Abstract
This chapter introduces fundamental models of grasp analysis. The overall model is a coupling of models that define contact behavior with widely used models of rigid-body kinematics and dynamics. The contact model essentially boils down to the selection of components of contact force and moment that are transmitted through each contact. Mathematical properties of the complete model naturally give rise to five primary grasp types whose physical interpretations provide insight for grasp and manipulation planning.
After introducing the basic model and types of grasps, this chapter focuses on the most important grasp characteristic: complete restraint. A grasp with complete restraint prevents loss of contact and thus is very secure. Two primary restraint properties are form closure and force closure. A form closure grasp guarantees maintenance of contact as long as the links of the hand and the object are well approximated as rigid and as long as the joint actuators are sufficiently strong. As will be seen, the primary difference between form closure and force closure grasps is the latterʼs reliance on contact friction. This translates into
requiring fewer contacts to achieve force closure than form closure.
Access provided by Autonomous University of Puebla. Download reference work entry PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
Background
Mechanical hands were developed to give robots the ability to grasp objects of varying geometric and physical properties. The first robotic hand designed for dexterous manipulation was the Salisbury hand [28.1]. It has three three-jointed fingers; enough to control all six degrees of freedom of an object and the grip pressure. The fundamental grasp modeling and analysis done by Salisbury provides a basis for grasp synthesis and dexterous manipulation research which continues today. Some of the most mature analysis techniques are embedded in the software GraspIt! [28.2]. GraspIt! contains models for several robot hands and provides tools for grasp selection, dynamic grasp simulation, and visualization.
The goal of this chapter is to give a thorough understanding of the all-important grasp properties of form and force closure. This will be done through detailed derivations of grasp models and discussions of illustrative examples. For an in-depth historical perspective and a treasure-trove bibliography of papers addressing a wide range of topics in grasping, the reader is referred to [28.3].
Models and Definitions
A mathematical model of grasping must be capable of predicting the behavior of the hand and object under the various loading conditions that may arise during grasping. Generally, the most desirable behavior is grasp maintenance in the face of unknown disturbing forces and moments applied to the object. Typically these disturbances arise from inertia forces which become appreciable during high-speed manipulation or applied forces such as those due to gravity. Grasp maintenance means that the contact forces applied by the hand are such that they prevent contact separation and unwanted contact sliding. The special class of grasps that can be maintained for every possible disturbing load is known as closure grasps. Figure 28.1 shows the Salisbury hand [28.1,4] executing a closure grasp of an object by wrapping its fingers around it and pressing the object against its palm. Formal definitions, analysis, and computational tests for closure will be presented in Sect. 28.5.
Figure 28.2 illustrates some of the main quantities that will be used to model grasping systems. Assume that the links of the hand and the object are rigid and that there is a unique, well-defined tangent plane at each contact point. Let {N} represent a conveniently chosen inertial frame fixed in the workspace. The frame {B} is fixed to the object with its origin defined relative to {N} by the vector p ∈ℝ3, where ℝ3 denotes three-dimensional Euclidean space. A convenient choice for p is the center of mass of the object. The position of contact point i in {N} is defined by the vector c
i
∈ℝ3. At contact point i, we define a frame {C}
i
, with axes  ({C}
i
is shown in exploded view). The unit vector
({C}
i
is shown in exploded view). The unit vector  contains c
i
is normal to the contact tangent plane, and is directed toward the object. The other two unit vectors are orthogonal and lie in the tangent plane of the contact.
contains c
i
is normal to the contact tangent plane, and is directed toward the object. The other two unit vectors are orthogonal and lie in the tangent plane of the contact.
Let the joints be numbered from 1 to n
q
. Denote by  the vector of joint displacements, where the superscript
the vector of joint displacements, where the superscript  indicates matrix transposition. Also, let
indicates matrix transposition. Also, let  represent joint loads (forces in prismatic joints and torques in revolute joints). These loads can result from actuator actions, other applied forces, and inertia forces. They could also arise from contacts between the object and hand. However, it will be convenient to separate joint loads into two components: those arising from contacts and those arising from all other sources. Throughout this chapter, noncontact loads will be denoted by τ.
represent joint loads (forces in prismatic joints and torques in revolute joints). These loads can result from actuator actions, other applied forces, and inertia forces. They could also arise from contacts between the object and hand. However, it will be convenient to separate joint loads into two components: those arising from contacts and those arising from all other sources. Throughout this chapter, noncontact loads will be denoted by τ.
Let  denote the vector describing the position and orientation of {B} relative to {N}. For planar systems n
u
= 3. For spatial systems, n
u
is three plus the number of parameters used to represent orientation, typically three (for Euler angles) or four (for unit quaternions). Denote by
denote the vector describing the position and orientation of {B} relative to {N}. For planar systems n
u
= 3. For spatial systems, n
u
is three plus the number of parameters used to represent orientation, typically three (for Euler angles) or four (for unit quaternions). Denote by  the twist of the object described in {N}. It is composed of the translational velocity v ∈ℝ3 of the point p and the angular velocity ω ∈ℝ3 of the object, both expressed in {N}. A twist of a rigid body can be referred to any convenient frame fixed to the body. The components of the referred twist represent the velocity of the origin of the new frame and the angular velocity of the body, both expressed in the new frame. For a rigorous treatment of twists and wrenches see [28.5,6]. Note that for planar systems, v ∈ℝ2 and ω ∈ℝ, and so n
ν
= 3.
the twist of the object described in {N}. It is composed of the translational velocity v ∈ℝ3 of the point p and the angular velocity ω ∈ℝ3 of the object, both expressed in {N}. A twist of a rigid body can be referred to any convenient frame fixed to the body. The components of the referred twist represent the velocity of the origin of the new frame and the angular velocity of the body, both expressed in the new frame. For a rigorous treatment of twists and wrenches see [28.5,6]. Note that for planar systems, v ∈ℝ2 and ω ∈ℝ, and so n
ν
= 3.
Another important point is  . Instead, these variables are related
by the matrix V as:
. Instead, these variables are related
by the matrix V as:

where the matrix  is not generally square but nonetheless satisfies
is not generally square but nonetheless satisfies  [28.7], I is the identity matrix, and the dot over the u implies differentiation with respect to time. Note that, for planar systems, V = I ∈ℝ3×3.
[28.7], I is the identity matrix, and the dot over the u implies differentiation with respect to time. Note that, for planar systems, V = I ∈ℝ3×3.
Let f ∈ℝ3 be the force applied to the object at the point p and let m ∈ℝ3 be the applied moment. These are combined into the object load, or wrench, vector denoted by  , where f and m are expressed in {N}. Like twists, wrenches can be referred to any convenient frame fixed to the body. One can think of this as translating the line of application of the force until it contains the origin of the new frame, then adjusting the moment component of the wrench to offset the moment induced by moving the line of the force. Last, the force and adjusted moment are expressed in the new frame. As done with the joint loads, the object wrench will be partitioned into two main parts: contact and noncontact wrenches. Throughout this chapter, g will denote the noncontact wrench on the object.
, where f and m are expressed in {N}. Like twists, wrenches can be referred to any convenient frame fixed to the body. One can think of this as translating the line of application of the force until it contains the origin of the new frame, then adjusting the moment component of the wrench to offset the moment induced by moving the line of the force. Last, the force and adjusted moment are expressed in the new frame. As done with the joint loads, the object wrench will be partitioned into two main parts: contact and noncontact wrenches. Throughout this chapter, g will denote the noncontact wrench on the object.
Velocity Kinematics
The material in this chapter is valid for a wide range of robot hands and other grasping mechanisms. The hand is assumed to be composed of a palm that serves as the common base for any number of fingers, each with any number of joints. The formulations given in this chapter are expressed explicitly in terms of only revolute and prismatic joints. However, most other common joints can be modeled by combinations of revolute and prismatic joints (e.g., cylindrical, spherical, and planar). Any number of contacts may occur between any link and the object.
Grasp Matrix and Hand Jacobian
Two matrices are of the utmost importance in grasp analysis: the grasp matrix G and the hand Jacobian J. These matrices define the relevant velocity kinematics and force transmission properties of the contacts. The following derivations of G and J will be done under the assumption that the system is three-dimensional. Changes for planar systems will be noted later.
Each contact should be considered as two coincident points: one on the hand and one on the object. The hand Jacobian maps the joint velocities to the twists of the hand expressed in the contact frames, while the transpose of the grasp matrix refers the object twist to the contact frames. Finger joint motions induce a rigid-body motion in each link of the hand. It is implicit in the terminology, twists of the hand, that the twist referred to contact i is the twist of the link involved in contact i. Thus these matrices can be derived from the transforms that change the reference frame of a twist.
To derive the grasp matrix, let ω obj N denote the angular velocity of the object expressed in {N} and let v i,obj N, also expressed in {N}, denote the velocity of the point on the object coincident with the origin of {C} i . These velocities can be obtained from the object twist referred to {N} as:

where

I
3×3 ∈ℝ3×3 is the identity matrix, and S(c
i
− p) is the cross-product matrix, that is, given a three-vector  , S(r) is defined as:
, S(r) is defined as:

The object twist referred to {C}
i
is simply the vector on the left-hand side of (28.2) expressed in {C}
i
. Let  represent the orientation of the i-th contact frame {C}
i
with respect to the inertial frame (the unit vectors
represent the orientation of the i-th contact frame {C}
i
with respect to the inertial frame (the unit vectors  ,
,  , and
, and  are expressed in {N}). Then the object twist referred to {C}
i
is given as:
are expressed in {N}). Then the object twist referred to {C}
i
is given as:

where  .
.
Substituting  from (28.2) into (28.4) yields the partial grasp matrix
from (28.2) into (28.4) yields the partial grasp matrix  , which maps the object twist from {N} to {C}
i
:
, which maps the object twist from {N} to {C}
i
:

where

The hand Jacobian can be derived similarly. Let ω i,hnd N be the angular velocity of the link of the hand touching the object at contact i, expressed in {N}, and define v i,hnd N as the translational velocity of contact i on the hand, expressed in {N}. These velocities are related to the joint velocities through the matrix Z i whose columns are the Plücker coordinates of the axes of the joints [28.5,6]. We have:

where  is defined as:
is defined as:

with the vectors d i,j , l i,j ∈ℝ3 defined as:

where ζ
j
is the origin of the coordinate frame associated with the j-th joint and  is the unit vector in the direction of the z-axis in the same frame, as shown in Fig. 28.11. Both vectors are expressed in {N}. These frames may be assigned by any convenient method, for example, the Denavit–Hartenberg method [28.8]. The
is the unit vector in the direction of the z-axis in the same frame, as shown in Fig. 28.11. Both vectors are expressed in {N}. These frames may be assigned by any convenient method, for example, the Denavit–Hartenberg method [28.8]. The  -axis is the rotational axis for revolute joints and the direction of translation for prismatic joints.
-axis is the rotational axis for revolute joints and the direction of translation for prismatic joints.
The final step in referring the hand twists to the contact frames is to change the frame of expression of v i,hnd N and ω i,hnd N to {C} i :

Combining (28.9) and (28.7) yields the partial hand Jacobian  , which relates the joint velocities to the contact twists on the hand:
, which relates the joint velocities to the contact twists on the hand:

where

To compact notation, stack all the twists of the hand and object into the vectors  and
and  as follows:
as follows:

Now the complete grasp matrix
 and the complete hand Jacobian
and the complete hand Jacobian
 relate the various velocity quantities as
relate the various velocity quantities as


where

The term complete is used to emphasize that all 6n c twist components at the contacts are included in the mapping. See Example 1, Part 1 and Example 3, Part 1 at the end of this chapter for clarification.
Contact Modeling
Three contact models useful for grasp analysis are reviewed here. For a complete discussion of contact modeling in robotics, readers are referred to Chap. 27.
The three models of greatest interest in grasp analysis are known as point contact without friction, hard finger, and soft finger [28.9]. These models select components of the contact twists to transmit between the hand and the object. This is done by equating a subset of the components of the hand and object twist at each contact. The corresponding components of the contact force and moment are also equated, but without regard for the constraints imposed by contact unilaterality and friction models (Sect. 28.5.2).
The point-contact-without-friction (PwoF) model is used when the contact patch is very small and the surfaces of the hand and object are slippery. With this model, only the normal component of the translational velocity of the contact point on the hand (i.e., the first component of ν i,hnd) is transmitted to the object. The two components of tangential velocity and the three components of angular velocity are not transmitted. Analogously, the normal component of the contact force is transmitted, but the frictional forces and moments are assumed to be negligible.
A hard-finger (HF) model is used when there is significant contact friction, but the contact patch is small, so that no appreciable friction moment exists. When this model is applied to a contact, all three translational velocity components of the contact point on the hand (i.e., the first three components of ν i,hnd) and all three components of the contact force are transmitted through the contact. None of the angular velocity components or moment components are transmitted.
The soft-finger (SF) model is used in situations in which the surface friction and the contact patch are large enough to generate significant friction forces and a friction moment about the contact normal. At a contact where this model is enforced, the three translational velocity components of the contact on the hand and the angular velocity component about the contact normal are transmitted (i.e., the first four components of ν i,hnd). Similarly, all three components of contact force and the normal component of the contact moment are transmitted.
Remark
The reader may see a contradiction between the rigid-body assumption and the soft-finger model. The rigid-body assumption is an approximation that simplifies all aspects of the analysis of grasping, but nonetheless it is sufficiently accurate in many real situations and grasp analysis would be impractical without. On the other hand, the need for a soft-finger model is a clear admission that the finger links and object are not rigid. However, it can be usefully applied in situations in which the amount of deformation required to obtain a large contact patch is small. Such situations occur when the local surface geometries are similar. If large finger or body deformations exist in the real system, the rigid-body approach presented in this chapter should be used with caution.
To develop the PwoF, HF, and SF models, define the relative twist at contact i as:

A particular contact model is defined through the matrix  , which selects ℓ
i
components of the relative contact twist and sets them to zero:
, which selects ℓ
i
components of the relative contact twist and sets them to zero:

These components are referred to as transmitted degrees of freedom (DOF). Define H i as:

where H iF and H iM are the translational and rotational component selection matrices, respectively. Table 28.2 gives the definitions of the selection matrices for the three contact models, where vacuous means that the corresponding block row matrix in (28.15) is void (i.e., it has zero rows and columns). Notice that, for the SF model, H iM selects rotation about the contact normal.
After choosing a transmission model for each contact, the contact constraint equations for all n c contacts can be written in compact form as:

where

and the number of twist components ℓ transmitted through the n
c contacts is given by  .
.
Finally, by substituting (28.12) and (28.13) into (28.16) one obtains:

where the grasp matrix and hand Jacobian are

For more details on the construction of H, the grasp matrix, and the hand Jacobian, readers are referred to [28.10,11,12] and the references therein.
See Example 1, Part 2 and Example 3, Part 2.
It is worth noting that (28.17) can be written in the following form:

where ν cc,hnd and ν cc,obj contain only the components of the twists that are transmitted by the contacts. Note that this equation implies that grasp maintenance is defined as the situation in which all these equations are maintained over time. Thus, when a contact is frictionless, contact maintenance implies continued contact, but sliding is allowed. However, when a contact is of the HF type, contact maintenance implies sticking contact, since sliding would violate the HF model. Similarly, for an SF contact, there may be no sliding or relative rotation about the contact normal.
For the remainder of this chapter, it will be assumed that ν cc,hnd = ν cc,obj, so the notation will be shortened to ν cc .
Planar Simplifications
Assume that the plane of motion is the (x, y)-plane of {N}. The vectors ν and g reduce in dimension from six to three by dropping components three, four, and five. The dimensions of the vectors c
i
and p reduce from three to two. The i-th rotation matrix becomes  (where the third components of
(where the third components of  and
and  are dropped) and (28.4) holds with
are dropped) and (28.4) holds with  . Equation (28.2) holds with:
. Equation (28.2) holds with:

where S 2 is the analog of the cross-product matrix for two-dimensional vectors, given as

Equation (28.7) holds with d i,j ∈ℝ2 and l i,j ∈ℝ defined as

The complete grasp matrix and hand Jacobian have reduced sizes:  and
and  .
.
As far as contact constraint is concerned, (28.15) holds with H iF and H iM in Table 28.3.
In planar cases, the SF and HF models are equivalent, because the object and the hand lie in a plane. Rotations about the contact normals would cause out-of-plane motions. Finally, the dimensions of the grasp matrix and hand Jacobian are reduced to the following sizes:  and
and  . See Example 1, Part 3 and Example 2, Part 1.
. See Example 1, Part 3 and Example 2, Part 1.
Dynamics and Equilibrium
The dynamic equations of the system can be written as:

where M
hnd(⋅) and M
obj(⋅) are symmetric positive-definite inertia matrices and b
hnd(⋅,⋅) and b
obj(⋅,⋅) are the velocity-product terms, g
app is the force and moment applied to the object by gravity and other external sources, τ
app is the vector of external loads and actuator actions, and the vector Gλ is the total wrench applied to the object by the hand. The vector λ contains the contact force and moment components transmitted through the contacts and expressed in the contact frames. Specifically,  , where
, where  . The subscripts indicate one normal (n) and two tangential (t, o) components of contact force f and moment m. For an SF, HF, or PwoF contact, λ
i
is defined as in Table 28.4. Finally, it is worth noting that
. The subscripts indicate one normal (n) and two tangential (t, o) components of contact force f and moment m. For an SF, HF, or PwoF contact, λ
i
is defined as in Table 28.4. Finally, it is worth noting that  is the wrench applied through contact i, where
is the wrench applied through contact i, where  and H
i
are defined in (28.6) and (28.15). The vector λ
i
is known as the wrench intensity vector for contact i.
and H
i
are defined in (28.6) and (28.15). The vector λ
i
is known as the wrench intensity vector for contact i.
Equation (28.20) represents the dynamics of the hand and object without regard for the kinematic constraints imposed by the contact models. Enforcing them, the dynamic model of the system can be written as:

subject to  , where
, where

One should notice that the dynamic equations are closely related to the kinematic model in (28.17). Specifically, just as J and  transmit only selected components of contact twists,
transmit only selected components of contact twists,  and G in (28.20) serve to transmit only the corresponding components of the contact wrenches.
and G in (28.20) serve to transmit only the corresponding components of the contact wrenches.
When the inertia terms are negligible, as occurs during slow motion, the system is said to be quasistatic. In this case, (28.22) becomes:

and does not depend on joint and object velocities. Consequently, when the grasp is in static equilibrium or moves quasistatically, one can solve the first equation and the constraint in (28.21) independently to compute λ,  , and ν. It is worth noting that such a force/velocity decoupled solution is not possible when dynamic effects are appreciable, since the first equation in (28.21) depends on the third one through (28.22).
, and ν. It is worth noting that such a force/velocity decoupled solution is not possible when dynamic effects are appreciable, since the first equation in (28.21) depends on the third one through (28.22).
Remark
Equation (28.21) highlights an important alternative view of the grasp matrix and the hand Jacobian. G can be thought of as a mapping from the transmitted contact forces and moments to the set wrenches that the hand can apply to the object, while  can be thought of as a mapping from the transmitted contact forces and moments to the vector of joint loads. Notice that these interpretations hold for both dynamic and quasistatic conditions.
can be thought of as a mapping from the transmitted contact forces and moments to the vector of joint loads. Notice that these interpretations hold for both dynamic and quasistatic conditions.
Controllable Twists and Wrenches
In hand design and in grasp and manipulation planning, it is important to know the set of twists that can be imparted to the object by movements of the fingers, and conversely, the conditions under which the hand can prevent all possible motions of the object. The dual view is that one needs to know the set of wrenches that the hand can apply to the object and under what conditions any wrench in ℝ6 can be applied through the contacts. This knowledge will be gained by studying the various subspaces associated with G and J [28.13].
The spaces, shown in Fig. 28.3, are the column spaces and null spaces of G,  , J, and
, J, and  . Column space (also known as range) and null space will be denoted by ℛ(⋅) and 𝒩(⋅), respectively. The arrows show the propagation of the various velocity and load quantities through the grasping system. For example, in the left part of Fig. 28.3 it is shown how any vector
. Column space (also known as range) and null space will be denoted by ℛ(⋅) and 𝒩(⋅), respectively. The arrows show the propagation of the various velocity and load quantities through the grasping system. For example, in the left part of Fig. 28.3 it is shown how any vector  can be decomposed into a sum of two orthogonal vectors in
can be decomposed into a sum of two orthogonal vectors in  and in 𝒩(J) and how
and in 𝒩(J) and how  is mapped to ℛ(J) by multiplication by J.
is mapped to ℛ(J) by multiplication by J.
It is important to recall two facts from linear algebra. First, a matrix A maps vectors from  to ℛ(A) in a one-to-one and onto fashion, that is, the map A is a bijection. The generalized inverse A
+ of A is a bijection that maps vectors in the opposite direction [28.14]. Also, A maps vectors in 𝒩(A) to zero. Finally, there is no nontrivial vector that A can map into
to ℛ(A) in a one-to-one and onto fashion, that is, the map A is a bijection. The generalized inverse A
+ of A is a bijection that maps vectors in the opposite direction [28.14]. Also, A maps vectors in 𝒩(A) to zero. Finally, there is no nontrivial vector that A can map into  . This implies that, if
. This implies that, if  is nontrivial, then the hand will not be able to control all degrees of freedom of the objectʼs motion. This is certainly true for quasistatic grasping, but when dynamics are important, they may cause the object to move along the directions in
is nontrivial, then the hand will not be able to control all degrees of freedom of the objectʼs motion. This is certainly true for quasistatic grasping, but when dynamics are important, they may cause the object to move along the directions in  .
.
Grasp Classifications
The four null spaces motivate a basic classification of grasping systems defined in Table 28.5. Assuming solutions to (28.21) exist, the following force and velocity equations provide insight into the physical meaning of the various null spaces:




In these equations, A + denotes the generalized inverse, henceforth pseudoinverse, of a matrix A, N(A) denotes a matrix whose columns form a basis for 𝒩(A), and α, β, γ, and η are arbitrary vectors that parameterize the solution sets. If not otherwise specified, the context will make clear whether the generalized inverse is left or right.
If the null spaces represented in the equations are nontrivial, then one immediately sees the first many-to-one mapping in the Table 28.5. To see the other many-to-one mappings, and in particular the defective class, consider (28.24). It can be rewritten with ν
cc
decomposed into components ν
rs and ν
lns in ℛ(J) and  , respectively, as follows:
, respectively, as follows:

Recall that every vector in  is orthogonal to every row of A
+. Therefore J
+
ν
lns = 0. If α and ν
rs are fixed in (28.28), then
is orthogonal to every row of A
+. Therefore J
+
ν
lns = 0. If α and ν
rs are fixed in (28.28), then  is unique. Thus it is clear that, if
is unique. Thus it is clear that, if  is nontrivial, then a subspace of twists of the hand at the contacts will map to a single joint velocity vector. Applying the same approach to the other three equations (28.25–28.27) yields the other many-to-one mappings listed in Table 28.5.
is nontrivial, then a subspace of twists of the hand at the contacts will map to a single joint velocity vector. Applying the same approach to the other three equations (28.25–28.27) yields the other many-to-one mappings listed in Table 28.5.
Equations (28.21) and (28.24–28.27), motivate the following definitions.
―
Definition 28.1 Redundant
A grasping system is said to be redundant if 𝒩(J) is nontrivial.
―
Joint velocities  in 𝒩(J) are referred to as internal hand velocities, since they correspond to finger motions, but do not generate motion of the hand in the constrained directions at the contact points. If the quasistatic model applies, it can be shown that these motions are not influenced by the motion of the object and vice versa.
in 𝒩(J) are referred to as internal hand velocities, since they correspond to finger motions, but do not generate motion of the hand in the constrained directions at the contact points. If the quasistatic model applies, it can be shown that these motions are not influenced by the motion of the object and vice versa.
―
Definition 28.2 Indeterminate
A grasping system is said to be indeterminate if  is
nontrivial.
is
nontrivial.
―
Object twists ν in  are called internal object twists, since they correspond to motions of the object, but do not cause motion of the object in the constrained directions at the contacts. If the static model applies, it can be shown that these twists cannot be controlled by finger motions.
are called internal object twists, since they correspond to motions of the object, but do not cause motion of the object in the constrained directions at the contacts. If the static model applies, it can be shown that these twists cannot be controlled by finger motions.
―
Definition 28.3 Graspable
A grasping system is said to be graspable if 𝒩(G) is nontrivial.
―
Wrench intensities λ in 𝒩(G) are referred to as internal object forces. These wrenches are internal because they do not contribute to the acceleration of the object, i.e., Gλ = 0. Instead, these wrench intensities affect the tightness of the grasp. Thus, internal wrench intensities play a fundamental role in maintaining grasps that rely on friction (Sect. 28.5.2).
―
Definition 28.4 Defective
A grasping system is said to be defective if  is nontrivial.
is nontrivial.
―
Wrench intensities λ in  are called internal hand forces. These forces do not influence the hand joint dynamics given in (28.20). If the static model is considered, it can be easily shown that wrench intensities belonging to
are called internal hand forces. These forces do not influence the hand joint dynamics given in (28.20). If the static model is considered, it can be easily shown that wrench intensities belonging to  cannot be generated by joint actions, but can be resisted by the structure of the hand.
cannot be generated by joint actions, but can be resisted by the structure of the hand.
See Example 1, Part 4; Example 2, Part 2; and Example 3, Part 3.
Limitations of Rigid-Body Assumption
The rigid-body dynamics equation (28.20) can be rewritten with Lagrange multipliers associated with the contact constraints as:

where  and
and

In order for this equation to determine the motion of the system completely, it is necessary that the matrix M
dyn be invertible. This case is considered in detail in [28.15], where the dynamics of multifinger manipulation is studied under the hypothesis that the hand Jacobian is full row rank,  . For all manipulation systems with noninvertible M
dyn, rigid-body dynamics fails to determine the motion and the wrench intensity vector. By observing that:
. For all manipulation systems with noninvertible M
dyn, rigid-body dynamics fails to determine the motion and the wrench intensity vector. By observing that:

the same arguments apply under the quasistatic conditions defined by (28.21) and (28.23). When  , the rigid-body approach fails to solve the first equation in (28.21), thus leaving λ indeterminate.
, the rigid-body approach fails to solve the first equation in (28.21), thus leaving λ indeterminate.
―
Definition 28.5 Hyperstatic
A grasping system is said to be hyperstatic if  is nontrivial.
is nontrivial.
―
In such systems there are internal forces (Definition 28.3) belonging to  that are not controllable as discussed for defective grasps. Rigid-body dynamics is not satisfactory for hyperstatic grasps since the rigid-body assumption leads to undetermined contact wrenches [28.16].
that are not controllable as discussed for defective grasps. Rigid-body dynamics is not satisfactory for hyperstatic grasps since the rigid-body assumption leads to undetermined contact wrenches [28.16].
See Example 3, Part 3.
Desirable Properties
For a general-purpose grasping system, there are three main desirable properties: control of the object twist ν, control of object wrench g, and control of the internal forces. Control of these quantities implies that the hand can deliver the desired ν and g with specified grip pressure by the appropriate choice of joint velocities and actions. The conditions on J and G equivalent to these properties are given in Table 28.6.
We derive the associated conditions in two steps. First, we ignore the structure and configuration of the hand (captured in J) by assuming that the contact point on the finger can be commanded to move in any direction transmitted by the chosen contact model. An important perspective here is that ν cc is seen as the independent input variable and ν is seen as the output. The dual interpretation is that the actuators can generate any contact force and moment in the constrained directions. Similarly, λ is seen as the input and g is seen as the output. The preliminary property of interest under this assumption is whether or not the arrangement and types of contacts on the object (captured in G) are such that a sufficiently dexterous hand could control its fingers so as to impart any twist ν ∈ℝ6 to the object and, similarly, to apply any wrench g ∈ℝ6 to the object.
All Object Twists Possible
Given a set of contact locations and types, by solving (28.19) for ν or observing the map G on the right side of Fig. 28.3, one sees that the achievable object twists are those in ℛ(G). Those in  could not be achieved by any hand using the given grasp. Therefore, to achieve any object twist, we must have:
could not be achieved by any hand using the given grasp. Therefore, to achieve any object twist, we must have:  , or equivalently, rank(G) = n
ν
. Any grasp with three non-collinear hard contacts or two distinct soft contacts satisfies this condition.
, or equivalently, rank(G) = n
ν
. Any grasp with three non-collinear hard contacts or two distinct soft contacts satisfies this condition.
All Object Wrenches Possible
This case is the dual of the previous case, so we expect the same condition. From (28.21), one immediately obtains the condition  , so again we have rank(G) = n
ν
.
, so again we have rank(G) = n
ν
.
To obtain the conditions needed to control the various quantities of interest, the structure of the hand cannot be ignored. Recall that the only achievable contact twists on the hand are in ℛ(J), which is not necessarily equal to ℝℓ.
Control All Object Twists
By solving (28.17) for ν, one sees that, in order to cause any object twist ν by choice of joint velocities  , we must have ℛ(GJ) =ℛ (G) and
, we must have ℛ(GJ) =ℛ (G) and  . These conditions are equivalent to rank(GJ) = rank(G) = n
ν
.
. These conditions are equivalent to rank(GJ) = rank(G) = n
ν
.
Control All Object Wrenches
This property is dual to the previous one. Analysis of (28.21) yields the same conditions: rank(GJ) = rank(G) = n ν .
Control All Internal Forces
Equation (28.20) shows that wrench intensities with no effect on object motion are only those in 𝒩(G). In general, not all the internal forces may be actively controlled by joint actions. In [28.12,17] it has been shown that all internal forces in 𝒩(G) are controllable if and only if  .
.
See Example 1, Part 5 and Example 2, Part 3.
Design Considerations of the Salisbury Hand
The
Salisbury hand in Fig. 28.4 was designed to have the smallest number of joints that would meet all the task requirements in Table 28.6. Assuming HF contacts, three non-collinear contacts is the minimum number such that rank(G) = n
ν
= 6. In this case, G has six rows and nine columns and the dimension of 𝒩(G) is three [28.1,4]. The ability to control all internal forces and apply an arbitrary wrench to the object requires that  , so the minimum dimension of the column space of J is nine. To achieve this, the hand must have at least nine joints, which Salisbury implemented as three fingers, each with three revolute joints.
, so the minimum dimension of the column space of J is nine. To achieve this, the hand must have at least nine joints, which Salisbury implemented as three fingers, each with three revolute joints.
The intended way to execute a dexterous manipulation task with the Salisbury hand is to grasp the object at three non-collinear points with the fingertips, forming a grasp triangle. To secure the grasp, the internal forces are controlled so that the contact points are maintained without sliding. Dexterous manipulation can be thought of as moving the fingertips to control the positions of the vertices of the grasp triangle.
Restraint Analysis
The most fundamental requirements in grasping and dexterous manipulation are the abilities to hold an object in equilibrium and control the position and orientation of the grasped object relative to the palm of the hand. The two most useful characterizations of grasp restraint are force closure and form closure. These names were in use over 125 years ago in the field of machine design to distinguish between joints that required an external force to maintain contact, and those that did not [28.18]. For example, some water wheels had a cylindrical axle that was laid in a horizontal semicylindrical groove split on either side of the wheel. During operation, the weight of the wheel acted to close the groove–axle contacts, hence the term force closure. By contrast, if the grooves were replaced by cylindrical holes just long enough to accept the axle, then the contacts would be closed by the geometry (even if the direction of the gravitational force were reversed), hence the term form closure.
When applied to grasping, form and force closure have the following interpretations. Assume that a hand grasping an object has its joint angles locked and its palm fixed in space; then the grasp has form closure, or the object is form closed, if it is impossible to move the object, even infinitesimally. Under the same conditions, the grasp has force closure, or the object is force closed, if for any noncontact wrench experienced by the object, contact wrench intensities exist that satisfy (28.20) and are consistent with the constraints imposed by the friction models applicable at the contact points. Notice that all form closure grasps are also force closure grasps. When under form closure, the object cannot move at all, regardless of the noncontact wrench. Therefore, the hand maintains the object in equilibrium for any external wrench, which is the force closure requirement.
Roughly speaking, form closure occurs when the palm and fingers wrap around the object forming a cage with no wiggle room such as the grasp shown in Fig. 28.5. This kind of grasp is also called a power grasp [28.19] or an enveloping grasp [28.20]. However, force closure is possible with fewer contacts, as shown in Fig. 28.6, but in this case force closure requires the ability to control internal forces. It is also possible for a grasp to have partial form closure, indicating that only a subset of the possible degrees of freedom are restrained by form closure [28.21]. An example of such a grasp is shown in Fig. 28.7. In this grasp, fingertip placement between the ridges around the periphery of the gasoline cap provide form closure against relative rotation about the axis of the helix of the threads and also against translation perpendicular to that axis, but the other three degrees of freedom are restrained through force closure. Strictly speaking, given a grasp of a real object by a human hand, it is impossible to prevent relative motion of the object with respect to the palm due to the compliance of the hand and object. Preventing all motion is possible only if the contacting bodies are rigid, as is assumed in most mathematical models employed in grasp analysis.
In the grasp depicted, contact with the ridges on the gasoline cap creates partial form closure in the direction of cap rotation (when screwing it in) and also in the directions of translation perpendicular to the axis of rotation. To achieve complete control over the cap, the grasp achieves force closure over the other three degrees of freedom
Form Closure
To
make the notion of form closure precise, introduce a gap function denoted by ψ
i
(u, q) at each of the n
c contact points between the object and the hand. The gap function is zero at each contact, becomes positive if contact breaks, and negative if penetration occurs. The gap function can be thought of as the distance between the contact points. In general, this function is dependent on the shapes of the contacting bodies. Let  and
and  represent the configurations of the object and hand for a given grasp; then:
represent the configurations of the object and hand for a given grasp; then:

The form closure condition can now be stated in terms of a differential change du of  :
:
―
Definition 28.6
A grasp  has form closure if and only if the following implication holds:
has form closure if and only if the following implication holds:

where ψ is the n c-dimensional vector of gap functions with i-th component equal to ψ i (u, q). By definition, inequalities between vectors imply that the inequality is applied between corresponding components of the vectors.
―
Expanding the gap function vector in a Taylor series about  yields infinitesimal form closure tests of various orders. Let β
ψ(u, q), β = 1, 2, 3,… denote the Taylor series approximation truncated after the terms of order β in du. From (28.30), it follows that the first-order approximation is:
yields infinitesimal form closure tests of various orders. Let β
ψ(u, q), β = 1, 2, 3,… denote the Taylor series approximation truncated after the terms of order β in du. From (28.30), it follows that the first-order approximation is:

where  denotes the partial derivative of ψ with respect to u evaluated at
denotes the partial derivative of ψ with respect to u evaluated at  . Replacing ψ with its approximation of order β in (28.31) implies three relevant cases of order β:
. Replacing ψ with its approximation of order β in (28.31) implies three relevant cases of order β:
-
1.
if there exists du such that
 has at least one strictly positive component, then the grasp does not have form closure of order β;
has at least one strictly positive component, then the grasp does not have form closure of order β;
-
2.
if for every nonzero du,
 has at least one strictly negative component, then the grasp has form closure of order β;
has at least one strictly negative component, then the grasp has form closure of order β;
-
3.
if neither case 1 nor case 2 applies for all
 , then higher-order analysis is required to determine the existence of form closure.
, then higher-order analysis is required to determine the existence of form closure.
Figure 28.8 illustrates form closure concepts using several planar grasps of gray objects by fingers shown as dark disks. The concepts are identical for grasps of three-dimensional objects, but are more clearly illustrated in a plane. The grasp on the left has first-order form closure. Note that first-order form closure only involves the first derivatives of the distance functions. This implies that the only relevant geometry in first-order form closure are the locations of the contacts and the directions of the contact normals. The grasp in the center has form closure of higher order, with the specific order depending on the degrees of the curves defining the surfaces of the object and fingers in the neighborhoods of the contacts [28.22]. Second-order form closure analysis depends on the curvatures of the two contacting bodies in addition to the geometric information used to analyze first-order form closure. The grasp on the right does not have form closure of any order, because the object can translate horizontally and rotate about its center.
First-Order Form Closure
First-order form closure exists if and only if the following implication holds:

The first-order form closure condition can be written in terms of the object twist ν:

where  . Because the gap functions only quantify distances, the product
. Because the gap functions only quantify distances, the product  is the vector of normal components of the instantaneous velocities of the object at the contact points (which must be nonnegative to prevent interpenetration). This in turn implies that the grasp matrix is the one that would result from the assumption that all contacts are of the type PwoF.
is the vector of normal components of the instantaneous velocities of the object at the contact points (which must be nonnegative to prevent interpenetration). This in turn implies that the grasp matrix is the one that would result from the assumption that all contacts are of the type PwoF.
An equivalent condition in terms of the contact wrench intensity vector  can be stated as follows. A grasp has first-order form closure if and only if:
can be stated as follows. A grasp has first-order form closure if and only if:

The physical interpretation of this condition is that equilibrium can be maintained under the assumption that the contacts are frictionless. Note that the components of λ n are the magnitudes of the normal components of the contact forces. The subscript (.)n is used to emphasize that λ n contains no other force or moment components.
Since g must be in the range of G n for equilibrium to be satisfied, and since g is an arbitrary element of ℝ6, then in order for condition (28.33) to be satisfied, the rank of G n must be six. Assuming rank(G n) = 6, another equivalent mathematical statement of first-order form closure is: there exists λ n such that the following two conditions hold [28.23]:

This means that there exists a set of strictly compressive normal contact forces in the null space of G n. In other words, one can squeeze the object as tightly as desired while maintaining equilibrium. A second interpretation of this condition is that the nonnegative span of the columns of G n must equal ℝ6. As will be seen, this interpretation will provide a conceptual link called frictional form closure that lies between form closure and force closure.
The duality of conditions (28.32) and (28.33) can be seen clearly by examining the set of wrenches that can be applied by frictionless contacts and the corresponding set of possible object twists. For this discussion, it is useful to give definitions of cones and their duals.
―
Definition 28.7
A cone 𝒞 is a set of vectors ς such that, for every ς in 𝒞, every nonnegative scalar multiple of ς is also in 𝒞.
―
Equivalently, a cone is a set of vectors closed under addition and nonnegative scalar multiplication.
―
Definition 28.8
Given a cone 𝒞 with elements ς, the dual cone 𝒞* with elements ς * is the set of vectors such that the dot product of ς * with each vector in 𝒞 is nonnegative. Mathematically:

―
See Example 4.
First-Order Form Closure Requirements
Several useful necessary conditions for form closure are known. In 1897 Somov proved that at least seven contacts are necessary to form close a rigid object with six degrees of freedom [28.24]. Lakshminarayana generalized this to prove that n ν + 1 contacts are necessary to form close an object with n ν degrees of freedom [28.21] (based on Goldman and Tucker 1956 [28.25]), see Table 28.7. This led to the definition of partial form closure that was mentioned above in the discussion of the hand grasping the gasoline cap. Markenscoff and Papadimitriou determined a tight upper bound, showing that, for all objects whose surfaces are not surfaces of revolution, at most n ν + 1 contacts are necessary [28.26]. Form closure is impossible to achieve for surfaces of revolution.
To emphasize the fact that n ν + 1 contacts are necessary and not sufficient, consider grasping a cube with seven or more points of contact. If all contacts are on one face, then clearly the cube is not form closed.
First-Order Form Closure Tests
Because form closure grasps are very secure, it is desirable to design or synthesize such grasps. To do this, one needs a way to test candidate grasps for form closure, and rank them so that the best grasp can be chosen. One reasonable measure of form closure can be derived from the geometric interpretation of the condition (28.34). The null space constraint and the positivity of λ n represent the addition of the columns of G n scaled by the components of λ n. Any choice of λ n closing this loop is in 𝒩(G n). For a given loop, if the magnitude of the smallest component of λ n is positive, then the grasp has form closure, otherwise it does not. Let us denote this smallest component by d. Since such a loop, and hence d, can be scaled arbitrarily, λ n should be bounded for computational expedency.
After verifying that G n has full row rank, a quantitative form closure test based on the above observations can be formulated as a linear program (LP) in the unknowns d and λ n as follows:





where  is the identity matrix and 1 ∈ℝn
c is a vector with all components equal to 1. The last inequality is designed to prevent this LP from becoming unbounded. A typical LP solution algorithm determines infeasibility or unboundedness of the constraints in the, so-called, phase I of the algorithm, and considers the result before attempting to calculate an optimal value [28.27]. If LP1 is infeasible, or if the optimal value d
* is zero, then the grasp is not form closed.
is the identity matrix and 1 ∈ℝn
c is a vector with all components equal to 1. The last inequality is designed to prevent this LP from becoming unbounded. A typical LP solution algorithm determines infeasibility or unboundedness of the constraints in the, so-called, phase I of the algorithm, and considers the result before attempting to calculate an optimal value [28.27]. If LP1 is infeasible, or if the optimal value d
* is zero, then the grasp is not form closed.
The quantitative form closure test (28.36–28.40) has n c + 8 constraints and n c + 1 unknowns. For a typical grasp with n c < 10, this is a small linear program that can be solved very quickly using the simplex method. However, one should note that the metric d * is dependent on the choice of units used when forming G n. It would be advisable to nondimensionalize the components of the wrenches to avoid dependence of the optimal d on ones choice of units. This could be done by dividing the first three rows of G by a characteristic force and the last three rows by a characteristic moment.
However, if one desires a binary test, LP1 can be converted into one by dropping the last constraint (28.40) and applying only phase I of the simplex algorithm.
In summary, form closure testing is a two-step process:
Form Closure Test
-
1.
Compute rank(G n).
-
1.
If rank(G n) ≠ n ν , then form closure does not exist. Stop.
-
2.
If rank(G n) = n ν , continue.
-
1.
-
2.
Solve LP1.
-
1.
If d * = 0, then form closure does not exist.
-
2.
If d * > 0, then form closure exists and d * is a crude measure of how far the grasp is from losing form closure.
-
1.
Variations of the Test
If the rank test fails, then the grasp could have partial form closure over as many as rank(G n) degrees of freedom. If one desires to test this, then LP1 must be solved using a new G n formed by retaining only the rows corresponding to the degrees of freedom for which partial form closure is to be tested. If d * > 0, then partial form closure exists. A second variation is to constrain d to be greater than some large negative value. If this is done, then d * < 0 is a crude measure of how far a grasp is from achieving form closure.
See Example 5.
Planar Simplifications
In the planar case, Nguyen [28.28] developed a graphical qualitative test for form closure. Figure 28.9 shows two form closure grasps with four contacts. To test form closure one partitions the normals into two groups of two. Let 𝒞1 be the nonnegative span of two normals in one pair and 𝒞2 be the nonnegative span of the other pair. A grasp has form closure if and only if 𝒞1 and 𝒞2 or −𝒞1 and −𝒞2 see each other for any pairings. Two cones see each other if the open line segment defined by the vertices of the cones lies in the interior of both cones. In the presence of more than four contacts, if any set of four contacts satisfies this condition, then the grasp has form closure. Notice that this graphical test can be difficult to execute for grasps with more than four contacts. Also, it does not extend to grasps of three-dimensional (3-D) objects and does not provide a closure measure.
Force Closure
A grasp has force closure, or is force closed, if the grasp can be maintained in the face of any object wrench. Force closure is similar to form closure, but relaxed to allow friction forces to help balance the object wrench. A benefit of including friction in the analysis is the reduction in the number of contact points needed for closure. A three-dimensional object with six degrees of freedom requires seven contacts for form closure, but for force closure, only two contacts are needed if they are modeled as soft fingers, and only three (non-collinear) contacts are needed if they are modeled as hard fingers.
Force closure relies on the ability of the hand to squeeze arbitrarily tightly in order to compensate for large applied wrenches that can only be resisted by friction. Figure 28.14 shows a grasped polygon (see Example 2). Consider applying a wrench to the object that is a pure force acting upward along the y-axis of the inertial frame. It seems intuitive that, if there is enough friction, the hand will be able to squeeze the object with friction forces preventing the objectʼs upward escape. Also, as the applied force increases in magnitude, the magnitude of the squeezing force will have to increase accordingly.
Since force closure is dependent on the friction models, common models will be introduced before giving formal definitions of force closure.
Friction Models
Recall the components of force and moment transmitted through contact i under the various contact models given earlier (Table 28.4). At contact point i, the friction law imposes constraints on the components of the contact force and moment. Specifically, the frictional components of λ i are constrained to lie inside a limit surface, denoted by ℒ i , that scales linearly with the product μ i f in, where μ i is the coefficient of friction at contact i. In the case of Coulomb friction, the limit surface is a circle of radius μ i f in. The Coulomb friction cone ℱ i is a subset of ℝ3:

More generally, the friction laws of interest have limit surfaces defined in the space of friction components,  , and friction cones ℱ
i
defined in the space of λ
i
,
, and friction cones ℱ
i
defined in the space of λ
i
,  . They can be written as
. They can be written as

where ||λ i || w denotes a weighted quadratic norm of the friction components at contact i. The limit surface is defined by ||λ i || w = f in.
Table 28.8 defines useful weighted quadratic norms for the three contact models: PwoF, HF, and SF. The parameter μ i is the friction coefficient for the tangential forces, υ i is the torsional friction coefficient, and a is the characteristic length of the object that is used to ensure consistent units in the terms of the norm of the SF model.
Remark
There are several noteworthy points to be made about the friction cones. First, all of them implicitly or explicitly constrain the normal component of the contact force to be nonnegative. The cone for SF contacts has a cylindrical limit surface with circular cross section in the (f it, f io)-plane and rectangular cross section in the (f it, m in)-plane. With this model, the amount of torsional friction that can be transmitted is independent of the lateral friction load. An improved model that couples the torsional friction limit with the tangential limit was studied by Howe and Cutkosky [28.29].
A Force Closure Definition
One common definition of force closure can be stated simply by modifying condition (28.33) to allow each contact force to lie in its friction cone rather than along the contact normal. Because this definition does not consider the handʼs ability to control contact forces, this definition will be referred to as frictional form closure. A grasp will be said to have frictional form closure if and only if the following conditions are satisfied:

where ℱ is the composite friction cone defined as:  , and each ℱ
i
is defined by (28.42) and one of the models listed in Table 28.8.
, and each ℱ
i
is defined by (28.42) and one of the models listed in Table 28.8.
Letting Int(ℱ) denote the interior of the composite friction cone, Murray et al. give the following equivalent definition [28.15]:
―
Definition 28.9
(Proposition 5.2, Murray et al.) A grasp has frictional form closure if and only if the following conditions are satisfied:
-
1.
rank(G) = n ν
-
2.
∃ λ such that Gλ = 0 and λ ∈ Int(ℱ).
―
These conditions define what Murray et al. call force closure. The force closure definition adopted here is stricter than frictional form closure; it additionally requires that the hand be able to control the internal object forces.
―
Definition 28.10
A grasp has force closure if and only if rank(G) = n
ν
,
 , and there exists λ such that Gλ = 0 and λ ∈ Int(ℱ).
, and there exists λ such that Gλ = 0 and λ ∈ Int(ℱ).
―
The full row rank condition on the matrix G is the same condition required for form closure, although G is different from G n used to determine form closure. If the rank test passes, then one must still find λ satisfying the remaining three conditions. Of these, the null space intersection test can be performed easily by linear programming techniques, but the friction cone constraint is quadratic, and thus forces one to use nonlinear programming techniques. While exact nonlinear tests have been developed [28.30], only approximate tests will be presented here.
Approximate Force Closure Tests
Any of the friction cones discussed can be approximated as the nonnegative span of a finite number n g of generators s ij of the friction cone. Given this, one can represent the set of applicable contact wrenches at contact i as follows:

where  and σ
i
is a vector of nonnegative generator weights. If contact i is frictionless, then n
g = 1 and
and σ
i
is a vector of nonnegative generator weights. If contact i is frictionless, then n
g = 1 and  .
.
If contact i is of type HF, we represent the friction cone by the nonnegative sum of uniformly spaced contact force generators (Fig. 28.10) whose nonnegative span approximates the Coulomb cone with an inscribed regular polyhedral cone. This leads to the following definition of S i :

where the index k varies from 1 to n g. If one prefers to approximate the quadratic friction cone by a circumscribing polyhedral cone, one simply replaces μ i in the above definition with μ i / cos (πn g).
The adjustment needed for the SF model is quite simple. Since the torsional friction in this model is decoupled from the tangential friction, its generators are given by  . Thus S
i
for the SF model is:
. Thus S
i
for the SF model is:

where b is the characteristic length used to unify units. The set of total contact wrenches that may be applied by the hand without violating the contact friction law at any contact can be written as:

where  and
and  .
.
It is convenient to reformulate the friction constraints in a dual form:

In this form, each row of F i is normal to a face formed by two adjacent generators of the approximate cone. For an HF contact, row i of F i can be computed as the cross product of s i and s i+1. In the case of an SF contact, the generators are of dimension four, so simple cross products will not suffice. However, general methods exist to perform the conversion from the generator form to the face normal form [28.25].
The face normal constraints for all contacts can be combined into the following compact form:

where  .
.
Let  be the first row of H
i
. Further let
be the first row of H
i
. Further let  and let
and let  . The following linear program is a quantitative test for frictional form closure. The optimal objective function value d
* is a measure of the distance the contact forces are from the boundaries of their friction cones, and hence a crude measure of how far a grasp is from losing frictional form closure.
. The following linear program is a quantitative test for frictional form closure. The optimal objective function value d
* is a measure of the distance the contact forces are from the boundaries of their friction cones, and hence a crude measure of how far a grasp is from losing frictional form closure.

The last inequality in LP2 is simply the sum of the magnitudes of the normal components of the contact forces. After solving LP2, if d * = 0 frictional form closure does not exist, but if d * > 0, then it does.
If the grasp has frictional form closure, the last step to determine the existence of force closure is to verify the condition  . If it holds, then the grasp has force closure. This condition is easy to verify with another linear program LP3.
. If it holds, then the grasp has force closure. This condition is easy to verify with another linear program LP3.

In summary, force closure testing is a three-step process:
Approximate Force Closure Test
-
1.
Compute rank(G).
-
1.
If rank(G) ≠ n ν , then force closure does not exist. Stop.
-
2.
If rank(G) = n ν , continue.
-
1.
-
2.
Solve LP2: Test frictional form closure.
-
1.
If d * = 0, then frictional form closure does not exist. Stop.
-
2.
If d * > 0, then frictional form closure exists and d * is a crude measure of how far the grasp is from losing frictional form closure.
-
1.
-
3.
Solve LP3. Test control of internal force.
-
1.
If d * > 0, then force closure does not exist.
-
2.
If d * = 0, then force closure exists.
-
1.
See Example 1, Part 6.
Planar Simplifications
In planar grasping systems, the approximate method described above is exact. This is because the SF models are meaningless, since rotations about the contact normal would cause motions out of the plane. With regard to the HF model, for planar problems, the quadratic friction cone becomes linear, with its cone represented exactly as:

Nguyenʼs graphical form closure test can be applied to planar grasps with two frictional contacts [28.28]. The only change is that the four contact normals are replaced by the four generators of the two friction cones. However, the test can only determine frictional form closure, since it does not incorporate the additional information needed to determine force closure.
Examples
Example 1: Grasped Sphere
Part 1:  and
and 
Figure 28.11
shows a planar projection of a three-dimensional sphere of radius r grasped by two fingers, which make two contacts at angles θ
1 and θ
2. The frames {C}1 and {C}2 are oriented so that their  -directions point out of the plane of the figure (as indicated by the small bold circle). The axes of the frames {N} and {B} were chosen to be axis-aligned with coincident origins located at the center of the sphere. The z-axes are pointing out of the page. Observe that, since the two joint axes of the left finger are perpendicular to the (x, y)-plane, it operates in that plane for all time. The other finger has three revolute joints. Because its first and second axes,
-directions point out of the plane of the figure (as indicated by the small bold circle). The axes of the frames {N} and {B} were chosen to be axis-aligned with coincident origins located at the center of the sphere. The z-axes are pointing out of the page. Observe that, since the two joint axes of the left finger are perpendicular to the (x, y)-plane, it operates in that plane for all time. The other finger has three revolute joints. Because its first and second axes,  and
and  , currently lie in the plane, rotation about
, currently lie in the plane, rotation about  will cause
will cause  to attain an out-of-plane component and would cause the finger tip at contact 2 to leave the plane.
to attain an out-of-plane component and would cause the finger tip at contact 2 to leave the plane.
In the current configuration, the rotation matrix for the i-th contact frame is defined as

The vector from the origin of {N} to the i-th contact point is given by

Substituting into (28.3) and (28.6) yields the complete grasp matrix for contact i:

where 0 ∈ℝ3×3 is the zero matrix and c
i
and s
i
are abbreviations for cos (θ
i
) and sin (θ
i
), respectively. The complete grasp matrix is defined as:  .
.
The accuracy of this matrix can be verified by inspection; for example, the first column is the unit wrench of the unit contact normal, the first three components are the direction cosines of  , and the last three are
, and the last three are  . Since
. Since  is collinear with (c
i
− p), the cross products (the last three components of the column) are zero. The last three components of the second column represent the moment of
is collinear with (c
i
− p), the cross products (the last three components of the column) are zero. The last three components of the second column represent the moment of  about the x-, y-, and z-axes of {N}. Since
about the x-, y-, and z-axes of {N}. Since  lies in the (x, y)-plane, the moments with the x- and y-axes are zero. Clearly
lies in the (x, y)-plane, the moments with the x- and y-axes are zero. Clearly  produces a moment of − r about the z-axis.
produces a moment of − r about the z-axis.
Construction of the complete hand Jacobian  for contact i requires knowledge of the joint axis directions and the origins of the frames fixed to the links of each finger. Figure 28.12 shows the hand in the same configuration as in Fig. 28.11, but with some additional data needed to construct the hand Jacobian. Assume that the origins of the joint frames lie in the plane of the figure.
for contact i requires knowledge of the joint axis directions and the origins of the frames fixed to the links of each finger. Figure 28.12 shows the hand in the same configuration as in Fig. 28.11, but with some additional data needed to construct the hand Jacobian. Assume that the origins of the joint frames lie in the plane of the figure.
In the current configuration, the quantities of interest for contact 1, expressed in {C}1 are:



The quantities of interest for contact 2, in {C}2 are:





Generally all of the components of the c − ζ and  vectors (including the components that are zero in the current configuration) are functions of q and u. The dependencies of the
vectors (including the components that are zero in the current configuration) are functions of q and u. The dependencies of the  vectors are shown explicitly.
vectors are shown explicitly.
Substituting into (28.14), (28.11), and (28.8) yields the complete hand Jacobian  :
:

The horizontal dividing line partitions  into
into  (on top) and
(on top) and  (on the bottom). The columns correspond to joints 1–5. The block diagonal structure is a result of the fact that finger i directly affects only contact i.
(on the bottom). The columns correspond to joints 1–5. The block diagonal structure is a result of the fact that finger i directly affects only contact i.
Example 1, Part 2: G and J
Assume that the contacts in Fig. 28.11 are both of type SF. Then the selection matrix H is given by

thus the matrices  and J ∈ℝ8×5 are constructed by removing rows 5, 6, 11, and 12 from
and J ∈ℝ8×5 are constructed by removing rows 5, 6, 11, and 12 from  and
and  :
:


Notice that changing the contact models is easily accomplished by removing more rows. Changing contact 1 to HF would eliminate the fourth rows from  and J, while changing it to PwoF would eliminate the second, third, and fourth rows of
and J, while changing it to PwoF would eliminate the second, third, and fourth rows of  and J. Changing the model at contact 2 would remove either just the eighth row or the sixth, seventh, and eighth rows.
and J. Changing the model at contact 2 would remove either just the eighth row or the sixth, seventh, and eighth rows.
Example 1, Part 3: Reduction to the Planar Case
The grasp shown in Fig. 28.11 can be reduced to a planar problem by following the explicit formulas given above, but it can also be done by understanding the physical interpretations of the various rows and columns of the matrices. Proceed by eliminating velocities and forces that are out of the plane. This can be done by removing the z-axes from {N} and {B}, and the  -directions at the contacts. Further, joints 3 and 4 must be locked. The resulting
-directions at the contacts. Further, joints 3 and 4 must be locked. The resulting  and J are constructed eliminating certain rows and columns.
and J are constructed eliminating certain rows and columns.  is formed by removing rows 3, 4, 7, and 8 and columns 3, 4, and 5. J is formed by removing rows 3, 4, 7, and 8 and columns 3 and 4, yielding:
is formed by removing rows 3, 4, 7, and 8 and columns 3, 4, and 5. J is formed by removing rows 3, 4, 7, and 8 and columns 3 and 4, yielding:


Example 1, Part 4: Grasp Classes
The first column of Table 28.9 reports the dimensions of the main subspaces of J and G for the sphere grasping example with different contact models. Only nontrivial null spaces are listed.
In the case of two HF contact models, all four null spaces are nontrivial, so the system satisfies the conditions for all four grasp classes. The system is graspable because there is an internal force along the line segment connecting the two contact points. Indeterminacy is manifested in the fact that the hand cannot resist a moment acting about that line. Redundancy is seen to exist since joint 3 can be used to move contact 2 out of the plane of the figure, but joint 4 can be rotated in the opposite direction to cancel this motion. Finally, the grasp is defective, because the contact forces and the instantaneous velocities along the  and
and  directions of contact 1 and 2, respectively, cannot be controlled through the joint torques and velocities. These interpretations are borne out in the null space basis matrices below, computed using r = 1, cos (θ
1) =−0.8=− cos (θ
2), sin (θ
1) = cos (θ
2) =−0.6, and l
7 = 0:
directions of contact 1 and 2, respectively, cannot be controlled through the joint torques and velocities. These interpretations are borne out in the null space basis matrices below, computed using r = 1, cos (θ
1) =−0.8=− cos (θ
2), sin (θ
1) = cos (θ
2) =−0.6, and l
7 = 0:


Notice that changing either contact to SF makes it possible for the hand to resist external moments applied about the line containing the contacts, so the grasp loses indeterminacy, but retains graspability (with squeezing still possible along the line of the contacts). However, if contact 2 is the SF contact, the grasp loses its redundancy. While the second contact point can still be moved out of the plane by joint 3 and back in by joint 4, this canceled translation of the contact point yields a net rotation about  (this also implies that the hand can control the moment applied to the object along the line containing the contacts). Changing to SF at contact 2 does not affect the handʼs inability to move contact 1 and contact 2 in the
(this also implies that the hand can control the moment applied to the object along the line containing the contacts). Changing to SF at contact 2 does not affect the handʼs inability to move contact 1 and contact 2 in the  and
and  directions, so the defectivity property is retained.
directions, so the defectivity property is retained.
Example 1, Part 5: Desirable Properties
Assuming contact model types of SF and HF at contacts 1 and 2, respectively, G is full row rank and so  (Table 28.9). Therefore, as long as the the hand is sufficiently dexterous, it can apply any wrench in ℝ6 to the object. Also, if the joints are locked, object motion will be prevented. Assuming the same problem values used in the previous part of this problem, the matrix
(Table 28.9). Therefore, as long as the the hand is sufficiently dexterous, it can apply any wrench in ℝ6 to the object. Also, if the joints are locked, object motion will be prevented. Assuming the same problem values used in the previous part of this problem, the matrix  is:
is:

Bases for the three nontrivial null spaces are:


Since ℛ(J) is four dimensional and 𝒩(G) is one dimensional, the maximum dimension of ℛ(J) +𝒩 (G) cannot be more than five, and therefore, the hand cannot control all possible object velocities, for example, the contact velocity  is in
is in  , and so cannot be controlled by the fingers. It is also equal to 0.6 times the third column of
, and so cannot be controlled by the fingers. It is also equal to 0.6 times the third column of  plus the fourth column of
plus the fourth column of  and therefore is in
and therefore is in  . Since the mapping between ℛ(G) and
. Since the mapping between ℛ(G) and  is one to one and onto, this uncontrollable contact velocity corresponds to a unique uncontrollable object velocity, ν = (0 0 0.6 1 0 0). In other words, the hand cannot cause the center of the sphere to translate in the z-direction, while also rotating about the x-axis (and not other axes simultaneously).
is one to one and onto, this uncontrollable contact velocity corresponds to a unique uncontrollable object velocity, ν = (0 0 0.6 1 0 0). In other words, the hand cannot cause the center of the sphere to translate in the z-direction, while also rotating about the x-axis (and not other axes simultaneously).
On the question of controlling all internal object forces, the answer is yes, since  . This conclusion is clear from the fact that 𝒩(G) has nonzero values in the first, second, and sixth positions, while all columns of
. This conclusion is clear from the fact that 𝒩(G) has nonzero values in the first, second, and sixth positions, while all columns of  have zeros in those positions.
have zeros in those positions.
Example 1, Part6: Force Closure
Again assume that contacts 1 and 2 on the grasped sphere were modeled as SF and HF contacts, respectively. Under this assumption, G is full row rank, and the internal force corresponds to equal and opposite contact forces. For frictional form closure to exist, the internal force must lie within the friction cones. Choosing r and the sines and cosines of θ
1 and θ
2 as in example 1, part 4, frictional form closure can be shown to exist if both friction coefficients are greater than 0.75. For this grasp, since  , frictional form closure is equivalent to force closure.
, frictional form closure is equivalent to force closure.
The plot in Fig. 28.13 was generated by fixing μ 2 =2.0 and varying μ 1. Notice that, for μ 1 <0.75, force closure does not exist. The metric increases smoothly until μ 1 becomes equal to μ 2. At this point, increasing μ 1 further does not improve force closure, since contact 2 becomes the limiting factor. To increase the metric further, both friction coefficients must be increased.
Example 2: Grasped Polygon in the Plane
Part 1: G and J
Figure 28.14 shows a planar hand grasping a polygon. Finger 1 (on the right) contains two joints numbered 1 and 2. Finger 2 contains joints 3–7, which are numbered in increasing order moving from the palm distally. The inertial frame has been chosen to lie inside the object, with its x-axis passing through contacts 1 and 2, and collinear with the normal vector of contact 2.
The rotation matrices are given by

Assuming HF contacts, G is given as

Notice that the first two columns of G correspond to the normal and tangential unit vectors at contact 1. The third and fourth columns correspond to contact 2.
Assuming HF contacts and that all joints are active (i.e., not locked), J is

The first two columns of  are the torques required to produce a unit force in the
are the torques required to produce a unit force in the  and
and  directions at contact 1. The horizontal line through the matrix partitions the contributions for the first finger (the upper part) and second finger. Notice that both
directions at contact 1. The horizontal line through the matrix partitions the contributions for the first finger (the upper part) and second finger. Notice that both  and G are full column rank.
and G are full column rank.
Example 2, Part 2: Grasp Classes
This example clearly illustrates the physical qualities of the various grasp classes without introducing features that can cloud the descriptions.
We now discuss the details of the four grasp classes using the previous planar example. During these discussions it is useful to choose nondimensional values for the parameters in the grasping system. Assume l 4 is the unit length. The other lengths as fractions of l 4 are:



Redundant
Redundancy exists if 𝒩(J) is nontrivial. Assuming that both contacts are hard contacts and that all the joints are active, rank(J) = 4, so 𝒩(J) is three dimensional. A basis for 𝒩(J) was obtained as

Since the first two rows are zero, 𝒩(J) does not include motions of the first finger (on the right of the palm). To understand this, assume that the object is fixed in the plane. Then the first finger cannot maintain sticking contact at contact 1 unless its joints are also fixed.
The three nonzero columns corresponding to finger 2 show that there are three basis motions of its joints that allow the finger contact to stick to the object contact. For example, the first column shows that, if joint 3 moves roughly as much as joints 4, 5, and 6, but in the opposite direction as joints 4 and 5 and in the same direction as joint 6, while joint 7 is more or less fixed, then contact 2 will be maintained.
Notice that finger 2 contains a parallelogram. Because of this geometry, one can see that the vector  is an element of 𝒩(J). The velocity interpretation of this vector is that the link of the finger connected to the palm, and the link touching the object remain fixed in space, while the parallelogram moves as a simple four-bar mechanism. Similarly, joint actions in 𝒩(J) do not affect the contact forces, but cause internal hand velocities. Also, notice that, since
is an element of 𝒩(J). The velocity interpretation of this vector is that the link of the finger connected to the palm, and the link touching the object remain fixed in space, while the parallelogram moves as a simple four-bar mechanism. Similarly, joint actions in 𝒩(J) do not affect the contact forces, but cause internal hand velocities. Also, notice that, since  , the entire space of possible generalized velocities and forces at the contacts can be generated by the joints.
, the entire space of possible generalized velocities and forces at the contacts can be generated by the joints.
Indeterminate
As noted above, with HF contact models, the system is graspable. However, replacing the HF models with PwoF models removes the tangent force components in the  and
and  directions. This effectively removes columns 2 and 4 from G, which guarantees that the system will be indeterminate. The reduced matrix is denoted by G
(1,3). In this case
directions. This effectively removes columns 2 and 4 from G, which guarantees that the system will be indeterminate. The reduced matrix is denoted by G
(1,3). In this case  is
is

Physically, this basis vector corresponds to moving the object such that the point coincident with the origin of {N} moves directly downward, while the object rotates counterclockwise. Also, if the analogous force and moment were applied to the object, the frictionless contacts could not maintain equilibrium.
Graspable
With two HF contact models in force, rank(G) = 3, so 𝒩(G) is one dimensional and the system is graspable. The null space basis vector of the grasp matrix is:

The physical interpretation of this basis vector is two opposing forces acting through the two contact points. Recall that, because the contact model is kinematic, there is no consideration of contact friction. However, given the direction of the contact normal relative to the line of the internal force, one can see that if the coefficient of friction is not greater than 0.75, squeezing tightly will cause sliding at contact 1, thus violating the kinematic contact model.
Defective
In a defective grasp,  . Given that the original J is full row rank, the grasp is not defective. However, it can be made defective by locking a number of joints and/or changing the handʼs configuration so that J is no longer full rank. For example, locking joints 4, 5, 6, and 7 makes finger 2 a single-link finger with only joint 3 active. In this new grasping system,
. Given that the original J is full row rank, the grasp is not defective. However, it can be made defective by locking a number of joints and/or changing the handʼs configuration so that J is no longer full rank. For example, locking joints 4, 5, 6, and 7 makes finger 2 a single-link finger with only joint 3 active. In this new grasping system,  is simply the first three rows of the original
is simply the first three rows of the original  given in (28.70), where the subscript is the list of indices of active joints. The null space basis vector is:
given in (28.70), where the subscript is the list of indices of active joints. The null space basis vector is:

This grasp is defective, since there is a subspace of contact velocities and forces that cannot be controlled by joint generalized velocities and forces. Since only the last component of  is nonzero, it would be impossible for the hand to give the contact point 2 on the object a velocity in the
is nonzero, it would be impossible for the hand to give the contact point 2 on the object a velocity in the  -direction while maintaining the contact. This is also clear from the arrangement of joint 3, contact 2, and the direction of the contact normal. The dual interpretation is that forces in
-direction while maintaining the contact. This is also clear from the arrangement of joint 3, contact 2, and the direction of the contact normal. The dual interpretation is that forces in  are resisted by the structure and the corresponding joint loads is zero, or equivalently that those forces are not controllable by the hand. Notice that if the model of contact 2 were changed to point without friction, then
are resisted by the structure and the corresponding joint loads is zero, or equivalently that those forces are not controllable by the hand. Notice that if the model of contact 2 were changed to point without friction, then  and the system would no longer be defective.
and the system would no longer be defective.
Example 3: Hyperstatic Grasps
Part 1:  and
and 
Figure 28.15 shows a planar projection of a three-dimensional sphere of radius l grasped by one finger only, with three revolute joints, through three contacts. The frames {C}1, {C}2, and {C}3 are oriented so that their  -directions point out of the plane of the figure (as indicated by the small bold circle). The axes of the frames {N} and {B} were chosen to be axis-aligned with coincident origins located at the center of the sphere. The z-axes are pointing out of the page. Observe that since the three joint axes of the finger are perpendicular to the (x, y)-plane, the grasp operates in that plane for all time.
-directions point out of the plane of the figure (as indicated by the small bold circle). The axes of the frames {N} and {B} were chosen to be axis-aligned with coincident origins located at the center of the sphere. The z-axes are pointing out of the page. Observe that since the three joint axes of the finger are perpendicular to the (x, y)-plane, the grasp operates in that plane for all time.
Assume that the width of all the links of the robotic hand is zero. Rotation matrices R
i
and vectors c
i
− p for i = 1,… , 3, can be computed as in (28.48) and (28.49) considering that θ
1 = π, for contact 1, θ
2 = π/2 and θ
3 = 0, for contacts 2 and 3, respectively. Finally, the complete grasp matrix is  where
where  is as defined in (28.50):
is as defined in (28.50):

Construction of the complete hand Jacobian  for contact i requires knowledge of the joint axis directions and the origins of the frames fixed to the links of each finger. Assume that the origins of the DH frames lie in the plane of the figure. In the current configuration, the quantities of interest for contact 1, expressed directly in {N}, are
for contact i requires knowledge of the joint axis directions and the origins of the frames fixed to the links of each finger. Assume that the origins of the DH frames lie in the plane of the figure. In the current configuration, the quantities of interest for contact 1, expressed directly in {N}, are

The quantities of interest for contact 2, in {N}, are

The quantities of interest for contact 3, in {N}, are

The complete hand Jacobian  (contact velocities are expressed in {C}
i
) is:
(contact velocities are expressed in {C}
i
) is:

The horizontal dividing line partitions  into
into  (on top),
(on top),  , and
, and  (on the bottom). The columns correspond to joints 1–3.
(on the bottom). The columns correspond to joints 1–3.
Example 3, Part 2: G and J
Assume that the three contacts in Fig. 28.15 are of type HF. Then the selection matrix H is given by

where I and 0 are in ℝ3×3, thus the matrices  and J ∈ℝ9×3 are obtained by removing rows related to rotations from
and J ∈ℝ9×3 are obtained by removing rows related to rotations from  and
and  :
:

Example 3, Part 3: Grasp Classes
The first column of Table 28.10 reports the dimensions of the main subspaces of  and G for the sphere grasping example with three hard-finger contacts. Only nontrivial null spaces are listed.
and G for the sphere grasping example with three hard-finger contacts. Only nontrivial null spaces are listed.
The system is defective because there are generalized contact forces belonging to the subspace that are resisted by the structure, which correspond to zero joint actions:

The first three columns represent generalized forces acting at the three contact points in a direction perpendicular to the plane of the Fig. 28.15. The fourth column corresponds to a contact force applied only along the  direction.
direction.
The system is graspable because the subspace of internal forces is three dimensional; a possible basis matrix is:

The three force vectors of the subspace N(G) are easily identified from Fig. 28.15. Note that all forces are expressed in local contact frames. The first column vector of N(G) represents opposed forces at contacts 1 and 2 along the line joining contacts 1 and 2. The second column vector parameterizes opposed forces at contacts 1 and 3 along the line joining contacts 1 and 3. The last vector represents forces along direction λ h, shown as the dashed lines in Fig. 28.15. Note that this direction (in wrench intensity space) corresponds to two upward friction forces at the left and right contacts and one downward with double the magnitude from the center of the top link in the work space.
Finally, the grasp is hyperstatic because

Hyperstatic forces in this subspace are internal forces that cannot be controlled through the hand joints. In Fig. 28.15 the internal force λ
h that is also in  is reported.
is reported.
The grasp in Fig. 28.15 is an example of a power grasp, a style of grasp mentioned earlier that uses many contact points not only on the fingertips but also on the links of fingers and the palm [28.4,20,31].
All power grasps are kinematically defective  and are usually hyperstatic. According to Sect. 28.4.2, rigid-body modeling is not sufficient to capture the overall system behavior, because the generalized contact forces in
and are usually hyperstatic. According to Sect. 28.4.2, rigid-body modeling is not sufficient to capture the overall system behavior, because the generalized contact forces in  leave the dynamics indeterminate.
leave the dynamics indeterminate.
Many approaches have been used to overcome the rigid-body limitation in hyperstatic grasps such as those proposed in [28.12,16,17] where viscoelastic contact models have been used to solve the force indeterminacy. In [28.32], the authors found that a sufficient condition for hyperstaticity is m > q + 6, where m is the dimension of the contact force vector.
Example 4: Duality
Consider a frictionless disc constrained to translate in the plane (Fig. 28.16). In this problem n ν = 2, so the space of applied contact forces and object velocities is the plane ℝ2. In the top pair of pictures, a single (fixed) contact point imposes a half-space constraint on the instantaneous velocity and limits the force at a frictionless contact to the ray. Both the ray and the (dark gray) half space are defined by the contact normal pointing into the object. Notice that the ray and half space are dual cones. When two contacts are present, the (light gray) force cone becomes the nonnegative span of the two contact normals and the velocity cone is its dual. With the addition of the third contact, the grasp has form closure, as indicated by the degeneration of the velocity cone to the origin and the expansion of the force cone to become equal to the plane.
It is important to point out that the discussion of the dual cones applies to three-dimensional bodies after replacing the contact normals with the columns of G.
Example 5: Form Closure
Form closure of a spatial object requires seven contacts, which is difficult to illustrate. Therefore, the only form closure example analyzed in this chapter is for the following planar problem.
The fundamental features of a planar grasp with four contacts are shown in Fig. 28.17. Notice that the normal at the fourth contact is well defined despite the contact occurring on the vertex of the object. The angle α of the finger is allowed to vary, and it can be shown that form closure exists if α lies in the interval  . Notice that a critical value of α occurs when the lower edge of 𝒞2 contains contact point 3 (α ≈1.0518) and contact point 2 (
. Notice that a critical value of α occurs when the lower edge of 𝒞2 contains contact point 3 (α ≈1.0518) and contact point 2 ( ).
).
Choosing the frame for analysis with origin at the fourth contact point, the grasp matrix for this example is

Form closure was tested for a range of angles as shown in the plot in Fig. 28.18, which indicates that the grasp farthest from losing form closure has α ≈1.22 radians, which is the configuration shown in the figure.
Conclusion and Further Reading
A great deal of understanding of grasping systems can be derived from the simple linear kinematic, dynamic, and contact models. The most widely used grasp classifications and closure properties can all be derived from these models under the rigid-body assumption. Linearizing these models leads to metrics and tests that can be computed efficiently using computational linear algebra and linear programming techniques. In-depth discussions of grasp kinematics and grasp classification can be found in [28.11,16,21,32,33,34,35,36]. When making simplifying assumptions, one has to wonder what insights have been lost. For the interested reader, there are a host of papers that analyze grasping system under more sophisticated assumptions. In general, bodies are curved and compliant [28.13,22,31,37,38,39]. Contact friction models are not quite as simple as the Coulomb approximation so widely adopted, and presented in this chapter; for example, if a contact has to resist a moment about its normal, its effective tangential friction coefficient is reduced [28.29]. In our analysis, the quadratic Coulomb friction cone was approximated by a polyhedral cone. The analysis problems are more difficult when using the quadratic cone, but they are quite tractable [28.30,40]. In principle, a properly designed hand–object system could be controlled to maintain all contacts, but worldly realities can lead to unwanted slipping or twisting.
Other important research topics within the area of grasping are: grasp synthesis, force distribution, stability, and dexterous manipulation. Grasp synthesis is the problem of choosing the posture of the hand and contact point locations to optimize a grasp quality metric. Note that this is quite a different issue from grasp acquisition, which refers to the act of achieving the chosen grasp. Grasp acquisition is an act of dexterous manipulation. One of the first studies of grasp synthesis for multifingered hands was undertaken by Jameson in 1985 [28.41] who designed a Levenberg–Marquardt algorithm to search the surface of an object for the locations of three points that would achieve force closure. Since this work, many other metrics and approaches to searching for high-quality grasps have been implemented (see, for example, [28.42,43,44,45,46,47]). A recent paper by Liu et al. provides an in-depth discussion of several quality metrics. They further demonstrate that, if one chooses finger contact locations by optimizing the metrics and if a force closure grasp exists, then the grasps obtained are force closed [28.48]. For grasping of several objects simultaneously, see [28.49].
The grasp force distribution problem is that of finding good joint actions and contact forces to balance a given external load applied to the object. This problem was studied in the context of walking machines first by McGhee and Orin [28.50] and later by several others [28.51,52]. Kumar and Waldron applied similar techniques to force distribution problems in grasping [28.53]. Recent work by Han et al. and Buss et al. has solved the force distribution problem with nonlinear friction cone constraints by taking advantage of second-order cone programming and related techniques [28.30,40,54]. In power grasps, this problem is more involved because contact forces that cannot be applied may exist, as studied in [28.17,19,20,55].
Grasp stability is too often equated to grasp closure, because all external forces can be balanced by the hand. However, grasp closure is really equivalent to the existence of equilibrium, which is a necessary condition for stability, but not a sufficient condition. The common definition of stability outside of the field of robotic grasping requires that, when a system is deflected from an equilibrium point, the system returns to this point. This was the approach taken by Hanafusa and Asada, who studied grasp stability for a hand with three elastic fingers [28.56]. Cutkosky took the analysis to three dimensions and accounted for finger and object curvatures [28.37]. He showed that stability was dependent on the stiffnesses of the fingers and controller and on the curvatures of the bodies in contact.
Dexterous manipulation research first appeared in the literature in the 1970s. Hanafusa and Asada developed a plan to turn a nut onto a bolt [28.57]. Since then a progression of increasingly complex manipulation tasks have been studied at varying degrees of detail. Mason and many of his students studied pushing tasks in the horizontal plane, see for example [28.58,59,60,61]. Other notable planar work can be found in [28.62,63,64,65,66]. The planning and execution of dexterous manipulation tasks in three dimensions continues to be an open problem in robotics. However, for several interesting approaches and many useful insights, the following reading is recommended [28.67,68,69,70,71,72].
Abbreviations
- DH:
-
Denavit–Hartenberg
- DOF:
-
degree of freedom
- HF:
-
hard-finger
- LP:
-
linear program
- PwoF:
-
point-contact-without-friction
- SF:
-
soft-finger
References
J.K. Salisbury: Kinematic and Force Analysis of Articulated Hands. Ph.D. Thesis (Stanford University, Stanford 1982)
A.T. Miller, P.K. Allen: GraspIt! A versatile simulator for robotic grasping, IEEE Robot. Autom. Mag. 11(4), 110–122 (2004)
A. Bicchi: Hands for dextrous manipulation and powerful grasping: A difficult road towards simplicity, IEEE Trans. Robot. Autom. 16, 652–662 (2000)
K. Salisbury, W. Townsend, B. Ebrman, D. DiPietro: Preliminary design of a whole-arm manipulation system (WAMS), Proc. IEEE Int. Conf. Robot. Autom. (1988) pp. 254–260
M.S. Ohwovoriole, B. Roth: An extension of screw theory, J. Mech. Des. 103, 725–735 (1981)
K.H. Hunt: Kinematic Geometry of Mechanisms (Oxford Univ. Press, Oxford 1978)
T.R. Kane, D.A. Levinson, P.W. Likins: Spacecraft Dynamics (McGraw Hill, New York 1980)
J.J. Craig: Introduction to Robotics: Mechanics and Control, 2nd edn. (Addison-Wesley, Reading 1989)
J.K. Salisbury, B. Roth: Kinematic and force analysis of articulated mechanical hands, J. Mech. Trans. Autom. Des. 105, 35–41 (1983)
M.T. Mason, J.K. Salisbury Jr: Robot Hands and the Mechanics of Manipulation (MIT Press, Cambridge 1985)
A. Bicchi: On the closure properties of robotic grasping, Int. J. Robot. Res. 14(4), 319–334 (1995)
D. Prattichizzo, A. Bicchi: Consistent task specification for manipulation systems with general kinematics, ASME J. Dyn. Syst. Meas. Contr. 119, 760–767 (1997)
J. Kerr, B. Roth: Analysis of multifingered hands, Int. J. Robot. Res. 4(4), 3–17 (1986)
G. Strang: Introduction to Linear Algebra (Wellesley-Cambridge, Wellesley 1993)
R.M. Murray, Z. Li, S.S. Sastry: A Mathematical Introduction to Robot Manipulation (CRC Press, Boca Raton 1993)
D. Prattichizzo, A. Bicchi: Dynamic analysis of mobility and graspability of general manipulation systems, IEEE Trans. Robot. Autom. 14(2), 241–258 (1998)
A. Bicchi: On the problem of decomposing grasp and manipulation forces in multiple whole-limb manipulation, Int. J. Robot. Auton. Syst. 13, 127–147 (1994)
F. Reuleaux: The Kinematics of Machinery (Macmillan, New York 1876), Republished by Dover, New York (1963)
T. Omata, K. Nagata: Rigid body analysis of the indeterminate grasp force in power grasps, IEEE Trans. Robot. Autom. 16(1), 46–54 (2000)
J.C. Trinkle: The Mechanics and Planning of Enveloping Grasps. Ph.D. Thesis (University of Pennsylvania, Philadelphia 1987)
K. Lakshminarayana: Mechanics of form closure, Amer. Soc. Mech. Eng. Tech. Rep. 78-DET-32 (1978)
E. Rimon, J. Burdick: Mobility of bodies in contact i: A 2nd order mobility index for multiple-finger grasps, IEEE Trans. Robot. Autom. 14(5), 696–708 (1998)
B. Mishra, J.T. Schwartz, M. Sharir: On the existence and synthesis of multifinger positive grips, Algorithmica 2(4), 541–558 (1987)
P. Somov: Über Schraubengeschwindigkeiten eines festen Körpers bei verschiedener Zahl von Stützflächen, Z. Math. Phys. 42, 133–153 (1897), (in German)
A.J. Goldman, A.W. Tucker: Polyhedral convex cones. In: Linear Inequalities and Related Systems, ed. by H.W. Kuhn, A.W. Tucker (Princeton Univ., York 1956) pp. 19–40
X. Markenscoff, L. Ni, C.H. Papadimitriou: The geometry of grasping, Int. J. Robot. Res. 9(1), 61–74 (1990)
D.G. Luenberger: Linear and Nonlinear Programming, 2nd edn. (Addison-Wesley, Reading 1984)
V.D. Nguyen: The synthesis of force closure grasps in the plane. M.S. Thesis (MIT, Cambridge 1985), AI-TR861
R.D. Howe, M.R. Cutkosky: Practical force-motion models for sliding manipulation, Int. J. Robot. Res. 15(6), 557–572 (1996)
L. Han, J.C. Trinkle, Z. Li: Grasp analysis as linear matrix inequality problems, IEEE Trans. Robot. Autom. 16(6), 663–674 (2000)
M.R. Cutkosky, I. Kao: Computing and controlling the compliance of a robotic hand, IEEE Trans. Robot. Autom. 5(2), 151–165 (1989)
J.C. Trinkle: On the stability and instantaneous velocity of grasped frictionless objects, IEEE Trans. Robot. Autom. 8(5), 560–572 (1992)
K.H. Hunt, A.E. Samuel, P.R. McAree: Special configurations of multi-finger multi-freedom grippers – a kinematic study, Int. J. Robot. Res. 10(2), 123–134 (1991)
D.J. Montana: The kinematics of multi-fingered manipulation, IEEE Trans. Robot. Autom. 11(4), 491–503 (1995)
Y. Nakamure, K. Nagai, T. Yoshikawa: Passive and active closures by constraining mechanisms, Int. J. Robot. Res. 8, 44–61 (1989)
J.S. Pang, J.C. Trinkle: Stability characterizations of rigid body contact problems with coulomb friction, Z. Angew. Math. Mech. 80(10), 643–663 (2000)
M.R. Cutkosky: Robotic Grasping and Fine Manipulation (Kluwer Academic, Norwell 1985)
W.S. Howard, V. Kumar: On the stability of grasped objects, IEEE Trans. Robot. Autom. 12(6), 904–917 (1996)
A.B.A. Cole, J.E. Hauser, S.S. Sastry: Kinematics and control of multifingered hands with rolling contacts, IEEE Trans. Autom. Contr. 34, 398–404 (1989)
M. Buss, H. Hashimoto, J. Moore: Dexterous hand grasping force optimization, IEEE Trans. Robot. Autom. 12(3), 406–418 (1996)
J. Jameson: Analytic Techniques for Automated Grasp. Ph.D. Thesis (Stanford University, Stanford 1985)
V. Nguyen: Constructing force-closure grasps, Int. J. Robot. Res. 7(3), 3–16 (1988)
N.S. Pollard: Parallel algorithms for synthesis of whole-hand grasps, Proc. IEEE Int. Conf. Robot. Autom. (1997)
Y.C. Park, G.P. Starr: Grasp synthesis of polygonal objects using a three-fingered robot hand, Int. J. Robot. Res. 11(3), 163–184 (1992)
I.M. Chen, J.W. Burdick: Finding antipodal point grasps on irregularly shaped objects, IEEE Trans. Robot. Autom. 9(4), 507–512 (1993)
B. Mishra: Grasp metrics: Optimality and complexity, Proc. Workshop Algorithmic Found. Robot. (Peters, Boston 1994)
J. Ponce, S. Sullivan, A. Sudsang, J.-D. Boissonnat, J.-P. Merlet: On computing four-finger equilibrium and force-closure grasps of polyhedral objects, Int. J. Robot. Res. 16(1), 11–35 (1997)
G.F. Liu, J. Xu, X. Wang, Z.X. Li: On quality functions for grasp synthesis, fixture planning, and coordinated manipulation, IEEE Trans. Autom. Sci. Eng. 1(2), 146–162 (2004)
K. Harada, M. Kaneko: Neighborhood equilibrium grasp for multiple objects, Proc. IEEE Int. Conf. Robot. Autom. (2000) pp. 2159–2164
R.B. McGhee, D.E. Orin: A mathematical programming approach to control of positions and torques in legged locomotion systems, Proc. ROMANCY (1976)
K. Waldron: Force and motion management in legged locomotion, IEEE J. Robot. Autom. 2(4), 214–220 (1986)
T. Yoshikawa, K. Nagai: Manipulating and grasping forces in manipulation by multi-fingered grippers, Proc. IEEE Int. Conf. Robot. Autom. (1987) pp. 1998–2007
V. Kumar, K. Waldron: Force distribution in closed kinematic chains, IEEE J. Robot. Autom. 4(6), 657–664 (1988)
M. Buss, L. Faybusovich, J. Moore: Dikin-type algortihms for dexterous grasping force optimization, Int. J. Robot. Res. 17(8), 831–839 (1998)
D. Prattichizzo, J.K. Salisbury, A. Bicchi: Contact and grasp robustness measures: Analysis and experiments. In: Experimental Robotics IV, Lecture Notes Contr. Inf. Sci., Vol. 223, ed. by O. Khatib, K. Salisbury (Springer, Berlin, Heidelberg 1997)
H. Hanafusa, H. Asada: Stable prehension by a robot hand with elastic fingers. In: Robot Motion: Planning and Control, ed. by M. Brady, J. Hollerbach, T. Johnson, T. Lozano-Perez, M. Mason (MIT Press, Cambridge 1982) pp. 323–336
H. Hanafusa, H. Asada: Handling of constrained objects by active elastic fingers and its applications to assembly, Trans. Soc. Instrum. Contr. Eng. 15(1), 61–66 (1979)
M.T. Mason: Manipulator Grasping and Pushing Operations. Ph.D. Thesis (Massachusetts Institute of Technology, Cambridge 1982), reprinted in Robot Hands and the Mechanics of Manipulation MIT Press, Cambridge 1985
R.C. Brost: Analysis and Planning of Planar Manipulation Tasks. Ph.D. Thesis (Carnegie Mellon University, Pittsburgh 1991)
M.A. Peshkin, A.C. Sanderson: Planning robotic manipulation strategies for workpieces that slide, IEEE J. Robot. Autom. 4(5), 524–531 (1988)
K. Lynch: Nonprehensile Manipulation: Mechanics and Planning. Ph.D. Thesis (Carnegie Mellon University, Pittsburgh 1996)
J.C. Trinkle, J.J. Hunter: A framework for planning dexterous manipulation, Proc. IEEE Int. Conf. Robot. Autom. (1991) pp. 1245–1251
J.C. Trinkle, R.C. Ram, A.O. Farahat, P.F. Stiller: Dexterous manipulation planning and execution of an enveloped slippery workpiece, Proc. IEEE Int. Conf. Robot. Autom., Vol. 2 (1993) pp. 442–448
K. Harada, M. Kaneko, T. Tsuji: Rolling based manipulation for multiple objects, Proc. IEEE Int. Conf. Robot. Autom. (2000) pp. 3887–3894
R.S. Fearing: Simplified grasping and manipulation with dextrous robot hands, IEEE J. Robot. Autom. RA-2(4), 188–195 (1986)
N.B. Zumel, M.A. Erdmann: Nonprehensible two palm manipulation with non-equilbrium transitions between stable states, Proc. IEEE Int. Conf. Robot. Autom. (1996) pp. 3317–3323
D.L. Brock: Enhancing the dexterity of a robot hand using controlled slip. M.S. Thesis (MIT, Cambridge 1987)
R. Fearing, S. Gopalswamy: Grasping polyhedral objects with slip, Proc. IEEE Int. Conf. Robot. Autom. (1989) pp. 296–301
M. Cherif, K.K. Gupta: Planning quasi-static fingertip manipulation for reconfiguring objects, IEEE Trans. Robot. Autom. 15(5), 837–848 (1999)
L. Han, J.C. Trinkle: Dextrous manipulation by rolling and finger gaiting, Proc. IEEE Int. Conf. Robot. Autom. (1998) pp. 730–735
L. Han, Z. Li, J.C. Trinkle, Z. Qin, S. Jiang: The planning and control of robot dexterous manipulation, Proc. IEEE Int. Conf. Robot. Autom. (2000) pp. 263–269
M. Higashimori, M. Kimura, I. Ishii, M. Kaneko: Friction independent dynamic capturing strategy for a 2d stick-shaped object, Proc. IEEE Int. Conf. Robot. Autom. (2007) pp. 217–224
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2008 Springer-Verlag
About this entry
Cite this entry
Prattichizzo, D., Trinkle, J.C. (2008). Grasping. In: Siciliano, B., Khatib, O. (eds) Springer Handbook of Robotics. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-30301-5_29
Download citation
DOI: https://doi.org/10.1007/978-3-540-30301-5_29
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-23957-4
Online ISBN: 978-3-540-30301-5
eBook Packages: EngineeringEngineering (R0)



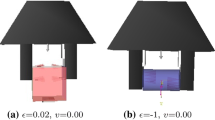








 has at least one strictly positive component, then the grasp does not have form closure of order β;
has at least one strictly positive component, then the grasp does not have form closure of order β;
 has at least one strictly negative component, then the grasp has form closure of order β;
has at least one strictly negative component, then the grasp has form closure of order β;
 , then higher-order analysis is required to determine the existence of form closure.
, then higher-order analysis is required to determine the existence of form closure.



 and
and 




 and
and 

 and causes hyperstaticity
and causes hyperstaticity


