A Multi-class Support Vector Machine Based on Geometric Margin Maximization

Abstract

Support vector machines (SVMs) are popular supervised learning methods. The original SVM was developed for binary classification. It selects a linear classifier by maximizing the geometric margin between the boundary hyperplane and sample examples. There are several extensions of the SVM for multi-class classification problems. However, they do not maximize geometric margins exactly. Recently, Tatsumi and Tanino have proposed multi-objective multi-class SVM, which simultaneously maximizes the margins for all class pairs. In this paper, we propose another multi-class SVM based on the geometric margin maximization. The SVM is formulated as minimization of the sum of inverse-squared margins for all class pairs. Since this is a nonconvex optimization problem, we propose an approximate solution. By numerical experiments, we show that the propose SVM has better performance in generalization capability than one of the conventional multi-class SVMs.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Support vector machines (SVMs) are popular supervised learning methods in machine learning. The original SVM [3, 9] was proposed for binary classification problems, i.e., tasks to learn a classifier separating two group of examples. The SVM determines a linear discriminant function based on the principle of margin maximization. It means that the linear function is selected such that the minimum distance between sample examples and the hyperplane associated with the linear function is maximized. It is based on geometric motivation that the neighborhood of a labeled example includes those of the same label as that example. In another viewpoint, the margin maximization is regarded as regularization in model selection.

There are various extensions of the binary SVM for multi-class classification problems, i.e., there are more than two groups which should be separated. A simple approach of extension is one-against-all (OAA) [7], which reduces a k-class problem to k binary problems to separate one class from the others, and applies the binary SVM to these problems. Another major approach is all-together (AT), which is formulated as minimization of the sum of regularization terms and errors of a classifier. Since optimization problems of AT-SVM includes more decision variables and constraints, computational costs are higher than OAA-SVM. On the other hand, Doğan et al. [4] showed that AT-SVMs outperform OAA-SVM in classification accuracy in the case of the linear kernel. (And they are comparable in the case of the RBF kernel.)

The above mentioned multi-class SVMs do not exactly maximize geometric margins. Especially, the existing AT-SVMs are derived from regularized model selection, instead of geometric interpretation. Recently, Tatsumi and Tanino [8] have pointed out geometric margin maximization in multi-class problems, and formulated a multi-objective optimization problem which simultaneously maximizes all of the class pair margins. The model is called multi-objective multi-class SVM (MMSVM).

To obtain Pareto solutions of multi-objective optimization problems, we need some scalarization method. Because of nonconvexity of MMSVM, almost all conventional scalarization methods cannot be computed efficiently. Tatsumi and Tanino [8] used the $\varepsilon$-constraint method, and showed that obtained classifiers have better classification accuracy than those of AT- and OAA-SVMs. However, the method needs high computational effort to find good parameter $\varepsilon$, and cannot maximize the margins of class pairs uniformly like weighted-sum scalarization.

In this paper, we propose a multi-class SVM which is another scalarizing formulation of MMSVM. It minimizes the sum of inverse-squared margins for all class pairs. To overcome nonconvexity of the scalarized MMSVM, we linearize its nonconvex parts and solve the modified convex optimization problem. Consequently, we obtain an approximation solution for the original problem. Moreover, we show an upper bound of the ratio of the objective function value of the approximation solution to the optimal value of the original problem. A special case of the proposed multi-class SVM coincides with the conventional AT-SVM in [2, 9, 10]. By numerical experiments, we show that the proposed multi-class SVM outperforms the AT-SVM in generalization capability.

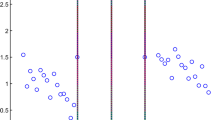
We demonstrate that large margin classifiers can be obtained by the proposed SVM. See Fig. 1. The left and right figures show classification boundaries of Wine Data Set obtained by AT-SVM and the proposed SVM, respectively. The tables after the figures show the values of margins for three class pairs (1, 2), (1, 3) and (2, 3). We can see that all of the margins of the classifier by the proposed SVM are larger than those by AT-SVM.

Fig. 1.

Separating lines obtained by AT-SVM (the left figure) and the proposed SVM (the right figure) for Wine Data Set. There are three classes—class 1: blue circles, class 2: orange triangles, class 3: yellow squares. The solid lines are the separating line with the margins of class pair 12. The broken lines are of class pair 13. The dotted lines are of class pair 23. The data are plotted in the 2-dimensional affine subspace passing through 3 normal vectors of 3 classes. (Color figure online)

This paper is organized as follows. In Sect. 2, binary and multi-class SVMs are introduced. In Sect. 3, we discuss the proposed multi-class SVM. We formulate the model minimizing the sum of inverse-squared margins, and propose the approximate solution. In Sect. 4, numerical experiments are presented to examine performance of the proposed SVM. Finally, in Sect. 5, concluding remarks are provided.

2 Multi-class SVMs

2.1 Multi-class Classification

In this paper, we deal with classification problems of supervised learning. Let n-dimensional real space $\mathbf {R}^n$ be an input space and $C = \{1,2,\dots ,c\}$, $c\ge 2$ be a class label set. A classification problem is to find a function $D:\mathbf {R}^n\rightarrow C$ from m input vectors $x^1,\dots ,x^m\in \mathbf {R}^n$ and class labels $y_1,\dots ,y_m\in C$. Such a function D is called a classifier. $S = ((x^1,y_1),\dots ,(x^m,y_m))$ is called a training set. We aim to find a function having high classification accuracy, i.e., it can correctly assign class labels to (unseen) input vectors. Let $M = \{1,\dots ,m\}$ be the index set of the training set. For $p\in C$, we define $M^p = \{i\in M\;|\;y_i = p\}$.

When $c = 2$, the problem is called binary classification. On the other hand, when $c \ge 3$, it is called multi-class classification. The SVM proposed in this paper can solve multi-class classification problems.

We consider a linear classifier D given in the following form: for $x\in \mathbf {R}^n$,

$$\begin{aligned} D(x) = \mathop {\mathrm{argmax}}\limits _{p\in C}\{f_p(x) = (w^p)^{\top }x + b_p\}, \end{aligned}$$

(1)

where $w^1,\dots ,w^c\in \mathbf {R}^n$ and $b_1,\dots ,b_c\in \mathbf {R}$. If there is more than one label p whose value $f_p(x)$ is the maximum, we arbitrarily select one label among them. Each $f_p(x)$ is called a linear discriminant function for the class label p. We propose a method to learn the parameters $(w^1,b_1),\dots ,(w^p,b_p)$ from the training set S, to construct the linear classifier D with high accuracy.

2.2 SVMs

SVMs (Support Vector Machines) are methods for binary classification to learn linear classifiers from examples. First, we mention the SVM for linearly separable binary classification problems. In binary classification, a linear classifier D is reduced to the following form: letting $f(x) = w^{\top } x + b$, $D(x) = 1$ if $f(x) > 0$; $D(x) = -1$ if $f(x) < 0$. Here, we suppose the class labels are 1 and $-1$. w and b are parameters of the linear classifier D. Input vectors x with $f(x) = 0$ are arbitrarily classified.

SVM selects a classifier whose boundary hyperplane having the largest margin. A margin of a hyperplane $f(x) = 0$ is the distance between the hyperplane and the nearest input vector in the training S, namely, $\frac{\min _{i\in M}|w^{\top }x^i + b|}{\Vert w\Vert }$, where $\Vert \cdot \Vert$ is the Euclidean norm. The largest-margin classifier is obtained by solving the following optimization problem.

$$\begin{aligned} \begin{aligned}&\mathop {\mathrm{minimize}}\limits _{w,b}&\frac{1}{2}\left( \frac{\min _{i\in M}|w^{\top } x^i + b|}{\Vert w\Vert }\right) ^{-2} \\&{{\mathrm{subject~to}}}&y_i(w^{\top } x^i + b) > 0,\; i\in M \end{aligned} \end{aligned}$$

(2)

Here, we consider the problem minimizing the inverse-squared margin instead of maximizing the margin. The constraint ensures that the selected hyperplane $w^{\top } x + b = 0$ correctly classifies all training points. The objective function is invariant if (w, b) is multiplied by a positive value. Hence, without loss of generality, we can fix $\min _{i\in M}|w^{\top } x^i + b| = 1$, and the above optimization problem is equivalent to the following.

(3)

For $i\in M$, let $\alpha _i$ be the optimal dual variable with respect to the constraint $y_i(w^{\top }x^i+b)\ge 1$. A training input vector $x^i$ is called a support vector if $\alpha _i > 0$ ¹. The optimal hyperplane $w^{\top }x+b = 0$ depends on the set of support vectors only.

The model (3) has no feasible solution if the positive class ($y_i=1$) and the negative class ($y_i=-1$) cannot be separated by any hyperplanes. Additionally, even if two classes are separable, a better hyperplane may be obtained by taking account of input vectors near to the hyperplane. To archive these ideas, we consider errors for training examples, and minimization of the sum of the errors. In this paper, we use the squared hinge loss function to assess the errors.

$$\begin{aligned} \begin{aligned}&\mathop {\mathrm{minimize}}\limits _{w,b}&\frac{1}{2}{\Vert w\Vert ^2} + \frac{\mu ^2}{2}\sum _{i\in M} L(y_i,f(x^i)), \end{aligned} \end{aligned}$$

(4)

where $L(y,f(x)) = (\max \{0,1-y(w^{\top } x + b)\})^2$. SVMs with tolerance of errors are called soft-margin. (On the other hand, the model (3) is called hard-margin.) In this formulation, the first term $\Vert w\Vert ^2/2$ of the margin minimization can be regarded as a regularization term to prevent overfitting of classifiers. $\mu$ is a hyperparameter to adjusting the effect of the sum of losses. It is equivalent to,

(5)

where $\xi = (\xi _1,\dots ,\xi _m)$ is the vector of additional decision variables.

2.3 Multi-class SVMs

We extend the SVM model (3) for multi-class problems. Let $f_p(x) = (w^p)^{\top }x + b_p$ be a linear discriminant function of class label $p\in C$. Additionally, let $C^{\bar{2}} = \{pq\;|\;p,q\in C,p<q\}$ be the set of class label pairs. For each class label pair $pq\in C^{\bar{2}}$, the boundary hyperplane separating two sets of p and q is $f_{pq}(x) = (w^p-w^q)^{\top }x + (b_p-b_q) = 0$. Similarly to (2), the optimization problem to minimize the sum of inverse-squared margins for all $pq\in C^{\bar{2}}$ is formulated as follows.

$$\begin{aligned} \begin{aligned}&\mathop {\mathrm{minimize}}\limits _{(w^p,b_p)}&\frac{1}{2} \left( \sum _{pq\in C^{\bar{2}}}\frac{\min _{i\in M^{pq}}|(w^p-w^q)^{\top } x^i + b_p-b_q|}{\Vert w^p-w^q\Vert }\right) ^{-2} \\&{{\mathrm{subject~to}}}&(w^p-w^q)^{\top } x^i + b_p-b_q> 0,\;i\in M^p,\;pq\in C^{\bar{2}},\\&&(w^q-w^p)^{\top } x^i + b_q-b_p > 0,\;i\in M^q,\;pq\in C^{\bar{2}}. \end{aligned} \end{aligned}$$

(6)

By the same reduction as (3), we fix $\min _{i\in M^{pq}}|(w^p-w^q)^{\top } x^i + b_p-b_q| = 1$. Then, we obtain the following optimization problem.

(7)

The multi-class SVM to construct a classifier using the linear discriminant functions obtained by problem (7) is called AT-SVM (All-Together SVM). The obtained classifier correctly separates all training input vectors. However, it may not be a margin maximization solution [8].

AT-SVM is also extended to soft-margin cases. There are several soft-margin models considering types of loss functions and functions to aggregate losses of training examples [4]. In this paper, we consider the following soft-margin model using the squared hinge loss function.

$$\begin{aligned} \begin{aligned}&\mathop {\mathrm{minimize}}\limits _{(w^p,b_p),\xi }&\frac{1}{2} \sum _{pq\in C^{\bar{2}}} {\Vert w^p-w^q\Vert ^2} + \frac{1}{2}\sum _{pq\in C^{\bar{2}}} \left( \sum _{i\in M^p}\xi _{qi}^2 + \sum _{i\in M^q} \xi _{pi}^2\right) \\&{{\mathrm{subject~to}}}&(w^p-w^q)^{\top } x^i + b_p-b_q + \xi _{qi} \ge 1,\; i\in M^p,\;pq\in C^{\bar{2}},\\&&(w^q-w^p)^{\top } x^i + b_q-b_p + \xi _{pi} \ge 1,\; i\in M^q,\;pq\in C^{\bar{2}}, \end{aligned} \end{aligned}$$

(8)

where $\xi = ((\xi _{1i})_{i\in M\setminus M^1},\dots ,(\xi _{ci})_{i\in M\setminus M^c})$.

3 Multi-class SVM Maximizing Geometric Margins

3.1 Geometric Margin Maximization

In this paper, we propose a new multi-class SVM based on minimization of the sum of inverse-squared margins (6). Let $s_{pq} = \left( \min _{i\in M^p\cup M^q} |\right.$ $\left. (w^p-w^q)^{\top } x^i + b_p-b_q|\right) ^2$ for $pq\in C^{\bar{2}}$, and $s = (s_{12},\dots ,s_{1c},s_{23},\dots ,s_{(c-1)c})$. The model (6) is reformulated as follows.

(9)

Let $((w^p,b_p)_{p\in C},s)$ be a feasible solution of (9) and $a > 0$. Then, $((aw^p,ab_p)_{p\in C},a^2s)$ is also a feasible solution and the objective function is invariant for the multiplication of a. Hence, without loss of generality, we can add constraints $s_{pq}\ge 1$ for $pq\in C^{\bar{2}}$.

(P1)

Let OPT1 be the optimal value of (P1).

3.2 Approximate Solutions

The optimization problem (P1) is nonconvex, because of $\sqrt{s_{pq}}$ in the right hand sides of the first and second constraints. Nonconvexity causes for difficulty in solving optimization problems. Hence, we replace $\sqrt{s_{pq}}$ with an affine function of $s_{pq}$, and make (P1) convex.

First, we put additional constraints $s_{pq}\le \rho ^2$ for $pq\in C^{\bar{2}}$, where $\rho$ is a hyperparameter.

(P2)

Let $\text {OPT}2(\rho )$ be the optimal value of (P2) with $\rho$. We have $\text {OPT}2(\rho )\ge \text {OPT}1$. Let $((\bar{w}^p,\bar{b}_p)_{p\in C},\bar{s})$ be an optimal solution of (P1) and $\bar{s}_{\min } = \min _{pq\in C^{\bar{2}}} \bar{s}_{pq}$. Then, $((\bar{w}^p/\sqrt{\bar{s}_{\min }},\bar{b}_p/\sqrt{\bar{s}_{\min }})_{p\in C},\bar{s}/\bar{s}_{\min })$ is also an optimal solution of (P1). If $\max _{pq\in C^{\bar{2}}} \bar{s}_{pq}/\bar{s}_{\min } \le \rho ^2$ then $((\bar{w}^p/\sqrt{\bar{s}_{\min }},\bar{b}_p/\sqrt{\bar{s}_{\min }})_{p\in C},\bar{s}/\bar{s}_{\min })$ is feasible for (P2). Therefore, it is optimal for (P2).

We replace $\sqrt{s_{pq}}$ in (P2) with $\frac{s_{pq}+\rho }{1+\rho }$, and obtain the following optimization problem.

(P3)

This is a second-order cone programming, which is a kind of convex optimization problems and can be easily solved by several software packages. Let $\text {OPT}3(\rho )$ be the optimal value of (P3) with $\rho$.

Figure 2 shows the relation between $\sqrt{s}$ and $(s+\rho )/(1+\rho )$. In the section $1\le s\le \rho ^2$, it holds that $\sqrt{s}\ge (s+\rho )/(1+\rho )$. Hence, we have $\text {OPT}3(\rho )\le \text {OPT}2(\rho )$. It leads that we obtain a lower bound of the optimal value of (P2) by solving the convex optimization problem (P3).

Fig. 2.

Approximating $\sqrt{s}$ by $(s+\rho )/(1+\rho )$ (when $\rho = 10$).

Let $((\bar{w}^p,\bar{b}_p)_{p\in C},\bar{s})$ be an optimal solution of (P3) with respect to $\rho$. For each $pq\in C^{\bar{2}}$, we define $s'_{pq} = \min _{i\in M^p\cup M^q}\left( (w^p-w^q)^{\top }x^i+b_p-b_q\right) ^2$. Remarking $1\le s'_{pq}\le \rho ^2$ for $pq\in C^{\bar{2}}$, solution $((\bar{w}^p,\bar{b}_p)_{p\in C},{s}')$ is feasible for (P2) with respect to $\rho$. We evaluate optimality of the solution $((\bar{w}^p,\bar{b}_p)_{p\in C},{s}')$. For each $pq\in C^{\bar{2}}$, the following inequality holds.

$$\begin{aligned} \frac{\Vert \bar{w}^p-\bar{w}^q\Vert ^2}{s'_{pq}}&= \frac{\Vert \bar{w}^p-\bar{w}^q\Vert ^2}{\min _{i\in M^{pq}}((\bar{w}^p-\bar{w}^q)^\top x^i + \bar{b}_p-\bar{b}_q)^2} \\&= \frac{\Vert \bar{w}^p-\bar{w}^q\Vert ^2}{\bar{s}_{pq}} \frac{\bar{s}_{pq}}{\min _{i\in M^{pq}}((\bar{w}^p-\bar{w}^q)^\top x^i + \bar{b}_p-\bar{b}_q)^2} \end{aligned}$$

$$\begin{aligned}&\le \bar{s}_{pq}\left( \frac{1+\rho }{\bar{s}_{pq}+\rho }\right) ^2 \frac{\Vert \bar{w}^p-\bar{w}^q\Vert ^2}{\bar{s}_{pq}} \\&\le \max _{1\le s \le \rho ^2} {s}\left( \frac{1+\rho }{{s}+\rho }\right) ^2 \frac{\Vert \bar{w}^p-\bar{w}^q\Vert ^2}{\bar{s}_{pq}} = \frac{(1+\rho )^2}{4\rho } \frac{\Vert \bar{w}^p-\bar{w}^q\Vert ^2}{\bar{s}_{pq}}. \end{aligned}$$

Therefore,

$$\begin{aligned} \text {OPT}2(\rho )&\le \sum _{pq\in C^{\bar{2}}} \frac{\Vert \bar{w}^p-\bar{w}^q\Vert ^2}{s'_{pq}} \le \frac{(1+\rho )^2}{4\rho } \sum _{pq\in C^{\bar{2}}}\frac{\Vert \bar{w}^p-\bar{w}^q\Vert ^2}{\bar{s}_{pq}} = \frac{(1+\rho )^2}{4\rho } \text {OPT}3(\rho ). \end{aligned}$$

We define $\theta (\rho ) = \frac{(1+\rho )^2}{4\rho }$. Consequently, the optimal value of (P2) is at most the optimal value of (P3) multiplied by $\theta (\rho )$.

Summarizing the above discussion, we have the following theorem.

Theorem 1

We have $1\le \frac{\text {OPT}\text {2}(\rho )}{\text {OPT}\text {3}(\rho )} \le \theta (\rho )$. Moreover, suppose that there exists an optimal solution $((w^p,b_p)_{p\in C},s)$ of (P1) such that $\frac{\max _{pq\in C^{\bar{2}}}s_{pq}}{\min _{pq\in C^{\bar{2}}}s_{pq}} \le \rho ^2$. Then, we have $1\le \frac{\text {OPT}\text {1}}{\text {OPT}\text {3}(\rho )} \le \theta (\rho )$.

This theorem implies that we obtain an approximation solution for (P1) and (P2) with $\rho$ by solving convex problem (P3) with $\rho$, and the ratio of approximation is at most $\theta (\rho )$.

The upper bound function $\theta$ monotonically increases with respect to $\rho$. The relationship of $\rho$ and $\theta$ is shown in Fig. 3. $\theta (\rho )$ is approximated by $\rho /4+1/2$, i.e., the upper bound of the ratio of approximation deteriorates linearly with respect to $\rho$. On the other hand, the range of $s_{pq}$ in (P2) and (P3) increases quadratically.

Fig. 3.

Function $\theta (\rho )$. $\rho \in [1,10]$.

When $\rho = 1$, (P2) and (P3) are reduced to (7). In other words, the proposed SVM is an extension of AT-SVM. Additionally, in the binary case: $C^{\bar{2}} = \{12\}$, the assumption of Theorem 1 holds for any $\rho$.

Corollary 1

For binary classification problems, we have $\text {OPT}\text {1} = \text {OPT}\text {2}(1) = \text {OPT}\text {3}(1)$.

3.3 Soft Margins

In this section, we consider a soft-margin formulation in the proposed multi-class SVM. Similarly to (8), we introduce slack variables $\xi _{ip}$ for $p\in C$ and $i\in M\setminus M^p$. The soft-margin model for (P3) is defined as follows.

(SP3)

In the same manner, we can define the soft-margin models for (P1) and (P2). Theorem 1 also holds in the soft-margin case without any modification.

The dual optimization problem of (SP3) is given as follows.

(SD3)

where $\alpha = ((\alpha _{1i})_{i\in M\setminus M^1},\dots ,(\alpha _{ci})_{i\in M\setminus M^c})$, $\beta ^{pq}\in \mathbf {R}^{n}$ for $pq\in C^{\bar{2}}$, $\gamma = (\gamma _{12},\dots ,\gamma _{1c},\gamma _{23},\dots ,\gamma _{(c-1)c})$ and $\delta = (\delta _{12},\dots ,\delta _{1c},\delta _{23},\dots ,\delta _{(c-1)c})$. In some software packages, the dual problem (SD3) can be solved more efficiently than the primal problem (SP3), since the dual problem has the smaller size of constraints², which significantly affects the speed of interior point methods. The dual problem is not a standard second-order cone programming, since $\alpha$ is included in the intersection of quadratic cones and cones of nonnegative regions. However, it is effectively handled in interior point methods.

3.4 The Proposed Method

We describe a training procedure using our SVM. It includes two phase. In the first phase, given the hyperparameters $\rho \ge 1$ and $\mu > 0$, we solve the optimization problem (SP3), and obtain $(\bar{w}^p,\bar{b}_p)_{p\in C}$ and $\bar{\xi }$. Calculate $\hat{s}_{pq}$ for $pq\in C^{\bar{2}}$:

$$\begin{aligned} \hat{s}_{pq}&= \min \{\min _{i\in M^p} \left( (\bar{w}^p-\bar{w}^q)^{\top }{x}^i + \bar{b}_p-\bar{b}_q + \bar{\xi }_{iq}\right) ^2,\\&\qquad \min _{i\in M^q} \left( (\bar{w}^q-\bar{w}^p)^{\top }x^i + \bar{b}_q-\bar{b}_p + \bar{\xi }_{ip}\right) ^2\}. \end{aligned}$$

In the second phase, we solve the soft-margin version of (P1) with $s_{pq} = \hat{s}_{pq}$ for $pq\in C^{\bar{2}}$, and obtain $(\hat{w}^p,\hat{b}_p)_{p\in C}$ and $\hat{\xi }$.

As mentioned in Introduction, Fig. 1 demonstrates that the proposed method archives larger margins than AT-SVM ($\rho =1$).

In the proposed SVM, regularization terms $\Vert w^p-w^q\Vert ^2$ are divided by $s_{pq}$. $s_{pq}$ is the minimum value of squared differences of discriminant functions $\left( f_p(x^i) - f_q(x^i)\right) ^2$ for $i\in M^p\cup M^q$. If $s_{pq}$ is large, we can say that the distance between two classes of p and q is large. In that case, the value $1/s_{pq}$ is small. Hence, the regularization by $\Vert w^p-w^q\Vert ^2$ gives little effect when the distance of two classes of p and q is large. Since the regularization term $\Vert w^p-w^q\Vert ^2$ is scaled by $s_{pq}$, we call the proposed SVM AT-SVM-SR (AT-SVM using Scaled Regularization terms).

4 Numerical Experiments

To examine generalization capability of the proposed SVM, we performed numerical experiments using 13 benchmark data sets in UCI Machine Learning Repository [5]. We compared classifiers obtained by AT-SVM-SR with $\rho = 100$ and AT-SVM (i.e. AT-SVM-SR with $\rho = 1$). To solve optimization problem (SD3), we used software package MOSEK [6]. Accuracy of classifiers was measured by 10-fold cross-validation with balancing class distribution.

We adapted the SVMs to nonlinear classification by kernel methods. The RBF kernel $k(x,y) = \exp \left( -\frac{\Vert x-y\Vert ^2}{2\sigma ^2}\right)$ was used in the experiments, where $x,y\in \mathbf {R}^n$ are input vectors and $\sigma$ is a parameter to control distances of feature vectors of examples. Furthermore, the feature vectors were projected to 200-dimensional real space by the kernel principal component analysis.

The parameter $\sigma$ of the RBF kernel was varied in $\{1,2,5,10,20,50,\dots ,1\times 10^4,2\times 10^4,5\times 10^4\}$. The hyperparameter $\mu$ of the SVMs was varied in $\{1,10,\dots ,1\times 10^4\}$.

For each benchmark data set, we performed two experiments. In one experiments, we did scaling the set of values of each variable so that the mean is 0 and the standard deviation is 1. In the other experiments, we did not that scaling.

Table 1 shows classification errors of classifiers measured in the numerical experiments. The first column shows the names of data sets with the numbers of sample examples and class labels. The next two columns show the results without scaling data sets. The last two columns show those with scaling. For each of non-scaling and scaling sections, we show the results of AT-SVM and AT-SVM-SR with $\rho = 100$. Each entry of the table shows the best (smallest) error in all of combinations of hyperparameters $\sigma$ and $\mu$. The selected values of $\sigma$ and $\mu$ following the best error. The numbers in bold type mean the best results (the smallest errors) for each dataset. In 7 data sets, whose names are shown in bold, AT-SVM-SR archived better classifiers than AT-SVM. On the other hand, in 2 data sets, whose names are shown in italic, AT-SVM archived better classifiers. We can say that the generalization capability of AT-SVM-SR is better than AT-SVM in general.

Table 1. The classification errors of AT-SVM and AT-SVM-SR with $\rho =100$. m and c in the first column indicate the numbers of objects and classes, respectively. The entry corresponding to each data set (non-scaling or scaling) and each method shows the classification error obtained by the cross validation. The selected parameters $\sigma$ and $\mu$ for each result are shown after the error.

5 Concluding Remarks

In this paper, we have proposed AT-SVM-SR, which is a new multi-class SVM derived from geometric margin maximization. In AT-SVM-SR, linear classifiers are provided by approximate solutions for the optimization problem of minimization of the sum of inverse-squared margins. Using Wine Data Set, we have demonstrated that the proposed AT-SVM-SR can obtain a classifier with larger margins comparing AT-SVM. The numerical experiments have shown that generalization capability of AT-SVM-SR outperforms that of AT-SVM in several data sets. One of the future work is detailed investigation on characteristics of AT-SVM-SR, e.g. the relationship between $\rho$ and classification accuracy.