An Overview of 2D Picture Array Generating Models Based on Membrane Computing

Abstract

A variety of two-dimensional array grammar models generating picture array languages have been introduced and investigated, utilizing and extending the well-established notions and techniques of formal string language theory. On the other hand the versatile computing model with a generic name of P system in the area of membrane computing, has turned out to be a rich framework for different kinds of problems in a variety of fields. Picture array generation in the field of two-dimensional (2D) languages is one such area where P systems with array objects and array rewriting, referred to as array P systems, have been fruitfully employed in increasing the generating power of the 2D grammar models. A variety of array P systems have been proposed in the literature. The objective of this survey is to review and describe the salient features of the major types of array P systems, which have served as the basis for developing other kinds of array P systems. Applications of these array P systems are also briefly described besides indicating possible new directions of investigation.

1 Introduction

The field of membrane computing [28, 30, 55] originated with Gh. Păun developing a new computing model around the year 2000, inspired by the structure and functioning of living cells. The basic version of this new computing model, with a generic name of P system (named in honour of the originator of this system) involves a hierarchical arrangement of membranes, one within another but all of them within one membrane, called the skin membrane and the membrane with no other membrane inside, being referred to as an elementary membrane. The regions delimited by the membranes can have objects and evolution rules. The minimal activity in a P system involves processing at the same time, the objects in all regions of the system by a nondeterministic and maximally parallel manner of application of the rules to the objects, thereby allowing the objects to evolve. The objects evolved can continue to remain in the same region or go to an adjacent region, with the communication being specified by a target indication. A computation halts when no object in all the regions can further evolve and the result of a computation is the number of objects in a specified membrane. Very many modifications and variants of the basic model of a P system have been proposed and studied but we do not enter into these details here. Instead our interest here is in a variant known as rewriting P system, initially introduced in [27] for the string case. The basic idea in a string rewriting P system is to consider the objects in the regions to be finite (structured) strings over an alphabet and the evolution rules as rewriting rules transforming a finite string in a region into another string. When the transformed string is passed through a membrane, it is sent as a whole in this kind of P system. There has been a number of investigations on rewriting P systems by several researchers (see, for example, [2,3,4, 9, 21, 22, 31]) introducing other features.

On the other hand, motivated by problems in the framework of image analysis and picture processing, several kinds of two-dimensional grammar models (see for example [17, 25, 33, 34, 45, 51] and references therein) have been introduced for picture array generation, with many of these models extending the rewriting feature in string grammars in formal language theory [35, 36]. Utilizing the rewriting rules in the two-dimensional grammar models, the string-rewriting P systems have been extended to arrays, resulting in a variety of array P systems (see for example [40]).

In this survey, some of the major types of array P systems are reviewed bringing out their constructions and their picture array generative power. Applications of the array P systems in the description of picture patterns are also indicated besides pointing out possible directions of study in future.

2 Preliminaries

We refer to [35, 36] for notions related to formal string grammars and languages. For picture array grammars and languages we refer to [15, 17] and for concepts relating to P systems to [28]. We briefly recall here certain needed notions.

An alphabet $\varSigma$ is a finite set of symbols. A word or a string $\alpha$ over $\varSigma$ is a finite sequence of symbols taken from $\varSigma$. The empty word with no symbols is denoted by $\lambda$. The set of all words over $\varSigma$ including $\lambda$, is denoted by $\varSigma ^{*}$. For any word $\alpha = a_1a_2 \ldots a_n$, we denote by ${}^t\alpha$ the word $\alpha$ written vertically, so that ${}^t\alpha = {}^t(\alpha )$.

For example, if $w = abb$ over $\{a,b\}$, then ${}^tw$ is $\begin{array}{c} a\\ b\\ b \end{array}.$

Interpreting the two-dimensional digital plane as a set of unit squares, a picture array in the two-dimensional plane (also called, simply as an array) over $\varSigma$, is composed of a finite number of labelled unit squares (also called pixels), with the labels taken from the alphabet $\varSigma .$ The set of all picture arrays over $\varSigma$ will be denoted by $\varSigma ^{**}$. The empty picture array is also denoted by $\lambda$ and $\varSigma ^{++} = \varSigma ^{**} - \{\lambda \}$. An empty unit square in the plane is indicated by the blank symbol $\# \notin \varSigma$.

A pictorial way of representing a picture array is done by showing the labels of the non-blank unit squares that constitute the picture array. For example, a picture array representing the digitized Chinese character “center” [52, p. 228] is shown in Fig. 1. Sometimes, if needed, the blank symbol is shown in some empty square but in general, we assume that the empty unit square in the plane contains this symbol even if the blank symbol is not shown. A picture array can be given in a formal manner by listing the coordinates of the non-blank unit squares of the picture array along with the corresponding labels of the unit squares. Note that a translation of the picture array in the two-dimensional plane changes only the coordinates of the unit squares of a picture array and hence only relative positions of the symbols in the non-blank unit squares are essential for describing a picture array. For example, for the picture array in Fig. 1, taking the origin (0, 0) at the lowermost non-blank unit square of the leftmost vertical line of $x's$, the coordinates of the non-blank unit squares of the picture array can be specified as follows:

$$\begin{aligned} \{ ((p,0),x), ((p,3),x) \mid 0 \le p \le 10 \} \cup \{ ((q,r),x) \mid q \in \{0,5,10\}, r \in \{1,2\} \} \end{aligned}$$

$$\begin{aligned} \cup \{((5,s),x) \mid s \in \{-1,-2,-3,4,5\}\}. \end{aligned}$$

Fig. 1

A picture array representing the chinese character “center” in digitized form

3 Array Grammars and Languages

Basically there are two types of array grammars, referred to as isometric array grammars [10,11,12, 15, 33] and non-isometric array grammars [34]. We first describe isometric array grammars. In an isometric array grammar, the geometric shape of an array is preserved while an array grammar rule is used in generating an array from another array.

3.1 Isometric Array Grammars

Analogous to the Chomsky hierarchy [35] in string grammars, there is a corresponding hierarchy [15] in the isometric array grammars. Here our interest is in the context-free type of rules which we recall now.

Definition 1

[14, 15] A context-free (CF) array grammar $G = (N, T, S, P, \#)$ , where N and T are finite sets of symbols, respectively called nonterminals and terminals with $V = N \cup T$ and N and T are disjoint. The symbol $S \in N$ is the start symbol. The set P is a finite set of array rewriting rules of the form $r:\alpha \rightarrow \beta$ where $\alpha$ and $\beta$ are arrays over $V \cup \#$ ($\#$ is the blank symbol) satisfying the following conditions:

• 1. the arrays $\alpha$ and $\beta$ have geometrically identical shapes;

• 2. exactly one square in $\alpha$ is labelled by a nonterminal in N while the remaining squares contain the blank symbol $\#$ but $\beta$ contains no blank symbol;

• 3. in rewriting $\alpha$ by $\beta$ by the rule $r:\alpha \rightarrow \beta$, the rule should be such that its application does not erase the non-blank symbols in $\alpha$ i.e a unit square with a non-blank symbol should not get replaced by the blank symbol $\#$;

• 4. the symbols of T that occur in $\alpha$ should be retained in their corresponding squares in $\beta$ while applying the rule;

• 5. the application of the rule $r:\alpha \rightarrow \beta$ should preserve the connectivity of the array in which rewriting is done.

For two arrays $\gamma , \delta$ over V and a rule r as above, we write $\gamma \Rightarrow _r \delta$ if $\delta$ can be obtained by replacing with $\beta$, a subarray of $\gamma$ identical to $\alpha .$ The reflexive and transitive closure of the relation $\Rightarrow$ is denoted by $\Rightarrow ^*$.

A CF array grammar is called regular, if the rules are of the following forms:

where A, B are nonterminals and a is a terminal.

The picture array language generated by G is

$$L(G)= \{\mathcal {A} \mid S \Rightarrow ^* \mathcal {A} \in T^{++} \}.$$

Note that the start array is indeed $\{((0,0), S)\}$ and it is understood that this square labelled S is surrounded by $\#$, denoting empty squares with no labels. We denote by L(AREG) and L(ACF) respectively the families of array languages generated by array grammars with regular and context-free array rewriting rules.

We illustrate with an example.

Example 1

Consider the context-free array grammar $G_p$ with rules

where S, A, B, C are nonterminals and a is a terminal. This grammar generates arrays with three arms over $\{ a \}$, but with the arms not necessarily of equal length where the length equals the number of $a's$ in an arm. In a derivation starting with S, the rule (1) is applied once. In other words, the first step of the derivation is as follows:

This can then be followed, for example, by the application of the rule (2) as many times as needed, thus growing the vertical upper arm and the growth can be terminated with an application of the rule (5). For example, if the rule (2) is applied twice, then the derivation takes place as follows:

Likewise, the horizontal right or left arm can be grown by the respective application of the rules (3), (4). Again the growth in these arms can be terminated by the respective application of the rules (6), (7), thus yielding an array in the form of the digitized Math symbol of perpendicularity (Fig. 2).

Fig. 2

A picture array representing the math symbol for perpendicularity in digitized form

It is known that analogous to the string case, CF array grammars are more powerful than regular array grammars in generating picture array languages.

Theorem 1

[5, 15] $L(AREG) \subset L(ACF).$

The inclusion is straightforward from the Definition 1 while the strict inclusion is seen by observing that the picture array language in Example 1 cannot be generated by regular array grammar rules as the rewriting in a regular array grammar cannot handle all three arms at the “junction” in the Fig. 2. In fact only two of the three arms can be generated by regular array grammar rules due to the nature of the rules.

Remark 1

Generation of geometric figures such as rectangles and squares by array grammars has been a problem of interest. One of the earliest studies in this direction has been done in [50]. Although regular array grammars have the simplest kind of rules and hence cannot have high generating power, it is interesting to note that Yamamoto, Morita and Sugata [50] have constructed regular array grammars for generating picture languages of rectangles and squares, utilizing the ability of the regular array grammars in sensing the blank symbol $\#$.

While context-free array grammar is an extension to two-dimensions of context-free string grammar of the Chomsky hierarchy [35], contextual array grammar [16] is an extension of the contextual string grammars [26] introduced by Marcus [24]. We now recall the definition of a two-dimensional contextual array grammar [16]. For our purposes of later relating this study to array P systems we consider the restriction as in [13], with the “selector” and the “context” being connected and labelled by only symbols from an alphabet and not the blank symbol $\#$ amounting to the case of the selector and the context having no empty unit squares.

Definition 2

[26] A contextual array grammar (CAG) is a construct $G= \left( V, P, A\right)$ where V is an alphabet, A is a finite set of axioms which are two-dimensional arrays in $V^{++}$ and P is a finite set of array contextual rules of the form $\left( \alpha , \beta \right)$ where

(i):

$\alpha$ is a function defined on $U_{\alpha }\subset \mathcal {Z\times Z}$ with values in V and $\left( U_\alpha , \alpha \right)$ is called the selector and $U_\alpha$, the selector area of the production $\left( \alpha , \beta \right) ;$ (Here $\mathcal {Z}$ is the set of all integers);

(ii):

$\beta$ is a function defined on $U_{\beta }\subset \mathcal {Z \times Z}$ with values in V where $\left( U_\beta , \beta \right)$ is called the context and $U_\beta$, the context area of the production $\left( \alpha , \beta \right)$;

(iii):

$U_{\alpha }$ and $U_{\beta }$ are finite and disjoint.

For arrays $\mathcal {C}_{1},\mathcal {C} _{2}\in V^{++}$, and a contextual rule $p:\left( \alpha , \beta \right)$, we have a derivation, denoted by $\mathcal {C} _{1} \Longrightarrow _{p} \mathcal {C} _{2}$, if in $\mathcal {C} _1$ we can find a sub-array that corresponds to the selector $\left( U_\alpha , \alpha \right)$, and if the positions corresponding to $\left( U_\beta , \beta \right)$ are labelled only by the blank symbol $\#$, so that we can add the context $\left( U_\beta ,\beta \right)$, thus obtaining $\mathcal {C} _2$. We then say that $\mathcal {C} _{2}$ is derivable from $\mathcal {C} _{1}$ and we write $\mathcal {C} _{1} \Longrightarrow _G \mathcal {C} _{2}.$ We denote the reflexive transitive closure of $\Longrightarrow _{G}$ by $\Longrightarrow _{G}^{*}.$ A t-mode of derivation, denoted by $\Longrightarrow _{G}^{t}$, is defined for arbitrary arrays $\mathcal {A}, \mathcal {B} \in V^{++}$ in the following manner: $\mathcal {A} \Longrightarrow _{G}^{t} \mathcal {B}$ if and only if $\mathcal {A} \Longrightarrow _{G}^{*} \mathcal {B}$ and there is no $\mathcal {C} \in V^{++}$ such that $\mathcal {B} \Longrightarrow _{G} \mathcal {C}.$ The picture array language generated by a CAG G in the t-mode is defined as follows:

$$ \begin{array}{lcl} L_{t}\left( G\right)= & {} \left\{ \mathcal {B}\in V^{++} \mid \mathcal {A}\Longrightarrow _{G}^{t}\mathcal {B} \text{ for } \text{ some } \mathcal {A}\in A\right\} . \end{array} $$

For a given CAG G, the t-mode (also called maximal mode) corresponds to collecting only the arrays produced by derivations which cannot be continued at some stage. On the other hand, in the $*$ -mode of derivation, all pictures derivable from an axiom are taken in the picture language generated. We consider here mainly the t-mode of derivation. The family of picture languages generated by contextual array grammars of the form $G = \left( V, P, A \right)$ in the t-mode will be denoted by $\mathcal {L}\left( cont, t\right)$.

We give an example illustrating the working of a contextual array grammar in t-mode, which generates an array language L consisting of picture arrays of solid squares of odd side length $4n-1, n \ge 1$, in the form as shown in Fig. 3 for $n = 2$, with the central square labelled c, surrounded by a single “layer” of $a'$s followed by a single “layer” of $c'$s and again followed by a single “layer” of $a'$s.

Fig. 3

A $5\times 5$ solid square with c in its central position

Example 2

Let $G= \left( \left\{ a, c\right\} ,P,A\right)$ be a contextual array grammar with A containing two axiom picture arrays $A_1, A_2$, which are given in pictorial form.

$$\begin{aligned}&A_1 := \begin{array}{ccc} a &{} a &{} a \\ a &{} c &{} a \\ a &{} a &{} a \end{array} ,\,\,A_2 := \begin{array}{ccc} c &{} &{} \\ a &{} a &{} a \\ a &{} c &{} a \\ a &{} a &{} a \end{array} \end{aligned}$$

Since the selector area $U_{\alpha }$ and the context area $U_{\beta }$ are disjoint in a contextual array production, the rules can be represented by patterns where the unit squares and symbols of the selector are indicated by enclosing these in boxes. The rules are defined as follows:

$$p_1 := \begin{array}{ccc} \fbox {c} &{} c &{} \\ \fbox {a} &{} \fbox {a} &{} \fbox {a} \\ \end{array} ,\,\,p_2 := \begin{array}{ccc} \fbox {c} &{} c &{} c \\ \fbox {a} &{} \fbox {a} &{} c \\ \end{array} ,\,\,p_3 := \begin{array}{cc} \fbox {a} &{} \fbox {c}\\ \fbox {a} &{} c \\ \fbox {a} &{} \\ \end{array} ,\,\,p_4 := \begin{array}{cc} \fbox {a} &{} \fbox {c}\\ \fbox {a} &{} c \\ c &{} c \\ \end{array},$$

$$p_5 := \begin{array}{ccc} \fbox {a} &{} \fbox {a} &{} \fbox {a} \\ &{} c &{} \fbox {c}\\ \end{array} ,\,\,p_6 := \begin{array}{ccc} c &{} \fbox {a} &{} \fbox {a} \\ c &{} c &{} \fbox {c}\\ \end{array} ,\,\,p_{7} := \begin{array}{cc} &{} \fbox {a} \\ c &{} \fbox {a} \\ \fbox {c} &{} \fbox {a} \\ \end{array} ,\,\,p_{7}^\prime := \begin{array}{cc} &{} \fbox {c} \\ c &{} \fbox {a} \\ \fbox {c} &{} \fbox {a} \\ \end{array} ,\,\,p_{8} := \begin{array}{cc} a&{} \\ c &{} \fbox {c} \\ \fbox {c} &{} \fbox {a} \\ \end{array},\,$$

$$r_1 := \begin{array}{ccc} \fbox {a} &{} a &{} \\ \fbox {c} &{} \fbox {c} &{} \fbox {c} \\ \end{array} ,\,\,r_2 := \begin{array}{ccc} \fbox {a} &{} a &{} a \\ \fbox {c} &{} \fbox {c} &{} a \\ \end{array} ,\,\,r_3 := \begin{array}{cc} \fbox {c} &{} \fbox {a}\\ \fbox {c} &{} a \\ \fbox {c} &{} \\ \end{array} ,\,\,r_4 := \begin{array}{cc} \fbox {c} &{} \fbox {a}\\ \fbox {c} &{} a \\ a &{} a \\ \end{array}, ,\,\, r_5 := \begin{array}{ccc} \fbox {c} &{} \fbox {c} &{} \fbox {c} \\ &{} a &{} \fbox {a}\\ \end{array}$$

$$ r_6 := \begin{array}{ccc} a &{} \fbox {c} &{} \fbox {c} \\ a &{} a &{} \fbox {a}\\ \end{array} ,\,\,r_{7} := \begin{array}{cc} &{} \fbox {c} \\ a &{} \fbox {c} \\ \fbox {a} &{} \fbox {c} \\ \end{array} ,\,\,r_{7}^\prime := \begin{array}{cc} &{} \fbox {a} \\ a &{} \fbox {c} \\ \fbox {a} &{} \fbox {c} \\ \end{array} ,\,\,r_{8} := \begin{array}{cc} c&{} \\ a &{} \fbox {a} \\ \fbox {a} &{} \fbox {c} \\ \end{array} ,\,\,r_{9} := \begin{array}{cc} a &{} \fbox {a} \\ \fbox {a} &{} \fbox {c} \\ \end{array} \,. $$

A maximal (that is, t-mode) derivation in G generating a $7 \times 7$ picture array of the language $L_1$ is shown below:

$$\begin{matrix} c &{} &{} \\ a &{} a &{} a \\ a &{} c &{} a\\ a &{} a &{} a \end{matrix} \,\Longrightarrow _{p_1}\, \begin{matrix} c &{} c &{} \\ a &{} a &{} a \\ a &{} c &{} a\\ a &{} a &{} a \end{matrix} \,\Longrightarrow _{p_2}\, \begin{matrix} c &{} c &{} c &{} c \\ a &{} a &{} a &{} c \\ a &{} c &{} a &{} \\ a &{} a &{} a &{} \end{matrix} \,\Longrightarrow _{p_3}\, \begin{matrix} c &{} c &{} c &{} c \\ a &{} a &{} a &{} c \\ a &{} c &{} a &{} c \\ a &{} a &{} a &{} \end{matrix} \,\Longrightarrow _{p_4}\, \begin{matrix} c &{} c &{} c &{} c \\ a &{} a &{} a &{} c \\ a &{} c &{} a &{} c \\ a &{} a &{} a &{} c \\ &{} &{} c &{} c \end{matrix} $$

$$\,\Longrightarrow _{p_5}\, \begin{matrix} c &{} c &{} c &{} c \\ a &{} a &{} a &{} c \\ a &{} c &{} a &{} c \\ a &{} a &{} a &{} c \\ &{} c &{} c &{} c \end{matrix} \,\Longrightarrow _{p_6}\, \begin{matrix} &{} c &{} c &{} c &{} c \\ &{} a &{} a &{} a &{} c \\ &{} a &{} c &{} a &{} c \\ c &{} a &{} a &{} a &{} c \\ c &{} c &{} c &{} c &{} c \end{matrix} \,\Longrightarrow _{p_7}\, \begin{matrix} &{} c &{} c &{} c &{} c \\ &{} a &{} a &{} a &{} c \\ c &{} a &{} c &{} a &{} c \\ c &{} a &{} a &{} a &{} c \\ c &{} c &{} c &{} c &{} c \end{matrix} \,\Longrightarrow _{p_7^\prime }\, \begin{matrix} &{} c &{} c &{} c &{} c \\ c&{} a &{} a &{} a &{} c \\ c &{} a &{} c &{} a &{} c \\ c &{} a &{} a &{} a &{} c \\ c &{} c &{} c &{} c &{} c \end{matrix} \,\Longrightarrow _{p_8}\, \begin{matrix} a &{} &{} &{} &{} \\ c &{} c &{} c &{} c &{} c \\ c &{} a &{} a &{} a &{} c \\ c &{} a &{} c &{} a &{} c \\ c &{} a &{} a &{} a &{} c \\ c &{} c &{} c &{} c &{} c \end{matrix}\,\, $$

$$\Longrightarrow _{r_1}\, \begin{matrix} a &{}a &{} &{} &{} \\ c &{} c &{} c &{} c &{} c \\ c &{} a &{} a &{} a &{} c \\ c &{} a &{} c &{} a &{} c \\ c &{} a &{} a &{} a &{} c \\ c &{} c &{} c &{} c &{} c \end{matrix}\,\, \Longrightarrow _{r_1}\, \begin{matrix} a &{} a&{}a &{} &{} \\ c &{} c &{} c &{} c &{} c \\ c &{} a &{} a &{} a &{} c \\ c &{} a &{} c &{} a &{} c \\ c &{} a &{} a &{} a &{} c \\ c &{} c &{} c &{} c &{} c \end{matrix} \,\, \Longrightarrow _{r_2}\, \begin{matrix} a &{} a&{}a &{} a&{} a&{}a\\ c &{} c&{} c &{} c &{} c&{}a \\ c &{} a &{} a &{} a &{} c&{} \\ c &{} a &{} c &{} a &{} c &{}\\ c &{} a &{} a &{} a &{} c &{}\\ c &{} c &{} c &{} c &{} c&{} \end{matrix} \,\, \Longrightarrow _{r_3}\, \begin{matrix} a &{} a&{}a &{} a&{} a &{}a\\ c &{} c&{} c &{} c &{} c &{}a\\ c &{} a &{} a &{} a &{} c &{}a\\ c &{} a &{} c &{} a &{} c&{} \\ c &{} a &{} a &{} a &{} c &{}\\ c &{} c &{} c &{} c &{} c&{} \end{matrix} $$

The derivation proceeds in this way due to the t-mode of derivation and halts when no rule is applicable. The resulting array is collected in the picture language of the CAG.

3.2 Non-isometric Array Grammars

We review here a basic non-isometric array grammar model introduced in [37] and extensively studied by different researchers and another comparatively recent model, which has been introduced in [41] and investigated in [1]. In these models, the picture arrays considered are rectangular arrays with the symbols defining a picture array being arranged in rows and columns. We first recall the two-dimensional grammar model (originally named as 2D matrix grammar [37]), which we call here as two-dimensional context-free grammar (2CFG), consistent with the terminology used in [17].

Definition 3

[17] A two-dimensional context-free grammar (2CFG) is $G = (V_h,V_v,V_i,T,S,R_h,R_v)$, where $V_h, V_v, V_i$ are finite sets of symbols, respectively called as horizontal nonterminals, vertical nonterminals and intermediate symbols; $V_i \subset V_v;$ T is a finite set of terminals; $S \in V_h$ is the start symbol; $R_h$ is a finite set of context-free rules of the form $X \rightarrow \alpha$, $X \in V_h, \alpha \in (V_h \cup V_i)^* ;$ $R_v$ is a finite set of right-linear rules of the form $X \rightarrow aY$ or $X \rightarrow a$, $X,Y \in V_i, a\in T \cup \{\lambda \}.$

When the rules in $R_h$ are regular grammar rules, then the 2CFG is called a two-dimensional right-linear grammar (2RLG).

There are two phases of derivation in a 2CFG. Starting with S, the context-free rules are applied in the first horizontal phase, generating strings over intermediates, which act as terminals of this first phase. The intermediate symbols in a string generated in the first phase, serve as the start symbols for the second vertical phase. The right-linear rules are applied in parallel to this string of intermediates in the second phase for generating the columns of the rectangular arrays over terminals. In this phase at a derivation step, either all the rules applied are of the form $X \rightarrow aY, \, a \in T$ or all the rules are of the form $X \rightarrow Y$ or all the rules are the terminating vertical rules of the form $X \rightarrow a, \, a \in T$ or all are of the form $X \rightarrow \lambda$. When the vertical generation halts, the picture array obtained over T, is collected in the picture language generated by the 2CFG. Note that the picture language generated by a 2CFG consists of rectangular arrays of symbols. We denote by L(2CFG), the family of picture array languages generated by two-dimensional context-free grammars and by L(2RLG), the family of picture array languages generated by two-dimensional right-linear grammars.

We illustrate the working of 2RLG with an example.

Example 3

We consider the 2RLG $G_1$ having in the first phase, the horizontal regular rules $S \rightarrow AX, X \rightarrow BY, Y \rightarrow AZ, Z \rightarrow B$ where A, B are the intermediate symbols and in the second phase the vertical right-linear rules $1: A \rightarrow aC, 2: C \rightarrow bC, 3: C \rightarrow bD, 4: D \rightarrow a, 5: B \rightarrow aB, 6: B \rightarrow a$ where a, b are the terminal symbols. The derivation in the first phase is as in a string grammar. The horizontal rules generate words of the form $ABA^nB, \, n \ge 1.$ In the second phase every symbol in such a word $ABA^nB$ is rewritten in parallel either by using the right-linear nonterminal rules rules 1 and 5 adding a row of the form $a^{n+3}$ followed by using the rules 2 or 3 and 5 adding a row of the form $bab^na.$ When the terminal rules 4 and 6 are applied in parallel, the derivation terminates adding a row of the form $a^{n+3}$ thus generating a rectangular picture array. Such a picture array for $n = 3$ is shown in Fig. 4. In fact, for this picture array, the derivation in the second phase is as follows:

$$\begin{array}{cccccc} A&B&A&A&A&B \end{array} \Rightarrow \begin{array}{cccccc}a &{} a &{} a &{} a &{} a &{} a \\ C&{}B&{}C&{}C&{}C&{}B \end{array} \Rightarrow \begin{array}{cccccc}a &{} a &{} a &{} a &{} a &{} a \\ b &{} a &{} b &{} b &{} b &{} a \\ C&{}B&{}C&{}C&{}C&{}B \end{array}$$

$$ \Rightarrow \begin{array}{cccccc}a &{} a &{} a &{} a &{} a &{} a \\ b &{} a &{} b &{} b &{} b &{} a \\ b &{} a &{} b &{} b &{} b &{} a \\ C&{}B&{}C&{}C&{}C&{}B \end{array} \Rightarrow \begin{array}{cccccc}a &{} a &{} a &{} a &{} a &{} a \\ b &{} a &{} b &{} b &{} b &{} a \\ b &{} a &{} b &{} b &{} b &{} a \\ b &{} a &{} b &{} b &{} b &{} a \\ D&{}B&{}D&{}D&{}D&{}B \end{array} \Rightarrow \begin{array}{cccccc} a &{} a &{} a &{} a &{} a &{} a \\ b &{} a &{} b &{} b &{} b &{} a \\ b &{} a &{} b &{} b &{} b &{} a \\ a &{} a &{} a &{} a &{} a &{} a\end{array} $$

The rules used are 1, 5 once, followed by 2, 5 two times, followed by 3, 5 once and finally 4, 6 once. Note that, if we interpret the symbol b as the blank symbol, then the picture array in Fig. 4a corresponds to the digitized form of the letter D over the symbol a Fig. 4b.

Fig. 4

i A picture array generated in Example 3 ii Digitized form of symbol D

An extension of the 2CFG (resp., 2RLG) which we call here as the two-dimensional tabled context-free grammar (2TCFG) (resp., tabled right-linear grammar (2TRLG)) was introduced in [39] (originally called as 2D tabled matrix grammar in [39]) to generate picture languages that cannot be generated by any 2CFG (resp., 2RLG). This kind of two-dimensional grammar is defined similar to 2CFG (resp., 2RLG) except that in the second phase, the right-linear rules are grouped into different sets, called tables such that (i) all the rules in a table are nonterminal rules of the form either $A \rightarrow aB$ only or $A \rightarrow B$ only or (ii) all are terminal rules of the form either $A \rightarrow a$ only or $A \rightarrow \lambda$ only and in the parallel derivation in the vertical direction, at a time rules in a single table are used. We denote by L(2TCFG) (resp., L(2TRLG)) the family of picture array languages generated by two-dimensional tabled context-free (resp., right-linear) grammars.

Another non-isometric array grammar model which is simple to handle yet expressive, is pure 2D context-free grammar introduced in [41] and subsequently investigated in [1]. We recall this 2D model now.

Definition 4

[41] A pure 2D context-free grammar (P2DCFG) is a 4-tuple

$$\begin{aligned} G = (\varSigma , P_1, P_2, \mathcal {M}_0) \end{aligned}$$

where

• (i) $\varSigma$ is a finite set of symbols;

• (ii) $P_1 = \{ c_i \mid 1 \le i \le p \}$, where $c_i$, called a column rule table, is a finite set of context-free rules of the form $a \rightarrow \alpha , a \in \varSigma , \alpha \in \varSigma ^*$ satisfying the condition that for any two rules $a \rightarrow \alpha , b \rightarrow \beta$ in $c_i$, $\alpha$ and $\beta$ have equal length;

• (iii) $P_2 = \{ r_j \mid 1 \le j \le q \}$, where $r_j$, called a row rule table, is a finite set of rules of the form $c \rightarrow {}^t\gamma , c \in \varSigma , \gamma \in \varSigma ^*$ such that for any two rules $c \rightarrow {}^t\gamma , d \rightarrow {}^t\delta$ in $r_j$, $\gamma$ and $\delta$ have equal length;

• (iv) $\mathcal {M}_0 \subseteq \varSigma ^{**} - \{ \lambda \}$ is a finite set of axiom arrays.

A derivation in a P2DCFG G is defined as follows: Let $A,B \in \varSigma ^{**}.$ The picture array B is derived in G from the picture array A, denoted by $A \Rightarrow B$, if B is obtained from A either (i) by rewriting in parallel all the symbols in a column of A, by rules in some column rule table or (ii) rewriting in parallel all the symbols in a row of A, by rules in some row rule table. All the rules used to rewrite a column (or a row) at a time should belong to the same table.

The picture language generated by G is the set of picture arrays $L(G) = \{M \in \varSigma ^{**} \mid M_0 \Rightarrow ^* M$ for some $M_0 \in \mathcal {M}_0 \}.$ The family of picture languages generated by P2DCFGs is denoted by L(P2DCFG).

Example 4

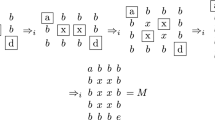
Consider the P2DCFG $G_2 = (\varSigma , P_1, P_2, \{M_0\})$ where $\varSigma = \{a,b,c,d \}$, $P_1 = \{c_t \}, P_2 = \{r_t \}$, where $c_t = \{a \rightarrow bab, c \rightarrow ada\},$ $r_t = \left\{ a \rightarrow \begin{array}{c} b\\ a\\ b \end{array}, d \rightarrow \begin{array}{c} a\\ c\\ a \end{array} \right\}$, and $M_{0} = \begin{array}{ccc} b&{}a&{}b \\ a&{}c&{}a \\ b&{}a&{}b \end{array}$. It can be seen that starting with the axiom array, the column table $c_t$ alone is applicable,which can be followed by an application of the row table $r_t$ only, giving a derivation as shown below:

$$\begin{array}{ccc} b&{}a&{}b \\ a&{}c&{}a\\ b&{}a&{}b \end{array} \Rightarrow \begin{array}{ccccc} b&{}b&{}a&{}b&{}b\\ a&{}a&{}d&{}a&{}a\\ b&{}b&{}a&{}b&{}b \end{array} \Rightarrow \begin{array}{ccccc} b&{}b&{}a&{}b&{}b\\ b&{}b&{}a&{}b&{}b\\ a&{}a&{}c&{}a&{}a\\ b&{}b&{}a&{}b&{}b\\ b&{}b&{}a&{}b&{}b \end{array}$$

Remark 2

It has been shown in [41] that the family L(P2DCFG) is incomparable with the family L(2CFG) (Definition 3) but is not disjoint with it.

4 P Systems for Picture Arrays

We now review the array P system models that have been proposed for handling picture array languages. In recent years, construction of rewriting P systems for the generation of two-dimensional picture languages has received more attention (see, for example, [40]). We consider here mainly the array-rewriting P systems that are based on the array grammar models reviewed in Sect. 3.

4.1 Array-Rewriting P System

The array P system introduced in [5] linked the two areas of membrane computing and picture grammars and is one of the earliest models in this direction, which has stimulated further research in the area of array P systems. We now review this system.

Definition 5

[5] An array-rewriting P system of degree $m\ge 1$ is a construct

$$\varPi =(V,T,\#,\mu ,F_1,\dots ,F_m, R_1,\dots ,R_m,i_o),$$

where

• (i) V is an alphabet;

• (ii) $T\subseteq V$ is the terminal alphabet;

• (iii) $\# \notin V$ is the blank symbol;

• (iv) $\mu$ is a membrane structure with m membranes labelled in a one-to-one correspondence with $1,2,\dots ,m$;

• (v) $F_i, \, 1 \le i \le m$ is a finite set of axiom arrays over V in the region $i, \, 1 \le i \le m$;

• (vi) $R_i, \, 1 \le i \le m$ is a finite set of context-free array rewriting rules over V in the region $i, \, 1 \le i \le m$ with the rules having attached targets here, out, in; and

• (vii) $i_o$ is the label of an elementary membrane of $\mu$, called the output membrane.

Here we consider array-rewriting P systems with context-free (CF) or regular (REG) array-rewriting rules.

A computation in an array-rewriting P system is defined analogous to the computation in a string rewriting P system [27]. But halting computations are considered as successful computations. Each array in every region of the system, that can be rewritten by a rule in that region, should be rewritten and the rewriting is sequential at the level of arrays in the sense that only one rule is applied to an array. The target associated with the rule used in rewriting an array decides to which region (immediately inner or immediately outer or the same region) the generated array is sent and these are indicated by the targets in, out, here. In fact here means that the array remains in the same region, out means that the array exits the current membrane (but if the rewriting was done in the skin membrane, then it exits the system and is “lost” in the environment) and in means that the array is immediately sent to one of the directly lower membranes, nondeterministically chosen if several there exist and if no internal membrane exists, then a rule with the target indication in cannot be used. A computation is successful only if it stops in the sense that no rule can be applied to the existing arrays in any of the regions. The result of an halting computation consists of the picture arrays composed only of symbols from T collected in the membrane with label $i_o$ in the halting configuration. The set of all such picture arrays generated or computed by an array-rewriting P system $\varPi$ is denoted by $AL(\varPi )$.

The family of all picture array languages $AL(\varPi )$ generated by such systems $\varPi$, with at most m membranes and with rules of type $\alpha \in \{REG, CF\}$ is denoted by $EAP_m(\alpha )$; if we have $V=T$ (referred to as non-extended systems), we ignore the condition to have at least one nonterminal unit square in the left hand side of rules and the family of picture languages in this case is written as $AP_m(\alpha )$.

We give an example of an array-rewriting P system with regular array grammar rules in the regions, generating a picture array language $L_p$ consisting of picture arrays representing the Math symbol of perpendicularity as in Fig. 2 but with all three “arms” of equal length, i.e., the number of symbols a in the middle vertical line equals the number of symbols in the horizontal bottom line in the portion to the right or to the left counting from the symbol in the “junction”.

Example 5

Consider the array-rewriting P system

$$\varPi _p = (\{A,B,B^\prime ,C,D,a\},\{a\},\#, [_1 [_2 [_3 \ ]_3 ]_2 ]_1, F_1,\emptyset ,\emptyset ,R_1,R_2,R_3,3),$$

where

In a computation in $\varPi _p$, only region 1 has an axiom array and so an application of the rewriting rule in region 1, to this array grows the middle column vertically up by one symbol a and the generated array is sent to region 2 due to the target indication in. In region 2, an application of the rule for B in this region, grows the bottommost horizontal arm to the right by one symbol and the array is sent to region 3. An application of the rule $\#\,\,\,C\rightarrow C\,\,\,a(out)$, grows the bottommost horizontal arm by one symbol to the left and the array is sent back to region 2 where the primed symbol $B^\prime$ is changed into B after which the array is sent back to region 1. The process can be repeated. If in region 3, the rule applied is $C\rightarrow D\,\,\,a$, then the array remains in the same region so that the application of the terminal rules $A\rightarrow a,B^\prime \rightarrow a,D\rightarrow a$ generates a picture array over a in the output region 3. The picture array is then collected in the language of the system. Note that in region 3, if $A, B^\prime$ are changed into a prior to an application of a rule for C and the nonterminal rule $\#\,\,\,C\rightarrow C\,\,\,a(out)$, is applied, then the array is sent to region 2 and remains stuck there. Note also that the lengths of the vertical arm, the left horizontal arm and the right horizontal arm of the picture array generated are of equal length.

In [5], the generative power of the array-rewriting P system is investigated in a very general sense. Since we are concerned here with array-rewriting P system mainly with CF or regular array grammar rules, we state a result on the generative power of the array-rewriting P system with only regular array grammar (Definition 1) rules in order to show the power of such array-rewriting P systems.

Theorem 2

[5] $EAP_3(REG) - ACF \ne \emptyset .$

The picture array language in Example 5 is in $EAP_3(REG)$ but it can be seen that this language $L_p$ cannot be generated by any context-free array grammar as in Definition 1 in view of the fact that the growth in the arms of the picture arrays of the language $L_p$ can take place independently on using context-free array grammar rules and cannot be controlled.

Remark 3

Recently, in [29], rewriting in parallel mode was employed on the arrays in the regions of the array-rewriting P system (Definition 5) and the constructions in [42] were improved in [29] resulting in a reduction in the number of membranes used.

4.2 Contextual Array P System

We now review an array P system which is based on contextual array grammar kind of rules and the method of application of the rules as described in Definition 2.

Definition 6

[13] A contextual array P system with $m\ge 1$ membranes is a construct

$$\varPi =(V,\#,\mu ,A_1,\dots ,A_m, P_1,\dots ,P_m,i_o),$$

where

• (i) V is an alphabet;

• (ii) $\# \notin V$ is the blank symbol;

• (iii) $\mu$ is a membrane structure with m membranes labelled in a one-to-one correspondence with $1,2,\dots ,m$;

• (iv) $A_i, \, 1 \le i \le m$ is a finite set of axiom arrays over V in the region $i, \, 1 \le i \le m$;

• (v) $P_i,\, 1 \le i \le m$ is a finite set of array contextual rules over V as in Definition 2; the rules have attached targets here, out, in $_j$, $1 \le j \le m$ or in and

• (vi) $i_o$ is the label of an elementary membrane of $\mu$, called the output membrane.

A computation in a contextual array P system is done analogous to the array-rewriting P system (Definition 5) again with the halting computations defined as successful computations. For each array $\mathcal {A}$ in each region of the system, if an array contextual rule p in the region, nondeterministically chosen can be applied to $\mathcal {A}$, then it should be applied and the application of a rule is sequential at the level of arrays. The resulting array, if any, is sent to the region indicated by the target associated with the rule used interpreting the attached target here, in, out in the usual manner as described in Definition 5. Also, $in_j$ is a target indication which means that the array is immediately sent to the directly lower membrane with label j. A computation is successful only if it stops such that a configuration is reached where no rule can be applied to the existing arrays. The result of a halting computation consists of the arrays collected in the membrane with label $i_o$ in the halting configuration. The set of all such arrays computed or generated by a system $\varPi$ is denoted by $CAL(\varPi )$. The family of all picture array languages $CAL(\varPi )$ generated by systems $\varPi$ as mentioned above, with at most m membranes, is denoted by $AP_m(cont)$.

Example 6

[13] Let $L_ l$ be a picture language consisting of arrays describing the digitized shape of the letter L with each square labelled by $\mathtt {a}$ except for the one in the uppermost position of the vertical arm which is labelled by $\mathtt {b}$ and both the arms having equal length i.e. equal number (at least three) of unit squares. A member of $L_l$ is shown in Fig. 5. A contextual array P system $\varPi _{l}$ with 2 membranes can generate $L_{l}$ and is given by $\varPi _{l} = (\{a, b\}, \#, \mu , A_1, A_2, P_1, P_2, 2)$ where $\mu = [_1\,[_ 2\,]_2\,]_1$ and $A_1 := \left\{ {\begin{matrix} a &{} \\ a &{} a \end{matrix}}\right\}$, $A_2 := \emptyset$. The rules are as follows:

Fig. 5

A picture array describing the digitized shape L

Starting from the axiom array ${\begin{matrix} a &{} \\ a&{} a \end{matrix}}$ in membrane 1, the rule $p_1$ is applied adjoining the context $\mathtt {a}$ to the selector $\mathtt {a}\,\mathtt {a}$ and then the resulting array ${\begin{matrix} a&{} &{} \\ a &{} a &{} a \end{matrix}}$ is sent to membrane 2 due to the target indication in attached to $p_1.$ Note that there is no initial array in membrane 2. If the rule $p_{2,1}$ is applied in membrane 2, then the context $\mathtt {a}$ will be adjoined resulting in the array ${\begin{matrix} a &{} &{} \\ a &{} &{} \\ a &{} \mathtt {a}&{} a \end{matrix}}$ which is sent back to membrane 1, due to the target indication out in rule $p_{2,1}^{}$. The rule $p_1$ in membrane 1, can now be applied and the resulting array is sent again to membrane 2. The process can be repeated. If rule $p_{2,2}$ is applied in membrane 2, then the uppermost square is “filled” with $\mathtt {b}$ and the picture remains in membrane 2 due to the target indication here. Note that the number of symbols in both the horizontal and vertical arms of the resulting L shaped picture will be the same so that the arms are of equal length (of at least three). Hence, only arrays from $L_l$ can be produced and all arrays of $L_l$ can be produced in this way.

We now state comparison results established in [13] for small number of membranes in contextual array P systems.

Theorem 3

$\mathcal {L}\left( cont,t\right) \,\subset \, AP_2(cont)$ where $\mathcal {L}\left( cont,t\right)$ is defined in Definition 2.

Theorem 4

$AP_2(cont)\,\subset \, AP_3(cont).$

An interesting result established in [13] is now stated which shows the existence of a proper infinite hierarchy with respect to the classes of languages described by contextual array P systems.

Theorem 5

For every $k \ge 1$, $AP_k(cont) \subset AP_{3k}(cont).$

5 Sequential/Parallel Array P Systems

Here we recall array P systems, called sequential / parallel array P systems [46], having the objects in the membranes as rectangular arrays and the rules as 2CFG or 2RLG type of rules as described in Definition 3.

Definition 7

[46] A sequential / parallel array P system of degree $m \ge 1$ is a construct $\pi = ( V_{1} \cup V_{2}, I, T, \mu , F_{1}, \cdots , F_{M}, R_{1},\cdots , R_{M}, i_{0})$ where

• (i) $V = V_{1}\cup V_{2}$ is an alphabet, $V_{1}- I$ is the set of horizontal nonterminals, $I \subseteq V_{1}$ is the set of intermediates, $V_{2} - T$ is the set of vertical non-terminals, $T \subseteq V_{2}$ is the set of terminals, $V_{2} - T$ includes the elements of I;

• (ii) $\mu$ is a membrane structure with m membranes labeled in a one-to-one manner with $1, 2, \cdots , m$;

• (iii) $F_{1},\cdots , F_{m}$ are finite sets (can be empty) of axiom strings in the regions of $\mu$ where horizontal rules are present; the regions where vertical rules are present, are initially empty;

• (iv) $R_{1},\cdots , R_{m}$ are finite sets of rules as in Definition 3 associated with the m regions of $\mu$; the rules can be either context free rules (called horizontal rules) of the form $A \rightarrow \alpha$, $A \in V_{1} - I,\, \alpha \in V_{1}^{*}$ or sets of right-linear nonterminal rules (called vertical nonterminal rules) of the form $X \rightarrow aY, X, Y \in V_{2} - T, \, a \in T \cup \{\lambda \}$ or sets of right-linear terminal rules (called vertical terminal rules) of the form $X \rightarrow a,\, X \in V_{2} - T,\, a \in T \cup \{\lambda \}$. The horizontal CF rules can be, in particular, regular rules of the form $A \rightarrow aB,\, A \rightarrow a, \, A \in V_{1}-I,\, w \in I^{*}.$ Horizontal rules and sets of vertical rules have attached targets, here, out, in (in general, here is omitted). A membrane has either horizontal rules or sets of vertical rules; horizontal rules are applied in a sequential manner; the vertical rules in a parallel manner in the vertical direction as in a 2CFG grammar;

• (v) Finally, $i_{o}$ is the label of an elementary membrane of $\mu$ which is the output membrane.

A computation in a sequential / parallel array P system is similar to a string rewriting P system; the successful computations are the halting ones; each object (either a string or a rectangular array), from each region of the system, which can be rewritten by suitable rules (a horizontal rule or a set of vertical rules) associated with that region, should be rewritten; The target (here, in, out) associated with the horizontal rule or the set of vertical rules, have the usual meaning as in other rewriting P systems (described earlier). A computation is successful only if it stops by reaching a configuration where no rule can be applied to the existing arrays. The result of a halting computation consists of the rectangular arrays composed only of symbols from T placed in the membrane with label $i_{o}$ in the halting configuration.

The set of all such arrays computed or generated by the system $\pi$ is denoted by $RAL(\pi )$. The family of all array languages $RAL(\pi )$ generated by systems $\pi$ as above, with at most m membranes, with horizontal rules of type $\alpha \in \{REG, CF\}$ is denoted by $S/P AP_{m}(\alpha )$ where $REG, \, CF$ stand respectively for regular or context-free type of rules.

Example 7

Consider the sequential / parallel array P system in the class $S/P AP_{4} (REG)$

$\varPi = (V_{1}\cup V_{2}, I, T, [_{4} [_{3} [_{2} [_{1} \, ]_{1} ]_{2} ]_{3} ]_{4}, S_1 B S_{2}, \emptyset , \emptyset , \emptyset , R_{1}, R_{2}, R_{3}, R_{4}, 4)$.

$V_{1} = \{ S_{1}, S_{2}, A, B \}$, $V_{2} = \{ A, B, C, a, b \}$, $I = \{ A, B \}, T = \{a,b \}$

$R_{1} = \{ S_1 \rightarrow A S_{1} (\textit{in}), S_1 \rightarrow A (\textit{in})\}$   $R_{2} = \{S_2 \rightarrow A S_{2} (\textit{out}), S_2 \rightarrow A (\textit{in})\}$, $R_{3} = \left\{ \left\{ A \rightarrow \begin{array}{c} a \\ C \end{array}, B \rightarrow \begin{array}{c} a \\ B \end{array}, C \rightarrow \begin{array}{c} b \\ C \end{array} \right\} , \left\{ C \rightarrow b, B \rightarrow a \right\} \right\}$, $R_{4} = \emptyset .$

Region 1 has the initial axiom word $S_1BS_2.$ There are no objects initially in the other regions. Starting with $S_1BS_2$ an application of the rule $S_1 \rightarrow A S_{1}$ generates the word $AS_1BS_2$ which is sent to region 2 where an application of the rule $S_2 \rightarrow A S_{2}$ sends the string $AS_1BAS_2$ generated back to region 1. When the terminating rule is applied in region 1, the string $AABAS_2$ generated is sent to region 2 where an application of the rule $S_2 \rightarrow A$ generates AABAA and sends it to region 3. An improper application of the rules in regions 1 and 2 will make the string get stuck in one of the regions. In general, the string sent to region 3 is of the form $A^nBA^n.$ In region 3, application in parallel of the vertical rules in the table $\left\{ A \rightarrow \begin{array}{c} a \\ C \end{array}, B \rightarrow \begin{array}{c} a \\ B \end{array}, C \rightarrow \begin{array}{c} b \\ C \end{array} \right\}$ allows growth in the vertical direction with an array generated being of the form

$$\begin{aligned}\begin{array} {ccc} a^n &{} a &{} a^n \\ b^n &{} a &{} b^n \\ &{}\cdots &{}\\ &{}\cdots &{}\\ b^n &{} a &{} b^n \\ C^n &{} B &{} C^n \end{array}. \end{aligned}$$

Application of the rules of the table $\left\{ C \rightarrow b, B \rightarrow a \right\}$ in parallel terminates the derivation, yielding arrays, one member of which is shown in Fig. 6. The picture language generated by $\varPi$ consists of rectangular arrays describing the letter T with equal “horizontal arms” over a (Fig. 6) to the left and right of the middle vertical arm, interpreting b as blank.

Now the generative power of the sequential/parallel array P systems is given in the following Theorem 6.

Theorem 6

• (i) $S/P RAP_{3} (REG) \supset L(2RLG);$

• (ii) $S/P RAP_{3} (CF)\supset L(2CFG);$

• (iii) $S/P RAP_{4} (REG) \subset S/P RAP_{4}(CF).$

Fig. 6

a A $5 \times 7$ array representing Letter T over a with equal “horizontal arms” b Digitized form of Letter T

5.1 Pure 2D Context-Free Grammar Based P System

We now recall an array P system that involves rules of pure 2D context-free grammars as in Definition 3.

Definition 8

[44] An array-rewriting P system (of degree $m \ge 1$) with pure 2D context-free rules is a construct

$$\varPi =(V, \mu ,F_1,\dots ,F_m, R_1,\dots ,R_m,i_o),$$

where V is an alphabet, $\mu$ is a membrane structure with m membranes labelled in a one-to-one way with $1,2,\dots ,m$; $F_i$ is a finite set of rectangular arrays over V associated with the region $i, \, 1 \le i \le m$, of $\mu$; $R_i$ is a finite set of column tables or row tables of context-free rules over V (as in a P2DCFG) associated with region  of $\mu$; the tables have attached targets here,out, in (in general, here is omitted), finally, $i_o$ is the label of an elementary membrane of $\mu$, which is the output membrane.

A computation in $\varPi$ is defined in the same way as in an array-rewriting P system with the successful computations being the halting ones: each rectangular array in each region of the system, which can be rewritten by a column/row table of rules (with the rewriting as in a P2DCFG) associated with that region, should be rewritten; this means that one table of rules is applied; the array obtained by rewriting is placed in the region indicated by the target associated with the table used (here means that the array remains in the same region, out means that the array exits the current membrane; and in means that the array is immediately sent to one of the directly lower membranes, nondeterministically chosen if several exist there; if no internal membrane exists, then a table with the target indication in cannot be used). A computation is successful only if it stops, a configuration is reached where no table of rules can be applied to the existing arrays. The result of a halting computation consists of rectangular arrays over V placed in the membrane with label $i_o$ in the halting configuration.

The set of all such arrays computed or generated by a system $\varPi$ is denoted by $AL(\varPi )$. The family of all array languages $AL(\varPi )$ generated by systems $\varPi$ as above, with at most m membranes, is denoted by $AP_m(P2DCFG)$.

We illustrate with an example.

Example 8

[44] Let

$$\begin{aligned} \varPi _1=(V, \mu ,F_1,F_2,F_3,F_4, R_1,R_2,R_3,R_4,i_o), \end{aligned}$$

where $V = \{u,u_t,u_b,u_l,u_l^\prime ,v,v_t,v_b,v_r,v_r^\prime ,x,y,z,w, s,s_1,s_2 \}$, $\mu = [_1[_2[_3 [_4 ]_4 ]_3]_2]_1$, indicating that the system has four regions, one within another, i.e. region 1 is the ‘skin’ membrane which contains region 2, which in turn contains region 3, and which in turn contains region 4. $i_0 = 4$ indicates that the region 4 is the output region.

$$\begin{aligned} R_1 = \{t_{c1} \}, \ R_2 = \{t_{c2}, t_{r3} \}, \ R_3 = \{ t_{r1}, t_{r2}\},\ R_4 = \emptyset . \end{aligned}$$

The tables of rules are given by

$$t_{c1} = \{u_t \rightarrow zu_tx, u \rightarrow yux, u_b \rightarrow wu_bx, s_1 \rightarrow ss_1x, s \rightarrow ssx \} (in), $$

$$t_{c2} = \{v_t \rightarrow v_tz, v \rightarrow vy, v_b \rightarrow v_bw, s_2 \rightarrow s_2s, s \rightarrow ss \} (in), $$

$$t_{r1} = \left\{ \begin{array}{ccc} &{} &{} u_l \\ u_l &{} \rightarrow &{} y\\ &{} &{} u \end{array},\begin{array}{ccc} &{} &{} s \\ s &{} \rightarrow &{} y \\ &{} &{} s \end{array},\begin{array}{ccc} &{} &{} s_1 \\ s_1 &{} \rightarrow &{} u \\ &{} &{} s \end{array} \right\} \bigcup \left\{ \begin{array}{ccc} &{} &{} x \\ x &{} \rightarrow &{} x \\ &{} &{} x \end{array},\begin{array}{ccc} &{} &{} s_2 \\ s_2 &{} \rightarrow &{} v \\ &{} &{} s \end{array},\begin{array}{ccc} &{} &{} v_r \\ v_r &{} \rightarrow &{} y \\ &{} &{} v \end{array} \right\} (in),$$

$$t_{r2} = \{u_l \rightarrow u_{l}^\prime , s \rightarrow s, s_1 \rightarrow s_1, x \rightarrow x, s_2 \rightarrow s_2, v_r \rightarrow v_{r}^\prime \} (out),$$

$$t_{r3} = \{u_{l}^\prime \rightarrow u_{l}, s \rightarrow s, s_1 \rightarrow s_1, x \rightarrow x, s_2 \rightarrow s_2, v_{r}^\prime \rightarrow v_{r}\} (out),$$

$F_1 = \{M_0 \}, F_2 = F_3 = F_4 = \emptyset$, $M_0 = \begin{array}{cccccc} z &{} z &{} u_t &{} v_t &{} z &{} z\\ u_l &{} s &{} s_1 &{} s_2 &{} s &{} v_r \\ w &{} w &{} u_b &{} v_b &{} w &{} w. \end{array}$

Starting with $M_0$ in the region 1, the rules of the column table $t_{c1}$ are applied and the array is sent to region 2 wherein the rules of the column table $t_{c2}$ are applied and the array is again sent to region 3. If in region 3, the rules of the row table $t_{r1}$ are applied, then the array is sent to region 4 wherein it remains and gets collected in the language generated. On the other hand, if in region 3, the rules of the row table $t_{r2}$ are applied changing $u_l$ into $u_l^\prime$ and $v_r$ into $v_r^\prime$, then the array is sent back to region 2 wherein the symbols $u_l^\prime$ and $v_r^\prime$ are respectively changed back into $v_l$ and $v_r$ and the array is sent to region 1. The process then repeats. An array M generated by $\varPi _1$ is shown in Fig. 7.

Fig. 7

An array M generated by $\varPi _1$

Results on comparison of generative power of array-rewriting P systems based on Pure 2D context-free grammars have been established in [44]. We state some of these here (Theorem 7).

Theorem 7

[44] (i) $L(P2DCFG) = AP_1(P2DCFG);$

(ii) $L(P2DCFG) \subset AP_2(P2DCFG);$

(iii) $L(2RLG) \subset L(T2RLG) \subseteq AP_2(P2DCFG);$

(iv) $L(2CFG) \subset L(T2CFG) \subseteq AP_2(P2DCFG);$

(v) $AP_2(P2DCFG) \setminus L(T2CFG) \ne \emptyset .$

6 Application to Picture Pattern Generation

Interesting classes of picture patterns can be generated using the array P systems. We illustrate by considering one of the systems discussed in the earlier sections, namely the array-rewriting P system based on P2DCFG type of rules. In the arrays generated by the array-rewriting P system with P2DCFG type of rules in the we use a well-known technique of replacing the letter symbols in the generated picture arrays by ‘primitive patterns’ (Fig. 8). Each symbol of a rectangular array M over an alphabet $\varSigma$ is considered to occupy a unit square in the rectangular grid so that a row of symbols or a column of symbols in the array respectively occupies a horizontal or a vertical sequence of adjacent unit squares. A mapping i, called an interpretation, from the alphabet $\varSigma = \{a_1, a_2, \ldots , a_n \}$ to a set of primitive picture patterns $\{p_1, p_2, \ldots p_m \}$ is defined such that for $1 \le i \le n$, $i(a_i) = p_j,$ for some $1 \le j \le m.$ Then i(M) is obtained by replacing every symbol $a \in M$ by the corresponding picture pattern i(a). In the Example 8, the interpretation i is given by $i(u_l)=i(u_t)=i(u_b)=i(u)=u,$ $i(z)=z,$ $i(x)=x,$ $i(s_1)=i(s_2)=i(s)=s,$ $i(v_r)=i(v_t)=i(v_b)=i(v)=v,$ $i(w)=w,$ $i(y)=y.$ The interpretation i applied to the array M gives a pattern commonly called a “kolam” pattern [38] (or a floor design) as in Fig. 9. The primitive kolam patterns are shown in Fig. 8.

Fig. 8

Primitive patterns of a “floor design”: x, y are called pupil, u, v fan, s diamond and z, w drop

Fig. 9

A “floor design” based on a “kolam” pattern

7 Conclusion and Discussion

We have reviewed here certain main types of array-rewriting P systems, with array objects and with two of these systems based on isometric type of array grammar rules and another two based on non-isometric type of array generating grammar rules. We have indicated an application of one of these systems in the description of floor-designs, commonly called “kolam” patterns [38].

Based on and following the types of array generating P systems reviewed here, several other kinds of array P systems have been proposed in the literature (see, for example, [6, 8, 18, 19, 43, 47]). The interesting application problem of generation of patterns of “floor-designs” has been considered in some of these array P systems (see, for example [19]). On the other hand string language generating models based on spiking neural P systems [7, 20, 53, 54, 56] have been proposed. It will be interesting to examine the possibility of picture array generation based on spiking neural P systems, which is an intensively investigated research area in recent times.

P systems with controlled computations have been introduced and investigated in [23]. In [32], study of the family of control languages of spiking neural P systems in comparison with other families of string languages, is undertaken. Recently, in [48, 49], besides considering 8-directional array P systems, control language study is also done. It will be interesting to investigate the effect of such a control language on the array P systems reviewed here, like the contextual array P system.