Abstract
Logic rules and inference are fundamental in computer science and have been studied extensively. However, prior semantics of logic languages can have subtle implications and can disagree significantly.
This paper describes a simple new semantics for logic rules, founded semantics, and its straightforward extension to another simple new semantics, constraint semantics, that unify the core of different prior semantics. The new semantics support unrestricted negation, as well as unrestricted existential and universal quantifications. They are uniquely expressive and intuitive by allowing assumptions about the predicates and rules to be specified explicitly. They are completely declarative and relate cleanly to prior semantics. In addition, founded semantics can be computed in linear time in the size of the ground program.
This work was supported in part by NSF under grants CCF-1414078, CNS-1421893, IIS-1447549, CCF-1248184, CCF-0964196, and CCF-0613913; and ONR under grants N000141512208 and N000140910651.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
- Datalog
- Unrestricted negation
- Existential and universal quantifications
- Fixed-point semantics
- Constraints
- Well-founded semantics
- Stable model semantics
- Fitting (Kripke-Kleene) semantics
- Supported model semantics
1 Introduction
Logic rules and inference are fundamental in computer science, especially for solving complex modeling, reasoning, and analysis problems in critical areas such as program analysis and verification, security, and decision support.
The semantics of logic rules and their efficient computations have been a subject of significant study, especially for complex rules that involve recursion and unrestricted negation and quantifications. Many different semantics and computation methods have been proposed, e.g., see surveys [1, 2]. Even those used in many Prolog-based systems and Answer Set Programming systems—negation as failure [3], well-founded semantics (WFS) [4], and stable model semantics (SMS) [5]—have subtle implications and differ significantly. Is it possible to create a simple semantics that also unifies these different semantics?
In practice, different semantics may be useful under different assumptions about the facts, rules, and reasoning used. For example, an application may have complete information about some predicates, i.e., sets and relations, but not other predicates. Capturing such situations is important for increasingly larger and more complex applications. Any semantics that is based on a single set of assumptions for all predicates cannot best model such applications. How can a semantics be created to support all different assumptions and still be simple and easy to use?
This paper describes a simple new semantics for logic rules, founded semantics, and its straightforward extension to another simple new semantics, constraint semantics.
-
The new semantics support unrestricted negation (both stratified and non-stratified), as well as unrestricted combinations of existential and universal quantifications.
-
They allow each predicate to be specified explicitly as certain (each assertion of the predicate has one of two values: true, false) or uncertain (has one of three values: true, false, undefined), and as complete (all rules defining the predicate are given) or not.
-
Completion rules are added for predicates that are complete, as explicit rules for inferring the negation of those predicates using the negation of the hypotheses of the given rules.
-
Founded semantics infers all true and false values that are founded, i.e., rooted in the given true or false values and exactly following the rules, and it completes certain predicates with false values and completes uncertain predicates with undefined values.
-
Constraint semantics extends founded semantics by allowing undefined values to take all combinations of true and false values that satisfy the constraints imposed by the rules.
Founded semantics and constraint semantics unify the core of previous semantics and have three main advantages:
-
1.
They are expressive and intuitive, by allowing assumptions about predicates and rules to be specified explicitly, by including the choice of uncertain predicates to support common-sense reasoning with ignorance, and by adding explicit completion rules to define the negation of predicates.
-
2.
They are completely declarative. Founded semantics takes the given rules and completion rules as recursive definitions of the predicates and their negation, and is simply the least fixed point of the recursive functions. Constraint semantics takes the given rules and completion rules as constraints, and is simply the set of all solutions that are consistent with founded semantics.
-
3.
They relate cleanly to prior semantics, including stratified semantics [6], first-order logic, Fitting semantics (also called Kripke-Kleene semantics) [7], supported models [6], as well as WFS and SMS, by precisely capturing corresponding assumptions about the predicates and rules.
Additionally, founded semantics can be computed in linear time in the size of the ground program, as opposed to quadratic time for WFS.
Finally, founded semantics and constraint semantics can be extended to allow uncertain, complete predicates to be specified as closed—making an assertion of the predicate false if inferring it to be true (respectively false) using the given rules and facts requires assuming itself to be true (respectively false)—and thus match WFS and SMS, respectively.
2 Motivation for Founded Semantics and Constraint Semantics
Founded semantics and constraint semantics are designed to be intuitive and expressive. For rules with no negation or with restricted negation, which have universally accepted semantics, the new semantics are consistent with the accepted semantics. For rules with unrestricted negation, which so far lack a universally accepted semantics, the new semantics unify the core of prior semantics with two basic principles:
-
1.
Assumptions about certain and uncertain predicates, with true (\(T\)) and false (\(F\)) values, or possibly undefined (\(U\)) values, and about whether the rules defining each predicate are complete must be made explicit.
-
2.
Any easy-to-understand semantics must be consistent with one where everything inferred that has a unique \(T\) or \(F\) value is rooted in the given \(T\) or \(F\) values and following the rules.
This section gives informal explanations.
Rules with no negation. Consider a set of rules with no negation in the hypotheses, e.g., a rule can be “q(x) if p(x)” but not “q(x) if not p(x)” for predicates p and q and variable x. The meaning of the rules, given a set of facts, e.g., a fact p(a) for constant a, is the set of all facts that are given or can be inferred by applying the rules to the facts, e.g., {p(a),q(a)} using the example rule and fact given. In particular,
-
1.
Everything is either \(T\) or \(F\), i.e., \(T\) as given or inferred facts, or \(F\) as otherwise. So one can just explicitly express what are \(T\), and the rest are \(F\).
-
2.
Everything inferred must be founded, i.e., rooted in the given facts and following the rules. So anything that always depends on itself, e.g., p(a), given only the rule “p(x) if p(x)”, is not \(T\).
In technical terms, the semantics is 2-valued, and the set of all facts, i.e., true assertions, is the minimum model, equal to the least fixed point of applying the rules starting from the given facts.
Rules with restricted negation. Consider rules with negation in the hypotheses, but with each negation only on a predicate all of whose facts can be inferred without using rules that contain negation of that predicate, e.g., one can have “q(x) if not p(x)” but not “p(x) if not p(x)”. The meaning of the rules is as for rules with no negation except that a rule with negation is applied only after all facts of the negated predicates have been inferred. In other words,
-
The true assertions of any predicate do not depend on the negation of that predicate. So a negation could be just a test after all facts of the negated predicate are inferred. The rest remains the same as for rules with no negation.
In technical terms, this is stratified negation; the semantics is still 2-valued, the minimum model, and the set of all true assertions is the least fixed point of applying the rules in order of the strata.
Rules with unrestricted negation. Consider rules with unrestricted negation in the hypotheses, where a predicate may cyclically depend on its own negation, e.g., “p(x) if not p(x)”. Now the value of a negated assertion needs to be established before all facts of the negated predicate have been inferred. In particular,
-
There may not be a unique \(T\) or \(F\) value for each assertion. For example, given only rule “p(x) if not p(x)”, p(a) cannot be \(T\) because inferring it following the rule would require itself be \(F\), and it cannot be \(F\) because it would lead to itself being \(T\) following the rule. That is, there may not be a 2-valued model.
In technical terms, the negation may be non-stratified. There are two best solutions to this that generalize a unique 2-valued model: a unique 3-valued model and a set of 2-valued models, as in well-founded semantics (WFS) and stable model semantics (SMS), respectively.
In a unique 3-valued model, when a unique \(T\) or \(F\) value cannot be established for an assertion, a third value, undefined (\(U\)), is used. For example, given only rule “p(x) if not p(x)”, p(a) is \(U\), in both WFS and founded semantics.
-
With the semantics being 3-valued, when one cannot infer that an assertion is \(T\), one should be able to express whether it is \(F\) or \(U\) when there is a choice. For example, given only rule “p(x) if p(x)”, p(a) is not \(T\), so p(a) may in general be \(F\) or \(U\).
-
WFS requires that such an assertion be \(F\), even though common sense generally says that it is \(U\). WFS attempts to be the same as in the case of 2-valued semantics, even though one is now in a 3-valued situation.
-
Founded semantics supports both, allowing one to choose explicitly when there is a choice. Founded semantics is more expressive by supporting the choice. It is also more intuitive by supporting the common-sense choice for expressing ignorance.
For a set of 2-valued models, similar considerations motivate our constraint semantics. In particular, given only rule “p(x) if not p(x)”, the semantics is the empty set, i.e., there is no model, in both SMS and constraint semantics, because no model can contain p(a) or not p(a), for any a, because p(a) cannot be \(T\) or \(F\) as discussed above. However, given only rule “p(x) if p(x)”, SMS requires that p(a) be \(F\) in all models, while constraint semantics allows the choice of p(a) being \(F\) in all models or being \(T\) in some models and \(F\) in other models.
Certain or uncertain. Founded semantics and constraint semantics first allow a predicate to be declared certain (i.e., each assertion of the predicate has one of two values: \(T\), \(F\)) or uncertain (i.e., each assertion of the predicate has one of three values: \(T\), \(F\), \(U\)) when there is a choice. If a predicate is defined (as conclusions of rules) with use of non-stratified negation, then it must be declared uncertain, because it might not have a unique 2-valued model. Otherwise, it may be declared certain or uncertain.
-
For a certain predicate, everything \(T\) must be given or inferred by following the rules, and the rest are \(F\), in both founded semantics and constraint semantics.
-
For an uncertain predicate, everything \(T\) or \(F\) must be given or inferred, and the rest are \(U\) in founded semantics. Constraint semantics then extends everything \(U\) to be combinations of \(T\) and \(F\) that satisfy all the rules and facts as constraints.
Complete or not. Founded semantics and constraint semantics then allow an uncertain predicate that is in the conclusion of a rule to be declared complete, i.e., all rules with that predicate in the conclusion are given.
-
If a predicate is complete, then completion rules are added to define the negation of the predicate explicitly using the negation of the hypotheses of all given rules and facts of that predicates.
-
Completion rules, if any, and given rules are used together to infer everything \(T\) and \(F\). The rest are \(U\) in founded semantics, and are combinations of \(T\) and \(F\) in constraint semantics as described above.
Closed or not. Finally, founded semantics and constraint semantics can be extended to allow an uncertain, complete predicate to be declared closed, i.e., an assertion of the predicate is made \(F\), called self-false, if inferring it to be \(T\) (respectively \(F\)) using the given rules and facts requires assuming itself to be \(T\) (respectively \(F\)).
-
Determining self-false assertions is similar to determining unfounded sets in WFS. Repeatedly computing founded semantics and self-false assertions until a least fixed point is reached yields WFS.
-
Among combinations of \(T\) and \(F\) values for assertions with \(U\) values in WFS, removing each combination that has self-false assertions that are not already \(F\) in that combination yields SMS.
Correspondence to prior semantics, more on motivation. Table 1 summarizes corresponding declarations that capture different assumptions under prior semantics; formal definitions and proofs for these and for additional relationships appear in the following sections. Founded semantics and constraint semantics allow additional combinations of declarations besides those in the table.
Some observations from the table may help one better understand founded semantics and constraint semantics.
-
The 4 wide rows cover all combinations of allowed declarations (for all predicates).
-
Wide row 1 is a special case of wide row 4, because being certain implies being complete and closed. So one could prefer to use only the latter two choices and omit the first choice. However, being certain is uniquely important, both for conceptual simplicity and practical efficiency:
-
(1)
It covers the vast class of database applications that do not use non-stratified negation, for which stratified semantics is universally accepted. It does not need to be understood by explicitly combining the latter two more sophisticated notions.
-
(2)
It allows founded semantics to match WFS for all example programs we found in the literature, with predicates being certain when possible and complete otherwise, but without the last, most sophisticated notion of being closed; and the semantics can be computed in linear time.
-
(1)
-
Wide rows 2 and 3 allow the assumption about predicates that are uncertain, not complete, or not closed to be made explicitly.
In a sense, WFS uses \(F\) for both false and some kinds of ignorance (no knowledge of something must mean it is \(F\)), uses \(T\) for both true and some kinds of ignorance inferred through negation of \(F\), and uses \(U\) for conflict, remaining kinds of ignorance from \(T\) and \(F\), and imprecision; SMS resolves the ignorance in \(U\), but not the ignorance in \(F\) and \(T\). In contrast,
-
founded semantics uses \(T\) only for true, \(F\) only for false, and \(U\) for conflict, ignorance, and imprecision;
-
constraint semantics further differentiates among conflict, ignorance, and imprecision—corresponding to there being no model, multiple models, and a unique model, respectively, consistent with founded semantics.
After all, any easy-to-understand semantics must be consistent with the \(T\) and \(F\) assertions that can be inferred by exactly following the rules and completion rules starting from the given facts.
-
Founded semantics is the maximum set of such \(T\) and \(F\) assertions, as a least fixed point of the given rules and completion rules if any, plus \(U\) for the remaining assertions.
-
Constraint semantics is the set of combinations of all \(T\) and \(F\) assertions that are consistent with founded semantics and satisfy the rules as constraints.
Founded semantics without closed predicates can be computed easily and efficiently, as a least fixed point, contrasting with an alternating fixed point or iterated fixed point for computing WFS.
3 Language
We first consider Datalog with unrestricted negation in hypotheses. We extend it in Sect. 7 to allow unrestricted combinations of existential and universal quantifications and other features.
Datalog with unrestricted negation. A program in the core language is a finite set of rules of the following form, where any \(P_i\) may be preceded with \(\lnot \), and any \(P_i\) and \(Q\) over all rules may be declared certain or uncertain, and declared complete or not:
Symbols \(\leftarrow \), \(\wedge \), and \(\lnot \) indicate backward implication, conjunction, and negation, respectively; \(h\) is a natural number, each \(P_i\) (respectively \(Q\)) is a predicate of finite number \(a_i\) (respectively \(a\)) of arguments, each \(X_{ij}\) and \(X_k\) is either a constant or a variable, and each variable in the arguments of \(Q\) must also be in the arguments of some \(P_i\).
If \(h = 0\), there is no \(P_i\) or \(X_{ij}\), and each \(X_k\) must be a constant, in which case \(Q(X_1, \ldots , X_a)\) is called a fact. For the rest of the paper, “rule” refers only to the case where \(h \ge 1\), in which case each \({P_i(X_{i1}, \ldots , X_{ia_i})}\) or \(\lnot P_i(X_{i1}, \ldots , X_{ia_i})\) is called a hypothesis of the rule, and \(Q(X_1, \ldots , X_a)\) is called the conclusion of the rule. The set of hypotheses of the rule is called the body of the rule.
A predicate declared certain means that each assertion of the predicate has a unique true (\(T\)) or false (\(F\)) value. A predicate declared uncertain means that each assertion of the predicate has a unique true, false, or undefined (\(U\)) value. A predicate declared complete means that all rules with that predicate in the conclusion are given in the program.
A predicate in the conclusion of a rule is said to be defined using the predicates or their negation in the hypotheses of the rule, and this defined-ness relation is transitive.
-
A predicate must be declared uncertain if it is defined transitively using its own negation, or is defined using an uncertain predicate; otherwise, it may be declared certain or uncertain and is by default certain.
-
A predicate may be declared complete or not only if it is uncertain and is in the conclusion of a rule, and it is by default complete.
In examples with no explicit specification of declarations, default declarations are used.
Rules of form (1) without negation are captured exactly by Datalog [8, 9], a database query language based on the logic programming paradigm. Recursion in Datalog allows queries not expressible in relational algebra or relational calculus. Negation allows more sophisticated logic to be expressed directly. However, unrestricted negation in recursion has been the main challenge in defining the semantics of such a language, e.g., [1, 2], including whether the semantics should be 2-valued or 3-valued, and whether the rules are considered complete or not.
Example. We use win, the win-not-win game, as a running example, with default declarations: move is certain, and win is uncertain and complete. A move from position x to position y is represented by a fact move(x,y). The following rule captures the win-not-win game: a position x is winning if there is a move from x to some position y and y is not winning. Arguments x and y are variables.

Note that the declarations for predicates move and win are different. Other choices of declarations can lead to different results, e.g., see the last example under least fixed point in Sect. 4. \(\blacksquare \)
Additional examples are given in Appendices A and B of [10].
Notations. In arguments of predicates, we use letter sequences for variables, and use numbers and quoted strings for constants.
In presenting the semantics, in particular the completion rules, we use equality and the notations below for existential and universal quantifications, respectively, in the hypotheses of rules, and use negation in the conclusions.

The quantifications return \(T\) iff for some or all, respectively, combinations of values of \(X_1,\ldots ,X_n\), the value of Boolean expression Y is \(T\). The domain of each quantified variable is the set of all constants in the program.
4 Formal Definition of Founded Semantics and Constraint Semantics
Atoms, literals, and projection. Let \(\pi \) be a program. A predicate is intensional in \(\pi \) if it appears in the conclusion of at least one rule; otherwise, it is extensional. An atom of \(\pi \) is a formula formed by applying a predicate symbol in \(\pi \) to constants in \(\pi \). A literal of \(\pi \) is an atom of \(\pi \) or the negation of an atom of \(\pi \). These are called positive literals and negative literals, respectively. The literals p and \(\lnot p\) are complements of each other. A set of literals is consistent if it does not contain a literal and its complement. The projection of a program \(\pi \) onto a set S of predicates, denoted \({ Proj}(\pi ,S)\), contains all facts of \(\pi \) whose predicates are in S and all rules of \(\pi \) whose conclusions contain predicates in S.
Interpretations, ground instances, models, and derivability. An interpretation of \(\pi \) is a consistent set of literals of \(\pi \). Interpretations are generally 3-valued: a literal p is true (\(T\)) in interpretation I if it is in I, is false (\(F\)) in I if its complement is in I, and is undefined (\(U\)) in I if neither it nor its complement is in I. An interpretation of \(\pi \) is 2-valued if it contains, for each atom A of \(\pi \), either A or its complement. An interpretation I is 2-valued for predicate P if, for each atom A for P, I contains A or its complement. Interpretations are ordered by set inclusion \(\subseteq \).
A ground instance of a rule R is any rule that can be obtained from R by expanding universal quantifications into conjunctions over all constants in the domain, and then instantiating the remaining variables with constants. For example, \({\texttt {q(a)}}~\leftarrow ~{\texttt {p(a)}}~\wedge ~{\texttt {r(b)}}\) is a ground instance of \({\texttt {q(x)}}~\leftarrow ~{\texttt {p(x)}}~\wedge ~\exists ~{\texttt {y}}~|~{\texttt {r(y)}}\). An interpretation is a model of a program if it contains all facts in the program and satisfies all rules of the program, interpreted as formulas in 3-valued logic [7], i.e., for each ground instance of each rule, if the body is true, then so is the conclusion. The one-step derivability operator \(T_\pi \) for program \(\pi \) performs one step of inference using rules of \(\pi \), starting from a given interpretation. Formally, \(C\in T_\pi (I)\) iff C is a fact of \(\pi \) or there is a ground instance R of a rule of \(\pi \) with conclusion C such that each hypothesis of R is true in interpretation I.
Dependency graph. The dependency graph \({ DG}(\pi )\) of program \(\pi \) is a directed graph with a node for each predicate of \(\pi \), and an edge from Q to P labeled \(\mathord {+}\) (respectively, \(\mathord {-}\)) if a rule whose conclusion contains Q has a positive (respectively, negative) hypothesis that contains P. If the node for predicate P is in a cycle containing only positive edges, then P has circular positive dependency in \(\pi \); if it is in a cycle containing a negative edge, then P has circular negative dependency in \(\pi \).
Founded semantics. Intuitively, the founded model of a program \(\pi \), denoted \({ Founded}(\pi )\), is the least set of literals that are given as facts or can be inferred by repeated use of the rules. We define \({ Founded}(\pi ) = { UnNameNeg}({ LFPbySCC}({ NameNeg}({ Cmpl}(\pi ))))\), where functions \({ Cmpl}\), \({ NameNeg}\), \({ LFPbySCC}\), and \({ UnNameNeg}\) are defined as follows.
Completion. The completion function, \({ Cmpl}(\pi )\), returns the completed program of \(\pi \). Formally, \({ Cmpl}(\pi )={ AddInv}({ Combine}(\pi ))\), where \({ Combine}\) and \({ AddInv}\) are defined as follows.
The function \({ Combine}(\pi )\) returns the program obtained from \(\pi \) by replacing the facts and rules defining each uncertain complete predicate Q with a single combined rule for Q, defined as follows. Transform the facts and rules defining Q so they all have the same conclusion \(Q(V_1, \ldots , V_a)\), where \(V_1,\ldots ,V_a\) are fresh variables (i.e., not occurring in the given rules defining Q), by replacing each fact or rule \(Q(X_1, \ldots , X_a) ~\leftarrow ~ H_1 \wedge \cdots \wedge H_h\) with \(Q(V_1,\ldots ,V_a) ~\leftarrow ~ (\exists ~Y_1,\ldots ,Y_k ~|~ V_1=X_1 \wedge \cdots \wedge V_a=X_a \wedge H_1 \wedge \cdots \wedge H_h)\), where \(Y_1,\ldots ,Y_k\) are all variables occurring in the given fact or rule. Combine the resulting rules for Q into a single rule defining Q whose body is the disjunction of the bodies of those rules. This combined rule for Q is logically equivalent to the original facts and rules for Q. Similar completion rules are used in Clark completion [3] and Fitting semantics [7].
Example. For the win example, the rule for win becomes the following. For readability, we renamed variables to transform the equality conjuncts into tautologies and then eliminated them.

\(\blacksquare \)
The function \({ AddInv}(\pi )\) returns the program obtained from \(\pi \) by adding, for each uncertain complete predicate Q, a completion rule that derives negative literals for Q. The completion rule for Q is obtained from the inverse of the combined rule defining Q (recall that the inverse of \(C~\leftarrow ~B\) is \(\lnot C~\leftarrow ~\lnot B\)), by putting the body of the rule in negation normal form, i.e., using laws of predicate logic to move negation inwards and eliminate double negations, so that negation is applied only to atoms.
Example. For the win example, the added rule is

\(\blacksquare \)
Least fixed point. The least fixed point is preceded and followed by functions that introduce and remove, respectively, new predicates representing the negations of the original predicates.
The function \({ NameNeg}(\pi )\) returns the program obtained from \(\pi \) by replacing each negative literal \(\lnot P(X_1, \ldots , X_a)\) with \({\texttt {n.}}P(X_1, \ldots , X_a)\), where the new predicate \({\texttt {n.}}P\) represents the negation of predicate P.
Example. For the win example, this yields:

\(\blacksquare \)
The function \({ LFPbySCC}(\pi )\) uses a least fixed point to infer facts for each strongly connected component (SCC) in the dependency graph of \(\pi \), as follows. Let \(S_1,\ldots ,S_n\) be a list of the SCCs in dependency order, so earlier SCCs do not depend on later ones; it is easy to show that any linearization of the dependency order leads to the same result for \({ LFPbySCC}\). For convenience, we overload S to also denote the set of predicates in the SCC.
Define \({ LFPbySCC}(\pi ) = I_n\), where \(I_0\) is the empty set and \(I_i = { AddNeg}({ LFP}(T_{I_{i-1} \cup { Proj}(\pi ,S_i)}), S_i)\) for \(i \in 1..n\). \({ LFP}\) is the least fixed point operator. The least fixed point is well-defined, because the one-step derivability function \(T_{I_{i-1} \cup { Proj}(\pi ,S_i)}\) is monotonic, because the program \(\pi \) does not contain negation. The function \({ AddNeg}(I, S)\) returns the interpretation obtained from interpretation I by adding completion facts for certain predicates in S to I; specifically, for each certain predicate P in S, for each combination of values \(v_1,\ldots ,v_a\) of arguments of P, if I does not contain \(P(v_1,\ldots ,v_a)\), then add \({\texttt {n.}}P(v_1,\ldots ,v_a)\).
Example. For the win example, the least fixed point calculation
-
1.
infers n.win(x) for any x that does not have move(x,y) for any y, i.e., has no move to anywhere;
-
2.
infers win(x) for any x that has move(x,y) for some y and n.win(y) has been inferred;
-
3.
infers more n.win(x) for any x such that any y having move(x,y) has win(y);
-
4.
repeatedly does 2 and 3 above until a fixed point is reached. \(\blacksquare \)
The function \({ UnNameNeg}(I)\) returns the interpretation obtained from interpretation I by replacing each atom \({\texttt {n.}}P(X_1, \ldots , X_a)\) with \(\lnot P(X_1, \ldots , X_a)\).
Example. For the win example, positions x for which win(x) is \(T\), \(F\), and \(U\), respectively, in the founded model correspond exactly to the well-known winning, losing, and draw positions, respectively. In particular,
-
1.
a losing position is one that either does not have a move to anywhere or has moves only to winning positions;
-
2.
a winning position is one that has a move to a losing position; and
-
3.
a draw position is one not satisfying either case above, i.e., it is in a cycle of moves that do not have a move to a losing position, called a draw cycle, or is a position that has only sequences of moves to positions in draw cycles. \(\blacksquare \)
Example. Suppose the running example uses the declaration that move is uncertain instead of the default of being certain. This means that moves not in the given move have \(U\) values, not allowing any n.win or win facts to be inferred. Therefore, the founded semantics infers that win is \(U\) for all positions. \(\blacksquare \)
Constraint semantics. Constraint semantics is a set of 2-valued models based on founded semantics. A constraint model of \(\pi \) is a consistent 2-valued interpretation M such that M is a model of \({ Cmpl}(\pi )\) and \({ Founded}(\pi ) \subseteq M\). We define \({ Constraint}(\pi )\) to be the set of constraint models of \(\pi \). Constraint models can be computed from \({ Founded}(\pi )\) by iterating over all assignments of true and false to atoms that are undefined in \({ Founded}(\pi )\), and checking which of the resulting interpretations satisfy all rules in \({ Cmpl}(\pi )\).
Example. For win, draw positions (i.e., positions for which win is undefined) are in draw cycles, i.e., cycles that do not have a move to a n.win position, or are positions that have only a sequence of moves to positions in draw cycles.
-
1.
If some SCC has draw cycles of only odd lengths, then there is no satisfying assignment of \(T\) and \(F\) to win for positions in the SCC, so there are no constraint models of the program.
-
2.
If some SCC has draw cycles of only even lengths, then there are two satisfying assignments of \(T\) and \(F\) to win for positions in the SCC, with the truth values alternating between \(T\) and \(F\) around each cycle, and with the second truth assignment obtained from the first by swapping \(T\) and \(F\). The total number of constraint models of the program is exponential in the number of such SCCs. \(\blacksquare \)
5 Properties of Founded Semantics and Constraint Semantics
Proofs of theorems appear in Appendix C of [10].
Consistency and correctness. The most important properties are consistency and correctness.
Theorem 1
The founded model and constraint models of a program \(\pi \) are consistent.
Theorem 2
The founded model of a program \(\pi \) is a model of \(\pi \) and \({ Cmpl}(\pi )\). The constraint models of \(\pi \) are 2-valued models of \(\pi \) and \({ Cmpl}(\pi )\).
Same SCC, same certainty. All predicates in an SCC have the same certainty.
Theorem 3
For every program, for every SCC S in its dependence graph, all predicates in S are certain, or all of them are uncertain.
Higher-order programming. Higher-order logic programs, in languages such as HiLog, can be encoded as first-order logic programs by a semantics-preserving transformation that replaces uses of the original predicates with uses of a single predicate holds whose first argument is the name of an original predicate [11]. For example, win(x) is replaced with holds(win,x). This transformation merges a set of predicates into a single predicate, facilitating higher-order programming. We show that founded semantics and constraint semantics are preserved by merging of compatible predicates, defined below, if a simple type system is used to distinguish the constants in the original program from the new constants representing the original predicates.
We extend the language with a simple type system. A type denotes a set of constants. Each predicate has a type signature that specifies the type of each argument. A program is well-typed if, in each rule or fact, (1) each constant belongs to the type of the argument where the constant occurs, and (2) for each variable, all its occurrences are as arguments with the same type. In the semantics, the values of predicate arguments are restricted to the appropriate type.
Predicates of program \(\pi \) are compatible if they are in the same SCC in \({ DG}(\pi )\) and have the same arity, same type signature, and (if uncertain) same completeness declaration. For a set S of compatible predicates of program \(\pi \) with arity a and type signature \(T_1,\ldots ,T_a\), the predicate-merge transformation \({ Merge}_S\) transforms \(\pi \) into a program \({ Merge}_S(\pi )\) in which predicates in S are replaced with a single fresh predicate holds whose first parameter ranges over S, and which has the same completeness declaration as the predicates in S. Each atom A in a rule or fact of \(\pi \) is replaced with \(MergeAtom_S(A)\), where the function \(MergeAtom_S\) on atoms is defined by: \(MergeAtom_S(P(X_1, \ldots , X_a))\) equals holds(“P”, \(X_1\), ..., \(X_a\)) if \(P \in S\) and equals \(P(X_1, \ldots , X_a)\) otherwise. We extend \(MergeAtom_S\) pointwise to a function on sets of atoms and a function on sets of sets of atoms. The predicate-merge transformation introduces S as a new type. The type signature of holds is \(S, T_1,\ldots , T_a\).
Theorem 4
Let S be a set of compatible predicates of program \(\pi \). Then \({ Merge}_S(\pi )\) and \(\pi \) have the same founded semantics, in the sense that \({ Founded}({ Merge}_S(\pi )) = MergeAtom_S({ Founded}(\pi ))\). \({ Merge}_S(\pi )\) and \(\pi \) also have the same constraint semantics, in the sense that \({ Constraint}({ Merge}_S(\pi ))\) \({}= MergeAtom_S({ Constraint}(\pi ))\).
6 Comparison with Other Semantics
Stratified semantics. Let \({ Stratified}(\pi )\) denote the unique 2-valued model of a program with stratified negation, as discussed in Sect. 2.
Theorem 5
For a program \(\pi \) with stratified negation and in which all predicates are certain, \({ Founded}(\pi )={ Stratified}(\pi )\).
First-order logic. The next theorem relates constraint models with the interpretation of a program as a set of formulas in first-order logic.
Theorem 6
For a program \(\pi \) in which all predicates are uncertain and not complete, the constraint models of \(\pi \) are exactly the 2-valued models of \(\pi \).
Fitting semantics. The Fitting model of a program \(\pi \), denoted \({ Fitting}(\pi )\), is the least model of a formula in 3-valued logic [7]; Sect. 6 of [10] summarizes the definition.
Theorem 7
For a program \(\pi \) in which all extensional predicates are certain, and all intensional predicates are uncertain and complete, \({ Founded}(\pi )={ Fitting}(\pi )\).
Theorem 8
(a) For a program \(\pi \) in which all intensional predicates are uncertain and complete, \({ Founded}(\pi ) \subseteq { Fitting}(\pi )\). (b) If, furthermore, some extensional predicate is uncertain, and some positive literal p for some uncertain extensional predicate does not appear in \(\pi \), then \({ Founded}(\pi ) \subset { Fitting}(\pi )\).
Theorem 9
(a) For a program \(\pi \) in which all predicates have default declarations as certain or uncertain and complete or not, \({ Fitting}(\pi ) \subseteq { Founded}(\pi )\). (b) If, furthermore, \({ Fitting}(\pi )\) is not 2-valued for some certain intensional predicate P, then \({ Fitting}(\pi ) \subset { Founded}(\pi )\).
Well-founded semantics. The well-founded model of a program \(\pi \), denoted \({ WFS}(\pi )\), is the least fixed point of a monotone operator \(W_\pi \) on interpretations [4]; Sect. 6 of [10] summarizes the definition.
Theorem 10
For every program \(\pi \), \({ Founded}(\pi ) \subseteq { WFS}(\pi )\).
Supported models. Supported model semantics of a logic program \(\pi \) is a set of 2-valued models [6], denoted \({ Supported}(\pi )\); Sect. 6 of [10] summarizes the definition.
Theorem 11
For a program \(\pi \) in which all extensional predicates are certain, and all intensional predicates are uncertain and complete, \({ Supported}(\pi )={ Constraint}(\pi )\).
Theorem 12
For a program \(\pi \) in which all intensional predicates are uncertain and complete, \({ Supported}(\pi ) \subseteq { Constraint}(\pi )\).
Theorem 13
For a program \(\pi \) in which all predicates have default declarations as certain or uncertain and complete or not, \({ Constraint}(\pi ) \subseteq { Supported}(\pi )\).
Stable models. Gelfond and Lifschitz define stable model semantics (SMS) of logic programs [5]. They define the stable models of a program \(\pi \) to be the 2-valued interpretations of \(\pi \) that are fixed points of a particular transformation. Let \({ SMS}(\pi )\) denote the set of stable models of \(\pi \).
Theorem 14
For a program \(\pi \) in which all predicates have default declarations as certain or uncertain, \({ SMS}(\pi ) \subseteq { Constraint}(\pi )\).
Example. For the win example with default declarations, Fitting semantics and WFS are the same as founded semantics in Sect. 4, and supported model semantics and SMS are the same as constraint semantics in Sect. 4. Additional examples can be found in Appendix B of [10]. \(\blacksquare \)
7 Computational Complexity and Extensions
Computing founded semantics and constraint semantics
Theorem 15
Computing founded semantics is linear time in the size of the ground program.
Proof
First ground all given rules, using any grounding. Then add completion rules, if any, by adding an inverse rule for each group of the grounded given rules that have the same conclusion, yielding ground completion rules of the same asymptotic size as the grounded given rules.
Now compute the least fixed point for each SCC of the resulting ground rules using a previous method [12]. To do so, first introduce a new intermediate predicate and rule for each conjunction and disjunction in the rules, yielding a new set of rules of the same asymptotic size. In computing the least fixed point, each resulting rule incurs at most one rule firing because there are no variables in the rule, and each firing takes worst-case \(O(1)\) time. Thus, the total time is worst-case linear in the size of all ground rules and therefore in the size of the grounded given rules. \(\blacksquare \)
The size of the ground program is polynomial in the size \(n\) of input data, i.e., the given facts, because each variable in each rule can be instantiated at most \(O(n)\) times (because the domain size is at most \(n\)), and there is a fixed number of variables in each rule, and a fixed size of the given rules. Precisely, the size of the ground program is in the worst case \(O(n^k\times r)\), where \(k\) is the maximum number of variables in a rule, and \(r\) is the size of the given rules.
Computing constraint semantics may take exponential time in the size of the input data, because in the worst case, all assertions of all predicates may have \(U\) values in founded semantics, and there is an exponential number of combinations of \(T\) and \(F\) values of all assertions, where each combination may be checked for whether it satisfies the constraints imposed by all rules.
These complexity analyses also apply to the extensions below except that computing founded semantics with closed predicates may take quadratic time in the size of the ground program, because of repeated computation of founded semantics and self-false assertions.
Closed predicate assumption. We can extend the language to support declaration of uncertain complete predicates as closed. Informally, this means that an atom A of the predicate is false in an interpretation I, called self-false in I, if every ground instance of rules that concludes A, or recursively concludes some hypothesis of that rule instance, has a hypothesis that is false or, recursively, is self-false in I. Self-false atoms are elements of unfounded sets [4].
Formally, \({ SelfFalse}_\pi (I)\), the set of self-false atoms of program \(\pi \) with respect to interpretation I, is defined in the same way as the greatest unfounded set of \(\pi \) with respect to I, except replacing “some positive hypothesis of R is in U” with “some positive hypothesis of R for a closed predicate is in U”. The founded semantics of this extended language is defined by repeatedly computing the semantics as per Sect. 4 and then setting self-false atoms to false, until a least fixed point is reached. Formally, the founded semantics is \({ FoundedClosed}(\pi )={ LFP}(F_\pi )\), where \(F_\pi (I) = { Founded}(\pi \cup I) \cup \lnot \cdot { SelfFalse}_\pi ({ Founded}(\pi \cup I))\).
The constraint semantics for this extended language includes only interpretations that contain the negative literals required by the closed declarations. Formally, a constraint model of a program \(\pi \) with closed declarations is a consistent 2-valued interpretation M such that M is a model of \({ Cmpl}(\pi )\), \({ FoundedClosed}(\pi ) \subseteq M\), and \(\lnot \cdot { SelfFalse}_\pi (M) \subseteq M\). Let \({ ConstraintClosed}(\pi )\) denote the set of constraint models of \(\pi \).
The next theorem states that changing predicate declarations from uncertain, complete, and closed to certain when allowed, or vice versa, preserves founded and constraint semantics. Theorem 3 implies that this change needs to be made for all predicates in an SCC.
Theorem 16
Let \(\pi \) be a program. Let S be an SCC in its dependence graph containing only predicates that are uncertain, complete, and closed. Let \(\pi '\) be a program identical to \(\pi \) except that all predicates in S are declared certain. Note that, for the declarations in both programs to be allowed, predicates in SCCs that follow S in dependency order must be uncertain, predicates in SCCs that precede S in dependency order must be certain, and predicates in S must not have circular negative dependency. Then \({ FoundedClosed}(\pi )={ FoundedClosed}(\pi ')\) and \({ ConstraintClosed}(\pi )={ ConstraintClosed}(\pi ')\).
Theorem 17
For a program \(\pi \) in which every uncertain predicate is complete and closed, \({ FoundedClosed}(\pi )={ WFS}(\pi )\).
Theorem 18
For a program \(\pi \) in which every uncertain predicate is complete and closed, \({ ConstraintClosed}(\pi ) = { SMS}(\pi )\).
Note, however, that founded semantics for default declarations (certain when possible and complete otherwise) allows the number of repetitions for computing self-false atoms to be greatly reduced, even to zero, compared with WFS that does repeated computation of unfounded sets.
In all examples we have found in the literature, and all natural examples we have been able to think of, founded semantics for default declarations, without closed predicate assumption, infers the same result as WFS. However, while founded semantics computes a single least fixed point without the outer repetition and is worst-case linear time, WFS computes an alternating fixed point or iterated fixed point and is worst-case quadratic. In fact, we have not found any natural example showing that an actual quadratic-time alternating or iterated fixed-point for computing WFS is needed.Footnote 1
Unrestricted quantifications in hypotheses. We extend the language to allow unrestricted combinations of existential and universal quantifications as well as negation, conjunction, and disjunction in hypotheses. The domain of each quantified variable is the set of all constants in the program.
Example. For the win example, the following two rules may be given instead:

\(\blacksquare \)
The semantics in Sect. 4 is easily extended to accommodate this extension: these constructs simply need to be interpreted, using their 3-valued logic semantics [7], when defining one-step derivability. Theorems 1–3 hold for this extended language. The other semantics discussed in Sect. 6 are not defined for this extension, thus we do not have theorems relating to them.
Negation in facts and conclusions. We extend the language to allow negation in given facts and in conclusions of given rules; such facts and rules are said to be negative. The Yale shooting example in Appendix B of [10] is a simple example.
The definition of founded semantics applies directly to this extension, because it already introduces and handles negative rules, and it already infers and handles negative facts. Note that \({ Combine}\) combines only positive facts and positive rules to form combined rules; negative facts and negative rules are copied unchanged into the completed program.
With this extension, a program and hence its founded model may be inconsistent; for example, a program could contain or imply p and \(\lnot {\texttt {p}}\). Thus, Theorem 1 does not hold for such programs. When the founded model is inconsistent, the inconsistent literals in it can easily be reported. When the founded model is consistent, the definition of constraint semantics applies directly, and Theorems 2 and 3 hold. The other semantics discussed in Sect. 6 are not defined for this extended language, so we do not have theorems relating to them.
8 Related Work and Conclusion
There is a large literature on logic language semantics and efficient computations. Several overview articles [1, 2, 14, 15] give a good sense of the challenges when there is unrestricted negation. We discuss major prior semantics here.
Clark [3] describes completion of logic programs to give a semantics for negation as failure. Numerous others, e.g., [16,17,18,19,20,21], describe similar additions. Fitting [7] presents a semantics, called Fitting semantics or Kripke-Kleene semantics, that aims to give a least 3-valued model. Apt et al. [6] defines supported model semantics, which is a set of 2-valued models; the models correspond to extensions of the Fitting model. Apt et al. [6] introduces stratified semantics. WFS [4] also gives a 3-valued model but aims to maximize false values. SMS [5] also gives a set of 2-valued models and aims to maximize false values. Other formalisms and semantics include partial stable models, also called stationary models [14], and FO(ID), for first-order logic with inductive definitions [22]. There are also many studies that relate different semantics, e.g., [23, 24].
Our founded semantics, which extends to constraint semantics, is unique in that it allows predicates to be specified as certain or uncertain, as complete or not, and as closed or not. These choices clearly and explicitly capture the different assumptions one can have about the predicates, rules, and reasoning, including the well-known closed-world assumption vs open-world assumption—i.e., whether or not all rules and facts about a predicate are given in the program—and allow both to co-exist naturally. These choices make our new semantics more expressive and intuitive. Instead of using many separate semantics, one just need to make the assumptions explicit; the same underlying logic is used for inference. In this way, founded semantics and constraint semantics unify different semantics.
In addition, founded semantics and constraint semantics are completely declarative, as a least fixed point and as constraint satisfaction, respectively. Our default declarations without closed predicates lead to the same semantics as WFS and SMS for all natural examples we have found. Additionally, founded semantics without closed predicates can be computed in linear time in the size of the ground program, as opposed to quadratic time for WFS.
There are many directions for future study, including additional relationships with prior semantics, further extensions, efficient implementations, and applications.
Notes
- 1.
Even a contrived example that demonstrates the worst-case quadratic-time computation of WFS has been challenging to find. For example, the quadratic-time example in [13] turns out to be linear in XSB; after significant effort between us and Warren, we found a much more sophisticated example that appears to take quadratic time, but a remaining bug in XSB makes the correctness of its computation unclear.
References
Apt, K.R., Bol, R.N.: Logic programming and negation: a survey. J. Log. Program. 19, 9–71 (1994)
Fitting, M.: Fixpoint semantics for logic programming: a survey. Theor. Comput. Sci. 278(1), 25–51 (2002)
Clark, K.L.: Negation as failure. In: Gallaire, H., Minker, J. (eds.) Logic and Databases, pp. 293–322. Plenum Press, New York (1978)
Van Gelder, A., Ross, K., Schlipf, J.S.: The well-founded semantics for general logic programs. J. ACM 38(3), 620–650 (1991)
Gelfond, M., Lifschitz, V.: The stable model semantics for logic programming. In: Proceedings of the 5th International Conference and Symposium on Logic Programming, pp. 1070–1080. MIT Press (1988)
Apt, K.R., Blair, H.A., Walker, A.: Towards a theory of declarative knowledge. In: Foundations of Deductive Databases and Logic Programming, pp. 89–148. Morgan Kaufman (1988)
Fitting, M.: A Kripke-Kleene semantics for logic programs. J. Log. Program. 2(4), 295–312 (1985)
Ceri, S., Gottlob, G., Tanca, L.: Logic Programming and Databases. Springer, Heidelberg (1990)
Abiteboul, S., Hull, R., Vianu, V.: Foundations of Databases: The Logical Level. Addison-Wesley, Reading (1995)
Liu, Y.A., Stoller, S.D.: The founded semantics and constraint semantics of logic rules. Computing Research Repository arXiv:1606.06269 [cs.LO] (Revised 2017) (2016)
Chen, W., Kifer, M., Warren, D.S.: HiLog: a foundation for higher-order logic programming. J. Log. Program. 15(3), 187–230 (1993)
Liu, Y.A., Stoller, S.D.: From datalog rules to efficient programs with time and space guarantees. ACM Trans. Program. Lang. Syst. 31(6), 1–38 (2009)
Zukowski, U.: Flexible computation of the well-founded semantics of normal logic programs. Ph.D. thesis, Faculty of Computer Science and Mathematics, University of Passau (2001)
Przymusinski, T.C.: Well-founded and stationary models of logic programs. Ann. Math. Artif. Intell. 12(3), 141–187 (1994)
Ramakrishnan, R., Ullman, J.D.: A survey of deductive database systems. J. Log. Program. 23(2), 125–149 (1995)
Lloyd, J.W., Topor, R.W.: Making Prolog more expressive. J. Log. Program. 1(3), 225–240 (1984)
Sato, T., Tamaki, H.: Transformational logic program synthesis. In: Proceedings of the International Conference on Fifth Generation Computer Systems, pp. 195–201 (1984)
Jaffar, J., Lassez, J.-L., Maher, M.J.: Some issues and trends in the semantics of logic programming. In: Shapiro, E. (ed.) ICLP 1986. LNCS, vol. 225, pp. 223–241. Springer, Heidelberg (1986). https://doi.org/10.1007/3-540-16492-8_78
Chan, D.: Constructive negation based on the completed database. In: Proceedings of the 5th International Conference and Symposium on Logic Programming, pp. 111–125. MIT Press (1988)
Foo, N.Y., Rao, A.S., Taylor, A., Walker, A.: Deduced relevant types and constructive negation. In: Proceedings of the 5th International Conference and Symposium on Logic Programming, pp. 126–139 (1988)
Stuckey, P.J.: Constructive negation for constraint logic programming. In: Proceedings of the 6th Annual IEEE Symposium on Logic in Computer Science, pp. 328–339 (1991)
Denecker, M., Ternovska, E.: A logic of nonmonotone inductive definitions. ACM Trans. Comput. Log. 9(2), 14 (2008)
Dung, P.M.: On the relations between stable and well-founded semantics of logic programs. Theor. Comput. Sci. 105(1), 7–25 (1992)
Lin, F., Zhao, Y.: Assat: computing answer sets of a logic program by sat solvers. Artif. Intell. 157(1–2), 115–137 (2004)
Acknowledgment
We thank David S. Warren, Michael Kifer, Anil Nerode, Tuncay Tekle, Molham Aref, Marc Denecker, Cordell Green, Goyal Gupta, Bob Kowalski, Fangzhen Lin, Alberto Pettorossi, Maurizio Proietti, Neng-Fa Zhou, and many others for helpful comments and discussions on logic languages, semantics, and efficient computations.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Comparison of Semantics for Well-Known Small Examples and More
A Comparison of Semantics for Well-Known Small Examples and More
Table 2 shows well-known example rules and more for tricky boundary cases in the semantics, where all uncertain predicates that are in a conclusion are declared complete, but not closed, and shows different semantics for them.
-
Programs 1 and 2 contain only negative cycles. All three of Founded, WFS, and Fitting agree. All three of Constraint, SMS, and Supported agree.
-
Programs 3 and 4 contain only positive cycles. Founded for certain agrees with WFS; Founded for uncertain agrees with Fitting. Constraint for certain agrees with SMS; Constraint for uncertain agrees with Supported.
-
Programs 5 and 6 contain no cycles. Founded for certain agrees with WFS and Fitting; Founded for uncertain has more undefined. Constraint for certain agrees with SMS and Supported; Constraint for uncertain has more models.
-
Programs 7 and 8 contain both negative and positive cycles. For program 7 where
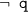 and q are disjunctive, all three of Founded, WFS, and Fitting agree; Constraint and Supported agree, but SMS has no model. For program 8 where
and q are disjunctive, all three of Founded, WFS, and Fitting agree; Constraint and Supported agree, but SMS has no model. For program 8 where 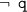 and q are conjunctive, Founded and Fitting agree, but WFS has q being \(F\); all three of Constraint, SMS, and Supported agree.
and q are conjunctive, Founded and Fitting agree, but WFS has q being \(F\); all three of Constraint, SMS, and Supported agree.
For all 8 programs, with default complete but not closed predicates, we have the following:
-
If all predicates are the default certain or uncertain, then Founded agrees with WFS, and Constraint agrees with SMS, with one exception for each:
-
(1)
Program 7 concludes q whether q is \(F\) or \(T\), so SMS having no model is an extreme outlier among all 6 semantics and is not consistent with common sense.
-
(2)
Program 8 concludes q if q is \(F\) and \(T\), so Founded semantics with q being \(U\) is imprecise, but Constraint has q being \(F\). WFS has q being \(F\) because it uses \(F\) for ignorance.
-
(1)
-
If predicates not in any conclusion are certain (not shown in Table 2 but only needed for q in programs 5 and 6), and other predicates are uncertain, then Founded equals Fitting, and Constraint equals Supported, as captured in Theorems 7 and 11, respectively.
-
If all predicates are uncertain, then Founded has all values being \(U\), capturing the well-known unclear situations in all these programs, and Constraint gives all different models except for programs 2 and 5, and programs 4 and 6, which are pair-wise equivalent under completion, capturing exactly the differences among all these programs.
Finally, if all predicates in these programs are not complete, then Founded and Constraint are the same as in Table 2 except that Constraint for uncertain becomes equivalent to truth values in first-order logic: programs 1 and 8 have an additional model, {q}, program 6 has an additional model, {\(\overline{\text{ p }}\), q}, and programs 2 and 5 have an additional model, {p,q}.
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG
About this paper
Cite this paper
Liu, Y.A., Stoller, S.D. (2018). Founded Semantics and Constraint Semantics of Logic Rules. In: Artemov, S., Nerode, A. (eds) Logical Foundations of Computer Science. LFCS 2018. Lecture Notes in Computer Science(), vol 10703. Springer, Cham. https://doi.org/10.1007/978-3-319-72056-2_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-72056-2_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-72055-5
Online ISBN: 978-3-319-72056-2
eBook Packages: Computer ScienceComputer Science (R0)





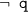 and
and 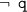 and
and