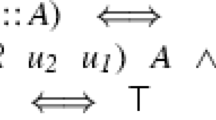Compositional Model Checking Is Lively

Abstract

Compositional model checking approaches attempt to limit state space explosion by iteratively combining behaviour of some of the components in the system and reducing the result modulo an appropriate equivalence relation. For an equivalence relation to be applicable, it should be a congruence for parallel composition where synchronisations between the components may be introduced. An equivalence relation preserving both safety and liveness properties is divergence-preserving branching bisimulation (DPBB). It is generally assumed that DPBB is a congruence for parallel composition, even in the context of synchronisations between components. However, so far, no such results have been published.

This work finally proves that this is the case. Furthermore, we discuss how to safely decompose an existing LTS network in components such that the re-composition is equivalent to the original LTS network. All proofs have been mechanically verified using the Coq proof assistant.

Finally, to demonstrate the effectiveness of compositional model checking with intermediate DPBB reductions, we discuss the results we obtained after having conducted a number of experiments.

This work is supported by ARTEMIS Joint Undertaking project EMC2 (grant nr. 621429).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Model checking [3, 9] is one of the most successful approaches for the analysis and verification of the behaviour of concurrent systems. However, a major issue is the so-called state space explosion problem: the state space of a concurrent system tends to increase exponentially as the number of parallel processes increases linearly. Often, it is difficult or infeasible to verify realistic large scale concurrent systems. Over time, several methods have been proposed to tackle the state space explosion problem. Prominent approaches are the application of some form of on-the-fly reduction, such as Partial Order Reduction [30] or Symmetry Reduction [7], and compositionally verifying the system, for instance using Compositional Reasoning [8] or Partial Model Checking [1, 2].

The key operations in compositional approaches are the composition and decomposition of systems. First a system is decomposed into two or more components. Then, one or more of these components is manipulated (e.g., reduced). Finally, the components are re-composed. Comparison modulo an appropriate equivalence relation is applied to ensure that the manipulations preserve properties of interest (for instance, expressed in the modal $\mu$-calculus [19]). These manipulations are sound if and only if the equivalence relation is a congruence for the composition expression.

Two prominent equivalence relations are branching bisimulation and divergence-preserving branching bisimulation (DPBB) [13, 15].¹ Branching bisimulation preserves safety properties, while DPBB preserves both safety and liveness properties.

In [14] it is proven that DPBB is the coarsest equivalence that is a congruence for parallel composition. However, compositional reasoning requires equivalences that are a congruence for parallel composition where new synchronisations between parallel components may be introduced, which is not considered by the authors. It is known that branching bisimulation is a congruence for parallel composition of synchronising Labelled Transition Systems (LTSs), this follows from the fact that parallel composition of synchronising LTSs can be expressed as a WB cool language [6]. However, obtaining such results for DPBB requires more work. To rigorously prove that DPBB is indeed a congruence for parallel composition of synchronising LTSs, a proof assistant, such as Coq [5], is required. So far, no results, obtained with or without the use of a proof assistant, have been reported.

A popular toolbox that offers a selection of compositional approaches is Cadp [12]. Cadp offers both property-independent approaches (e.g., compositional model generation, smart reduction, and compositional reasoning via behavioural interfaces) and property-dependent approaches (e.g., property-dependent reductions [25] and partial model checking [1]). The formal semantics of concurrent systems are described using networks of LTSs [22], or LTS networks for short. An LTS network consists of n LTSs representing the parallel processes. A set of synchronisation laws is used to describe the possible communication, i.e., synchronisation, between the process LTSs.

In this setting, this work considers parallel composition of synchronising LTS networks. Given two LTS networks $\mathcal {M}$ and $\mathcal {M}'$ of size n related via a DPBB relation $B$, another LTS network $\mathcal {N}$ of size m, and a parallel composition operator $\parallel _\sigma$ with a mapping $\sigma$ that specifies synchronization between components, we show there is a DPBB relation $C$ such that

$$ \mathcal {M}\;\;B\;\; \mathcal {M}' \implies \mathcal {M}\parallel _\sigma \mathcal {N}\;\;C\;\; \mathcal {M}' \parallel _\sigma \mathcal {N}$$

This result subsumes the composition of individual synchronising LTSs via composition of LTS networks of size one. Moreover, generalization to composition of multiple LTS networks can be obtained via a reordering of the processes within LTS networks.

Contributions. In this work, we prove that divergence-preserving branching bisimulation is a congruence for parallel composition of synchronising LTSs. Furthermore, we present a method to safely decompose an LTS network in components such that the composition of the components is equivalent to the original LTS network. The proofs have been mechanically verified using the Coq proof assistant and are available online.²

Finally, we discuss the effectiveness of compositionally constructing state spaces with intermediate DPBB reductions in comparison with the classical, non-compositional state space construction. The discussion is based on results we obtained after having conducted a number of experiments using the Cadp toolbox. The authors of [11] report on experiments comparing the run-time and memory performance of three compositional verification techniques. As opposed to these experiments, our experiments concern the comparison of compositional and classical, non-compositional state space construction.

Structure of the paper. Related work is discussed in Sect. 2. In Sect. 3, we discuss the notions of LTS, LTS network, so-called LTS network admissibility, and DPBB. Next, the formal composition of LTS networks is presented in Sect. 4. We prove that DPBB is a congruence for the composition of LTS networks. Section 5 is on the decomposition of an LTS network. Decomposition allows the redefinition of a system as a set of components. In Sect. 6 we apply the theoretical results to a set of use cases comparing a compositional construction approach with non-compositional state space construction. In Sect. 7 we present the conclusions and directions for future work.

2 Related Work

Networks of LTSs are introduced in [21]. The authors mention that strong and branching bisimulations are congruences for the operations supported by LTS networks. Among these operations is the parallel composition with synchronisation on equivalent labels. A proof for branching bisimulation has been verified in PVS and a textual proof was written, but both the textual proof and the PVS proof have not been made public [23]. An axiomatisation for a rooted version of divergence-preserving branching bisimulation has been performed in a Master graduation project [33]. However, the considered language does not include parallel composition. In this paper, we formally show that DPBB is also a congruence for parallel composition with synchronisations between components. As DPBB is a branching bisimulation relation with an extra case for explicit divergence, the proof we present also formally shows that branching bisimulation is a congruence for parallel composition with synchronisations between components.

Another approach supporting compositional verification is presented in [22]. Given an LTS network and a component selected from the network the approach automatically generates an interface LTS from the remainder of the network. This remainder of the network is called the environment. The interface LTS represents the synchronisation possibilities that are offered by the environment. This requires the construction and reduction of the system LTS of the environment. The advantage of this method is that transitions and states that do not contribute to the system LTS can be removed. In our approach only the system LTS of the considered component must be constructed. The environment is left out of scope until the components are composed.

Many process algebras support parallel composition with synchronisation on labels. Often a proof is given showing that some bisimulation is a congruence for these operators [10, 20, 24, 26]. However, to the best of our knowledge no such proofs exist considering DPBB. Furthermore, if LTSs can be derived from their semantics (such as is the case with Structural Operational Semantics) then the fact that DPBB is a congruence for such a parallel composition can be directly derived from our results.

To generalize the congruence proofs a series of meta-theories have been proposed for algebras with parallel composition [6, 34, 35]. In [35] the panth format is proposed. They show that strong bisimulation is a congruence for algebras that adhere to the panth format. The focus of the work is on the expressiveness of the format. The author of [6] proposes WB cool formats for four bisimulations: weak bisimulation, rooted weak bisimulation, branching bisimulation, and rooted branching bisimulation. It is shown that these bisimulations are congruences for the corresponding formats. In [34] similar formats are proposed for eager bisimulation and branching bisimulation. Eager bisimulation is a kind of weak bisimulation wich is sensitive to divergence. The above mentioned formats do not consider DPBB. In our work we have shown that DPBB is a congruence for parallel composition of LTS networks and LTSs.

In earlier work, we presented decomposition for LTS transformation systems of LTS networks [36]. The work aims to verify the transformation of a component that may synchronise with other components. The paper proposes to calculate so called detaching laws which are similar to our interface laws. The approach can be modelled with our method. In fact, we show that the derivation of these detaching laws does not amount to a desired decomposition, i.e., the re-composition of the decomposition is not equivalent to the original system (see Example 3 discussed in Sect. 5).

A projection of an LTS network given a set of indices is presented in [12]. Their projection operator is similar to the consistent decomposition of LTS networks that we proposed. In fact, with a suitable operator for the reordering of LTS networks our decomposition operation is equivalent to their projection operator. The current paper contributes to these results that admissibility properties of the LTS network are indeed preserved for such consistent decompositions.

3 Preliminaries

In this section, we introduce the notions of LTS, LTS network, and divergence-preserving branching bisimulation of LTSs. The potential behaviour of processes is described by means of LTSs. The behaviour of a concurrent system is described by a network of LTSs [22], or LTS network for short. From an LTS network, a system LTS can be derived describing the global behaviour of the network. To compare the behaviour of these systems the notion of divergence-preserving branching bisimulation (DPBB) is used. DPBB is often used to reduce the state space of system specifications while preserving safety and liveness properties, or to compare the observable behaviour of two systems.

The semantics of a process, or a composition of several processes, can be formally expressed by an LTS as presented in Definition 1.

Definition 1

(Labelled Transition System). An LTS $\mathcal {G}$ is a tuple $( \mathcal {S}_{\mathcal {G}}, \mathcal {A}_{\mathcal {G}},$ $\mathcal {T}_{\mathcal {G}}, \mathcal {I}_{\mathcal {G}} )$, with

• $\mathcal {S}_{\mathcal {G}}$ a finite set of states;

• $\mathcal {A}_{\mathcal {G}}$ a set of action labels;

• $\mathcal {T}_{\mathcal {G}} \subseteq \mathcal {S}_{\mathcal {G}} \times \mathcal {A}_{\mathcal {G}} \times \mathcal {S}_{\mathcal {G}}$ a transition relation;

• $\mathcal {I}_{\mathcal {G}} \subseteq \mathcal {S}_{\mathcal {G}}$ a (non-empty) set of initial states.

Action labels in $\mathcal {A}_{\mathcal {G}}$ are denoted by a, b, c, etc. Additionally, there is a special action label $\tau$ that represents internal, or hidden, system steps. A transition $( s, a, s' ) \in \mathcal {T}_{\mathcal {G}}$, or $s \xrightarrow {a}_\mathcal {G}s'$ for short, denotes that LTS $\mathcal {G}$ can move from state s to state $s'$ by performing the a-action. The transitive reflexive closure of $\xrightarrow {a}_\mathcal {G}$ is denoted as , and the transitive closure is denoted as .

LTS Network. An LTS network, presented in Definition 2, describes a system consisting of a finite number of concurrent process LTSs and a set of synchronisation laws that define the possible interaction between the processes. We write $1..n$ for the set of integers ranging from 1 to n. A vector $\bar{v}$ of size n contains n elements indexed from 1 to n. For all $i \in 1..n$, $\bar{v}_i$ represents the $i^{th}$ element of vector $\bar{v}$. The concatenation of two vectors v and w of size n and m respectively is denoted by $v \parallel w$. In the context of composition of LTS networks, this concatenation of vectors corresponds to the parallel composition of the behaviour of the two vectors.

Definition 2

(LTS network). An LTS network $\mathcal {M}$ of size n is a pair $( \varPi , \mathcal {V})$, where

• $\varPi$ is a vector of n concurrent LTSs. For each $i \in 1..n$, we write $\varPi _i = ( \mathcal {S}_{i}, \mathcal {A}_{i}, \mathcal {T}_{i}, \mathcal {I}_{i})$.

• $\mathcal {V}$ is a finite set of synchronisation laws. A synchronisation law is a tuple $(\bar{v}, a)$, where $\bar{v}$ is a vector of size n, called the synchronisation vector, containing synchronising action labels, and a is an action label representing the result of successful synchronisation. We have $\forall i \in 1..n .\;\bar{v}_i \in \mathcal {A}_{i}\cup \{ \bullet \}$, where $\bullet$ is a special symbol denoting that $\varPi _i$ performs no action. The set of result actions of a set of synchronisation laws $\mathcal {V}$ is defined as $\mathcal {A}_{\mathcal {V}} = \{ a \mid (\bar{v}, a)\in \mathcal {V}\}$.

The explicit behaviour of an LTS network $\mathcal {M}$ is defined by its system LTS $\mathcal {G}_\mathcal {M}$ which is obtained by combining the processes in $\varPi$ according to the synchronisation laws in $\mathcal {V}$ as specified by Definition 3. The LTS network model subsumes most hiding, renaming, cutting, and parallel composition operators present in process algebras. For instance, hiding can be applied by replacing the a component in a law by $\tau$.

Definition 3

(System LTS). Given an LTS network $\mathcal {M}= ( \varPi , \mathcal {V})$, its system LTS is defined by $\mathcal {G}_\mathcal {M}= ( \mathcal {S}_{\mathcal {M}}, \mathcal {A}_{\mathcal {M}},$ $\mathcal {T}_{\mathcal {M}}, \mathcal {I}_{\mathcal {M}})$, with

• $\mathcal {I}_{\mathcal {M}}= \{ \langle s_1, \dots , s_n \rangle \mid s_i \in \mathcal {I}_{i}\}$;

• $\mathcal {T}_{\mathcal {M}}$ and $\mathcal {S}_{\mathcal {M}}$ are the smallest relation and set, respectively, satisfying $\mathcal {I}_{\mathcal {M}}\subseteq \mathcal {S}_{\mathcal {M}}$ and for all $\bar{s}\in \mathcal {S}_{\mathcal {M}}$, $a \in \mathcal {A}_{\mathcal {V}}$, we have $\bar{s}\xrightarrow {a}_{\mathcal {M}} \bar{s}'$ and $\bar{s}' \in \mathcal {S}_{\mathcal {M}}$ iff there exists $(\bar{v}, a)\in \mathcal {V}$ such that for all $i \in 1..n$:

  $$ {\left\{ \begin{array}{ll} \bar{s}_i = \bar{s}'_i &{} \text {if}\ \bar{v}_i = \bullet \\ \bar{s}_i \xrightarrow {\bar{v}_i}_{\varPi _i} \bar{s}'_i &{} \text {otherwise} \end{array}\right. } $$

• $\mathcal {A}_{\mathcal {M}}= \{ a \mid \exists \bar{s}, \bar{s}' \in \mathcal {S}_{\mathcal {M}}. \bar{s}\xrightarrow {a}_{\mathcal {M}} \bar{s}' \}$.

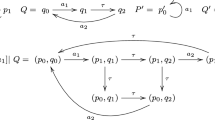
In Fig. 1, an example of an LTS network $\mathcal {M}=( \langle \varPi _1, \varPi _2\rangle , \mathcal {V})$ with four synchronisation laws is shown on the left, and the corresponding system TLS $\mathcal {G}_\mathcal {M}$ is shown on the right. Initial states are coloured black. The states of the system LTS $\mathcal {G}_\mathcal {M}$ are constructed by combining the states of $\varPi _1$ and $\varPi _2$. In this example, we have $\langle 1 , 3 \rangle , \langle 1 , 4 \rangle , \langle 2 , 3 \rangle \in \mathcal {S}_{\mathcal {M}}$, of which $\langle 1 , 3 \rangle$ is the single initial state of $\mathcal {G}_\mathcal {M}$.

Fig. 1.

An LTS network $\mathcal {M}=( \varPi , \mathcal {V})$ (left) and its system LTS $\mathcal {G}_\mathcal {M}$ (right)

The transitions of the system LTS in Fig. 1 are constructed by combining the transitions of $\varPi _1$ and $\varPi _2$ according to the set of synchronisation laws $\mathcal {V}$. Law $( \langle c, c \rangle , c )$ specifies that the process LTSs can synchronise on their c-transitions, resulting in c-transitions in the system LTS. Similarly, the process LTSs can synchronise on their d-transitions, resulting in a d-transition in $\mathcal {G}_\mathcal {M}$. Furthermore, law $( \langle a, \bullet \rangle , a )$ specifies that process $\varPi _1$ can perform an a-transition independently resulting in an a-transition in $\mathcal {G}_\mathcal {M}$. Likewise, law $( \langle \bullet , b \rangle , b )$ specifies that the b-transition can be fired independently by process $\varPi _2$. Because $\varPi _1$ does not participate in this law, it remains in state $\langle 1 \rangle$ in $\mathcal {G}_\mathcal {M}$. The last law states that a- and e-transitions can synchronise, resulting in f-transitions, however, in this example the a- and e-transitions in $\varPi _1$ and $\varPi _2$ are never able to synchronise since state $\langle 2 , 4 \rangle$ is unreachable.

An LTS network is called admissible if the synchronisation laws of the network do not synchronise, rename, or cut $\tau$-transitions [22] as defined in Definition 4. The intuition behind this is that internal, i.e., hidden, behaviour should not be restricted by any operation. Partial model checking and compositional construction rely on LTS networks being admissible [12]. Hence, in this paper, we also restrict ourselves to admissible LTS networks when presenting our composition and decomposition methods.

Definition 4

(LTS network Admissibility). An LTS network $\mathcal {M}= ( \varPi , \mathcal {V})$ of length n is called admissible iff the following properties hold:

• 1. $\forall (\bar{v}, a)\in \mathcal {V}, i \in 1..n .\;\bar{v}_i = \tau \implies \lnot \exists j \ne i .\;\bar{v}_j \ne \bullet$; (no synchronisation of $\tau$’s)

• 2. $\forall (\bar{v}, a)\in \mathcal {V}, i \in 1..n .\;\bar{v}_i = \tau \implies a = \tau$; (no renaming of $\tau$’s)

• 3. $\forall i \in 1..n .\;\tau \in \mathcal {A}_{i} \implies \exists (\bar{v}, a)\in \mathcal {V}.\;\bar{v}_i = \tau$. (no cutting of $\tau$’s)

Divergence-Preserving Branching Bisimulation. To compare LTSs, we use DPBB, also called branching bisimulation with explicit divergence [13, 15]. DPBB supports abstraction from actions and preserves both safety and liveness properties. To simplify proofs we use DPBB with the weakest divergence condition ($\text {D}_4$) presented in [15] as presented in Definition 5. This definition is equivalent to the standard definition of DPBB [15]. The smallest infinite ordinal is denoted by $\omega$.

Definition 5

(Divergence-Preserving Branching bisimulation). A binary relation B between two LTSs $\mathcal {G}_1$ and $\mathcal {G}_2$ is a divergence-preserving branching bisimulation iff for all $s \in \mathcal {S}_{\mathcal {G}_1}$ and $t \in \mathcal {S}_{\mathcal {G}_2}$, $s \;B\;t$ implies:

• 1. if $s \xrightarrow {a}_{\mathcal {G}_1} s'$ then

  • (a) either $a = \tau$ with $s' \;B\;t$;

  • (b) or $t \xrightarrow {\tau }\!\!^*_{\mathcal {G}_2} \hat{t} \xrightarrow {a}_{\mathcal {G}_2} t'$ with $s \;B\;\hat{t}$ and $s' \;B\;t'$.

• 2. symmetric to 1.

• 3. if there is an infinite sequence of states $(s^k)_{k\in \omega }$ such that $s = s^0$, $s^k \xrightarrow {\tau }_{\mathcal {G}_1} s^{k+1}$ and $s^k \;B\;t$ for all $k \in \omega$, then there exists a state $t'$ such that $t \xrightarrow {\tau }\!\!^+_{\mathcal {G}_2} t'$ and $s^k \;B\;t'$ for some $k \in \omega$.

• 4. symmetric to 3.

Two states $s \in \mathcal {S}_{\mathcal {G}_1}$ and $t \in \mathcal {S}_{\mathcal {G}_2}$ are divergence-preserving branching bisimilar, denoted by $s \;\underline{\leftrightarrow }_b^\Delta \;t$, iff there is a DPBB relation B such that $s \;B\;t$. We say that two LTSs $\mathcal {G}_1$ and $\mathcal {G}_2$ are divergence-preserving branching bisimilar, denoted by $\mathcal {G}_1 \;\underline{\leftrightarrow }_b^\Delta \;\mathcal {G}_2$, iff $\forall s_1 \in \mathcal {I}_{\mathcal {G}_1}. \exists s_2 \in \mathcal {I}_{\mathcal {G}_2} .\;s_1 \;\underline{\leftrightarrow }_b^\Delta \;s_2$ and vice versa.

4 Composition of LTS Networks

This section introduces the compositional construction of LTS networks. Composition of process LTSs results in a system LTS that tends to grow exponentially when more processes are considered.

An LTS network can be seen as being composed of several components, each of which consists of a number of individual processes in parallel composition, with intra-component synchronisation laws describing how the processes inside a component should synchronise with each other. Furthermore, inter-component synchronisation laws define how the components as a whole should synchronise with each other. Compositional construction of a minimal version of the final system LTS may then be performed by first constructing the system LTSs of the different components, then minimising these, and finally combining their behaviour. Example 1 presents an example of a network with two components and an inter-component synchronisation law.

Example 1

(Component). Consider an LTS network $\mathcal {M}= ( \varPi , \mathcal {V})$ with processes $\varPi = \langle \varPi _1, \varPi _2, \varPi _3 \rangle$ and synchronisation laws $\mathcal {V}= \{( \langle a, \bullet , \bullet \rangle , a ), ( \langle \bullet , b, b \rangle , b ), ( \langle c, c, c \rangle , c )\}$. We may split up the network in two components, say $M_1 = ( \langle \varPi _1 \rangle , \mathcal {V}_1 )$ and $\mathcal {M}_{\{2,3\}} = ( \langle \varPi _2, \varPi _3 \rangle , \mathcal {V}_{\{2,3\}} )$. Then, $( \langle c,c,c \rangle , c )$ is an inter-component law describing synchronisation between $\mathcal {M}_1$ and $\mathcal {M}_{\{2,3\}}$. The component $\mathcal {M}_1$ consists of process $\varPi _1$, and the set of intra-component synchronisation laws $\mathcal {V}_1 = \{( \langle a, \bullet , \bullet \rangle , a )\}$ operating solely on $\varPi _1$. Similarly, component $\mathcal {M}_{\{2,3\}}$ consists of $\varPi _2$ and $\varPi _3$, and the set of intra-component synchronisation laws $\mathcal {V}_{\{2,3\}} = \{ ( \langle \bullet , b, b \rangle , b ) \}$ operating solely on $\varPi _2$ and $\varPi _3$.

The challenge of compositional construction is to allow manipulation of the components while guaranteeing that the observable behaviour of the system as a whole remains equivalent modulo DPBB. Even though synchronisation laws of a component may be changed, we must somehow preserve synchronisations with the other components. Such a change of synchronisation laws occurs, for instance, when reordering the processes in a component, or renaming actions that are part of inter-component synchronisation laws.

In this paper, we limit ourselves to composition of two components: a left and a right component. This simplifies notations and proofs. However, the approach can be generalised to splitting networks given two sets of indices indicating which processes are part of which component, i.e., a projection operator can be used to project distinct parts of a network into components.

In the remainder of this section, first, we formalise LTS networks composition. Then, we show that admissibility is preserved when two admissible networks are composed. Finally, we prove that DPBB is a congruence for composition of LTS networks.

Composing LTS networks. Before defining the composition of two networks, we introduce a mapping indicating how the inter-component laws should be constructed from the interfaces of the two networks. An inter-component law can then be constructed by combining the interface vectors of the components and adding a result action. This is achieved through a given interface mapping, presented in Definition 6, mapping interface actions to result actions.

Definition 6

(Interface Mapping). Consider LTS networks $\mathcal {M}_\varPi = ( \varPi , \mathcal {V})$ and $\mathcal {M}_\mathrm {P}= ( \mathrm {P}, \mathcal {W})$ of size n and m, respectively. An interface mapping between $\mathcal {M}_\varPi$ and $\mathcal {M}_\mathrm {P}$ is a mapping $\sigma : \mathcal {A}_{\mathcal {V}}\setminus \{\tau \} \times \mathcal {A}_{\mathcal {W}}\setminus \{\tau \} \times \mathcal {A}_{\sigma }$ describing how the interface actions of $\mathcal {M}_\varPi$ should be combined with interface actions of $\mathcal {M}_\mathrm {P}$, and what the action label should be resulting from successful synchronisation. The set $\mathcal {A}_{\sigma }$ is the set of actions resulting from successful synchronisation between $\varPi$ and $\mathrm {P}$. The actions mapped by $\sigma$ are considered the interface actions.

An interface mapping implicitly defines how inter-component synchronisation laws should be represented in the separate components. These local representatives are called the interface synchronisation laws. A mapping between $\mathcal {M}_\varPi = ( \varPi , \mathcal {V})$ and $\mathcal {M}_\mathrm {P}= ( \mathrm {P}, \mathcal {W})$ implies the following sets of interface synchronisation laws:

$$ \mathcal {V}_\sigma = \{ ( \bar{v}, a ) \in \mathcal {V}\mid \exists b, c .\;( a, b, c ) \in \sigma \} $$

$$ \mathcal {W}_\sigma = \{ ( \bar{w}, b ) \in \mathcal {W}\mid \exists a, c .\;( a, b, c ) \in \sigma \} $$

An interface synchronisation law makes a component’s potential to synchronise with other components explicit. An interface synchronisation law has a synchronisation vector, called the interface vector, that may be part of inter-component laws. The result action of an interface synchronisation law is called an interface action. These notions are clarified further in Example 2.

Example 2

(Interface Vector and Interface Law). Let $\mathcal {M}=( \langle \varPi _1, \varPi _2, \varPi _3 \rangle , \mathcal {V})$ be a network with inter-component synchronisation law $( \langle a,a,b \rangle , c ) \in \mathcal {V}$ and a component $M_{\{1,2\}} = ( \langle \varPi _1, \varPi _2 \rangle , \mathcal {V}_{\{1,2\}})$. Then, $\langle a , a \rangle$ is an interface vector of $M_{\{1,2\}}$, and given a corresponding interface action $\alpha$, the interface law is $( \langle a , a \rangle , \alpha )$.

Together the interface laws and interface mapping describe the possible synchronisations between two components, i.e., the interface laws and interface mapping describe inter-component synchronisation laws. Given two sets of laws $\mathcal {V}$ and $\mathcal {W}$ and an interface mapping $\sigma$, the inter-component synchronisation laws are defined as follows:

$$ \sigma (\mathcal {V}, \mathcal {W}) = \{( \bar{v}\parallel \bar{w}, a ) \mid ( \bar{v}, \alpha ) \in \mathcal {V}\wedge ( \bar{w}, \beta ) \in \mathcal {W}\wedge ( \alpha , \beta , a ) \in \sigma \} $$

The mapping partitions both $\mathcal {V}$ and $\mathcal {W}$ into two sets of synchronisation laws: the interface and non-interface synchronisation laws.

The application of the interface mapping, i.e., formal composition of two LTS networks, is presented in Definition 7. We show that a component may be exchanged with a divergence-preserving branching bisimilar component iff the interface actions are not hidden. In other words, the interfacing with the remainder of the networks is respected when the interface actions remain observable.

Definition 7

(Composition of LTS networks). Consider LTS networks $\mathcal {M}_\varPi = ( \varPi , \mathcal {V})$ of size n and $\mathcal {M}_\mathrm {P}= ( \mathrm {P}, \mathcal {W})$ of size m. Let $\sigma : \mathcal {A}_{\mathcal {V}}\setminus \{\tau \} \times \mathcal {A}_{\mathcal {W}}\setminus \{\tau \} \times \mathcal {A}_{ }$ be an interface mapping describing the synchronisations between $\mathcal {M}_\varPi$ and $\mathcal {M}_\mathrm {P}$. The composition of $\mathcal {M}_\varPi$ and $\mathcal {M}_\mathrm {P}$, denoted by $\mathcal {M}_\varPi \parallel _\sigma \mathcal {M}_\mathrm {P}$, is defined as the LTS network $( \varPi \parallel \mathrm {P}, (\mathcal {V}\setminus \mathcal {V}_\sigma )^\bullet \cup \;^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma ) \cup \sigma (\mathcal {V},\mathcal {W}) )$, where $(\mathcal {V}\setminus \mathcal {V}_\sigma )^\bullet = \{( \bar{v}\parallel \bullet ^m, a ) \mid (\bar{v}, a)\in \mathcal {V}\setminus \mathcal {V}_\sigma \}$ and $^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma ) = \{( \bullet ^n \parallel \bar{v}, a ) \mid (\bar{v}, a)\in \mathcal {W}\setminus \mathcal {W}_\sigma \}$ are the sets of synchronisation laws $\mathcal {V}\setminus \mathcal {V}_\sigma$ padded with m $\bullet$’s and $\mathcal {W}\setminus \mathcal {W}_\sigma$ padded with n $\bullet$’s, respectively.

As presented in Proposition 1, LTS networks that are composed (according to Definition 7) from two admissible networks are admissible as well. Therefore, composition of LTS networks is compatible with the compositional verification approaches of [12].

Proposition 1

Let $\mathcal {M}_\varPi = ( \varPi , \mathcal {V})$ and $\mathcal {M}_\mathrm {P}= ( \mathrm {P}, \mathcal {W})$ be admissible LTS networks of length n and m, respectively. Furthermore, let $\sigma : \mathcal {A}_{\mathcal {V}}\setminus \{\tau \} \times \mathcal {A}_{\mathcal {W}}\setminus \{\tau \} \times \mathcal {A}_{ }$ be an interface mapping. Then, the network $\mathcal {M}= \mathcal {M}_\varPi \parallel _\sigma \mathcal {M}_\mathrm {P}$, composed according to Definition 7, is also admissible.

Proof

We show that $\mathcal {M}$ satisfies Definition 4:

• No synchronisation and renaming of $\tau$ ’s. Let $( \bar{v}, a ) \in (\mathcal {V}\setminus \mathcal {V}_\sigma )^\bullet \cup {^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma )} \cup \sigma (\mathcal {V},\mathcal {W})$ be a synchronisation law with $\bar{v}_i = \tau$ for some $i \in 1..(n + m)$. We distinguish two cases:

  • $( \bar{v}, a ) \in (\mathcal {V}\setminus \mathcal {V}_\sigma )^\bullet \cup {^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma )}$. By construction of $(\mathcal {V}\setminus \mathcal {V}_\sigma )^\bullet$ and ${^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma )}$, and admissibility of $\mathcal {M}_\varPi$ and $\mathcal {M}_\mathrm {P}$, we have $\forall j \in 1..n .\;\bar{v}_j \ne \bullet \implies i = j$, $\forall j \in (n+1)..(n+m) .\;\bar{v}_j \ne \bullet \implies i = j$ and $a = \tau$. Hence, it holds that $\forall j \in 1..(n+m) .\;\bar{v}_j \ne \bullet \implies i = j$ (no synchronisation of $\tau$’s) and $a = \tau$ (no renaming of $\tau$’s).

  • $( \bar{v}, a ) \in \sigma (\mathcal {V}, \mathcal {W})$. By definition of $\sigma (\mathcal {V},\mathcal {W})$, there are interface laws $( \bar{v}', \alpha ' ) \in \mathcal {V}$ and $( \bar{v}'', \alpha '' ) \in \mathcal {W}$ such that $( \alpha ', \alpha '', a ) \in \sigma$. Hence, either $1 \le i \le n$ with $\bar{v}'_i = \tau$ or $n < i \le n+m$ with $\bar{v}''_{i-n} = \tau$. Since $\mathcal {M}_\varPi$ and $\mathcal {M}_\mathrm {P}$ are admissible, we must have $\alpha ' = \tau$ or $\alpha '' = \tau$, respectively. However, the interface mapping does not allow $\tau$ as interface actions, therefore, the proof follows by contradiction.

  It follows that $\mathcal {M}$ does not allow synchronisation and renaming of $\tau$’s.

• No cutting of $\tau$ ’s. Let $(\varPi \parallel \mathrm {P})_i$ be a process with $\tau \in \mathcal {A}_{(\varPi \parallel \mathrm {P})_i}$ for some $i \in 1 .. (n+m)$. We distinguish the two cases $1 \le i \le n$ and $n<i <m$. It follows that $\tau \in \mathcal {A}_{\varPi _i}$ for the former case and $\tau \in \mathcal {A}_{\mathrm {P}_{i-n}}$ for the latter case. Since both $\mathcal {M}_\varPi$ and $\mathcal {M}_\mathrm {P}$ are admissible and no actions are removed in $(\mathcal {V}\setminus \mathcal {V}_\sigma )^\bullet$ and ${^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma )}$, in both cases there exists a $(\bar{v}, a)\in \ (\mathcal {V}\setminus \mathcal {V}_\sigma )^\bullet \cup {^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma )} \cup \sigma (\mathcal {V},\mathcal {W})$ such that $\bar{v}_i = \tau$. Hence, the composite network $\mathcal {M}$ does not allow cutting of $\tau$’s.

Since the three admissibility properties hold, the composed network $\mathcal {M}$ satisfies Definition 4.   $\square$

DPBB is a congruence for LTS network composition. Proposition 2 shows that DPBB is a congruence for the composition of LTS networks according to Definition 7. It is worth noting that an interface mapping does not map $\tau$’s, i.e., synchronisation of $\tau$-actions is not allowed. In particular, this means that interface actions must not be hidden when applying verification techniques on a component.

Note that Proposition 2 subsumes the composition of single LTSs, via composition of LTS networks of size one with trivial sets of intra-component synchronisation laws.

Proposition 2

Consider LTS networks $\mathcal {M}_\varPi = ( \varPi , \mathcal {V})$, $\mathcal {M}_{\varPi '} = ( \varPi ', \mathcal {V}' )$ of size n, and $\mathcal {M}_\mathrm {P}= ( \mathrm {P}, \mathcal {W})$ of size m. Let $\sigma$ be an interface mapping describing the coupling between the interface actions in $\mathcal {A}_{\mathcal {V}}$ and $\mathcal {A}_{\mathcal {W}}$. The following holds

Proof

Intuitively, we have $\mathcal {M}_\varPi \parallel _\sigma \mathcal {M}_\mathrm {P}\;\underline{\leftrightarrow }_b^\Delta \;\mathcal {M}_{\varPi '} \parallel _\sigma \mathcal {M}_\mathrm {P}$ because $\mathcal {M}_\varPi \;\underline{\leftrightarrow }_b^\Delta \;\mathcal {M}_{\varPi '}$ and the interface with $\mathcal {M}_\mathrm {P}$ is respected. Since $\mathcal {M}_\varPi \;\underline{\leftrightarrow }_b^\Delta \;\mathcal {M}_{\varPi '}$, whenever a transition labelled with an interface action $\alpha$ in $\mathcal {M}_\varPi$ is able to perform a transition together with $\mathcal {M}_\mathrm {P}$, then $\mathcal {M}_{\varPi '}$ is able to simulate the interface $\alpha$-transition and synchronise with $\mathcal {M}_\mathrm {P}$. It follows that the branching structure and divergence is preserved. For the sake of brevity we define the following shorthand notations: $\mathcal {M}= \mathcal {M}_\varPi \parallel _\sigma \mathcal {M}_\mathrm {P}$ and $\mathcal {M}' = \mathcal {M}_{\varPi '} \parallel _\sigma \mathcal {M}_\mathrm {P}$. We show $\mathcal {M}_\varPi \;\underline{\leftrightarrow }_b^\Delta \;\mathcal {M}_{\varPi '} \implies \mathcal {M}\;\underline{\leftrightarrow }_b^\Delta \;\mathcal {M}'$.

Let $B$ be a DPBB relation between $\mathcal {M}_\varPi$ and $\mathcal {M}_{\varPi '}$, i.e., $\mathcal {M}_\varPi \;\underline{\leftrightarrow }_b^\Delta \;\mathcal {M}_{\varPi '}$. By definition, we have $\mathcal {M}\;\underline{\leftrightarrow }_b^\Delta \;\mathcal {M}'$ iff there exists a DPBB relation C with $\mathcal {I}_{\mathcal {M}}\;\underline{\leftrightarrow }_b^\Delta \;\mathcal {I}_{\mathcal {M}'}$. We define $C$ as follows:

The component that is subject to change is related via the relation B that relates the states in $\varPi$ and $\varPi '$. The unchanged component of the network is related via the shared state $\bar{r}$, i.e., it relates the states of $\mathrm {P}$ to themselves.

To prove the proposition we have to show that $C$ is a DPBB relation. This requires proving that $C$ relates the initial states of $\mathcal {M}$ and $\mathcal {M}'$ and that $C$ satisfies Definition 5.

$\bullet \;$ $C$ relates the initial states of $\mathcal {M}$ and $\mathcal {M}'$, i.e.,  $\mathcal {I}_{\mathcal {M}} \;C\;\mathcal {I}_{\mathcal {M}'}$. We show that $\forall \bar{s}\in \mathcal {I}_{\mathcal {M}}.\;\exists \bar{t}\in \mathcal {I}_{\mathcal {M}'} .\;\bar{s}\;C\;\bar{t}$, the other case is symmetrical. Take an initial state $\bar{s}\parallel \bar{r}\in \mathcal {I}_{\mathcal {M}}$. Since $\mathcal {I}_{\mathcal {M}_\varPi } \;B\;\mathcal {I}_{\mathcal {M}_{\varPi '}}$ and $\bar{s}\in \mathcal {I}_{\mathcal {M}_\varPi }$, there exists a $\bar{t}\in \mathcal {I}_{\mathcal {M}_{\varPi '}}$ such that $\bar{s}\;B\;\bar{t}$. Therefore, we have $\bar{s}\parallel \bar{r}\;C\;\bar{t}\parallel \bar{r}$. Since $\bar{s}\parallel \bar{r}$ is an arbitrary state in $\mathcal {I}_{\mathcal {M}}$ the proof holds for all states in $\mathcal {I}_{\mathcal {M}}$. Furthermore, since the other case is symmetrical it follows that $\mathcal {I}_{\mathcal {M}} \;C\;\mathcal {I}_{\mathcal {M}'}$.

$\bullet \;$ If $\bar{s}\;C\;\bar{t}$ and $\bar{s}\xrightarrow {a}_{\mathcal {M}} \bar{s}'$ then either $a = \tau \wedge \bar{s}' \;C\;\bar{t}$, or $\bar{t}\xrightarrow {\tau }\!\!^*_{\mathcal {M}'} \hat{\bar{t}} \xrightarrow {a}_{\mathcal {M}'} \bar{t}' \wedge \bar{s}\;C\;\hat{\bar{t}} \wedge \bar{s}' \;C\;\bar{t}'$. To better distinguish between the two parts of the networks, we unfold C and reformulate the proof obligation as follows: If $\bar{s}\;B\;\bar{t}$ and $\bar{s}\parallel \bar{r}\xrightarrow {a}_{\mathcal {M}} \bar{s}' \parallel \bar{r}'$ then either $a = \tau \wedge \bar{s}' \;B\;\bar{t}\wedge \bar{r}= \bar{r}'$, or $\bar{t}\parallel \bar{r}\xrightarrow {\tau }\!\!^*_{\mathcal {M}'} \hat{\bar{t}} \parallel \bar{r}\xrightarrow {a}_{\mathcal {M}'} \bar{t}'\parallel \bar{r}' \wedge \bar{s}\;B\;\hat{\bar{t}} \wedge \bar{s}' \;B\;\bar{t}'$. Consider synchronisation law $( \bar{v}\parallel \bar{w}, a ) \in (\mathcal {V}\setminus \mathcal {V}_\sigma )^\bullet \cup {^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma )} \cup \sigma (\mathcal {V}, \mathcal {W})$ enabling the transition ${\bar{s}\parallel \bar{r}\xrightarrow {a}_{\mathcal {M}} \bar{s}' \parallel \bar{r}'}$. We distinguish three cases:

• 1. $( \bar{v}\parallel \bar{u}, a ) \in (\mathcal {V}\setminus \mathcal {V}_\sigma )^\bullet$. It follows that $\bar{w}=\bullet ^m$, and thus, subsystem $\mathcal {M}_\mathrm {P}$ does not participate. Hence, we have $\bar{r}= \bar{r}'$ and $(\bar{v}, a)\in \mathcal {V}$ enables a transition $\bar{s}\xrightarrow {a}_{\mathcal {M}_\varPi } \bar{s}'$. Since $\bar{s}\;B\;\bar{t}$, by Definition 5, we have:

  • $a = \tau$ with $\bar{s}' \;B\;\bar{t}$. Because $\bar{s}' \;B\;\bar{t}$ and $\bar{r}= \bar{r}'$, the proof trivially follows.

  • $\bar{t}\xrightarrow {\tau }\!\!^*_{\mathcal {M}_{\varPi '}} \hat{\bar{t}} \xrightarrow {a}_{\mathcal {M}_{\varPi '}} \bar{t}'$ with $\bar{s}\;B\;\hat{\bar{t}}$ and $\bar{s}' \;B\;\bar{t}'$. These transitions are enabled by laws in $\mathcal {V}'\setminus \mathcal {V}'_\sigma$. The set of derived laws are of the form $( \bar{v}' \parallel \bullet ^m, \tau ) \in (\mathcal {V}'\setminus \mathcal {V}'_\sigma )^\bullet$ enabling a $\tau$-path from $\bar{t}\parallel \bar{r}$ to $\hat{\bar{t}} \parallel \bar{r}$, and there is a law $( \bar{v}' \parallel \bullet ^m, a )\in (\mathcal {V}'\setminus \mathcal {V}'_\sigma )^\bullet$ enabling $\hat{\bar{t}} \parallel \bar{r}\xrightarrow {a}_{\mathcal {M}'} \bar{t}' \parallel \bar{r}$. Take $\bar{r}' := \bar{r}$ and the proof obligation is satisfied.

• 2. $( \bar{v}\parallel \bar{w}, a ) \in {^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma )}$. It follows that $\bar{v}= \bullet ^n$, and thus, subsystems $\mathcal {M}_\varPi$ and $\mathcal {M}_{\varPi '}$ do not participate; we have $\bar{s}= \bar{s}'$ and $\bar{r}\xrightarrow {a}_{\mathcal {M}_\mathrm {P}} \bar{r}'$. We take $\bar{t}' := \bar{t}$. Hence, we can conclude $\bar{t}\parallel \bar{r}\xrightarrow {\tau }\!\!^*_{\mathcal {M}'} \bar{t}\parallel \bar{r}\xrightarrow {a}_{\mathcal {M}} \bar{t}' \parallel \bar{r}'$, $\bar{s}\;B\;\bar{t}$, and $\bar{s}' \;B\;\bar{t}'$.

• 3. $( \bar{v}\parallel \bar{w}, a ) \in \sigma (\mathcal {V},\mathcal {W})$. Both parts of the network participate in the transition ${\bar{s}\parallel \bar{r}\xrightarrow {a}_{\mathcal {M}} \bar{s}' \parallel \bar{r}'}$. By definition of $\sigma (\mathcal {V}, \mathcal {W})$, there are $( \bar{v}, \alpha ) \in \mathcal {V}$, $( \bar{w}, \beta ) \in \mathcal {W}$ and $( \alpha , \beta , a ) \in \sigma$ such that $( \bar{v}, \alpha )$ enables a transition $\bar{s}\xrightarrow {\alpha }_{\mathcal {M}_\varPi } \bar{s}'$ and $( \bar{u}, \beta )$ enables a transition $\bar{r}\xrightarrow {\beta } \bar{r}'$. Since $\bar{s}\;B\;\bar{t}$, by Definition 5, we have:

  • $\alpha = \tau$ with $\bar{s}' \;B\;\bar{t}$. Since $\alpha \in \mathcal {A}_{\mathcal {V}}\setminus \{\tau \}$ we have a contradiction.

  • $\bar{t}\xrightarrow {\tau }\!\!^*_{\mathcal {M}'_{\varPi '}} \hat{\bar{t}} \xrightarrow {\alpha }_{\mathcal {M}'_{\varPi '}} \bar{t}'$ with $\bar{s}\;B\;\hat{\bar{t}}$ and $\bar{s}' \;B\;\bar{t}'$. Since $\tau$ actions are not mapped by the interface mapping we have a set of synchronisation laws of the form $( \bar{v}' \parallel \bullet ^m, \tau ) \in (\mathcal {V}'\setminus \mathcal {V}'_\sigma )^\bullet$ enabling a $\tau$-path $\bar{t}\parallel \bar{r}\xrightarrow {\tau }\!\!^*_{\mathcal {M}'} \hat{\bar{t}} \parallel \bar{r}$.

    Let $( \bar{v}', \alpha ) \in \mathcal {V}'$ be the synchronisation law enabling the $\alpha$-transition. Since $( \alpha , \beta , a) \in \sigma$, $\alpha$ is an interface action and does not occur in $\mathcal {V}' \setminus \mathcal {V}'_\sigma$. It follows that $( \bar{v}', \alpha ) \in \mathcal {V}'_\sigma$, and consequently $( \bar{v}' \parallel \bar{w}, a ) \in \sigma (\mathcal {V}',\mathcal {W})$. Law $( \bar{v}' \parallel \bar{w}, a )$ enables the transition $\hat{\bar{t}} \parallel \bar{r}\xrightarrow {a}_{\mathcal {M}'} \bar{t}' \parallel \bar{r}'$, and the proof follows.

$\bullet \;$ If $\bar{s}\;C\;\bar{t}$ and $\bar{t}\xrightarrow {a}_{\mathcal {M}'} \bar{t}'$ then either $a = \tau \wedge \bar{s}' \;C\;\bar{t}$, or $\bar{s}\xrightarrow {\tau }\!\!^*_{\mathcal {M}} \hat{\bar{s}} \xrightarrow {a}_{\mathcal {M}} \bar{s}' \wedge \bar{s}\;C\;\hat{\bar{t}} \wedge \bar{s}' \;C\;\bar{t}'$. This case is symmetric to the previous case.

$\bullet \;$ If $\bar{s}\;C\;\bar{t}$ and there is an infinite sequence of states  $(\bar{s}^k)_{k\in \omega }$ such that $\bar{s}= \bar{s}^0$, $\bar{s}^k \xrightarrow {\tau }_{\mathcal {M}} \bar{s}^{k+1}$  and $\bar{s}^k \;C\;\bar{t}$ for all $k \in \omega$, then there exists a state  $\bar{t}'$ such that $\bar{t}\xrightarrow {\tau }\!\!^+_{\mathcal {M}'} \bar{t}'$ and $\bar{s}^k \;C\;\bar{t}'$ for some $k \in \omega$. Again we reformulate the proof obligation to better distinguish between the two components: if $\bar{s}\parallel \bar{r} \;C\;\bar{t}\parallel \bar{r}$ and there is an infinite sequence of states $(\bar{s}^k \parallel \bar{r}^k )_{k\in \omega }$ such that $\bar{s}\parallel \bar{r} = \bar{s}^0 \parallel \bar{r}^0$, $\bar{s}^k \parallel \bar{r}^k \xrightarrow {\tau }_{\mathcal {M}} \bar{s}^{k+1} \parallel \bar{r}^{k+1}$ and $\bar{s}^k \;B\;\bar{t}$ for all $k \in \omega$, then there exists a state $\bar{t}'$ such that $\bar{t}\parallel \bar{r} \xrightarrow {\tau }\!\!^+_{\mathcal {M}'} p' \parallel \bar{r}$ and $\bar{s}^k \;B\;\bar{t}'$ for some $k \in \omega$.

We distinguish two cases:

• 1. All steps in the $\tau$-sequence are enabled in $\mathcal {M}_\varPi$, i.e., $\forall k \in \omega .\;\bar{s}^k \xrightarrow {\tau }_{\mathcal {M}_\varPi } \bar{s}^{k+1}$. Since $\bar{s}\;B\;\bar{t}$, by condition 3 of Definition 5, it follows that there is a state $\bar{t}'$ with $\bar{t}\xrightarrow {\tau }\!\!^+ \bar{t}'$ and $\bar{s}^k \;B\;\bar{t}'$ for some $k \in \omega$. Since $\tau$ is not an interface action, the synchronization laws enabling $\bar{t}\xrightarrow {\tau }\!\!^+ \bar{t}'$ are also present in $\mathcal {M}'$. Hence, we have $\bar{t}\parallel \bar{r} \xrightarrow {\tau }\!\!^+ \bar{t}' \parallel \bar{r}$ and $\bar{s}^k \;B\;\bar{t}'$ for $k \in \omega$.

• 2. There is a $k \in \omega$ with $\lnot \bar{s}^k \xrightarrow {\tau }_{\mathcal {M}_\varPi } \bar{s}^{k+1}$. We do have $\bar{s}^k \parallel \bar{r}^k \xrightarrow {\tau }_{\mathcal {M}} \bar{s}^{k+1} \parallel \bar{r}^{k+1}$ with $\bar{s}^k \;B\;\bar{t}$ (see antecedent at the start of the ‘divergence’ case). Since the $\tau$-transition is not enabled in $\mathcal {M}_\varPi$ the transition must be enabled by a synchronisation law $( \bar{v}\parallel \bar{w}, \tau ) \in {^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma )} \cup \mathcal {\sigma (\mathcal {V},\mathcal {W})}$. We distinguish two cases:

  • $( \bar{v}\parallel \bar{w}, \tau ) \in {^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma )}$. The transition $\bar{s}^k \parallel \bar{r}^k \xrightarrow {\tau }_{\mathcal {M}} \bar{s}^{k+1} \parallel \bar{r}^{k+1}$ is enabled by $( \bar{v}\parallel \bar{w}, \tau ) \in {^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma )}$. Therefore, there is a transition $\bar{r}^k \xrightarrow {\tau }_{\mathcal {M}_\mathrm {P}} \bar{r}^{k+1}$ enabled by $( \bar{w}, \tau ) \in \mathcal {W}\setminus \mathcal {W}_\sigma$. Since this transition is part of an infinite $\tau$-sequence, there is a path $\bar{s}\parallel \bar{r} \xrightarrow {\tau }\!\!^*_\mathcal {M}\bar{s}^k \parallel \bar{r}^k$. Furthermore, condition 1 of Definition 5 holds for $C$, hence, there is a state $\bar{t}' \in \mathcal {S}_{\mathcal {M}_{\varPi '}}$ and a transition $\bar{t}\parallel \bar{r} \xrightarrow {\tau }\!\!^*_{\mathcal {M}_\mathrm {P}} \bar{t}' \parallel \bar{r}^k$ with $\bar{s}^{k} \parallel \bar{r}^{k} \;C\;\bar{t}' \parallel \bar{r}^k$. Therefore, we have $\bar{t}\parallel \bar{r} \xrightarrow {\tau }\!\!^+_{\mathcal {M}'} \bar{t}' \parallel \bar{r}^{k+1}$. Finally, since $\bar{s}^{k} \parallel \bar{r}^{k} \;C\;\bar{t}' \parallel \bar{r}^k$, it follows that $\bar{s}^{k} \;B\;\bar{t}'$.

  • $( \bar{v}\parallel \bar{w}, \tau ) \in \sigma (\mathcal {V},\mathcal {W})$. By definition of $\sigma (\mathcal {V},\mathcal {W})$, there are two laws $( \bar{v}, \alpha ) \in \mathcal {V}$ and $( \bar{u}, \beta ) \in \mathcal {W}$ with $( \alpha , \beta , \tau ) \in \sigma$. The laws enable transitions $\bar{s}^k \xrightarrow {\alpha }_{\mathcal {M}_\varPi } \bar{s}^{k+1}$ and $\bar{r}^k \xrightarrow {\beta }_{\mathcal {M}_\mathrm {P}} \bar{r}^{k+1}$ respectively. Since $\bar{s}^k \;B\;\bar{t}$ and $\alpha \ne \tau$, by Definition 5, there are states $\hat{\bar{t}}, \bar{t}' \in \mathcal {S}_{\mathcal {M}_{\varPi '}}$ such that there is a sequence $\bar{t}\xrightarrow {\tau }\!\!^*_{\mathcal {M}_{\varPi '}} \hat{\bar{t}} \xrightarrow {\alpha }_{\mathcal {M}_{\varPi '}} \bar{t}'$ with $\bar{s}\;B\;\hat{\bar{t}}$ and $\bar{s}^{k+1} \;B\;\bar{t}'$. Let $( \bar{v}', \alpha ) \in \mathcal {V}'$ be the law enabling the $\alpha$-transition. Since $( \alpha , \beta , \tau ) \in \sigma$, and consequently $( \bar{v}' \parallel \bar{w}, \tau ) \in \sigma (\mathcal {X}', \mathcal {Y})$. Furthermore, the $\tau$-path from $\bar{t}$ to ${\hat{\bar{t}}}$ is enabled by laws of the form $( \bar{v}'', \tau ) \in \mathcal {V}'\setminus \mathcal {V}'_\sigma$. Hence, there is a series of transitions $\bar{t}\parallel \bar{r}\xrightarrow {\tau }\!\!^*_{\mathcal {M}'} \hat{\bar{t}} \parallel \bar{r}^k \xrightarrow {\tau }_{\mathcal {M}'} \bar{t}' \parallel \bar{r}^{k+1}$. Finally, recall that $\bar{s}^{k+1} \;B\;\bar{t}'$. Hence, also in this case the proof obligation is satisfied.

$\bullet \;$ If $\bar{s}C\bar{t}$ and there is an infinite sequence of states $(\bar{t}^k)_{k\in \omega }$ such that $\bar{t}= \bar{t}^0$, $\bar{t}^k \xrightarrow {\tau }_{\mathcal {G}_2} \bar{t}^{k+1}$ and $\bar{s}C\bar{t}^k$ for all $k \in \omega$, then there exists a state $\bar{s}'$ such that $\bar{s}\xrightarrow {\tau }\!\!^+_{\mathcal {G}_1} \bar{s}'$ and $\bar{s}' C\bar{t}^k$ for some $k \in \omega$. This case is symmetric to the previous case.    $\square$

5 Decomposition of LTS Networks

In Sect. 4, we discuss the composition of LTS networks, in which a system is constructed by combining components. However, for compositional model checking approaches, it should also be possible to correctly decompose LTS networks. In this case the inter-component laws are already known. Therefore, we can derive a set of interface laws and an interface mapping specifying how the system is decomposed into components.

To be able to apply Proposition 2 for compositional state space construction, the composition of the decomposed networks must be equivalent to the original system. If this holds we say a decomposition is consistent with respect to $\mathcal {M}$.

Definition 8

(Consistent Decomposition). Consider a network $\mathcal {M}= ( \Sigma , \mathcal {X})$. Say network $\mathcal {M}$ is decomposed into components $\mathcal {N}= ( \varPi , \mathcal {V})$ and $\mathcal {O} = ( \mathrm {P}, \mathcal {W})$ with interface laws $\mathcal {V}_\sigma$ and $\mathcal {W}_\sigma$, where $\sigma$ is the implied interface mapping. The decomposition of $\mathcal {M}$ in to components $\mathcal {N}$ and $\mathcal {O}$ is called consistent with respect to $\mathcal {M}$ iff $\mathcal {M}= \mathcal {N}\parallel _\sigma \mathcal {O}$, i.e., we must have $\Sigma = \varPi \parallel \mathrm {P}$ and $\mathcal {X}= (\mathcal {V}\setminus \mathcal {V}_\sigma )^\bullet \cup \;^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma ) \cup \sigma (\mathcal {V},\mathcal {W})$.

To show that a decomposition is consistent with the original system it is sufficient to show that the set of inter-component laws of the original system is equivalent to the set of inter-component laws generated by the interface-mapping:

Lemma 1

Consider a network $\mathcal {M}= ( \varPi \parallel \mathrm {P}, \mathcal {V}^\bullet \cup {^\bullet \mathcal {W}} \cup \mathcal {X})$, with $\mathcal {X}$ the set of inter-component laws and disjoint sets $\mathcal {V}^\bullet$, ${^\bullet \mathcal {W}}$ and $\mathcal {X}$. A consistent decomposition of $\mathcal {M}$ into components $\mathcal {N}= ( \varPi , \mathcal {V}\cup \mathcal {V}_\sigma )$ and $\mathcal {O} = ( \mathrm {P}, \mathcal {W}\cup \mathcal {W}_\sigma )$, with interface laws $\mathcal {V}_\sigma$ and $\mathcal {W}_\sigma$ disjoint from V and W, respectively, is guaranteed iff $\mathcal {X}= \sigma (\mathcal {V}_\sigma , \mathcal {W}_\sigma )$.

Proof

The decomposition is consistent iff $\mathcal {V}^\bullet \cup {^\bullet \mathcal {W}} \cup \mathcal {X}= (\mathcal {V}\setminus \mathcal {V}_\sigma )^\bullet \cup \;^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma ) \cup \sigma (\mathcal {V}\cup \mathcal {V}^\sigma ,\mathcal {W}\cup \mathcal {W}^\sigma )$ and $\varPi \parallel \mathrm {P}= \varPi \parallel \mathrm {P}$. The latter is trivial. Furthermore, since $\mathcal {V}\cap \mathcal {V}_\sigma = \emptyset$ ($\mathcal {W}\cap \mathcal {W}_\sigma = \emptyset$) and by definition of $\mathcal {V}_\sigma$ ($\mathcal {W}_\sigma )$, we have $\mathcal {V}^\bullet = (\mathcal {V}\setminus \mathcal {V}_\sigma )^\bullet$ (${^\bullet \mathcal {W}} = {^\bullet (\mathcal {W}\setminus \mathcal {W}_\sigma )}$). It follows from $\mathcal {V}\cap \mathcal {V}_\sigma = \emptyset$, $\mathcal {W}\cap \mathcal {W}_\sigma = \emptyset$, and Definition 7 that $\sigma (\mathcal {V}\cup \mathcal {V}^\sigma ,\mathcal {W}\cup \mathcal {W}^\sigma ) = \sigma (\mathcal {V}_\sigma , \mathcal {W}_\sigma )$. Hence, the decomposition is consistent iff $\mathcal {X}= \sigma (\mathcal {V}_\sigma , \mathcal {W}_\sigma )$.    $\square$

Indeed, it is possible to derive an inconsistent decomposition as shown in Example 3.

Example 3

(Inconsistent Decomposition). Consider a set of inter-component laws $\mathcal {X}= \{( \langle a, b \rangle , c ), ( \langle b, a \rangle , c ) \}$. Partitioning the laws results in the sets of interface laws $\mathcal {V}_\sigma = \{ (\langle a \rangle , \gamma ), (\langle b \rangle , \gamma ) \}$ and $\mathcal {W}_\sigma = \{( \langle b \rangle , \gamma ), ( \langle a \rangle , \gamma )\}$ derived from some $\mathcal {V}$ and $\mathcal {W}$, respectively. This system implies the interface mapping $\sigma = \{ (\gamma , \gamma , c) \}$. The derived set of inter-component laws is $\sigma (\mathcal {V}, \mathcal {W}) = \{( \langle a, a \rangle , c ), ( \langle a, b \rangle , c ), ( \langle b, a \rangle , c ), ( \langle b, b \rangle , c )\} \ne \mathcal {X}$. Hence, this decomposition is not consistent with the original system.

However, a consistent composition can always be derived. In Proposition 3 we show how to construct two sets of interface laws $\mathcal {V}_\sigma$ and $\mathcal {W}_\sigma$, and an interface mapping $\sigma$ for component $\mathcal {M}_\varPi = ( \varPi , \mathcal {V} \cup \mathcal {V}_\sigma )$ and $\mathcal {M}_\mathrm {P}= ( \mathrm {P}, \mathcal {W}\cup \mathcal {W}_\sigma )$ such that the decomposition is consistent. Consider a synchronisation law $( \bar{v}\parallel \bar{w}, a)$, the idea is to encode this synchronisation law directly in the interface mapping, i.e., we create unique result actions $\alpha _{\bar{v}}$ and $\alpha _{\bar{w}}$ with $( \alpha _{\bar{v}}, \alpha _{\bar{w}}, a ) \in \sigma$. This way it is explicit which interface law corresponds to which inter-component law.

Proposition 3

Consider a network $\mathcal {M}= ( \varPi \parallel \mathrm {P}, \mathcal {V}^\bullet \cup {^\bullet \mathcal {W}} \cup \mathcal {X})$. We define the sets of interface laws as follows:

$$ \mathcal {V}_\sigma = \{ ( \bar{v}, \alpha _{\bar{v}} ) \mid ( \bar{v}\parallel \bar{w}, a ) \in \mathcal {X}\}, \mathcal {W}_\sigma = \{ ( \bar{w}, \alpha _{\bar{w}} ) \mid ( \bar{v}\parallel \bar{w}, a ) \in \mathcal {X}\} $$

where $\alpha _{\bar{v}}$ and $\alpha _{\bar{w}}$ are unique interface result actions identified by the corresponding interface law, that is, $\forall ( \bar{v}', a ) \in \mathcal {V}\cup \mathcal {V}_\sigma .\;a = \alpha _{\bar{v}} \implies \bar{v}' = \bar{v}$ and $\forall ( \bar{w}', a ) \in \mathcal {W}\cup \mathcal {W}_\sigma .\;a = \alpha _{\bar{w}} \implies \bar{w}' = \bar{w}$.

Finally, the interface mapping is defined as $\sigma = \{ ( \alpha _{\bar{v}}, \alpha _{\bar{w}}, a ) \mid ( \bar{v}\parallel \bar{w}, a ) \in \mathcal {X}\}$. The decomposition into $\mathcal {M}_\varPi = (\varPi , \mathcal {V}\cup \mathcal {V}_\sigma )$ and $\mathcal {M}_\mathrm {P}= (\mathrm {P}, \mathcal {W}\cup \mathcal {W}_\sigma )$ is consistent.

Proof

By Lemma 1, we have to show $\mathcal {X}= \sigma (\mathcal {V}_\sigma ,\mathcal {W}_\sigma )$.

$$ \begin{aligned} \sigma (\mathcal {V}_\sigma ,\mathcal {W}_\sigma )&\mathop {=}\limits ^{(1)} \{( \bar{v}\parallel \bar{w}, a ) \mid ( \bar{v}, \alpha _{\bar{v}} ) \in \mathcal {V}_\sigma \wedge ( \bar{w}_{\bar{w}}, \beta ) \in \mathcal {W}_\sigma \wedge ( \alpha _{\bar{v}}, \alpha _{\bar{w}}, a ) \in \sigma \}&\\&\mathop {=}\limits ^{(2)} \{( \bar{v}\parallel \bar{w}, a ) \mid ( \bar{v}\parallel \bar{w}, a) \in \mathcal {X}\} = \mathcal {X}\end{aligned} $$

where at (1) the definition of $\sigma (\mathcal {V}_\sigma ,\mathcal {W}_\sigma )$ is unfolded, and (2) follows from construction of $\mathcal {V}_\sigma$, $\mathcal {W}_\sigma$, and $\sigma$. Hence, the decomposition is consistent with $\mathcal {M}$.    $\square$

Proposition 4 shows that LTS networks resulting from the consistent decomposition of an admissible LTS network are also admissible. Hence, consistent decomposition is compatible with the compositional verification approaches presented in [12].

Proposition 4

Consider an admissible LTS network $\mathcal {M}= ( \varPi \parallel \mathrm {P}, \mathcal {V}^\bullet \cup {^\bullet \mathcal {W}} \cup \mathcal {X})$ of length $n+m$. If the decomposition is consistent, then the decomposed networks $\mathcal {M}_\varPi = ( \varPi , \mathcal {V}\cup \mathcal {V}_\sigma )$ and $\mathcal {M}_\mathrm {P}= ( \mathrm {P}, \mathcal {W}\cup \mathcal {W}_\sigma )$ are also admissible.

Proof

We show that $\mathcal {M}_\varPi$ and $\mathcal {M}_\mathrm {P}$ satisfy Definition 4:

No synchronisation and renaming of $\tau$ ’s. Let $(\bar{v}, a)\in \mathcal {V}\cup \mathcal {V}_\sigma$ be a synchronisation law such that $\bar{v}_i = \tau$ for some $i \in 1..n$. We distinguish two cases:

• $(\bar{v}, a)\in \mathcal {V}_\sigma$. Since $(\bar{v}, a)$ is an interface law and the decomposition is consistent, its result action a may not be $\tau$. However, since $\mathcal {M}$ is admissible, no renaming of $\tau$’s is allowed. By contradiction it follows that $(\bar{v}, a)\not \in \mathcal {V}_\sigma$ completing this case.

• $(\bar{v}, a)\in \mathcal {V}^\bullet$. By construction, there exists a law $( \bar{v}\parallel \bullet ^m, a) \in \mathcal {V}^\bullet$. Since $\mathcal {V}^\bullet \subseteq \mathcal {V}^\bullet \cup {^\bullet \mathcal {W}} \cup \mathcal {X}$, by admissibility of $\mathcal {M}$, we have $\forall j \in 1..n .\;\bar{v}_j \ne \bullet \implies i = j$ (no synchronisation of $\tau$’s) and $a = \tau$ (no renaming of $\tau$’s).

Hence, $\mathcal {M}_\varPi$ does not synchronize or rename $\tau$’s. The proof for $\mathcal {M}_\mathrm {P}$ is similar.

No cutting ofZ $\tau$ ’s. Let $\varPi _i$ be a process with $i \in 1..n$ such that $\tau \in \mathcal {A}_{\varPi _i}$. Since $\mathcal {M}$ is admissible there exists a law $( \bar{v}\parallel \bar{w}, a ) \in \mathcal {V}^\bullet \cup {^\bullet \mathcal {W}} \cup \mathcal {X}$ such that $(\bar{v}\parallel \bar{u})_i = \tau$. We distinguish three cases:

• $( \bar{v}\parallel \bar{w}, a ) \in \mathcal {V}^\bullet$. Since $(\bar{v}\parallel \bar{w})_i = \tau$ and $i \le n$ it follows that $\bar{v}_i = \tau$. By construction of $\mathcal {V}^\bullet$, there is a $(\bar{v}, a)\in V$ with $\bar{v}_i = \tau$.

• $( \bar{v}\parallel \bar{w}, a ) \in {^\bullet \mathcal {W}}$. In this case we must have $i > n$ which contradicts our assumption: $i \in 1 .. n$. The proof follows by contradiction.

• $( \bar{v}\parallel \bar{w}, a ) \in \mathcal {X}$. Then, $( \bar{v}\parallel \bar{w}, a )$ is an inter-component law with at least one participating process for each component. Hence, there exists a $j \in (n+1)..m$ such that $(\bar{v}\parallel \bar{w})_j \ne \bullet$. Moreover, since $\mathcal {M}$ is admissible, no synchronisation of $\tau$’s are allowed. Therefore, since $(\bar{v}\parallel \bar{w})_j \ne \bullet$, we must have $j = i$. However, this would mean $j \in 1..n$, contradicting $j \in (n+1) .. m$. By contradiction the proof follows.

We conclude that $\mathcal {M}_\varPi$ does not cut $\tau$’s. The proof for $\mathcal {M}_\mathrm {P}$ is symmetrical.

All three admissibility properties hold for $\mathcal {M}_\varPi$ and $\mathcal {M}_\mathrm {P}$. Hence, the networks resulting from the decomposition satisfy Definition 4.    $\square$

6 Application

In order to compare compositional approaches with the classical, non-compositional approach, we have employed Cadp to minimise a set of models modulo DPBB.

Each model is minimised with respect to a given liveness property. To achieve the best minimisation we applied maximal hiding [25] in all approaches. Intuitively, maximal hiding hides all actions except for the interface actions and actions relevant for the given liveness-property.

Table 1. Experiments: smart reduction vs. root reduction

As composition strategy we have used the smart reduction approach described in [11]. In Cadp, the classical approach, where the full state space is constructed at once and no intermediate minimisations are applied, is the root reduction strategy. At the start, the individual components are minimised before they are combined in parallel composition, hence the name. We have measured the running time and maximum number of states generated by the two methods.

For compositional approaches, the running time and largest state space considered depends heavily on the composition order, i.e., the order in which the components are combined. The smart reduction approach uses a heuristic to determine the order in which to compose processes. In [11], it has been experimentally established that this heuristic frequently works very well. After each composition step the result is minimised.

Measurements. The results of our experiments are shown in Table 1. The Model column indicates the test case model corresponding to the measurements.

The smart and root sub-columns denote the measurement for the smart reduction and root reduction approaches, respectively.

In the Running time (sec.) column the running time until completion of the experiment is shown in seconds. Indicated in bold are the shortest running times comparing the smart and root sub-columns. The maximum running time of an experiment was set to 80 hours, after which the experiment was discontinued (indicated with −).

The columns Max. #states and Max. #transitions show the largest number of states and transitions, respectively, generated during the experiment. Of both methods the best result is indicated in bold.

The number of states and transitions after minimisation are shown in the Reduced #states and Reduced #transitions columns, respectively.

The experiments were run on the DAS-5 cluster [4] machines. They have an Intel Haswell E5-2630-v3 2.4 GHz CPU, 64 GB memory, and run CentOS Linux 7.2.

As test input we selected twelve case studies: four mCRL2 [10] models distributed with its toolset, seven Cadp models, and one from the Beem database [29].

Discussion. In terms of running time smart reduction performs best for eight of the models, whereas root reduction performs best in four of the models. In general, the smart reduction approach performs better for large models where the state space can be reduced significantly before composition. This is best seen in the HAVi-LE’, Le Lann, and Peterson use cases, where smart reduction is several hours faster.

In this set of models, root reduction performs best in relatively small models; 1394, ACS, Cache, Lamport, and ODP. However, the difference in running times is negligible. Smart reduction starts performing better in the moderately sized models such as Transit and Wafer stepper. For smaller models the overhead of the smart reduction heuristic is too high to obtain any benefits from the nominated ordering.

In summary, compositional reduction is most efficient when it is expected that components reduce significantly and highly interleaving components are added last.

7 Conclusions

In this paper we have shown that DPBB is a congruence for parallel composition of LTS networks where there is synchronisation on given label combinations. Therefore, the DPBB equivalence may be used to reduce components in the compositional verification of LTS networks. It had already been shown that compositional verification of LTS networks is adequate for safety properties. As DPBB preserves both safety and liveness properties, compositional verification can be used to verify liveness properties as well.

Furthermore, we have discussed how to safely decompose an LTS network in the case where verification has to start from the system as a whole. Both the composition and consistent decomposition of LTS networks preserve the admissibility property of LTS networks. Hence, the composition operator remains compatible with the compositional verification approaches for LTS networks described by [12].

The proofs in this paper have been mechanically verified using the Coq proof assistant³ and are available online (see footnote 2).

Although our work focuses on the composition of LTS networks, the results are also applicable on composition of individual LTSs. Our parallel composition operator subsumes the usual parallel composition operators of standard process algebra languages such as CCS [27], CSP [32], mCRL2 [10], and LOTOS [18].

Finally, we have run a set of experiments to compare compositional and traditional DPBB reduction. The compositional approach applies Cadp’s smart reduction employing a heuristic to determine an efficient compositional reduction order. The traditional reduction generates the complete state space before applying reduction. The compositional approach performed better in the medium to large models where the intermediate state space can be kept small.

Future work. An interesting direction for future work is the integration of the proof in a meta-theory for process algebra. This integration would give a straightforward extension of our results to parallel composition for process algebra formalisms.

This work has been inspired by an approach for the compositional verification of transformations of LTS networks [31, 36,37,38,39]. We would like to apply the results of this paper to the improved transformation verification algorithm [31], thus guaranteeing its correctness for the compositional verification of transformations of LTS networks.

In future experiments, we would like to involve recent advancements in the computation of branching bisimulation, and therefore also DPBB, both sequentially [16, 17] and in parallel on graphics processors [41]. It will be interesting to measure the effect of applying these new algorithms to compositionally solve a model checking problem.

Finally, by encoding timing in the LTSs, it is possible to reason about timed system behaviour. Combining approaches such as [40, 42] with our results would allow to compositionally reason about timed behaviour. We plan to investigate this further.