Diagnostic competences of teachers are considered important for students’ learning success. However, there is little empirical evidence about cognitive processes of teachers in (informal) diagnostic situations and the knowledge they use in such situations. The concern of the reported study is to extend this state of research from a domain-specific point of view. For this purpose, processes and knowledge resources mathematics teachers apply in informal diagnostic situations (evaluating tasks and students’ solutions) are identified empirically and described theoretically. The findings show that the teachers in the study proceed predominantly in a systematic way and use a variety of different types of mathematical knowledge.

1 Introduction: Diagnostic Competence

In everyday teaching we find various kinds of diagnostic situations. They can be characterized with regard to their purpose and position in a learning process (e.g., Ingenkamp & Lissmann, 2008; Wiliam, 2007).

At the beginning of a learning process an initial assessment can yield information about students’ previous knowledge and preconditions for planning lessons. During a learning process, formative assessment can be used to support students individually or adapt lessons. Summative assessment at the end of a learning process can be used for assessing learning results, grading or evaluating instruction (Fig. 1).

Fig. 1
figure 1

Diagnostic situations in a learning process

Full size image

Another way to characterize diagnostic situations is their level of formality. In addition to formal assessment (e.g., by standardized diagnostic tests), informal assessment (e.g., by observation) plays an important role in the classroom, e.g., by selecting appropriate tasks or reacting to students’ mistakes.

Within diagnostic situations one can also distinguish a preactional, an actional and a postactional phase, each phase characterized by different types of diagnostic judgments (Klug, Bruder, Kelava, Spiel, & Schmitz, 2013): In the preactional phase, teachers plan diagnostic actions by selecting methods, aims, criteria, and so on. In the actional phase, they collect data, interpret and draw conclusions and in the postactional phase they enact instructional measures (Klug et al., 2013). This tripartite model allows a broader understanding of diagnostic situations as it includes diagnostic activities of teachers before and after the actual diagnostic judgment.

Diagnostic competence can be defined as the individuals’ dispositions that are necessary to manage diagnostic situations successfully, and it can be seen as one of the key competences for teaching (Helmke, Hosenfeld, & Schrader, 2004). There is a broad agreement that diagnostic competence is essential for the quality of teaching; for example, when teachers have to select adequate measures such as modifying the difficulty of a task or when they have to adapt educational methods (Helmke et al., 2004; Anders, Kunter, Brunner, Krauss, & Baumert, 2010; Schwarz, Wissmach, & Kaiser, 2008). However, we find hints that diagnostic competence of teachers is not sufficiently developed (e.g., Krauss & Brunner, 2011).

In recent studies diagnostic competence often is described as the ability of a person to judge people accurately and is measured as the precision of certain judgments (Schrader, 2011). In these judgments teachers have to estimate the level, the variance and the ranking order of students’ attributes or of tasks. Such a numerical precision can be regarded as an indicator for diagnostic competence. However, this approach does not provide any understanding of the way teachers generate diagnostic judgments and their underlying cognitive processes (for a detailed discussion see Leuders, Dörfler, Leuders & Philipp 2018 – chapter “Diagnostic Competence of Mathematics Teachers: Unpacking a Complex Construct” in this book).

In order to support the development of diagnostic competence of teachers, it is important to understand the processes and identify the knowledge teachers apply during these processes (Barth & Henninger, 2012). Furthermore, it would be a matter of particular interest to clarify the domain-specificity (or even topic-specificity) of diagnostic competence and its structure. We find indications that diagnostic competence should not be understood as a general ability, but rather as a construct composed of multiple partial competences (Spinath, 2005). In conclusion, we still need further research to develop a better theoretical understanding of processes that underlie teachers’ diagnostic judgments (see also the concept of diagnostic thinking in Leuders et al. 2018 in this book).

Accordingly, the analysis in this chapter deals with the following questions: (1) How do teachers arrive at their diagnostic judgments, and (2) what kind of knowledge do they need in diagnostic processes? The study reported here focuses on informal diagnostic situations in mathematics, such as evaluating tasks and evaluating students’ solutions. These situations can be described as the actional phase in which teachers have to gather and interpret information about tasks and students’ knowledge. Both diagnostic situations can occur at every position in a learning process.

In the following section the theoretical framework of the study is described, particularly recurring on models that may help understand diagnostic processes and knowledge resources of teachers in these diagnostic situations.

2 Theoretical Framework

In order to describe diagnostic competence(s) as judgment processes within a theoretical framework, it is helpful to take a closer look at suitable models that focus on cognitive processes and their underlying knowledge resources, that is, which tap diagnostic thinking (within the general model of diagnostic competence as a continuum, cf. chapter “Diagnostic Competence of Mathematics Teachers: Unpacking a Complex Construct” in this book). In this section three theoretical approaches were taken into consideration to identify the cognitive processes and knowledge resources in diagnostic situations. The models vary in their domain-specificity and therefore provide an insight from different perspectives on diagnostic activities. First, the focus is on processes in estimating other people’s knowledge in general and then mathematical knowledge resources for teachers were delineated. The third approach gives a first insight into the interaction of processes and knowledge resources in diagnostic situations.

2.1 Diagnostic Processes as an Alternation of Anchoring and Adjustment

Diagnostic situations in the classroom require the evaluation of the current level of students’ knowledge by the teacher. With the exception of the use of standardized measuring instruments, such diagnostic situations can be related to situations described in the field of research on expertise: The rating of other people’s knowledge, especially the rating of the knowledge of novices by experts (Ostermann, Leuders, & Philipp, 2017; Philipp & Leuders, 2014).

Nickerson (1999) proposes a model (see Fig. 2) to describe this process in three steps: (1) The expert uses his or her knowledge as a basis (model of own knowledge) and keeps the exclusivity of his or her knowledge in mind (e.g., specific knowledge of teachers). This leads to a default model of a random other’s knowledge. This default model represents a kind of common knowledge of any person (or a group of persons) and builds the foundation for further, more specific, models. (2) The consideration of information such as the affiliation to a specific group of people (e.g., class level) and information from former experience are used to modify the model and result in an initial model of a specific other’s knowledge. This model construction is not necessarily a conscious process. (3) The process of rating other people’s knowledge continues in gaining information about a specific person (e.g., in conversation) and leads to a working model of a specific other’s knowledge. So the development of a model of other people’s knowledge is a permanent refinement and update. The whole process can be characterized as a heuristic of “anchoring an adjustment” (Tversky & Kahnemann, 1974), in which the own knowledge of the expert as starting point plays an important role. In considering aspects of knowledge continuously, this heuristic leads to different steps of a model of other peoples’ knowledge. The different steps then can be understood as anchors in building the starting point for further adjustment.

Fig. 2
figure 2

Model of rating other people’s knowledge (From Nickerson, 1999, p. 740)

Full size image

In the classroom teachers frequently have to assess the knowledge of students, groups of students or a whole class. The continuous process of modifying and updating such assessments (regarded as anchoring and adjustment process) may occur constantly during a lesson and enables adaptive teaching. Nickerson’s model, when applied on pedagogical situations, can be helpful to understand diagnostic processes; especially, since it helps to explain biases, which frequently occur – generally and in the pedagogical context:

  • False-consensus effect: Own opinions and attitudes are considered to be opinions and attitudes of the majority of people (Brown, 1982).

  • Egocentric bias: The attribution of general knowledge to other people is strongly connected to own general knowledge (Nickerson, 1999).

  • Curse of expertise: With increasing expertise challenges for novices are underestimated (e.g., Camerer, Loewenstein, & Weber, 1989).

  • Illusion of simplicity: Experts misjudge topics as simple because they are familiar with it (Kelley, 1999).

  • Hindsight bias: It is difficult to reconstruct the own state of previous knowledge (Fischhoff, 1975).

This shows that tendencies of overestimating knowledge of others are frequent. Such tendencies can be explained by insufficient adaptation in Nickerson’s model or deficient awareness of the exclusivity of one’s own knowledge. In pedagogical situations this can have severe consequences: The discrepancy of mathematical expert knowledge of teachers (after several years of teacher education and teaching practice) and the knowledge of students is enormous. Furthermore, it is difficult to adopt a novice’s perspective: “Every beginning instructor discovers sooner or later that his first lectures were incomprehensible because he was talking to himself, so to say, mindful only of his own point of view. He realizes only gradually and with difficulty that it is not easy to place oneself in the shoes of students who do not know what he knows about the subject matter of his course” (Piaget, 1962, p. 5, in Nickerson, 1999, p. 747).

A transfer to pedagogical situations seems plausible – the assessment of students’ knowledge guides the teachers’ actions in the classroom. On the other hand, in the classroom there is also an important difference to the kind of situations Nickerson refers to: Teachers usually do have prior knowledge about the knowledge of their students. Even if they teach a new class, they do not only refer to their own knowledge to assess students’ knowledge, but also consider general information such as age and class level. It can be assumed that such models of knowledge are increasingly used as foundation with growing teaching experience.

The typical misjudgments referred to above also exist in pedagogical situations: The curse of expertise often appears in context of achievement tests in which teachers falsely interpret correct results as confirmation of students’ knowledge and thereby overestimate the knowledge of students. However, the reverse also occurs: Teachers sometimes underestimate the knowledge of students, supposing that they had no learning opportunity outside the classroom (Clarke et al., 2002; Selter, 1995). In Nickerson’s model this can be interpreted as attributing a lack of knowledge, for example, to first-graders. In other situations, it is apparent that teachers use the knowledge of good students as standard for the whole class (Schrader & Helmke, 1987). The awareness of such biases can also be used in a productive way; for example, in teaching mathematics the hindsight bias can be used in designing teaching situations bearing in mind a “preview-perspective” of students that are not familiar with a content and a “review-perspective” of the teacher (Ruf & Gallin, 2005). These examples show that Nickerson’s model can be used to understand frequent tendencies of over- or underestimating students’ knowledge in pedagogical context and it also highlights the significance of own knowledge.

With regard to diagnostic situations in the classroom Nickerson’s model is helpful for understanding the process of generating judgments and it also helps to gain insight into resources people use when assessing other people’s knowledge. Besides, typical misjudgment tendencies can be interpreted within the model. The model is very general and therefore can be transferred to a variety of situations. This generality also leads to limitations: It does not contribute to our understanding of domain-specific processes.

2.2 Diagnostic Competences as Facet of Professional Knowledge for Teaching Mathematics

In order to analyze diagnostic processes, it is not sufficient to describe the processes of generating knowledge on students, as in section 2.1. One should also be aware of different types of knowledge that are relevant in the process.

Several attempts to describe domain-specific types of teacher knowledge can be traced back to the framework of Shulman who categorized teacher knowledge and introduced pedagogical content knowledge as “the category most likely to distinguish the understanding of the content specialist from the pedagogue” (Shulman, 1987, p. 8). Pedagogical content knowledge includes knowledge about typical difficulties of students and their pre- or misconceptions (Shulman, 1986). This category already hints at the concept of diagnostic competence.

For the domain of mathematics, Shulmans’ categories were refined and substantiated in various studies by Ball and colleagues (Ball, Lubienski, & Mewborn, 2001; Ball, Thames, & Phelbs, 2008; Hill, Ball, & Schilling, 2008), for example. Their detailed analyses of teaching practice led to a categorization of mathematical knowledge applied in teaching (Ball et al., 2008, Fig. 3). In their job analysis, they considered teaching situations in the classroom and activities connected to teaching such as lesson planning, managing homework or evaluating students’ work.

Fig. 3
figure 3

Domains of mathematical knowledge for teaching (From Ball et al., 2008, p. 403)

Full size image

When considering competences required in diagnostic situations, several of these knowledge domains can be regarded as relevant:

  • First of all, in diagnostic situations it is essential to evaluate the mathematical correctness of a solution. The knowledge needed for this pertains to the domain of common content knowledge (CCK). In diagnostic situations it is often necessary to decide very quickly if a solution is correct or a solution attempt is adequate.

  • In contrast to common content knowledge specialized content knowledge (SCK) is considered as a kind of subject matter knowledge that is required only for teaching. It goes beyond the understanding of mathematical contents people in other fields need because the teaching of mathematical contents requires a deeper understanding to make it learnable for students. In diagnostic situations it is used, for example, to modify the difficulty of tasks or find patterns in students’ errors. Note that this kind of knowledge draws on mathematical knowledge and does not require knowledge about students.

  • The domain knowledge of content and students (KCS) is characterized by a close connection of mathematical knowledge and knowledge about students and may be the most important for diagnostic situations. For example, it is crucial to know typical errors or students’ (mis-)conceptions within mathematical topics to follow their way of thinking.

The theoretical approach of Ball and colleagues to identify and substantiate several domains of mathematical knowledge for teaching is also useful to capture knowledge for diagnostic activities of teachers; particularly, because the mentioned knowledge domains are closely connected to typical activities of mathematics teachers. Although the model does not describe diagnostic processes directly, it can be helpful in understanding different kinds of mathematical knowledge needed in diagnostic situations and contributes to clarify knowledge resources which teachers use in such situations.

2.3 Diagnostic Processes as Unpacking Learning Goals

Morris, Hiebert, and Spitzer (2009) construct a theoretical model for teacher thinking which applies to a specific diagnostic situation. They consider the ability to “unpack” the sub-goals of a task as important for planning and evaluating students’ learning processes. They describe this ability as a type of mathematical knowledge that is special for teaching quite similar to the SCK by Ball et al. (2008), as described above. As an example, Morris et al. decompose the learning goal “students will understand how to add fractions and will understand the concepts underlying this operation” into six sub-goals that are necessary to attain the learning goal (Morris et al., 2009, p. 499):

  1. 1.

    A quantity is identified as the quantity “one.”

  2. 2.

    We obtain units of size 1/n by partitioning the “one” into n equal parts.

  3. 3.

    The numerator is the number of units of size 1/n.

  4. 4.

    The addends must both be expressed in terms of the same-sized unit.

  5. 5.

    The addends must be joined.

  6. 6.

    The sum must be expressed in terms of a unit of size 1/n.

This kind of analysis is a mathematical one and does not require any knowledge about individual student solutions. The authors emphasize that other decompositions of the learning goal are also possible. The identified sub-goals can be interpreted as subconcepts of students, and used to clarify students’ errors.

In their study preservice teachers had to complete four written tasks. They had to (1) anticipate an ideal student response, (2) evaluate a student’s incorrect response, (3) evaluate a student’s correct response, and (4) analyze a classroom lesson (Morris et al., 2009). Especially, the activities in tasks (2) and (3) can be understood as diagnostic activities. One result of the study is that the participants do not decompose learning goals spontaneously but they could be supported to do so when referring to subconcepts in the tasks explicitly.

Such a decomposition of learning goals provides a better understanding of the students’ failure and helps to localize it. However, the authors’ example is a very specific one, since it is mostly based on an analysis of procedures. Typical misconceptions of students such as the idea of “division makes the result smaller”, which is a learning obstacle when students go from natural numbers to fractions (e.g., Swan, 2001, p. 154) are not taken into consideration. As we can see by this example, it is not only the mathematical structure of a task, but also the structure of the learners’ knowledge that leads to errors in students’ solutions. Nevertheless, the decomposition of learning goals can be considered as an important facet of diagnostic competence. With regard to the identification of diagnostic processes and knowledge resources, the approach of Morris et al. comprises two aspects: The process of decomposing learning goals requires specialized content knowledge and knowledge about typical pre- or misconceptions of students (knowledge of content and students) (Ball et al., 2008).

The models discussed in the preceding sections contribute valuable theoretical ideas and empirical findings regarding diagnostic activities of teachers. Nickerson (1999) provides a very general model of an expert-novice-situation. This situation is similar to a diagnostic situation in the classroom although the author himself does not transfer the model into pedagogical context. Knowledge about frequent tendencies of under- or overestimating knowledge in the process of assessing other people’s knowledge can be helpful for a deeper understanding of fundamental processes concerning own knowledge. Ball et al. (2008) suggest different domains of mathematical knowledge by analyzing teaching situations which are also helpful for identifying knowledge resources required in diagnostic situations. Morris et al. (2009) outline a very specific process of decomposing mathematical knowledge which can be considered relevant for diagnostic situations, for example, for analyzing a task. Thus, all these models, though of very different scope, can be useful for a deeper understanding of diagnostic processes and the knowledge resources needed. However, they have their limitations. Nickerson (1999) describes cognitive processes in a judgment process but is not clear to what extent such processes are relevant in the pedagogical context, especially, in diagnostic situations of mathematics teachers. On the other hand, the model of decomposing learning goals (Morris et al., 2009) seems to be too specific to describe diagnostic processes extensively. The ability to decompose can be understood as an important part of diagnostic competences but it does not consider students’ misconceptions. Both models take knowledge resources needed in the processes into account only partially. The domains of mathematical knowledge (Ball et al., 2008) provide a framework that differentiates mathematics teachers’ knowledge but it is not focused on diagnostic processes.

Taken together these models can be helpful in the understanding of diagnostic processes and knowledge resources and their interaction in diagnostic situations. However, an empirical analysis is needed that accounts for the specificity of diagnostic situations on the one hand and the variety of phenomena encountered when analyzing teacher behavior on the other.

3 Investigating Processes and Knowledge Resources in Diagnostic Situations

The study reported here focuses on informal diagnostic situations in which mathematics teachers (1) judge tasks and (2) evaluate students’ solutions. Such diagnostic situations occur rather often: Teachers have to select and use tasks and have to react to students’ solutions and mistakes spontaneously. To investigate the diagnostic competence of mathematics teachers, it seems essential to study real processes and the knowledge resources needed in such diagnostic situations. So, the research questions are:

  1. 1.

    What kind of processes do teachers show in their diagnostic judgments?

  2. 2.

    What kind of knowledge do teachers rely on during these processes?

Investigating these questions can result in a deeper understanding of diagnostic processes on the one hand and a clarification of constituent parts of diagnostic competence in mathematics on the other. Another (long-term) objective connected with these questions is to derive consequences for teacher education (Philipp & Leuders, 2014).

3.1 Design

In order to gain knowledge on diagnostic processes and on knowledge resources, two-phased interviews were conducted. In the first phase the teachers first had to evaluate two tasks. Then three students’ solutions were presented successively to each task to initiate a diagnostic process. In the second phase the participants had to reflect on their own process in describing or explaining it. This procedure was expected to be beneficial for catching most of the relevant diagnostic processes and knowledge resources by triggering the participants with the tasks and students’ solutions and afterwards having them describe their own processes and give some additional statements. The reasoning in both phases was captured by means of think-aloud interviews (Ericsson & Simon, 1993).

The participants were six experienced mathematics teachers, three of them additionally experienced in mathematics teacher education. That way it was possible to draw on practical experience and theoretical knowledge similarly. The aim was to find a broad variety of different processes and knowledge resources used in diagnostic situations. Think-aloud-protocols of the interviews provide the data for the analyses which were a total of 12 evaluations of tasks and 36 evaluations of students’ solutions. The tasks were chosen from the topic of fractions due to the fact that broad systematic knowledge about typical students (mis-)conceptions in this field is available.

Figure 4 shows the two tasks and the three students’ solutions to each task used in the interviews. The students’ solutions were selected with regard to typical mistakes and misconceptions occurring frequently. The tasks and the interview guidelines were developed in a pilot study. In the first phase of the interview the participants were asked the following: “Please evaluate the task. How can you use it in the classroom?”, and then, to evaluate students’ solutions: “Please evaluate the students’ solution. Which conclusions do you draw?” In the second phase the participants reflected their own processes by answering the questions: “How did you come to your evaluation? Please describe and give reasons for your procedure. What kind of knowledge did you use?”

Fig. 4
figure 4

Tasks and students’ solutions (From: Wartha, 2007)

Full size image

3.2 Data Analysis

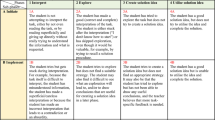
For the analysis of the data interpretative content analysis, techniques were used (Mayring, 1983). The objectives were to build a theory of processes in diagnostic situations (research question 1) and generate hypotheses for further research in this area. To answer the second research question, the same data was analyzed with a focus on different types of knowledge that influence diagnostic processes. In order to answer both research questions, the following steps were carried out: First theoretical categories were built based on the models mentioned before for both processes and knowledge resources. Initial point for the analysis built the categories in table 1.

Table 1 Theoretical categories for processes and knowledge resources
Full size table

Based on the think-aloud-protocols code descriptions, examples and coding rules were defined. In the next step new categories were continually supplemented and specified by identifying further processes or knowledge resources. Thus, the development of deductive and inductive categories was necessary. The analyses were carried out using the qualitative data analysis software, MAXQDA.

To capture diagnostic processes, the think-aloud-protocols in the two diagnostic situations, the evaluation of tasks and the evaluation of students’ solutions (first phase of the interview) were analyzed along with the reflection of the own processes (second phase of the interview). These different approaches provided an insight into a broad variety of diagnostic processes. Table 2 shows the identified processes in detail.

Table 2 Diagnostic processes
Full size table

The same data was analyzed again to answer the question which knowledge teachers rely on in such diagnostic situations (see Table 3). For example, the teacher statement “So that 1/4 is larger than 1/3. So the typical error, that, that it turns around, when it is in the denominator. With larger and smaller.” can illustrate the proceeding in the analysis. With a focus on processes, this excerpt can be interpreted as identifying deficits. The same statement also gives an indication of knowledge resources the teacher draws on: a typical mistake. So, this example strikingly shows the interaction of processes and knowledge resources, although this is not the case in every statement in equal measure.

Table 3 Knowledge resources used in diagnostic situations
Full size table

The generation of all codes, both processes and knowledge resources, were discussed several times in a group of researchers in mathematics education. In addition, they were used at two different points in time for the same data to assure the consistency of the assignments to categories.

In a further step of data analysis, relationships between the identified codes were investigated. Such relations were frequently occurring sequences of two (or more) codes or their simultaneous appearance. Also relationships between processes and knowledge resources were included in the analysis in order to achieve a more comprehensive view. The main result of this step of the analysis is a model of diagnostic processes presented in section 3.3.

3.3 Results

The intention of this section is not only to report the results of the study but also to point out their relation to the theoretical approaches mentioned above. By considering the relations of the identified codes, the diagnostic processes (first research question) can for the most part be interpreted as sequence of steps. It should be noted that not all of the participants showed all processes and there are also different qualities of individual processes observable in every step. This may be due to the use of different knowledge resources in the steps.

Figure 5 shows an idealized model of diagnostic processes and their relations: When the participants have to evaluate a task, the starting point often is an own solution approach. Then the participants identified prerequisites required by the task, and also potential barriers. In order to evaluate a student’s solution, it is necessary to follow the student’s argumentation. Thereby, strengths as well as deficits in the student’s approaches can be identified. Possible reasons for mistakes or misconceptions can be expressed by error hypotheses. In addition, measures to investigate if an error hypothesis is correct can be proposed.Footnote 1

Fig. 5
figure 5

Model of diagnostic processes

Full size image

Apart from these steps in a diagnostic situation, processes were found that typically comprise more than one step. These processes can be interpreted as strategies in diagnostic situations (Table 3). When the participants made an own solution approach, identified prerequisites and barriers of a task or followed the students’ solution (first three steps), it became clear that they took the student’s perspective. For example, they tried to adopt the thinking of an imaginary student in analyzing a task or tried to reconstruct the thinking of a particular student in analyzing the given students’ solutions. A very common strategy is to decompose tasks or students’ solutions and analyze them step by step. In order to identify strengths and deficits students’ solutions are compared; for example, with own solution approaches or typical mistakes.

With reference to the theoretical models, the relevance of the teachers’ own knowledge becomes apparent. It constitutes the fundament for diagnostic processes, as can be seen in the own solution approach, for example. This is also essential in the model Nickerson (1999) proposes as starting point of the process of assessing other people’s knowledge. In Nickerson’s approach the model of other people’s knowledge then is refined and adjusted. This is similar to the process of taking a students’ perspective in diagnostic situations; for example, when a teacher considers skills or typical strategies of a 6th grader, and can be seen as adaptation of an initial model of other peoples’ knowledge. When tasks or solutions are analyzed step by step, this can be interpreted as a kind of decomposition described by Morris and his colleagues (2009). Although it is not the specific decomposing of a learning goal, the decomposing of the prerequisites of a task, for example, so the strategy seems to be similar. This strategy also occurs in the evaluation of students’ solutions by analyzing their way of thinking stepwise. In the same manner decomposing is not restricted to learning goals. Thus, the understanding of decomposing here is an extended one.

Concerning the second research question regarding the knowledge resources teachers rely on in diagnostic situations, the codes can be related to different types of (mathematical) knowledge:

  • Teachers refer to the correctness of a solution when they have to decide which approaches are mathematically productive. This is mathematical content knowledge.

  • The use of mental models and different representations is helpful when teachers evaluate tasks, for example. Having multiple approaches available can be useful to identify prerequisites or barriers of a task. This can be described as knowledge only teachers need.

  • Topic-specific knowledge about typical mistakes, typical misconceptions or student strategies is a type of mathematical knowledge that includes knowledge about students.

  • Furthermore, knowledge of diagnostic methods seems to be essential when teachers have to locate possible reasons for errors.

Teachers use these categories of knowledge resources in diagnostic situations as found in the empirical analysis correspond largely with domains of mathematical knowledge which Ball and colleagues propose. The first category concurs with common content knowledge and is characterized as a type of general knowledge that is needed in different professions, not only in teaching. However, the second category is knowledge that no other profession needs (specialized content knowledge). The third category in addition implies knowledge about students and is conform to the domain knowledge of content and students. The last category seems to be rather a type of general pedagogical knowledge (Shulman, 1986, 1987) with being also subject-specific, or even topic-specific. It is a type of mathematical knowledge needed especially in diagnostic situations.

To sum up, the results of the study can be seen in connection with theoretical frameworks that do not only focus on diagnostic competence and therefore can be understood as a specification of such frameworks with respect to the category of diagnostic situations. The empirically found types of mathematical knowledge largely fit into the theoretical framework of Ball et al. (2008) and contain knowledge about methods to localize reasons for errors or misconceptions. A main strategy in diagnostic situations, that is to analyze step by step, resembles the process of decomposing mathematical learning goals Morris et al. (2009) delineate, but goes beyond, for instance, when misconceptions lead to errors that cannot be deduced this way. The results also show that own knowledge plays an important role in diagnostic situations, just as Nickerson illustrates in his model of assessing other peoples’ knowledge.

4 Discussion

The main objective of the study was to gain a deeper insight into diagnostic processes of teachers. The broad variety of identified processes shows that informal diagnostic situations make high demands on mathematics teachers. Furthermore, it was possible to point out that different types of (mathematical) knowledge are needed in the above-mentioned diagnostic situations. This may be a reason for different qualities of individual diagnostic processes. This became manifest, for instance, when the participants showed differences in the degree of flexibility, for example, in the number of solution approaches or representations. So, this seems to have an effect on the quality of their analyses in several diagnostic steps. In further studies these differences should be investigated. A possible setting could be to analyze differences between experts and novices with the objective to find indicators for diagnostic competence of mathematics teachers.

Another main objective of the reported study was the identification of different types of mathematical knowledge which teachers use in informal diagnostic situations. The findings provide evidence that in addition to content knowledge, specialized content knowledge and knowledge about content and students, knowledge about diagnostic methods is useful in diagnostic situations.

The present study analyzed diagnostic processes and competences of individuals at a given time in their career. For teacher education, it would be relevant to investigate in what way individuals acquire and develop these diagnostic competences, and which of them can be learned and taught in which way.

Systematic relationships between processes and knowledge resources could not be examined. This may be due to fact that the sample is too small for such analyses. Still diagnostic processes, knowledge resources and their interaction seem to be fundamental for understanding diagnostic competence of mathematics teachers, which involves not only knowledge but also abilities and attitudes. This question is of interest for deriving consequences for teacher education. Further questions arise, for example, how such knowledge can be taught at university.

The model of diagnostic processes is beneficial in that it is possible to classify individuals and so it offers the possibility to compare people or groups of people (e.g., experts and novices). Differences can be made visible, so in further research potential diagnostic types of teachers could be investigated. Furthermore, the identified processes and knowledge resources can be used for the development of concepts in teacher education or teacher further education with fostering of diagnostic competence in mind.