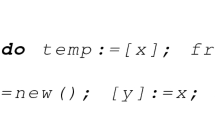1 Introduction

Program verification can be described as the problem of deciding whether a given program exhibits a desired behaviour, often called its specification. Temporal logic, in its various flavours [24] is a very popular and widely studied specification formalism due to its relative simplicity and expressive power: a wide variety of safety (“something bad cannot happen”) and liveness properties (“something good eventually happens”) can be captured [20].

Historically, perhaps the most popular approach to verify temporal properties of programs has been model checking: one first builds an abstract model that overapproximates all possible executions of the program, and then checks that the desired temporal property holds for this model (see e.g. [10, 12, 15]). However, this approach has been applied mainly to integer programs; the situation for memory-aware programs over heap data structures becomes significantly more challenging, mainly because of the difficulties in constructing suitable abstract models. One possible approach is simply to translate such heap-aware programs into integer variables, in such a way that properties such as memory safety or termination of the original program follows from a corresponding property in its integer translation [12, 15, 22]. However, for more general temporal properties, this technique might produce unsound results. In general, it is not clear whether it is feasible to provide suitable translations from heap to integer programs for any temporal property; in particular, numerical abstraction of heap programs often removes important information about the exact shape of heap data structures, which might be needed to prove some temporal properties.

Example 1

Consider a “server” program that, given an acyclic linked list with head pointer \(\mathtt {x}\), nondeterministically alternates between adding an arbitrary number of “job requests” to the head of the list and removing all requests in the list:

figure a

Memory safety of this program can be proven using a simple numeric abstraction recording emptiness/nonemptiness of the list. Proving instead that it is always possible for the heap to become empty, expressed in CTL as \(AGEF(\mathsf {emp})\), requires a finer abstraction, recording the length of the list. However, such an abstraction is still not sufficient to prove the property that the heap is always a nil-terminating acyclic list from x to nil, expressed in CTL as AG(ls(x, nil)) (where ls is the standard list segment predicate of separation logic [26]), because the information about acyclicity is lost.

Thus, although it is often possible to provide numeric abstractions to suit specific programs and temporal properties, it is not clear that this is so for arbitrary programs and properties.

In this paper, we instead approach the above problem via the main (perhaps less fashionable) alternative to model checking, namely the direct deductive verification of pointer programs. We formulate a cyclic proof system manipulating temporal judgements about programs, and employ automatic proof search in this system to verify that a program has a given temporal property. Given some fixed program, the judgements of our system express a temporal property of the program when started from any state satisfying a precondition written in a fragment of separation logic, a well-known language for describing heap memory [26]. The core of the proof system is a set of symbolic execution rules that simulate program execution steps. To handle the fact that symbolic execution can in general be applied ad infinitum, we employ cyclic proof [6, 7, 9, 29], in which proofs are finite cyclic graphs subject to a global soundness condition. Using this approach, we are frequently able to verify temporal properties of heap programs in an automatic and sound way without the need of abstractions or program translations. Moreover, our analysis has the added benefit of producing independently checkable proof objects.

Our proof system is tailored to CTL program properties over separation logic assertions; subsequently, we show how to adapt this system to handle fairness constraints, where nondeterministic branching may not unfairly favour one branch over another. We have also adapted our system to (fair) LTL properties, though we do not present this adaptation in this paper due to space constraints.

We provide an implementation of our proof system as an automated verification tool within the Cyclist theorem proving framework [9], and evaluate its performance on a range of examples. The source code, benchmark and executable binaries of the implementation are publicly available online [1]. Our tool is able to discover surprisingly complex cyclic proofs of temporal properties with times often in the millisecond range. Practically speaking, the advantages and disadvantages of our approach are entirely typical of deductive verification: on the one hand, we do not need to employ abstraction or program translation, and we guarantee soundness; on the other hand, our algorithms might fail to terminate, and (at least currently) we do not provide counterexamples in case of failure. Thus we believe our approach should be understood as a useful complement to, rather than a replacement for, model checking.

The remainder of this paper is structured as follows. Section 2 introduces our programming language, the memory state assertion language, and temporal (CTL) assertions over these. Section 3 introduces our proof system for verifying temporal properties of programs, and Sect. 4 modifies this system to account for fair program executions. Section 5 presents our implementation and experimental evaluation, Sect. 6 discusses related work and Sect. 7 concludes.

2 Programs and Assertions

In this section we introduce our programming language, our language of assertions about memory states (based on a fragment of separation logic) and our language for expressing temporal properties of programs, given by CTL over memory assertions.

Programming language. We use a simple language of while programs with pointers and (de)allocation, but without procedures. We assume a countably infinite set Var of variables and a first-order language of expressions over \(\textsf {Var}\). Branching conditions B and commands C are given by the following grammar:

$$\begin{aligned} \begin{array}{lll} B &{} {::=} &{} E = E \mid E \ne E \mid \mathsf {*}\\ C &{} {::=} &{} \text {x} := [E] \mid [E] := E \mid \text {x} := \mathbf{alloc }() \mid \mathbf{free }(E) \mid \text {x} := E \mid \\ &{}&{} \mathbf{skip } \mid {\mathbf{if }\;{B}\;\mathbf{then }\;{C}\;\mathbf{else }\;{C}\;\mathbf{fi }} \mid {\mathbf{while }\;{B}\;\mathbf{do }\;{C}\;\mathbf{od }} \mid C ; C \mid \epsilon \end{array} \end{aligned}$$

where \(x \in \textsf {Var}\) and E ranges over expressions. We write \(\epsilon \) for the empty command, \(\mathsf {*}\) for a nondeterministic condition, and [E] for dereferencing of expression E.

We define the semantics of the language in a stack-and-heap model employing heaps of records. We fix a set Val of values, and a set \(\textsf {Loc} \subset \textsf {Val}\) of addressable memory locations. A stack is a map \(s: \textsf {Var} \rightarrow \textsf {Val}\) from variables to values. The semantics \([\![E]\!]s\) of expression E under stack s is standard; in particular, \([\![x]\!]s = s(x)\) for \(x \in \textsf {Var}\). We extend stacks pointwise to act on tuples of terms. A heap is a partial, finite-domain function \(h : \textsf {Loc} \rightharpoonup _{\text {fin}} (\textsf {Val}\ \textsf {List})\), mapping finitely many memory locations to records, i.e. arbitrary-length tuples of values; we write \(\mathrm {dom}(h)\) for the set of locations on which h is defined. We write e for the empty heap, and \(\uplus \) to denote composition of domain-disjoint heaps: \(h_1 \uplus h_2\) is the union of \(h_1\) and \(h_2\) when \(\mathrm {dom}(h_1) \cap \mathrm {dom}(h_2) = \varnothing \) (and undefined otherwise). If f is a stack or a heap then we write \(f[x \mapsto v]\) for the stack or heap defined as f except that \(f[x \mapsto v](x) = v\). A paired stack and heap, (s, h), is called a (memory) state.

A (program) configuration \(\gamma \) is a triple \(\langle {C} , {s} , {h} \rangle \) where C is a command, s a stack and h a heap. If \(\gamma \) is a configuration, we write \(\gamma _{C}, \gamma _{s}\), and \(\gamma _{h}\) respectively for its first, second and third components. A configuration \(\gamma \) is called final if \(\gamma _C = \epsilon \). The small-step operational semantics of programs is given by a binary relation \(\leadsto \) on program configurations, where \(\gamma \leadsto \gamma '\) holds if the execution of the command \(\gamma _C\) in the state \((\gamma _s,\gamma _h)\) can result in the program configuration \(\gamma '\) in one step. We write \(\leadsto ^*\) for the reflexive-transitive closure of \(\leadsto \). The special configuration \(\mathsf {fault}\) is used to denote a memory fault, e.g., if a command tries to access non-allocated memory. For brevity, we omit the operational semantics here, since it is essentially standard.

An execution path is a (maximally finite or infinite) sequence \((\gamma _i)_{i \ge 0}\) of configurations such that \(\gamma _i \leadsto \gamma _{i+1}\) for all \(i \ge 0\). If \(\pi \) is a path, then we write \(\pi _i\) for the ith element of \(\pi \). A path \(\pi \) starts from configuration \(\gamma \) if \(\pi _0 = \gamma \).

Remark 1

In temporal program verification, it is relatively common to consider all program execution paths to be infinite, and all temporal properties to quantify over infinite paths. This can be achieved either (i) by modifying programs to contain an infinite loop at every exit point, or (ii) by modifying the operational semantics so that final configurations loop infinitely (i.e. \(\langle {\epsilon } , {s} , {h} \rangle \leadsto \langle {\epsilon } , {s} , {h} \rangle \)).

Here, instead, our temporal assertions quantify over paths that are either infinite or else maximally finite. This has the same effect as directly modifying programs or their operational semantics, but seems to us slightly cleaner.

Memory state assertions. We express properties of memory states (s, h) using a standard symbolic-heap fragment of separation logic (cf. [2]) extended with user-defined (inductive) predicates, typically needed to express data structures in the memory. We omit the schema for inductive predicates and their interpretations here, since they are identical to those used, e.g., in [7,8,9, 27].

Definition 1

A symbolic heap is given by a disjunction of assertions each of the form \(\varPi : \varSigma \), where \(\varPi \) is a finite set of pure formulas of the form \(E = E\) or \(E \ne E\), and \(\varSigma \) is a spatial formula given by the following grammar:

$$ \varSigma \,\, {::=} \,\, \mathsf {emp}\mid E \mapsto \mathbf {E} \mid \varSigma *\varSigma \mid \varPsi (\mathbf {E}) , $$

where E ranges over expressions, \(\mathbf {E}\) over tuples of expressions and \(\varPsi \) over predicate symbols (of arity matching the length of \(\mathbf {E}\) in \(\varPsi (\mathbf {E})\)).

Definition 2

Given a state s, h and symbolic heap \(\varPi : \varSigma \), we write \(s,h \,\models \, \varPi :\varSigma \) if \(s,h \,\models \, \varpi \) for all pure formulas \(\varpi \in \varPi \), and \(s,h \,\models \, \varSigma \), where the relation \(s,h \,\models \, A\) between states and formulas is defined by

$$\begin{array}{r@{}c@{}l} s,h \,\models \, E_1 = E_2 &{}\Leftrightarrow &{} [\![E_1]\!]s = [\![E_2]\!]s \\ s,h \,\models \, E_1 \ne E_2 &{}\Leftrightarrow &{} [\![E_1]\!]s \ne [\![E_2]\!]s \\ s,h \,\models \, \mathsf {emp}&{}\Leftrightarrow &{} \mathrm {dom}(h) = \varnothing \\ s,h \,\models \, E \mapsto \mathbf {E} &{}\Leftrightarrow &{} \mathrm {dom}(h) = \{[\![E]\!]s\}\,\, and \,\, h([\![E]\!]s) = [\![\mathbf {E}]\!]s \\ s,h \,\models \, \varPsi (\mathbf {E}) &{}\Leftrightarrow &{} ([\![\mathbf {E}]\!]s,h) \in [\![\varPsi ]\!] \\ s,h \,\models \, \varSigma _1 *\varSigma _2 &{} \Leftrightarrow &{} h = h_1 \uplus h_2 \,\, and \,\, s,h_1 \,\models \, \varSigma _1 \,\, and\,\, s,h_2 \,\models \, \varSigma _2 \\ s,h \,\models \, \varOmega _1 \vee \varOmega _2 &{}\Leftrightarrow &{} s,h \,\models \, \varOmega _1 \,\, or\,\, s,h \,\models \, \varOmega _2 \end{array}$$

Note that the semantics of a predicate symbol, \([\![\varPsi ]\!] \subseteq \mathsf {Val\ List}\, \times \,\mathsf {Heaps}\), is typically obtained from an inductive definition of \(\varPsi \) in a standard way (see e.g. [6]).

Temporal assertions. We describe temporal properties of our programs using temporal assertions, built from the memory state assertions given above using standard operators of computation tree logic (CTL) [11], where the temporal operators quantify over execution paths from a given configuration.

Definition 3

CTL assertions are described by the grammar:

$$\begin{array}{r@{}c@{}l} \varphi &{} {::=} &{} P \mid \mathsf {error}\mid \mathsf {final}\mid \varphi \wedge \varphi \mid \varphi \vee \varphi \mid \Diamond \varphi \mid \Box \varphi \\ &{}&{} \mid EF\varphi \mid AF\varphi \mid EG\varphi \mid AG\varphi \mid E(\varphi U \varphi ) \mid A(\varphi U \varphi ) \end{array}$$

where P ranges over memory state assertions (Definition 1).

Note that \(\mathsf {final}\) and \(\mathsf {error}\) denote final, respectively faulting configurations.

Definition 4

A configuration \(\gamma \) is a model of the CTL assertion \(\varphi \) if the relation \(\gamma \,\models \, \varphi \) holds, defined by structural induction as follows:

Judgements in our system are given by \(P \vdash C : \varphi \), where P is a symbolic heap, C is a command sequence and \(\varphi \) is a temporal assertion.

Definition 5

(Validity). A CTL judgement \(P \vdash C \;:\varphi \) is valid if and only if, for all memory states (s, h) such that \(s,h \,\models \, P\), we have \(\langle {C} , {s} , {h} \rangle \,\models \, \varphi \).

3 A Cyclic Proof System for Verifying CTL Properties

In this section, we present a cyclic proof system for establishing the validity of our CTL judgements on programs, as described in the previous section.

Our proof rules for CTL judgements are shown in Fig. 1. The symbolic execution rules for commands are adapted from those in the proof system for program termination in [7], accounting for whether a diamond \(\Diamond \) or box \(\Box \) property is being established. The dichotomy between \(\Diamond \) and \(\Box \) is only visible for the nondeterministic components of a program. In the specific case of our language, the nondeterministic constructs are (i) nondeterministic while; (ii) nondetreministic if; and (iii) memory allocation; it is only for these constructs that we need a specific rule for each case, as shown in our symbolic execution rules. Incidentally, the difference between E properties and A properties is basically the same as the difference between \(\Diamond \) and \(\Box \), but extended to execution paths rather than individual steps.

We also introduce faulting execution rules to allow us to prove that a program faults. The logical rules comprise standard rules for the logical connectives and standard unfolding rules for the temporal operators and inductive predicates in memory assertions. For brevity, we omit here the somewhat complex unfolding rule for inductive predicates, but similar rules can be found in, e.g., [7,8,9, 27].

Fig. 1.
figure 1

Proof rules for CTL judgements. We write \(\tiny \bigcirc \varphi \) to mean “either \(\Box \varphi \) or \(\Diamond \varphi \)”.

Full size image

Proofs in our system are cyclic proofs: standard derivation trees in which open subgoals can be closed either by applying an axiom or by forming a back-link to an identical interior node. To ensure that such structures correspond to sound proofs, a global soundness condition is imposed. The following definitions, adaptations of similar notions in e.g. [6,7,8,9, 27], formalise this notion.

Definition 6

(Pre-proof). A leaf of a derivation tree is called open if it is not the conclusion of an axiom. A pre-proof is a pair \(\mathcal {P} = (\mathcal {D,L})\), where \(\mathcal {D}\) is a finite derivation tree constructed according to the proof rules and \(\mathcal {L}\) is a back-link function assigning to every open leaf of \(\mathcal {D}\) a companion: an interior node of \(\mathcal {D}\) labelled by an identical proof judgement.

A pre-proof \(\mathcal {P} = (\mathcal {D,L})\) can be seen as a finite cyclic graph by identifying each open leaf of \(\mathcal {D}\) with its companion. A path in \(\mathcal {P}\) is then a path in this graph. It is easy to see that a path in a pre-proof corresponds to one or more paths in the execution of a program, interleaved with logical inferences.

To qualify as a proof, a cyclic pre-proof must satisfy a global soundness condition, defined using the notion of a trace along a path in a pre-proof.

Definition 7

(Trace). Let \((J_i = P_{i} \vdash C_{i} :\varphi _{i})_{i \ge 0}\) be a path in a pre-proof \(\mathcal {P}\). The sequence of temporal formulas along the path, \((\varphi _{i})_{i \ge 0}\), is a \(\Box \)-trace (\(\Diamond \)-trace) following that path if there exists a formula \(\psi \) such that, for all \(i \ge 0\):

  • the formula \(\varphi _i\) is of the form \(AG \psi \) (\(EG \psi \)) or \(\Box AG \psi \) (\(\Diamond EG \psi \)); and

  • \(\varphi _i = \varphi _{i+1}\) whenever \(J_i\) is the conclusion of the consequence rule (Cons).

We say that a trace progresses whenever a symbolic execution rule is applied. A trace is infinitely progressing if it progresses at infinitely many points.

We also take account of precondition traces arising from inductive predicates in the precondition, as employed in [7]. Roughly speaking, a precondition trace tracks an occurrence of an inductive predicate in the preconditions of the judgements along the path, progressing whenever the predicate occurrence is unfolded. Again, see [7,8,9, 27] for similar notions.

Definition 8

(Proof). A pre-proof \(\mathcal {P}\) is a proof if it satisfies the following global soundness condition: for every infinite path \((P_{i} \vdash C_{i} :\varphi _{i})_{i \ge 0}\) in \(\mathcal {P}\), there is an infinitely progressing \(\Box \)-trace, \(\Diamond \)-trace or precondition trace following some tail \((P_{i} \vdash C_{i} :\varphi _{i})_{i \ge n}\) of the path.

Example 2

Consider the server-like program in Example 1 in the Introduction. We can show that, given that the heap is initially a linked list from \(\mathtt {x}\) to \(\mathsf {nil}\), it is always possible for the heap to become empty at any point during program execution. Writing C for our server program, this property is expressed as the judgement \(ls(x,nil) \vdash C: AG EF(\mathsf {emp})\).

Figure 2 shows an outline cyclic proof of this judgement in our system (we suppress the internal judgements for space reasons, but show the cycle structure and rule applications). Note that the back-links depicted in blue do not form infinite loops as they all point to a companion that eventually leads to a (Check) axiom. The red back-links do give rise to infinite paths; one can see that the pre-proof qualifies as a valid cyclic proof since there is an infinitely progressing \(\Box \)-trace along every infinite path.

Fig. 2.
figure 2

Single threaded monolithic server example (Color figure online)

Full size image

We now show that our proof system is sound.

Lemma 1

Let \(J = (P \vdash C :\varphi )\) be the conclusion of a proof rule R. If J is invalid under (s, h), then there exists a premise of the rule \(J' = P' \vdash C' : \varphi '\) and a model \((s',h')\) such that \(J'\) is not valid under \((s',h')\) and, furthermore,

  1. 1.

    if there is a \(\Box \)-trace \((\varphi ,\varphi ')\) following the edge \((J, J')\) then, letting \(\psi \) be the unique subformula of \(\varphi \) given by Definition 7, there is a configuration \(\gamma \) such that \(\gamma \not \models \, \psi \), and the finite execution path \(\pi ' = \langle {C'} , {s'} , {h'} \rangle \ldots \gamma \) is well-defined and a subpath of \(\pi = \langle {C} , {s} , {h} \rangle \ldots \gamma \). Therefore \(\mathrm {length}(\pi ') \le \mathrm {length}(\pi )\). Moreover, \(\mathrm {length}(\pi ) < \mathrm {length}(\pi ')\) when R is a symbolic execution rule.

  2. 2.

    if there is a \(\Diamond \)-trace \((\varphi , \varphi ')\) following the edge \((J,J')\) then, letting \(\psi \) be the unique subformula of \(\varphi \) given by Definition 7, there is a smallest finite execution tree \(\kappa \) with root \(\langle {C} , {s} , {h} \rangle \), each of whose leaves \(\gamma \) satisfies \(\gamma \not \models \, \psi \). Moreover, \(\kappa \) has a subtree \(\kappa '\) with root \(\langle {C'} , {s'} , {h'} \rangle \) and whose leaves are all leaves of \(\kappa \). Therefore \(\mathrm {height}(\kappa ') \le \mathrm {height}(\kappa )\). Moreover, \(\mathrm {height}(\kappa ') < \mathrm {height}(\kappa )\) when R is a symbolic execution rule.

Theorem 1

(Soundness). If \(P \vdash C:\varphi \) is provable, then it is valid.

Proof

(Sketch) Suppose for contradiction that there is a cyclic proof \(\mathcal {P}\) of \(J=P \vdash C:\varphi \) but J is invalid. That is, for some stack s and heap h, we have \((s,h) \,\models \, P\) but \(\langle {C} , {s} , {h} \rangle \not \models \, \varphi \). Then, by local soundness of the proof rules, we can construct an infinite path \((P_i \vdash C_i :\varphi _i)_{i \ge 0}\) in \(\mathcal {P}\) of invalid judgements. Since \(\mathcal {P}\) is a cyclic proof, by Definition 8 there exists an infinitely progressing trace following some tail \((P_{i} \vdash C_{i} :\varphi _{i})_{i \ge n}\) of the path.

If this trace is a \(\Box \)-trace, using condition 1 of Lemma 1, we can construct an infinite sequence of finite paths to a fixed configuration \(\gamma \) of infinitely decreasing length, contradiction. A similar argument related to the height of computation trees applies in the case of a \(\Diamond \)-trace. A precondition trace yields an infinitely decreasing sequence of ordinal approximations of some inductive predicate, also a contradiction; see [7] for details.

The inductive-coinductive dichotomy shows nicely in our trace condition. Coinductive (G) properties need to show that something happens infinitely often whereas inductive (F) properties have to show that something cannot happen infinitely often. Both cases give us a progress condition: for coinductive properties, we essentially need program progress on the right of the judgements. For inductive properties, we need an infinite descent on the left of the judgements (or for the proof to be finite).

Readers familiar with Hoare-style proof systems might wonder about relative completeness of our system, i.e., whether all valid judgements are derivable if all valid entailments between formulas are derivable. Typically, such a result might be established by showing that for any program C and temporal property \(\varphi \), we can (a) express the logically weakest precondition for C to satisfy \(\varphi \), say \(wp(C,\varphi )\), and (b) derive \(wp(C,\varphi ) \vdash C : \varphi \) in our system. Relative completeness then follows from the rule of consequence, (Cons). Unfortunately, it seems certain that such weakest preconditions are not expressible in our language. For example, in [7], the multiplicative implication of separation logic, , is needed to express weakest preconditions, whereas it is not present in our language due to the problems it poses for automation (a compromise typical of most separation logic analyses). Indeed, it seems likely that we would need to extend our precondition language well beyond this, since [7] only treats termination, whereas we treat arbitrary temporal properties. Since our focus in this paper is on automation, we leave such an analysis to future work.

4 Fairness

An important component in the verification of reactive systems is a set of fairness requirements to guarantee that no computation is neglected forever. These fairness constraints are usually categorised as weak and strong fairness [20]. However, since weak fairness requirements are usually restricted to the parallel composition of processes, a property that our programming language lacks, we limit ourselves to the treatment of strong fairness.

Definition 9

(Fair execution). Let C be a program command and \(\pi = (\pi _i)_{i \ge 0}\) a program execution. We say that \(\pi \) visits C infinitely often if there are infinitely many distinct \(i \ge 0\) such that \(\pi _i = \langle {C} , {\_\ } , {\_\ } \rangle \). A program execution \(\pi \) is fair for commands \(C_i, C_j\) if it is the case that \(\pi \) visits \(C_i\) infinitely often if and only if \(\pi \) visits \(C_j\) infinitely often. Furthermore, \(\pi \) is fair for a program C if it is fair for all pairs of commands \(C_i,C_j\) such that C contains a command of the form \({{\varvec{if}}}\,\, {*}\,\, {{\varvec{then}}}\,\, {C_i}\,\, {{\varvec{else}}}\,\,{C_j}\,\, {{\varvec{fi}}}\,\, \) or \( \,\, {{\varvec{while}}}\,\, {*} \,\, {{\varvec{do}}}\,\, {C_i} \,\, {{\varvec{od}}}\,\, \; C_j\).

Note that every finite program execution is trivially fair. Also, for the purposes of fairness, we consider program commands to be uniquely labelled (to avoid confusion between different instances of the same command).

We now modify our cyclic CTL system to treat fairness constraints. First, we adjust the interpretation of judgements to account for fairness, then we lift the definition of fairness from program executions to paths in a pre-proof.

Definition 10

(Fair CTL judgement). A fair CTL judgement \({P} \vdash _{f} {C} \;:{\varphi }\) is valid if and only if, for all memory states (s, h) such that \(s,h \,\models \, P\), we have \(\langle {C} , {s} , {h} \rangle \models _f \,\varphi \), where \(\models _f\) is the satisfaction relation obtained from \(\models \) in Definition 4 by interpreting the temporal operators as quantifying over fair paths, rather than all paths. For example, the clause for AG becomes

Definition 11

A path in a pre-proof \((J_i = {P_{i}} \vdash _{f} {C_{i}} \;:{\varphi _{i}})_{i \ge 0}\) is said to visit C infinitely often if there are many distinct \(i \ge 0\) such that \(J_{i_C} = C\). A path in a pre-proof is fair for commands \(C_i, C_j\) if it is the case that \((J_i)_{i \ge 0}\) visits \(C_i\) infinitely often if and only if \((J_i)_{i \ge 0}\) visits \(C_j\) infinitely often. Finally, the path is fair for program C iff it is fair for all pairs of commands \(C_i,C_j\) such that C contains a command of the form \({{\varvec{if}}}\,\, {*}\,\, {{\varvec{then}}}\,\, {C_i}\,\, {{\varvec{else}}}\,\,{C_j}\,\, {{\varvec{fi}}}\,\, \) or \( \,\, {{\varvec{while}}}\,\, {*} \,\, {{\varvec{do}}}\,\, {C_i} \,\, {{\varvec{od}}}\,\, \; C_j\).

Given these new definitions, the global soundness condition of our proofs is restricted to account only for fair paths in a pre-proof.

Definition 12

(Bad pre-proof). A pre-proof \(\mathcal {P}\) is bad if there is an infinite path in \(\mathcal {P}\) such that the rule \((\text {Wh*}\,\Diamond \text {1})/(\text {If*}\,\Diamond \text {1})\) is applied infinitely often and \((\text {Wh*}\,\Diamond \text {2})/(\text {If*}\,\Diamond \text {2})\) is applied only finitely often, or vice versa.

Definition 13

(Fair proof). A pre-proof \(\mathcal {P}\) is a fair cyclic proof if it is not bad, and for every infinite fair path \(({P_{i}} \vdash _{f} {C_{i}} \;:{\varphi _{i}})_{i \ge 0}\) in \(\mathcal {P}\), there is an infinitely progressing \(\Box \)-trace, \(\Diamond \)-trace or precondition trace following some tail \(({P_{i}} \vdash _{f} {C_{i}} \;:{\varphi _{i}})_{i \ge n}\) of the path.

Proposition 1

(Decidable soundness condition). It is decidable whether a pre-proof is a valid fair cyclic proof.

Proof

(Sketch) To check that a pre-proof \(\mathcal {P}\) is not bad, we construct two Büchi automata; the first one \(\mathcal {A}_{B_1}\) accepts all infinite paths in \(\mathcal {P}\) such that the rule \(((\text {Wh*}\,\Diamond \text {1}))/(\text {If*}\,\Diamond \text {1})\) is applied infinitely often. The second Büchi automata \(\mathcal {A}_{B_2}\) accepts all infinite paths such that the rule \((\text {Wh*}\,\Diamond \text {2})/(\text {If*}\,\Diamond \text {2})\) is applied infinitely often. We then check that the following relation holds of the languages accepted by each automata: \(\mathcal {L}(\mathcal {A}_{B_1}) \subseteq \mathcal {L}(\mathcal {A}_{B_2})\) and \(\mathcal {L}(\mathcal {A}_{B_2}) \subseteq \mathcal {L}(\mathcal {A}_{B_1})\), where language inclusion of Büchi automata is decidable.

Moreover, to check that there exists an infinitely progressing trace along every infinite path of \(\mathcal {P}\) we construct two automata over strings of nodes of \(\mathcal {P}\). The fair automata \(\mathcal {A}_{\textit{Fair}}\) that accepts all infinite fair paths in \(\mathcal {P}\) is a Streett automata with acceptance condition formed of conjuncts of the form \((\mathrm {Fin}(i) \vee \mathrm {Inf}(j)) \wedge (\mathrm {Fin}(j) \vee \mathrm {Inf}(i))\) for each pair of fairness constraints (i, j). The trace automata \(\mathcal {A}_{\textit{Trace}}\) is a Büchi automata that accepts all infinite paths in \(\mathcal {P}\) such that an infinitely progressing trace exists along the path (cf. [5]). \(\mathcal {P}\) is then a valid cyclic proof if and only if \(\mathcal {A}_{\textit{Trace}}\) accepts all strings accepted by \(\mathcal {A}_{\textit{Fair}}\). We are then done since Streett automata can be transformed into Büchi automata [21] and inclusion between Büchi automata is decidable.

Fig. 3.
figure 3

Single threaded monolithic server example

Full size image

Example 3

We return to our server program from Examples 1 and 2. Suppose we wish to prove, not that it is always possible for the heap to become empty, i.e. \(AG EF(\mathsf {emp})\), but that the heap will always eventually become empty, i.e. \(AG AF(\mathsf {emp})\). Our server program in fact does not satisfy this property, because the program can always choose to execute the second inner loop infinitely often, adding job requests to the list forever. However, it does satisfy this property under the assumption of fair execution, which prevents the second loop from being executed infinitely often without executing the first loop.

Figure 3 shows the proof of this property in the adaptation of our system that is aware of fairness constraints as described above. Adding the fairness constraints relaxes the conditions under which back-links can be formed. This relaxed condition can be seen in back-links depicted in green as they cause an infinite path with no valid trace to be formed. Yet, because this infinite path is unfair, it is not considered in the global soundness condition. Our pre-proof qualifies as a valid cyclic proof since along every fair infinite path there is either a \(\Box \)-trace or a precondition trace progressing infinitely often.

Theorem 2

(Soundness). If \({P} \vdash _{f} {C} \;:{\varphi }\) is provable, then it is valid.

Proof

(Sketch) Suppose for contradiction that there is a fair cyclic proof \(\mathcal {P}\) of \(J={P} \vdash _{f} {C} \;:{\varphi }\) but J is invalid. That is, for some stack s and heap h, we have \((s,h) \,\models \, P\) but \(\langle {C} , {s} , {h} \rangle \not \models _f \, \varphi \). Then, by local soundness of the proof rules, we can construct an infinite path \(({P_i} \vdash _{f} {C_i} \;:{\varphi _i})_{i \ge 0}\) in \(\mathcal {P}\) of invalid sequents. By Definition 13 we know that said infinite path is a fair path (as any unfair path has been ruled out by requiring that \(\mathcal {P}\) is not a bad pre-proof according to Definition 12). Since the path is an infinite fair path, by Definition 13 we also know that there is an infinitely progressing \(\Box \)-trace, \(\Diamond \)-trace or precondition trace following some tail of the path. Showing that the existence of an infinitely progressing trace along the path leads to a contradiction follows the same argument as in Sect. 3.

5 Implementation and Evaluation

We implement our proof systems on top of the Cyclist theorem prover [9], a mechanised cyclic theorem proving framework. The implementation, source code and benchmarks are publicly available at [1] (under the subdirectory titled as the present paper).

Our implementation performs iterative depth-first search, aimed at closing open nodes in the proof by either applying an inference rule or forming a back-link. If an open node cannot be closed, we attempt to apply symbolic execution; if this is not possible, we try unfolding temporal operators and inductive predicates in the precondition to enable symbolic execution to proceed. Forming back-links typically requires the use of the consequence rule (i.e. a lemma proven on demand) to re-establish preconditions altered by symbolic executions (as can be seen in Figs. 2 and 3). When all open nodes have been closed, a global soundness check of the cyclic proof is performed automatically. Entailment queries over symbolic heaps in separation logic, which arise at backlinks and when applying the (Check) axiom or checking rule side conditions, are handled by a separate instantiation of \(\textsc {Cyclist }\) for separation logic entailments [9].

We evaluate the implementation on handcrafted nondeterministic and nonterminating programs similar to Example 1. Our test suite can be seen as an adaptation of the common model checking benchmarks presented in [14, 15] for the verification of temporal properties of nondeterministic programs. Roughly speaking, operations/iterations on integer variables in the original benchmarks are replaced in favour of operations/iterations on heap data structures.

Our test suite comprises the following programs:

  1. (i)

    Examples discussed in the paper are named Exmp;

  2. (ii)

    Fin-Lock - a finite program that acquires a lock and, once obtained, proceeds to free from memory the elements of a list and reset the lock;

  3. (iii)

    Inf-Lock wraps the previous program inside an infinite loop;

  4. (iv)

    Nd-In-Lock is an infinite loop that nondeterministically acquires a lock, then proceeds to perform a nondeterministic number of operations before releasing the lock;

  5. (v)

    Inf-List is an infinite loop that nondeterministically adds a new element to the list or advances the head of the list by one element on each iteration;

  6. (vi)

    Insert-List has a nondeterministic if statement that either adds a single elements to the head of the list or deletes all elements but one, and is followed by an infinite loop;

  7. (vii)

    Append-List appends the second argument to the end of the first argument;

  8. (viii)

    Cyclic-List is a nonterminating program that iterates through a non-empty cyclic list;

  9. (ix)

    Inf-BinTRee is an infinite loop that nondeterministically inserts nodes to a binary three or performs a random walk of the three;

  10. (x)

    The programs named with Branch define a somewhat arbitrary nesting of nondeterministic if and while statements, aimed at testing the capability of the tool in terms of lines of code and nesting of cycles;

  11. (xi)

    Finally we also cover sample programs taken from the Windows Update system (Win Update), the back-end infrastructure of the PostgreSQL database server (PostgreSQL) and an implementation of the acquire-release algorithm taken from the aforementioned benchmarks (Acq-Rel).

We show the results of the evaluation of the CTL system and its extension to consider fairness constraints in Table 1. For each test, we report whether fairness constraints were needed to verify the desired property and the time taken in seconds. The tests were carried out on an Intel x-64 i5 system at 2.50 GHz.

Table 1. Experimental results.
Full size table

Our experiments demonstrate the viability of our approach: our runtimes are mostly in the range of milliseconds and show similar performance to existing tools for the model checking benchmarks. Overall, the execution times in the evaluation are quite varied as they depend on a few factors such as the complexity of the program in question and temporal property to verify, but sources of potential slowdown can be witnessed by different test cases. Even at the level of pure memory assertions, the base case rule (Check) has to check entailments \(P \,\models \, Q\) between symbolic heaps, which involves calling an inductive theorem prover; this is reasonably fast in some cases, but very costly in others (e.g. the Append-List example). Another source of slowdown is in attempting to form back-links too eagerly (e.g. when encountering the same command at two different program locations); since we check soundness when forming a back-link, which involves calling a model checker (cf. [9]), this too is an expensive operation, as can be seen in the runtimes of test cases with suffix Branch.

Note that despite the encouraging results, the implementation is not without limitations as it might, in some cases, fail to terminate and produce a valid proof. Generalising, our proof search tends to fail either when the temporal property in question does not hold, or when we fail to establish a sufficiently general “invariant” to form backlinks in the proof.

6 Related Work

Related work on the automated verification of temporal program properties can broadly be classified into two main schools, model checking and deductive verification. In recent years, model checking has been the more popular of these two. Although earlier work in model checking focused on finite-state transition systems (e.g. [11, 25]), recent advances in areas such as state space restriction [3], precondition synthesis [12], CEGAR [15], bounded model checking [10] and automata theory [13] have enabled the treatment of infinite transition systems.

The present paper takes the deductive verification approach. A common limitation of early proof systems for various temporal logics is their restriction to finite state transition systems [4, 18, 19]. In the realm of infinite state systems, previous proof systems for verifying temporal properties of arbitrary transition systems [23, 30] have shed some light on the soundness and relative completeness of deductive verification. However, these early systems have typically relied upon complex verification conditions that are seemingly difficult to fully automate, arguably the most cited argument against deductive verification. In contrast, our proof system can handle infinite state, non-terminating programs, even under fairness restrictions, and we provide an implementation and evaluation, showing that it can indeed work in practice.

Of particular relevance here are those proof systems for temporal properties based on cyclic proof. Our work can be seen as an extension of the cyclic termination proofs in [7] to arbitrary temporal properties. In [4], a procedure for the verification of CTL* properties is developed that employs a cyclic proof system for LTL as a sub-procedure. A subtle but important difference when compared to our work is the lack of cut/consequence rule (used e.g. to generalise precondition formulas or to apply intermediary lemmas). A side benefit of this restriction is a simplification of the soundness condition on cyclic proofs.

A cyclic proof system for the verification of CTL* properties of infinite-state transition systems is presented in [30]. Focusing on generality, this system avoids considering details of state formulas and their evolution throughout program execution by assuming an oracle for a general transition system. The system relies on a soundness condition that is similar to Definition 8, but does not track progress in the same way, imposing extra conditions on the order in which rules are applied. The success criterion for validity of a proof also presents some differences; it relies on finding ranking functions, intermediate assertions and checking for the validity of Hoare triples, and it is far from clear that such checks can be fully automated. In contrast, we rely on a relatively simple \(\omega \)-regular condition, which is decidable and can be automatically checked by \(\textsc {Cyclist }\) [5, 9, 29].

7 Conclusions and Future Work

Our main contribution in this paper is the formulation, implementation and evaluation of a deductive cyclic proof system for verifying temporal properties of pointer programs, building on previous systems for separation logic and for other temporal verification settings [4, 7, 30]. We present two variants of our system and prove both systems sound. We have implemented these proof systems, and proof search algorithms for them, in the \(\textsc {Cyclist }\) theorem prover, and evaluated them on benchmarks drawn from the literature.

The main advantage of our approach is that we never obtain false positive results. This advantage is not in fact exclusive to deductive verification: some automata-theoretic model checking approaches are also proven to be sound [32]. Nonetheless, when compared to such approaches, our treatment of the temporal verification problem has the advantage of being direct. Owing to our use of separation logic and a deductive proof system, we do not need to apply approximation or transformations to the program as a first step; in particular, we avoid the translation of temporal formulas into complex automata [33] and the instrumentation of the original program with auxiliary constructs [13].

One natural direction for future work is to develop improved mechanised techniques, such as generalisation/abstraction, to enhance the performance of proof search in our system(s). Another possible direction is to consider larger classes of programs. In particular, concurrency is one very interesting such possibility, perhaps building on existing verification techniques for concurrency in separation logic (e.g. [31]). A different direction to explore is the enrichment of our assertion language, for example to CTL* [17] or \(\mu \)-calculus [16]. The structure of CTL* formulas and their classification into path and state subformulas suggest a possible combination of our CTL system with an LTL system to produce a proof object composed of smaller proof structures (cf. [4, 30]). The encoding of CTL* into \(\mu \)-calculus [16] and the applicability of cyclic proofs for the verification of \(\mu \)-calculus properties (see e.g. [28]) hint at the feasibility of such an extension.