Genomic Selection: State of the Art

Abstract

Genomic prediction is an important approach that recently emerged to guide plant and animal breeding efforts. Much of this optimism is based on the success of genomic selection (GS) to predict breeding values, when compared with the traditional results of marker-assisted selection (MAS) and phenotypic evaluations. Its effective implementation depends, however, on important theoretical and practical aspects related to the breeding program composition and the genetic background of the species under investigation. This chapter covers topics related with GS implementation and concepts that underlies its predictive ability. Requirements necessary to the population definition, statistical methods, GS influence on the expected genetic gain, examples of success in tropical crops, and challenges are discussed in order to guide future studies. Finally, we provide a critical analysis about the potential of GS to reshape traditional breeding schemes, without ignoring conventional breeding practices and genetic studies.

1 Introduction

Plant breeding underpins successful crop production and involves the modification of genotypes to improve yield, field performance, host plant resistance to pests, and end use quality. Traditionally, genetic progress has been achieved by phenotypic evaluations in field trials. It is undeniable that important advances were obtained in the last decades. It is important, however, to take into account the time required to achieve these gains. In practice, approaches based in phenotypic metrics are coupled with long testing phases resulting in slow genetic gain per unit of time.

Since the 1980s, with the advent of molecular markers and the perception of its advantages, new opportunities were opened for its use in breeding programs. The central purpose is to assist (or support) the selection using DNA information. Named as marker-assisted selection (MAS ), the application was motivated by the opportunity to reduce cost and time and, consequently, increase the expected genetic gain (Lande and Thompson 1990). Additionally, the use of markers was seen as an important alternative to increase the understanding of the genetic architecture of a quantitative trait, which has always been unclear and intriguing.

Among the MAS methods , the first to be widely accepted in the animal and plant breeding was termed quantitative trait loci (QTL) mapping . Quantitative traits refer to phenotypes that are controlled by two or more genes (i.e., multigenes) and affected by environmental factors, thus resulting in continuous variation in a population (Mackay et al. 2009). QTL are regions in the genome that harbor genes that govern a quantitative trait of interest (Doerge 2002). The concept that underlies QTL analysis is to split the mapping task into two components: (1) identifying QTL and (2) estimating their effect (Jannink et al. 2010).

Despite the importance of elucidating the genetic bases of quantitative loci, the QTL mapping approach has drawbacks that prevent its routine application in breeding programs (Bernardo 2008). The linkage disequilibrium induced in experimental populations, for instance, restricts the relevance of results to the families (or population) under study (Heffner et al. 2009). Additionally, QTL mapping has a better performance for traits controlled by major genes, which is an unusual scenario for traits with agronomic importance (Goddard and Hayes 2007). Supported by these inconveniences, Meuwissen et al. (2001) proposed a promised methodology that was popularized later as genomic selection (GS). It is opportune a brief description about the facts that drive the development of the GS methodology.

As previously mentioned, QTL mapping failed in its practical application (Dekkers 2004; Bernardo and Yu 2007; Xu 2008). In addition, high-throughput genotyping was boosted by next-generation sequencing techniques (NGS ) that significantly reduced the cost per marker (Poland and Rife 2012). The availability of cheap and abundant molecular markers changed, in different aspects, the form in which DNA information could be inserted in genetic studies. Firstly, genotyping was automated and, in some cases, outsourced, permitting a routine and feasible application. Secondly, a vast number of genome-wide single nucleotide polymorphism (SNP ) markers were discovered in many species (He et al. 2014). Lastly, computational and statistical methods converged to handle the effective analysis of the vast amount of molecular data. All of these contributed to the development of a new method of marker-assisted selection, with greater success.

Hence, if, on the one hand, traditional QTL analysis is based on the detection, mapping, and use of QTL with large effect on a trait selection, on the other hand, GS works by simultaneously selecting hundreds or thousands of markers covering the genome so that the majority of quantitative trait loci are in linkage disequilibrium (LD) with such markers (Meuwissen et al. 2001). Formally, the core of GS is the absence of any statistical test to declare if a marker has a statistically significant effect. Even effects that might be too small will be used to compute the genomic estimated breeding value. In addition, when markers covering the whole genome are used, LD is assumed between QTL and markers across all families resulting in wider applications, even for traits with low heritability (Goddard and Hayes 2007).

It has been predicted for over two decades that molecular information have the potential to redirecting resources and activities in breeding programs (Meuwissen et al. 2001; Goddard and Hayes 2007; Crossa et al. 2010; Jannink et al. 2010; Nakaya and Isobe 2012). GS has emerged as the method closest to achieving this goal. In this chapter, theory and practice will be discussed to detail how the methodology may reshape breeding programs and facilitate selection gains.

2 Practical and Theoretical Requirements for Genomic Selection Implementation

The previously mentioned features make GS a product of this millennium with real prospects for success. To this end, some practical and theoretical requirements are necessary for an effective implementation. In practical terms, genotyping and the definition of training and testing data sets constitute important aspects. In theoretical terms, biological and genetic concepts will be reflected by the final GS performance. This following section intends to present some details about the practical and theoretical factors which underlie GS implementation.

2.1 Practical Implementation

For a consolidated breeding program, with breeding schemes well defined that are consistently supported by good germplasm and experimentation, practical usage of genomic prediction can be considered straightforward. In general, it depends on critical decisions about which materials should be predicted and, in particular, financial and physical resources to be available for genotyping and phenotyping . These requirements are formally summarized by the subdivision of the program in three data sets, generically named “populations.” The population term, in GS context, should be interpreted as a set of genotypes, where the predictive models will be trained, validated, and applied. These concepts have a close relationship with terms commonly used in the statistical learning area, especially topics on resampling and cross-validation (James et al. 2013).

The first data set is the training population (TRN ). This set is also known as the reference population or discovery data set (Goddard and Hayes 2007; Nakaya and Isobe 2012; Desta and Ortiz 2014). In this step, a predictive model is defined, and the allelic effects are estimated. The individuals belonging to TRN (accesses, lines, clones, double haploid, families, etc.) must be genotyped and phenotyped for the traits of interest. A common challenge is the definition of which individuals should compose this reference population. There is not a standard way to answer this question. In theory, this population is composed by promising materials, on which the breeder has particular interest to apply selection methods and, hence, obtain new cultivars. As will be described in the next topic, this specification will have important consequences on the predictive ability of GS.

Next, a second data set called the validation or testing population (TST) should be defined (Goddard and Hayes 2007; Nakaya and Isobe 2012; Desta and Ortiz 2014). In general, this population is slightly smaller than the TRN and also includes individuals that must be genotyped and phenotyped. The role of the TST , simply stated, is to check the efficiency predictive equation defined in the previous step. The genome-estimated breeding values (GEBVs ) are obtained using the marker effect estimated in the TNR and correlated with the true phenotypic values (Desta and Ortiz 2014). This result is called predictive accuracy (Ould Estaghvirou et al. 2013) and has been commonly reported as the standard metric to evaluate GS efficiency. Its magnitude will provide an important measure of GS ability to predict phenotypes, based solely on genotypic data.

The last data set is commonly called the breeding population (Goddard and Hayes 2007; Nakaya and Isobe 2012; Desta and Ortiz 2014). This is the population where GS will be directly applied, so it is the major focus of the breeding programs. Given the satisfactory accuracy value obtained in the last step, the molecular markers become the unit of evaluation in the breeding program. The effects estimated in the TST and validated in the TRN will be used, therefore, to predict new phenotypes. At this moment, selection will be guided solely by marker information (Lorenz et al. 2011). For this reason, selection can be performed at early stages (e.g., seedlings inside greenhouses), thus resulting saving of time and field evaluations (assuming that costs of genotyping are smaller).

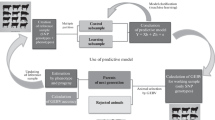
Figure 2.1 shows the importance of these populations. As illustrated, all of them are connected, and the effects estimated in the first step will be used in all subsequent steps. In this sense, the use of an appropriate genomic model is a critical step (an in-depth discussion is provided in the Statistical Method section ). Although populations are presented as physically separated, a single population may serve all the three functions.

Fig. 2.1

Genomic selection (GS) implementation . Allele effects (β) estimated in the training data set (TRN) are used in all subsequent steps. In the testing data set (TST), these effects are used to predict the genomic estimated breeding values (GEBV), which are correlated with the true phenotypic values. This correlation value is termed as predictive accuracy (r), and it is an important indicator of efficiency. Breeding data set is the GS target. Prediction based on molecular information is performed, and genotypes are selected in early stages (seedlings), using the alleles effects as selection criteria

Genotyping and phenotyping are important aspects to consider for practical implementation. The final state of a trait will be the cumulative result of a number of causal interactions between the genetic makeup of the genotype and the environment in which the plant developed (Malosetti et al. 2013). Therefore, it is common that genetic and nongenetic sources are decomposed and studied, making the experimental design and agricultural practices two fundamental aspects to be considered during the data set definition. Certainly, GS success is closely dependent of the environment in which the phenotypes are measured and on the presence of genotype-by-environment (GxE ) interaction.

Regarding the genotyping , as already mentioned, procedures have been advanced by the rapid progress of NGS methodologies. Genotyping by sequencing (GBS ) is a product of this rapid advance and combined the possibility to simultaneously perform marker discovery (SNPs) and genotyping across the population of interest (Elshire et al. 2011). Unlike the traditional genotyping methods where these two steps are performed separately, GBS is a one-step approach which makes the technique truly rapid, flexible, and perfectly suited for GS studies (Poland and Rife 2012). Although markers based on solid arrays (chips) or PCR may be used in GS studies, the number of reports using GBS and its variants is significantly higher. However, the number of genotyping methods techniques is under constant development, and we will certainly see more progress in this area in the next years.

2.2 Theoretical Aspects Related to Predictive Capacity

The predictive ability will be dependent on the genetic and nongenetic factors under analysis. Having a reasonable understanding of theoretical aspects that underlie these factors helps to guide GS implementation and, hence, improve the predictions. A central concept, closely linked with the theoretical definition of GS, is the linkage disequilibrium (LD). Also known as allelic association , LD is the “nonrandom association of alleles at different loci” (Flint-Garcia et al. 2003). The correlation between polymorphisms is caused by their shared history of mutation and recombination. The terms linkage and LD are often confused. Although LD and linkage are related concepts, they are intrinsically different. Linkage refers to the correlated inheritance of loci through the physical connection on a chromosome, whereas LD refers to the correlation between alleles in a population (Ott et al. 2011). Generally, all of the sources that affect Hardy Weinberg (HW) equilibrium could potentially have an influence on LD patterns (Flint-Garcia et al. 2003). In the GS context, LD concept plays a key role, as the distance along which LD persists will determine the number and density of markers and experimental design needed to perform an association analysis (Flint-Garcia et al. 2003; Mackay and Powell 2007).

Several studies have been proposed to elucidate other factors which affect predictive ability. If a large number of QTL contribute to trait variation, the following equation described by Daetwyler et al. (2013) is appropriate to predict the expected accuracy: $\sqrt{N_{\mathrm{p}}{h}^2{\left[{N}_{\mathrm{p}}{h}^2+{M}_{\mathrm{e}}\right]}^{-1}}$, where N _p is the number of individuals in the TRN,h ² is the heritability of the trait, and M _e is the number of independent chromosome segments.

A critical parameter is M _e, since it is inversely proportional to the accuracy. The success of GS is directly associated with the genetic distance between the reference population (TRN), where the model is trained, and the breeding population, where the estimated marker effects are used as unit of selection. This equation formalizes the idea, considering that one always expects a reduction in the predictive ability when the genetic distance increases. As a practical consequence, it is expected to have lower predictive accuracy when generations are far apart, for instance. Thus, understanding the genetic background where the model will be trained for the selection target (the breeding population) is essential to success.

The population size is another factor in the formula. Its importance is clear for two reasons, as pointed out by de Los Campos et al. (2013). First, the accuracy of estimated marker effects increases with sample size, because bias and variance of estimates of marker effects decrease with increasing sample size. Second, an increase in sample size may also increase the extent of the genetic relationship between TRN and TST data sets, which was previously described as an important factor. Population size has been highly variable in GS studies. In a revision on the subject, Nakaya and Isobe (2012) showed that, for cereals such as maize, barley, and wheat, an average size of 258 individuals has been used in the TRN data set. On the other hand, this value is larger in forest studies, where, on average, 673 individuals constitute the TRN. Studies in plants have been shown that smaller TRN sizes are required, relative to studies in animal. The authors point out two factors for this: (1) the narrow genetic diversity in plant populations, which is mainly caused by self-crossing reproduction, and (2) the quality of phenotypic evaluations, as good experimental design is more common in plant than in animal breeding.

Heritability is the biological factor highlighted in the formula. Heritability is defined as the proportion of phenotypic variance among individuals in a population that is due to heritable genetic effects. It is, therefore, expected to increase accuracy for traits governed by genetic factors and with less environmental effects. The direct relationship between accuracy and heritability is supported by simulation (Daetwyler et al. 2013).

3 Statistical Methods Applied to Genomic Predictions

GS studies involve the prediction of breeding values using DNA information (Fig. 2.1). For this, the inference of marker effects and their connection to phenotypes is considered the final stage. Given its importance, this section was designated to describe the use of linear models to predict breeding values, highlighting differences between philosophies of analysis in statistical learning. As a final topic, we discuss GS models that have been commonly used in plant breeding.

3.1 Linear Models and a Gentle Introduction to Statistical Learning

Prediction begins with the specification of a model involving effects and other parameters that try to describe an observed phenomenon. In GS context, a statistical model is proposed to associate phenotypic observations with variations at the DNA level . A large number of models may be defined to link these variables. A particularly useful class are linear models, where various effects are added and assumed to cause the observed values (Garrick et al. 2014). A linear relationship is considered the simplest attempt to describe the dependency between variables. For this reason, it is often the starting point to model some phenomena. Supported by a consolidated theory, this class of models has a statistical value and genetic interpretation that are useful for biometric research.

The attempt to develop an accurate model, which can be used to predict some important metric, is called statistical learning (James et al. 2013). In many GS implementations, linear regression models are used to this end to describe the genetic values. Linear regression, simply stated, is a method that summarizes how the average values of an outcome variable vary over subpopulations defined by linear functions of predictor variables (Gelman and Hill 2007). In the context of genomic prediction context, phenotypes are the response (or dependent) variable, and they are regressed on the markers (predictors or independent variable) using a regression function. As pointed out by de Los Campos et al. (2013), this regression function should be viewed as an approximation to the true unknown genetic values, which can be interpreted as a complex function involving the genotype of the ith individual at a large number of genes, as well as its interactions with environmental conditions.

In statistical notation, a regression model may be represented by:

$$ {y}_i={\beta}_0+\sum_{j=1}^p{\beta}_j{x}_{ij}+{\epsilon}_i $$

This means that the phenotypic observation of the individual i is made up of the sum of the following components: β ₀ is an intercept, x _ij is the genotype of the ith individual (i = 1,...,n) at the jth marker (j = 1, …, p), and β _j is the regression coefficient, corresponding to marker effects. The ϵ _i term represents random variables capturing nongenetic effects, which can emerge due to imperfect linkage disequilibrium between markers and QTL or model misspecification.

As noted, the phenotypic response is influenced by more than one predictor variable, as expected for quantitative traits. The postulated model may be an idealized oversimplification of the complex real-word situation, but in such cases, empirical models provide useful approximations of the relationship among variables (Rencher and Schaalje 2008). Intuitively, the regression model boils down to a mathematical construct used to represent what we believe may represent the mechanism that generates the observations at hand.

In matrix notation , the same model may be represented as y = XB + e, where y is a n × 1 phenotypic vector, X is a n × p marker genotype matrix, B is a p × 1 vector of marker effects, and e is a n × 1 vector of residual effects. Again, the response vector is made up of the value of the linear predictor plus the vector of residuals. The linear predictor consists of the product of the marker genotype (matrix X) and the estimated marker effects $\left(\overset{\wedge }{B}\right)$. Thus, the linear predictor $\left(X\overset{\wedge }{B}\right)$ is another vector containing the expected value of the response, given the covariates, for each individual i.

In essence, statistical learning refers to a set of approaches for estimating the regression coefficients (James et al. 2013). There are two main reasons one may wish to estimate these coefficients: prediction and inference. GS studies, in general, are focused in predictions. A set of inputs X (molecular markers) are readily available, and the output y (phenotypic values) should be predicted. In this setting, the way in which the coefficients are estimated is often treated as a black box, in the sense that one is not typically concerned with the exact form of B but whether it yields accurate predictions for the phenotypic values. Strictly speaking, this is the main difference between prediction and inference. In inference studies, we wish to estimate these coefficients and know their exact form, in order to understand which predictors are associated with the response.

In regression analysis, inference on the regression coefficient (marker effects) can be performed using different approaches. For example, one approach might be to derive a function for the marker effects that maximizes the correlation between predicted values and their unobserved true values. Alternatively, another approach might be to minimize the prediction error variance, which is the expected value of the squared difference between predicted values and their unobserved true values (Garrick et al. 2014). This last criterion is referred to as ordinary least squares (Rencher and Schaalje 2008) and is widely used in regression analysis . Intuitively, the idea is sensible: given that we are trying to predict an outcome using other variables, we want to do so in such a way as to minimize the error of our prediction (Gelman and Hill 2007).

A direct relation between regression and quantitative genetic concepts can be formulated. Considering regression models with one predictor, under an additive model and two alleles at a locus, the estimated regression coefficient may be interpreted in terms of the average effect of an allelic substitution, which quantifies the variation of the phenotypic values when an allele is replaced by its alternative (Falconer and Mackay 1996). As a biological consequence, two copies of the second allele have twice as much effect as one copy, and no copies have zero effect. The underlying assumption here is that the marker will only affect the trait if it is in linkage disequilibrium with an unobserved QTL.

Some points deserve attention during regression analysis with multiple predictors. First is the interpretation of the regression coefficients. The interpretation for any given coefficient is, in part, contingent on the other variables in the model (Rencher and Schaalje 2008). Typical advice is to interpret each coefficient “with all the other predictors held constant.” Secondly, the dimensionality problems occur when the number predictor vastly exceeds the number of records. In this case, the use of usual theory to infer marker effects is not adequate. In traditional QTL studies, this inconvenience was avoided because predictors were added on regression models if they significantly improved the fit of existing models. As a statistical consequence, the data dimensionality was maintained, and least square estimators could be used without further problems. However, GS models suggest using all available molecular markers as covariates in a unique linear model. This leads to a situation where some kind of penalization is required in order to maintain the data dimensionality.

Dimensionality is a topic commonly discussed in statistical learning and deserves some comments. Predictive accuracy was previously mentioned as the gold standard metric in GS studies. Although the mathematical proof is beyond the scope of this chapter, it is possible to show that two statistical components are directly associated with this task. In order to minimize the error, it is necessary to select a statistical learning method that simultaneously achieves low variance and low bias. High variance refers to more flexible models, meaning that any small change in the original data set causes considerable change in regression coefficient estimative. In GS context, it means that marker effects have more variation between training sets. On the other hand, bias refers to the difference between an estimator’s expectation and the true value of the parameter being estimated. In another words, it is the error introduced by approximating a real-life problem considering simpler models. As a general rule, more flexible models result in higher variance and lower bias. The balance between both metrics determines the predictive ability, and, for this, the term bias-variance trade-off is commonly used (James et al. 2013).

Next, we discuss how data dimensionality and bias-variance trade-off are considered under the frequentist and Bayesian framework . Genetic assumptions used in each approach are also discussed.

3.2 Modeling Philosophy: Frequentist × Bayesian Approach

Two philosophies to estimate genomic breeding values have been widely discussed in the literature. See, for example, Heslot et al. (2012); Kärkkäinen and Sillanpää (2012); Gianola (2013); de Los Campos et al. (2013).

The frequentist approach, in general, uses markers for estimating the realized relationships, directly computing the breeding value in a mixed model context. On the other hand, a Bayesian framework focuses on the inference of marker effects, and the genetic value of an individual is obtained by the sum of these estimated effects. Regardless of the modeling philosophy, the central problem for both approaches is how to deal with the number of markers (p) which vastly exceeds the number of individuals (n) or, in a statistical learning context, how to deal with the bias-variance trade-off.

In traditional analysis (in matrix notation), the least square estimator of B (regression coefficients) treats X as a fixed matrix and satisfies the system of equations: X′XB = X′y, where B may not be a unique solution. If n << p, X′X is singular having a zero determinant, the B estimator is not unique, and the variance is infinite. Thus, an infinite number of solutions can be obtained, and these estimators cannot be used either as an inferential or as a predictive machine (Gianola 2013). One way of tackling the data dimensionality issue is by considering the introduction of constraining (or shrinking) on the size of the estimated coefficients. This approach, referred as regularization (James et al. 2013), can often substantially reduce the variance at the cost of increasing the bias.

Frequentist and Bayesian approaches have different perspectives on how this penalty should be considered. Frequentists derive an estimator by adding a penalty to the loss function (e.g., penalized maximum likelihood) (Kärkkäinen and Sillanpää 2012; James et al. 2013). In the Bayesian context, regularization is inserted directly into the model formulation by specifying an appropriate prior density for the regression coefficients (Gianola 2013; de Los Campos et al. 2013). As a consequence, Bayesians consider the assumptions of model sparseness as a part of the model formulation (prior density), while in the frequentist view it is assumed part of the estimator (Kärkkäinen and Sillanpää 2012).

In what follows, the most useful GS models and their genetic assumptions will be presented. Frequentist and Bayesian methods are divided and discussed for clarity purposes. Here, the idea is not to advocate for one over the other, rather to discuss some relevant points that differentiate them.

3.2.1 Frequentist Approaches

Oversaturated models are addressed in a frequentist framework by adding a penalty during the parameter estimation, which significantly reduces their variance. See, for example, Whittaker et al. (2000); James et al. (2013); de Los Campos et al. (2013). In the machine-learning literature, this is attained via ad hoc penalty functions that produce regularization (Gianola 2013). In penalized regressions or shrinkage methods, estimators are derived as solutions to an optimization problem that balances model goodness of fit to the training data and model complexity. Several penalized estimation procedures have been proposed, and they differ on the choice of penalty function (de Los Campos et al. 2013).

One of the first methods proposed for genomic prediction was Ridge Regression (RR) (Whittaker et al. 2000), which is equivalent to best linear unbiased prediction (BLUP) in the context of mixed models (Habier et al. 2007). Another special penalized regression method is known as least absolute angle and selection operator (LASSO) (Tibshirani 1996). There is an assumed penalty function which underlies the difference between these methods: LASSO makes the regression coefficients shrink more strongly than RR. Additionally, the penalty induced by LASSO may involve zeroing out some coefficients and shrinkage estimates of the remaining effects; therefore, LASSO combines shrinkage and an indirect variable selection (hence the “selection operator” in its name). Regardless of the penalty function used, penalized regressions will result in biased estimators of the marker effects. However, the small bias induced is paid off with reduced variance for the parameters (de Los Campos et al. 2013).

As pointed out in the last topic, the least squares approach estimates the regression coefficients using the value that minimizes the residual sum of squares (RSS ). Following the previous statistical notation:

$$ \mathrm{RSS}=\sum_{i=1}^n{\left({y}_i-{\beta}_0-\sum_{j=1}^p{\beta}_j{x}_{ij}\right)}^2 $$

Ridge Regression is similar to least squares, except that the coefficients are estimated by minimizing the RSS plus by a penalty function

$$ \sum_{i=1}^n{\left({y}_i-{\beta}_0-\sum_{j=1}^p{\beta}_j{x}_{ij}\right)}^2+\lambda {\beta}_j^2=\mathrm{RSS}+\lambda {\beta}_j^2 $$

The second term in the Ridge Regression formula is called shrinkage penalty and is responsible for the regularization (Whittaker et al. 2000; James et al. 2013). The central question is deciding how stringent the regularization process should be. As the penalty grows, the degree of shrinkage becomes stronger, and eventually all of the marker effects are shrunk to zero. A model with all regression coefficients close to null values is not desirable, as it does have any power to prediction. However, when this is close to the null value, the penalty term has no effect, and RR will produce the least square estimates. Hence, an ideal scheme is one that can selectively shrink the regression coefficients; i.e., markers with small or no effects should be severely penalized, whereas those with larger effects should not be shrunk at all (Xu and Hu 2010).

The penalty assumed in the RR will shrink all of the coefficients toward zero, but none of them will be set equal to zero. As pointed out by James et al. (2013), this may not be a problem for prediction studies, but it can create some challenges during the interpretation, given the number of predictors is quite larger. In this sense, the LASSO approach is an alternative to ridge regression, and the coefficients are estimated with the following equation (Tibshirani 1996):

$$ \sum_{i=1}^n{\left({y}_i-{\beta}_0-\sum_{j=1}^p{\beta}_j{x}_{ij}\right)}^2+\lambda \mid {\beta}_j\mid =\mathrm{RSS}+\lambda \mid {\beta}_j\mid $$

LASSO and RR present a similar formulation. However, the LASSO penalty has the effect of forcing some of the coefficients to be exactly zero. For this reason, LASSO is known to perform not only regularization but also variable selection. Models with this feature are referred in the literature as sparse models, given the ability to subset variables (James et al. 2013). Additional details about regularization are presented by James et al. (2013) and Habier et al. (2009).

In the context of GS, an important relation is commonly addressed. There is a close connection between Ridge Regression and kinship-BLUP, a methodology where the breeding values are predicted based on their kinship. Best linear unbiased prediction (BLUP ) was developed by Henderson (1949, 1950) in seminal articles applied to genetic and breeding. The main purpose was to estimate fixed effects and breeding values simultaneously. Important properties of BLUP were incorporated in its name: Best means it maximizes the correlation between true and predicted breeding values or minimizes prediction error variance; Linear because predictors are linear functions of observations; Unbiased is a desired statistical propriety related to the estimation of realized values for a random variable; and Prediction involves predicting the true breeding value. BLUP has found widespread usage in the genetic evaluation of domestic animals because of its desirable statistical properties (Mrode and Thompson 2005).

The traditional BLUP approach relies on pedigree information to define the covariance between relatives. Formally, the vector of random effects (e.g., breeding values) is assumed to be multivariate normal, where the variance parameter is indexed by the numerator relationship matrix (called A matrix). The connection between traditional BLUP and GS studies is the computation of this covariance using DNA information: genomic relationship matrix (called G matrix) (VanRaden 2008). The replacement of the A matrix by the G matrix constitute the theoretical bases of the GBLUP approach, the standard method used in GS studies.

Though conceptually similar, GBLUP and BLUP have distinct performance. The main difference is the possibility to compute a realized kinship matrix using molecular information, instead of using only expected values based on pedigree record. As pointed out by Mrode and Thompson (2005), “in pedigree populations, G discriminates among sibs, and other relatives, allowing us to say whether these sibs are more or less alike than expected, so we can capture information on Mendelian sampling.” Heffner et al. (2009) point out four mechanisms responsible for the divergence between realized relationships from their expectations: random Mendelian segregation, segregation distortion, selection, and pedigree recording errors.

GBLUP has some other important features that make it widely used in GS (Mrode and Thompson 2005; VanRaden 2008; Crossa et al. 2014): (1) the accuracy of an individual’s genomic estimated breeding value (GEBV ) can be calculated in the same way as in pedigree-based BLUP, using software and concepts well known in breeding routines; (2) GBLUP information can be incorporated with pedigree information in a single-step method; and (3) in contrast with the penalized regression (RR and LASSO), the dimensions of the genetic effects are reduced from p × p (where p is the number of markers) to n × n (where n is the number of individuals), which is more efficient for computing purposes. An important assumption assumed in these methods is that markers are random effects with a common variance. Under a genetic perspective, this assumption may be unrealistic because markers may contribute differently to genetic variance. This is addressed by Bayesian models, discussed in the following topic.

3.2.2 Bayesian Approach

Before describing the most useful Bayesian models applied in GS studies, a brief description of central concepts in Bayesian inference is presented.

Simply stated, Bayesian inference determines what can be inferred about unknown parameters, given the observed data (Kruschke et al. 2012). From another perspective, Gelman et al. (2014) point out that: “by Bayesian data analysis, we mean practical methods for making inferences from data using probability models for quantities we observe and for quantities about which we wish to learn. The essential characteristic of Bayesian methods is their explicit use of probability for quantifying uncertainty in inferences based on statistical data analysis.”

Formally, Bayesian analysis begins with the definition of a descriptive model, just as in classical statistics. Likewise, inference and prediction continue to be few of the major objectives. The great convenience, as described by Gelman et al. (2014), is the possibility to yield a complete distribution over the joint parameter space. So, the inference of a parameter is made in terms of probability statements, which has a commonsense interpretation (Kruschke et al. 2012).

All Bayesian inference is derived from a simple mathematical relation about conditional probabilities. When the rule is applied to parameters and data, Bayes’ theorem can be conventionally written as:

$$ p\left(\theta |y\right)=\frac{p\left(y|\theta \right)\times p\left(\theta \right)}{p(y)} $$

Termed as Bayes’ rule, y is the observed data, and θ is a vector of parameters in the descriptive model. The posterior distribution, p(θ|y), specifies the relative credibility of every combination of parameters given the data. This is a probability distribution and, hence, provides the most complete inference that is mathematically possible about the parameters values. The term p(y|θ) is the likelihood and represents the probability that the data is generated by the model with parameter. The term p(θ) is called the prior distribution and represents the strength of our belief in θ without any observation. Finally, p(y) is called the “evidence,” or marginal likelihood, and is the probability of the data according to the model determined by summing across all possible parameters values weighted by the strength of belief in those parameters values. For details, see Kruschke (2011) and Gelman et al. (2014).

GS models are simple expansion of Bayes’ rule assuming a hierarchical multiple linear regression as the explicit model (Meuwissen et al. 2001; Gianola et al. 2009). The term hierarchical (also named multilevel) is used when information is available on several different levels of observational units. Figure 2.2 is an adaptation from Kruschke et al. (2012) and is used for an intuitive explanation of the multiple layers (levels) assumed during a regression analysis.

Fig. 2.2

Hierarchical Bayesian multiple linear regression . At the bottom of the diagram, the data Yi depends of the regression model and illustrates the likelihood function. The arrow has a “~” symbol to indicate that the data are normally distributed with a mean and a standard deviation. The ellipsis next to arrows denotes the repeated dependency across the observations. Moving up the diagram, the “=” signs indicate a deterministic dependency. The regression coefficients and the standard deviation are the parameters of the regression model. One layer above is represented the beliefs (prior) on these parameters. The prior distribution is a joint distribution across the five-dimensional parameter space, defined as the product of five independent distributions. The last layer is the hyperparameters and expresses our belief about the distribution of the regression coefficients and the standard deviation (Adapted from Kruschke et al. (2012))

The fact that GS models are just an expansion of these ideas is important. As pointed out by Kärkkäinen and Sillanpää (2012), it is a common challenge to understand the “widespread fashion of mixing the model and the parameter estimation in a way that it is hard to follow what is the model, the likelihood, and the priors and what is the estimator.” Much of this critical view is directed to the collection of the Bayesian methods used for genomic predictions. The term “Bayesian alphabet ” was coined by Gianola et al. (2009) to refer to the number of letters of the alphabet used to denote various Bayesian linear regression used in GS studies. These models are specified as Bayesian hierarchical regression and, in general, differ in the priors adopted for the regression coefficients, while sharing the same sampling model: a Gaussian distribution with a mean vector represented by a regression on the markers (SNP) and a residual variance. For a formal mathematical description, a notation similar to that presented by de Los Campos et al. (2013) is used here:

$$ p\left(\mu, \beta, {\sigma}^2|y,\omega \right)\propto p\left(y|\mu, \beta, {\sigma}^2\right)\times p\left(\mu, \beta, {\sigma}^2|\omega \right) $$

$$ p\left(\mu, \beta, {\sigma}^2|y,\omega \right)\propto p\left(y|\mu, \beta, {\sigma}^2\right)\times p\left(\mu \right)\times p\left(\beta |\omega \right)\times p\left({\sigma}^2\right) $$

where p(μ, β, σ ²|y, ω) is the posteriori density of model to unknowns μ, β, σ ² given the data (y) and hyperparameters (ω); p (y|μ, β, σ ²) is the likelihood of the data given the unknowns, which for continuous traits are commonly independent normal densities, with mean Xβ and variance σ ²; and p(μ, β, σ ²|y, ω), factorized in the equation, is the join prior density of model unknowns, including the intercept (μ) that is commonly assigned a flat prior; the regression coefficients (β), for which are commonly assigned IID informative priors; and the residual variance (σ ²), for which is commonly assigned a scaled inverse chi-square prior with degree of freedom d.f and scale parameter S (Gianola 2013; Pérez and de los Campos 2014).

The basic idea behind the model description was shown in Fig. 2.2. Some prior distributions may be changed, but the concept is the same; GS models should be interpreted as a variant of multiple regression models, described hierarchically. For example, the BayesA method, initially proposed by Meuwissen et al. (2001), may be formally described in layers, where at the first stage a normal multiple regression is assumed; at the second a normal conditional prior is assigned to each marker effect, all possessing a null mean but with a variance that is specific to each marker; and, lastly, it assigns the same scaled inverse chi-squared distribution for the hyperparameters.

As previously mentioned, the central point is how to deal with oversaturated models. In a Bayesian context the sparseness is included in the model by specifying an appropriate prior density for the regression coefficients. Supported by the infinitesimal model , which states that a quantitative trait is controlled by an infinite number of unlinked loci and each locus has an infinitely small effect (Fisher 1919), it is reasonable a priori belief that most of the predictors have only a negligible effect, while there are a few predictors with possibly large effect sizes. A prior density which represents these beliefs has a probability mass-centered near zero and distributed over nonzero values, with a reasonably high probability for large values (Kärkkäinen and Sillanpää 2012).

In-depth discussions about prior densities assigned to marker effects, as well as the hyperparameter definition, are presented by Kärkkäinen and Sillanpää (2012), Gianola (2013), and de Los Campos et al. (2013). Based on how much mass these densities have in the neighborhood of zero and how thick or flat the tails are, a general classification into three big categories was presented by de Los Campos et al. (2013).

Starting with the Gaussian prior, methods that assign this prior to the marker effects are referred to as Bayesian Ridge Regression (BRR ) (Pérez et al. 2010). This mimics the RR approach (or the BLUP) when a specific penalty is assumed. RR-BLUP and BRR both perform shrinkage step that is homogeneous across markers. The second class of densities is called “thick-tailed priors .” Two widely accepted methods which represent this class are BayesA (Meuwissen et al. 2001) and Bayesian LASSO (Park and Casella 2008). Relative to the Gaussian prior, these densities have higher and thicker tails. This induces shrinkage of marker effect estimates toward zero for smaller effects and less shrinkage for markers with larger effect estimates.

There is a third group of models (“point of mass at zero and slab priors”), which include BayesB (Meuwissen et al. 2001) and BayesC (Habier et al. 2011). For this class, the prior assumption is that marker effects have identical and independent mixture distributions, where each has a point mass at zero with probability Ï€ and a univariate-t distribution (BayesB) or a univariate-normal distribution (BayesC) with probability 1 − π. When π=0, BayesB can be seen as a special case of BayesA; and the BayesC is identical to RR-BLUP. Alternative Bayesian models are discussed by Gianola (2013), which largely are expansions of the mentioned theory.

An important point under investigation, when different prior densities are tested, is the search for a better description of the genetic architecture (Gianola 2013; de Los Campos et al. 2013). For example, the BRR approach considers the marker effects as sampled from a normal distribution with fixed variance; hence, as a practical consequence, the effects are shrinking to the same degree assuming our beliefs that the trait is controlled by many loci with small effects. In contrast, the BayesB makes the assumption that most loci have no effect on the trait and thus more markers are left out of the prediction model; so, our preliminary hypothesis is that the trait is controlled by relatively few loci, whose effect vary in size.

The central question which underlies the choice for a Bayesian model is “What distribution should be used?” As previously noted, the answer is closely associated with the genetic architecture of a trait, which is commonly seldom known. Motivated by this, it has been a common practice in GS research to start by testing different models which represent the biological phenomenon.

3.2.3 Practical Lessons About Statistical Methods Used for Genomic Selection

Recently, a significant number of simulated and empirical studies were published comparing genomic prediction models (Heslot et al. 2012; Resende et al. 2012b; Crossa et al. 2013; Daetwyler et al. 2013). Among the additive models, Bayesian regressions and the GBLUP method have mainly been used in animal and plant breeding. GBLUP is attractive due to its straightforward implementation using existing mixed model software, relative simplicity, and limited computing time. Bayesian methods were not widely used until around 20 years ago, given the release of several packages that allowed Bayesian analysis to be performed easily and quickly on a standard desktop computer (Stephens and Balding 2009).

A summary of some models commonly used in GS studies is given in Table 2.1. Alternative methodologies are discussed by Heslot et al. (2012), de Los Campos et al. (2013), Zhou et al. (2013), Desta and Ortiz (2014), and Gianola (2013). The methods described were classified according to the approach used for the analysis, maintaining the same structure used in the last section. Table 2.1 highlights some attributes , such as genetic architecture, regularization, and variable selection. Genetic architecture is cited as a generic way to determine which models are able to weight markers of small and large effects. The regularization is a common feature for all GS methods; however some models are able to combine regularization and variable selection. A software commonly used and a classification of complexity are also presented. Here, complexity was defined as the number of parameters estimated during the inference. Bayesian models with variable selection and a mixture of distributions were classified as having high complexity (given the higher number of parameters to be estimated).

Table 2.1 Genomic selection methods and their particularity commonly applied to plant breeding

Currently, a great number of software/packages are freely available. As a general rule, “push a button” interfaces are not provided, and, hence, a minimal background in statistics and computation is required. Sampling methods (Monte Carlo Markov Chain), commonly used in Bayesian approaches, require more computational demand and, consequently, more time for performing the analysis.

Regarding the performance of these models in practice, simulation studies using frequentist and Bayesian methods have shown similar results for traits governed by many loci, which closely resemble the infinitesimal genetic model (de Los Campos et al. 2013; Daetwyler et al. 2013; Wang et al. 2015). A slight advantage of variable selection methods was observed for simulated traits where fewer loci contributed to genetic variation (Coster et al. 2010; Daetwyler et al. 2013). Empirical studies have been conducted to confirm the results of simulation studies (Moser et al. 2009; Heslot et al. 2012; Resende et al. 2012b; Ferrão et al. 2016a). When models are compared, in a large majority of the cases, small differences in predictive ability are observed. Some hypotheses have been proposed to explain these differences. One is related to intrinsic features of the data (e.g., the ration between number of markers and records, span of LD, genetic architecture, etc.) that hinder model regularization and, consequently, result in similar results. Another possible argument is discussed by Tempelman (2015) and involves statistical and computational challenges associated with the Bayesian inference. The author pointed out some general issues concerning the hyperparameter specification, MCMC diagnostics and the problem of data dimensionality.

The final message about practical lessons of the statistical methods is that no single method has emerged as a benchmark model for genomic predictions. Hence, evaluation and reflection about advantages and drawbacks of each one model should be considered as an imperative step during the GS implementation. However, given that so much effort would be taken for data recording, it seems reasonable to test a number of models before applying them in real-word situations.

4 Genomic Selection and Plant Breeding

The biometric models accounting for genomic prediction became mature after building on Henderson’s mixed linear model equations for BLUP of breeding values using pedigree and phenotype data. Their accuracy remains an active area of research, but genomic selection has already led to increased rates of genetic gain, particularly for traits with low heritability. For example, dairy cattle has improved as a result of decreasing generation intervals and increasing significantly selection intensity. Simulations and empirical studies have demonstrated that GS has potential to accelerate the breeding cycle, maintain genetic diversity, and increase the genetic gain per unit of time in plant breeding (Bernardo and Yu 2007; Heffner et al. 2009; Heffner et al. 2010; Resende et al. 2012b). All of these factors have created a lot of excitement and high expectations in the plant breeding communities. Furthermore, Rajsic et al. (2016) provide a general average cost framework to quantify prediction accuracy of effects and varying cost ratios of phenotyping to genotyping for comparing the economic performance of GS vis-à-vis phenotypic selection. They found that GS appears promising for traits with heritability below 0.25 unless the phenotyping costs is higher than genotyping and the effective chromosome segment number 100 or more. The following section describes how genomic predictions can be integrated into breeding efforts and result in higher genetic gains.

4.1 Expected Genetic Gain: The Breeder’s Equation

The expected genetic gain is an important metric to quantify the progress of a breeding program. For this reason, it is known as the breeder’s equation . One version of this equation weights the expected genetic gain by the cycle size, as follows (Desta and Ortiz 2014): $\mathrm{GP}=\raisebox{1ex}{$i{r}_{\mathrm{a}}{\sigma}_{\mathrm{a}}^2$}\!\left/ \!\raisebox{-1ex}{$L$}\right.$, where i is the selection intensity, r _a is the selection accuracy, ${\sigma}_{\mathrm{a}}^2$ is the square root of additive genetic variance, and L is the cycle length.

Using this equation, GS has potential to capitalize on all four of the components (Desta and Ortiz 2014). First is operating under the selective accuracy. The use of molecular markers can be leveraged to estimate a relationship matrix or applied directly into regression models and increase the selection gain. It is well established in the literature that conclusions based on molecular information tends to be more reliable. In a mixed model context, the kinship computed via DNA information is able to consider the realized relationship among individuals, instead of an expected value supported by pedigree records.

The second term is the cycle length . This term has a special importance in perennial crops, where the breeding cycle is longer. In order to advance generations and accelerate the gain per unit of time, genomic predictions can be performed during seedling phase. In addition to saving time, this reduces cost by avoiding the necessity to maintain populations for several years in the field. A good perspective on the relationship between cost and gain is presented by Heffner et al. (2010). The authors reported that, for many crops, the time for a breeding cycle using GS might represent one-third or less than that used by phenotypic selection.

The use of many cycles per year directly affects the selection intensity and genetic variance, the two remaining components in the equation. In general, the selection intensity is raised by the ability to evaluate a large breeding population and consider a big screening nursery. Consequently, new genes and combination of them, not present in the breeding program, may be incorporated in the evaluation process.

At this point it would be helpful to contextualize the relationship between expected genetic gains and a cost-benefit approach. Although GS has been announced as a potential tool to assist selection in breeding programs, there are a number of practical problems in conventional breeding programs that GS cannot eliminate or suppress. A reflection about them should be considered before deploying GS as a breeding tool. Heslot et al. (2015) point out some challenges: (1) the choice of germplasm on which to apply MAS, once the germplasm should represent the final objectives expected in GS applications; (2) trade-offs between family size and number of families created for MAS; (3) integration of information for multiple traits, balanced between phenotypic selection and MAS at a constant budget; (4) disconnection between the population used to train the models and the elite breeding germplasm (breeding population); and (5) logistical issues involved with the integration of molecular information in breeding programs.

Most of these points are related to resource allocation toward phenotyping, genotyping, the genetic architecture of traits under analysis, and population size, as described by Heslot et al. (2015). According to the authors, the use of markers to achieve breeding gains requires consideration of the genetic gain achieved by the breeding program with and without GS. Looking only at the expected genetic gain formula, it seems clear that GS in contrast to traditional breeding schemes will increase genetic gain. However a cost-benefit analysis will take into account that genotyping all candidates might require reducing the size of the breeding population and result in a negative impact on breeding gains. A practical example: on the base of a breeding program flow, as general rule, the number of candidates to be evaluated is higher, and they are not fully inbred, making the logistics of genotyping and prediction more complicated and expensive. For this reason, Heslot et al. (2015) point out “This trade-off is even stronger in a phenotypic breeding program, because large populations early in the cycle are combined with high selection intensity on highly heritable traits (high plot-basis heritability), which can be extremely efficient and relatively Inexpensive. It is probably beneficial to use markers to select on a low heritability trait, such as yield, early in the cycle; in most crops, yield cannot be measured accurately on segregating populations, single plants, or small plots. At the same time, most of the individuals in early generations can be discarded efficiently using inexpensive phenotyping.”

Important insights about the cut-benefit trade-off have been reported in empirical studies. Meuwissen (2009), in animal breeding, computed the expected accuracy for reference populations considering different sizes and different heritabilities. In traits with low heritability, an accuracy of 0.20 can be obtained with a large reference population (2000–5000 animals). In contrast, Akanno et al. (2014) simulated a case of limited resources considering a small training population in animal breeding (1000 individuals). In this case, the population size was considered appropriate; however, it required multigeneration training populations and the reestimation of marker effects after two generations of selection. Although these simulations were proposed in an animal scenario, the results reinforce the ability of genomic prediction to improve the genetic gain. The level of this improvement is strongly associated with resource allocation.

4.2 Genomic Selection and Plant Breeding Schemes

The previous section describes how GS has the potential to raise expected genetic gain. In this regard, some empirical studies have supported GS superiority compared with traditional phenotypic methods. In tree breeding, for example, the selection efficiency per unit of time was estimated to be 53–112% higher than phenotypic selection, thus resulting in a time reduction of 50% in the breeding cycle (Resende et al. 2012a). Higher genetic gain, compared with phenotypic selection and other conventional MAS, was also reported in biparental wheat populations (Heffner et al. 2011). Likewise, GS appears to be more effective than pedigree-based phenotypic selection for improving genetic gains in grain yield under drought in tropical maize (Beyene et al. 2016). These are some examples of success that have encouraged GS application in practical breeding programs. However, open questions remain about how to implement these ideas in well-established plant breeding programs (Jonas and de Koning 2013). This is a reality for many crops, especially in non-private institutions.

Innovative studies have been performed by the International Maize and Wheat Improvement Center (CIMMYT) , and a good perspective about the subject was presented by Crossa et al. (2014). As a general rule, genomic information has been useful for the investigation of unknown population structure, predicting on unrecorded pedigree structure, correcting incorrect pedigrees, and predicting the genetic value of Mendelian sampling terms (random sampling of the genome of each parent, which should be interpreted as a deviation of the average effects of additive genes an individual receives from both parents from the average effects of genes from the parents common to all offspring). In terms of the algorithms/models used for predictions, in CIMMYT trials , no prediction model fits all situations (Crossa et al. 2013; Perez-Rodriguez et al. 2013; Crossa et al. 2014). Further, it is noteworthy to consider the context where these studies were performed. In particular, the investigation of GxE interaction (Burgueño et al. 2012; Lopez-Cruz et al. 2015), predictions in structured populations, and the response of the GS across years and breeding cycle (Arief et al. 2015; Jarquín et al. 2016) have revealed new perspectives on the use of molecular information in plant breeding. In this sense, the studies applied to maize and wheat, developed at CIMMYT, have been used as benchmark for others crops with similar objectives.

An interesting viewpoint of practical recommendations was described by Bassi et al. (2015). In wheat, a comparative analysis showed equivalence in costs between phenotypic evaluations and GS. Authors reported how GS methods may reshape traditional breeding schemes, in order to increase the genetic gain. In short, GS and on-field evaluations are interleaved, and there are no significant changes in traditional schemes. Selection based on molecular markers can be performed using plants in a seedling phase (inside greenhouse), avoiding additional costs with experimental area and phenotyping and, consequently, shorting the length of each cycle. It is worth mentioning that GS and on-field evaluations are proposed as complementary methods, such that neither completely replaces the other. GS has several advantages, but it should be stressed that phenotypic evaluations will always be necessary.

In order to summarize how the aforementioned ideas could be incorporated in classical breeding schemes, an intuitive representation is shown in Fig. 2.3, where a schematic of breeding inbred lines is presented using doubled haploids (originally discussed by Heslot et al. (2015)). As pointed out, GS can be use at each stage of cultivar development. At the bottom of Fig. 2.3, we present our personal perspective on GS implication in intrapopulational recurrent selection schemes applied to coffee (Coffea canephora). A remarkable feature of the coffee breeding program is the long testing phase, since it is a perennial species with a long juvenile period. Historically, coffee experiments have been performed in multiple locations and harvests (years of production), which results in high cost and a long time to achieve the final product. Figure 2.3 highlights the ability to advance generations by implementing GS during the seedling phase, inside greenhouse. As an immediate consequence, the breeding cycle will be reduced and the selection intensity increased. In contrast to conventional methods of recurrent selection in C. canephora, this technique is to reduce the total time required to advance a generation by two-thirds (5–6 years).

Fig. 2.3

Simple scheme of a breeding cycle with genomic selection (GS). For each stage, the figure presents side-by-side characteristics of classic breeding (in black) and potential applications of GS (in gray). The schematic of breeding inbred line, on the top, was originally described by Heslot et al. (2015), while the schematic of intrapopulational recurrent selection, on the bottom, is based on a Coffea canephora breeding program

The C. canephora scheme may be expanded for other tropical species. As a general rule, any breeding scheme is based on three steps: crossing, evaluation, and selection. Directional selection occurs when a breeder induces the phenotypic mean of a trait to move in the desired direction over one or more generations. To achieve this, breeders impose a selection threshold, such that an evaluation guarantees that individuals above this threshold are selected as the progenitor of the next generation. As a consequence, these individuals will intercross and compose a new breeding cycle (crossing step). The assumption behind each of these concepts is that the selected individuals provide genetic progress, which involves allelic transmission and increases the frequency of selected alleles in the breeding population .

Different metrics can be used to drive the selection step. GS accuracies support the use of GEBV, rather than phenotypic metrics, to guide selection in plant breeding. In this scenario, phenotyping plays a crucial role in the process of estimating and/or reestimating marker effects. New germplasm that may eventually feed breeding programs and improve the base population, under the GS regime, will be useful for composing a training population, which will increase the sample size and allows new alleles be sampled. Field experimentation emerges as a crucial step at the end of the process when candidates that were selected by their GEBV should be tested in multiple environments.

It is noteworthy that marker effects may change as result of allele frequency changes or of epistatic interactions. Hence, model updating within breeding cycle should mitigate reduced gains caused by these mechanisms. In this context, there is an important routine of genotyping in the breeding program. For this end, maintaining a physical structure to genotyping may be expensive, and one solution is to outsource these services.

5 Challenges, Perspectives, and Trends

Previously, practical and theoretical aspects were discussed in order to elucidate GS application. It is clear that this new scenario not only reshapes the expectations of plant breeding but also brings a new context to investigate questions that raised researchers. This topic addresses challenges, perspectives, and trends that have been investigated in the plant breeding literature. The last subject in this section is a perspective on future directions in GS investigations.

5.1 A Multidisciplinary Solution to the Challenge of Big Data

GS is a multidisciplinary approach that involves interconnected areas, e.g., plant breeding, genetics, molecular biology, statistical genetics, and bioinformatics. The primary challenge during GS application is to connect all of these areas in an efficient framework. In practical terms this means collaborative work, where shared decisions among researchers, with different expertise, should guide the breeding program.

A challenge in this context is the “Big Data question ” (James et al. 2013; Adams 2015). The term “Big Data” was designated for data sets that are so large or complex that traditional data processing applications are inadequate or inefficient. In GS studies, data sets with this magnitude are coming from new phenotyping technology, which are able to generate millions of measurements every day, and from “omics” projects that have been feeding huge public and private database with biological and molecular information. The necessity to store, process, and draw conclusion from such information is a challenge and necessity for modern breeders.

Although advances have been reported, it is noteworthy that the potential of GS does not invalidate or reduce the importance of two other areas in breeding programs: field evaluations and the continuity of traditional MAS research. In terms of field evaluation, the composition of good populations, the use of appropriated experimental designs, and the choice of promising parents continue to be important steps. These assignments are commonly activities of the so-called conventional breeder and, even in the presence of GS, remain as key point for success of plant breeding. In terms of traditional MAS approaches, we are reinforcing the importance to continue genetic mapping and QTL mapping researches. Genetic mapping studies have been important in modern genomic studies, especially during the genome assembly, which is useful for SNP prospection and subsequent genetic analysis. On the other hand, QTL mapping remains as the most appropriate approach for genetic architecture studies.

5.2 Genotype-by-Environment (GxE) Interaction

Recently, a large number of studies have been performed to address GxE interaction , and, therefore, different statistical models are reported in the literature. See, for example, Smith et al. (2005); Crossa (2012); Malosetti et al. (2013). GxE interaction occurs because different genotypes do not necessary response in the same way to equal conditions. An important point is the attempt to predict genotype performance over an environmental space.

In a mixed model context , genotypic performances across the environments have been modeled as correlated traits considering structured and unstructured covariance functions. A natural advantage is the flexible way in which these functions may be tested to describe the interactions and residual variance (Smith et al. 2005). Furthermore, when genetic effects are assumed as random, pedigree information can be incorporated, and more accurate breeding values may be computed via best linear unbiased prediction (BLUP). In coffee, for example, it was reported differences in the predictive accuracy of 10–17%, when comparing models that considered and ignored interaction effect (Ferrão et al. 2016b). Increases in the predictive ability by GxE modeling were reported by Burgueño et al. (2012), Lado et al. (2016), and Malosetti et al. (2016).

More recently, studies have advanced in order to incorporate modern information about environmental covariates (Jarquín et al. 2013; Heslot et al. 2014) and the explicit modeling of interaction between markers and environment (MxE ) (Schulz-Streeck et al. 2013; Crossa et al. 2015; Lopez-Cruz et al. 2015). An important point in these studies is the possibility to decompose the effects into components that are constant across groups (environments or populations) and deviations that are group specific. From a quantitative genetics perspective, it is reasonable to expect that SNP effects may differ across populations and environments. In a breeding program, this may aid in the selection of generalist genotypes (good performance in all conditions, i.e., broad adaptation) or specialist genotypes (performance directed for a specific condition, i.e., narrow adaptation). In general terms, these insights are related with the classical breeding concepts about adaptability and stability.

5.3 GS in the Presence of Population Structure

Commonly, GS methods assume homogeneity of allele effects across individuals. However, this assumption ignores the fact that systematic differences in allele frequency and in patterns of linkage disequilibrium can induce group-specific marker effects (de Los Campos and Sorensen 2014). Although rarely discussed in GS context, population structure is a real prospect in plant breeding. These substructures are commonly caused by natural activities inside a breeding program, e.g., artificial selection, drift, and exchange of materials.

In genome-wide association (GWAS ), it is known that population structure is an important source of spurious association between genetic variants and phenotypes. Principal components (PCs) methods are frequently used to account the population structure and “correct” for population stratification. Although important, such methods as the PCs induce a mean correction that does not account for heterogeneity of marker effects (de Los Campos et al. 2015b). Moreover, there are good reasons that support the hypothesis that, in heterogeneous populations, markers effects should be allowed to vary between groups. It is reasonable to capture this variation instead of treating it as potential confounder or ignoring it.

5.4 Epistasis and Dominance

GS models have been limited mostly to fit marker (or haplotypic) additive effects, either explicitly estimating the marker effects or implicitly through the so-called “genomic” relationship matrix (GBLUP method) (Vitezica et al. 2013). As previously cited, there is a natural trend to consider additive models as a starting point in GS investigations. Besides to capture a large portion of the genetic variation, additivity might be straightforward implemented. However, if most of the studies have addressed prediction taking into account only genes with additive effects, there is still a lack of reports dealing with the total genetic value, which include additive and nonadditive effects (Denis and Bouvet 2011).

Nonadditive variations result from interactions between alleles at the same locus (intra-locus) or interactions from different locus (inter-locus). Formally, intra-locus interactions are called dominance effects and can be defined as the difference between the genotypic value and the breeding value of a particular genotype (Falconer and Mackay 1996; Lynch and Walsh 1998). From the statistical point of view, dominance effects are interaction effects or within-locus interaction. On the other hand, interaction deviations or epistatic deviations refer to additional deviations when more than one locus are analyzed (Falconer and Mackay 1996; Lynch and Walsh 1998). Hence, the additivity assumed in GS studies may be derived from two sources: under a narrow view, refers to genes at one locus and means the absence of dominance, and in a broad view, refers to genes at different loci and means the absence of epistasis. In both cases, nonadditivity constitutes a major challenge for plant breeder (Holland 2001).

Considering dominance effects, recent studies have been shown superiority of models that took into account this source of variation. Dominance has theoretical and practical interest, because it is frequently used in crosses of animal breeds and plant lines. In tree breeding, for example, higher predictive accuracies were observed when dominance-additive variance ratio increases (Denis and Bouvet 2011). These results have been particularly interesting for tree improvement, where clonal cultivars can be produced. Considering animal and simulated data, Vitezica et al. (2013) point out advantages in recovering information when the dominance is modeled. In a similar direction, advantages to consider dominance effects are reported by Nishio and Satoh (2014) and Lopes et al. (2015).

There are well-defined cases of interactions at molecular level between gene products, but the real relationship between molecular interactions and complex phenotypes is often unclear. Considering classical quantitative genetics methods, the genetic component of variance are often poorly estimated providing the false impression that this source of variation is not important, as pointed out by Holland (2001). Lorenzana and Bernardo (2009) reported that including epistatic effects in prediction models will only improve accuracy if two conditions were considered: (1) if epistasis is present and (2) if it is accurately modeled. Currently, contrasting results have been reported adding some controversy about their importance in quantitative genetic analysis. Increased in predictive ability by the epistasis modeling is discussed by Hu et al. (2011), whereas Lorenzana and Bernardo (2009) have indicated that predictions were adversely affected. These results point out that importance of epistasis modeling can vary between species, type of crossing, and trait under analysis. It seems clear that, given the complexity of the subject, further research should be performed.

A critical viewpoint is presented by Lorenz et al. (2011): “if the predictive accuracy is lower when the epistasis is included, clearly epistasis was poorly modeled with the population sizes in this study.” Another result that reinforce the epistasis importance is presented by Dudley and Johnson (2009), who concluded that epistatic effects are more important than additive effects in determination of oil, protein, and starch contents of maize. These results, and other reported in the literature, not only are remarkable for the importance of epistatic effects but also deserve attention for the necessity to better the description of nonadditive modeling in GS studies.

5.5 Polyploid Species

The GS application changes when polyploid species are considered. Challenges in this sense are not exclusive to GS but also include QTL, genetic mapping, and GWAS research. Important polyploid crops include sugarcane, wheat, potato, coffee, cotton, and some fruit species (e.g., apple and strawberry). Commonly, analytical frameworks assume a specific mode of inheritance and relation between alleles, based in diploid species, which does not fit in polyploid context (Dufresne et al. 2014). This difficulty is due to several complications evidenced in the polyploidy analysis, as follows: (1) larger number of genotypic classes, (2) poorly understood behavior of the chromosomes, (3) lack of molecular and statistical methods to precisely and efficiently estimate the genotypic classes, (4) ploidy level of the species, and (5) complexity of the interactions between alleles (Mollinari and Serang 2015).

Despite the significant number of polyploid tropical species and the increases of availability genomic data, there remain important gaps in the knowledge about polyploid genetics (Dufresne et al. 2014). A common practice adopted in polyploid analysis has been the interchange of knowledge and methods applied to diploid level. Although it is an approximation, it is a naive way of handling the problem, given the unrealistic and simplified assumptions that are assumed (Garcia et al. 2013).

Appropriate methods applied to genomic prediction in polyploid analysis are still in their infancy. The challenge begins before the modeling steps of genotype-phenotype relationship. Genotypic classification and SNP calling are not trivial tasks. A good perspective about the subject is presented by Garcia et al. (2013) and Mollinari and Serang (2015).

In polyploids, a locus may carry multiple doses of a particular nucleotide. Traditional molecular markers (e.g., AFLP and SSR) do not allow a straightforward estimation of this dosage at a given polymorphic locus. The development of modern genotyping technologies opened an important opportunity to evaluating the relative abundance of each allele (Mollinari and Serang 2015). Although progress were observed in tetrasomic polyploid species (e.g., potato species), more complex polyploid species, such as sugarcane and some forage crops, have not yet fully benefited from molecular marker information (Garcia et al. 2013). To circumvent these problems, the vast majority of genetic research in complex polyploids utilize only single-dose markers during the genetic analysis. So, all the modeling is performed considering the presence of polymorphisms in just one homologous chromosome per homology group. Among the limitations of this approach, it is noteworthy the impossibility to study the effects of allelic dosage, i.e., the effects of the number of copies of each allele at a particular locus in a polyploid genotype. Some studies have been shown that allelic dosage may be extremely important in gene expression in several polyploid species (Garcia et al. 2013; Mollinari and Serang 2015).

In order to advance in polyploid analysis, the measurement of relative abundances (dosage) of alleles is an important step. These estimated dosages may be modeled in association studies. The packages SuperMASSA (Serang et al. 2012) and fitTetra (Voorrips et al. 2011) are theoretical implementations of these ideas, however considering different approaches. It seems clear that subsequent steps involve the accommodation of these estimated allelic dosages into the predictive models. In addition, important gaps remain in our knowledge about the importance of additive and nonadditive effects during the genetic modeling, a critic subject in polyploids given their complex nature (e.g., multiple alleles and loci, mixed inheritance patterns, association between ploidy and mating system variation) (Dufresne et al. 2014). Nevertheless, studies in this direction are still modest and constitute a current challenge in future GS studies.

5.6 Genomic Selection 2.0: The Future Is Coming

Recently, GS studies have been not focusing only on predictive abilities but also in two other important features: identifying SNPs associated with the trait and understanding its genetic architecture (MacLeod et al. 2016). For this end, previous biological information and emphasis on estimated marker effects have been considered. Likewise, it has been a challenge in the incorporation of previous genetic evidence in new statistic methods. Some authors have named this current period as “Genomic Selection 2.0” (Hickey 2013; Boichard et al. 2016), representing the new era where information from sequencing data can be generated on millions of individuals and prior biologic results, such as causal mutation, may be considered in predictive models. The challenge in this scenario is determining which of these millions of variants are causal mutations, since the size of effects of such causal mutation is likely to be small.

Good perspectives are presented by Hickey (2013), who coined the term “Genomic Selection 2.0” (GS 2.0). According to the author, until the present, three types of GS investigations have been applied in breeding programs. The so-called GS 0.0 was the first method applied to genomic prediction and “assumed linkage disequilibrium between markers and causative mutations would drive prediction.” One step forward, the GS 1.0 “primarily utilize linkage information via realized relationships with close relatives because training populations, although large by historical standards, are far from sufficiently large for linkage disequilibrium information to be very useful for making predictions about quantitative traits.” The GS 2.0 is a label given to the current status, which involves large population sizes, millions of molecular data and automated phenotyping.

Considering animal breeding as our benchmark, the 1000 bull genomes project includes whole-genome sequences from 1682 cattle of 55 breeds, from which 67.3 million of genetic variants were identified – including 64.8 million SNP and 2.5 million of indels. The challenge is determining which genetic variants are causal mutations that underlying variations in complex traits. Mapped the causal mutations, these information may be included in genomic prediction investigations.

Broadly speaking, the problem of identifying relevant SNPs in high-dimensional data sets approximates GS methods with contemporaneous genome-wide association algorithm (GWAS). The primary rationale of GWAS investigations is to investigate the underlying biological phenomenon mapping variant genetics associated with important traits. Thus, it is reasonable to hypothesize that modern GS analysis may borrow particularity from GWAS method, i.e., identify important covariates and learn about underlying biological process and use them for prediction tasks.

In a statistical context, the scientific question behind these algorithms is naturally framed as a variable selection problem. Simply stated, “which variable (SNPs) under investigation are useful for prediction the outcome (phenotype)?” Mostly existing GWAS analysis is based on “single-SNP” approach (simply test each SNP, one at time, for association with the phenotype). An alternative is to consider the Bayesian variable selection regression (BVSR) approach , which resembles GS models except because the primary goal is to map SNPs with a biological signal, instead of to predict the genetic merit. In analytical terms, it stands out that Bayesian approach could access the predictive value of the SNP effects simply by computing the posterior probability (i.e., the posterior probability that its coefficient is not zero). Other natural advantages include the possibility to estimate heritability of complex traits, allowing for both polygenic and sparse models, and incorporating external genomic data into the priors, which can increase power and yield new biological insights (Guan and Stephens 2011).

There are many possible approaches to BVRS; see for a review O’Hara and Sillanpää (2009). Models based on a sparse (“spike and slab”) prior for the coefficients of linear regression are few of the most widely used for GS purposes – previously discussed on the Statistical Methods topic. Regardless of the BVRS method , current studies have been focused in some important points: (1) traditional algorithms are based on computationally intensive MCMC methods; hence, advances have been driven to be able to perform analysis in a practical time frame considering large-scale problems; (2) typical genomic prediction studies do not produce easily interpretable measures of confidence that individual covariates have nonzero regression coefficients. A modern tendency may consider methods that are able to extract more information from signals (biological evidence) that exist in the data, instead of to be purely a predictive approach; (3) Bayesian framework has been continuously investigated for inferential and predictive purposes. In BVRS scenario, the hyperparameter definition has a crucial importance, given they are responsible for reflecting the sparsity of model and the typical size of nonzero regression coefficients. Both features are important on the inference about the genetic architecture and model complexity. Several rules to define hyperparameter have been suggested in the literature with a lack of consensus among different authors. In this sense, aggregate information from previous QTL mapping and GWAS studies have potential to drive these definitions. For instance, it is possible to consider assumptions that functional SNPs may tend to cluster near one another in the genome or make some SNPs that are better candidates for affecting the trait than other (O’Hara and Sillanpää 2009; Guan and Stephens 2011; Carbonetto and Stephens 2012).

From this perspective, MacLeod et al. (2016) reported the use of GS combined with mapping of causal variants. The BayesRC method incorporates prior biological evidence considering classes of variants to be enriched for causal mutation. In short, previous important evidence originated by variant annotation analysis or from a list of candidate genes may be used to enrich the data analysis. In a similar direction, but considering mapped QTLs as a priori known, Bernardo (2014) points out higher predictive ability when these information are considered as fixed effects in GS models. In wheat, Crossa et al. (2015) showed results considering the importance to identify markers with stable or specific effects across environments. Indirectly, this matter was addressed in the GxE Interaction section. However, it is noteworthy the focus study on the markers effects, rather than solely on predictive capacity. In rice, GS analysis has been proposed in conjunction with GWAS, in order to perform prediction and help on the genetic architecture comprehension (Spindel et al. 2015).

In terms of genotyping and bioinformatic steps, the example of the 1000 bull genomes project reflects the tendency to consider whole-genome sequences in thousands of individuals. Use of whole-genome sequences is supported by simulation studies, which show that SNP densities identified by this approach may provide 40% more accurate predictions than SNP identified by the available genotyping platforms (Meuwissen and Goddard 2010). In this scenario, costs per individual sequenced should be low, and, hence, an alternative may be to sequence all individuals at low coverage. By sequencing coverage, we mean the number of reads sequenced for a determinate site in the genome. In low-coverage data sets, among the drawbacks, a potential challenge in diploid species is the high probability that only one of the two chromosomes has been sampled at a site during the sequencing. As consequence, the genotype definition may be hampered (Nielsen et al. 2011). For this end, the development of computational and imputation methods that are able to deal with this scenario to, firstly, build consensus haplotypes and, then, impute full sequence information on the basis of these consensus haplotypes is important.

An area impacted by GS 2.0 is the phenotyping of quantitative traits that was relatively ignored until recently. In GS context, the perception that phenotype-marker association studies may only be useful considering reliable phenotyping have boosted the so-called high-throughput phenotyping platforms (HTPP) . This new branch includes large set of available instruments (robotic and computing) to obtaining detailed measurements of plant characteristics (Cabrera-Bosquet et al. 2012). In general lines, HTPP allows to scan thousands of plants a day in an approach to science akin to high-throughput DNA sequencing (Finkel 2009). On one hand, accurate metrics for physiological process can be observed; but, in the other, the huge capacity of data acquisition required statistical and computational approaches able to summarize the information. Another perspective is the greater of flexibility to choose the traits to be considered in breeding programs. Many initiatives are under way to generate reference populations for traits that were long believed to be impossible to select.

At this point, it is helpful to review what we are attempting to achieve in this topic. Factually, GS research – like in all “omic” – have dynamic advances. As pointed out by Hickey (2013), GS 2.0 can be considered the state of the art. Our personal view is in accordance with the author, however, with additional remarks: (1) the importance to include biological information from multiple areas (e.g., chromatin structure analysis, candidate genes, causal mutation, and epigenetics); (2) continuous advances on the development of algorithms applied to imputation and haplotype construction, in special, for low-coverage sequencing; and (3) improvement of high-throughput phenotyping platforms, in order to achieve better phenotypic metrics and consider traits that are hard to be investigated by conventional methods.

6 Conclusions

Genomic prediction for selection is one of the most remarkable breeding proposals in recent years (Habier 2010; Hickey 2013). It may also address important connections between classical quantitative genetics and molecular biology, considering GS context (Gianola et al. 2009; de Los Campos et al. 2015a). Much of these optimistic discourses came from the success of GS in predictions of breeding values, when compared with the traditional MAS results. In fact, it is an undeniable huge potential. In animal breeding, in special, GS overlap the barrier of a simple promise and, currently, constitute in a reality (Hickey 2013). In plant breeding, the examples of success are still restricted for the so-called main crops, such as maize, rice, soybean, and wheat (Poland et al. 2012; Crossa et al. 2013; Jarquín et al. 2014; Crossa et al. 2014; Bassi et al. 2015; Spindel et al. 2015).

One point to be considered in tropical crops is that some species are not proper model systems. The term model systems is used in order to highlight some points that hinder or difficult GS application. Beyond the financial questions, some crops present long life cycles and traits are expressed in later stages of their cycle, some have high genetic load and inbreeding depression, for others large experimental areas are necessary, and for many there is the absence of a suitable genotyping platform. These are only some factors that can be pointed out. In these scenarios, we recommend that GS should be initially treated as an alternative branch in the conventional breeding programs, but it is necessary to include GS in breeding scenarios. This means considering small projects in the beginning, in order to understand the scenario that the crop is inserted.

In conclusion, we are highlighting the GS as a promising and innovative tool to be applied in plant breeding programs. However, to achieve this objective, a critical reflection about the problem of resource allocation is needed. The ideas regarded in this chapter addressed some practical and theoretical issues useful in this process of reshaping breeding.