Supervised Approaches for Function Prediction of Proteins Contact Networks from Topological Structure Information

Abstract

The role performed by a protein is directly connected to its physico-chemical structure. How the latter affects the behaviour of these molecules is still an open research topic. In this paper we consider a subset of the Escherichia Coli proteome where each protein is represented through the spectral characteristics of its residue contact network and its physiological function is encoded by a suitable class label. By casting this problem as a machine learning task, we aim at assessing whether a relation exists between such spectral properties and the protein’s function. To this end we adopted a set of supervised learning techniques, possibly optimised by means of genetic algorithms. First results are promising and they show that such high-level spectral representation contains enough information in order to discriminate among functional classes. Our experiments pave the way for further research and analysis.

1 Introduction

A protein is a biological macromolecule that is at the basis of every biological process, e.g. enzyme catalysis, DNA replication, response to stimuli, molecules transport, cell structures, and the like. A protein is composed by one or more long chains of amino-acids residues linked in a chain by peptide bonds. There are 20 different kinds of amino-acid residues and the particular sequence of amino-acids that composes a protein is called primary structure.

When in solution, protein molecules assume their specific 3D structure by a process called protein folding. The particular 3D shape of a protein is at the basis of its physiological role, moreover this configuration undergoes (slight but crucial) changes to adapt to its micro-environment. Indeed, the deformation affects the interaction potentials between the protein’s atoms and the external environment, allowing it to carry out a specific function. In this regard, a protein can be conceived as a nano-machine equipped with sensors and actuators, and engineered—i.e. evolved—to be, from a chemical point of view, as stable as possible.

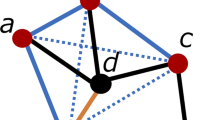
There is a deep relation between the function and the structure of a protein, and investigating the latter is a fundamental step in understanding the former. A thorough comprehension of how a protein works is in turn of great significance for a variety of practical settings, like drug design and the diagnosis of diseases. In this work we approach this problem from a topological point of view by a minimalist representation of the protein structure, called protein contact network (PCN) [1].

The main objective of this work is to investigate how the structure of a protein is related to its function by exploiting supervised machine learning techniques, building upon the spectral properties of the relative PCN. It is worth noting until now that there has been no consistent effort in relating functional and structural properties of proteins in a systematic way. This work takes into account a set of proteins of the Escherichia Coli proteome [2] represented as PCNs. Within this set we consider two classes, i.e. the subset of enzymes and its complement, non-enzymes, where each element of the first class is associated with an Enzyme Commission number [3], that describes the chemical reactions it catalyses, as the ground-truth class label.

This problem is then reformulated as a classification task. Specifically, the target of the classification task is to predict the particular class of each protein starting from a spectral representation of the corresponding protein contact network.

The remainder of this paper is structured as follows: in Sect. 2 we will discuss some essential concepts and definitions regarding graphs and their properties, along with PCNs and their graph-based representation; in Sect. 3 we will present the set of algorithms we used for our analysis, along with the pre-processing stage in order to map PCNs in suitable real-valued features vectors; in Sect. 4 we will show the obtained results and, finally, in Sect. 5 we will draw some conclusions, along with interesting extensions and future works.

2 Definitions

2.1 Fundamentals of Graph Theory and Graph Spectra

Graphs are objects capable of describing data and structures both under a topological and semantic point of view, often used to represent conveniently a set of objects and their relations in many data science fields and applications.

Formally, a graph $G=(V,E)$ is composed by a set of nodes (or vertices) V and a set of edges (or links) E, where $|V|=N$ and $|E|=M$ with N not necessarily equal to M; an edge $e=(v_i,v_j) \in E$ is a link between nodes $v_i$ and $v_j$.

A graph can be described by means of the adjacency matrix $\mathbf {A}$, a binary matrix defined as:

$$\begin{aligned} \mathbf {A}_{i,j} = {\left\{ \begin{array}{ll} 1 &{} \quad \text {if } (v_i,v_j) \in E\\ 0 &{} \quad \text {otherwise}\\ \end{array}\right. } \end{aligned}$$

(1)

and if the graph is undirected (that is, if $e=(v_i,v_j) \in E$, then $e=(v_j,v_i) \in E$), such matrix is symmetric by definition. The degree D of node i is defined as the number of nodes connected to it:

$$\begin{aligned} D(i)=\sum _{j=1}^{N}\mathbf {A}_{i,j} \end{aligned}$$

(2)

Starting from (2), the degree matrix $\mathbf {D}$ has the form

$$\begin{aligned} \mathbf {D}_{i,j} = {\left\{ \begin{array}{ll} D(i) &{} \quad \text {if } i=j\\ 0 &{} \quad \text {otherwise}\\ \end{array}\right. } \end{aligned}$$

(3)

which is diagonal by definition. Given $\mathbf {D}$ and $\mathbf {A}$, the Laplacian matrix $\mathbf {L}$ of a graph is defined as

$$\begin{aligned} \mathbf {L}=\mathbf {D}-\mathbf {A} \end{aligned}$$

(4)

and its normalised version has the form

$$\begin{aligned} \varvec{\mathcal {L}}=\mathbf {D}^{-\frac{1}{2}}\mathbf {L}\mathbf {D}^{-\frac{1}{2}} \end{aligned}$$

(5)

The normalised graph Laplacian matrix has an interesting property [4] in case of unweighted and undirected graphs, which will turn useful for our analysis:  

Property. :

The set of eigenvalues of $\varvec{\mathcal {L}}$ (i.e. its spectrum) $S=\lbrace \lambda _i\rbrace _{i=1}^N$ lies in range [0; 2], independently of the number of eigenvalues of $\varvec{\mathcal {L}}$.

 

2.2 Protein Contact Networks and Kernel Density Estimator

A protein can effectively be described as a 3D object defined by the location (i.e. 3D coordinates) of the amino-acids which compose the protein itself [1]. Amino-acids, being the monomers of the protein (polymer) are also called residues. Inter-residue interactions determine the unique spatial arrangement of the protein and therefore a graph is a convenient representation for such a configuration, where residues are the nodes of the graph and edges indicate spatial proximity between different residues.

Specifically, if the distance between two nodes is below a given threshold (typically $8\AA$), the two nodes can be considered adjacent. However, some authors (e.g. [5, 6]) consider two nodes as adjacent if their distance in the 3D space is between 4 and 8 $\AA$. The lower threshold is set in order to ignore first-neighbour contacts on the protein’s linear chain, since they are expected in every protein and provide no additional information on its spatial organisation. In this work, we adopt this convention.

Since proteins can be described as graphs, we can evaluate PCNs adjacency matrices and spectra as in Sect. 2.1. Notice that in this unlabelled graph representation, the different chemical properties of amino-acids have been deliberately neglected.

The property stated in Sect. 2.1 provides the following, precious, insight: since the aforementioned [0; 2] range in which eigenvalues lie is independent from N, one can think of processing graphs (e.g. evaluating dissimilarity) having different number of nodes. However, the number of eigenvalues is still function of N and in order to overcome this problem, we estimate [6] the graph spectral density p(x) by means of a Kernel Density Estimator (KDE) [7]. Amongst the several kernel functions available, the Gaussian kernel is one of the mostly used:

$$\begin{aligned} p(x)=\dfrac{1}{N}\sum _{i=1}^{N}\dfrac{1}{\sqrt{2\pi \sigma ^2}}e^{\dfrac{-(x-\lambda _i)^2}{2\sigma ^2}} \end{aligned}$$

(6)

where $\sigma$ is the kernel bandwidth. We define the distance between two graphs ($G_1$ and $G_2$) as the squared difference between their corresponding spectral densities ($p_1(x)$ and $p_2(x)$, respectively) all over the [0; 2] range:

$$\begin{aligned} d(G_1,G_2)=\int _{0}^{2}(p_1(x)-p_2(x))^2 dx \end{aligned}$$

(7)

2.3 Enzyme Commission Number

The Enzyme Commission number (hereinafter EC) is a numerical coding scheme utilised for classifying the physiological role of enzymes. In particular, the EC number of an enzyme encodes the chemical reaction it catalyses. An EC number is a sequence of four digits, separated by dots, in which the first digit (1–6) indicates one of the six major groups¹ and the latter three digits represent a progressively finer functional classification of the enzyme. As we will deal with supervised machine learning algorithms (Sect. 3.2), it is easy to map each protein in our dataset with its group which will serve as the label. However, not all proteins are enzymes and therefore for some of them the EC number might not exist: in this case, such proteins will have label 7, which means not-enzyme.

3 Proposed Approach

3.1 Preprocessing

We start considering our proteins as a set of plain text files, each of which describes a given graph. All graphs are undirected and we do not consider weights on edges between amino-acids. In order to feed this dataset to our algorithms (which take as input $N_F$-dimensional real-valued vectors, Sect. 3.2, where $N_F$ is the number of features) a mandatory pre-processing stage is performed on the basis of Sect. 2. Indeed, for each graph:

• 1. the adjacency matrix is evaluated according to (1)

• 2. the degree matrix is evaluated according to (3)

• 3. Laplacian and normalised Laplacian matrices are evaluated according to (4) and (5), respectively

• 4. normalised Laplacian matrix eigenvalues are evaluated

The set of eigenvalues represents our pattern which, to this stage, is a vector in $\mathbb {R}^{N}$ where the number of nodes N might be different from protein to protein.

3.2 Supervised Algorithms

Support Vector Machines. Amongst the chosen algorithms, the first competitor will be a One-Against-All non-linear Support Vector Machines (SVMs) [10] ensemble with Gaussian Radial Basis Function (GRBF) kernel.

$$\begin{aligned} GRBF(\mathbf {a},\mathbf {b})=e^{-\gamma \cdot d^2(\mathbf {a},\mathbf {b})} \end{aligned}$$

(8)

where $d^2(\cdot )$ is the squared Euclidean distance.

The two main parameters, namely the regularisation term C and the kernel shape $\gamma$, will be tuned according to a grid search ($log_2C=[-20;20] \times log_2\gamma =[-20;+20]$) with cross-validation.

K -Nearest Neighbours. Conversely to SVMs, K-Nearest Neighbours (K-NN) is an instance-based algorithm [9] and therefore it does not require any training phase. The only parameter to be tuned is K, the number of neighbours to be considered in the classification stage. As our dataset does not have prohibitive dimensions (in terms of number of patterns), we will gather the optimal K using a bruteforce approach; that is, trying every K from 1 up to the number of patterns in the Training Set and select the best K as the value that leads to the minimum error rate on the Validation Set.

CURE Support Vector Machines. The CURE² Support Vector Machines is an optimised and extended version of the plain Support Vector Machines described above. Specifically:

• (a) albeit the Gaussian kernel (6) is widely used, it might not be the most suitable choice for the problem at hand and how to select the right bandwidth $\sigma$ deserves some attention

• (b) the very same SVMs parameter (C and $\gamma$) can be tuned in a smarter way, if compared to a grid-search approach

• (c) some features (i.e. KDE samples, Sect. 4.1) might be more important than others, thus the dissimilarity measure can be tuned according to a weights vector

The CURE Support Vector Machines overcome these problems thanks to an optimisation/tuning procedure orchestrated by a genetic algorithm (GA) [8] in which the genetic code which identifies the generic individual from a given population has the form:

$$\begin{aligned} \begin{bmatrix}C&\gamma&\mathbf {w}&KT&\sigma \end{bmatrix} \end{aligned}$$

(9)

where $\mathbf {w}$ is the weights vector which tunes the dissimilarity measure in the GRBF kernel function (8). The latter can therefore be restated as

$$\begin{aligned} wGRBF(\mathbf {a},\mathbf {b})=e^{-\gamma \cdot d_w^2(\mathbf {a},\mathbf {b},\mathbf {w})} \end{aligned}$$

(10)

where in turn

$$\begin{aligned} d_w^2(\mathbf {a},\mathbf {b},\mathbf {w})=\sum _{i=1}^{N_F} \mathbf {w}_i (\mathbf {a}_i-\mathbf {b}_i)^2 \end{aligned}$$

(11)

Moreover, in (9), KT is an integer in range [1; 4] which indicates the kernel type (1 = Gaussian, 2 = Epanechnikov, 3 = rectangular box, 4 = triangular) and $\sigma$ is the bandwidth used by kernel KT.

Each SVM will be trained and optimised independently in order to separate a given class (marked as positive) from all other classes (marked as negatives). To do so, each individual from the genetic population will train such SVM on the Training Set by using the set of parameters written in its genetic code: C will regularise the penalty value in the SVMs convex optimisation problem, $\gamma$ and $\mathbf {w}$ will tune the dissimilarity/kernel function (10)–(11), KT and $\sigma$ will select the KDE and its bandwidth in order to extract the set of samples which represent a given PCN.

However, separate tuning of such SVMs, due to heavy labels unbalancing (Table 1), might lead the GA towards apparently good solutions, if the error rate is selected as (part of) the linear convex combination³, i.e. the fitness function. In order to overcome this problem, the fitness function (to be minimised) has been re-stated as well as the linear convex combination between the complement of the F-score⁴ and the percentage of patterns elected as Support Vectors⁵.

4 Experimental Results

4.1 Dataset Description

In order to validate our algorithms, we used the 454-patterns Escherichia Coli dataset introduced in [11, 12], named ds-g- . Such dataset has been introduced in [2], where the Authors collected the whole Escherichia Coli proteome. However, of the 3173 proteins collected, only 454 have their 3D structure available from [13], starting from which we were able to build their respective graphs. Moreover, we processed such graphs according to Sect. 3.1 with the following caveats:

• 1. we generated a first dataset (hereinafter scott ) by evaluating the Gaussian KDE (6) with bandwidth (i.e. parameter $\sigma$) according to the Scott’s rule⁶ [14]

• 2. we generated a second dataset (hereinafter hscott ) by setting $\sigma$ as half the Scott’s rule

Finally, $N_F=100$ samples linearly spaced in [0; 2] have been extracted from the density function evaluated with Eq. (6). Such final 100 samples unambiguously identify our pattern which, to this stage, is a vector in $\mathbb {R}^{100}$ and in turn the dissimilarity measure between patterns, formerly (7), collapses into the Euclidean distance.

However, both hscott and scott will not substitute in any case the original dataset in which each record is the set of eigenvalues for a given protein since the CURE SVMs will be free to evaluate different KDEs; indeed, such SVMs will basically repeat the above steps of evaluating the KDE with a given bandwidth and extracting 100 samples, where the KDE does not necessarily has to be Gaussian and the bandwidth does not necessarily has to be (a function of) the Scott’s rule.

We split the 454-patterns dataset into three non-overlapping sets, namely Training Set, Validation Set and Test Set. Roughly, the Training Set contains 50% of the total number of patterns (229 patterns), whereas the Validation and Test Sets contain 25% of the remaining patterns (111 and 114 patterns, respectively) and such split has been done in a stratified fashion; that is, preserving proportions amongst labels. For the sake of completeness, Table 1 summarises labels distribution in the aforementioned three splits:

Table 1. Labels distribution in Training, Validation and Test Sets. In brackets, the respective percentage value.

4.2 Test Results

Coherently with the CURE SVMs approach and in order to ensure a fair comparison, each of the algorithms described in Sect. 3.2 has been restated in a One-Against-All fashion; that is, there will be as many classifiers as there are labels and the i ^th classifier will be trained in order to separate the i ^th class (marked as positive) from all other classes (marked as negatives).

The set of parameters considered for comparison are:

• 1. $\text {accuracy} = \dfrac{TP+TN}{TP+TN+FP+FN}$

• 2. $\text {sensitivity (or recall)} = \dfrac{TP}{TP+FN}$

• 3. $\text {specificity} = \dfrac{TN}{TN+FP}$

• 4. $\text {negative predictive value} = \dfrac{TN}{TN+FN}$

• 5. $\text {positive predictive value (or precision)} = \dfrac{TP}{TP+FP}$

where TP, TN, FP and FN are the true positives, true negatives, false positives and false negatives, respectively.

Tables 2 and 3 summarise the K-NN and SVM performances on hscott , respectively. In such Tables, the i ^th row corresponds to the i ^th classifier which, recall, has been trained to recognise the i ^th class as positive. Also values marked as “NaN” are the outcome of a 0-by-0 division.

Table 2. K-Nearest Neighbours results on hscott

Table 3. Support Vector Machines results on hscott

In a similar way, Tables 4 and 5 summarise the K-NN and SVM performances on scott , respectively.

Table 4. K-Nearest Neighbours results on scott

Table 5. Support Vector Machines results on scott

From Tables 2, 3, 4 and 5 it is clear that both algorithms, in both cases, tend to predict all patterns as negatives, as shown by NaNs in positive predictive value⁷ (PPV) and very high negative predictive value (NPV) and specificity. Interestingly, the 7^th classifier (for both algorithms in both cases) does not return such results and recalling that the 7^th classifier is in charge of separating enzymes from not-enzymes, indicates an approximate spectrum/EC number mapping, encoded by the data-driven classifier function. This in turn suggests the existence of a relation between protein structure and function, that is preserved by the spectral representation employed in this work.

Let us further investigate by showing the CURE SVMs results in Table 6. Given the randomness in GAs, such results have been obtained by averaging five GA runs.

Table 6. The CURE Support Vector Machines results

As first observation, the SVMs are much more robust with respect to positive predictions, this as the result of choosing (a function of the) F-score as the fitness value in the GA; indeed, the F-score by considering both precision and recall intrinsically considers also false positives and false negatives, “stretching” the confusion matrix to be as much diagonal as possible. Second, the 7^th SVM over-performs the other 7^th classifiers, thanks to the optimisation procedure. Third, the (sub)-optimal kernel type as returned by the GA is the Gaussian kernel, which proves our first assumption in introducing (see (6)) and using such type of kernel for our first experiments.

5 Conclusions and Future Works

The classification task we face in this work is highly challenging and (at least to our knowledge) has never been faced in a systematic manner. It is worth noting that proteins are nano-machines whose basic structure has not a unique “optimisation target”, such as performing a specific physiological function (like the catalysis of a given chemical reaction). Conversely, protein molecules must at the same time accommodate many chemico-physical constraints, the most demanding one being probably to be soluble in water [15].

One of the many constraints the particular 3D configuration of a functional protein molecule must obey is the efficient transmission of allosteric signals through the structure [16]. Allostery is the mechanism that allows the protein to sense its micro-environment and to transmit a relevant message, sensed by a different part of the molecule (allosteric site) through the entire structure, to reach the “active site” (in the case of an enzyme the part of the structure devoted to the catalytic work). This mechanism allows the molecule to modify active site configuration so to adapt the reaction kinetics according to the particular physiological needs. Network formalisation, while surely extremely minimalistic, is highly effective as for signal transmission efficiency description, being able to get rid of many aspects of allosteric mechanism [17].

In our opinion, the largely unexpected success of functional prediction from PCN, stems from the focus on signal transmission of the PCN formalisation. This is evident when considering the statistics of the dichotomic separation of non-enzymes (class 7) from all the other classes. This is a somewhat “semantically asymmetric” case, like the Alice in Wonderland not-birthdays, since there are many modes to be a not-enzyme (structural proteins, motor proteins, membrane pores, ...). This is why (see Table 6) we are not disturbed by the low sensitivity of the class 7 prediction task (sensitivity = 53%), but at the same time, the specificity is extremely high (93%). This means that the corresponding synthesised SVM (see Table 6) was pretty sure of ’what-is-not-a-not-enzyme’ and, in more plain terms, the system is very effective in classifying a protein as an enzyme. While, at least in principle, all the proteins must sense their micro-environment and adapt to it [18], the allosteric properties are expected to be more prominent for enzymes than for non-enzymatic molecules. This is in line with the behaviour of the 7^th CURE SVM prediction that recognises very well the enzymatic/non-enzymatic character of patterns.

Finer details (the recognition of specific ECs) of the proposed structure/function recognition are still difficult to interpret and need to enlarge the dataset, but the obtained results seem to go along a biophysically motivated avenue.

We will further study this machine learning-based way of predicting functional behaviour starting from proteins topological information and some further analyses can be carried out. Indeed, it is possible to check how the classifiers performances change as the aforementioned $[4;8]\AA$ (Sect. 2.2) range changes. Moreover, several variants of the CURE SVMs can be applied, by considering linear classification or other different KDEs or different (dis)similarity measures in the Gaussian RBF kernel. Finally, a hierarchical classifier can be applied in order to improve between-enzymes classification.