A New Evolutionary Algorithm for Synchronization

Abstract

A synchronizing word brings all states of a finite automaton to the one particular state. From practical reasons the synchronizing words should be as short as possible. Unfortunately, the decision version of the problem is NP-complete. In this paper we present a new evolutionary approach for finding possibly short synchronizing words for a given automaton. As the optimization problem has two contradicting goals (the word’s length and the word’s rank) we use a 2 population feasible-infeasible approach. It is based on the knowledge on words’ ranks of all prefixes of a given word. This knowledge makes the genetic operators more efficient than in case of the standard letter-based operators.

J. Kowalski—Supported in part by the National Science Centre, Poland under project number 2014/13/N/ST6/01817.

A. Roman—Supported in part by the National Science Centre, Poland under project number 2015/17/B/ST6/01893.

1 Introduction

The synchronization problem is to find a word that brings all states of a finite automaton to the one, fixed state. Such word is called a synchronizing word and an automaton for which it exists is called synchronizing. In 1964 Černý [1] conjectured that for every synchronizing automaton with n states there exists a synchronizing word of length at most $(n-1)^2$. This conjecture remains open and it stimulated a huge research in the field of automata theory.

Synchronization is not only a theoretical problem, but has many practical applications. Some most important examples are:

• model-based testing of reactive systems, where we test conformance of a system under test with its model [2, 3]

• biocomputing, where a computing process is modeled by a “soup of automata” built with DNA molecules and after the computations all automata need to be restarted to the initial state [4]

• part orienting problem, where some parts of a defined shape arrive at manufacturing sites and they need to be sorted and oriented before assembly [5, 6].

It is clear that for the practical reasons we need to find – for a given automaton – the shortest possible synchronizing word. Unfortunately, the decision version of this problem is NP-complete [5, 7]. There exist some heuristic algorithms to compute the synchronizing word ([5, 8,9,10]), but they do not guarantee the optimal solution. Of course, the algorithms that are able to return the shortest synchronizing word are exponential, thus not very practical (for example [11,12,13]). Finally, there are some attempts that utilize artificial intelligence, like simple genetic algorithm [14] in which chromosomes directly represent synchronizing words.

In this paper we continue the research on the artificial intelligence methods for finding shortest possible synchronizing words. The evolutionary algorithm we present in this paper realizes a good trade-off between the runtime and the quality of results measured in terms of the length of a synchronizing word found.

Instead of the plain GA approach we used a more sophisticated algorithm, FI-2POP [15], and found it better suited for the task of synchronization. Moreover, we introduce domain-knowledge-based operators which significantly improve the quality of synchronizing words produced.

The paper is organized as follows. In Sect. 2 we introduce the basic definitions on automata and synchronization. We also present some ideas from [14] that show how it is possible to represent the problem of finding a short reset word in terms of a genetic algorithm machinery. In Sect. 3 we present our approach to the synchronization problem. We give the details about the evolutionary algorithm and its features constructed in a way to make the process of searching the space of possible solutions efficient and effective. Section 4 is devoted to the experiments and comparison of our approach with other known algorithms. Finally, Sect. 5 gives some conclusions and final remarks.

2 Automata Synchronization

2.1 Basic Notions and Definitions

A finite automaton is a triple $(Q, \varSigma , \delta )$, where Q is a finite, nonempty set of states, $\varSigma$ is a finite, nonempty set of input symbols (called an alphabet) and $\delta : Q \times \varSigma \rightarrow Q$ is a transition function. By $\varSigma ^*$ we denote the free monoid over $\varSigma$, that is the set of all words over $\varSigma$. The length of a word $w \in \varSigma ^*$ is the number of its letters. An empty word $\varepsilon \in \varSigma ^*$ has length 0. Without introducing any ambiguities, the transition function can be naturally extended to the set $2^Q$ of states from Q and to words over A: $\delta (P, \varepsilon )=P$, $\delta (P, aw)=\delta (\delta (P, a), w)$ for all $P \subseteq Q$, $a \in \varSigma$, $w \in \varSigma ^*$.

For a given $\mathcal {A}=(Q, \varSigma , \delta )$ and $w \in \varSigma ^*$ we define the deficiency of w as $df(w)=|Q|-|\delta (Q, w)|$. The deficiency may be viewed as a “completeness” of the synchronization process. For an empty word we have $df(\varepsilon )=0$. If w is a synchronizing word, then we achieve the maximal deficiency, $df(w)=|Q|-1$. A rank of the word w is defined as $rk(w)=|Q|-df(w)=|\delta (Q, w)|$. For a word $w=a_1a_2...a_k$ let us put $r_i = rk(a_1...a_i)$ for $1 \le i \le k$, $r_0 := |Q|$, $r_t := 0$ for $t>k$. We say that a subword $v=a_ia_{i+1}...a_j$ of w ($i<j)$ is a compressing word if $r_{i-1}>r_i=r_{i+1}=...=r_{j-1}>r_j$. A single letter $a_i$ is a compressing word if $r_{i-1}>r_i>r_{i+1}$.

Let $\mathcal {A}=(Q, A, \delta )$ be a finite automaton. We say that a word $w \in \varSigma ^*$ synchronizes $\mathcal {A}$ iff $|\delta (Q, w)|=1$ or, equivalently, that $\forall p, q \in Q\ \delta (p, w)=\delta (q, w)$. Such w is called a synchronizing word. Notice that if w is a synchronizing word, then so is any word of the form uwv, $u, v \in \varSigma ^*$. Therefore, it is natural to ask about the shortest possible synchronizing word. Such a word is called a minimal synchronizing word. The famous Černý conjecture states, that the length of a minimal synchronizing word for the n-state synchronizing automaton does not exceed $(n-1)^2$.

For the sake of simplicity, when it is clear what is the transition function, we will use the notation Qw instead of $\delta (Q, w)$.

Fig. 1.

An exemplary 4-state synchronizing automaton over 2-letter alphabet.

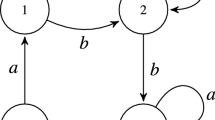
Let us consider the automaton $\mathcal {A}=(\{1,2,3,4\}, \{a, b\}, \delta )$ from Fig. 1. It is easy to check that the word $w=bbaabb$ is a synchronizing word, because for each state $q \in Q$ we have $\delta (q, bbaabb)=3$. It can be shown that this is also the minimal synchronizing word for this automaton.

2.2 Genetic Algorithm for Synchronization

Simple Genetic Algorithm (SGA) operates on the populations of possible solutions S to a given problem in a way that imitates nature. A population P consists of a number of chromosomes. Each chromosome $c \in P \subset S$ encodes a possible solution to a problem. To evaluate the quality of this solution, a fitness function $f: S \rightarrow [0, \infty )$ is introduced. It is used to perform the selection of the best individuals that are further subjected to genetic operators: crossover and mutation.

The idea of a crossover is to construct from two good individuals $c_1, c_2$ a third one, $c_3$, that is possibly better than its parents, that is $f(c_3) > f(c_i)$ for $i=1, 2$. The mutation allows us to introduce the diversity to the population. This way the genetic algorithm is able to effectively explore a potentially very big solution search space.

In case of a synchronization problem we search for a word w that is a possibly short synchronizing word for a given automaton $\mathcal {A}=(Q, \varSigma , \delta )$. As each word is a linear representation of its letters, $w=a_1a_2\ldots a_n$, $a_i \in \varSigma$, $i=1, \ldots , n$, we may represent w directly as a chromosome with genes $a_i \in \varSigma$. Notice that we do not need to encode the solution: the chromosome is already a solution.

In [14] a modified version of SGA, named SynchroGA, was used for the problem of finding the short synchronizing words. Two most important modifications were:

• the variable length of the chromosome – as we evaluate the solutions by their length,

• the number of possible genes – SGA operates on a binary alphabet of two genes: 0 and 1; in case of synchronization each gene corresponds to one letter from $\varSigma$, so the number of different genes is equal to the size $|\varSigma |$ of the input alphabet.

The modified SGA also used an experimentally constructed fitness function:

$$f(w) = \frac{df^4(w)}{\root 4 \of {|w|}}.$$

The fitness function evaluated two things at the same time: the deficiency of the found word (the larger, the better) and the length of this word (the shorter, the better). This approach is not very effective, because it imposes fixed coefficients that represent the importance of these two factors.

3 Algorithm

In this section we describe in details our evolutionary SynchroGA-2POP algorithm. We provide arguments for using 2-population GA, point out the improvements from the previous approaches and present the set of implemented operators.

3.1 Feasible-Infeasible 2-Population Approach

The feasible-infeasible two population (FI-2POP) genetic algorithm [15] seems naturally well-suited for the task of DFA synchronization, as it has been developed especially to handle constrained optimization problems. The FI-2POP algorithm has been successfully used especially for search-based procedural content generation [16], including game level generation [17, 18] and music generation [19].

In the synchronization problem, there exist two types of words, synchronizing and non-synchronizing, corresponding to feasible and infeasible population respectively. Non-synchronizing words can be very close to the optimal solution (e.g. by one letter deletion). Let us consider again the automaton from Fig. 1. A word babaabb brings the whole set of states to its subset $\{2, 3\}$. However, when we remove the first occurrence of a, the word bbaabb becomes a synchronizing one.

The goals for both populations are different, which encourages us to use different operators. To improve the non-synchronizing word and advance to the feasible population, we have to reduce its rank (which can be easiest achieved by making it longer). To improve a synchronizing word, from the other hand, we have to reduce its length. As stated in [15], maintaining two distinct populations is more natural in such case than using e.g. penalty functions, as it was done in SynchroGA [14].

3.2 Rank-Based Model

Let $\mathcal {A}$ be a deterministic finite automaton with $|Q|=n$ states and the alphabet of size k. For a given a word w, checking if w synchronizes $\mathcal {A}$ is equal to computing Qw, which requires $\varTheta (n|w|)$ time. We have that $rk(w)=|Qw|$ is a word’s rank, and w is synchronizing iff $rk(w)=1$.

The natural model used in the previous approach utilizing a genetic algorithm [14] was to base fitness function on the word’s rank. However, this information turns out to be very limited. In particular, knowing that $w=va$ is synchronizing, we have no information if v is synchronizing. Thus in many cases computed words can be trivially improved. This problem was raised as one of the conclusions in [14].

Our solution is to extend the output given by the checking procedure, without increasing its complexity. Instead of returning just the rank for a word w, the procedure returns the ranks of all prefixes of w (which are computed anyway, as they are required to compute the rank of the whole word). So, for a word $w=a_1a_2\ldots a_{|w|}$, we compute $r_1, r_2, \ldots , r_{|w|}$ (recall that for every $i\le |w|$, $r_i$ is the rank of the word $a_1a_2\ldots a_i$).

This information allows us not only to remove the unnecessary suffixes of synchronizing words but also to introduce more sophisticated genetic operators, based on the compressing words.

3.3 Operators

In our algorithm we have implemented multiple genetic operators, to choose the combinations which provide the best results. Apart from the standard operators based on the plain strings, in most cases we also defined their rank-based counterparts.

Initialization. Let P be the size of the entire population. The initialization operator generates 2P random words. It is twice much as the population size in order to increase the chance of generating the feasible words and to have the feasible and infeasible populations more balanced. The uniform(l) operator creates the words of length $l\cdot n$, where every letter is chosen with the uniform probability.

The rank of a letter a is the size of the |Qa| set. The rank-based(l) initialization creates the words of length $l\cdot n$, where every letter is chosen using the roulette wheel method, using letter rank as the weight. Alternatively, reverse-rank-based(l) operator uses as the roulette wheel weights the values $n-r_a+1$, where $r_a$ is the rank of letter a. Adding one in this formula ensures that the probability will be nonzero in case of letters being the permutations of states.

Selection. For every subpopulation (feasible and infeasible) of size $P'$, the $\lfloor \frac{P'}{2}\rfloor$ pairs of parents are chosen. The tournament(s) selection operator chooses every parent as the best among s randomly selected individuals. The tournaments are repeated until a pair containing different parents is chosen. The mostly used uniform selection operator, is the special case of the tournament selection with s equal to one. The sampling is performed with repetitions.

Crossover. We have tested standard crossover operators: one-point, two-point and uniform. Each one has also its rank-based equivalent. For the rank-based crossovers, the cutting points have to be defined at the end of the compressing words.

Mutation. It is the main operator whose task is to push a given population to its goal. Thus, we mostly use different mutations for the feasible and infeasible population.

The letter-exchange(p) mutation changes every letter in a word with a given probability p. The new letter is chosen with the uniform probability among the letters different than the actual one.

The first operator designed for the infeasible population is the letter-insertion(p) mutation. After every existing letter it inserts, with a probability p, a new, uniformly chosen letter. The adaptive version of the operator makes the probability dependent on the best fitness value among the individual’s parents. Let r be the lowest rank of the parent’s words. The probability of the individual letter insertion is equal to $\min \{p \cdot r,1\}$.

Let $LC(P_f)$ be the set of the last compressing words for all elements of the feasible population $P_f$. The lastwords operator extends the chromosome by adding at the end one randomly chosen element from $LC(P_f)$. If the feasible population is empty, it uses a random word of length 0.1n.

The compressing-word-insertion inserts one random compressing word of length $\ge 5$ (not necessarily the last one) from the current feasible population, or a random word of length 0.1n if it is empty. The word is inserted always between the existing compressing words. We use the heuristic stating that the rank based crossovers preserve compressing words (which is certainly true only before the first cutting point).

Finally, the letter-deletion(p) mutation, designed for the feasible population, removes a letter with a given probability. The adaptive version uses the probability $\min \{p \cdot l/l_{min}, 1\}$, where l is the length of the shortest parent word and $l_{min}$ the length of the shortest word in the feasible population.

Replication. All our experiments use one replication operator. From the joint population of the parents and offsprings with removed duplicates it chooses best $\frac{P}{2}$ synchronizing words for the new feasible population, and best $\frac{P}{2}$ non-synchronizing words for the new infeasible population. If there are no valid individuals to fill one of the populations, the other one is properly extended to always maintain P individuals in total.

Fitness Function and Termination Criteria. We used two fitness functions: the word’s rank for the infeasible population, and the word’s length for the feasible population. The goal for every population is to minimize its fitness function value. The evolution stops after a given generation.

3.4 Preliminary Experiments

The preliminary experiments were intended to choose the best combination of operators. They have been performed using randomly generated automata: over binary alphabet with 25, 50, 75, 100 states, and over 3 and 4 letters alphabet with 25, 50, and 75 states. Each sample contained 100 automata and each automaton has been tested 100 times. We have used the population of size 60 (30 feasible + 30 infeasible), and the maximum generation has been set to 500.

The parameter settings were tested using the hill climbing strategy. After the initial run containing different combinations of operators, in each turn we modified the individual operators in a few most promising settings, evaluated the new settings, and repeated the process a few times, until no score increase has been observed.

In total, we have tested more than 110 settings. The partial results are presented in Table 1. For every tested combination of operators we have calculated the fraction of cases where a minimal synchronizing word has been found (column 2). The average generation in which it happened is presented in column 3. Let us point out that in all cases we were able to find some synchronizing word. The next columns show the ratio of the length of the found synchronizing word and the lengths returned by the other algorithms. MLSW stands for the length of a minimal synchronizing word calculated using the exponential algorithm [11]. COFFLSW stands for the result of Cut-Off IBFS$_n$ [10], which is so far the most accurate heuristic algorithm described. EPPLSW denotes the length provided by the classical Eppstein algorithm [5]. Ratio below 1 means that our algorithm provides shorter synchronizing words than the algorithm we are comparing to.

Table 1. Results for preliminary selection of operators. The table presents the best 20 combinations of operators according to % of MLSW found by the evolutionary algorithm with this set of operators. The last row presents the best setting that does not use any rank-based operator. Abbreviations used in the table: Init = initialization operator (uni = uniform, rb = rank-based, rrb = reverse-rank-based); $C_{FI}$ = feasible population crossover, $C_{IF}$ = infeasible population crossover (1pL = one-point standard, i.e. letter-based, 1pRB = one-point rank-based, 2pRB = two-point rank-based); $M_{FI}$ = feasible population mutation (ald(p) = adaptive letter-deletion with probability p); $M_{IF}$ = infeasible population mutation (lw = lastwords, cwi = compressing-word-insertion, ali(p) = adaptive letter-insertion with probability p).

The next four columns show the average percent of advancements between the succeeding populations. IF$\rightarrow$FI is counted when a child of infeasible parents is feasible. IF++ is counted when a child of infeasible parents is improved, i.e. it is feasible or its rank is lower than the lowest rank of its parents. Similarly, FI$\rightarrow$FI is counted when a child remains in feasible population, and FI++ when it is improved (it is shorter then the shortest of its parents). Remaining columns describe the operators used. For all presented combinations we used the uniform selection operator.

All leading operator settings have very similar performance. The difference in the percent of founded MLSW between the leader and the first ten settings is less than 0.5%, and for the first twenty it is less than 1%. The first combination of operators which does not contain any rank-based operator has been classified as 52 with the score nearly 2% worse than the leader. On the other hand, some of the tested combinations, using e.g. 3 elements tournament selection and letter-exchange mutation obtained MLSW scores below 60%.

Let us discuss the performance of the individual operators. It seems that the initial population size (ranging from 0.5n to 2.5n, where n is the number of states) does not have any significant impact on the number of generations. Performance of the rank-based and uniform initialization operators is alike, which is expected due to the fact that the probability values they use are similar for the random automata. However, the reverse-rank-based initialization which differentiate probabilities more, scores visibly worse (positions 12 and 13 at best).

Surprisingly, the dominant crossover operator for the feasible individuals is not based on the knowledge on compressing words, but it is a standard one-point crossover. It seems that the only top-score alternative is the two-point rank-based crossover within an entry ranked as 14. The best rank-based equivalent of the one-point crossover achieved the score of 74.6% and is ranked as 29th. No other operator appears in the table unless close to the bottom.

On the other hand, the rank-based crossovers seems to be the only reasonable choice for the infeasible parents, especially the two-point crossover. The best letter-based crossover is the one ranked 52. Also, we have to point out that the uniform crossovers, both letter- and rank-based, do not work well for the task of synchronization. They tend to destroy word’s structure too much, and failed for both population types.

The only operator directly suited to improving feasible individuals is letter-deletion. The letter-exchange mutation preserves the word length, so the score increase mostly relies on the crossover operation. We have tested different probability values combined with both adaptive and non-adaptive version. We observed that the adaptive version behaves better, as it is more cautious for short synchronizing words while simultaneously more aggressive for the long words. The best combination of operators using non-adaptive letter-deletion is ranked 68th. We also found that the slightly higher or slightly lower probability values usually result in a worse score. Note that increasing the probability actually decreases a chance to preserve or improve a feasible individual.

The lastwords operator totally dominates the other options for the infeasible individuals mutation. The heuristic that the last compression words tend to synchronize the remaining, thus the hardest to synchronize, states is surprisingly effective. Note that the compressing word insertion has significantly higher percent factor of improving the infeasible population, so we can assume that the lastwords seems to prefer quality over the quantity. The first entry with a letter-insertion operator is ranked as 49, with less than 74% of found MLSW and population improvement factor below 3%. Similarly, as in case of the letter-deletion operator, the adaptive version results in undeniably better scores.

For the further experiments we usually use just the combination of operators ranked as first. However, in some cases we also test the behavior of other operator sets which are same how representative (ranked 2nd, 14th, 19th, and 52nd).

4 Experiments and Results

In this section we provide the results of three experiments with our algorithm. First one checks the algorithm performance for the so-called extremal automata. These are the automata with very long ($\varOmega (|Q|^2)$) minimal synchronizing words, thus they are the ‘hardest to synchronize’. We use some well-known series of such automata, for which it is known what is the exact length of their MLSW, hence, we are able to compare the algorithm results with the optimal solutions.

The second experiment compares our approach with the genetic algorithm from [14]. We perform this experiment on the same set of the extremal automata, so the results of the first two experiments are put together in the next subsection.

The third experiment checks how our algorithm deals with the random automata having large number of states. We also compare it with the Eppstein and Cut-Off IBFS algorithms.

We do not provide running time comparisons because of the used architecture. Implementations of all other algorithms are written in the highly optimized C++ code, while our SynchroGA2-POP is mainly written in Lua, and refers to C++ implementation only when testing ranks of the words.

4.1 Extremal Automata and Comparison with SynchroGA

In this section we present the comparison of our approach with the genetic algorithm from [14]. We tested both algorithms for the series of extremal automata B, C, $D'$, $D''$, E, F, G, H, W and two simpler series a and b (see Table 2 for the details) for 11, 21, 31, 41, 51 and 61 states.

There are two main reasons for testing these automata. First, they are hard to synchronize. Second, for each type we can construct an automaton with an arbitrary number of states and we know exactly what are the minimal synchronizing words for all these automata (for proofs, see the ‘Reference’ column in Table 2).

For each automaton of a given type and number of states both algorithms were run 20 times. Each run included 1000 steps. Population size was 40 in case of the genetic algorithm and 20 feasible + 20 infeasible in case of our approach. After each run we collected the following information:

• rk – the minimal rank among the ranks of all the words from all populations for this run,

• length – the length of the word with minimal rank,

• firstPop – the number of the first population in which the best word was found.

Table 2. Description of the extreme automata series and two special series a and b analyzed in the experiment.

Based on this information we were able to compare the algorithms in three different ways: (1) comparison for the optimal runs, where only the runs with the minimal synchronizing words found were analyzed; (2) comparison for the runs in which any synchronizing word was found; (3) general comparison, taking into account all the runs. The results are presented respectively in Tables 3, 4 and Fig. 2.

As for the optimal runs we can see that our algorithm was able to find the minimal synchronizing words in case of $D'_{21}$, $D''_{11}$, $D''_{21}$, $G_{11}$, $G_{21}$, $W_{11}$ and for all a and b automata. The genetic algorithm was not able to find the synchronizing word for $a_{51}$, $a_{61}$, $b_{51}$ and $b_{61}$, despite the fact that their MLSW are relatively short (linear in the number of states). We may also observe that for a and b automata our algorithm was able to find the minimal synchronizing words much faster than SynchroGA.

Table 3. Comparison of algorithms for runs in which minimal synchronizing words were found. SGA2 = our SynchroGA-2POP approach, SGA = SynchroGA.

When comparing the runs in which any (not necessarily minimal) synchronizing word was found we may observe that in case of SynchroGA the algorithm was usually not able to find a synchronizing word for automata with large number of states. Our algorithm found the synchronizing word for all types of automata, but the differences between their lengths and the MLSW values increase with the number of states.

Fig. 2.

Comparison of algorithms for runs in which any synchronizing words was found.

Table 4. Comparison of algorithms for all runs. SGA2 = our SynchroGA-2POP approach, SGA = SynchroGA.

Fig. 3.

The mean found length by the algorithms for random binary automata.

The analysis of all runs shows that our algorithm deals generally much better than SynchroGA. First, it was able to find the synchronizing words for all types and sizes of the analyzed automata. Only in few cases the mean rank of the best word found is greater than 1, which means that in some (out of 20) runs for some automata types our algorithm was not able to find the synchronizing word. The results for SynchroGA are much worse. For some automata ($B_{41}$, $C_{31}$, $C_{41}$, $D''_{41}$, $E_{31}$, $E_{41}$, $F_{41}$, $H_{31}$) it was not able to find a synchronizing word within all 20 runs.

4.2 Computing Reset Words of Large Automata

The next test was performed for the large random automata over 2-letter alphabet. In this case, computing the length of a minimal synchronizing word is computationally too expensive, and instead of the exact algorithm the heuristic procedures are used to obtain as good approximation as possible. We have tested how SynchroGA-2POP behaves for such large data, and compared it against the Eppstein algorithm and Cut-Off IBFS$_n$.

We tested automata with the number of states n between 100 and 600 (with step 100). For each n we tested 1000 automata, and for each automaton we run our algorithm 10 times. The results of the experiment are presented in Fig. 3. We used the same settings as in the preliminary experiments, i.e. population of size 60 and generation limit set to 500. We run the experiment using various operator combinations, which are appointed by the rank presented in Fig. 1.

It can be seen that the difference between the best three selected variants is very small, and all of them performed better than the Eppstein algorithm for DFA with less than 400 states. On the other hand, the difference between them, and the variant ranked as 19, which differs mainly in the mutation operator for the infeasible population, is clearly visible. The results of Cut-Off IBFS$_n$ are very close to the estimated length of a minimal reset word proposed in [11], and SynchroGA-2POP reaches comparable lengths only for $n \le 100$. Lastly, the quality of the results provided by the best letter-based-only variant (ranked as 52 in the preliminary experiment) emphasizes the benefits from using more sophisticated rank-based operators.

5 Conclusions

In this paper we presented a new heuristic algorithm for finding short synchronizing words. We used a 2 population feasible-infeasible approach. This allowed us to manage two usually contradicting goals when considering them as the components of the fitness function: rank of the word and its length. Usually, for random words, short ones have large ranks. From the other hand, providing the words with low rank requires them to be very long.

In [14] both these contradicting goals were put into one fitness function. In our approach we used the 2 population scheme, which allowed us to ‘split’ the fitness function into two independent components. The mutation operator for the feasible population took into account the result from the infeasible one, therefore it was able to ‘adapt’ to a given automaton and allowed to mutated words to be still synchronizing, but shorter.

The performed experiments show that our algorithm generally works better than SynchroGA. However, comparing to the Cut Off-IBFS approach, it gives worse results for big random automata. Also, for bigger automata, Eppstein algorithm outperforms our approach. However, the genetic algorithm is much more flexible than the two above mentioned solutions. We may define the size of the population (therefore, controlling the memory used) and the exit criterion (therefore, controlling the runtime). The experiments show that our algorithm fits well for small automata and – comparing with the SynchroGA algorithm – for the ones that are hard to synchronize.