Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Networks are ubiquitous in our daily lives and many real-life applications focus on mining information from the networks. A fundamental problem in network mining is how to learn the desirable network representations [4, 22]. To address this problem, network embedding is presented to learn the distributed representations of nodes in the network. The main idea of network embedding is to find a dense, continuous, and low-dimensional vector for each node as its distributed representation. Representing nodes into the distributed vectors can form up a potentially powerful basis to generate high-quality node features for many data mining and machine learning tasks, such as node classification [6], link prediction [11] and recommendation [24, 27].

Most related works investigate the topology information for network embedding, such as DeepWalk [16], LINE [19], Node2Vec [6] and SDNE [22]. The basic assumption of these topology-driven embedding methods is that nodes with similar topology context should be distributed closely in the learned low dimensional representation space. However, in many real scenarios, it is insufficient to learn desirable node representations by purely relying on the network topology structure. For example in the social networks, it is possible that two users share very similar interests but they are not connected and share no common friends, thus their similarity on interests cannot be effectively captured by the topology based network embedding methods. In such a case, other types of information should be incorporated as the complementary content to help us learn better representations.

Usually, nodes in the network may be associated with a set of properties, such as the profiles of each user in a social network and the metadata of each paper in a citation network. Node property information is also important to measure the similarity between nodes, but are largely ignored by previous network embedding methods. For example in a social network, if two users share some common tags or tweet topics, they are very likely to be similar even if they are topologically far away from each other. Since the node properties potentially encode different types of information from the network topology, integrating them into the embedding process is expected to achieve a better performance. As the first attempt, TADW [25] incorporates the text features of nodes into network embedding process under a framework of matrix factorization. However, there are two limitations of TADW. Firstly, the very time and memory consuming matrix factorization process of TADW makes it infeasible to scale up to large networks. Secondly, TADW only considers the texts associated to each node, and it is difficult to apply TADW to handle the node properties of rich types in general.

In this paper, we propose a general network embedding framework which can effectively encode both the topology information of the network and the rich properties of the nodes. This task is difficult to address due to the following challenges. Firstly, nodes in a network may contain several types of properties, and in different networks, the types of node properties are different. It is non-trivial to model various types of properties into an unified format and utilize these property information. Secondly, although combining network topology and node properties into the embedding process is expected to achieve better performance, it is not obvious how best to do this under a general framework. There are sophisticated interactions between network topology and node properties, and it is difficult to integrate node properties into the existing topology-derived models. For example, DeepWalk and Node2Vec cannot easily handle additional information during the random walk process in a network.

To address the above challenges, we propose a general and flexible property preserving network embedding model PPNE. We formulate the learning process of property preserving network embedding as a joint optimization problem, where the topology-derived and property-derived objective functions are optimized jointly. Specifically, we propose a negative sampling based objective function to capture the topology information, which aims to maximize the likelihood of the prediction of the center node given a specific contextual node. Besides, we extract a set of constraints according to the property similarity between each pair of nodes, and a property-derived objective function is proposed to restrict the learned representation vectors to satisfy the extracted constraints. Finally, we utilize the stochastic gradient descent (SGD) algorithm to solve this joint optimization problem.

To summarize, we make the following contributions:

  • In this paper we propose and study the novel problem of property preserving network embedding, and propose a general embedding framework to effectively incorporate both network topological information and node property information into the network embedding process.

  • To utilize the property similarity information, we propose two ways of extracting constraints from the property similarity matrix. A carefully designed objective function with such constraints is also proposed.

  • We extensively evaluate our approach through multi-class classification and link prediction tasks on five datasets. Experimental results show the superior performance of PPNE over state-of-the-art embedding methods.

The rest of this paper is organized as follows. Section 2 summarizes the related works. Section 3 formally defines the problem of property preserving network embedding. Section 4 introduces the proposed model PPNE in details. Section 5 presents the experimental results. Finally we conclude this work in Sect. 6.

2 Related Work

Network embedding aims to learn a distributed representation vector for each node in a network, which essentially is an unsupervised feature learning process. In general, network embedding is related to the problem of graph embedding or dimensionality reduction. Most existing network embedding methods can be categorized into two broad categories: matrix factorization based and neural network based methods.

Matrix factorization based methods first express the input network with a affinity matrix in which the entries represent the relationships between nodes, and then embed the affinity matrix into a low dimensional space using matrix factorization techniques. Locally linear embedding [17] seeks a lower-dimensional projection of the input affinity matrix which preserves distances within local neighborhoods. Spectral Embedding [2] is one method to calculate the non-linear embeddings. It finds a low dimensional representation of the input data using a spectral decomposition of the graph Laplacian. Sparse random projection [10] reduces the dimensionality of data by projecting the original input space using a sparse random matrix. However, matrix factorization based methods rely on the decomposition of the affinity matrix, which is too expensive to scale efficiently to large real-world networks. Besides, the manually predefined node similarity measurements are needed to construct the affinity matrix, which can significantly affect the quality of learned representation vectors.

Recently neural network based models are introduced to solve the network embedding problem. As the first attempt, DeepWalk [16] introduces an word embedding algorithm (Skip-Gram) [14] to learn the representation vectors of nodes. Tang et al. propose LINE [19], which optimizes a carefully designed objective function that preserves both the local and global structure. Wang et al. propose SDNE [22], a deep embedding model to capture the highly non-linear network structure and preserve the global and local structures. SDNE exploits the first-order and second-order proximities to preserve the network structure. Node2Vec [6] learns a mapping of nodes to a low-dimensional space of features that maximizes the likelihood of preserving distances between network neighborhoods of nodes. TADW [25] incorporates the text features of nodes into network embedding process under a framework of matrix factorization. Compared to the matrix factorization based methods, neural network based methods are easier to generalize and own strong representation ability. However, most previous works only take the network topology information into consideration. Different from the previous typology-only works, our work aims to propose a general property preserving network embedding model which integrate the rich types of node properties in the network into the embedding process.

Finally, there is a body of works focus on the problem of node classification [8, 20, 21, 26] or link prediction [11, 13]. However, the objective of our work is totally different from these works. We aim to learn better representation vectors for nodes, while the node classification or link prediction tasks are only utilized to evaluate the quality of the embedding results.

3 Problem Definition

In this section, we formally define the studied problem. The input network G is defined as \(G = (V, T, P)\), where V represents nodes in the network. The topology matrix \(T \in \mathbb {R}^{|V| \times |V|} \) is the adjacency matrix of the network. P is the property similarity matrix with each entry \(P_{i,j} \in [0,1]\) denoting the property similarity score between node i and j. Here we formally define the problem of property preserving network embedding:

Definition 1

(Property Preserving Network Embedding): Given a network G = (V, T, P), the problem of property preserving network embedding aims to learn a matrix \(X \in \mathbb {R}^{|V| \times d}\), where d is the number of latent dimensions with \(d \ll |V|\). Each row vector \(X_{i}\) in X is the embedding vector of node i. The objective of property preserving network embedding is to make the learned representation vectors explicitly preserve both the network topology and node property information.

4 Property Preserving Network Embedding

In this section, we present the details of the proposed property preserving network embedding model PPNE. Firstly we briefly introduce the framework of PPNE. Then the topology-derived objective function and property-derived objective function are introduced separately. After that we present the joint optimization process of the above two objective functions. Finally we discuss several practical issues of the proposed model.

4.1 Framework

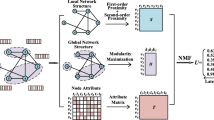
Figure 1 shows the framework of PPNE. One can see that each node in the network is associated with a set of properties. The first step of PPNE is to construct two matrices from the input network: the topology matrix and the property similarity matrix. Topology matrix is a 0–1 adjacency matrix which represents the connections among nodes. The property similarity matrix contains the property similarities between each pair of nodes, which is calculated by a predefined similarity measurement. Given a particular machine learning or data mining task, users can flexibly choose or design the property similarity measurement. For example, in order to serve a geographic mining task, the geography related properties (address, geographic tag) should be more important than other properties. How to calculate the node property similarities is not the focus of this paper, as it varies to different networks and applications. We assume the property similarity matrix has been given by domain experts. For the topology matrix, we utilize the random walk algorithm to generate a set of node sequences. A topology-derived objective function is proposed to capture topology information preserved in the node sequences. For the property similarity matrix, we extract a set of constraints, which ensures the embedding vectors of nodes with similar properties should be distributed closely in the learned representation space. Here we define two kinds of constraints: inequality constraints and numeric constraints. We also propose a property-derived objective function for each type of the constraints. Finally, the topology-derived and property-derived objective functions are jointly optimized sharing same parameters.

Fig. 1.
figure 1

Framework of PPNE.

Full size image

4.2 Topology-Derived Objective Function

Following the idea of DeepWalk [16], we assume that nodes with similar topology context tend to be similar. With such an assumption, we aim to maximize the likelihood of the prediction of the center node given a specific contextual node. The contextual nodes of a center node are defined as a fixed-size window w of its previous nodes and after nodes in the node sequences generated by random walk. We propose an novel negative sampling based optimization objective function in which the node representation vectors are considered as the parameters. In the optimization procedure, the representation vectors are updated and the finally learned vectors preserve the topology information.

Firstly, the network topology matrix T is converted into a set of node sequences \(\mathcal {C}\) by random walk. In a random walk iteration, for each node n in V, we generate a node sequence of length t which starts from node n. This iteration will repeat r times to generate enough sequences.

Based on the node sequences \(\mathcal {C}\), we try to solve the following objective function:

$$\begin{aligned} \small maximize \ \ \ D_{T} = \prod _{\begin{array}{c} n \in \mathcal {C} \end{array}} \prod _{\begin{array}{c} z \in context(n) \end{array}} \prod _{\begin{array}{c} u \in \lbrace \lbrace n \rbrace \cup NEG(n) \rbrace \end{array}} p(u|z) \end{aligned}$$
(1)

Given a sampled center node n and its contextual nodes context(n), NEG(n) is the set of negative samples of the center node n with a predefined size ns. Nodes far away from the center node have a larger chance to be picked as the negative samples. p(u|z) defines the probability of the center node u given the contextual node z. Given the contextual node z, we aim to maximize the probability of the positive samples \(u \in \lbrace n \rbrace \), while minimize the probability of the negative samples \(u \in NEG(n)\).

For each node n in V, we design two corresponding vectors: the embedding vector and the parameter vector. The embedding vector \(\upsilon _{n}\) is the representation of node n when it is treated as the contextual node, while the parameter vector \(\theta _{n}\) is the representation of n when it is treated as the center node. In our model, p(u|z) is defined as

$$\begin{aligned} \small p(u|z)=\left\{ \begin{aligned} \sigma (\upsilon _{z}^\mathrm {T}\theta _{u}),&\ \ \ \ \ \ \ \ \ \ L^{n}(u) = 1&\\ 1 - \sigma (\upsilon _{z}^\mathrm {T}\theta _{u}),&\ \ \ \ \ \ \ \ \ \ L^{n}(u) = 0&\\ \end{aligned} \right. \end{aligned}$$

in which \(\sigma \) is the sigmoid function:

$$\begin{aligned} \small \sigma (\upsilon _{z}^\mathrm {T}\theta _{u}) = \frac{1}{1 + e^{-(\upsilon _{z}^\mathrm {T}\theta _{u})}}&\end{aligned}$$

\( L^{n}(u)\) is an indicator function:

$$\begin{aligned} \small L^{n}(u)=\left\{ \begin{aligned} 1,&\ \ \ \ \ \ \ \ \ \ u \in \lbrace n \rbrace&\\ 0,&\ \ \ \ \ \ \ \ \ \ u \in NEG(n)&\\ \end{aligned} \right. \end{aligned}$$

Moreover, p(u|z) can be represented as

$$\begin{aligned} \small p(u|z) = [\sigma (\upsilon _{z}^\mathrm {T}\theta _{u})] ^{L^{n}(u)} \cdot [1 - \sigma (\upsilon _{z}^\mathrm {T}\theta _{u})] ^ {1 - L^{n}(u)} \end{aligned}$$

Hence, the objective function can be rewritten as follows:

$$\begin{aligned} \small maximize \ \ \ D_{T} = \prod _{\begin{array}{c} n \in \mathcal {C} \end{array}} \prod _{\begin{array}{c} z \in context(n) \end{array}} \prod _{\begin{array}{c} u \in \lbrace \lbrace n \rbrace \cup NEG(n) \rbrace \end{array}}&\nonumber \\ [\sigma (\upsilon _{z}^\mathrm {T}\theta _{u})] ^{L^{n}(u)} \cdot [1 - \sigma (\upsilon _{z}^\mathrm {T}\theta _{u})] ^ {1 - L^{n}(u)} \end{aligned}$$
(2)

By maximizing the likelihood of prediction of positive samples and minimizing the likelihood of negative samples, the proposed objective function encodes the topology information into the representation vectors of nodes.

Compare to DeepWalk, a popular topology-derived method, the proposed model is faster and more effective. Firstly, the objective function of DeepWalk is defined as

$$\begin{aligned} \small maximize \ \ \ D = \prod _{\begin{array}{c} n \in \mathcal {C} \end{array}} \prod _{\begin{array}{c} z \in context(n) \end{array}} p(z|n) \end{aligned}$$

The hierarchical softmax method is introduced to design the probability p(z|n), which reduces the computational complexity of calculating p(z|n) from O(|V|) to \(O(\log _2 |V |)\). Hence the computational complexity of DeepWalk is \(O( |\mathcal {C}| \cdot 2 w \cdot \log _2 |V|)\), in which w is the window size of the contextual nodes. In the objective function (2), the computational complexity is further reduced to \(O( |\mathcal {C}| \cdot 2 w \cdot (ns + 1))\), in which ns is a constant number irrelevant to the size of network. Thus the model training time is significantly reduced. Secondly, by choosing the negative samples according to their distances from the center node, the rich global topology information is integrated into our model. This strategy ensures our model not only considers the local information of the contextual nodes, but also can encode the information of the nodes which have farther topological distance from the center node.

4.3 Property-Derived Objective Function

In this subsection we present the details of the property-derived objective function. In natural language processing area, SWE [12] and RC-NET [23] incorporate the semantic knowledges into the word embedding process. Inspired by the above works, we propose two ways to extract constraints from the property similarity matrix P. Based on these constraints, we introduce the property-derived objective functions.

Related works incorporate the original property features of single type into the embedding process [25]. Different from such works, in our approach the property matrix \(P \in \mathbb {R}^{|V| \times |V|} \) contains the property similarity scores between each pair of nodes, which is calculated by a predefined similarity measurement. According to the requirements of targeting data mining tasks and the types of networks, users can flexibly design an appropriate property similarity measurement to cast the input network into the property similarity matrix. This strategy guarantees the proposed embedding framework can be applied on various kinds of networks and serves different types of data mining tasks.

Inequality Constraints. The first way we proposed to utilize the property similarity matrix P is to extract a set of inequalities from matrix P as the constraints. For each node n in V, according to the matrix P, we construct its most similar node set \(pos_{n}\) and most dissimilar node set \(neg_{n}\). \(pos_{n}\) contains top k similar nodes of n and \(neg_{n}\) contains top k dissimilar nodes, where \(k \ll |V|/2 \). With \(pos_{n}\) and \(neg_{n}\), we can obtain the following inequalities for node n:

$$\begin{aligned} P_{np} > P_{nq} ~~~ p \in pos_{n},q \in neg_{n}&\end{aligned}$$

in which \(P_{np}\) is the property similarity score between node n and p. The final representation vectors of the corresponding nodes should satisfy the following constraint:

$$\begin{aligned} sim(\upsilon _{n},\upsilon _{p}) > sim(\upsilon _{n},\upsilon _{q}) ~~~ p \in pos_{n} ~ q \in neg_{n}&\end{aligned}$$

in which \(\upsilon _{n}\) is the embedding vector of node n. \(sim(\upsilon _{n},\upsilon _{p})\) is the cosine similarity between the embedding vectors of node n and p. After constructing such constraints for all the nodes, we can obtain a set of constraints \(\mathcal {S}\), which contains triples in the form of \( \lbrace (i, j, k), ~ sim(\upsilon _{i},\upsilon _{j}) > sim(\upsilon _{i},\upsilon _{k}) \rbrace \).

Based on the constraint set \(\mathcal {S}\) and the node sequences \(\mathcal {C}\), we propose the following objective function to force the embedding vectors to satisfy the extracted constraints:

$$\begin{aligned} minimize \ \ D_{I} = \sum _{n \in \mathcal {C}} \sum _{\begin{array}{c} (i,j,k) \in \mathcal {S} \end{array}} I_{i,j,k}(n) \cdot f(i,j,k) \end{aligned}$$
(3)

where \(I_{i,j,k}(n)\) is an indicator function:

$$\begin{aligned} I_{i,j,k}(n) = \left\{ \begin{aligned} 1, ~~~&i = n ~ or ~ j = n ~ or ~ k = n&\\ 0, ~~~&else&\\ \end{aligned} \right. \end{aligned}$$

The function f(.) is a normalization hinge loss function:

$$\begin{aligned} f(i,j,k) = max(0, sim(\upsilon _{i},\upsilon _{k}) - sim(\upsilon _{i},\upsilon _{j}))&\end{aligned}$$

The objective function \(D_{I}\) ensures that the similarity score between embedding vectors of two nodes with similar properties should be no less than the nodes with dissimilar properties. For a sampled node in the sequences, we select the inequality constraints associated with this node and judge whether the current embedding vectors of the corresponding nodes satisfy these constraints. If the constraints are satisfied, these embedding vectors will remain unchanged, otherwise they will be updated towards the direction of satisfying these constraints.

Numeric Constraints. The second way of utilizing the matrix P is to consider the property similarity scores as the numeric constraints for refining the network embedding process. The motivation is that the learned representation vectors of two nodes should be distributed closer to each other if they have similar properties, namely their property similarity score in P is high.

Similar to the generation process of the inequality constraints, according to the matrix P, for each node n in |V| we select its top k similar and dissimilar node sets as the \(pos_{n}\) and \(neg_{n}\). Nodes in the two sets own strong discrimination ability over node n. Based on the property similarity matrix P and node sequences \(\mathcal {C}\), we propose the following objective function:

$$\begin{aligned} minimize ~~ D_{N} = \sum _{n \in \mathcal {C}}\sum _{\begin{array}{c} i \in \lbrace pos_{n} \cup neg_{n} \rbrace \end{array}} P_{ni}d(\upsilon _{n},\upsilon _{i}) \end{aligned}$$
(4)

in which \(d(\upsilon _{i},\upsilon _{j})\) is the Euler distance function to measure the distance between the embedding vectors of node i and j: \(d(\upsilon _{i},\upsilon _{j}) = \sqrt{(\upsilon _{i} - \upsilon _{j})^{T}(\upsilon _{i} - \upsilon _{j})}\).

One can see that the optimization process of the objective function \(D_{N}\) is affected by the property similarity score \(P_{ni}\), and the distances between nodes with similar properties decrease faster than that between dissimilar ones. Hence, \(D_{N}\) can ensure that nodes with similar properties are distributed closer in the learned embedding space.

4.4 Joint Optimization

In this subsection, we show the joint optimization process of the topology-derived and property-derived objective functions. Here we propose two types of PPNE model: \(\mathrm {PPNE_{ineq}}\) and \(\mathrm {PPNE_{num}}\). \(\mathrm {PPNE_{ineq}}\) aims to jointly optimize the topology-derived objective function \(D_{T}\) and the inequality constraint based objective function \(D_{I}\). \(\mathrm {PPNE_{num}}\) aims to jointly optimize \(D_{T}\) and the property-derived function \(D_{N}\) with numeric constraints. We utilize the SGD algorithm to solve the optimization problems. Firstly we introduce the optimization process of \(D_{T}\), \(D_{I}\) and \(D_{N}\) separately, and the derivative results are utilized to jointly update the embedding vectors.

To maximize the objective function \(D_{T}\) in the Formula (2), we try to maximize the following log-likelihood function:

$$\begin{aligned} \small&\log D_{T} = \sum _{\begin{array}{c} n \in \mathcal {C} \end{array}}\sum _{\begin{array}{c} z \in context(n) \end{array}} \sum _{\begin{array}{c} u \in \lbrace \lbrace n \rbrace \cup NEG(n) \rbrace \end{array}}&\\&\quad \quad \quad \quad \lbrace L^{n}(u) \cdot \log [\sigma (\upsilon _{z}^\mathrm {T}\theta _{u})] + [1 - L^{n}(u)] \cdot \log [1 - \sigma (\upsilon _{z}^\mathrm {T}\theta _{u})] \rbrace&\end{aligned}$$

Given a sample of (n, context(n)) in \(\mathcal {C}\), with sampled z and u, we set

$$\begin{aligned} \small \mathcal {L} = L^{n}(u) \cdot \log [\sigma (\upsilon _{z}^\mathrm {T}\theta _{u})] + [1 - L^{n}(u)] \cdot \log [1 - \sigma (\upsilon _{z}^\mathrm {T}\theta _{u})] \end{aligned}$$
(5)

Firstly we calculate the following partial derivative:

$$\begin{aligned} \small \small \frac{\partial \mathcal {L}}{\partial \theta _{u}} = [L^{n}(u) - \sigma (\upsilon _{z}^\mathrm {T}\theta _{u})]\cdot \upsilon _{z}&\end{aligned}$$

Thus \(\theta _{u}\) can be updated by

$$\begin{aligned} \theta _{u} = \theta _{u} + \eta [L^{n}(u) - \sigma (\upsilon _{z}^\mathrm {T}\theta _{u})]\cdot \upsilon _{z} \end{aligned}$$
(6)

where parameter \(\eta \) is the learning rate. In Formula (5), \(\theta _{u}\) and \(\upsilon _{z} \) are symmetric, so \(\upsilon _{z}\) can be updated as

$$\begin{aligned} \upsilon _{z} = \upsilon _{z} + \eta \sum _{\begin{array}{c} u \in \lbrace \lbrace n \rbrace \cup NEG(n) \rbrace \end{array}} [L^{n}(u) - \sigma (\upsilon _{z}^\mathrm {T}\theta _{u})]\cdot \theta _{u} \end{aligned}$$
(7)

Then we show the optimization process of \(D_{I}\) in Formula (3). For convenience, we use \(s_{np}\) to represent \(sim(\upsilon _{n},\upsilon _{p})\). Given a sampled (n, context(n)) in \(\mathcal {C}\), firstly we calculate the partial derivative of \(D_{I}\):

$$\begin{aligned} \small \frac{\partial D_{I}}{\partial \upsilon _{n}}&= \sum _{\begin{array}{c} (i,j,k) \in S \end{array}} f' \cdot (\delta _{ik}(n)\frac{\partial s_{ik}}{\partial \upsilon _{n}} - \delta _{ij}(n)\frac{\partial s_{ij}}{\partial \upsilon _{n}}) \end{aligned}$$
(8)

in which \(\delta _{ij}(n)\) are defined as

$$\begin{aligned} \delta _{ij}(n) = \left\{ \begin{aligned} 1, ~~~&i = n ~ or ~ j = n&\\ 0, ~~~&others&\\ \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} f' = \left\{ \begin{aligned} 1, ~~~&s_{ij} < s_{ik}&\\ 0, ~~~&s_{ij} \ge s_{ik}&\\ \end{aligned} \right. \end{aligned}$$

The partial derivatives in Formula (8) can be easily calculated. For example, given a constraint contains n and assume \(i=n\), we can get

$$\begin{aligned} \frac{\partial s_{ij}}{\partial \upsilon _{n}} = \frac{\partial s_{nj}}{\partial \upsilon _{n}} = -\frac{s_{nj}\upsilon _{n}}{|\upsilon _{n}|^{2}} + \frac{\upsilon _{j}}{|\upsilon _{n}||\upsilon _{j}|}&\end{aligned}$$

For the sample (n, context(n)), the embedding vectors of node n will be updated as follows:

$$\begin{aligned} \upsilon _{n} = \upsilon _{n} - \beta \cdot \eta \sum _{\begin{array}{c} (i,j,k) \in S \end{array}} \frac{\partial D_{I}}{\partial \upsilon _{n}} \end{aligned}$$
(9)

in which \(\beta \) is the balance parameter to control the weight of the node properties in the embedding process.

Here we present the optimization process of \(D_{N}\) in Formula (4). Given a sampled (n, context(n)), we calculate the partial derivative of \(D_{N}\):

$$\begin{aligned} \small \frac{\partial D_{N}}{\partial \upsilon _{n}} = \sum _{\begin{array}{c} i \in \lbrace pos_{n} \cup neg_{n} \rbrace \end{array}}P_{ni} \cdot (\upsilon _{n} - \upsilon _{i}) [(\upsilon _{n} - \upsilon _{i})^{T}(\upsilon _{n} - \upsilon _{i})]^{-\frac{1}{2}}&\end{aligned}$$

The embedding vector of node n will be updated as follows:

$$\begin{aligned} \upsilon _{n} = \upsilon _{n} - \beta \cdot \eta \sum _{\begin{array}{c} i \in \lbrace pos_{n} \cup neg_{n} \rbrace \end{array}} \frac{\partial D_{N}}{\partial \upsilon _{n}} \end{aligned}$$
(10)

Finally, Algorithm 1 shows the joint optimization process of \(\mathrm {PPNE_{ineq}}\) model. For \(\mathrm {PPNE_{num}}\) model, we only need to modify line 14 to update embedding vector following Formula (10).

figure a

4.5 Discussion

We discuss several issues of the PPNE model in detail.

Choice of the Measurements. We choose the cosine similarity measurement to measure the similarity between embedding vectors, and the Euler distance to measure the distance between embedding vectors. The proposed model is still effective with these simple and popular measurements, which can better show the generality of our model.

Property Similarity Matrix. The property similarity matrix of the input network is the basis of the proposed model. For a large network, the calculation process of the pairwise similarities between nodes seems to be time consuming. However there are several effective strategies which can significantly reduce the time cost. Firstly, we can precompute the norm of each vector and store it using a lookup table. Secondly, this process can be implemented easily in parallel. These improvements has been implemented in a popular machine learning toolkit: scikit-learnFootnote 1. With scikit-learn, it takes only several hours to construct the similarity matrix for the largest network in our experiments.

5 Experiments

In this section, firstly we introduce the datasets and baseline methods used in this work. Then we thoroughly evaluate our proposed methods through two classic data mining tasks on four paper citation networks and one social network. Finally we analyze the quantitative experimental results and investigate the sensitivity across parameters.

5.1 Experiment Setup

Datasets. In order to thoroughly evaluate the proposed methods, we conduct experiments on four paper citation networks and one social network with different scale of nodes. Table 1 shows the detailed information of the five datasets. The four paper citation networks are CiteseerFootnote 2, Cora (see Footnote 2), PubMed (see Footnote 2) [18] and DBLPFootnote 3 [9]. In the paper citation networks, nodes refer to papers and links refer to the citation relationships among papers. Papers are classified into several categories according to the belonged domains. In Citeseer, Wiki and PubMed networks, each paper has abstract as its property, and in DBLP dataset, each paper has properties like title, authors, publication venue and abstract. Google+ (see Footnote 3) is a social network in which nodes refer to users and links represent friend relationships among users. Each user has gender, job title, university and workplace as his properties. The institution of each user is considered as his category. We select top 6 popular institutions as the final categories. For the networks with single type of node property (Citeseer, Cora and PubMed), the property similarity matrix contains the pairwise cosine similarity scores between nodes. For the networks with richer and more complex node properties (DBLP and Google+), we calculate the cosine similarity between nodes over each type of properties separately, and then weighted linearly combine them. The weights are tuned in a few random sampled instances.

Embedding Methods. We compare PPNE with the following baseline methods:

  • DeepWalk: DeepWalk [16] is a topology-only network embedding method, which introduces the Skip-Gram algorithm to learn the node representation vectors.

  • LINE: LINE [19] is a popular topology-only network embedding method, which considers the first-order and second-order proximities information.

  • Property Features: In this method nodes are represented by the property features.

  • Naive Combination: We simply concatenate the vectors from both Property Features and DeepWalk as the final representation vectors.

  • TADW: TADW [25] incorporates the text features of each node into the embedding process under a framework of matrix factorization.

  • \(\mathbf {PPNE_{ineq}:}\) \(\mathrm {PPNE_{ineq}}\) is the PPNE model with the inequality constrains.

  • \(\mathbf {PPNE_{num}:}\) \(\mathrm {PPNE_{num}}\) is the proposed PPNE model with the numeric constrains.

Table 1. Statistics of the datasets
Full size table

Parameter Setup. For all datasets, the dimension of the learned representation vector is set to d = 160. In DeepWalk method, parameters are set as window size w = 10, walks per node r = 80 and walk length t = 40. In LINE method, the parameters are set as follows: negative = 5 and samples = 10 million. In Property Features method, we reduce the dimension of node property features to 160 via SVD [7] algorithm. In TADW method the parameters are set to the same as given in the original paper. In PPNE method, the number of negative samplings \(ns = 5\), the balance parameter \(\beta = 0.3\), learning rate \(\eta = 0.1\), walks per node \(r = 80\), walk length t = 40.

5.2 Multi-class Classification

We utilize the representation vectors generated by various network embedding methods to perform multi-class node classification task. The representation vector of each node is treated as its feature vector, and then we use a linear support vector machine model [3] to return the most likely category. The classification model is implemented using scikit-learn. For each dataset, a portion (\(T_{r}\)) of the labeled nodes are randomly picked as the training data, and the rest of nodes are the test data. We repeat this process 10 times, and report the average performance in terms of classification accuracy.

Table 2. Classification performance (Accuracy) on four datasets.
Full size table

Table 2 shows the classification performance on four datasets. Here “-” means TADW can not handle large networks due to its very time and memory consuming process of matrix factorization. From Table 2, one can see PPNE consistently outperforms other baseline methods. For Citeseer dataset, \(\mathrm {PPNE_{ineq}}\) achieves the best performance and beat the best baseline TADW by 5%. In Wiki dataset, \(\mathrm {PPNE_{ineq}}\) beat baselines by 3%. \(\mathrm {PPNE_{ineq}}\) improves the classification performance by 5% on DBLP dataset and \(\mathrm {PPNE_{num}}\) beat the best baseline by nearly 6% on Google+ dataset. Besides, the improvement over TADW is statistically significant (sign test, p-value \(<0.05\)) on Citeseer and Wiki datasets. \(\mathrm {PPNE_{ineq}}\) extracts the inequalities between nodes from the property similarity matrix, which is a robust method to represent the similarity information. As a more delicate method, the optimization process of \(\mathrm {PPNE_{num}}\) is affected by the numeric similarity scores, which essentially introduces the degree of inequalities between nodes. If these degrees match the label information, such as in Google+, \(\mathrm {PPNE_{num}}\) performs better than \(\mathrm {PPNE_{ineq}}\), otherwise it may introduce noise into \(\mathrm {PPNE_{num}}\) as shown on Citeseer, Wiki and DBLP datasets.

The experimental results demonstrate the effectiveness of the proposed embedding methods. By incorporating the network topology and node property information into a unified embedding framework, the quality of the learned representation vectors are improved. Meanwhile, PPNE performs consistently better when training data is small.

Parameter Sensitivity Analysis. PPNE has two major parameters: dimension d and the balance parameter \(\beta \). We fix the training proportion to 30% and test the classification accuracies with different d and \(\beta \). We let \(\beta \) varies from 0.1 to 0.9 and d varies from 10 to 500. Figure 2 shows the classification performances with different \(\beta \) and d on Citeseer and Wiki datasets. With the increase of \(\beta \), the classification accuracy first increases and then decreases. When we increase the dimension d, the classification accuracy first increases and then keeps stable. It shows that, PPNE achieves the best performance when \(\beta \) varies within a reasonable range and d is larger than a specific threshold.

Fig. 2.
figure 2

The classification performance w.r.t the balance parameter \(\beta \) and dimension d.

Full size image

5.3 Link Prediction

Given a snapshot of the current network, the link prediction task refers to predicting the edges that will be added in the future time [1, 13]. Link prediction can show the predictability of different network embedding methods. To process the link prediction task, a portion of existing links (50%) are removed from the input network. Based on the residual network, node representation vectors are learned by different embedding methods. Node pairs in the removed edges are considered as the positive samples. We also randomly sample the same number of node pairs that are not connected as the negative samples. Positive and negative samples form a balanced data set. Given a node pair in the samples, the cosine similarity score is calculated according to their representation vectors. Area Under Curve (AUC) [5] is used to evaluate the consistency between the labels and the similarity scores of the samples. We also choose \(Common \ Neighbors\) as a baseline method because it has been proved as an effective method [11, 15].

Table 3. Link prediction performance (AUC score)
Full size table

Table 3 shows the experimental results. One can see that PPNE outperforms other embedding methods. Compare to TADW, \(\mathrm {PPNE_{ineq}}\) improves the AUC score by 4% in Citeseer and 5% in PubMed, which demonstrates the effectiveness of PPNE in learning good node representation vectors for the task of link prediction.

6 Conclusion

This paper proposes a general network embedding model PPNE to incorporate both network topology information and node property information. We formulate the learning of property preserving network embedding as a joint optimization problem. Firstly we propose the topology-derived objective function and property-derived objective function, and then the above objective functions are optimized jointly sharing the same parameters. Experimental results on the multi-class classification and link prediction tasks over five datasets demonstrate the effectiveness of PPNE.