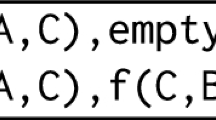Learning Constraint Satisfaction Problems: An ILP Perspective

Abstract

We investigate the problem of learning constraint satisfaction problems from an inductive logic programming perspective. Constraint satisfaction problems are the underlying basis for constraint programming and there is a long standing interest in techniques for learning these. Constraint satisfaction problems are often described using a relational logic, so inductive logic programming is a natural candidate for learning such problems. So far, there is however only little work on the intersection between learning constraint satisfaction problems and inductive logic programming. In this article, we point out several similarities and differences between the two classes of techniques that may inspire further cross-fertilization between these two fields.

1 Introduction

Constraint programming (CP) is an active research area in the field of artificial intelligence. It is concerned with solving combinatorial problems that are formalised as constraint satisfaction problems (CSPs). CP has been used in numerous applications in domains such as time-tabling, scheduling, packing, bioinformatics, etc.

On the other hand, inductive logic programming (ILP) is a research area that has studied the learning of logic programs and relational descriptions for more than twenty years now. ILP has also been applied in a wide variety of contexts, including bio- and chemo-informatics, natural language processing, engineering, etc.

CP has – like ILP – its origins in the field of logic programming and uses a declarative representation. However, while learning traditional logic programs is popular (thanks to ILP), the learning of constraint programs and CSPs has received much less attention, even though several techniques for learning CSPs have been contributed in the past ten years, cf. [1, 5, 7, 10, 19, 20]. The motivation for learning is that formulating the CSP for a particular application is a non-trivial task.

Most of the techniques to learn logic programs and to learn constraint satisfaction problems have been developed independently of one another (but see [19]). This is surprising as both problems are – as we will show – essentially logical and relational learning problems. This paper contributes to bridging the gap between CP and ILP by surveying the CP-learning techniques from the perspective of ILP. This will allow us to point out differences and similarities between the two approaches and to also indicate opportunities for further research.

This paper is organized as follows. In Sect. 2, we introduce the relevant context on the modelling of constraint satisfaction problems (CSPs). In Sect. 3, we introduce the task of learning CSPs, and we relate this task to ILP in Sect. 4. In Sect. 5, we give an overview of existing systems for solving this task, and we describe them in terms of ILP concepts. Section 6 provides a summary and discussion of the different systems and Sect. 7 concludes this paper.

2 Constraint Satisfaction Problems

Constraint programming (CP) is concerned with solving constraint satisfaction problems (CSPs). A CSP is a constraint network $p=(\mathcal{V},D,\mathcal{C})$, defined by

• a finite set of variables $\mathcal{V} = \{v_1, \ldots , v_n\}$;

• a domain D, which maps every variable $v\in \mathcal{V}$ to a set of possible values D(v); and

• a finite set of constraints $\mathcal{C} = \{c_1, \ldots , c_n\}$, where each constraint $c_i \in \mathcal{C}$ is essentially a relation $c_i \subseteq D(v_{i_1}) \times \cdots \times D(v_{i_{m_i}})$, that can be specified extensionally or intensionally.

The key question of constraint satisfaction problems is to find an assignment of values to the variables so that all constraints in the constraint network are satisfied. The constraints hence form one big conjunction. Let us now illustrate CSPs using three well-known examples: n-queens, sudoku and graph coloring.

In n-queens, the goal is to put n queens on an n-by-n board, so that no queen attacks another one (queens can attack if they are in the same row, column or diagonal, as per the chess rules), cf. Figs. 1 and 2. The valid solutions of the n-queens problem are completely determined by the value of n.

Fig. 1.

A 4$\,\times \,$4 chessboard

Fig. 2.

...and a 4-queens solution.

In Sudoku, one is given a 9$\,\times \,$9 grid. The goal of a Sudoku is to enter in each cell a number between 1 and 9, such that no number occurs twice in the same row, column or block. In a Sudoku puzzle, a number of values are already given while guaranteeing that there is a unique solution to the puzzle, cf. Figs. 3 and 4. In a CSP these initial values can be encoded as additional constraints.

Fig. 3.

An unsolved 3$\,\times \,$3 Sudoku...

Fig. 4.

...and its solution.

In graph coloring, one is given a graph and a set of colors. The goal is to assign a color to each node in the graph such that adjacent nodes have a different color. In a CSP the graph structure can be encoded by using auxiliary variables and constraints on them. An example is shown in Figs. 5 and 6.

Fig. 5.

An uncolored graph

Fig. 6.

... and a valid 3-coloring. (Color figure online)

CSPs can be expressed in terms of local constraints. These constraints express simple relationships between a bounded number of individual variables, for example, $v_1 = v_2, v_3 \not = v_4, v_5 = v_6 + v_7 + v_8$.

However, the number of such constraints in a CSP can become very large. CSPs are therefore often expressed in terms of global constraints. What we call a global constraint is in fact a class of constraints involving any (unbounded) number of variables. The semantics of the global constraint is given by a Boolean function of unbounded arity; thus an instance of the global constraint can be posted on any number of variables and may represent a whole set of local constraints. Global constraints have two main advantages: they simplify the model by reducing the number of constraints, and solvers can more easily exploit the relationships between the constraints in the set. The standard example of a global constraint is the alldifferent constraint. For example, the constraint $alldifferent ([v_1, v_2, v_3])$ is equivalent to the set $v_{1} \not = v_{2}, v_{1} \not = v_{3}, v_{2} \not = v_{3}$. Additionally, higher level languages for expressing CSPs (such as MiniZinc [23] and B-prolog [28]) offer constructs for compactly expressing loops (e.g., foreach).

Listing 1.1 shows an example of an n-queens constraint specification in B-prolog. It uses a list of variables Q, with N such variables (line 2), each with a domain of values from 1 to N (line 3). In this representation, the assignment $Q[i] = j$ means that the queen on row i is at column j (using the knowledge that there can be only one queen per row). Lines 5–9 represent the constraints. Line 5 uses the global alldifferent constraint and states that no two queens can be on the same column. Line 6 uses a foreach construct to state that queens can not be on a $\setminus$-diagonal (example: $Q[2]=2$ and $Q[3]=3$) while line 8 states the same for a /-diagonal (example: $Q[3]=3$ and $Q[4]=2$).

This model contains both a choice on how to represent the queens, as well as how to formulate the constraints. Other representations for the queens are also possible, such as one Boolean variable per board position or one integer variable per column. Other ways to formulate the constraints are also possible, such as with a decomposition of the alldifferent constraints.

In this paper, we will review different techniques that have been investigated for learning constraints, as well as their relationship to ILP.

3 The Learning Task

In its basic form, the learning task consists in learning the constraints of a CSP from example assignments. Given is

• a finite set of variables $\mathcal{V} = \{v_1, \ldots , v_n\}$;

• a domain D that maps every variable $v\in \mathcal{V}$ to a set of possible values D(v);

• a set of positive and negative examples that take the form of assignments $\theta = \{v_1 = a_1, \ldots , v_n = a_n\}$ to the variables $\mathcal{V}$ that satisfy or violate the CSP;

• a language of possible constraints $\mathcal{L}_\mathcal{C}$, such that each $c \in \mathcal{L}_\mathcal{C}$ is of the form $r(t_1, \ldots ,t_m)$ with r / m a relation of arity m defined in the background, where the terms $t_i$ correspond to a constant, a variable in $\mathcal{V}$ or a list of variables that are a subset of $\mathcal{V}$.¹

The goal then is to find a hypothesis $h \subseteq \mathcal{L}_\mathcal{C}$ that is satisfied by all positive examples and no negative examples.

For the n-queens problem in Listing 1.1, the set of variables would have cardinality n, and the domain for each would be the set $\{1, \ldots , n\}$ (note how the variable representation is part of the learning problem). For 4-queens, a positive example would be $\{Q_1 = 3, Q_2=1, Q_3=4, Q_4=2\}$ and a negative example would be $\{Q_1 = 3, Q_2=3, Q_3=4, Q_4=2\}$; example constraints could be binary predicates for equality and inequality; ternary predicates for addition and multiplication and a unary predicate for the alldifferent constraint, among others.

Observations. Several observations can be made about this problem statement:

• CSPs are conjunctive descriptions and CP is heavily focussed on dealing with conjunctions as these impose strong constraints that – unlike disjunctive descriptions – propagate well in the search;

• The above definition assumes that all variables are explicit, and no new (auxiliary) variables are introduced to formulate certain constraints;

• Unlike in traditional machine learning and ILP, one typically assumes a noise-free setting;

• The number of constraints in CSPs can be quite large, especially when considering ground representations in which foreach loops are unrolled; it is typically much larger than the typical clauses learned in ILP; for instance, the Sudoku problem involves $927=36\times 27$ constraints.

• Redundancy amongst constraints is a key problem. For instance, the constraints $x = y$ and $y =z$ imply $x=z$. Together with the high number of variables that is available, this causes severe problems for traversing the search space as there are many syntactic variants. These are hypotheses that are formulated differently and hence syntactically different (like $x = y \wedge y =z$ and $x = y \wedge y =z \wedge x =z$) but semantically equivalent. Clever ways for dealing with this are necessary.

• Standard ILP systems often start from a large set of positive and negative examples. The number of solutions to a CSP problem is often small and it can already be hard to generate a single positive one. Therefore, several researchers are learning CSPs from queries [7, 8] and from small sets of examples [5, 19]; these queries, as we shall discuss, do not always ask for the classification of a complete example (consisting of a value assignment to all variables in $\mathcal{V}$).

4 Relation to Inductive Logic Programming

Inductive Logic Programming (ILP) is a machine learning methodology that uses first-order logic to represent the data as well as the learned hypotheses. This use of first-order logic sets it apart from other machine learning techniques. It is often used in a concept learning setting, where the goal is to find a hypothesis that covers all of the positive examples and none of the negative ones. See [13] for a gentle introduction to ILP.

In the ILP literature, there is a well-known distinction between learning from entailment and learning from interpretations [12], which is also quite relevant in the present context. When learning from entailment, each example is presented as a ground fact and additional knowledge about the examples and the domain is provided as background knowledge. The goal is to find (a set of) clauses that, combined with the background knowledge, logically entail the positive examples, and do not entail the negative examples.

Several state of the art CSP learning approaches (such as Conacq [10] and QuAcq [7]) map directly to this setting. However, in contrast to traditional ILP, they focus on learning a single clause.

The CSP $p=(\mathcal{V},D,\mathcal{C})$ can be represented by a single conjunctive clause of the following form:

$$\begin{aligned} p(v_1,\ldots ,v_n) \text { :- }&d(v_1), \ldots , d(v_n), \\&c_1(v_{{c_1}_1}, v_{{c_1}_2}, \ldots , v_{{c_1}_r}), \\&\ldots , \\&c_m(v_{{c_m}_1}, v_{{c_m}_2}, \ldots , v_{{c_m}_s}). \end{aligned}$$

where $\mathcal{V} = \{v_1, \ldots , v_n\}$, $d(v_x)$ represents the domain of $v_x$ and there are m constraints $c_i$, each involving a subset of the variables in $\mathcal{V}$. In this setting, learning a CSP corresponds to learning a single clause for which in addition $vars(head) = vars(body)$ as no existential variables are allowed in the body of the clause. The definition of the $c_i$ is then part of the background knowledge; cf. below. The goal is then to learn the definition of $p(v_1,\ldots ,v_n)$ given this background knowledge and positive and negative examples. Observe that this formulation of the constraint learning problem is closely related to the learnability results for single rules by [18] or conjunctive concepts in structural domains by [17], two settings that have been well-studied within the context of ILP.

Example. For the n-queens problem with $n=4$, we could have the positive example queens4(2, 3, 1, 4) and the negative example queens4(2, 1, 3, 4). The background knowledge consists of the declaration of the domains, equality operators and simple mathematical functions.

The goal is to find a set of clauses of the form

$$\begin{aligned} queens4(q_1, q_2, q_3, q_4) \text { :- } body(q_1, q_2, q_3, q_4) \end{aligned}$$

such that the body of at least one of the clause is satisfied for the substitution $\{ q_1/2, q_2/3, q_3/1, q_4/4 \}$ and the body of none of the clauses is satisfied for the substitution $\{ q_1/2, q_2/1, q_3/3, q_4/4 \}$.

The n-queens problem for $n=4$ can be formulated as

$$\begin{aligned} queens4( q_1, q_2, q_3, q_4 ) \text { :- }&q_1 \in [1,4], q_2 \in [1,4], q_3 \in [1,4], q_4 \in [1,4], \\&q_1 \not = q_2, q_1 \not = q_3, q_1 \not = q_4, q_2 \not = q_3, q_2 \not = q_4, q_3 \not = q_4, \\&| q_1 - q_2 | \not = 1, | q_1 - q_3 | \not = 2, | q_1 - q_4 | \not = 3, \\&| q_2 - q_3 | \not = 1, | q_2 - q_4 | \not = 2, | q_3 - q_4 | \not = 1. \end{aligned}$$

The second line could be replaced with $alldifferent (q_1,q_2,q_3,q_4)$ if that constraint is available.

Alternatively, the learning of CSPs can also be viewed as a learning from interpretations task as originally tackled in the Clausal Discovery system Claudien [14]. In this approach an example is a set of ground facts (typically a Herbrand interpretation). This set is a complete description of the knowledge about the example, that is, facts that are not in the example are considered to be false. In this setting, there is no explicit target predicate such as queens.

Furthermore, a hypothesis H is said to cover an example e if the example e is a model of H. Hypotheses are represented in clausal logic, that is, Claudien learns a conjunctive set of clauses of the form $h_1 \vee \cdots \vee h_m \leftarrow b_1 \wedge \cdots \wedge b_n$, where the $h_i$ and $b_j$ are first-order terms. All variables in such a clause are universally quantified.

Also with this representation, it is possible to represent a CSP $p=(\mathcal{V},D,\mathcal{C})$. The form that this could take is to add a predicate $v_i/1$ to represent each variable in $\mathcal{V}$ and then employ for each variable $v_i \in \mathcal{V}$ the following clauses:

$$v_i(X) \wedge v_i(Y) \rightarrow X=Y$$

$$v_i(e_{i,1}) \vee \cdots \vee v(e_{i,i_n})$$

with $D(v_i) = \{e_{i,1}, \ldots , e_{i,i_n}\}$ the domain of the variable $v_i$. These clauses guarantee that any model will have to take exactly one value e for each variable $v \in \mathcal{V}$. Furthermore, for each constraint $c_j$ we add the clause:

$$ v_1(X_1) \wedge v_2(X_2) \wedge \cdots \wedge v_n(X_n) \rightarrow c_j(X_1, X_2, \ldots , X_n) $$

where $X_i$ are the different variables involved in the constraint $c_j$. This constraint guarantees that any model of the theory will satisfy all the constraints in the CSP. Notice again that we assumed here that the number of variables is given and fixed. If so, the learning setting is essentially propositional and closely related to that of Valiant’s seminal PAC-learning setting [27]. However, it is often possible to generalize the setting towards any number of variables as in the first order extension to j, k-clausal theories [15] of Valiant’s setting. It is this setting that formed the basis for learning from interpretations in ILP. We achieve this transformation by replacing each predicate $v_i(X)$ by a predicate v(i, X), that is, by making the variable index a variable itself. We illustrate this on the n-queens example.

Example. We can represent a solution to the 4-queens problem as the following interpretation:

$$\{ size(4), q(1,2), q(2,4), q(3,1), q(4,3) \}$$

where q(R, C) indicates that there is a queen at position (R, C) on the board. The set of clauses that fully determines the n-queens problem for examples represented in this language is

$$\begin{aligned} q(R_1, C_1) \wedge q(R_2, C_2) \wedge R_1 \not = R_2&\rightarrow C_1 \not = C_2 \\ q(R_1, C_1) \wedge q(R_1, C_1) \wedge R_1 \not = R_2&\rightarrow | R_1-R_2 | \not = | Q_1-Q_2 | \\ q(R_1, C_1) \wedge q(R_2, C_2) \wedge C_1 \not = C_2&\rightarrow R_1 \not = R_2 \\ size(N) \wedge q(R, C)&\rightarrow between(C,1,N) \\ size(N) \wedge q(R, C)&\rightarrow between(R,1,N) \\ size(N) \wedge between(R,1,N)&\rightarrow exists_{row}(R) \end{aligned}$$

where $exists_{row}$ is defined in the background knowledge as

$$\begin{aligned} q(R,C) \rightarrow exists_{row}(R). \end{aligned}$$

Similar clauses could be added for $exists_{col}$ but they are redundant. In the common CSP formulation of this problem (see Listing 1.1) the last 4 constraints are implicitly encoded in the representation of the variables as a list of row positions of the queens. Note that this definition can be learned from examples of different sizes.

One interesting consequence of these different representations is the following. The single clause representation is essentially a propositional one, while the representation as a conjunctive set of clauses (CNF) also allows for relational descriptions. The propositional techniques will learn constraints for one specific CSP instance (e.g., n-queens for one specific n or graph coloring for one specific graph), while relational approaches have the potential of learning the general CSP (e.g., n-queens for all n at the same time or graph coloring for arbitrary graphs). Indeed, given that in the single clause representation the arity of the target predicate is fixed and $vars(head) = vars(body)$, it is not possible to learn one clause that will work for any number of queens.

As an example, let us examine the graph coloring problem. Using a propositional representation (either the single clause or the propositional CNF one), one will essentially learn the constraints governing a particular graph. This is easy to see when considering the single clause representation. What will be learned will be a set of inequalities. Each such inequality corresponds to one edge in the graph. This is unusual from an ILP perspective, as there it would typically be assumed that the edges are given. If the edges are given, it is possible to learn the overall concept of graph-coloring using a clause such as

$$ edge(X,Y), color(X,CX), color(Y,CY) \rightarrow CX \not = CY$$

5 CSP Learning Systems

In the literature there are several examples of learning systems that focus on the problem of learning CSPs. To describe these learning systems, we shall proceed along a number of dimensions, which are often used to characterize ILP systems. It will be convenient to realize this by answering the following questions:

• 1. What is the representation language for the examples (or instances in the data)?

• 2. What is the hypotheses space or language ?

• 3. What type of background knowledge is used ?

• 4. What search strategy is used ?

• 5. How are the resulting hypotheses scored or ranked ?

In the remainder of this section we briefly discuss five different constraint learning systems by answering these questions.

5.1 Learning a CNF

Clausal Discovery (Claudien) [14]. Claudien was developed as a general purpose learning system, not focussed in particular on learning CSPs.

• 1. Examples are represented as Herbrand interpretations. These interpretations can contain additional information about the problem instance, for example the graph structure in the case of graph coloring. Claudien is capable of learning from only positive examples, or both positive and negative examples.

• 2. Hypotheses are represented as a conjunctive set of clauses.

• 3. Background knowledge contains global knowledge, for example, definitions of global constraints that are available. This knowledge is typically represented as clauses or predicate definitions.

• 4. Search in Claudien is performed on a lattice based on $\theta$-subsumption. It is guided by a refinement operator which can be specified in the $\mathcal {D}LAB$ bias specification language, which specifies which literals can be added to a clause during the search.

• 5. Claudien computes the most specific hypothesis, that is the one that covers the fewest interpretations.²

Lallouet et al. [19]. The system proposed by Lallouet et al. essentially solves the same learning task as Claudien. However, instead of learning a set of clauses in universally quantified conjunctive normal form (UCNF) directly, they exploit the duality between UCNF and clauses in existentially quantified disjunctive normal form (EDNF) [11]. This duality can be expressed by the following property:

$$( \exists l_{1,1} \wedge \cdots \wedge l_{1,n_1}) \vee \cdots \vee (\exists l_{k,1} \wedge \cdots \wedge l_{k,n_1k})$$

is a solution to an EDNF concept learning task with positive examples P and negative examples N if and only if

$$( \forall \lnot l_{1,1} \vee \cdots \vee \lnot l_{1,n_1}) \wedge \cdots \wedge (\forall \lnot l_{k,1} \vee \cdots \vee \lnot l_{k,n_1k})$$

is a solution to an UCNF concept learning task with N as positive examples and P as negative examples. The clausal theory is thus obtained by learning a EDNF on the examples where the class labels are flipped (so positive become negative and vice versa) and by then taking the negation of the obtained formula, which is in UCNF. The main motivation for this approach is the availability of EDNF learning algorithm implementations such as Aleph [26].

An important difference between Claudien and this approach is the use of positive versus negative examples. Claudien learns primarily on positive examples with possible additional information from negative examples, while the approach by Lallouet et al. primarily learns from negative examples due to the class flipping step.

• 1. same as Claudien

• 2. same as Claudien

• 3. same as Claudien

• 4. The authors observe that neither top-down search as bottom-up search provided the necessary scalability. They propose a bi-directional search method that combines top-down and bottom-up search similar to Mitchell’s Candidate Elimination [21].

• 5. Selection is part of the bidirectional search of the DNF learning algorithm.

ModelSeeker [5]. ModelSeeker searches for global constraints starting from an unstructured list of variables. It does not perform search over individual variables but it searches over blocks of variables instead. These blocks are generated by a generator function that extracts certain structures from the example (e.g. rows of a matrix). This approach consists of two steps:

• 1. Find a generator that can be applied on the given example. The generator will enumerate blocks of variables (e.g. the rows of a matrix).

• 2. Find a global constraint, defined on all variables in a given block (e.g. row), that holds for all blocks generated by that generator.

ModelSeeker defines a number of generator templates that can be instantiated. For example, $scheme(n, m_1, m_2, size_1, size_2)$ interprets a sample of length n as a matrix of size $m_1 \times m_2$, and extracts non-overlapping blocks of size $size_1 \times size_2$. Valid instances of this template can be found using Prolog as follows

where factor(N,M1,M2) computes a pair of integers $M_1$ and $M_2$ such that $N = M_1 \times M_2$. For a $9 \times 9$ Sudoku with 81 variables, possible generators include schema(81, 1, 81, 1, 81) (a list), schema(81, 3, 27, 3, 3) (a 3-by-27 matrix where blocks of 3-by-3 are extracted), and schema(81, 9, 9, 1, 9) (where the rows of a $9 \times 9$ matrix are extracted).

In the second phase, ModelSeeker searches for a constraint that is satisfied by all blocks belonging to the specific generator instance selected in the first phase. In a Sudoku, for example, the constraint alldifferent(Vars) holds for all sets of variables extracted by schema(81, 9, 9, 1, 9) (i.e. the rows of the matrix). The constraints that are considered are a large subset of those available in the global constraint catalog [3].

Table 1 shows the output of ModelSeeker for the Sudoku problem.

Table 1. Model found by ModelSeeker for the standard Sudoku problem.

In an ILP formulation, we can write this as

$$\begin{aligned} scheme(81,9,9,1,9, Block)&\rightarrow permutation(Block) \\ scheme(81,9,9,9,1, Block)&\rightarrow permutation(Block) \\ scheme(81,9,9,3,3, Block)&\rightarrow permutation(Block) \end{aligned}$$

Note that the generator is described using constants. This indicates that ModelSeeker cannot generalize over problems of different sizes. The enumeration of this kind of clauses requires a very specialized language bias. Thanks to its tailored bias, ModelSeeker is capable of learning from a single example.

ModelSeeker can also introduce auxiliary variables as parameters of global constraints. It then assumes that all constraints over a set of variable subsets (e.g. rows of a matrix) share the same parameter. This is for example the case when learning magic squares, where each row (and column) sums to the same number.

• 1. Examples are unstructured lists of numbers. They are typically the output that one would expect from a CP solver.

• 2. Hypotheses consist of a generator and a global constraint.

• 3. Two sets of background knowledge are provided: a set of predefined generator templates and a set of global constraints. Some (handcrafted) meta information is available about subsumption between constraints.

• 4. The search strategy is a clever generate and test strategy. It consists of finding all combinations of generator and global constraint that are satisfied in the example.

• 5. ModelSeeker uses a combination of techniques for ranking and selecting hypotheses. The Constraint Seeker returns a ranked list of constraints, where the ranking is based on a number of properties as described in [4]. ModelSeeker essentially selects the most specific hypothesis. However, ModelSeeker considers the global constraints to be black-boxes on which no automated reasoning is possible. Generality tests are therefore purely based on available hand-crafted meta-data. This meta-data can be used to express, among others, implication (e.g. permutation implies alldifferent), contractibility and expandability (e.g. alldifferent(a,b,c) implies alldifferent(a,b), etc.)

5.2 Learning a Single Clause

Conacq [6, 8]. Conacq employs a version-space like approach (Mitchell’s FIND-S algorithm [21]). The version space is the space of all possible constraint networks that can be built on a given set of variables with constraints belonging to a given language. Conacq iterates over the examples to reduce the version space.

• 1. All examples are complete assignments on a set $\mathcal V$ of variables taking values in a domain D. Each example is labelled positive or negative depending on whether it satisfies or not all the constraints of the problem. For instance for 4-queens: $(Q_1=3,Q_2=1,Q_3=4,Q_4=2)$ is a positive example.

• 2. The hypotheses are subsets of a set $\mathcal B$ of the basis constraints, that is, all constraints that possibly participate to the definition of the constraint network. For instance, $\mathcal B$ could contain all binary constraints $Q_i\diamond Q_j$ where $\diamond \in \{=,\ne ,<,\le ,\ge ,>,\ldots \}$.

• 3. The background knowledge contains the definition of these constraints, and can also include any interdependency between constraints that could hold between subsets of constraints. For instance, $X\le Y\wedge Y\le Z\rightarrow X\le Z$ tells us that each time constraints $Q_i\le Q_j$ and $Q_j\le Q_k$ are learned, we can derive $Q_i\le Q_k$. This is intended to recognize syntactic variants and work more at a semantic level of generalization that is reminiscent of Buntine’s generalized subsumption [9] and the notion of semantic closure [16]. Working at the semantic level allows one to significantly decrease the number of candidate hypotheses in the version space.

• 4. The version space is compactly represented by a SAT formula. Each model is a hypothesis that accepts all positive examples and rejects all negative ones. Strategies for updating/simplifying the SAT formula involve unit propagation or backbone detection (i.e., detecting constraints that belong to all hypotheses of the version space.

• 5. No ranking/evaluation function was proposed for selecting hypotheses. The by default function is to take the most specific one.

The active version of Conacq (Conacq2) [8] asks membership queries until the version space has converged on a single hypothesis.

• 1. as in Conacq

• 2. as in Conacq

• 3. as in Conacq

• 4. The strategy usually used for asking membership queries that will produce a fast decrease in the size of the version space is an adaptation of the near-miss strategy [25]. For instance, given a negative example $e_1$ violating a set $\kappa$ of constraints, we try to ask the user to classify an example $e_2$ that violates a single constraint of $\kappa$. If the example is classified positive, that constraint is removed from the candidate constraints. If it is negative, it is learned as belonging to the constraint network. This strategy is reminiscent of Mitchell’s FIND-S algorithm [22]. Interdependencies between constraints can make impossible the generation of near-miss queries, leading to slower decrease in the size of the version space (Constraints networks have been shown to be non learnable in a polynomial sequence of membership queries).

• 5. Conacq2 can be stopped at any time, but it has been presented to be run until convergence. In such a case, it is not necessary to rank the hypotheses as there is only remaining one in the version space.

QuAcq [7]. QuAcq is an extension of Conacq2 that is able to ask partial queries to reduce the number of queries required for convergence.

Thanks to this feature, for each example classified as negative, QuAcq uses a dichotomic search to elucidate one constraint of the constraint network with a number of queries logarithmic in the size of the negative example. As a result, QuAcq learns the constraint network in a polynomial number of queries (namely, $t\cdot n$, where t is the size of the network and n the number of its variables) and proves convergence in a number of queries linear in the size of the basis $\mathcal B$.

• 1. examples are partial or complete assignments on the set $\mathcal V$ of variables. Each example is labelled positive or negative depending on whether it satisfies or not all the constraints of the problem whose variables are involved in the example. For instance for 4-queens: $(Q_1=3,Q_2=2,Q_3=4)$ is a negative example because $Q_1$ and $Q_2$ are on the same diagonal;

• 2. as in Conacq;

• 3. QuAcq does not use any background knowledge other than the definition of the operators;

• 4. for each example classified as positive, QuAcq rules out from the candidate constraints all those that are violated by the example. For each example classified as negative, QuAcq uses a dichotomic search to elucidate one constraint of the constraint network with a number of queries logarithmic in the size of the negative example. This step requires the use of partial queries.

• 5. as Conacq2, QuAcq is supposed to be run until convergence.

Example. Consider the 4-queens problem. Suppose the example $e=(Q_1=3,Q_2=1,Q_3=3,Q_4=2)$ has been classified as negative by the user. This means there is at least one constraint of the network to learn that rejects e (actually there are several). To elucidate such a constraint, QuAcq splits e in two parts of equal size (to guarantee logarithmic convergence) and asks the user the query $(Q_1=3,Q_2=1)$. As the two remaining queens in this example do not attack each other, the user classifies this partial example as positive and QuAcq removes from the set of candidate constraints all those that are violated by $(Q_1=3,Q_2=1)$ (e.g., $Q_1= Q_2$). Then QuAcq extends the example to $Q_3$. The query $(Q_1=3,Q_2=1,Q_3=3)$ is negative. Hence, QuAcq knows that there is a constraint between $\{Q_1,Q_2\}$ and $Q_3$. QuAcq generates the query $(Q_1=3,Q_3=3)$, which is classified as negative. At this point QuAcq knows there is a constraint on the scope $(Q_1,Q_3)$, and it knows this constraint forbids the tuple (3, 3). What remains to do is to generate queries on $(Q_1,Q_3)$ that will allow QuAcq to find which constraint leads to the rejection of $(Q_1=3,Q_3=3)$. Suppose that the remaining candidate constraints that could reject $(Q_1=3,Q_3=3)$ are $\{\ne ,<,>\}$. After having asked $(Q_1=3,Q_3=2)$ and $(Q_1=2,Q_3=3)$, both classified positive, QuAcq rules out $Q_1<Q_3$ and $Q_1>Q_3$ as candidate constraints, and $Q_1\ne Q_3$ is added to the learned network.

Table 2. Categorization of systems. The question answered are (1) Does the system learn a single clause or multiple ones? (2) Is the system propositional or relational? (3) Does it use active learning? (4) What type of examples does it need (positive, negative, partial)? (5) How does it handle redundancy (logic-based, lattice-based, ruleset-based) (6) Can it learn from examples of difference sizes?

6 Discussion

We will now analyze these different systems based on a number of dimensions. Table 2 gives an overview of this section.

Propositional vs. Relational. For the systems we discussed, Claudien and Lallouet use first-order logic to learn constraint models, while Conacq and QuAcq are based on propositional logic. Many constraint satisfaction problems have some form of global structure that can be captured very well by first-order logic, but would require many constraints in propositional logic.

ModelSeeker is a mix between the two. It allows one to capture global structure using global constraints, but it only learns a restricted form of clauses. Its output can be considered to be a domain-specific language that can be mapped to a clausal theory, but it lacks the expressivity of the latter.

Active vs. Passive Learning. Most of the systems are passive learning systems, that is, they take examples and produce a model without user interaction. However, Conacq2 and QuAcq are based on posing queries to the user, which allows them to quickly converge to the correct solution, even when no positive examples have been seen. In a sense, it allows the system to learn the model and solve it at the same time. From a machine learning point of view, the use of partial queries is new and unexplored in the context of ILP, cf. [2].

Requirements on Examples. An important aspect of learning CSPs is the availability of examples. Some CSPs have many solutions, some have only one. The systems discussed in this paper have different requirements for the examples.

Claudien and the approach of Lallouet et al. start from examples as sets of ground facts. This allows them to learn from structured examples (for example, containing a graph). Both approaches typically require a substantial number of examples, depending on the complexity of the input language and the available background information in the form of language bias. The main difference between both approaches is that Claudien learns a theory on positive examples, while Lallouet et al. starts from negative examples. Both approaches can incorporate information from both positive and negative examples.

Conacq, QuAcq and ModelSeeker start from examples in the form of assignments to the variables in the model. This means they fix the number of variables at the start of the learning task.

ModelSeeker assumes that some structure can be imposed on the variables on which global constraints can be found. It often can learn a good model from just a single positive example. ModelSeeker can not incorporate information from a negative example.

QuAcq can start from partial examples, which means that it can be used to learn problems for which no solution has been found yet.

Redundancy. All systems support some form of redundancy elimination. In Claudien, Lallouet et al., Conacq and QuAcq this is based on logical inference. In ModelSeeker, this is based on metadata provided with the constraints.

7 Conclusion and Future Work

We see the learning of CSPs as a modern challenge in which many of the techniques and insights from ILP can play an important role. The connection between constraint programming and inductive logic programming has been made before by Lallouet et al. [19] for learning CSPs and by Abdennadher and Rigotti [1] for learning propagation rules for CSP solvers. In this survey, we have given an overview of techniques for learning CSPs and relate them to concepts from the ILP community, with the intention of inspiring further cross-fertilization between these two fields.

Each of the systems described in this paper contributes its own ideas. The expert driven ModelSeeker [5] introduces the idea of generators and uses a very well developed search strategy which makes it capable of learning relatively complex CSPs from a small number of examples. However, techniques from ILP can still contribute (1) by making it possible to structure the search space better by using more-general-than relations between the available constraints and the generators, (2) by allowing ModelSeeker to incorporate negative examples, and (3) by making it able to learn from examples of different sizes [24].

The propositional systems Conacq [10] and QuAcq [7] are interesting because they start from a sound theoretical basis and can therefore provide guarantees on the complexity of the learning task. The QuAcq system is especially of interest because it can learn from partial queries to the user. This allows it to learn a CSP for which no solutions are known yet. This setting has never been studied in an ILP setting.

In conclusion, we believe that ILP-based techniques can make a valuable contribution for the task of learning CSPs, and that techniques studied for learning CSPs can be used to improve the effectiveness of ILP systems.