Multiple-Aggregate Games

Abstract

Consider an environment in which individuals are organised into groups, they contribute to the collective action of their group, and are influenced by the collective actions of other groups; there are externalities between groups that are transmitted through the aggregation of groups’ actions. The theory of ‘aggregative games’ has been successfully applied to study games in which players’ payoffs depend only on their own strategy and a single aggregation of all players’ strategies, but the setting just described features multiple aggregations of actions—one for each group—in which the nature of the intra-group strategic interaction may be very different to the inter-group strategic interaction. The aim of this contribution is to establish a framework within which to consider such ‘multiple aggregate games’; present a method to analyse the existence and properties of Nash equilibria; and to discuss some applications of the theory to demonstrate how useful the technique is for analysing strategic interactions involving individuals in groups.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Richard and I had many interesting discussions about aggregative games and games in which there are multiple aggregates, and it was firmly on both of our agendas to pursue joint research on multiple aggregate games. As is often the case, momentum in pursuing ideas takes time to establish, and it was very unfortunate that we were not afforded the opportunity to work closely on developing these ideas before Richard sadly passed away in 2015. It is a great honour to have the opportunity to communicate the current state of my thoughts on multiple aggregate games in this volume dedicated to Richard: the aim has been to provide an accessible exposition of the ideas and establish a framework for analysis, rather than to derive the most general results under the weakest assumptions, that I believe Richard would appreciate. The work has undoubtedly benefitted from the discussions I had with Richard, as well as with Roger Hartley, and it is also without doubt that what is presented here is inferior to what might have been achieved had Richard co-authored the contribution: he had amazing intuition and an ability to explain complex ideas in a simple way, that only comes from having a truly deep understanding. I hope to have done the ideas justice.

In a strategic decision making environment there is strategic interdependence between individuals playing a non-cooperative game; each is influenced by, and influences, the other players in the game. Sometimes individuals care about exactly which of their adversaries does what, but in many interesting economic applications players care only about the aggregation of other players’ actions, since it is this that influences their payoff. Such games are called aggregative games. Often, individuals within an environment are organised into groups and they contribute to the collective action of their group which in part determines their payoff, but they are also affected by the collective actions of other groups: there are externalities between groups that are transmitted through the aggregation of groups’ actions. Whilst the theory of aggregative games has been successfully applied to study games with a single aggregate, the setting just described features multiple aggregations of actions, one for each group, and the nature of the intra-group strategic interaction—where players contribute to the collective action of their group—may be very different to the inter-group strategic interaction. The aim of this paper is to establish a framework in which to consider such ‘multiple aggregate games’; present a method to analyse the existence and properties of equilibria; and to discuss some applications of the theory—to contests; public goods games; and bilateral oligopoly—to demonstrate how useful the technique is for analysing strategic interactions between groups of individuals.

Consider a simultaneous-move game of complete information involving i = 1, …, N individuals where each has to decide on a single action $x_{i} \in \mathbb{R}_{+}$. Each player’s payoff depends on their own action and the vector of all other players’ actions. The game is an ‘aggregative game’ if each player cares only about the aggregation of other players’ actions, X _−i  = X − x _i , where X is the sum of all players’ actions. The standard approach to finding a Nash equilibrium involves identifying each player’s best response function, b _i (X _−i ); this is player i’s action consistent with a Nash equilibrium in which the aggregate actions of other players is X _−i . The problem is that for each player this is defined on a different domain, and therefore the joint best response function, of which a fixed point must be found, has as many dimensions as there are players. An aggregative approach does something different: rather than finding a best response, instead consider the action of player i consistent with a Nash equilibrium in which the aggregate of all players, including player i, takes the value X. This gives the ‘replacement function’¹ r _i (X), so called because finding it involves replacing X _−i with X − x _i in the equation that defines the best response and then solving for x _i . A Nash equilibrium is identified at the level of the aggregation of actions, and requires aggregate consistency between individual actions and the aggregate; that is, for X to be such that the sum of replacement functions evaluated at X exactly equals X. This is a much simpler problem than finding mutually consistent best responses! Existence, uniqueness and comparative static properties can be investigated by understanding the properties of replacement functions and their aggregation, which is tractable even in a game with heterogeneous players; and whether these players are active in equilibrium or not can be deduced by evaluating their replacement function at the equilibrium aggregate.

The methods of aggregative games have been used to good effect in the study of Cournot oligopoly (Novshek 1985); public goods games (Cornes and Hartley 2007); and Tullock contests (Cornes et al. 2005); among others. In contests, a contestant’s share of the aggregate action naturally features in their payoff function, and in the analysis of the game it is often convenient to use share functions rather than replacement functions; since s _i (X) = r _i (X)∕X can be monotonically decreasing in X when r _i (X) is not. Aggregate consistency with share functions requires their sum to take the value 1. The share function approach was first introduced by Cornes and Hartley (2000) in studying joint production games. In addition to exploring the use of aggregative games in particular applications, there have been some general treatments including those by Corchon (1994), Jensen (2010) (who considers that the aggregation of players’ actions can be more general than the simple unweighted sum), Cornes and Hartley (2012), and Acemoglu and Jensen (2013).

In a ‘multiple aggregate game’ each player is a member of a single group and their action contributes to the collective action of their group. Individuals within a group care about their own action, the collective action of their group, and also the collective actions of other groups: there is intra-group strategic interaction which takes the form of an aggregative game; and inter-group spill-overs that transmit through the aggregate actions of groups. The applicability of this framework that extends the scope of aggregative games is clear. Inspiration for the study of multiple aggregate games comes from the analysis of bilateral oligopoly (see, for example, Dickson and Hartley 2008) in which there is a set of buyers and a set of sellers and, in essence, each group of traders plays a simple Tullock contest in which they receive a proportional share of a prize, the size of which is determined by the aggregate actions of the other group of traders.

The method used to analyse multiple aggregate games first resolves the intra-group strategic interaction, and then essentially treats groups as players that choose an aggregate action to resolve the inter-group interaction. First, a group is selected and the aggregate actions of other groups are fixed at arbitrary levels. This defines a ‘partial game’ that involves only the members of the selected group, and since each group member cares only about their own action and the aggregation of other group members’ actions, this is an aggregative game. Within the partial game, aggregative methods can be applied to identify a Nash equilibrium: individual replacement or share functions are derived that represent the consistent behaviour of group members; then aggregate consistency within the group is imposed to identify the Nash equilibrium in the partial game, which reveals the ‘group best response’. This is repeated for each group, and the resulting group best responses represent the collective action of each group consistent with a Nash equilibrium in which the aggregate actions of other groups take a particular value, having accounted for the strategic tension within groups. A Nash equilibrium in the full game can then be identified at the level of group aggregates, that requires the aggregate action of each group to be a group best response to the aggregate actions of the other groups.

Whilst identifying Nash equilibrium is a fixed point problem, it involves the joint group best response and therefore only has as many dimensions as there are groups even though there are heterogeneous players within each group. This may be as few as two, as in bilateral oligopoly. As such, exploiting the aggregative nature of the game considerably simplifies the analysis and, since group best responses are found using the aggregation of replacement or share functions whose properties are easily deduced, the features of Nash equilibrium can be easily understood.

In some games there is more structure to the group interaction: a ‘nested aggregative game’ has the feature that individuals not only care just about the aggregation of others’ actions within their group, they also care only about the aggregation of other groups’ actions. Such games are aggregative both at the level of individuals within groups, and at the level of groups. The analysis slightly differs to exploit this additional aggregative structure: within ‘partial games’ individual and group consistency with a Nash equilibrium in which the aggregate of all groups’ actions takes a particular value is sought to define ‘group replacement functions’, following which overall consistency is required for a Nash equilibrium, which needs the sum of group replacement functions to be equal to the aggregate action, a simpler problem than finding mutually consistent group best responses. Thus, consistency in aggregation is required twice: once at the level of individuals within groups in partial games; and once at the level of groups within the full game. The analysis of a game between individuals using aggregative techniques renders the study of equilibrium tractable and permits uniqueness of equilibrium to be considered even in the presence of heterogeneous players, and the same is true of a nested aggregative game with heterogeneous groups and heterogeneity of players within groups, which is explored here in a general setting.

There is some existing literature on strategic interactions between individuals within groups that is related to the ideas presented here. Cornes et al. (2005) consider a model in which individuals in groups contribute to a public good enjoyed by their group, and there are also spill-overs in the public good provided by each group. Restrictions are imposed on the nature of the spill-overs that ensure the game has the form of what has been called here a nested aggregative game, and the idea of both group and overall consistency to identify Nash equilibria is introduced. Nitzan and Ueda (2014) study a ‘collective contest’ in which individuals in groups contribute effort to the group in contesting a rent. The cost of effort is heterogeneous among group members, as is their valuation of the rent, and the approach taken to analyse a Nash equilibrium recognises that it is a nested aggregative game and appeals to group and overall consistency to analyse the effect of heterogeneity within groups.

In strategic interactions where group structure is important, some contributions have used ideas that are similar to the partial game approach taken here. In particular, Baik (2008) studies a collective contest and uses the idea of a ‘group-specific equilibrium’ to analyse the game, albeit in a simple setting since there is essentially a single active player in each group. Kolmar and Rommeswinkel (2013) study a contest between groups in which there are complementarities in effort within groups, and use the idea of a group best response function to identify Nash equilibria.

In the setting explored here each individual belongs to a single group and contributes only to the aggregate of that group; there are multiple aggregates because there are multiple groups. In other settings there might be multiple aggregations of actions where all players contribute to all aggregates. Models of production and appropriation fall into this category and, whilst aggregative methods can be used to analyse such models (Cornes et al. 2010), the lack of group structure means they fall outside the remit of the current exposition.

The remainder of the paper is structured as follows. Section 2 presents the economic environment, defines the game that is played, and introduces the idea of partial games and group best responses. In Sect. 3 partial games are analysed by exploiting their aggregative properties to derive group best responses, and in Sect. 4 Nash equilibrium in the full game is studied by considering mutual consistency of group best responses. Section 5 considers the special case of nested aggregative games. In Sect. 6 some applications of the method—to contests; bilateral oligopoly; and public goods—are considered, and conclusions follow. All proofs are contained in an Appendix.

2 The Economic Framework

Consider a strategic interaction between individuals that are exogenously organised in groups where each individual belongs to a single group and their payoffs depend on the actions of their fellow group members and on the actions of members of other groups, perhaps in a fundamentally different way than within the group. It is natural to think of the influence of members of other groups working through the aggregation (i.e., the sum) of those groups’ actions, and attention is restricted to this case. The (finite) set of groups is J = { 1, …, j, …, N} and the (finite) set of individuals in group j is I ^j = { 1, …, i, …, N ^j}. Subscripts are used to identify individuals, superscripts to identify the group they belong to. Each individual must simultaneously choose a single action $x_{i}^{\,j} \in \mathbb{R}_{+}$; capitals are used to represent aggregations of actions, and vectors of actions are in boldface, as the following statement makes clear.

Notation

$\mathbf{x} =\{ x_{i}^{\,j}\}_{i\in I^{j},j\in J}$ is the vector of all players’ actions. $\mathbf{x}^{\,j} =\{ x_{i}^{\,j}\}_{i\in I^{j}}$ is the vector of all actions of members of group j, and x _−i ^j = x ^j ∖x _i ^j . $X^{j} =\sum _{i\in I^{j}}x_{i}^{\,j}$ is the aggregation of actions of the members of group j, and X _−i ^j = X ^j − x _i ^j . X ={ X ^j } _j∈J is the vector of all group aggregates, and X ^−j = X ∖X ^j . Where appropriate, X = ∑ _j∈J X ^j is the aggregation of all groups’ aggregate actions, and X ^−j = X − X ^j .

In a strategic environment individuals’ actions have external consequences for others, so typically an individual’s payoff will depend both on their own action and on the actions chosen by all other individuals. Here, an individual’s actions have external consequences both within and outside their group, and the effect on members of other groups comes only through the aggregation of the group’s actions. As such, each individual cares about the actions of members of other groups only through their aggregation, so the payoff to a typical individual in group j can be written

$$\displaystyle{ u_{i}^{\,j}(x_{ i}^{\,j},\mathbf{x}_{ -i}^{\,j};\mathbf{X}^{-j}). }$$

This allows externalities between players within a group as well as externalities between groups that work the level of aggregate group actions to be considered, where the nature of the strategic interaction within groups may be very different to that between groups: for example, an individual’s actions may have negative consequences for the members of their own group, and positive consequences for the members of other groups, or vice versa.

The game $\mathcal{G}$ is the simultaneous-move game of complete information with player set ∪ _j ∈ J I ^j; actions $x_{i}^{\,j} \in \mathbb{R}_{+}$; and payoffs u _i ^j(x _i ^j, x _−i ^j; X ^−j): the equilibrium concept is Nash equilibrium in pure strategies. If no further attention was paid to the group structure of the game, the analysis would proceed by attempting to find a vector of actions, one for each player, that constitute mutually consistent best responses. This involves finding a fixed point of the joint best response function, that has as many dimensions as there are players in the game; whilst there are well-known approaches for studying the existence of such fixed points, understanding the properties of equilibrium is a more difficult task. This is particularly true when the game does not exhibit strategic complementarities so the tools of supermodular games cannot be exploited, which is likely to be the case in many interesting applications given the potentially different nature of the intra- and inter-group interaction.

By recognising the group structure of the game, a somewhat different approach to identifying Nash equilibria can be taken. The method follows a two-step procedure. First, select a group and fix the actions of the members of all other N − 1 groups, so the aggregate action of each of these groups (which is what the members of the group in question care about) takes a particular value. Consider the strategic interaction among the members of the group in question, seeking to find actions that are consistent with a Nash equilibrium in the game in which the other groups’ aggregate actions take the specified values. Repeat this for each group (fixing the aggregate actions of the other N − 1 groups in turn), which identifies consistent behaviour within groups taking as fixed the aggregate actions of all other groups. The second step then looks at between-group consistency. The aggregation of the consistent individual actions found in the first step gives a ‘group best response’ to the aggregate actions of other groups; a Nash equilibrium of the game requires mutual consistency of these group best responses at the level of group aggregates. Once an equilibrium has been identified, individual actions can be deduced from the characterisation of equilibrium behaviour within groups from step 1, evaluated at the equilibrium values of the aggregate actions of other groups.

More precisely, select a group j and fix the aggregate actions of other groups at some levels collected in X ^−j. Define a ‘partial game’ $\mathcal{G}^{j}(\mathbf{X}^{-j})$ amongst the members of group j, in which the aggregate actions of all other groups are fixed. The analysis of the intra-group strategic interaction involves finding a Nash equilibrium of this partial game. Restrictions will be imposed ensuring uniqueness of equilibrium within each partial game for any X ^−j; the action of individual i in this Nash equilibrium is written $\tilde{x}_{i}^{\,j}(\mathbf{X}^{-j})$ and the aggregation of group j’s equilibrium actions is $\tilde{X}^{j}(\mathbf{X}^{-j}) =\sum _{i\in I^{j}}\tilde{x}_{i}^{\,j}(\mathbf{X}^{-j})$. Having resolved the strategic interaction within the group, this function gives the ‘group-j best response’ to the aggregate actions of the other groups contained in X ^−j. This is then repeated for all other N − 1 groups to deduce a group best response function for each group. The remaining task is to ensure between-group consistency, which requires mutual consistency of group best responses: to identify a Nash equilibrium in the game $\mathcal{G}$ a vector of group aggregates X ^∗ is sought such that $X^{j{\ast}} =\tilde{ X}^{j}(\mathbf{X}^{-j{\ast}})$ for all j ∈ J; the equilibrium action of each player will consequently be $x_{i}^{\,j{\ast}} =\tilde{ x}_{i}^{\,j}(\mathbf{X}^{-j{\ast}})$. Essentially, having ensured intra-group consistency groups are treated as players in an N-player game where they ‘choose’ aggregate actions and have best response functions given by $\tilde{X}^{j}(\mathbf{X}^{-j})$.

The following proposition establishes that the two-step procedure just outlined is valid in identifying Nash equilibria in the game $\mathcal{G}$, since mutually consistent group best responses are in one-to-one correspondence with Nash equilibria in the game.

Proposition 1

Consider the N partial games $\{\mathcal{G}^{j}(\mathbf{X}^{-j})\}_{j\in J}$ of the game $\mathcal{G}$ in which the player set is the members of group j, their actions are $x_{i}^{\,j} \in \mathbb{R}_{+}$ , and their payoffs are u _i ^j (x _i ^j , x _−i ^j ; X ^−j ) where X ^−j is considered fixed. Suppose a Nash equilibrium in $\mathcal{G}^{j}(\mathbf{X}^{-j})$ exists and is unique for any $\mathbf{X}^{-j} \in \mathbb{R}_{+}^{N-1}$ , and write $\tilde{x}_{i}^{\,j}(\mathbf{X}^{-j})$ for the equilibrium strategy of player i and $\tilde{X}^{j}(\mathbf{X}^{-j}) =\sum _{i\in I^{j}}\tilde{x}_{i}^{\,j}(\mathbf{X}^{-j})$ for the aggregation of group j’s actions in the Nash equilibrium. Then x ^∗ is a Nash equilibrium in $\mathcal{G}$ if and only if $X^{j{\ast}} =\tilde{ X}^{j}(\mathbf{X}^{-j{\ast}})$ for all j ∈ J, where $x_{i}^{\,j{\ast}} =\tilde{ x}_{i}^{\,j}(\mathbf{X}^{-j{\ast}})$ .

This proposition supposes there is a unique Nash equilibrium in each partial game. To understand the conditions under which this will be true attention is restricted to strategic interactions where, within each group, individuals only care about the aggregation of other group members’ actions. In this case, a player’s payoff can (with a slight abuse of notation) be written

$$\displaystyle{ u_{i}^{\,j}(x_{ i}^{\,j},X_{ -i}^{j};\mathbf{X}^{-j}). }$$

With this structure, which is a common feature of many games with continuous strategies, a typical individual’s payoff depends on their own action, the aggregation of their group’s actions, and the vector of all other groups’ aggregate actions, since it can be written

$$\displaystyle{ \tilde{u}_{i}^{\,j}(x_{ i}^{\,j},X^{j};\mathbf{X}^{-j}) \equiv u_{ i}^{\,j}(x_{ i}^{\,j},X^{j} - x_{ i}^{\,j};\mathbf{X}^{-j}). }$$

(1)

As such, once the vector of other groups’ aggregate actions is fixed, each partial game $\mathcal{G}^{j}(\mathbf{X}^{-j})$ is an aggregative game, and this aggregative structure will be exploited to establish uniqueness of equilibrium within partial games. The game $\mathcal{G}$, being constituted of N aggregative games, is thus a ‘multiple-aggregate game’.

In the special case of a ‘nested aggregative game’ individuals in group j not only care just about the aggregation of other group members’ actions, they also care only about the aggregation of other groups’ actions. Then payoffs (again with a slight abuse of notation) can be written

$$\displaystyle{ \tilde{u}_{i}^{\,j}(x_{ i}^{\,j},X^{j};X^{-j}). }$$

Since X ^−j = X − X ^j, in such games an individual’s payoff will depend on their own action, the aggregation of their group’s action, and the aggregation of all groups’ actions, since

$$\displaystyle{ \hat{u}_{i}^{\,j}(x_{ i}^{\,j},X^{j};X) \equiv \tilde{ u}_{ i}^{\,j}(x_{ i}^{\,j},X^{j};X - X^{j}). }$$

This special case is the focus of attention in Sect. 5.

3 Study of Group Partial Games

In the partial game $\mathcal{G}^{j}(\mathbf{X}^{-j})$ with X ^−j fixed, a Nash equilibrium among the N ^j members of group j is sought. The payoff functions of these players, as noted in (1), can be written $\tilde{u}_{i}^{\,j}(x_{i}^{\,j},X^{j};\mathbf{X}^{-j})$; consequently, the group-j partial game is an aggregative game since with X ^−j fixed each player’s payoff depends only on their own action and the aggregation of all players’ actions (within that player’s group) which will be exploited to study the Nash equilibria of the partial game and understand the features of group best response functions $\tilde{X}^{j}(\mathbf{X}^{-j})$.

Basically, the aim is to define for each player a ‘share function’ that represents their behaviour consistent with a Nash equilibrium in a partial game in which the group aggregate takes a particular value, and show that there is a Nash equilibrium in the partial game if and only if the sum of shares equals one. If share functions are strictly decreasing in the group aggregate then the sum of shares will inherit this property, so if the sum of shares exceeds one when the group aggregate is small, and is less than one when it is large, there will be a unique Nash equilibrium in the partial game. Under what conditions is this true?

If a player’s payoff function u _i ^j is strictly concave in own strategy, which will be assumed, their best response will be unique and the best response function, denoted b _i ^j(X _−i ^j; X ^−j), is identified by the necessary and sufficient first-order condition. Thus, b _i ^j(X _−i ^j; X ^−j) = max{0, x _i ^j} where x _i ^j satisfies

$$\displaystyle{ \frac{\partial u_{i}^{\,j}(x_{i}^{\,j},X_{-i}^{j};\mathbf{X}^{-j})} {\partial x_{i}^{\,j}} = 0. }$$

(2)

A player’s best response gives their action consistent with a Nash equilibrium in $\mathcal{G}^{j}(\mathbf{X}^{-j})$ in which the actions of all other players in group j sum to X _−i ^j.

Rather than working with best responses, an aggregative approach considers the strategy of a player that is consistent with a Nash equilibrium in which the aggregate action of all members of the group, including the player in question, takes a particular value X ^j. This will be given by the player’s ‘replacement function’ r _i ^j(X ^j; X ^−j) which is defined by

$$\displaystyle{ r_{i}^{\,j}(X^{j};\mathbf{X}^{-j}) \equiv b_{ i}^{\,j}(X^{j} - r_{ i}^{\,j}(X^{j};\mathbf{X}^{-j});\mathbf{X}^{-j}). }$$

Note that the replacement function is given by r _i ^j(X ^j; X ^−j) = max{0, x _i ^j} where x _i ^j is defined by

$$\displaystyle{ \frac{\partial u_{i}^{\,j}(x_{i}^{\,j},X^{j} - x_{i}^{\,j};\mathbf{X}^{-j})} {\partial x_{i}^{\,j}} = 0 }$$

(3)

so long as r _i ^j(X ^j; X ^−j) ≤ X ^j, otherwise the function is deemed undefined.

A player’s replacement function gives their individual action consistent with a Nash equilibrium in the game $\mathcal{G}^{j}(\mathbf{X}^{-j})$ in which the aggregate action of all members of group j is X ^j. Consistency of individual group members’ actions with the aggregate of the group requires the sum of their actions consistent with a particular group aggregate to be exactly equal to that group aggregate. This simple equilibrium identification condition in the partial game, which involves finding a fixed point of $\sum _{i\in I^{j}}r_{i}^{\,j}(X^{j};\mathbf{X}^{-j}): \mathbb{R}_{+} \rightarrow \mathbb{R}_{+}$ at the level of the aggregate action of the group, makes clear the appeal of an aggregative game approach.

Proposition 2

x ^j∗ is a Nash equilibrium in the game $\mathcal{G}^{j}(\mathbf{X}^{-j})$ if and only if

$$\displaystyle{ \sum _{i\in I^{j}}r_{i}^{\,j}(X^{j{\ast}};\mathbf{X}^{-j}) = X^{j{\ast}}. }$$

(4)

An aggregate action by the members of group j that satisfies the consistency condition (4) constitutes a ‘group best response’ in $\mathcal{G}^{j}(\mathbf{X}^{-j})$, which is denoted $\tilde{X}^{j}(\mathbf{X}^{-j})$. Whether Nash equilibria in partial games are unique, so $\tilde{X}^{j}(\mathbf{X}^{-j})$ can be considered a function, will rely on the monotonicity properties of the representation of consistent individual behaviour with respect to the group aggregate. Rather than working with levels of a player’s action, represented by the replacement function, it is often more convenient to work with their share of the group aggregate, σ _i ^j = x _i ^j∕X ^j, as this can be monotonically decreasing in X ^j when replacement functions are not. For X ^j > 0, an individual’s ‘share function’ is² s _i ^j(X ^j; X ^−j) = r _i ^j(X ^j; X ^−j)∕X ^j which is implicitly defined by s _i ^j(X ^j; X ^−j) = max{0, σ _i ^j} where σ _i ^j satisfies

$$\displaystyle{ l_{i}^{\,j}(\sigma _{ i}^{\,j},X^{j};\mathbf{X}^{-j}) \equiv \frac{\partial u_{i}^{\,j}(\sigma _{ i}^{\,j}X^{j},X^{j}[1 -\sigma _{ i}^{\,j}];\mathbf{X}^{-j})} {\partial x_{i}^{\,j}} = 0 }$$

(5)

so long as σ _i ^j ≤ 1, otherwise the share function is undefined.

The analogue of individual actions summing to the aggregate action that achieves aggregate consistency within group j is that the shares of the members of group j sum to one. As such, the group-j best response must satisfy

$$\displaystyle{ \sum _{i\in I^{j}}s_{i}^{\,j}(X^{j};\mathbf{X}^{-j}) = 1. }$$

(6)

Clearly, the properties of share functions are important in determining the properties of the group best response, elucidating the details of which is turned to next. In applications, it is often straightforward to understand what conditions on the primitives imply share functions are monotonically decreasing in X ^j. The following assumption details the conditions on preferences required in the general model.

Assumption 1

For each individual i ∈ I ^j , suppose that u _i ^j is continuously differentiable as many times as required, and that:

• a) $\frac{\partial ^{2}u_{ i}^{\,j}} {\partial (x_{i}^{\,j})^{2}} < 0$ ;

• b) if $\frac{\partial ^{2}u_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X_{-i}^{j}} < 0$ then $\left \vert \frac{\partial ^{2}u_{ i}^{\,j}} {\partial (x_{i}^{\,j})^{2}} \right \vert > \left \vert \frac{\partial ^{2}u_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X_{-i}^{j}}\right \vert$ ; and

• c) $\frac{\partial ^{2}u_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X_{-i}^{j}} +\sigma _{ i}^{\,j}\left [ \frac{\partial ^{2}u_{ i}^{\,j}} {\partial (x_{i}^{\,j})^{2}} - \frac{\partial ^{2}u_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X_{-i}^{j}}\right ] < 0$ for all σ _i ^j ∈ (0,1].

In addition, $\lim _{x_{i}^{\,j}\rightarrow \infty }\frac{\partial u_{i}^{\,j}(x_{ i}^{\,j},\cdot;\cdot )} {\partial x_{i}^{\,j}} < 0$ .

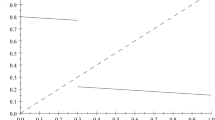
Thus, payoffs are strictly concave, as previously noted; the substitutability or complementarity of actions within groups must not be too strong; and players will always use a finite action. The following proposition details the properties of share functions; Fig. 1 illustrates.

Fig. 1

Illustrating share functions. For individual 1, X ₁ ^j(X ^−j) > 0; for individual 2 X ₂ ^j(X ^−j) = 0 and $\bar{X}_{2}^{\,j}(\mathbf{X}^{-j}) > 0$. For individual 3 $\underline{X}_{3}^{\,j}(\mathbf{X}^{-j}) =\bar{ X}_{3}^{\,j}(\mathbf{X}^{-j}) = 0$ and therefore their share function is zero for all X ^j > 0. The diagram also illustrates the aggregation of share functions for these three players and, assuming they constitute group j, the equilibrium aggregate action in the partial game is identified

Proposition 3

Suppose the preferences of player i ∈ I ^j satisfy Assumption  1 . Each player’s share function s _i ^j (X ^j ; X ^−j ) is defined for all X ^j ≥ X _i ^j( X ^−j ) which is X ^j such that l _i ^j (1,X ^j ; X ^−j ) = 0 if this is strictly positive, otherwise the share function is defined for all X ^j > 0. Define player i’s drop-out value as $\bar{X}_{i}^{\,j}(\mathbf{X}^{-j})$ which is X ^j such that l _i ^j (0,X ^j ; X ^−j ) = 0 if this exists, or + ∞ if it does not. Then the share function has the following properties:

• a) s _i ^j (X ^j ; X ^−j ) = 0 for all $X^{j} \geq \bar{ X}_{i}^{\,j}(\mathbf{X}^{-j})$ ;

• b) it is continuous and, where it is defined, strictly decreasing in $X^{j} <\bar{ X}_{i}^{\,j}(\mathbf{X}^{-j})$ ; and

• c) if X _i ^j( X ^−j ) > 0 then s _i ^j(X _i ^j( X ^−j ); X ^−j ) = 1, otherwise $\lim _{X^{j}\rightarrow 0}s_{i}^{\,j}(X^{j};\mathbf{X}^{-j}) =\bar{ s}_{i}^{\,j}(\mathbf{X}^{-j})$ .

The consistency condition (6) that identifies an equilibrium in the partial game $\mathcal{G}^{j}(\mathbf{X}^{-j})$ requires X ^j to be such that the sum of individual share functions equals one, for then the sum of the individual actions consistent with a Nash equilibrium in which the aggregate action is X ^j will sum precisely to X ^j. Note that if X _i ^j(X ^−j) > 0 for any member of group j then the aggregate share function is defined only where all members’ share functions are defined, i.e. for $X^{j} \geq \max _{i\in I^{j}}\{\underline{X}_{i}^{\,j}(\mathbf{X}^{-j})\}$. If individual share functions are strictly decreasing in X ^j, the aggregation of these will also be strictly decreasing, so under the conditions of Proposition 3 there will be at most one Nash equilibrium. For large enough values of X ^j it can be shown that the aggregate share function will take values less than one, so whether a Nash equilibrium exists depends on whether, when X ^j is small, the aggregate share function exceeds one. The following proposition makes the conditions for the existence of a unique Nash equilibrium clear.

Proposition 4

Suppose the preferences of all members of group j satisfy Assumption  1 . Then there is a unique Nash equilibrium in the partial game $\mathcal{G}^{j}(\mathbf{X}^{-j})$ in which the aggregate action of the members of group j is X ^j > 0 if either X _i ^j( X ^−j ) > 0 for any i ∈ I ^j , or $\sum _{i\in I^{j}}\bar{s}_{i}^{\,j}(\mathbf{X}^{-j}) > 1$ .

Under the conditions stated in the proposition the group best response function $\tilde{X}^{j}(\mathbf{X}^{-j})$ satisfies

$$\displaystyle{ \sum _{i\in I^{j}}s_{i}^{\,j}(\tilde{X}^{j}(\mathbf{X}^{-j});\mathbf{X}^{-j}) = 1. }$$

(7)

The equilibrium action of individual i ∈ I ^j is given by $\tilde{X}^{j}(\mathbf{X}^{-j})\sum _{i\in I^{j}}s_{i}^{\,j}(\tilde{X}^{j}(\mathbf{X}^{-j});\mathbf{X}^{-j})$, which is positive if $\tilde{X}^{j}(\mathbf{X}^{-j}) <\bar{ X}_{i}^{\,j}(\mathbf{X}^{-j})$; for some players this inequality may not hold in which case their equilibrium action is zero. If the conditions stated in the proposition are not satisfied then the only Nash equilibrium involves all group members choosing x _i ^j = 0 and so $\tilde{X}^{j}(\mathbf{X}^{-j}) \equiv 0$ in these circumstances.³

4 Nash Equilibrium in the Full Game

Having established the existence and uniqueness of Nash equilibrium in group partial games, which has allowed group best response functions $\tilde{X}^{j}(\mathbf{X}^{-j})$ to be defined, attention now turns to consider mutual consistency of these group best response functions and Nash equilibrium in the full game $\mathcal{G}$. Inter-group consistency of actions occurs with a vector of group aggregates X ^∗ such that $X^{j{\ast}} =\tilde{ X}^{j}(\mathbf{X}^{-j{\ast}})$ for all j ∈ J. Finding group aggregate actions that are mutually consistent in the sense of group best responses is analogous to finding mutually consistent individual actions within an N-player game; as with the standard problem, understanding the characteristics of best response functions is important in understanding the features of the equilibrium.

The group structure of the game makes it natural to assume that the members within each group are influenced by the actions of other groups in the same way, captured in the following definition.

Definition

The members of group j are ‘qualitatively symmetric’ if, for any h, i ∈ I ^j, $\mathop{\mathrm{sgn}}\nolimits \{ \frac{\partial ^{2}u_{ h}^{j}} {\partial x_{h}^{j}\partial X^{k}}\} =\mathop{ \mathrm{sgn}}\nolimits \{ \frac{\partial ^{2}u_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X^{k}}\}$ and $\mathop{\mathrm{sgn}}\nolimits \{ \frac{\partial u_{h}^{j}} {\partial X^{k}} \} =\mathop{ \mathrm{sgn}}\nolimits \{ \frac{\partial u_{i}^{\,j}} {\partial X^{k}}\}$ for all k ≠ j ∈ J.

Formally, only the first of the conditions, that says the marginal payoff of each group member is influenced by the actions of another group in the same direction, is required but it is very natural to also assume the externality from other groups takes the same sign for members of the same group. Note that assuming the members of group j are qualitatively symmetric does not impose that individuals within groups are homogeneous, nor does it restrict the effect of any two different groups on the members of group j to be the same.

The following proposition clarifies the behaviour of group best response functions.

Proposition 5

Suppose the preferences of all members of all groups satisfy Assumption  1 and that the members of each group are qualitatively symmetric. Then for each j ∈ J and all k ≠ j ∈ J, $\tilde{X}^{j}(\mathbf{X}^{-j})$ is a continuous function of X ^k , and, defining $\bar{\mathcal{X}}^{j} \subset \mathbb{R}_{+}^{N-1}$ as the set of values of X ^−j where $\tilde{X}^{j}(\mathbf{X}^{-j}) = 0$ ,

$$\displaystyle{ \mathop{\mathrm{sgn}}\nolimits \left \{\frac{\partial \tilde{X}^{j}(\mathbf{X}^{-j})} {\partial X^{k}} \right \} =\mathop{ \mathrm{sgn}}\nolimits \left \{ \frac{\partial ^{2}u_{i}^{\,j}} {\partial x_{i}^{\,j}\partial X^{k}}\right \} }$$

for all $\mathbf{X}^{-j} \in \mathbb{R}_{+}^{N-1}\setminus \bar{\mathcal{X}}^{j}$ . Moreover, if the strategic effects within group j are stronger than the strategic effects between group j and group k, which requires that $\left \vert \frac{\partial ^{2}u_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X^{k}}\right \vert < \left \vert \sigma _{i}^{\,j} \frac{\partial ^{2}u_{ i}^{\,j}} {\partial (x_{i}^{\,j})^{2}} + [1 -\sigma _{i}^{\,j}] \frac{\partial ^{2}u_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X_{-i}^{j}}\right \vert$ for all σ _i ^j ∈ [0,1], for all i ∈ I ^j , then $\left \vert \frac{\partial \tilde{X}^{j}(\mathbf{X}^{-j})} {\partial X^{k}} \right \vert < 1$ .

Mutual consistency of group best responses requires the identification of a fixed point of the N-dimensional joint group best response function. Since strong assumptions about the differentiability of individuals’ payoffs are made, group best responses are continuous functions and therefore the existence of a Nash equilibrium is ensured by Brouwer’s fixed point theorem (so long as an assumption of bounded aggregate strategy spaces can also be made). In applications, careful consideration might also be given to whether this fixed point lies in the interior of the aggregate action space, or whether some groups are inactive in equilibrium (i.e. if $\mathbf{X}^{-j} \in \bar{\mathcal{X}}^{j}$ for any j ∈ J).

It may be possible to say something not only of existence, but also of uniqueness; and to study the comparative static properties of equilibrium: using the approach of group best responses, a comparative static exercise will reveal the effect on group aggregates directly, which are often of primary interest, without having to first deduce the effect on individual equilibrium behaviour that is then aggregated. In applications group best response functions may have clear properties that allow definitive statements about the nature of equilibrium to be made. Whilst it is difficult to draw conclusions in such a general setting as this, the following two statements can be made:

• 1. If $\tilde{X}^{j}(\mathbf{X}^{-j})$ is increasing in X ^k for all k ≠ j ∈ J, then the strategic interaction at the level of groups exhibits complementarities, and the insights from the study of supermodular games (see, for example, Vives 1990) can be used to understand the comparative static properties of the equilibrium group aggregates at the extremal equilibria.⁴

• 2. If N = 2 and the absolute value of the slope of group best response functions for each group (that can be drawn in the space of aggregate group actions) is less than 1, the conditions for which are presented in Proposition 5, the joint group best response will be a contraction and so there will be a unique Nash equilibrium.⁵ Whilst there might be many heterogeneous players within groups, using a multiple aggregate game approach renders the study of the comparative static properties of the equilibrium relatively simple, for the effect of a change in the economic environment on group aggregates in the two-group case will follow from a simple diagrammatic exercise.

5 Nested Aggregative Games

If a strategic interaction has the features of a ‘nested aggregative game’ more structure can be added to the analysis to draw conclusions about uniqueness of Nash equilibrium in the full game, denoted $\hat{\mathcal{G}}$, even when there are several groups. In such games the members of each group care about their own action, their group’s aggregate action, and the aggregation of all other groups’ aggregate actions, so payoffs can be written $\hat{u}_{i}^{\,j}(x_{i}^{\,j},X^{j};X)$. To analyse this game, the share function approach will be applied twice: once at the level of individuals in groups to replace the fixed point problem of finding consistent actions within groups, as with the analysis so far; and then at the level of groups to replace the fixed point problem of finding consistent aggregate actions between groups.

First fix a value for the aggregate actions of all groups, X, select a group j, and define a ‘partial game’ $\hat{\mathcal{G}}^{j}(X)$ in which only the members of group j are considered. The analysis of the partial games is slightly different since whilst the aggregate X is treated as fixed, the influence of players within the group on this aggregate must be accounted for. The aim is to find a group aggregate action that is consistent with a Nash equilibrium in $\hat{\mathcal{G}}$ in which the aggregate of all individuals is X, which means that the group aggregate action must be consistent with the behaviour of members of the group.

Thus, in $\hat{\mathcal{G}}^{j}(X)$ consider the actions of each member of the group consistent with a Nash equilibrium in which the aggregate of all players is X, and the aggregate of the members of group j is X ^j. Share functions that represent consistent individual behaviour in this partial game are denoted $\hat{s}_{i}^{\,j}(X^{j};X)$, and take the form $\hat{s}_{i}^{\,j}(X^{j};X) =\max \{ 0,\sigma _{i}^{\,j}\}$ where σ _i ^j is the solution to

$$\displaystyle{ \hat{l}_{i}^{\,j}(\sigma _{ i}^{\,j},X^{j};X) \equiv \frac{\text{d}\hat{u}_{i}^{\,j}(\sigma _{ i}^{\,j}X^{j},X^{j};X)} {\text{d}x_{i}^{\,j}} = \frac{\partial \hat{u}_{i}^{\,j}} {\partial x_{i}^{\,j}} + \frac{\partial \hat{u}_{i}^{\,j}} {\partial X^{j}} + \frac{\partial \hat{u}_{i}^{\,j}} {\partial X} = 0 }$$

(8)

so long as this does not exceed 1, otherwise the share function is undefined. Consistency of the aggregate action of the members of group j requires individual actions to sum to this aggregate action, or for $\sum _{i\in I^{j}}\hat{s}_{i}^{\,j}(X^{j};X) = 1$. On varying X, this gives the ‘group replacement function’ $\hat{X}^{j}(X)$, and to find a Nash equilibrium in the game $\hat{\mathcal{G}}$ an aggregate action X must be found that is consistent with the collective behaviour of groups.

Proposition 6

In a nested aggregative game $\hat{\mathcal{G}}$ , x ^∗ is a Nash equilibrium if and only if

$$\displaystyle{ \sum _{j\in J}\hat{X}^{j}(X^{{\ast}}) = X^{{\ast}}. }$$

As with individuals within groups, it is often more convenient to work with a group’s share of the overall aggregate action, rather than the group aggregate itself. For X > 0, the ‘group share function’ is $\hat{S}^{j}(X) =\hat{ X}^{j}(X)/X$; letting $\Lambda ^{j} = X^{j}/X$ the group share function (if it is positive) is that value of $\Lambda ^{j}$ that satisfies

$$\displaystyle{ \hat{L}^{j}(\Lambda ^{j},X) \equiv \sum _{ i\in I^{j}}\hat{s}_{i}^{\,j}(\Lambda ^{j}X;X) - 1 = 0 }$$

(9)

so long as the resulting $\Lambda ^{j}$ does not exceed 1, in which case the group share function is undefined. Accordingly, taking the aggregation of group share functions to be defined only for values of X where the group share function of all groups is defined, there is a Nash equilibrium in the game $\hat{\mathcal{G}}$ with aggregate action X > 0 if and only if

$$\displaystyle{ \sum _{j\in J}\hat{S}^{j}(X) = 1. }$$

The next proposition collects the features of group share functions that allow conclusions about uniqueness of Nash equilibrium to be drawn (in the proof the properties of individual share functions that are relied on to construct the aggregate share functions are also elucidated).

Proposition 7

Suppose that for each i ∈ I ^j ,j ∈ J utility $\hat{u}_{i}^{\,j}$ is continuously differentiable in each argument as many times as required, and that $\frac{\text{d}\hat{u}_{i}^{\,j}(\sigma _{ i}^{\,j}X^{j},X^{j};X)} {\text{d}x_{i}^{\,j}}$ is strictly decreasing in each of its arguments. Then within each partial game $\hat{\mathcal{G}}^{j}(X)$ the group share function $\hat{S}^{j}(X)$ is defined for all $X \geq \hat{\underline{ X}}^{j}$ which is X such that $\hat{L}^{j}(1,X) = 0$ if this is strictly positive, otherwise it is defined for all X > 0 with $\lim _{X\rightarrow 0}\hat{S}^{j}(X) =\hat{\bar{ S}}^{j}$ ; and it is positive for all $X <\hat{\bar{ X}}^{j}$ which is X such that $\hat{L}^{j}(0,X) = 0$ . Where it is defined and positive, the group share function is strictly decreasing in X. Consequently, there is at most one Nash equilibrium with X > 0 in $\hat{\mathcal{G}}$ , and if either $\hat{\underline{X}}^{j} > 0$ for any j ∈ J, or $\sum _{j\in J}\hat{\bar{S}}^{j} > 0$ if $\hat{\underline{X}}^{j} = 0$ for all j ∈ J, there is exactly one such Nash equilibrium.

Thus, in a nested aggregative game the aggregative properties of the game are exploited twice: once at the level of individuals within groups; and once at the level of groups. Deductions concerning the uniqueness of equilibrium can then be made even when there are many groups of heterogeneous players and indeed, once an equilibrium has been identified, whether all groups are active, and whether all individuals within active groups are active, can be understood: in particular, if there is a Nash equilibrium with aggregate X ^∗ and $\hat{\bar{X}}^{j} \geq X^{{\ast}}$ then group j will be inactive in equilibrium. If a comparative static exercise were to be undertaken for a nested aggregative game, the effect of a change in the economic environment on individual and therefore group share functions must first be understood, and then the effect on the equilibrium aggregate action can be determined, which may in fact be of primary interest; if desired, the effect on the equilibrium aggregate actions of each group can then be considered, along with the effect on individual group members’ actions.

6 Applications

6.1 Group Contests

In a standard (Tullock-style) contest each of several individuals chooses the level of ‘effort’ to exert in contesting a rent, and their success in doing so is determined by the contest success function. In a ‘winner-take-all’ contest the rent is indivisible and the contest success function determines the probability of a contestant being awarded the rent; hence the contest (imperfectly) discriminates between contestants, giving a higher probability of winning to contestants that exert more effort. In a ‘rent-sharing’ contest the rent is perfectly divisible and the contest success function determines the share of the rent awarded to each contestant. This discussion considers contests of the latter variety.

If the set of contestants is {1, …, i, …, N}, the effort chosen by contestant i is e _i  ≥ 0, the aggregate effort of all contestants is E, and E _−i  = E − e _i , then in a simple Tullock contest the contest success function is given by $\frac{e_{i}} {e_{i}+E_{-i}}$ (if E > 0, otherwise it is 1∕N), and so if R is the contested rent and there is a unit cost of effort each contestant’s payoff takes the form $\frac{e_{i}} {e_{i}+E_{-i}}R - e_{i}$. Extensions to this simple model include non-linear costs of effort c _i (e _i ); endogenous determination of the rent whereby R = f(E) (Chung 1996); and of course more general contest success functions in which the impact of effort in the contest is given by p _i (e _i ) and the contest success function takes the form $\frac{p_{i}(e_{i})} {\sum _{h=1}^{N}p_{h}(e_{h})}$ (see, for example, Cornes et al. 2005). With these extensions, contests capture a multitude of interesting economic environments, so understanding their properties is of upmost importance. There is, of course, a substantial literature on contests, and several contributions have used the techniques of aggregative games to undertake the analysis; it is clear from the contest success function that a contestant’s share of the aggregate is important, and it was indeed in the study of a ‘joint production game’—in which the collective output of individuals is determined by their aggregate input, which is then shared in proportion to those inputs; a simple Tullock contest with an endogenous rent—that the Cornes-Hartley duo first utilised the share function approach (Cornes and Hartley 2000).

While standard contests are appropriate for modelling many economic environments, in some settings individuals are naturally organised into groups and the group plays at least some role in the outcome of the contest. There are, inter alia, three interesting scenarios to consider in the context of group contests:

• 1. In a collective contest each individual belongs to a group and decides on a level of effort to contribute to the group. The collective effort of a group then determines the share of the rent received by that group (or the probability of winning the rent in a winner-take-all contest) which then becomes a public good for the group enjoyed equally by all group members irrespective of their initial choice of effort.

• 2. In an intra- and inter-group contest each individual belongs to a group and decides on a level of effort that contributes to the collective effort of the group which determines the share of the rent awarded to that group (as in a collective contest); and a group member’s contribution to this collective effort also influences their allocation of the rent within the group.⁶

• 3. Individuals within groups may be engaged in a contest in which there are spill-overs between groups, captured by the size of the rent that each group enjoys itself being influenced by the actions of other groups. Individuals within groups might be engaged in otherwise independent contests, so the actions of members of other groups only influence the rent being contested within each group. Alternatively, groups might be engaged in a contest with each other where the valuation of the rent by each group is influenced by the actions of other groups, which then either becomes a public good for the group members (as in a collective contest), or is contested within the group (as in an intra- and inter-group contest).

6.1.1 Collective Contests

In a collective contest individual i in group j chooses a level of effort x _i ^j to contribute to the group. X ^j is then the collective effort of the group. The relative effort of group j, X ^j∕X, determines the share of an exogenously given rent R awarded to group j that becomes a public good for its members. Let v _i ^j be individual i’s valuation of the rent and c _i ^j(⋅ ) their cost of effort, which are possibly different for different individuals within each group. Then the payoff to a typical contestant is given by

$$\displaystyle{ \hat{u}_{i}^{\,j}(x_{ i}^{\,j},X^{j};X) = \frac{X^{j}} {X} v_{i}^{\,j} - c_{ i}^{\,j}(x_{ i}^{\,j}). }$$

As such, it is clear that collective contests exhibit the features of a nested aggregative game, since payoffs depend only on individual actions, the aggregate action of the group, and the aggregation of all groups’ actions.

Such contests capture the essence of collective action; as Konrad (2009, p. 129) notes, “[given the aggregate effort of other groups] the individual effort contributions to the aggregate group effort are contributions to a public good”: the quantity of the public good is X ^j∕X and individual i’s valuation of it is (X ^j∕X)v _i ^j. It is of course very interesting to understand the effect of collective action on the outcome of the contest, and there is no lack of literature on this subject. Katz et al. (1990) show that when the cost of effort is linear and the valuation of the rent of each member of a group is the same the aggregate effort of each group is uniquely determined and independent of group size, but there is indeterminacy over the split of aggregate effort within the group. In this case the fact that individuals are in groups plays very little role in the outcome, since groups act as though they are one individual, despite the presence of a free-rider problem within groups. Baik (2008) allows for heterogeneous valuations and shows that only the highest-valuation individuals choose positive effort in equilibrium, the remaining individuals free-riding, so consequently there is under-investment in effort by the group. The analysis of this game is very much in the spirit of the idea of partial games since it proceeds by focussing on a group, fixing the actions of the agents in other groups, and considering what is termed the “group [j]-specific equilibrium”, which has a straightforward solution given that a single player in each group contributes to collective effort, or if more than one player contributes then those players are necessarily identical.

That all members of a group except those that value the good highest free-ride on the highest valuation members is sensitive to the assumption of linear costs of effort. If costs are convex (but the same for all group members) then all members of a group will contribute to collective effort, as explained by Esteban and Ray (2001) and neatly summarised in Corchón (2007, Sect. 4.2). In these collective contests with convex costs the idea of the “group size paradox”—that free riding is more acute in large groups, meaning smaller groups are more effective—can be explored: however, it is found that whilst individual effort is lower in larger groups the aggregate effort of the group is higher, in contrast to the paradox. This is true where the group see the contested rent as a public good, and even when there is some congestion of it, so long as it is not too strong. Nitzan and Ueda (2014) have extended this literature to allow for members of groups to have both different valuations and different costs, which they do by utilising what has been called here a nested aggregative game approach to derive group share functions and establish consistency of aggregate actions to identify the Nash equilibrium. Being very tractable, this method of analysis allows free riders within groups that make no contribution to group effort to be identified, and the effect of heterogeneity on a group’s performance and the contest outcome to be carefully considered.

6.1.2 Intra- and Inter-Group Contests

In an intra- and inter-group contest it is again the relative collective effort of groups that determine their share of the rent (which is taken to have a common value for all group members), but the allocation of that rent share within the group is influenced by the relative effort of group members. In Nitzan (1991) the intra-group allocation is partially determined by the relative effort of group members, with the remaining rent being distributed in an egalitarian way. If α ^j is the proportion of the rent that is equally distributed within group j, the payoff to contestant i in group j is given by

$$\displaystyle{ \hat{u}_{i}^{\,j}(x_{ i}^{\,j},X^{j};X) = \left [\alpha ^{j} \frac{1} {N^{j}} + (1 -\alpha ^{j})\frac{x_{i}^{\,j}} {X^{j}}\right ]\frac{X^{j}} {X} R - c_{i}^{\,j}(x_{ i}^{\,j}), }$$

which is again a nested aggregative game.

If α ^j = 0 for all groups then the X ^j in the intra-group contest success function cancels with that in the inter-group contest success function, and the group structure becomes irrelevant as the contest can be seen as a standard Tullock contest with ∑ _j ∈ J N ^j contestants; hence the characteristics of groups plays no role in the outcome of the contest. If α ^j = 1 then the case collapses to a contest that is similar to a collective contest in which the value of the contested rent to group j is given by R∕N ^j. Nitzan (1991) undertook an in-depth analysis of this contest by appealing to the symmetry of contestants within groups by assuming a linear cost of effort and symmetry of sharing rules for groups, showing that as a larger proportion of the rent within groups is allocated based on relative effort, so the collective effort of groups, and consequently the aggregate effort and dissipation of the rent, increases.

By using a nested aggregative game approach, unrealistic symmetry assumptions can be avoided, allowing contestants to have convex costs of effort that can be different. The analysis would proceed by first fixing the aggregate effort of all groups at X and considering consistency of actions among the members of group j. This will define individual share functions, and the value of X ^j such that the sum of these share functions is equal to one will give the group-j reaction function, revealing the aggregate effort of group j consistent with a Nash equilibrium in which the aggregate effort of all groups is X. The Nash equilibrium can be found by identifying the level of aggregate effort of all groups that generates consistent group efforts that exactly sum to it, which is where the sum of group share functions is equal to one.

As Konrad (2009) notes, when groups have different sharing rules it is not necessarily the case that all groups will be active in equilibrium, and indeed it will be the case that when contestants within a group have different costs not all contestants will be active. The multiple aggregate game approach, being very tractable in terms of the representation of behaviour consistent with equilibrium, allows for a full understanding of the composition of equilibrium effort to be understood: once group share functions have been aggregated and the equilibrium aggregate effort of all groups found, each group’s share function merely needs evaluating at the equilibrium aggregate effort to check whether or not it is zero; and for those groups where it is strictly positive the share functions of individuals within groups can be evaluated to understand which group members are active. The approach holds much hope for understanding the fine details of the equilibrium in group contests, even in quite general settings.

6.1.3 Contests with Group Spill-Overs

An area where multiple aggregate games is likely to make a strong contribution to the analysis of contests in the future is where there are spill-overs between groups’ collective effort in terms of the value of the rent being contested by the group, and there is heterogeneity both within and between groups. This can be captured specifying that the value of the rent contested by group j is given by f ^j(X ^j, X ^−j). This specification allows the rent to be influenced by the group’s own aggregate effort, but not necessarily so. If ∂ f ^j∕∂ X ^k > ( < )0 then there are positive (negative) externalities between group k and group j. With this rent structure, there might be no other inter-group conflict as contestants within groups contest their group’s rent in N otherwise independent group contests; or there may be additional inter-group conflict since the rent, which is valued differently by different groups, is contested between groups as in a collective contest, which could also be coupled with an inter-group contest. The payoff to a typical contestant in the former case would be of the form u _i ^j(x _i ^j, X ^j; X ^−j) = (x _i ^j∕X ^j)f ^j(X ^j, X ^−j) − c _i ^j(x _i ^j), and for the latter case it would be

$$\displaystyle{ u_{i}^{\,j}(x_{ i}^{\,j},X^{j};\mathbf{X}^{-j}) = \left [\alpha ^{j} \frac{1} {N^{j}} + (1 -\alpha ^{j})\frac{x_{i}^{\,j}} {X^{j}}\right ]\frac{X^{j}} {X} f^{j}(X^{j},\mathbf{X}^{-j}) - c_{ i}^{\,j}(x_{ i}^{\,j}), }$$

both of which are multiple aggregate games, but not nested aggregative games.

Contests with group spill-overs hold a wealth of interest in terms of applications. In industrial organisation, the framework could be used to capture Cournot competition (which is a simple Tullock contest where effort is output and the rent is endogenously determined as total revenue in the market) between two (or more) groups of sellers who each produce a homogeneous good that acts as a substitute or complement to the other, so the aggregate actions of one group of sellers influence the total revenue that the other group is contesting. In political settings, individuals within political allegiances might contest a rent and the value of this rent is influenced by the actions of competing groups during the campaign. In international trade, groups of traders located in different countries interact both with each other in the home market and, because of trade, the value of this activity will be influenced by the aggregate actions of firms in different locations.

Using the framework of multiple aggregate games, by first resolving the within-group strategic interaction having fixed the behaviour of other groups, and then seeking mutual consistency of behaviour at the level of groups, gives hope for developing an understanding of the features of equilibrium in these as well as other settings to generate new insight concerning these relatively under-explored yet interesting economic environments.

6.2 Bilateral Oligopoly

Bilateral oligopoly is a model of trade in which there is market power on both sides of the market. Given this, a group-based analysis is likely to be fitting as the actions of traders on each side of the market will affect each other, and they will also affect, and be affected by, the actions of traders on the opposite side of the market in the aggregate. One approach to modelling bilateral oligopoly is using a two-commodity version of a Shapley-Shubik strategic market game (Shapley and Shubik 1977) in which one of the goods takes the role of money, and each trader is endowed either with the good or money. This model was originally introduced by Gabszewicz and Michel (1997) and has seen careful study in the literature by Dickson and Hartley (2008), which inspires this discussion, and Amir and Bloch (2009).

Consider an economic environment in which there is a single good g, and money m, that is populated by traders who have preferences that can be represented by utility functions v _i (g, m). Suppose that the set of traders is partitioned into two groups: group 1 contains individuals that are endowed with e _i ¹ > 0 units of the good but no money, and are called sellers; group 2 contains individuals endowed with e _i ² > 0 units of money but none of the good, and are called buyers. Each seller decides on an offer of the good to make to the market x _i ¹ ≥ 0 to be exchanged for money; and each buyer decides on an amount of money to send to the market x _i ² ≥ 0 to be exchanged for the good.⁷ The market aggregates these offers and bids, and then sellers are awarded a share of the aggregate amount of money sent to the market in proportion to their offer, so receive $\frac{x_{i}^{1}} {X^{1}} X^{2}$ units of money; and similarly buyers are awarded their proportional share of the aggregate amount of the good in the market, so receive $\frac{x_{i}^{2}} {X^{2}} X^{1}$ units of the good.⁸

Bilateral oligopoly is therefore a game between two groups where, within each group, individuals engage in a simple Tullock contest in which they choose actions to contest a perfectly divisible prize, the value of which is determined by the aggregation of actions of members of the other group. Payoffs in this game take the form

$$\displaystyle{ u_{i}^{\,j}(x_{ i}^{\,j},X_{ -i}^{j};\mathbf{X}^{-j}) = \left \{\begin{array}{ll} v_{i}\left (e_{i}^{1} - x_{ i}^{1}, \frac{x_{i}^{1}} {x_{i}^{1}+X_{-i}^{1}} X^{2}\right )&\text{if }\ j = 1\text{, or} \\ v_{i}\left ( \frac{x_{i}^{2}} {x_{i}^{2}+X_{-i}^{2}} X^{1},e_{i}^{2} - x_{i}^{2}\right )&\text{if }\ j = 2, \end{array} \right. }$$

and so the game is a multiple (two) aggregate game, but is not a nested aggregative game.

An analysis using the approach outlined here involves first fixing the actions of the buyers and considering the partial game played by the sellers to deduce a function $\tilde{X}^{1}(X^{2})$ that represents the aggregate offers from the sellers consistent with a Nash equilibrium in which the aggregate bid made by the buyers is X ²; and second considering the partial game played by the buyers when the actions of the sellers are considered fixed to deduce the consistent aggregate bid function of the buyers $\tilde{X}^{2}(X^{1})$. When traders’ preferences are ‘binormal’, which requires the (absolute value of) the marginal rate of substitution of the good for money ($\frac{\partial v_{i}/\partial g} {\partial v_{i}/\partial m}$) to be decreasing as consumption of the good increases and increasing as consumption of money increases, the share function of every trader is strictly decreasing in the aggregate on their side of the market (Dickson and Hartley 2008; Dickson 2013). Moreover, as Dickson (2013) showed, if for each seller the ratio of the marginal rate of substitution to m is decreasing in m then the consistent aggregate offer function will be increasing in the aggregate bid; and if for each buyer the product of the marginal rate of substitution and g is increasing in g then the consistent aggregate bid function will be increasing in the aggregate offer, as illustrated in Fig. 2.

Fig. 2

Consistent aggregate bid and offer functions in bilateral oligopoly

Under these conditions on preferences there are ‘group complementarities’, and therefore the ideas of supermodular games applied to group best response functions could be used to discern some comparative static properties of the extremal equilibria. In the illustration there is a single Nash equilibrium, but in this case, since the game has features that mean the group best responses begin from the origin, uniqueness of (non-null) Nash equilibrium cannot be ascertained by appealing to the contraction principle for, if the slope of each group best response is everywhere below 1 they will never cross in the interior of aggregate action space. Another possibility is to consider that the slope at the origin exceeds 1 and the group best response functions are concave: in practice many standard utility functions give rise to this property, but deriving an intuitive general statement on preferences is difficult.

To circumvent these issues, Dickson and Hartley (2008) characterised the individual and aggregate behaviour of the two groups consistent with a Nash equilibrium in which the ratio of the aggregate money bid to the aggregate amount of commodity offered—which is the price of the good—takes a particular value. For the sellers this is a strategic supply function, and when the consistent aggregate bid of the buyers is divided by the price it is a strategic demand function. Nash equilibria in bilateral oligopoly are identified by the intersections of these strategic versions of Marshallian supply and demand functions, which are monotonic in the expected direction under the stated conditions on preferences and so intersect only once.

This analysis, and in particular study of the uniqueness of Nash equilibrium which is tackled in an environment of heterogeneous traders, is made possible only by taking a multiple aggregate game approach and fixing one side of the market to consider consistent behaviour in the partial game played on the other side of the market. Once the within-group strategic interaction has been resolved and the consistent aggregate behaviour derived, the intersection of strategic supply and demand functions ensures consistency between the sides of the market.

After determining the equilibrium price, equilibrium values of the aggregate offer and bid can be deduced, following which individual traders’ strategies can be found, revealing whether there are any inactive traders on either side of the market. Comparative statics are relatively straightforward to undertake to develop an understanding of, for example, the effect of increasing the number of traders on one side of the market, or of increasing the endowment of goods for some sellers, where the effect on the number of sellers that are active in equilibrium might be of relevance.

6.3 Group Public Goods

In an unpublished manuscript, Cornes et al. (2005) consider the provision of public goods within groups when there are spill-overs between groups, capturing the principal of the free-rider problem but where there is also group inter-dependence. If x _i ^j is the contribution of player i to the public good of group j then the quantity of the public good provided by group j is X ^j and, because of the spill-overs between groups the level of the public good consumed by individuals in group j is given by X ^j + ∑ _{k ≠ j ∈ J} θ ^j, k X ^k, where θ ^j, k is the spill-over parameter capturing how the public good provided by group k influences the members of group j. If there is concordance of interests between group k and j then θ ^j, k > 0, whilst if their interests are conflicting θ ^j, k < 0. The consumption of the private good is m _i ^j − c _i ^j x _i ^j where m _i ^j is income and c _i ^j the cost of public good provision. The payoff to a typical player is thus

$$\displaystyle{ u_{i}^{\,j}(x_{ i}^{\,j},X^{j};\mathbf{X}^{-j}) = v_{ i}^{\,j}(m_{ i}^{\,j} - x_{ i}^{\,j},X^{j} +\sum _{ k\neq j\in J}\theta ^{j,k}X^{k}), }$$

where v _i ^j(⋅ , ⋅ ) is the player’s utility defined over private good consumption and public good consumption. More general formulations of the ‘public good production function’ for each group could be considered that might account for complementarities between public goods, for example. So long as it is only the aggregate provision of public goods by other groups that matters to an individual, this is a multiple aggregate game.

If the spill-over parameter is common for all groups, i.e. θ ^j, k = θ for all k ≠ j ∈ J, for all j ∈ J, then the quantity of the public good consumed by group j can be written θ X + (1 −θ)X ^j. In this case, payoffs are

$$\displaystyle{ \hat{u}_{i}^{\,j}(x_{ i}^{\,j},X^{j},X) = v_{ i}^{\,j}(m_{ i}^{\,j} - x_{ i}^{\,j},\theta X + (1-\theta )X^{j}), }$$

and therefore the game is a nested aggregative game.

Cornes et al. (2005) investigate the latter formulation using a replacement function approach. Individual replacement functions $\hat{r}_{i}^{\,j}(X^{j};X)$ give the contribution of player i in group j consistent with a Nash equilibrium in which the aggregate contribution of group j is X ^j, and the aggregate contribution of all groups is X. They seek group consistency by requiring, for a given X, that $\sum _{i\in I^{j}}r_{i}^{\,j}(X^{j};X) = X^{j}$ for each j ∈ J which gives the group-j consistent contribution $\hat{X}^{j}(X)$, which is a group replacement function. Overall consistency then requires $\sum _{j\in J}\hat{X}^{j}(X) = X$.

They are able to show that with appropriate restrictions on preferences individual replacement functions are decreasing in X ^j and therefore the group-j consistent contribution is unique, so group replacement functions are indeed functions. Moreover, if groups’ interests are concordant then individual replacement functions are also decreasing in X which implies that group replacement functions are decreasing in X, so there is a unique value of X where $\sum _{j\in J}\hat{X}^{j}(X) = X$ and so a unique Nash equilibrium. If group interests are conflicting then group replacement functions are increasing in X, but so long as the conflict is not too strong the function $\sum _{j\in J}\hat{X}^{j}(X)$ will be a contraction (its slope will be less than one) with a unique fixed point and therefore a unique Nash equilibrium. Given uniqueness of equilibrium, found under quite general conditions, understanding the comparative static properties of equilibrium is a relatively straightforward task.

Cornes et al. (2005) suggest an extension to the case where the good generated by contributions of individuals does not become a pure nonexcludable good, but is distributed among group members according to some sharing rule. This could be captured by considering that the good becomes a private good and is shared among group members according to the rule $[\alpha \frac{1} {N^{j}} + \frac{x_{i}^{\,j}} {X^{j}} ]$, as in Nitzan (1991). This preserves the nested aggregate nature of the game, and is consistent with the idea of contests between groups where the size of the contested rent is influenced by the actions of other groups, introduced previously, and so could be analysed using the tools of multiple aggregate games.

7 Concluding Remarks

This contribution considers the theory of multiple aggregate games, in which individuals are organised into groups and there are both within-group and between-group strategic tensions that can be very different in nature. This general framework captures environments in which there is a collective element to individual actions within groups, and externalities between groups’ aggregate actions. The within-group strategic interaction is assumed to have the features of an aggregative game, and this is exploited in the method proposed to analyse these games, which follows a two step procedure: first, the intra-group strategic interaction is resolved through study of group ‘partial games’ to derive group best responses; then the inter-group game is analysed by considering mutual consistency of these group best responses at the level of group aggregates. If ‘aggregativeness’ also pervades the between-group interaction, as in a nested aggregative game, then rather than using group best responses, group replacement functions can be derived that have a much simpler consistency requirement to identify equilibria.

Exploiting the aggregative properties of games makes for a very tractable analysis since the structure of the game is used to reduce the dimensionality of the problem. Replacement (or share) functions often have very clear properties in terms of their monotonicity and where they drop to zero, that are preserved when they are aggregated. Establishing existence and uniqueness of Nash equilibrium; understanding which players are active in equilibrium; and undertaking a comparative static analysis (that may involve adding players) are all relatively straightforward tasks.

By using this method within groups and, if appropriate, also between groups, the analysis of multiple aggregate games becomes much less daunting even with heterogeneity of players in groups, and heterogeneity between groups. In applications, this permits a rather general analysis to be undertaken that has the scope to answer many interesting questions that might be posed, particularly related to the effect of heterogeneity within and between groups. Some applications that have been considered in the literature—collective contests; group provision of public goods; bilateral oligopoly—have been discussed, and others speculated upon. Some of these, as well as many others, fit within a model of group contests with group spill-overs, careful study of which seems to be a fruitful direction for future research. I hope that the exposition of multiple aggregate games presented here is useful in pursuing this and other lines of research, and I also hope that I have done justice to the ideas that Richard and I discussed.

Appendix: Proofs

Proof of Proposition 1

The proof is by simple definition chasing. If x ^∗ is a Nash equilibrium in $\mathcal{G}$, then by definition $x_{i}^{\,j{\ast}} =\tilde{ x}_{i}^{\,j}(\mathbf{X}^{-j{\ast}})$ for all i ∈ I ^j, j ∈ J. But then for each j ∈ J, $X^{j{\ast}} =\sum _{i\in I^{j}}\tilde{x}_{i}^{\,j}(\mathbf{X}^{-j{\ast}}) =\tilde{ X}^{j}(\mathbf{X}^{-j{\ast}})$. Conversely, if $X^{j{\ast}} =\tilde{ X}^{j}(\mathbf{X}^{-j{\ast}})$ for all j ∈ J, then by definition x ^j∗ where $x_{i}^{\,j{\ast}} =\tilde{ x}_{i}^{\,j}(\mathbf{X}^{-j{\ast}})$ for each i ∈ I ^j is a Nash equilibrium in $\mathcal{G}^{j}(\mathbf{X}^{-j{\ast}})$ for all j ∈ J; it then follows that x ^∗ is a Nash equilibrium. □ 

Proof of Proposition 2

The proof is again by definition chasing. First, if x ^j∗ is a Nash equilibrium then x _i ^j∗ = b _i ^j(X _−i ^j∗; X ^−j) for all i ∈ I ^j. This implies x _i ^j∗ = b _i ^j(X ^j∗− x _i ^j∗; X ^−j), and so by definition x _i ^j∗ = r _i ^j(X ^j∗; X ^−j) for all i ∈ I ^j; and therefore $\sum _{i\in I^{j}}r_{i}^{\,j}(X^{j{\ast}};\mathbf{X}^{-j}) = X^{j{\ast}}$. To prove necessity, suppose $\sum _{i\in I^{j}}r_{i}^{\,j}(X^{j{\ast}};\mathbf{X}^{-j}) = X^{j{\ast}}$ and consider the strategy x _i ^j∗ = r _i ^j(X ^j∗; X ^−j). By definition of the replacement function, x _i ^j∗ = b _i ^j(X ^j∗− x _i ^j∗; X ^−j), and since $X^{j{\ast}} =\sum _{i\in I^{j}}r_{i}^{\,j}(X^{j{\ast}};\mathbf{X}^{-j})$ it follows that $X^{j{\ast}}- x_{i}^{\,j{\ast}} =\sum _{h\neq i\in I^{j}}r_{h}^{j}(X^{j{\ast}};\mathbf{X}^{-j}) = X_{-i}^{j{\ast}}$. As such, x _i ^j∗ = b _i ^j(X _−i ^j∗; X ^−j) for all i ∈ I ^j, so x ^j∗ is a Nash equilibrium in $\mathcal{G}^{j}(\mathbf{X}^{-j})$. □ 

Proof of Proposition 3

A player’s share function is the value of σ _i ^j that makes l _i ^j, defined in (5), equal to 0—however, if this is below zero the share function is defined as zero; and if it is above 1 the share function is undefined. First, note that under Assumption 1

$$\displaystyle\begin{array}{rcl} \frac{\partial l_{i}^{\,j}} {\partial \sigma _{i}^{\,j}} & = X^{j}\left [ \frac{\partial ^{2}u_{ i}^{\,j}} {\partial (x_{i}^{\,j})^{2}} + \frac{\partial ^{2}u_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X_{-i}^{j}}\right ] < 0\ \text{ and}& {}\\ \frac{\partial l_{i}^{\,j}} {\partial X^{j}}& =\sigma _{ i}^{\,j} \frac{\partial ^{2}u_{ i}^{\,j}} {\partial (x_{i}^{\,j})^{2}} + [1 -\sigma _{i}^{\,j}] \frac{\partial ^{2}u_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X_{-i}^{j}} < 0.& {}\\ \end{array}$$

The first inequality implies there is at most one σ _i ^j ∈ [0, 1] where l _i ^j = 0 so the share function is indeed a function. Continuity of this function, where it is defined, follows from l _i ^j varying continuously in all its arguments by virtue of the assumed differentiability of utility functions.

If X _i ^j(X ^−j) > 0, by definition, l _i ^j(1, X _i ^j(X ^−j); X ^−j) = 0, so s _i ^j(X _i ^j(X ^−j), X ^−j) = 1 and the monotonicity properties just stated imply that for all X ^j < X _i ^j(X ^−j), l _i ^j > 0 for all σ _i ^j ≤ 1, and therefore the share function is undefined. In addition, again by definition, if $\bar{X}_{i}^{\,j}(\mathbf{X}^{-j}) < \infty$ then $l_{i}^{\,j}(0,\bar{X}_{i}^{\,j}(\mathbf{X}^{-j});\mathbf{X}^{-j}) = 0$ so $s_{i}^{\,j}(\bar{X}_{i}^{\,j}(\mathbf{X}^{-j});\mathbf{X}^{-j}) = 0$ and the monotonicity properties of l _i ^j imply that for all $X^{j} >\bar{ X}_{i}^{\,j}(\mathbf{X}^{-j})$, l _i ^j = 0 only when σ _i ^j < 0, and therefore by definition s _i ^j(X ^j; X ^−j) = 0.

Where it is positive and defined, implicit differentiation of the first-order condition that defines the share function, (5), gives

$$\displaystyle{ \frac{\partial s_{i}^{\,j}} {\partial X^{j}} = -\frac{\frac{\partial l_{i}^{\,j}} {\partial X^{j}}} {\frac{\partial l_{i}^{\,j}} {\partial \sigma _{i}^{\,j}} } < 0, }$$

where the inequality follows from the deductions above.

If X _i ^j(X ^−j) = 0 the share function is defined for all X ^j > 0 where it takes values in the compact set [0, 1], so (taking subsequences if necessary) the limit as X ^j → 0 will exist, which is denoted $\bar{s}_{i}^{\,j}(\mathbf{X}^{-j})$. □ 

Proof of Proposition 4

If $\bar{X}_{i}^{\,j}(\mathbf{X}^{-j}) < \infty$ the share function of individual i ∈ I ^j is equal to zero for all $X^{j} \geq \bar{ X}_{i}^{\,j}(\mathbf{X}^{-j})$. If not, then since it is assumed that $\lim _{x_{i}^{\,j}\rightarrow \infty }\frac{\partial u_{i}^{\,j}(x_{ i}^{\,j},\cdot;\cdot )} {\partial x_{i}^{\,j}} < 0$ the first-order condition (5) can hold as X ^j → ∞ only if $\lim _{X^{j}\rightarrow \infty }\sigma _{i}^{\,j}X^{j} < \infty$ which requires σ _i ^j → 0, implying the share function vanishes in the large X ^j limit. This implies there is an $\bar{x}^{\,j}(\mathbf{X}^{-j})$ such that $\sum _{i\in I^{j}}s_{i}^{\,j}(X^{j};\mathbf{X}^{-j}) < 1$ for all $X^{j} >\bar{ x}^{\,j}(\mathbf{X}^{-j})$. The function $\sum _{i\in I^{j}}s_{i}^{\,j}(X^{j};\mathbf{X}^{-j})$ is continuous and strictly decreasing in X ^j for all $\max _{i\in I^{j}}\{\underline{X}_{i}^{\,j}(\mathbf{X}^{-j})\} < X^{j} <\bar{ x}^{\,j}(\mathbf{X}^{-j})$, and is therefore equal to 1 for at most one value of X ^j. If X _i ^j(X ^−j) > 0 for any i ∈ I ^j then $\sum _{i\in I^{j}}s_{i}^{\,j}(\max _{i\in I^{j}}\{\underline{X}_{i}^{\,j}(\mathbf{X}^{-j})\},\mathbf{X}^{-j}) \geq 1$ and so there is a unique value of X ^j where $\sum _{i\in I^{j}}s_{i}^{\,j}(X^{j},\mathbf{X}^{-j}) = 1$. If X _i ^j(X ^−j) = 0 for all i ∈ I ^j then the aggregate share function is defined for all X ^j > 0, with $\lim _{X^{j}\rightarrow 0}\sum _{i\in I^{j}}s_{i}^{\,j}(X^{j},\mathbf{X}^{-j}) =\sum _{i\in I^{j}}\bar{s}_{i}^{\,j}(\mathbf{X}^{-j})$. As such, the existence of a (unique) Nash equilibrium requires $\sum _{i\in I^{j}}\bar{s}_{i}^{\,j}(\mathbf{X}^{-j}) > 1$. □ 

Proof of Proposition 5

For $\mathbf{X}^{-j} \in \mathbb{R}_{+}^{N-1}\setminus \bar{\mathcal{X}}^{j}$, the group best response is implicitly defined by (7). Continuity of the group best response follows from continuity of individual share functions in each of its arguments, which follows from the assumed differentiability of utility functions. With apology⁹ implicit differentiation of (7) gives

$$\displaystyle{ \frac{\partial \tilde{X}^{j}(\mathbf{X}^{-j})} {\partial X^{k}} = -\frac{\sum _{i\in I^{j}} \frac{\partial s_{i}^{\,j}} {\partial X^{k}}} {\sum _{i\in I^{j}}\frac{\partial s_{i}^{\,j}} {\partial X^{j}}}. }$$

(10)

Where an individual’s share function is positive, recall that it is defined by the first-order condition l _i ^j(σ _i ^j, X ^j; X ^−j) = 0 as in (5). As deduced previously,

$$\displaystyle{ \frac{\partial s_{i}^{\,j}} {\partial X^{j}} = -\frac{\frac{\partial l_{i}^{\,j}} {\partial X^{j}}} {\frac{\partial l_{i}^{\,j}} {\partial \sigma _{i}^{\,j}} } = \frac{\sigma _{i}^{\,j} \frac{\partial ^{2}u_{ i}^{\,j}} {\partial (x_{i}^{\,j})^{2}} + [1 -\sigma _{i}^{\,j}] \frac{\partial ^{2}u_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X_{-i}^{j}}} {X^{j}\left [ \frac{\partial ^{2}u_{i}^{\,j}} {\partial (x_{i}^{\,j})^{2}} - \frac{\partial ^{2}u_{i}^{\,j}} {\partial x_{i}^{\,j}\partial X_{-i}^{j}}\right ]} < 0 }$$

under Assumption 1. In addition,

$$\displaystyle{ \frac{\partial s_{i}^{\,j}} {\partial X^{k}} = -\frac{\frac{\partial l_{i}^{\,j}} {\partial X^{k}}} {\frac{\partial l_{i}^{\,j}} {\partial \sigma _{i}^{\,j}} } = - \frac{ \frac{\partial ^{2}u_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X^{k}}} {X^{j}\left [ \frac{\partial ^{2}u_{i}^{\,j}} {\partial (x_{i}^{\,j})^{2}} - \frac{\partial ^{2}u_{i}^{\,j}} {\partial x_{i}^{\,j}\partial X_{-i}^{j}}\right ]}. }$$

Since the denominator is negative under Assumption 1, $\mathop{\mathrm{sgn}}\nolimits \{ \frac{\partial s_{i}^{\,j}} {\partial X^{k}}\} =\mathop{ \mathrm{sgn}}\nolimits \{ \frac{\partial ^{2}u_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X^{k}}\}$. As such, since group members are qualitatively symmetric, it follows that $\mathop{\mathrm{sgn}}\nolimits \{ \frac{\partial \tilde{X}^{j}(\mathbf{X}^{-j})} {\partial X^{k}} \} =\mathop{ \mathrm{sgn}}\nolimits \{ \frac{\partial ^{2}u_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X^{k}}\}$, as stated.

$\left \vert \frac{\partial \tilde{X}^{j}(\mathbf{X}^{-j})} {\partial X^{k}} \right \vert < 1$ if the numerator in (10) is less than the denominator, a sufficient (but by no means necessary) condition for which is $\left \vert \frac{\partial s_{i}^{\,j}} {\partial X^{k}}\right \vert < \left \vert \frac{\partial s_{i}^{\,j}} {\partial X^{j}}\right \vert$ for all i ∈ I ^j, which is implied by the inequality in the proposition. □ 

Proof of Proposition 6

If x ^∗ is a Nash equilibrium, then by definition of share functions $x_{i}^{\,j{\ast}} = X^{j{\ast}}\hat{s}_{i}^{\,j}(X^{j{\ast}};X^{{\ast}})$ for all i ∈ I ^j, j ∈ J. As such, $\sum _{i\in I^{j}}\hat{s}_{i}^{\,j}(X^{j{\ast}};X^{{\ast}}) = 1$ and therefore $X^{j{\ast}} =\hat{ X}^{j}(X^{{\ast}})$ for all j ∈ J, implying $X^{{\ast}} =\sum _{j\in J}\hat{X}^{j}(X^{{\ast}})$. For necessity of the condition, define a player’s best response in a nested aggregative game as b _i ^j(X _−i ^j; X ^−j). Consider the strategy $x_{i}^{\,j{\ast}} =\hat{ X}^{j}(X^{{\ast}})\hat{s}_{i}^{\,j}(X^{j{\ast}};X^{{\ast}})$. By definition of share functions and the consistency of $\hat{X}^{j}(X^{{\ast}})$ within group j (which implies $\hat{X}^{j}(X^{{\ast}}) - x_{i}^{\,j{\ast}} = X_{-i}^{j{\ast}}$), $x_{i}^{\,j{\ast}} = b_{i}^{\,j}(X_{-i}^{j{\ast}};X^{{\ast}}-\hat{ X}^{j}(X^{{\ast}}))$. When $X^{{\ast}} =\sum _{j\in J}\hat{X}^{j}(X^{{\ast}})$, it follows that $X^{{\ast}}-\hat{ X}^{j}(X^{{\ast}}) = X^{-j{\ast}}$, and therefore x _i ^j∗ = b _i ^j(X _−i ^j∗; X ^−j∗) for all i ∈ I ^j, j ∈ J, giving the conclusion that x ^∗ is a Nash equilibrium. □ 

Proof of Proposition 7

The properties of individual share functions in $\hat{\mathcal{G}}^{j}(X)$ are first deduced. The conditions stated on preferences are equivalent to assuming

$$\displaystyle\begin{array}{rcl} \frac{\partial \hat{l}_{i}^{\,j}} {\partial \sigma _{i}^{\,j}} & =& X^{j}\left [ \frac{\partial ^{2}\hat{u}_{ i}^{\,j}} {\partial (x_{i}^{\,j})^{2}} + \frac{\partial ^{2}\hat{u}_{i}^{\,j}} {\partial x_{i}^{\,j}\partial X^{j}} + \frac{\partial ^{2}\hat{u}_{i}^{\,j}} {\partial x_{i}^{\,j}\partial X}\right ] < 0, {}\\ \frac{\partial \hat{l}_{i}^{\,j}} {\partial X^{j}}& =& \sigma _{i}^{\,j} \frac{\partial ^{2}\hat{u}_{ i}^{\,j}} {\partial (x_{i}^{\,j})^{2}} + \frac{\partial ^{2}\hat{u}_{i}^{\,j}} {\partial x_{i}^{\,j}\partial X^{j}} +\sigma _{ i}^{\,j} \frac{\partial ^{2}\hat{u}_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X^{j}} + \frac{\partial ^{2}\hat{u}_{i}^{\,j}} {\partial (X^{j})^{2}} +\sigma _{ i}^{\,j} \frac{\partial ^{2}\hat{u}_{ i}^{\,j}} {\partial x_{i}^{\,j}\partial X} + \frac{\partial ^{2}\hat{u}_{i}^{\,j}} {\partial X^{j}\partial X} < 0,\text{ and} {}\\ \frac{\partial \hat{l}_{i}^{\,j}} {\partial X} & =& \frac{\partial ^{2}\hat{u}_{i}^{\,j}} {\partial x_{i}^{\,j}\partial X} + \frac{\partial ^{2}\hat{u}_{i}^{\,j}} {\partial X^{j}\partial X} + \frac{\partial ^{2}\hat{u}_{i}^{\,j}} {\partial (X)^{2}} < 0. {}\\ \end{array}$$

Under the first two conditions (as previously) two thresholds $\hat{\underline{X}}_{i}^{\,j}(X)$ (which is X ^j > 0 such that $\hat{l}_{i}^{\,j}(1,X^{j};X) = 1$) and $\hat{\bar{X}}_{i}^{\,j}(X)$ (which is X ^j such that $\hat{l}_{i}^{\,j}(0,X^{j};X) = 1$ if such an X ^j exists, otherwise it is defined as + ∞) can be defined, between which the share function is defined and takes positive values, and where

$$\displaystyle{ \frac{\partial \hat{s}_{i}^{\,j}} {\partial X^{j}} = -\frac{\frac{\partial \hat{l}_{i}^{\,j}} {\partial X^{j}}} {\frac{\partial \hat{l}_{i}^{\,j}} {\partial \sigma _{i}^{\,j}} } < 0. }$$

If $\hat{\underline{X}}_{i}^{\,j}(X)$ as defined above does not exist then the share function is defined for all X ^j > 0 with $\lim _{X^{j}\rightarrow 0}\hat{s}_{i}^{\,j}(X^{j};X) =\hat{\bar{ s}}_{i}^{\,j}(X)$.

As before, the aggregation of individual share functions is taken to be defined only for values of X ^j where all group members’ share functions are defined. Noting that share functions are either equal to zero for large enough X ^j, or are vanishing in the large X ^j limit, if either $\hat{\underline{X}}_{i}^{\,j}(X) > 0$ for any i ∈ I ^j, or $\sum _{i\in I^{j}}\hat{\bar{s}}_{i}^{\,j}(X) > 1$ then there is a single consistent aggregate action $\hat{X}^{j}(X)$ in $\hat{\mathcal{G}}^{j}$ which is such that $\sum _{i\in I^{j}}\hat{s}_{i}^{\,j}(\hat{X}^{j}(X);X) = 1$. If this is not the case then $\hat{X}^{j}(X) = 0$.

Consider now varying X to change the partial game played by group j. Group j’s share of the total aggregate is $\hat{S}^{j}(X) =\hat{ X}^{j}(X)/X$, defined by (9) if the resulting share is between 0 and 1. Note that

$$\displaystyle\begin{array}{rcl} \frac{\partial \hat{L}^{j}} {\partial \Lambda ^{j}}& =& X\sum _{i\in I^{j}} \frac{\partial \hat{s}_{i}^{\,j}} {\partial X^{j}}\text{ and} {}\\ \frac{\partial \hat{L}^{j}} {\partial X} & =& \sum _{i\in I^{j}}\Lambda ^{j} \frac{\partial \hat{s}_{i}^{\,j}} {\partial X^{j}} + \frac{\partial \hat{s}_{i}^{\,j}} {\partial X}. {}\\ \end{array}$$

Now,

$$\displaystyle{ \frac{\partial \hat{s}_{i}^{\,j}} {\partial X} = -\frac{\frac{\partial \hat{l}_{i}^{\,j}} {\partial X} } {\frac{\partial \hat{l}_{i}^{\,j}} {\partial \sigma _{i}^{\,j}} } < 0, }$$

which, combined with the monotonicity of share functions with respect to group aggregate, implies both of the expressions above are negative. Given this, the thresholds and the monotonicity of group share functions stated in the proposition can be derived analogously to the case within groups, so the details are omitted. Aggregate share functions are either equal to zero for $X >\hat{\bar{ X}}^{j}$ or, if this is not finite, vanish in the large X limit—this follows by recalling that individual share functions vanish in the large X ^j limit, so as X → ∞ (9) can hold only if $\lim _{X\rightarrow \infty }\Lambda ^{j}X < \infty$ which requires $\Lambda ^{j} \rightarrow 0$. Given this, if either $\hat{\underline{X}}^{j} > 0$ for any j ∈ J, or $\sum _{j\in J}\hat{\bar{S}}^{j} > 0$ if $\hat{\underline{X}}^{j} = 0$ for all j ∈ J, the aggregate share function will exceed one for small enough X and since it is strictly decreasing in X will be equal to one at exactly one value of X, so consequently there is a unique Nash equilibrium. □