Abstract
Concurrent program logics are frameworks for constructing proofs, which ensure that concurrent programs work correctly. However, most conventional concurrent program logics do not consider the complexities of modern memory structures, and the proofs in the logics do not ensure that programs will work correctly. To the best of our knowledge, Independent Reads Independent Writes (IRIW), which is known to have non-intuitive behavior under relaxed memory consistency models, has not been fully studied under the context of concurrent program logics. One reason is the gap between theoretical memory consistency models that program logics can handle and the realistic memory consistency models adopted by actual computer architectures. In this paper, we propose observation variables and invariants that fill this gap, releasing us from the need to construct operational semantics and logic for each specific memory consistency model. We describe general operational semantics for relaxed memory consistency models, define concurrent program logic sound to the operational semantics, show that observation invariants can be formalized as axioms of the logic, and verify IRIW under an observation invariant. We also obtain a novel insight through constructing the logic. To define logic that is sound to the operational semantics, we dismiss shared variables in programs from assertion languages, and adopt variables observed by threads. This suggests that the so-called bird’s-eye view of the whole computing system disturbs the soundness of the logic.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Relaxed memory consistency model
- Concurrent program logic
- Rely/guarantee method
- Observation
- Independent Reads Independent Writes
1 Introduction
Memory structures are becoming increasingly complicated as computing systems continue to grow. This can be overwhelming when attempting to write programs that work on architectures consisting of complicated memory structures. Since conventional program verification considers architectures with simple memory structures, it struggles to deal with architectures that consist of complicated memory structures.
To illustrate the problem, consider an example racy program. Readers may consider that racy programs should be prohibited as their behaviors are specified undefined in C++11 [12]. However, in lower-level programming (e.g., on virtual machine or computer architecture), racy programs are necessary to implement register algorithms, which provide mutual exclusion etc. Although such racy programs are not typically large, their non-intuitive behaviors make it difficult to verify them.
Figure 1 shows Independent Reads Independent Writes (IRIW) [4]. Variables x and y are shared, and variables \(r_0\), \(r_1\), \(r_2\), and \(r_3\) are thread-local. We assume that all variables are initialized to 0. IRIW consists of four threads. Two threads are readers, which read values from the shared variables x and y. The other two threads are writers. One writes 1 to x, and the other writes 1 to y. If the write to x is performed before the write to y, then \(r_2 \le r_3\) seems to hold, since \(r_2 > r_3\) (i.e., \(r_2=1\) and \(r_3=0\)) does not hold for the following reason:
-
1.
\(r_2 = 1\) implies \(y = 1\), and
-
2.
we assume that the write to x is performed before the write to y;
-
3.
therefore, when x is read (to \(r_3\)), its value is 1.
Similarly, if the write to y is performed before the write to x, then \(r_0 \le r_1\) seems to hold. Therefore, it would appear that  .
.
However, this is not always the case, because an architecture may realize a form of shared memory, as shown in Fig. 2. This means that the first reader and writer share the same physical memory, and the second reader and writer share another physical memory. Shared memory is realized by any mechanism for data transfer (denoted by \(\leftrightarrows \)) between the physical memories. The architecture that has mechanism for data transfer is sensitive to the so-called remote-write-atomicity [11] (also called multi-copy-atomicity in [24]). Remote-write-atomicity claims that if two thread write values to (possibly distinct) locations, then the other threads must observe the same order between the two write operations.
Here, let us assume that physical memories do not enjoy remote-write-atomicity, that is, effects on one memory cannot be immediately transferred to the other memory. Under this architecture, while the first reader may observe that the write to x is performed before the write to y, the second reader may observe that the write to y is performed before the write to x. Therefore, there is no guarantee that  .
.
Thus, in modern program verification, we cannot ignore remote-write-atomicity. However, to the best of our knowledge, there exists no concurrent program logic in which remote-write-atomicity can be switched on and off. One reason is the existence of a gap between theoretical memory consistency models, which concurrent program logics can handle, and realistic memory consistency models, which are those adopted by actual computer architectures. While theoretical memory consistency models (axioms written in assertion languages) in concurrent program logics describe relations between expressions, which are often the orders of values that are evaluated by expressions, realistic memory consistency models (which are often written in natural languages rather than formal languages) describe the orders of executions of statements on actual computer architectures. In this paper, we propose observation variables and invariants that fill this gap, thus releasing us from the need to construct operational semantics and logic for each specific memory consistency model. We define general operational semantics to consider cases in which threads own their memories, and construct concurrent program logic in which we give proofs that ensure certain properties hold when programs finish. We can control observation invariants as uniform axioms of the logic. This enables us to show that a property holds when a program finishes under an observation invariant, whereas the property does not hold when the program finishes without the observation invariant. In Sect. 9, we verify IRIW using this logic under an observation invariant induced by a realistic memory consistency model like SPARC-PSO [27].
To the best of our knowledge, the derivation shown in Sect. 9 is the first to ensure that a property holds in concurrent program logic that handles relaxed memory consistency models like SPARC-PSO, although the behavior of IRIW under more relaxed memory consistency models that refute the property has been discussed several times in the literature (e.g., [4, 22, 24, 25, 31]).
In constructing the concurrent program logic, we obtained a novel insight into the use of shared variables in an assertion language for operational semantics with relaxed memory consistency models. First, we extend an assertion language in the logic by introducing the additional variable \(x^i\) to denote x as observed by the i-th thread. The value of \(x^i\) is not necessarily the same as that of x. Next, we restrict the assertion language by dismissing shared variables in programs from assertion languages. This prohibits us from describing the value of x. By designing this assertion language, we can construct a concurrent program logic that is sound to operational semantics (explained in Sect. 4) with relaxed memory consistency models. This suggests that, in concurrent computation, the so-called bird’s-eye view that overlooks the whole does not exist, and that each thread runs according to its own observations, and some (or all) threads sometimes reach a consensus.
The rest of this paper is organized as follows. Section 2 discusses related work, and Sect. 3 presents some definitions that are used throughout this paper. Section 4 gives operational semantics (based on the notion of state transition systems) for relaxed memory consistency models. Section 5 explains our concurrent program logic. Section 6 defines validity of judgments. Section 7 introduces the notion of observation invariants. Section 8 then presents our soundness theorem. In Sect. 9, we provide example derivations for concurrent programs. Section 10 concludes the paper and discusses ideas for future work.
2 Related Work
Stølen [28] and Xu et al. [35, 36] provided concurrent program logics based on rely/guarantee reasoning [13]. However, they did not consider relaxed memory consistency models containing observation invariants, that is, they handle strict consistency, the strictest memory consistency model. This paper handles relaxed memory consistency models. The memory consistency models with observation invariants in this paper are more relaxed than those obeying strict consistency.
Ridge [23] developed a concurrent program logic for x86-TSO [26] based on rely/guarantee reasoning by introducing buffers. However, buffers to one shared memory are known to be insufficient to cause the behavior of IRIW. This paper handles more relaxed memory consistency models than x86-TSO, as threads have their own memories to deal with observation invariants.
Ferreira et al. [7] introduced a concurrent separation logic that is parameterized by invariants, and explained the non-intuitive behavior of IRIW. Their motivation for constructing a parametric logic coincides with ours. However, their logic is based on command subsumptions, which describe the execution orders of statements. This is different from our notion of observations; their approach therefore has no direct connection to our logic, and gave no sufficient condition to ensure the correctness of IRIW. Any connection between their logic and ours remains an open question.
Vafeiadis et al. presented concurrent separation logics for restricted C++11 memory models [30, 32]. The restricted C++11 semantics are so weak that the property for IRIW (shown in Sect. 1) does not hold without additional assumptions. However, unlike our approach, they did not handle programs that contain write operations to distinct locations, such as IRIW. In another paper [15], Lahav and Vafeiadis described an Owicki–Gries style logic and verified a program consisting of multiple reads and writes in the logic. This program is different from IRIW, as the reads/writes are from/to the same location. The essence of IRIW is to write to distinct locations x and y. Our paper proposes the notion of observation invariants, constructs a simple concurrent program logic, formalizes the axioms of our logic, and gives a formal proof for IRIW. This simplification provides the insight explained in Sect. 1.
The authors proposed a notion of program graphs, representations of programs with memory consistency models, gave operational semantics and construct program logic for them [1]. However, the semantics and logic cannot handle the non-intuitive behavior of IRIW since remote-write-atomicity is implicitly assumed.
There also exist verification methods that are different from those using concurrent program logics. Model checking based on exhaustive searches is a promising program verification method [2, 10, 14, 17]. Given a program and an assertion, model checking is good at detecting execution traces that violate the assertions, but is less suitable for ensuring that the assertion holds.
Some reduction methods to Sequential Consistency (SC) via race-freedom of programs are well-known (e.g., [5, 20, 21]). However, verification of racy programs like concurrent copying protocols is one of the authors’ concerns [3], and programs that have non-SC behaviors are our main targets.
Boudol et al. proposed an operational semantics approach to represent a relaxed memory consistency model [5, 6]. They defined a process calculus, equipped with buffers that hold the effects of stores, and its operational semantics to handle the non-intuitive behavior of IRIW. He proved Data Race Freedom (DRF) guarantee theorem that DRF programs have the same behaviors as those under SC. However, IRIW is not DRF.
Owens et al. reported that x86-CC [25] allows the non-intuitive behavior of IRIW, and designed x86-TSO [22] that prohibits the behavior. He also extended DRF to Triangular Race Freedom (TRF) that TRF programs have the same behaviors under x86-TSO as those under SC [21]. Although IRIW is surely TRF, a slight modification of IRIW in which additional writes to distinct variables at the start on the reader threads are inserted is not TRF. Since the program has a non-SC behavior, verification of the program under SC cannot ensure correctness of the program under x86-TSO. Our verification method to use observation invariants is robust to such slight changes. In addition, our method is not specific to a certain memory consistency model like x86-TSO. An observation invariant introduced in Sect. 7 for IRIW is independent of the slight change, and we can construct a derivation for the program that is similar to the derivation for IRIW explained in Sect. 9.3.
3 Concurrent Programs
In this section, we formally define our target concurrent programs.
Similar to the conventional program logics (e.g., [8]), sequential programs are defined as sequences of statements. Let r denote the thread-local variables that cannot be accessed by other threads, \(x, y, \ldots \) denote shared variables, and e denote thread-local expressions (thread-local variables, constant values \( val \), arithmetic operations, and so on). A sequential program can then be defined as follows:

In the above definition, the superscript i represents (an identifier of) the thread on which the associated statement will be executed. In the rest of this paper, this superscript is often omitted when the context is clear. The \(\texttt {SK}^{}\) statement denotes an ordinary no-effect statement (SKip). As in conventional program logics, \(\texttt {MV}^{} \, {r} \, {e}\) denotes an ordinary variable substitution (MoVe). The load and store statements denote read and write operations, respectively, for shared variables (LoaD and STore). The effect of the store statement issued by one thread may not be immediately observed by the other threads. The \(\texttt {IF}\) and \(\texttt {WL}\) statements denote ordinary conditional branches and iterations, respectively, where we adopt ternary conditional operators (IF-then-else-end and WhiLe-do-end). Finally, S; S denotes a sequential composition of statements.
We write  , \(\varphi \wedge \psi \), \(\varphi \leftrightarrow \psi \), and
, \(\varphi \wedge \psi \), \(\varphi \leftrightarrow \psi \), and  as
as  ,
,  , \((\varphi \supset \psi ) \wedge (\psi \supset \varphi )\), and
, \((\varphi \supset \psi ) \wedge (\psi \supset \varphi )\), and  , respectively. In the following, we assume that \(\lnot \), \(\wedge \),
, respectively. In the following, we assume that \(\lnot \), \(\wedge \),  , and \(\supset \) are stronger with respect to their connective powers. In addition to the above definition, \(\top \) is defined as the tautology
, and \(\supset \) are stronger with respect to their connective powers. In addition to the above definition, \(\top \) is defined as the tautology  .
.
A concurrent program with N threads is defined as the composition of sequential programs by parallel connectives \(\parallel \) as follows:

In this paper, the number of threads N is fixed during program execution. Parentheses are often omitted, and all operators except \(\supset \) are assumed to be left associative.
4 Operational Semantics
In this section, we define small-step operational semantics for the programming language defined in Sect. 3. Specifically, the semantics is defined as a standard state transition system, where a state (written as \( st \)) is represented as a pair of \(\langle \sigma ,\varSigma \rangle \). The first element of the pair, \(\sigma \), consists of the values of thread-local variables and shared variables that threads observe on registers and memories; formally, a function from thread identifiers and (thread-local and shared) variables to values. The second element, \(\varSigma \), represents buffers that temporarily buffer the effects of store operations to shared variables. It may be worth noting that, in the present paper, buffers are not queues, that is, each buffer stores only the latest value written to its associated variable, for simplicity. This is because the present paper focuses on verifying IRIW, and storing the latest value suffices for the purpose. Replacing buffers with queues is straightforward and not shown in the present paper. \(\varSigma ^{i,j}\) refers to thread j’s buffer for effects caused by thread i’s statements. If \(i\ne j\), then thread j cannot observe the effects that are buffered. If \(i = j\), then thread j can observe the effects that are buffered.
Using Fig. 3, we now present an informal explanation of buffers and memories. Thread 0 executes statement \(\texttt {ST}^{0} \, {x} \, {1}\), and buffers \(\varSigma ^{0,0}\) and \(\varSigma ^{0,1}\) are updated. Next, thread 1 executes statement \(\texttt {LD}^{1} \, {r_1} \, {x}\). If the effect of \(\texttt {ST}^{0} \, {x} \, {1}\) has not yet reached \(\sigma ^1\), thread 1 cannot observe it, and reads the initialized value 0. If the effect of \(\texttt {ST}^{0} \, {x} \, {1}\) has already reached \(\sigma ^1\), thread 1 reads 1. Finally, thread 0 executes statement \(\texttt {LD}^{0} \, {r_0} \, {x}\). Whether the effect of \(\texttt {ST}^{0} \, {x} \, {1}\) has reached \(\sigma ^1\) or not, thread 0 can observe it. Therefore, thread 0 reads a value of 1. Updates from \(\varSigma \) to \(\sigma \) are performed without the need for statements.
Formally, in the following, a function from triples formed of two thread identifiers and shared variables to values is evaluated by currying all functions, for the convenience of partial applications. We assume that the set of values contains a special constant value \(\texttt {udf}\) to represent uninitialized or invalidated buffers. We often write \(\sigma i\), \(\varSigma i\), and \(\varSigma i j\) as \(\sigma ^i\), \(\varSigma ^i\), and \(\varSigma ^{i,j}\), respectively, for readability. We define the following two operations for update functions as in Fig. 4 where f ranges over each among \(\sigma \), \(\sigma ^i\), \(\varSigma \), \(\varSigma ^i\), and \(\varSigma ^{i,j}\).
Figure 5 shows the rules of the operational semantics, where \(\langle \!|e|\!\rangle _{\sigma ^i}\) denotes the valuation of an expression e as follows:

and \(\sigma ^i \vDash \varphi \) denotes the satisfiability of \(\varphi \) on \(\sigma ^i\) in the standard manner, which is defined as follows:

A pair of a program and a state is called a configuration. Each rule is represented by a one-step transition between configurations  , which indicates that a statement causes \(\langle P, st \rangle \) to transit to \(\langle P', st ' \rangle \), where \(\delta \) is \(\mathrm {c}\) or \(\mathrm {e}\).
, which indicates that a statement causes \(\langle P, st \rangle \) to transit to \(\langle P', st ' \rangle \), where \(\delta \) is \(\mathrm {c}\) or \(\mathrm {e}\).
Specifically, Rule \(\text {O-ENV}\) denotes a transition that requires no statement in P, which means that other threads are executing statements or memories are being updated from buffers. Although the rule was originally introduced to mean that other threads consume statements in conventional operational semantics for concurrent programming languages (with strict consistency) [35, 36], the rule has the additional meaning here that memories are updated from buffers in constructing operational semantics for relaxed memory consistency models.
Readers unfamiliar with operational semantics for an imperative concurrent programming language (and its rely/guarantee reasoning) may consider  to be nonsense because
to be nonsense because  seems to allow any transitions. However, it is restricted to being admissible under a rely-condition by the notion of validity for judgments (called rely/guarantee specifications), as defined in Sect. 6. This is similar to the context of Hoare logic, where transitions consuming statements are defined to be large at first, and the transitions are restricted to be admissible ones under pre-conditions by the notion of validity for Hoare triples. This is one of the standard methods of defining operational semantics for an imperative concurrent programming language (e.g., as seen in [35, 36]), and is not caused by handling relaxed memory consistency models. Here, in accordance with the standard, a transition
seems to allow any transitions. However, it is restricted to being admissible under a rely-condition by the notion of validity for judgments (called rely/guarantee specifications), as defined in Sect. 6. This is similar to the context of Hoare logic, where transitions consuming statements are defined to be large at first, and the transitions are restricted to be admissible ones under pre-conditions by the notion of validity for Hoare triples. This is one of the standard methods of defining operational semantics for an imperative concurrent programming language (e.g., as seen in [35, 36]), and is not caused by handling relaxed memory consistency models. Here, in accordance with the standard, a transition  that consumes no statements is defined to be the product of states.
that consumes no statements is defined to be the product of states.
Rule \(\text {O-MV}\) evaluates e and updates \(\sigma \) with respect to r. Rule \(\text {O-LD}\) evaluates x on \(\varSigma ^{i,i}\), if \(\varSigma ^{i,i} x\) is defined (i.e., effects on x by statements on thread i itself are buffered), and on \(\sigma ^i\) otherwise, and updates \(\sigma ^i\) with respect to r. \(\text {O-ST}\) evaluates e and updates \(\varSigma ^{i,j}\) (not \(\sigma ^i\)) with respect to x for any j; i.e., the rule indicates that the effect of the store operation is buffered in \(\varSigma ^{i,j}\). Rule \(\text {O-IT}\) handles a branch statement by asserting that \(\varphi \) is satisfied under state \(\sigma ^i\), and P is chosen. If \(\sigma ^i\) is not satisfied, rule \(\text {O-IE}\) is applied and Q is chosen. Rule \(\text {O-WT}\) handles a loop statement by asserting that \(\varphi ^i\) is satisfied under state \(\sigma \), and an iteration is performed. If \(\sigma ^i\) is not satisfied, rule \(\text {O-WE}\) is applied, and the program exits from the loop. Rules \(\text {O-SQ}\) and \(\text {O-PR}\) handle sequential and parallel compositions of programs, respectively.
5 Concurrent Program Logic
In this section, we define our concurrent program logic. Our assertion language is defined as follows:

where E represents a pseudo-expression denoting thread-local variables r, observation variables \(x^i\), next thread-local variables \(\underline{r}\), next observation variables \(\underline{x^i}\), constant values \( val \), arithmetic operations, and so on. Our assertion language does not contain a shared variable x that occurs in programs. This means that nobody observes the whole system. This novelty is a key point of this paper. We often write r as \(r^i\) when referring to r being a thread-local variable on the i-th thread. The observation variable \(x^i\) represents the value written to the shared variable x by \(\texttt {ST}\) on a thread with identifier i. The next variable \(\underline{v}\) represents the value of v on a state to which the current state transits under the operational semantics.
Figure 6 shows the judgment rules. They are defined in the styles of Stølen and Xu’s proof systems [28, 35, 36], which have two kinds of judgments. Each judgment of the form \(\vDash \varPhi \) refers to satisfiability in the first-order predicate logic with equations in a standard manner. Each judgment of the form \(\{ pre , rely \} \, {P} \, \{ guar , post \}\) (where \( pre \) and \( post \) have no next variable) states that, if program P runs under pre-condition \( pre \) and rely-condition \( rely \) (which are guaranteed by the other threads as well as the environments, as explained in Sect. 6) according to the operational semantics of Sect. 4, then the guarantee-condition \( guar \) (on which the other threads rely) holds, as in conventional rely/guarantee systems. In the rest of this paper, we write \(\vdash \{ pre , rely \} \, {P} \, \{ guar , post \}\) if \(\{ pre , rely \} \, {P} \, \{ guar , post \}\) can be derived from the judgment rules of Fig. 6.
More specifically, rule \(\text {L-MV}\) of Fig. 6 handles the substitution of thread-local variables with expressions. This is the same as in conventional rely/guarantee proof systems. \([e{\slash }v]\) represents the substitution of v with e. The first assumption means that \( pre \) must be a sufficient condition that implies \( post \) with respect to the substitution. We define \(\vDash \varPhi \) as \(\langle \sigma ,\varSigma \rangle , \langle \sigma ',\varSigma ' \rangle \vDash \varPhi \) for any \(\langle \sigma ,\varSigma \rangle , \langle \sigma ',\varSigma ' \rangle \), where \(\langle \sigma ,\varSigma \rangle , \langle \sigma ',\varSigma ' \rangle \vDash \varPhi \) is defined in a similar manner to a conventional rely/guarantee system, as shown in Fig. 7. In the following, we often write \(\langle \sigma ,\varSigma \rangle \vDash \varPhi \) when \(\varPhi \) has no next variable. The second assumption means that \( pre \) must be a sufficient condition that implies \( guar \) under an invariant about V before and after an execution of an assignment C (formally defined as \(\lceil C \rceil ^{V}\)), where C is \(\texttt {MV}^{} \, {r} \, {e}\), \(\texttt {LD}^{} \, {r} \, {x}\), or \(\texttt {ST}^{} \, {x} \, {e}\), and V is a finite set of non-next variables that occur in \( guar \). A formula \(\lceil \texttt {MV}^{i} \, {r} \, {e} \rceil ^{V}\) is defined as \(\underline{r} = e \wedge \bigwedge {\text {I}}(V {\setminus } \{r\})\), which means that the value of \(\underline{r}\) is equal to the evaluation of e while the values of variables in \(V {\setminus } \{r\}\) are assignment-invariant, where \({\text {I}}(V)\) is \(\{\, v = \underline{v} \mid v \in V \,\}\). Its formal definition is shown in Fig. 8. The third assumption means that \( pre \) and \( post \) are stable under the \( rely \) condition guaranteed by another thread, where we denote that \(\varPhi \) is stable under \(\varPsi \) (written as \(\varPhi \mathrel {\bot } \varPsi \)) as \(\varPhi (\varvec{v}) \wedge \varPsi (\varvec{v}, \underline{\varvec{v}}) \supset \varPhi (\underline{\varvec{v}})\), where \(\varvec{v}\) denotes a sequence of variables.
Rule \(\text {L-SK}\) states that an ordinary no-effect statement does not affect anything.
Rule \(\text {L-LD}\) handles the substitution of thread-local variables with shared variables. Note that r is substituted with the observation variables \(x^i\), instead of the shared variables x. Rule \(\text {L-ST}\) handles the substitution of shared variables with expressions. Note that, as for \(\text {L-LD}\), this rule considers the observation variable \(x^i\) instead of the shared variable x.
Rules \(\text {L-IF}\) and \(\text {L-WL}\) handle branch and loop statements, respectively. Careful readers may have noticed that Xu et al.’s papers [35, 36] do not require the third assumption, which is implicitly assumed because these logics adopt the restriction that rely/guarantee-conditions are reflexive (as in [19, 29]). This restriction often makes it difficult to write down derivations. Therefore, in this paper, we do not adopt the restriction, following van Staden [33]. As suggested by Nieto in [19], reflexivity is used to ensure soundness. However, we do not adopt the reflexivity of rely/guarantee-conditions, but instead use the third assumption regarding \(\text {L-IF}\) and \(\text {L-WL}\), which prohibits the so-called stuttering transitions [16], as explained in Sect. 6.
Rule \(\text {L-SQ}\) handles the sequential composition of programs. Rule \(\text {L-WK}\) is the so-called consequence rule. \(\text {L-PR}\) handles parallel compositions of programs in a standard rely/guarantee system. The third assumption means that \(P_1\)’s rely-condition \( rely _1\) must be guaranteed by the global rely-condition \( rely \) or \(P_0\)’s guarantee-condition \( guar _0\). The fourth assumption is similar. The fifth assumption means that \( guar \) must be guaranteed by either \( guar _0\) or \( guar _1\).
6 Validity for Judgments
We now define computations of programs, and validity for judgments.
We define the set of computations \( Cmp (P)\) of P as a finite or infinite sequence \( c \) of configurations whose adjacent configurations are related by  or
or  defined in Sect. 4. We write \( Cfg ( c ,i)\), \( Prg ( c ,i)\), and \( St ( c ,i)\) as the i-th configuration, program, and state of \( c \), respectively. By definition, the program \( Prg ( c ,0)\) is P. As mentioned in Sect. 5, we do not assume that the rely/guarantee-conditions are reflexive. Therefore, our logic does not unconditionally ensure that the guarantee conditions hold on computations that contain
defined in Sect. 4. We write \( Cfg ( c ,i)\), \( Prg ( c ,i)\), and \( St ( c ,i)\) as the i-th configuration, program, and state of \( c \), respectively. By definition, the program \( Prg ( c ,0)\) is P. As mentioned in Sect. 5, we do not assume that the rely/guarantee-conditions are reflexive. Therefore, our logic does not unconditionally ensure that the guarantee conditions hold on computations that contain  , as Xu et al. noted in [36].
, as Xu et al. noted in [36].
The length of a computation of c is denoted by \(| c |\). If \( c \) is an infinite sequence, then \(| c |\) is the smallest limit ordinal \(\omega \). Let \( c '\) be a computation that satisfies \( St ( c ',| c '| -1) = St ( c ,0)\). We define \( c ' \cdot c \) as a concatenation of \( c '\) and \( c \). We define \(\vDash \{ pre , rely \} \, {P} \, \{ guar , post \}\) as \( Cmp (P) \cap A( pre , rely ) \subseteq C( guar ,post)\), which means that any computation under pre/rely-conditions satisfies guarantee/post-conditions, as shown in Fig. 9. Thus, this paper does not handle post-conditions in non-terminating computations. This kind of validity is called partial correctness [34].
Careful readers may have noticed that the second arguments of \(\varSigma \) and substitutions to \(\varSigma ^{i,j} \; (i \ne j)\) at rule \(\text {O-ST}\) are redundant, as  , which satisfies a rely-condition, is allowed at any time, and our assertion language cannot describe \(\varSigma ^{i,j} \; (i\ne j)\). Strictly speaking, although technically unnecessary and redundant, we have adopted these arguments to explain admissible computations more intuitively. A computation that formally represents the non-intuitive behavior of IRIW without remote-write-atomicity in Sect. 9.3 may help readers understand how memories are updated by effects from buffers.
, which satisfies a rely-condition, is allowed at any time, and our assertion language cannot describe \(\varSigma ^{i,j} \; (i\ne j)\). Strictly speaking, although technically unnecessary and redundant, we have adopted these arguments to explain admissible computations more intuitively. A computation that formally represents the non-intuitive behavior of IRIW without remote-write-atomicity in Sect. 9.3 may help readers understand how memories are updated by effects from buffers.
7 Observation Invariant
In this section, we propose an observation invariant, which is an invariant written by observation variables. Formally, we define an observation invariant as a formula of the first-order predicate logic with the equations of Sect. 5.
We adopt observation invariants as axioms of the logic in Sect. 5. For example, let \(x^0 = x^1\) be an observation invariant, which means that the value of x observed by thread 0 coincides with the value of x observed by thread 1. Adopting the observation invariant as an axiom means handling execution traces that always satisfy \(\sigma ^0 [\varSigma ^{0,0}] x = \sigma ^1 [\varSigma ^{1,1}] x\).
Let us consider three examples of observation invariants. The program shown in Fig. 10 is called Dependence Cycle (DC). Although we intuitively think that either \(r_0\) or \(r_1\) has an initial value of 0, \(r_0 = 1 \wedge r_1 =1\) may not hold under a relaxed memory consistency model such as C++11 memory models. Memory consistency models for programming languages are often very relaxed in consideration of compiler optimization.
Our intuition that either \(r_0\) or \(r_1\) has an initial value is supported by no speculation regarding store statements on distinct threads, which is assumed under SPARC-PSO and similar architectures. For DC, this can be represented as \(y^0 = 0 \supset y^1 = 0\), \(x^1 \le \underline{x^1} \supset x^0 \le \underline{x^0}\), \(x^1 = 0 \supset x^0 = 0\), and \(y^0 \le \underline{y^0} \supset y^1 \le \underline{y^1}\) if the buffers are empty with respect to x and y when DC launches, and a rely-condition ensures no store operation to x and y. The first formula, \(y^0 = 0 \supset y^1 = 0\), means that thread 1 observes \(y = 0\) as long as thread 0 observes \(y = 0\). This is because thread 0 is the only thread that has a store statement to y in DC. The second formula, \(x^1 \le \underline{x^1} \supset x^0 \le \underline{x^0}\), means that thread 0 observes that x is monotone if thread 1 observes x is monotone. Thread 0 cannot observe x is not monotone, because thread 1 (which has a store statement to x and can see its own buffer) observes x is monotone. The third and fourth formulas are similar.
Next, let us consider an observation invariant for the One Reader One Writer (1R1W) program shown in Fig. 11, which consists of one reader thread and one writer thread. The reader thread in 1R1W has no store statement. Therefore, \(\underline{y^1} \le x^1 \supset \underline{y^0} \le x^0\) is an observation invariant for 1R1W under x86-TSO [26]. This prohibits the reordering of effects of store statements, where we assume that the buffers are empty with respect to x and y when 1R1W launches, and a rely-condition ensures no store operations to x and y. Note that this is not an invariant under SPARC-PSO, which allows the effects of store statements to be reordered. The transfer of monotonicity \(x^1 \le \underline{x^1} \supset x^0 \le \underline{x^0}\) is also an observation invariant, even under SPARC-PSO, since the reader thread has no store statement to x.
Finally, let us consider an observation invariant for IRIW. Similar to DC, the transfer of monotonicity (\(x^2 \le \underline{x^2} \supset x^0 \le \underline{x^0}\), \(x^2 \le \underline{x^2} \supset x^1 \le \underline{x^1}\), \(y^3 \le \underline{y^3} \supset y^0 \le \underline{y^0}\), and \(y^3 \le \underline{y^3} \supset y^1 \le \underline{y^1}\)) holds, because the reader threads in IRIW have no store statement. In addition, \(\underline{x^0} = \underline{x^1}\) and \(\underline{y^0} = \underline{y^1}\) are invariants under remote-write-atomicity (which is assumed under SPARC-PSO and similar architectures), as threads 0 and 1 can detect nothing in their own buffers, and share a common observation of a shared memory. Note that the invariants are properly weaker than the strict consistency assumed by conventional concurrent program logics [13, 28, 35, 36], which forces the variable updates to be immediately observed by all threads, that is, \(\underline{x^0} = \underline{x^1} = \underline{x^2} = \underline{x^3}\) and \(\underline{y^0} = \underline{y^1} = \underline{y^2} = \underline{y^3}\).
8 Soundness
In this section, we present the soundness of the operational semantics defined in Fig. 5. In Sect. 5, we derived a concurrent program logic that is sound to the operational semantics defined in Fig. 5. However, the logic is actually insufficient to derive some valid judgments.
Auxiliary variables are known to enhance the provability of concurrent program logics [28]. Auxiliary variables are fresh variables that do not occur in the original programs, and are used only for the description of assertions. By using auxiliary variables in assertions, we can describe the progress of thread executions as rely/guarantee-conditions. In Sect. 9.3, we show a typical usage of auxiliary variables.
We extend our logic to contain the following inference rule (called the auxiliary variables rule [28, 35]):

where \({\text {fv}}(\varPhi )\) denotes free variables that occur in \(\varPhi \) in a standard manner, and \({(P_0)}_{\varvec{z}}\) is defined as the program that coincides with \(P_0\), except that an assignment A is removed if
-
A is an assignment whose left value belongs to \(\varvec{z}\),
-
no variable in \(\varvec{z}\) occurs in assignments whose left values do not belong to \(\varvec{z}\), and
-
no variable in \(\varvec{z}\) freely occurs in conditional statements.
Let \( c \) be  for any \(0 \le i\). We write \( tr ( c ,i)\) as \(\delta _i\). Given \( c \in Cmp (P_0 \parallel P_1)\), \( c _0 \in Cmp (P_0)\), and \( c _1 \in Cmp (P_1)\), a ternary relation \( c = c _0 \parallel c _1\) is defined if \(| c | = | c _0| = | c _1|\) and
for any \(0 \le i\). We write \( tr ( c ,i)\) as \(\delta _i\). Given \( c \in Cmp (P_0 \parallel P_1)\), \( c _0 \in Cmp (P_0)\), and \( c _1 \in Cmp (P_1)\), a ternary relation \( c = c _0 \parallel c _1\) is defined if \(| c | = | c _0| = | c _1|\) and
-
1.
\( St ( c ,i) = St ( c _0,i) = St ( c _1,i)\),
-
2.
\( tr ( c ,i) = \mathrm {c}\) implies either of \( tr ( c _0,i) = \mathrm {c}\) or \( tr ( c _1,i) = \mathrm {c}\) holds,
-
3.
\( tr ( c ,i) = \mathrm {e}\) implies \( tr ( c _0,i) = \mathrm {e}\) and \( tr ( c _1,i) = \mathrm {e}\) hold, and
-
4.
\( Prg ( c ,i) = Prg ( c _0,i) \parallel Prg ( c _1,i)\)
for \(0 \le i < | c |\). We write \({\text {prefix}}( c ,i)\) and \({\text {postfix}}( c ,i)\) as the prefix of \( c \) with length \(i+1\) and the sequence that is derived from \( c \) by removing \({\text {prefix}}( c ,i-1)\), respectively.
Proposition 1
\( Cmp (P_0 \parallel P_1) = \{\, c _0 \parallel c _1 \mid c _0 \in Cmp (P_0), c _1 \in Cmp (P_1) \,\}\).
Lemma 2
Assume \(\vdash \{ pre _0 \wedge pre _1 , rely \} \, {P_0 \parallel P_1} \, \{ guar , post _0 \wedge post _1\}\) by \(\text {L-PR}\), \( Cmp (P_0) \cap A( pre _0, rely _0) \subseteq C( guar _0, post _0)\), \( Cmp (P_1) \cap A( pre _1, rely _1) \subseteq C( guar _1, post _1)\),  ,
,  ,
,  , and \( c \in Cmp (P_0 \parallel P_1) \cap A( pre _0 \wedge pre _1 , rely ) \). In addition, we take \( c _0 \in Cmp (P_0)\) and \( c _1 \in Cmp (P_1)\) such that \( c = c _0 \parallel c _1\) by Proposition 1.
, and \( c \in Cmp (P_0 \parallel P_1) \cap A( pre _0 \wedge pre _1 , rely ) \). In addition, we take \( c _0 \in Cmp (P_0)\) and \( c _1 \in Cmp (P_1)\) such that \( c = c _0 \parallel c _1\) by Proposition 1.
-
1.
\( St ( c ,i) , St ( c ,i+1) \vDash guar _0\) and \( St ( c ,i) , St ( c ,i+1) \vDash guar _1\) hold for any
 and
and  , respectively.
, respectively. -
2.
 and
and  hold for any
hold for any 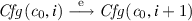 and
and  , respectively.
, respectively. -
3.
 for any
for any  holds.
holds. -
4.
Assume
 . Then,
. Then,  holds.
holds.
Proof
1. Let us consider the former case. Without loss of generality, we can assume that \( St ( c ,i), St ( c ,i+1) \not \vDash guar _0\) where \( St ( c ,j) , St ( c ,j+1) \vDash guar _0\) and \( St ( c ,j) , St ( c ,j+1) \vDash guar _1\) for any \(0 \le j < i\).
By the definition, there exists  or
or  corresponding to
corresponding to  for any \(0 \le k \le i\). Therefore,
for any \(0 \le k \le i\). Therefore,  holds. By
holds. By  ,
,  holds. Since
holds. Since  holds, in particular,
holds, in particular,  holds. This contradicts
holds. This contradicts  . The latter case is similar.
. The latter case is similar.
2. Immediate from the definition of \(c = c_0 \parallel c_1\) and 1.
4. By 2,  , and
, and  , \( c _0 \in A( pre _0, rely _0)\) and \( c _1 \in A( pre _1, rely _1)\) hold.
, \( c _0 \in A( pre _0, rely _0)\) and \( c _1 \in A( pre _1, rely _1)\) hold.
By \( Cmp (P_0) \cap A( pre _0, rely _0) \subseteq C( guar _0, post _0)\) and \( Cmp (P_1) \cap A( pre _1, rely _1) \subseteq C( guar _1, post _1)\), \( St ( c ,| c |) \vDash post _0\) and \( St ( c ,| c | -1) \vDash post _1\) hold. Therefore,  holds. \(\square \)
holds. \(\square \)
Theorem 3
\(\vdash \{ pre , rely \} \, {P} \, \{ guar , post \}\) implies \(\vDash \{ pre , rely \} \, {P} \, \{ guar , post \}\).
Proof
By induction on derivation and case analysis of the last inference rule.
First, assume \(\text {L-ST}\). Let  . By \(\text {O-ST}\), there exist \(\sigma _0, \varSigma _0, \ldots \) such that
. By \(\text {O-ST}\), there exist \(\sigma _0, \varSigma _0, \ldots \) such that  ,
,

\(\langle \sigma _0,\varSigma _0 \rangle \vDash pre \), and \(\langle \sigma _j,\varSigma _j \rangle , \langle \sigma _{j+1},\varSigma _{j+1} \rangle \vDash rely \) for any \(0 \le j < n\). By \(\vDash pre \mathrel {\bot } rely \), \(\langle \sigma _n,\varSigma _n \rangle \vDash pre \). By the definition,  . By
. By  ,
,  , that is,
, that is,  . In addition, assume \(| c | < \omega \). By \(\vDash pre \supset [e/x^i] post \), \(\langle \sigma _n,\varSigma _n \rangle \vDash [e/x^i] post \). By the definition,
. In addition, assume \(| c | < \omega \). By \(\vDash pre \supset [e/x^i] post \), \(\langle \sigma _n,\varSigma _n \rangle \vDash [e/x^i] post \). By the definition,  , that is, \(\langle \sigma _{n+1},\varSigma _{n+1} \rangle \vDash post \). By \(\vDash post \mathrel {\bot } rely \), \(\langle \sigma _{| c | -1},\varSigma _{| c | -1} \rangle \vDash post \).
, that is, \(\langle \sigma _{n+1},\varSigma _{n+1} \rangle \vDash post \). By \(\vDash post \mathrel {\bot } rely \), \(\langle \sigma _{| c | -1},\varSigma _{| c | -1} \rangle \vDash post \).
Second, assume \(\text {L-WL}\). Let \( c \in Cmp (\texttt {WL}^{i} \, {\varphi }\mathord {?}{S^i_0}) \cap A( pre , rely )\), which consists of the following five segments:
-
 ,
, -
 where \(\sigma _{k_0} \vDash \varphi \),
where \(\sigma _{k_0} \vDash \varphi \), -
 where \(\sigma _{k_0} \not \vDash \varphi \),
where \(\sigma _{k_0} \not \vDash \varphi \), -
\(\langle S^i_0 ; S^i,\langle \sigma _{k_0},\varSigma _{k_0} \rangle \rangle \longrightarrow ^*\langle S^i,\langle \sigma _{k_n},\varSigma _{k_n} \rangle \rangle \).
-
\(\langle S^i_0 ; S^i,\langle \sigma _{k_0},\varSigma _{k_0} \rangle \rangle \longrightarrow \cdots \) which does not reach \(S^i\).
where \(\langle \sigma ',\varSigma ' \rangle , \langle \sigma '',\varSigma '' \rangle \vDash rely \) for any  in the five segments. By \(\vDash pre \mathrel {\bot } rely \), \(\langle \sigma _{k_0},\varSigma _{k_0} \rangle \vDash pre \). Let \(c'\) be \(\langle S^i_0,\langle \sigma _{k_0},\varSigma _{k_0} \rangle \rangle \longrightarrow ^*\langle \texttt {SK}^{i},\langle \sigma _{k_n},\varSigma _{k_n} \rangle \rangle \). By induction hypothesis, \(\langle \sigma ',\varSigma ' \rangle , \langle \sigma '',\varSigma '' \rangle \vDash guar \) holds for any
in the five segments. By \(\vDash pre \mathrel {\bot } rely \), \(\langle \sigma _{k_0},\varSigma _{k_0} \rangle \vDash pre \). Let \(c'\) be \(\langle S^i_0,\langle \sigma _{k_0},\varSigma _{k_0} \rangle \rangle \longrightarrow ^*\langle \texttt {SK}^{i},\langle \sigma _{k_n},\varSigma _{k_n} \rangle \rangle \). By induction hypothesis, \(\langle \sigma ',\varSigma ' \rangle , \langle \sigma '',\varSigma '' \rangle \vDash guar \) holds for any  in \(c'\) holds. The case that c does not reach \(S^i\) is similar. Therefore, since \(\vDash pre \supset {\text {I}}(V) \supset guar \) holds, \(\langle \sigma ',\varSigma ' \rangle , \langle \sigma '',\varSigma '' \rangle \vDash guar \) holds for any
in \(c'\) holds. The case that c does not reach \(S^i\) is similar. Therefore, since \(\vDash pre \supset {\text {I}}(V) \supset guar \) holds, \(\langle \sigma ',\varSigma ' \rangle , \langle \sigma '',\varSigma '' \rangle \vDash guar \) holds for any  in c holds. In addition, assume \(| c | < \omega \). By \(\vDash pre \mathrel {\bot } rely \) and induction hypothesis,
in c holds. In addition, assume \(| c | < \omega \). By \(\vDash pre \mathrel {\bot } rely \) and induction hypothesis,  holds. By
holds. By  and
and  ,
,  .
.
Third, assume \(\text {L-SQ}\). Let  . There exist \( st _0, \delta _0, \ldots \) such that
. There exist \( st _0, \delta _0, \ldots \) such that

\( st _0 \vDash pre \), and \( st _j , st _{j+1} \vDash rely \) for any \(0 \le j < n\). Let \( c '\) and \( c ''\) be  and \({\text {postfix}}( c ,n)\), respectively. Obviously, \( c ' \in Cmp (P^i_0) \cap A( pre , rely )\) holds. By induction hypothesis, \( c ' \in C( guar ,\varPhi )\) holds. By the definition,
and \({\text {postfix}}( c ,n)\), respectively. Obviously, \( c ' \in Cmp (P^i_0) \cap A( pre , rely )\) holds. By induction hypothesis, \( c ' \in C( guar ,\varPhi )\) holds. By the definition,  holds. Therefore,
holds. Therefore,  holds. By induction hypothesis, \( c '' \in C( guar , post )\) holds. Therefore, \( c \in C( guar , post )\) holds.
holds. By induction hypothesis, \( c '' \in C( guar , post )\) holds. Therefore, \( c \in C( guar , post )\) holds.
Fourth, assume \(\text {L-PR}\). By Lemmas 2.3 and 2.4.
Fifth, assume \(\text {L-AX}\). Let  . There exist \(\sigma _0, \varSigma _0, \delta _0, \ldots \) such that
. There exist \(\sigma _0, \varSigma _0, \delta _0, \ldots \) such that

 . Since
. Since  ,
,  , and \(\varvec{z} \cap ({\text {fv}}( pre ) \cup {\text {fv}}( rely ) \cup {\text {fv}}( guar ) \cup {\text {fv}}( post )) = \varnothing \), there exist \(P'_0, \sigma '_0, \varSigma '_0, \ldots \) such that
, and \(\varvec{z} \cap ({\text {fv}}( pre ) \cup {\text {fv}}( rely ) \cup {\text {fv}}( guar ) \cup {\text {fv}}( post )) = \varnothing \), there exist \(P'_0, \sigma '_0, \varSigma '_0, \ldots \) such that

and \(P'_0 = P\), \({(P'_n)}_{\varvec{z}} = P_n\), \({\sigma '_j}^i v = {\sigma _j}^i v\), \({\varSigma '_j}^{i,i'} v = {\varSigma _j}^{i,i'} v\), \(\langle \sigma '_0,\varSigma '_0 \rangle \vDash pre \wedge pre _0\), and \(\langle \sigma '_j,\varSigma '_j \rangle , \langle \sigma '_{j+1},\varSigma '_{j+1} \rangle \vDash rely \wedge rely _0\) for any \(v \not \in \varvec{z}\), \(0 \le i,i' < N\) and \(0 \le j < n\). Therefore, \( c ' \in Cmp (P) \cap A( pre \wedge pre _0, rely \wedge rely _0)\) holds. By induction hypothesis, \( c ' \in C( guar , post )\) holds. Therefore, \( c \in C( guar , post )\) holds.
The other cases are similar and omitted due to space limitation. \(\square \)
9 Examples
In this section, we verify several example racy programs.
9.1 Verification of DC
The first example program is DC, introduced in Sect. 7. The verification property, a judgment consisting of the post-condition  under appropriate pre/rely-conditions, is shown with a derivation for DC.
under appropriate pre/rely-conditions, is shown with a derivation for DC.
Figure 12 shows an essential part of a derivation for DC, where

and D, \(\underline{D}\) are  and
and  , respectively. Some assumptions regarding the inference rules are omitted when the context renders them obvious.
, respectively. Some assumptions regarding the inference rules are omitted when the context renders them obvious.
A key point is that  and
and  are derived from the observation invariants for DC,
are derived from the observation invariants for DC,  ,
,  , \(x^1 = 0 \supset x^0 = 0\), and \(y^0 \le \underline{y^0} \supset y^1 \le \underline{y^1}\) introduced in Sect. 7 at the final inference by \(\text {L-PR}\).
, \(x^1 = 0 \supset x^0 = 0\), and \(y^0 \le \underline{y^0} \supset y^1 \le \underline{y^1}\) introduced in Sect. 7 at the final inference by \(\text {L-PR}\).
9.2 Verification of 1R1W
Let us consider a relaxed memory consistency model that prohibits the reordering of the effects of store statements. Therefore, we expect \(r_0 \le r_1\) under an appropriate condition when the program in Fig. 11 finishes.
Figure 13 shows an essential part of a derivation for 1R1W, where
\(\text{1R } \equiv \texttt {LD}^{0} \, {r_0} \, {y}; \texttt {LD}^{0} \, {r_1} \, {x}\), \(\text{1W } \equiv \texttt {ST}^{1} \, {x} \, {1}; \texttt {ST}^{1} \, {y} \, {1}\), and some assumptions of the inference rules are omitted when the context renders them obvious.
A key point here is that  and
and  are derived from the observation invariants for 1R1W, \(\underline{y^1} \le x^1 \supset \underline{y^0} \le x^0\) and \(x^1 \le \underline{x^1} \supset x^0 \le \underline{x^0}\) introduced in Sect. 7 at the final inference by \(\text {L-PR}\).
are derived from the observation invariants for 1R1W, \(\underline{y^1} \le x^1 \supset \underline{y^0} \le x^0\) and \(x^1 \le \underline{x^1} \supset x^0 \le \underline{x^0}\) introduced in Sect. 7 at the final inference by \(\text {L-PR}\).
As explained in Sect. 7, under SPARC-PSO,  is not implied, since \(y^1 \le x^1 \supset y^0 \le x^0\) is not an observation invariant.
is not implied, since \(y^1 \le x^1 \supset y^0 \le x^0\) is not an observation invariant.
9.3 Verification of IRIW
Finally, we demonstrate the verification of the program introduced in Sect. 1. The verification property is a judgment consisting of the post-condition  under appropriate pre/rely-conditions, although the judgment is formally shown as (2) in this section since the pre/rely-conditions require some notation.
under appropriate pre/rely-conditions, although the judgment is formally shown as (2) in this section since the pre/rely-conditions require some notation.
First, note that the post-condition does not always hold without axioms for remote-write-atomicity. Actually, the following computation:

implies this fact, where we write the substitutions \([v^i \mapsto n]\) and \([v^{i,j} \mapsto n]\) as  and
and  , respectively, for readability. Additionally, \(\sigma \) and \(\varSigma \) are constant functions to 0 and \(\texttt {udf}\), respectively. Note that we must confirm that
, respectively, for readability. Additionally, \(\sigma \) and \(\varSigma \) are constant functions to 0 and \(\texttt {udf}\), respectively. Note that we must confirm that  satisfies the rely-condition of (2).
satisfies the rely-condition of (2).
Thus, the post-condition does not always hold with no additional axiom. Let us show that the post-condition holds under appropriate pre/rely/guarantee-conditions with axioms for remote-write-atomicity. To construct a derivation, we add the auxiliary variables \(z_0\) and \(z_1\), as shown in Fig. 14.
We construct a derivation on each thread. The following three judgments:

are derived by \(\text {L-LD}\) and \(\text {L-MV}\), where \({\text {M}}(V)\) is \(\bigwedge \{\, v \le \underline{v} \mid v \in V \,\}\), and


is derivable by \(\text {L-SQ}\). Similarly, so is

from symmetricity, where

Let D and \(\underline{D}\) be  and
and  , respectively. Note that \(v < v' \wedge D \wedge \underline{D}\) means \(v = 0 \wedge v'=1\).
, respectively. Note that \(v < v' \wedge D \wedge \underline{D}\) means \(v = 0 \wedge v'=1\).
By \(\text {L-ST}\), \(\{D , rely ^2\} \, {\texttt {ST}^{} \, {y} \, {1}} \, \{ guar ^2 , \top \}\) and \(\{D , rely ^3\} \, {\texttt {ST}^{} \, {x} \, {1}} \, \{ guar ^3 , \top \}\) are derivable, where
Let us construct separate derivations corresponding to Independent Reads (IR), Independent Writes (IW), and IRIW. To construct a derivation for IR, it is sufficient that

is satisfied, as this implies

under \(\text {L-PR}\) and \(\text {L-WK}\), where \( pre _{01} \equiv x^0=0 \wedge y^0=0 \wedge x^1=0 \wedge y^1=0\). Therefore, we can deduce

by \(\text {L-AX}\) and \(\text {L-WK}\), where \( rely ^{01} \equiv {\text {M}}\{x^0,y^0,x^1,y^1\} \wedge {\text {I}}\{r_0,r_1,r_2,r_3\}\).
Similarly, to construct a derivation for IW, it is sufficient that

is satisfied, since this allows us to deduce that  .
.
We now construct the following derivation for IRIW

it is sufficient that the following is satisfied:

Let us recall the observation invariants \(\underline{x^0} = \underline{x^1}\) and \(\underline{y^0} = \underline{y^1}\) under the remote-write-atomicity explained in Sect. 7. Obviously, the observation invariants imply (1). Additionally, the transfer of monotonicity implies (3). Thus, under remote-write-atomicity, which is more relaxed than strict consistency (and therefore under SPARC-PSO), IRIW is guaranteed to work correctly.
10 Conclusion and Future Work
This paper has proposed the notion of observation invariants to fill the gap between theoretical and realistic relaxed memory consistency models. We have derived general small-step operational semantics for relaxed memory consistency models, introduced additional variables \(x^i\) to denote a value of x observed by i in an assertion language, and stated a concurrent program logic that is sound with respect to the operational semantics. Our analysis suggests that the non-existence of shared variables without observations by threads in the assertion language ensures the soundness. We have successfully constructed a formal proof for the correctness of IRIW via the notion of observation invariants. To the best of our knowledge, the derivation in this paper is the first to verify IRIW in a logic that handles relaxed memory consistency models like SPARC-PSO.
There are four directions for future work. The first is to invent systematic construction of observation invariants and to find further applications of observation invariants. The observation invariants shown in this paper are given in ad-hoc ways. The example programs that are verified in this paper are small. Systematic construction of observation invariants will tame observation invariants for larger programs, provide further applications of observation invariants, and enable us to compare our method with existing methods. The second is to implement a theorem prover that can verify programs in the logic in this paper. Manual constructions of derivations, which are done in this paper, are tedious and error-prone. The third is to compare our logic with doxastic logic [18], which is based on the notion of belief. We introduced the additional variable \(x^i\) to denote x as observed by thread i, but this variable does not always coincide with x on physical memories. Therefore, \(x^i\) may be considered to be x as believed by thread i. The fourth is a mathematical formulation of our logic. Although mathematical formulations of rely/guarantee-reasoning have been stated in some studies (e.g., [9]), they assume that (program) shared variables are components in assertion languages (called a cheat in [9]). Since the insight provided in this paper dismisses shared variables from assertion languages, the assumption cannot be admissible, and a new mathematical formulation of our logic based on rely/guarantee-reasoning is significant.
References
Abe, T., Maeda, T.: Concurrent program logic for relaxed memory consistency models with dependencies across loop iterations. J. Inf. Process. (2016, to appear)
Abe, T., Maeda, T.: A general model checking framework for various memory consistency models. Int. J. Softw. Tools Technol. Transferr (2016, to appear). doi:10.1007/s10009-016-0429-y
Abe, T., Ugawa, T., Maeda, T., Matsumoto, K.: Reducing state explosion for software model checking with relaxed memory consistencymodels. In: Proceedings of SETTA. LNCS, vol. 9984 (2016, to appear). doi:10.1007/978-3-319-47677-3_8
Boehm, H.J., Adve, S.V.: Foundations of the C++ concurrency memory model. In: Proceedings of PLDI, pp. 68–78 (2008)
Boudol, G., Petri, G.: Relaxed memory models: an operational approach. In: Proceedings of POPL, pp. 392–403 (2009)
Boudol, G., Petri, G., Serpette, B.P.: Relaxed operational semantics of concurrent programming languages. In: Proceedings of EXPRESS/SOS, pp. 19–33 (2012)
Ferreira, R., Feng, X., Shao, Z.: Parameterized memory models and concurrent separation logic. In: Gordon, A.D. (ed.) ESOP 2010. LNCS, vol. 6012, pp. 267–286. Springer, Heidelberg (2010). doi:10.1007/978-3-642-11957-6_15
Hoare, C.A.R.: An axiomatic basis for computer programming. Commun. ACM 12(10), 576–580, 583 (1969)
Hoare, T., Möller, B., Struth, G., Wehrman, I.: Concurrent Kleene algebra and its foundations. J. Log. Algebraic Program 80(6), 266–296 (2011)
Holzmann, G.J.: The SPIN Model Checker. Addison-Wesley, Reading (2003)
Intel Corporation: A Formal Specification of Intel Itanium Processor Family Memory Ordering (2002)
ISO, IEC 14882: 2011: Programming Language C++ (2011)
Jones, C.B.: Development methods for computer programs including a notion of interference. Ph.D. thesis, Oxford University (1981)
Jonsson, B.: State-space exploration for concurrent algorithms under weak memory orderings: (preliminary version). SIGARCH Comput. Archit. News 36(5), 65–71 (2008)
Lahav, O., Vafeiadis, V.: Owicki-Gries reasoning for weak memory models. In: Halldórsson, M.M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) ICALP 2015. LNCS, vol. 9135, pp. 311–323. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47666-6_25
Lamport, L.: The temporal logic of actions. ACM TOPLAS 16(3), 872–923 (1994)
Linden, A., Wolper, P.: An automata-based symbolic approach for verifying programs on relaxed memory models. In: Pol, J., Weber, M. (eds.) SPIN 2010. LNCS, vol. 6349, pp. 212–226. Springer, Heidelberg (2010). doi:10.1007/978-3-642-16164-3_16
Meyer, J.J.C.: Modal epistemic and doxastic logic. In: Gabbay, D.M., Guenthner, F. (eds.) Handbook of Philosophical Logic, vol. 10, 2nd edn, pp. 1–38. Springer, Dordrecht (2004)
Nieto, L.P.: The rely-guarantee method in Isabelle/HOL. In: Degano, P. (ed.) ESOP 2003. LNCS, vol. 2618, pp. 348–362. Springer, Heidelberg (2003). doi:10.1007/3-540-36575-3_24
Oracle Corporation: The Java Language Specification. Java SE 8 Edition (2015)
Owens, S.: Reasoning about the implementation of concurrency abstractions on x86-TSO. In: D’Hondt, T. (ed.) ECOOP 2010. LNCS, vol. 6183, pp. 478–503. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14107-2_23
Owens, S., Sarkar, S., Sewell, P.: A better x86 memory model: x86-TSO. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 391–407. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03359-9_27
Ridge, T.: A rely-guarantee proof system for x86-TSO. In: Leavens, G.T., O’Hearn, P., Rajamani, S.K. (eds.) VSTTE 2010. LNCS, vol. 6217, pp. 55–70. Springer, Heidelberg (2010). doi:10.1007/978-3-642-15057-9_4
Sarkar, S., Sewell, P., Alglave, J., Maranget, L., Williams, D.: Understanding POWER multiprocessors. In: Proceedings of PLDI, pp. 175–186 (2011)
Sarkar, S., Sewell, P., Nardelli, F.Z., Owens, S., Ridge, T., Braibant, T., Myreen, M.O., Alglave, J.: The semantics of x86-CC multiprocessor machine code. In: Proceedings of POPL, pp. 379–391 (2008)
Sewell, P., Sarkar, S., Owens, S., Nardelli, F.Z., Myreen, M.O.: x86-TSO: a rigorous and usable programmer’s model for x86 multiprocessors. Commun. ACM 53(7), 89–97 (2010)
SPARC International Inc.: The SPARC Architecture Manual, Version 9 (1994)
Stølen, K.: Development of parallel programs on shared data-structures. Technical report UMCS-91-1-1, Department of Computer Science, University of Manchester (1991)
Tofan, B., Schellhorn, G., Bäumler, S., Reif, W.: Embedding rely-guarantee reasoning in temporal logic. Technical report, Institut für Informatik, Universität Augsburg (2010)
Turon, A., Vafeiadis, V., Dreyer, D.: GPS: Navigating weak memory with ghosts, protocols, and separation. In: Proceedings of OOPSLA. 691–707(2014)
Vafeiadis, V.: Formal reasoning about the C11 weak memory model. In: Proceedings of CPP (2015)
Vafeiadis, V., Narayan, C.: Relaxed separation logic: a program logic for C11 concurrency. In: Proceedings of OOPSLA, pp. 867–884 (2013)
Staden, S.: On rely-guarantee reasoning. In: Hinze, R., Voigtländer, J. (eds.) MPC 2015. LNCS, vol. 9129, pp. 30–49. Springer, Heidelberg (2015). doi:10.1007/978-3-319-19797-5_2
Winskel, G.: The Formal Semantics of Programming Languages. MIT Press, Cambridge (1993)
Xu, Q.: A theory of state-based parallel programming. Ph.D. thesis, Oxford University Computing Laboratory (1992)
Xu, Q., de Roever, W.P., He, J.: The rely-guarantee method for verifying shared variable concurrent programs. Formal Aspects Comput. 9(2), 149–174 (1997)
Acknowledgments
Some definitions in this paper are inspired by Qiwen Xu’s PhD thesis [35]. The authors would like to thank him for answering our questions respectfully. The authors also thank the anonymous reviewers for several comments to improve the paper. This work was supported by JSPS KAKENHI Grant Number 16K21335.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Abe, T., Maeda, T. (2016). Observation-Based Concurrent Program Logic for Relaxed Memory Consistency Models. In: Igarashi, A. (eds) Programming Languages and Systems. APLAS 2016. Lecture Notes in Computer Science(), vol 10017. Springer, Cham. https://doi.org/10.1007/978-3-319-47958-3_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-47958-3_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-47957-6
Online ISBN: 978-3-319-47958-3
eBook Packages: Computer ScienceComputer Science (R0)
















 and
and  , respectively.
, respectively. and
and  hold for any
hold for any 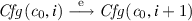 and
and  , respectively.
, respectively. for any
for any  holds.
holds. . Then,
. Then,  holds.
holds. .
. ,
, where
where  where
where 

