Complexity of Discrete Energy Minimization Problems

Abstract

Discrete energy minimization is widely-used in computer vision and machine learning for problems such as MAP inference in graphical models. The problem, in general, is notoriously intractable, and finding the global optimal solution is known to be NP-hard. However, is it possible to approximate this problem with a reasonable ratio bound on the solution quality in polynomial time? We show in this paper that the answer is no. Specifically, we show that general energy minimization, even in the 2-label pairwise case, and planar energy minimization with three or more labels are exp-APX-complete. This finding rules out the existence of any approximation algorithm with a sub-exponential approximation ratio in the input size for these two problems, including constant factor approximations. Moreover, we collect and review the computational complexity of several subclass problems and arrange them on a complexity scale consisting of three major complexity classes – PO, APX, and exp-APX, corresponding to problems that are solvable, approximable, and inapproximable in polynomial time. Problems in the first two complexity classes can serve as alternative tractable formulations to the inapproximable ones. This paper can help vision researchers to select an appropriate model for an application or guide them in designing new algorithms.

1 Introduction

Discrete energy minimization, also known as min-sum labeling [69] or weighted constraint satisfaction (WCSP)¹ [25], is a popular model for many problems in computer vision, machine learning, bioinformatics, and natural language processing. In particular, the problem arises in maximum a posteriori (MAP) inference for Markov (conditional) random fields (MRFs/CRFs) [43]. In the most frequently used pairwise case, the discrete energy minimization problem (simply “energy minimization” hereafter) is defined as

$$\begin{aligned} \min _{x\in \mathcal {L}^\mathcal {V}} \sum _{u\in \mathcal {V}} f_u(x_u) + \sum _{(u,v)\in \mathcal {E}} f_{uv}(x_u,x_v), \end{aligned}$$

(1)

where $x_u$ is the label for node u in a graph $\mathcal {G}=(\mathcal {V}, \mathcal {E})$. When the variables $x_u$ are binary (Boolean): $\mathcal {L}= \mathbb {B}= \{0,1\}$, the problem can be written as a quadratic polynomial in x [11] and is known as quadratic pseudo-Boolean optimization (QPBO) [11].

In computer vision practice, energy minimization has found its place in semantic segmentation [51], pose estimation [71], scene understanding [57], depth estimation [44], optical flow estimation [70], image in-painting [59], and image denoising [8]. For example, tree-structured models have been used to estimate pictorial structures such as body skeletons or facial landmarks [71], multi-label Potts models have been used to enforce a smoothing prior for semantic segmentation [51], and general pairwise models have been used for optimal flow estimation [70]. However, it may not be appreciated that the energy minimization formulations used to model these vision problems have greatly varied degrees of tractability or computational complexity. For the three examples above, the first allows efficient exact inference, the second admits a constant factor approximation, and the third has no quality guarantee on the approximation of the optimum.

The study of complexity of energy minimization is a broad field. Energy minimization problems are often intractable in practice except for special cases. While many researchers analyze the time complexity of their algorithms (e.g., using big O notation), it is beneficial to delve deeper to address the difficulty of the underlying problem. The two most commonly known complexity classes are P (polynomial time) and NP (nondeterministic polynomial time: all decision problems whose solutions can be verified in polynomial time). However, these two complexity classes are only defined for decision problems. The analogous complexity classes for optimization problems are PO (P optimization) and NPO (NP optimization: all optimization problems whose solution feasibility can be verified in polynomial time). Optimization problems form a superset of decision problems, since any decision problem can be cast as an optimization over the set $\{$yes, no$\}$, i.e., P $\subset$ PO and NP $\subset$ NPO. The NP-hardness of an optimization problem means it is at least as hard as (under Turing reduction) the hardest decision problem in the class NP. If a problem is NP-hard, then it is not in PO assuming P $\ne$ NP.

Although optimal solutions for problems in NPO, but not in PO, are intractable, it is sometimes possible to guarantee that a good solution (i.e., one that is worse than the optimal by no more than a given factor) can be found in polynomial time. These problems can therefore be further classified into class APX (constant factor approximation) and class exp-APX (inapproximable) with increasing complexity (Fig. 1). We can arrange energy minimization problems on this more detailed complexity scale, originally established in [4], to provide vision researchers a new viewpoint for complexity classification, with a focus on NP-hard optimization problems.

In this paper, we make three core contributions, as explained in the next three paragraphs. First, we prove the inapproximability result of QPBO and general energy minimization. Second, we show that the same inapproximability result holds when restricting to planar graphs with three or more labels. In the proof, we propose a novel micro-graph structure-based reduction that can be used for algorithmic design as well. Finally, we present a unified framework and an overview of vision-related special cases where the energy minimization problem can be solved in polynomial time or approximated with a constant, logarithmic, or polynomial factor.

Fig. 1.

Discrete energy minimization problems aligned on a complexity axis. Red/boldface indicates new results proven in this paper. This axis defines a partial ordering, since problems within a complexity class are not ranked. Some problems discussed in this paper are omitted for simplicity (Color figure online)

Binary and Multi-label Case (Sect. 3). It is known that QPBO (2-label case) and the general energy minimization problem (multi-label case) are NP-hard [12], because they generalize such classical NP-hard optimization problems on graphs as vertex packing (maximum independent set) and the minimum and maximum cut problems [27]. In this paper, we show a stronger conclusion. We prove that QPBO as well as general energy minimization are complete (being the hardest problems) in the class exp-APX. Assuming P $\ne$ NP, this implies that a polynomial time method cannot have a guarantee of finding an approximation within a constant factor of the optimal, and in fact, the only possible factor in polynomial time is exponential in the input size. In practice, this means that a solution may be essentially arbitrarily bad.

Planar Three or More Label Case (Sect. 4). Planar graphs form the underlying graph structure for many computer vision and image processing tasks. It is known that efficient exact algorithms exist for some special cases of planar 2-label energy minimization problems [55]. In this paper, we show that for the case of three or more labels, planar energy minimization is exp-APX-complete, which means these problems are as hard as general energy minimization. It is unknown that whether a constant ratio approximation exists for planar 2-label problems in general.

Subclass Problems (Sect. 5). Special cases for some energy minimization algorithms relevant to computer vision are known to be tractable. However, detailed complexity analysis of these algorithms is patchy and spread across numerous papers. In Sect. 5, we classify the complexity of these subclass problems and illustrate some of their connections. Such an analysis can help computer vision researchers become acquainted with existing complexity results relevant to energy minimization and can aid in selecting an appropriate model for an application or in designing new algorithms.

1.1 Related Work

Much of the work on complexity in computer vision has focused on experimental or empirical comparison of inference methods, including influential studies on choosing the best optimization techniques for specific classes of energy minimization problems [26, 62] and the PASCAL Probabilistic Inference Challenge, which focused on the more general context of inference in graphical models [1]. In contrast, our work focuses on theoretical computational complexity, rather than experimental analysis.

On the theoretical side, the NP-hardness of certain energy minimization problems is well studied. It has been shown that 2-label energy minimization is, in general, NP-hard, but it can be in PO if it is submodular [30] or outerplanar [55]. For multi-label problems, the NP-hardness was proven by reduction from the NP-hard multi-way cut problem [13]. These results, however, say nothing about the complexity of approximating the global optimum for the intractable cases. The complexity involving approximation has been studied for classical combinatorial problems, such as MAX-CUT and MAX-2SAT, which are known to be APX-complete [46]. QPBO generalizes such problems and is therefore APX-hard. This leaves a possibility that QPBO may be in APX, i.e., approximable within a constant factor.

Energy minimization is often used to solve MAP inference for undirected graphical models. In contrast to scarce results for energy minimization and undirected graphical models, researchers have more extensively studied the computational complexity of approximating the MAP solution for Bayesian networks, also known as directed graphical models [42]. Abdelbar and Hedetniemi first proved the NP-hardness for approximating the MAP assignment of directed graphical models in the value of probability, i.e., finding x such that

$$\begin{aligned} \frac{p(x^*)}{p(x)} \le r(n) \end{aligned}$$

(2)

with a constant or polynomial ratio $r(n) \ge 1$ is NP-hard and showing that this problem is poly-APX-hard [2]. The probability approximation ratio is closest to the energy ratio used in our work, but other approximation measures have also been studied. Kwisthout showed the NP-hardness for approximating MAPs with the measure of additive value-, structure-, and rank-approximation [40–42]. He also investigated the hardness of expectation-approximation of MAP and found that no randomized algorithm can expectation-approximate MAP in polynomial time with a bounded margin of error unless NP $\subseteq$ BPP, an assumption that is highly unlikely to be true [42].

Unfortunately, the complexity results for directed models do not readily transfer to undirected models and vice versa. In directed and undirected models, the graphs represent different conditional independence relations, thus the underlying family of probability distributions encoded by these two models is distinct, as detailed in Appendix B. However, one can ask similar questions on the hardness of undirected models in terms of various approximation measures. In this work, we answer two questions, “How hard is it to approximate the MAP inference in the ratio of energy (log probability) and the ratio of probability?” The complexity of structure-, rank-, and expectation-approximation remain open questions for energy minimization.

2 Definitions and Notation

There are at least two different sets of definitions of what is considered an NP optimization problem [4, 45]. Here, we follow the notation of Ausiello et al. [4] and restate the definitions needed for us to state and prove our theorems in Sects. 3 and 4 with our explanation of their relevance to our proofs.

Definition 2.1

(Optimization Problem, [4] Definition 1.16). An optimization problem $\mathcal {P}$ is characterized by a quadruple $(\mathcal {I},\mathcal {S},m,\mathrm {goal})$ where

• 1. $\mathcal {I}$ is the set of instances of $\mathcal {P}$.

• 2. $\mathcal {S}$ is a function that associates to any input instance $x\in \mathcal {I}$ the set of feasible solutions of x.

• 3. m is the measure function, defined for pairs (x, y) such that $x\in \mathcal {I}$ and $y\in \mathcal {S}(x)$. For every such pair (x, y), m(x, y) provides a positive integer.

• 4. $\mathrm {goal} \in \{\min , \max \}$.

Notice the assumption that the cost is positive, and, in particular, it cannot be zero.

Definition 2.2

(Class NPO, [4] Definition 1.17). An optimization problem $\mathcal {P}= (\mathcal {I},\mathcal {S},m, \mathrm {goal})$ belongs to the class of NP optimization (NPO) problems if the following hold:

• 1. The set of instances $\mathcal {I}$ is recognizable in polynomial time.

• 2. There exists a polynomial q such that given an instance $x\in \mathcal {I}$, for any $y\in \mathcal {S}(x)$, $|y| < q(x)$ and, besides, for any y such that $|y| < q(x)$, it is decidable in polynomial time whether $y\in \mathcal {S}(x)$.

• 3. The measure function m is computable in polynomial time.

Definition 2.3

(Class PO, [4] Definition 1.18). An optimization problem $\mathcal {P}$ belongs to the class of PO if it is in NPO and there exists a polynomial-time algorithm that, for any instance $x\in \mathcal {I}$, returns an optimal solution $y\in \mathcal {S}^*(x)$, together with its value $m^*(x)$.

For intractable problems, it may be acceptable to seek an approximate solution that is sufficiently close to optimal.

Definition 2.4

(Approximation Algorithm [4] Definition 3.1). Given an optimization problem $\mathcal {P}= (\mathcal {I},\mathcal {S},m,\mathrm {goal})$ an algorithm $\mathcal {A}$ is an approximation algorithm for $\mathcal {P}$ if, for any given instance $x\in \mathcal {I}$, it returns an approximate solution, that is a feasible solution $\mathcal {A}(x) \in \mathcal {S}(x)$.

Definition 2.5

(Performance Ratio, [4], Definition 3.6). Given an optimization problem $\mathcal {P}$, for any instance x of $\mathcal {P}$ and for any feasible solution $y\in \mathcal {S}(x)$, the performance ratio, approximation ratio or approximation factor of y with respect to x is defined as

$$\begin{aligned} R(x,y) = \max \Big \{\frac{m(x,y)}{m^*(x)}, \frac{m^*(x)}{m(x,y)}\Big \}, \end{aligned}$$

(3)

where $m^*(x)$ is the measure of the optimal solution for the instance x.

Since $m^*(x)$ is a positive integer, the performance ratio is well-defined. It is a rational number in $[1,\infty )$. Notice that from this definition, it follows that if finding a feasible solution, e.g. $y\in \mathcal {S}(x)$, is an NP-hard decision problem, then there exists no polynomial-time approximation algorithm for $\mathcal {P}$, irrespective of the kind of performance evaluation that one could possibly mean.

Definition 2.6

( r(n)-approximation, [4], Definition 8.1). Given an optimization problem $\mathcal {P}$ in NPO, an approximation algorithm $\mathcal {A}$ for $\mathcal {P}$, and a function $r:\mathbb {N}\rightarrow (1,\infty )$, we say that $\mathcal {A}$ is an r(n)-approximate algorithm for $\mathcal {P}$ if, for any instance x of $\mathcal {P}$ such that $\mathcal {S}(x) \ne \varnothing$, the performance ratio of the feasible solution $\mathcal {A}(x)$ with respect to x verifies the following inequality:

$$\begin{aligned} R(x,\mathcal {A}(x)) \le r(|x|). \end{aligned}$$

(4)

Definition 2.7

( F -APX, rn [4], Definition 8.2). Given a class of functions F, F-APX is the class of all NPO problems $\mathcal {P}$ such that, for some function $r\in F$, there exists a polynomial-time r(n)-approximate algorithm for $\mathcal {P}$.

The class of constant functions for F yields the complexity class APX. Together with logarithmic, polynomial, and exponential functions applied in Definition 2.7, the following complexity axis is established:

$$\begin{aligned} \hbox {PO }\subseteq \hbox { APX }\subseteq \hbox { log-APX } \subseteq \hbox { poly-APX } \subseteq \hbox { exp-APX }\subseteq \hbox { NPO}. \end{aligned}$$

Since the measure m needs to be computable in polynomial time for NPO problems, the largest measure and thus the largest performance ratio is an exponential function. But exp-APX is not equal to NPO (assuming P $\ne$ NP) because NPO contains problems whose feasible solutions cannot be found in polynomial time. For an energy minimization problem, any label assignment is a feasible solution, implying that all energy minimization problems are in exp-APX.

The standard approach for proofs in complexity theory is to perform a reduction from a known NP-complete problem. Unfortunately, the most common polynomial-time reductions ignore the quality of the solution in the approximated case. For example, it is shown that any energy minimization problem can be reduced to a factor 2 approximable Potts model [48], however the reduction is not approximation preserving and is unable to show the hardness of general energy minimization in terms of approximation. Therefore, it is necessary to use an approximation preserving (AP) reduction to classify NPO problems that are not in PO, for which only the approximation algorithms are tractable. AP-preserving reductions preserve the approximation ratio in a linear fashion, and thus preserve the membership in these complexity classes. Formally,

Definition 2.8

(AP-reduction, [4] Definition 8.3). Let $\mathcal {P}_1$ and $\mathcal {P}_2$ be two problems in NPO. $\mathcal {P}_1$ is said to be AP-reducible to $\mathcal {P}_2$, in symbols $\mathcal {P}_1 \mathbin {{\le }_{\mathrm{AP}}}\mathcal {P}_2$, if two functions $\pi$ and $\sigma$ and a positive constant $\alpha$ exist such that²:

• 1. For any instance $x\in \mathcal {I}_1$, $\pi (x) \in \mathcal {I}_2$.

• 2. For any instance $x\in \mathcal {I}_1$, if $S_1(x) \ne \varnothing$ then $S_2(\pi (x)) \ne \varnothing$.

• 3. For any instance $x\in \mathcal {I}_1$ and for any $y \in S_2(\pi (x))$, $\sigma (x, y) \in S_1(x)$.

• 4. $\pi$ and $\sigma$ are computable by algorithms whose running time is polynomial.

• 5. For any instance $x\in \mathcal {I}_1$, for any rational $r > 1$, and for any $y \in S_2(\pi (x))$,

  $$\begin{aligned} R_2(\pi (x),y) \le r \quad \text {implies} \end{aligned}$$

  (5)
  $$\begin{aligned} R_1(x, \sigma (x, y)) \le 1 + \alpha (r-1). \end{aligned}$$

  (6)

AP-reduction is the formal definition of the term ‘as hard as’ used in this paper unless otherwise specified. It defines a partial order among optimization problems. With respect to this relationship, we can formally define the subclass containing the hardest problems in a complexity class:

Definition 2.9

( $\mathcal {C}$ -hard and  $\mathcal {C}$ -complete, [4] Definition 8.5). Given a class $\mathcal {C}$ of NPO problems, a problem $\mathcal {P}$ is $\mathcal {C}$-hard if, for any $\mathcal {P}' \in \mathcal {C}$, $\mathcal {P}' \mathbin {{\le }_{\mathrm{AP}}}\mathcal {P}$. A $\mathcal {C}$-hard problem is $\mathcal {C}$-complete if it belongs to $\mathcal {C}$.

Intuitively, a complexity class $\mathcal {C}$ specifies the upper bound on the hardness of the problems within, $\mathcal {C}$-hard specifies the lower bound, and $\mathcal {C}$-complete exactly specifies the hardness.

3 Inapproximability for the General Case

In this section, we show that QPBO and general energy minimization are inapproximable by proving they are exp-APX-complete. As previously mentioned, it is already known that these problems are NP-hard [12], but it was previously unknown whether useful approximation guarantees were possible in the general case. The formal statement of QPBO as an optimization problem is as follows:

Problem 1

QPBO

• instance: A pseudo-Boolean function $f :\mathbb {B}^\mathcal {V}\rightarrow \mathbb {N}:$

  $$\begin{aligned} f(x) = \sum _{v\in \mathcal {V}} f_u(x_u) + \sum _{u,v\in \mathcal {V}} f_{uv}(x_u,x_v), \end{aligned}$$

  (7)

  given by the collection of unary terms $f_u$ and pairwise terms $f_{uv}$.

• solution: Assignment of variables $x \in \mathbb {B}^\mathcal {V}$.

• measure: $\min f(x) > 0$.

Theorem 3.1

QPBO is exp-APX-complete.

Proof Sketch

(Full proof in Appendix A).

• 1. We observe that W3SAT-triv is known to be exp-APX-complete [4]. W3SAT-triv is a 3-SAT problem with weights on the variables and an artificial, trivial solution.

• 2. Each 3-clause in the conjunctive normal form can be represented as a polynomial consisting of three binary variables. Together with representing the weights with the unary terms, we arrive at a cubic Boolean minimization problem.

• 3. We use the method of [24] to transform the cubic Boolean problem into a quadratic one, with polynomially many additional variables, which is an instance of QPBO.

• 4. Together with an inverse mapping $\sigma$ that we define, the above transformation defines an AP-reduction from W3SAT-triv to QPBO, i.e. W3SAT-triv $\mathbin {{\le }_{\mathrm{AP}}}$ QPBO. This proves that QPBO is exp-APX-hard.

• 5. We observe that all energy minimization problems are in exp-APX and thereby conclude that QPBO is exp-APX-complete.

This inapproximability result can be generalized to more than two labels.

Corollary 3.2

k-label energy minimization is exp-APX-complete for $k \ge 2$.

Proof Sketch

(Full proof in Appendix A). This theorem is proved by showing QPBO $\mathbin {{\le }_{\mathrm{AP}}}$ k-label energy minimization for $k \ge 2$.

We show in Corollary B.1 the inapproximability in energy (log probability) transfer to probability in Eq. (2) as well.

Taken together, this theorem and its corollaries form a very strong inapproximability result for general energy minimization³. They imply not only NP-hardness, but also that there is no algorithm that can approximate general energy minimization with two or more labels with an approximation ratio better than some exponential function in the input size. In other words, any approximation algorithm of the general energy minimization problem can perform arbitrarily badly, and it would be pointless to try to prove a bound on the approximation ratio for existing approximation algorithms for the general case. While this conclusion is disappointing, these results serve as a clarification of grounds and guidance for model selection and algorithm design. Instead of counting on an oracle that solves the energy minimization problem, researchers should put efforts into selecting the proper formulation, trading off expressiveness for tractability.

Fig. 2.

Complexity for planar energy minimization problems. The “general case” implies no restrictions on the pairwise interaction type. This paper shows that the third category of problems is not efficiently approximable

4 Inapproximability for the Planar Case

Efficient algorithms for energy minimization have been found for special cases of 2-label planar graphs. Examples include planar 2-label problems without unary terms and outerplanar 2-label problems (i.e., the graph structure remains planar after connecting to a common node) [55]. Grid structures over image pixels naturally give rise to planar graphs in computer vision. Given their frequency of use in this domain, it is natural to consider the complexity of more general cases involving planar graphs. Figure 2 visualizes the current state of knowledge of the complexity of energy minimization problems on planar graphs. In this section, we prove that for the case of planar graphs with three or more labels, energy minimization is exp-APX-complete. This result is important because it significantly reduces the space of potentially efficient algorithms on planar graphs. The existence of constant ratio approximation for planar 2-label problems in general remains an open question⁴.

Theorem 4.1

Planar 3-label energy minimization is exp-APX-complete.

Proof Sketch

(Full proof in Appendix A).

• 1. We construct elementary gadgets to reduce any 3-label energy minimization problem to a planar one with polynomially many auxiliary nodes.

• 2. Together with an inverse mapping $\sigma$ that we define, the above construction defines an AP-reduction, i.e., 3-label energy minimization $\mathbin {{\le }_{\mathrm{AP}}}$ planar 3-label energy minimization.

• 3. Since 3-label energy minimization is exp-APX-complete (Corollary 3.2) and all energy minimization problems are in exp-APX, we thereby conclude that planar 3-label energy minimization is exp-APX-complete.

Corollary 4.2

Planar k-label energy minimization is exp-APX-complete, for $k \ge 3$.

Proof Sketch

(Full proof in Appendix A). This theorem is proved by showing planar 3-label energy minimization $\mathbin {{\le }_{\mathrm{AP}}}$ planar k-label energy minimization, for $k \ge 3$.

These theorems show that the restricted case of planar graphs with 3 or more labels is as hard as general case for energy minimization problems with the same inapproximable implications discussed in Sect. 3.

The most novel and useful aspect of the proof of Theorem 4.1 is the planar reduction in Step 1. The reduction creates an equivalent planar representation to any non-planar 3-label graph. That is, the graphs share the same optimal value. The reduction applies elementary constructions or “gadgets” to uncross two intersecting edges. This process is repeated until all intersecting edges are uncrossed. Similar elementary constructions were used to study the complexity of the linear programming formulation of energy minimization problems [48, 49]. Our novel gadgets have three key properties at the same time: (1) they are able to uncross intersecting edges, (2) they work on non-relaxed problems, i.e., all indicator variables (or pseudomarginals to be formal) are integral; and (3) they can be applied repeatedly to build an AP-reduction.

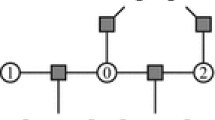
The two gadgets used in our reduction are illustrated in Fig. 3. A 3-label node can be encoded as a collection of 3 indicator variables with a one-hot constraint. In the figure, a solid colored circle denotes a 3-label node, and a solid colored rectangle denotes the equivalent node expressed with indicator variables (white circles). For example, in Fig. 3, $a=1$ corresponds to the blue node taking the first label value. The pairwise potentials (edges on the left part of the figures) can be viewed as edge costs between the indicator variables (black lines on the right), e.g., $f_{uv}(3, 2)$ is placed onto the edge between indicator c and e and is counted into the overall measure if and only if $c = e = 1$. In our gadgets, drawn edges represent zero cost while omitted edges represent positive infinity⁵. While the set of feasible solutions remains the same, the gadget encourages certain labeling relationships, which, if not satisfied, cause the overall measure to be infinity. Therefore, the encouraged relationships must be satisfied by any optimal solution. The two gadgets serve different purposes:

Split A 3-label node (blue) is split into two 2-label nodes (green). The shaded circle represents a label with a positive infinite unary cost and thus creates a simulated 2-label node. The encouraged relationships are

• $a = 1 \Leftrightarrow d = 1 \text { and } f = 1$.

• $b = 1 \Leftrightarrow g = 1$.

• $c = 1 \Leftrightarrow e = 1 \text { and } f = 1$.

Thus (d, f) encodes a, (d, g) and (e, g) both encode b and (e, f) encodes c.

UncrossCopy The values of two 2-label nodes are encouraged to be the same as their diagonal counterparts respectively (red to red, green to green) without crossing with each other. The orange nodes are intermediate nodes that pass on the values. All types of lines represent the same edge cost, which is 0. The color differences visualize the verification for each of the 4 possible states of two 2-label nodes. For example, the cyan lines verify the case where the top-left (green) node takes the values (1, 0) and the top-right (red) node takes the value (0, 1). It is clear that the encouraged solution is for the bottom-left (red) node and the bottom-right (green) node to take the value (0, 1) and (1, 0) respectively.

Fig. 3.

Gadgets to represent a 3-label variable as two 2-label variables (Split) and to copy the values of two diagonal pairs of 2-label variables without edge crossing (UncrossCopy) (Color figure online)

Fig. 4.

Planar reduction for 3-label problems

These two gadgets can be used to uncross the intersecting edges of two pairs of 3-label nodes (Fig. 4, left). For a crossing edge ($x_u$, $x_v$), first a new 3-label node $x_{v'}$ is introduced preserving the same arbitrary interaction (red line) as before (Fig. 4, middle). Then, the crossing edges (enclosed in the dotted circle) are uncrossed by applying Split and UncrossCopy four times (Fig. 4, right). Without loss of generality, we can assume that no more than two edges intersect at a common point except at their endpoints. This process can be applied repeatedly at each edge crossing until there are no edge crossings left in the graph [49].

5 Complexity of Subclass Problems

In this section, we classify some of the special cases of energy minimization according to our complexity axis (Fig. 1). This classification can be viewed as a reinterpretation of existing results from the literature into a unified framework.

5.1 Class PO (Global Optimum)

Polynomial time solvability may be achieved by considering two principal restrictions: those restricting the structure of the problem, i.e., the graph G, and those restricting the type of allowed interactions, i.e., functions $f_{uv}$.

Structure Restrictions. When G is a chain, energy minimization reduces to finding a shortest path in the trellis graph, which can be solved using a classical dynamic programming (DP) method known as the Viterbi algorithm [20]. The same DP principle applies to graphs of bounded treewidth. Fixing all variables in a separator set decouples the problem into independent optimization problems. For treewidth 1, the separators are just individual vertices, and the problem is solved by a variant of DP [47, 54]. For larger treewidths, the respective optimization procedure is known as junction tree decomposition [43]. A loop is a simple example of a treewidth 2 problem. However, for a treewidth k problem, the time complexity is exponential in k [43]. When G is an outer-planar graph, the problem can be solved by the method of [55], which reduces it to a planar Ising model, for which efficient algorithms exist [60].

Interaction Restrictions. Submodularity is a restriction closely related to problems solvable by minimum cut. A quadratic pseudo-Boolean function f is submodular iff its quadratic terms are non-positive. It is then known to be equivalent with finding a minimum cut in a corresponding network [21]. Another way to state this condition for QPBO is $\forall (u, v) \in \mathcal {E}, f_{uv}(0, 1) + f_{uv}(1, 0) \ge f_{uv}(0, 0) + f_{uv}(1, 1).$ However, submodularity is more general. It extends to higher-order and multi-label problems. Submodularity is considered a discrete analog of convexity. Just as convex functions are relatively easy to optimize, general submodular function minimization can be solved in strongly polynomial time [56]. Kolmogorov and Zabin introduced submodularity in computer vision and showed that binary 2^nd order and 3^rd order submodular problems can be always reduced to minimum cut, which is much more efficient than general submodular function minimization [34]. Živný et al. and Ramalingam et al. give more results on functions reducible to minimum cut [50, 68]. For QPBO on an unrestricted graph structure, the following dichotomy result has been proven by Cohen et al. [16]: either the problem is submodular and thus in PO or it is NP-hard (i.e., submodular problems are the only ones that are tractable in this case).

For multi-label problems Ishikawa proposed a reduction to minimum cut for problems with convex interactions, i.e., where $f_{uv}(x_u,x_v) = g_{uv}(x_u - x_v)$ and $g_{uv}$ is convex and symmetric [23]. It is worth noting that when the unary terms are convex as well, the problem can be solved even more efficiently [22, 31]. The same reduction [23] remains correct for a more general class of submodular multi-label problems. In modern terminology, component-wise minimum $x \wedge y$ and component-wise maximum $x \vee y$ of complete labelings x, y for all nodes are introduced ($x,y \in \mathcal {L}^\mathcal {V}$). These operations depend on the order of labels and, in turn, define a lattice on the set of labelings. The function f is called submodular on the lattice if $f(x \vee y) + f(x \wedge y) \le f(x) + f(y)$ for all x, y [65]. In the pairwise case, the condition can be simplified to the form of submodularity common in computer vision [50]: $f_{uv}(i, j+1) + f_{uv}(i+1, j) \ge f_{uv}(i, j) + f_{uv}(i+1, j+1).$ In particular, it is easy to see that a convex $f_{uv}$ satisfies it [23]. Kolmogorov [32] and Arora et al. [3] proposed maxflow-like algorithms for higher order submodular energy minimization. Schlesinger proposed an algorithm to find a reordering in which the problem is submodular if one exists [53]. However, unlike in the binary case, solvable multi-label problems are more diverse. A variety of problems are generalizations of submodularity and are in PO, including symmetric tournament pair, submodularity on arbitrary trees, submodularity on arbitrary lattices, skew bisubmodularity, and bisubmodularity on arbitrary domains (see references in [64]). Thapper and Živný [63] and Kolmogorov [33] characterized these tractable classes and proved a similar dichotomy result: a problem of unrestricted structure is either solvable by LP-relaxation (and thus in PO) or it is NP-hard. It appears that LP relaxation is the most powerful and general solving technique [72].

Mixed Restrictions. In comparison, results with mixed structure and interaction restrictions are rare. One example is a planar Ising model without unary terms [60]. Since there is a restriction on structure (planarity) and unary terms, it does not fall into any of the classes described above. Another example is the restriction to supermodular functions on a bipartite graph, solvable by [53] or by LP relaxation, but not falling under the characterization [64] because of the graph restriction.

Algorithmic Applications. The aforementioned tractable formulations in PO can be used to solve or approximate harder problems. Trees, cycles and planar problems are used in dual decomposition methods [9, 35, 36]. Binary submodular problems are used for finding an optimized crossover of two-candidate multi-label solutions. An example of this technique, the expansion move algorithm, achieves a constant approximation ratio for the Potts model [13]. Extended dynamic programming can be used to solve restricted segmentation problems [18] and as move-making subroutine [67]. LP relaxation also provides approximation guarantees for many problems [5, 15, 28, 37], placing them in the APX or poly-APX class.

5.2 Class APX and Class Log-APX (Bounded Approximation)

Problems that have bounded approximation in polynomial time usually have certain restriction on the interaction type. The Potts model may be the simplest and most common way to enforce the smoothness of the labeling. Each pairwise interaction depends on whether the neighboring labellings are the same, i.e. $f_{uv}(x_u,x_v) = c_{uv}\delta (x_u, x_v)$. Boykov et al. showed a reduction to this problem from the NP-hard multiway cut [13], also known to be APX-complete [4, 17]. They also proved that their constructed alpha-expansion algorithm is a 2-approximate algorithm. These results prove that the Potts model is in APX but not in PO. However, their reduction from multiway cut is not an AP-reduction, as it violates the third condition of AP-reducibility. Therefore, it is still an open problem whether the Potts model is APX-complete. Boykov et al.also showed that their algorithm can approximate the more general problem of metric labeling [13]. The energy is called metric if, for an arbitrary, finite label space $\mathcal {L}$, the pairwise interaction satisfies a) $f_{uv}(\alpha , \beta ) = 0$, b) $f_{uv}(\alpha , \beta ) = f_{uv}(\beta , \alpha ) \ge 0$, and c) $f_{uv}(\alpha , \beta ) \le f_{uv}(\beta , \gamma ) + f_{uv}(\beta , \gamma )$, for any labels $\alpha$, $\beta$, $\gamma \in \mathcal {L}$ and any $uv \in \mathcal {E}$. Although their approximation algorithm has a bound on the performance ratio, the bound depends on the ratio of some pairwise terms, a number that can grow exponentially large. For metric labeling with k labels, Kleinberg et al.proposed an $O(\log k \log \log k)$-approximation algorithm. This bound was further improved to $O(\log k)$ by Chekuri et al. [14], making metric labeling a problem in log-APX⁶.

We have seen that a problem with convex pairwise interactions is in PO. An interesting variant is its truncated counterpart, i.e., $f_{uv}(x_u,x_v) = w_{uv}\min \{d(x_u - x_v), M\}$, where $w_{uv}$ is a non-negative weight, d is a convex symmetric function to define the distance between two labels, and M is the truncating constant [66]. This problem is NP-hard [66], but Kumar et al. [39] have proposed an algorithm that yields bounded approximations with a factor of $2+\sqrt{2}$ for linear distance functions and a factor of $O(\sqrt{M})$ for quadratic distance functions⁷. This bound is analyzed for more general distance functions by Kumar [38].

Another APX problem with implicit restrictions on the interaction type is logic MRF [6]. It is a powerful higher order model able to encode arbitrary logical relations of Boolean variables. It has energy function $f(x) = \sum _i^n w_iC_i$, where each $C_i$ is a disjunctive clause involving a subset of Boolean variables x, and $C_i = 1$ if it is satisfied and 0 otherwise. Each clause $C_i$ is assigned a non-negative weight $w_i$. The goal is to find an assignment of x to maximize f(x). As disjunctive clauses can be converted into polynomials, this is essentially a pseudo-Boolean optimization problem. However, this is a special case of general 2-label energy minimization, as its polynomial basis spans a subspace of the basis of the latter. Bach et al. [6] proved that logic MRF is in APX by showing that it is a special case of MAX-SAT with non-negative weights.

6 Discussion

The algorithmic implications of our inapproximability have been discussed above. Here, we focus on the discussion of practical implications. The existence of an approximation guarantee indicates a practically relevant class of problems where one may expect reasonable performance. In structural learning for example, it is acceptable to have a constant factor approximation for the inference subroutine when efficient exact algorithms are not available. Finley and Joachims proved that this constant factor approximation guarantee yields a multiplicative bound on the learning objective, providing a relative guarantee for the quality of the learned parameters [19]. An optimality guarantee is important, because the inference subroutine is repeatedly called, and even a single poor approximation, which returns a not-so-bad worst violator, will lead to the early termination of the structural learning algorithm.

However, despite having no approximation ratio guarantee, algorithms such as the extended roof duality algorithm for QPBO [52] are still widely used. This gap between theory and application applies not only to our results but to all other complexity results as well. We list several key reasons for the potential lack of correspondence between theoretical complexity guarantees and practical performance.

Complexity Results Address the Worst Case Scenario. Our inapproximability result guarantees that for any polynomial time algorithm, there exists an input instance for which the algorithm will produce a very poor approximation. However, applications often do not encounter the worst case. Such is the case with the simplex algorithm, whose worst case complexity is exponential, yet it is widely used in practice.

Objective Function is Not the Final Evaluation Criterion. In many image processing tasks, the final evaluation criterion is the number of pixels correctly labeled. The relation between the energy value and the accuracy is implicit. In many cases, a local optimum is good enough to produce a high labeling accuracy and a visually appealing labeling.

Other Forms of Optimality Guarantee or Indicator Exist. Approximation measures in the distance of solutions or in the expectation of the objective value are likely to be prohibitive for energy minimization, as they are for Bayesian networks [40–42]. On the other hand, a family of energy minimization algorithms has the property of being persistent or partial optimal, meaning a subset of nodes have consistent labeling with the global optimal one [10, 11]. Rather than being an optimality guarantee, persistency is an optimality indicator. In the worst case, the set of persistent labelings could be empty, yet the percentage of persistent labelings over the all the nodes gives us a notion of the algorithm’s performance on this particular input instance. Persistency is also useful in reducing the size of the search space [29, 58]. Similarly, the per-instance integrality gap of duality based methods is another form of optimality indicator and can be exponentially large for problems in general [37, 61].

7 Conclusion

In this paper, we have shown inapproximability results for energy minimization in the general case and planar 3-label case. In addition, we present a unified overview of the complexity of existing energy minimization problems by arranging them in a fine-grained complexity scale. These altogether set up a new viewpoint for interpreting and classifying the complexity of optimization problems for the computer vision community. In the future, it will be interesting to consider the open questions of the complexity of structure-, rank-, and expectation-approximation for energy minimization.