Keywords

1 Introduction

We detail the OpenMP parallelization of two new data classification algorithms. A classification algorithm sorts the data into different classes such that the similarity within a class is stronger than that between different classes. This is a standard problem in machine learning. Recently, novel algorithms have been proposed [1] that are motivated by PDE-based image segmentation methods and are modified to apply to discrete data sets [4]. Serial results show that these algorithms improve both accuracy of solution and efficiency of the computation and can be potentially faster in parallel than various classification algorithms such as spectral clustering with k-means [6]. In this paper we describe parallel implementations and optimizations of the new algorithms. We focus on shared memory many-core parallelization schemes that will be applicable to next generation architectures such as the upcoming Intel Knights Landing processor. After analyzing the computational hotspots, we find that an optimized implementation of the Nyström eigensolver is the computational challenge. We implement directive-based OpenMP parallelization on the most time-consuming part and implement steps of optimizations to speed up and achieve almost ideal performance.

The rest of this paper is organized as follows: Sect. 2 presents the background of the image classification algorithms and the Nyström extension eigensolver. In Sect. 3 we discuss Math library usage and optimization for the serial code. We show our OpenMP parallelization strategies, optimization steps and arithmetic intensity analysis in Sect. 4. Finally, Sect. 5 presents some conclusions and future work.

2 Graph-Based Classification Algorithms

2.1 Introduction

We approach the classification problem using graph cut ideas. The novel classification algorithms consider each data point as a node in a weighted graph and the similarity (weight) between two nodes \(Z_i\) and \(Z_j\) is given by formula:

$$\begin{aligned} w_{ij} = exp(-dis(Z_i,Z_j)/\tau ), \end{aligned}$$
(1)

where \(\tau \) is a parameter [5, 6]. The weight matrix is \(W=\{w_{ij}\}\). In this paper, we use cosine distance since we use the hyperspectral imagery as the test data set and cosine distance is standard in this field. So

$$\begin{aligned} dis(Z_i,Z_j) = \frac{<Z_i,Z_j>}{||Z_i||_2||Z_j||_2}. \end{aligned}$$
(2)

The classification problem is approached using ideas from graph-cuts [2]. Given a weighted undirected graph, the goal is to find the minimum cut (measured by a summation of the weights along the graph cut) for this problem. This is equivalent to assigning a scalar or vector value \(u_i\) to each \(i^{th}\) data point and minimizing the graph total variation (TV) \(\sum _{ij} |u_i - u_j | w_{ij}\) [3]. Instead of directly solving a graph-TV minimization problem, we transform the graph TV to graph-based Ginzburg-Laudau (GL) functional [8]:

$$\begin{aligned} E(u) = \epsilon <L_su, u> + \frac{1}{\epsilon } \sum _i (W(u_i)) \end{aligned}$$
(3)

where W(u) is a double well potential, for example \(W(u)=\frac{1}{4}(u^2-1)^2\) in a binary partition and multi-well potential for more classes. \(L_s\) is the normalized symmetric graph Laplacian which is defined as \(L = I - D^{-\frac{1}{2}}WD^{-\frac{1}{2}}\), where D is a diagonal matrix with diagonal elements \(d_i = \sum _{j\in V} w(i,j)\).

In the vanishing \(\epsilon \) limit a variant of (3) has been proved to converge to the graph TV functional [7]. Different fidelity items are added to GL functional for semi-supervised and unsupervised learning respectively. The GL functional is minimized using gradient descent [9]. An alternative is to directly minimize the GL functional using the MBO scheme [11] or a direct compressed sensing method [12]. We use the MBO scheme in this paper in which one alternates solving the heat (diffusion) equation for u and thresholding to maintain distinct class structure. Computation of the entire graph Laplacian is prohibitive for large data so we use the Nyström extension to randomly sample the graph and compute a modest number of leading eigenvalues and eigenfunctions of the graph Laplacian [10]. By projecting all vectors onto this sub-eigenspace, the iteration step reduces to a simple coefficient update.

2.2 Semi-supervised and Unsupervised Algorithms

We outline the semi-supervised and the unsupervised algorithms. For the semi-supervised algorithm, the fidelity (a small amount of “ground truth”) is known and the rest needs to be classified according to the categories of the fidelity. For the unsupervised algorithm, there is no prior knowledge of the labels of the data. We use the Nyström extension algorithm beforehand for both algorithms to calculate the eigenvalues and eigenvectors as the inputs. In practice, these two algorithms converge very fast and give accurate classification results.

Semi-supervised Graph MBO Algorithm. [11]

figure a

Unsupervised Graph MBO Algorithm. [13]

figure b

2.3 Nyström Extension Method

In both the semi-supervised and unsupervised algorithms, we calculate the leading eigenvalues and eigenvectors of the graph Laplacian using the Nyström method [10] to accelerate the computation. This is achieved by calculating an eigendecomposition on a smaller system of size \(M< <N\) and then expanding the results back up to N dimensions. The computational complexity is almost O(N). We can set \(M<<N\) without any significant decrease in the accuracy of the solution.

Suppose \(Z=\{Z_k\}_{k=1}^N\) is the whole set of nodes on the graph. By randomly selecting a small subset X, we can partition Z as \(Z=X\bigcup Y\), where X and Y are two disjoint set, \(X=\{Z_i\}_{i=1}^M\) and \(Y = \{Z_j\}_{j=1}^{N-M}\) and \(M<<N\). The weight matrix W can be written as

$$ W= \left[ {\begin{array}{cc} W_{XX}&{} W_{XY} \\ W_{YX} &{} W_{YY} \\ \end{array} } \right] , $$

where \(W_{XX}\) denotes the weights of nodes in set X, \(W_{XY}\) denotes the weights between set X and set Y, \(W_{YX} = W_{XY}^T\) and \(W_{YY}\) denotes the weights of nodes in set Y. It can be shown that the large matrix \(W_{YY}\) can be approximated by \(W_{YY} \approx W_{YX}W_{XX}^{-1}W_{XY}\), and the error is determined by how many of the rows of \(W_{XY}\) span the rows of \(W_{YY}\). We only need to compute \(W_{XX}\), \(W_{XY} = W_{YX}^T\), and it requires only \((|X|\cdot (|X|+|Y|))\) computations versus \((|X|+|Y|)^2\) when the whole matrix is used. For the data set we use in this paper, \(M=100\) and \(N=13,475,840\).

Nyström Extension Algorithm

figure c

3 Math Library Usage and Optimizations

All the data are in matrix form and there are intensive linear algebra calculations. We apply a Singular Value Decomposition (SVD) to two small matrices. We make use of the LAPACK (Linear Algebra PACKage) and BLAS (Basic Linear Algebra Subprograms) libraries in the codes. The LAPACK provides routines for the SVD and the BLAS provides routines for vector-vector (Level 1), matrix-vector (Level 2) and matrix-matrix (Level 3) operations. BLAS and LAPACK are also highly vectorized and multithreaded using OpenMP.

We use the Intel Performance Tool VTune Amplifier to analyze the performance and to find bottlenecks [21]. The hotspots collection shows some computationally expensive parts are related to calculating the inner product of two vectors. In the unsupervised graph MBO algorithm, this operation occurs when calculating the matrix P and takes 84 % of the run time. Also, it occurs when calculating the matrix \(W_{XY}\) in the Nyström extension algorithm and takes 90 % of the run time. We optimize this procedure by forming all the vectors into matrices and doing the inner product of two matrices. In this way, we make use of BLAS 3 (matrix-matrix) instead of BLAS 1 (vector-vector). The part of calculating the matrix P in the unsupervised algorithm is 22.5\(\times \) faster using BLAS 3. This optimization is based on the fact that BLAS 1,2 are memory bound and BLAS 3 is computation bound [14, 15].

4 Parallelization of the Nyström Extension

Parallelization of these two classification algorithms involves a parallel for. It is critical to further optimize the OpenMP implementation to get nearly ideal scaling. We detail this process using more complex features of OpenMP such as SIMD and vectorization. Then we use the uniform sampling and chunk of data to get the best performance.

We consider the data set, described in more detail in [16], composed of hyperspectral video sequences recording the release of chemical plumes at the Dugway Proving Ground. We use the 329 frames of the video. Each frame is a hyperspectral image with dimension \(128\times 320\times 129\), where 129 is the dimension of the channel of each pixel. The total number of pixels is 13,475,840. Since we are dealing with very large data set we choose binary form for smaller storage space and faster I/O. Our test data is 13.91 GB in binary form and the I/O is 36.8\(\times \) faster than the txt format when testing on Cori Phase I.

We conduct our experiments on single nodes of systems at the National Energy Research Scientific Computing Center (NERSC). Cori Phase I is the newest supercomputer system at NERSC [22]. The system is a Cray XC based on the Intel Haswell multi-core processor. Each node has 128 GB of memory and two 2.3 GHz 16-core Haswell processors. Each core has its own L1 and L2 caches, with 64 KB (32 KB instruction cache, 32 KB data) and 256 KB, respectively; there is also a 40-MB shared L3 cache per socket. Peak performance per node is about 1.2 TFlop/s and peak bandwidth is about 120 GB/s. The resultant machine balance of 10 flops per byte strongly motivates the use of BLAS 3 like computations. Cori Phase II will be a Cray XC system based on the second generation of Intel Xeon Phi Product Family, called Knights Landing (KNL) Many Integrated Core (MIC) Architecture. The test system available to us now features 64 cores with 1.3 GHz clock frequency (Bin-3 configuration) with support for four hyper-threads each. Each core additionally has two 512bit-wide vector processing units. Additionally, the chip is equipped with 16 GB on-package memory shared between all cores. it is referred to as HBM or MCDRAM with a maximum bandwidth of 430 GB/s measured using the STREAM triad benchmark. The 512 KB L2 cache is shared between two cores (i.e. within a tile) and the 16 KB L1 cache is private to the core. Furthermore, the single socket KNL nodes are equipped with 96 GB DDR4 6-channel memory with a maximum attainable bandwidth of 90 GB/s.

Fig. 1.
figure 1

The procedure of calculating \(W_{XY}\):

Full size image

4.1 OpenMP Parallelization

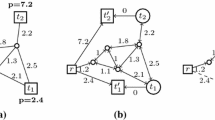
Analysis with VTune shows that the most time consuming phase of both two classification algorithms is the construction of \(W_{XY}\) in the Nyström extension procedure. This phase is a good candidate for OpenMP parallelization because each element of \(W_{XY}\) can be computed independently. The procedure of calculating \(W_{XY}\) is shown in Fig. 1. We form the data in a N by d matrix Z. Each row of Z corresponds to a data point and it’s a vector of dimension d. In computation, we store Z in an array in row major. We randomly select M rows to form the sampled data set \(X=\{Z_i\}_{i=1}^{M}\). The other rows form the data set \(Y=\{Z_j\}_{j=1}^{N-M}\). Then we use the nested for-loop to calculate the values of \(W_{XY}\) by the formula (1). We then put the corresponding value in an array which represent the M by \(N-M\) matrix \(W_{XY}\).

Reordering Loops. We have tested re-ordering loops as a means to optimize the algorithm. With analysis, we notice the j-loop is far larger than the i-loop. There are still two ways to do the parallelization. One way is to parallelize the j-loop as inner loop and the other way is to parallelize the j-loop as outer loop. We tried both ways and compared the results.

figure d

The results show that parallelizing the outer j-loop is much faster. The run time decreases by a factor of 7. This is because on Cori, each core has its own L1 and L2 cache. When parallelizing the outer j-loop, all the \(X_i\)s can be read and reside on the L2 of each core and can be used repeatedly. If instead we parallelize the inner j-loop, there are more reads of the \(X_i\) and thus the calculation takes more time. Parallelizing the outer j loop also means each thread has more work to do, since the inner i-loop is also part of the j-loop. In this way less overhead and more load balance can be achieved. While if we parallelize the inner j-loop, not only each thread has less work and large load imbalance, but also there are multiple times of thread creation and overhead.

Vectorization and Chunk. We further optimize the OpenMP parallelization using vectorization. First, we notice, the norms of \(Z_i\)s are computed repeatedly in the i-loop. So, we normalize all the \(Z_i\)s in the previous step, calculating \(W_{XX}\), and store all the normalized \(Z_i\)s in a new matrix \(X_{mat}\). Then we can calculate the inner product of each \(Z_j\) and all the \(Z_i\)s (\(X_{mat}\)) all at once. This make use of BLAS 2 instead of the previous BLAS 1. Also, we can vectorize the loop when calculating \(W_{XY}\). This optimization reduce the run time of calculating \(W_{XY}\) by a factor of 3.

Step C: Calculating \(W_{XY}\), normalize and form all \(Z_i\) s to \(X_{mat}\)

figure e

The Nyström extension algorithm is based on a random partition of the whole dataset Z into two disjoint data sets X and Y, where \(X=\{Z_i\}_{i=1}^M\) and \(Y = \{Z_j\}_{j=1}^{N-M}\) and \(M<<N\). Assuming we can uniformly partition the dataset, so that \(Z_i\)s are evenly distributed, we can form chunks of \(Z_j\)s to matrix and further optimize this calculation. The procedure is shown in Fig. 2. First, when calculating \(W_{XX}\), we evenly sample \(Z_i\)s and normalized them. We form the normalized \(Z_i\)s to a matrix \(X_{mat}\). Then all the data in between two consecutive \(Z_i\)s are the chunk of \(Z_j\)s. Since the chunk size is still very large, we further decompose each Y-chunk into sub-chunks. There are several considerations for choosing the sub-chunk size. If it is too small, we waste potential of combining expensive operations. If it is too large, the sub-chunk may run out of lower level cache and needs to be put into the higher cache levels, up to the point where they spill over into DRAM which may cause a substantial performance hit. The optimal value depends on the cache hierarchy, their respective sizes, their latency and so on. For a different architecture, one may consider choosing another value. We pick the the \(subchunksize=64\) when running the codes on Cori Phase I and it can be further optimized.

Fig. 2.
figure 2

Uniform sampling and dividing Y into chunks and sub-chunks

Full size image

Then for each sub-chunk, we calculate the Euclidean norm of each row and store them in a vector \(n2_{vec}\). This calculation can be vectorized since calculating the norm of each row is independent. We then calculate the matrix multiplication \(X_{mat}\cdot Y_{submat}\) using BLAS 3 function DGEMM. The result is a \(m \times subchunksize\) matrix \(n12_{mat}\). It is the result of all the inner product of rows in \(X_{mat}\) and rows in \(Y_{submat}\). Then we can vectorize the final calculation of values in \(W_{XY}\).

Step D: Calculating \(W_{XY}\) using uniform sampling and chunked Y matrices

figure f

In this uniform sampling, the chunk size is defined as \(chunksize = floor(N/M)\). When M is not divisible by N, the last chunk is larger than the other chunks. Also, subchunksize may not be divisible by chunksize. So the size of the last sub-chunk in each chunk needs to be adjusted. The procedure of uniform sampling gives good results as compared to the random sampling and further improves the performance by a factor of 1.7.

Thread Affinity. We also consider the effect of thread affinity. We choose the thread affinity setting as “OMP_PROC_BIND=scatter” and “OMP_PLACES=cores (or threads)”, because it uses one hardware thread per core. While if we use the thread affinity setting to be “OMP_PROC_BIND=close” and “OMP_PLACES=threads”, it puts more threads on each physical core and leaves other cores idle, which affects scaling performance.

Fig. 3.
figure 3

The run time of different optimization steps on Cori Phase I. Step A: parallelizing the inner j-loop and BLAS 3 optimization on Graph MBO. Step B: parallelizing the outer j-loop. Step C: normalizing and forming all \(Z_i\)s to \(X_{mat}\). Step D: using uniform sampling and chunked Y matrices. (Color figure online)

Full size image
Fig. 4.
figure 4

The scaling results of the OpenMP parallelization of the Nyström loop on Cori Phase I. The black line with squares, the red line with circles and the blue line with triangles show the scaling results of step B, C and D respectively. The pink line with upside down triangles shows the ideal scaling. (Color figure online)

Full size image

Experiment Results. Cori Phase I: We examined optimization steps on a single node of Cori Phase I. The run time decrease and scaling results of different steps of optimizing the OpenMP parallelization are shown in Fig. 3. We show the significant speed up of the Nyström loop part. In Step A, in addition to parallelizing the Nyström loop, we also use BLAS 3 optimization on the graph MBO algorithm. Since we use BLAS and LAPACK in the serial part of Nyström algorithm and the graph MBO algorithm, their run time also decrease when using multi-cores. We show the OpenMP thread scaling results on Cori Phase I in Fig. 4. Almost ideal scaling results are acheived. Each Cori Phase 1 node has two sockets (NUMA domain) and each socket has 16 cores. Although the absolute performance increases when using more than 16 threads on a single node, the NUMA effect is observed. The scaling slows down due to the remote memory access to a far NUMA domain.

Knight’s Landing: We employed the same optimizations already used for the Haswell optimization with three exceptions: we have compiled the code with AVX-512 support to make use of the wider vector units as well as doubled the sub-chunk size as depicted in Fig. 2 accordingly.Footnote 1 Furthermore, we have enabled fast floating point model and imprecise divides with -fp-model fast=2 and -no-prec-div respectively. The (strong) thread scaling of the various sections of the code is depicted in Fig. 5 for one hyper-thread per core. We found that this configuration delivered the best performance. Utilizing two or more hyper-threads significantly decreased the performance, especially that of the Nystrom loop. We observe that our code obtains good strong scaling up to all 64 cores. We are currently investigating the hyper-threads performance and improving the scaling of step D.

Fig. 5.
figure 5

The scaling results of the OpenMP parallelization of the Nyström loop on KNL white box. The black line with squares, the red line with circles and the blue line with triangles show the scaling results of step B, C and D respectively. The pink line with upside down triangles shows the ideal scaling which matches step D. (Color figure online)

Full size image

4.2 Arithmetic Intensity and Roofline Model

Arithmetic intensity is the ratio of floating-point operations (FLOP’s) performed by a given code (or code section) to the amount of data movement (Bytes) that are required to support those operations. Arithmetic intensity in conjunction with the Roofline Model [17] can be used to bound kernel performance and qualify performance in a manner more nuanced than percent-of-peak. Figure 6 shows the result of using the Roofline Toolkit [18] to characterize the performance of a Cori Phase I node (full 32 cores). The resultant lines (“ceilings”) are bounds on performance. Clearly, in order to attain high performance, one must design algorithms that deliver high arithmetic intensity. In order to characterize the Nyström loop, we used Intel’s Software Development Emulator Toolkit (SDE) to record FLOP’s and Intel’s VTune Amplifier to collect data movement when running on 32 cores of a Cori Phase I node [19, 20]. We can then compare the results to a theoretical estimate based on the inherent requisite computation and data movement.

Fig. 6.
figure 6

Empirical Roofline Toolkit results for a Cori Phase I node. Observe, DRAM bandwidth constrains performance for a wide range of arithmetic intensities.

Full size image

As shown in Fig. 1, the memory access has two major components — one must read data from the matrix Z from DRAM and then write the results in to a matrix \(W_{XY}\). The size of data matrix Z is \(N\times d\), where \(N=13,475,840\) and \(d=129\) for our test data. As we store the data in double precision, the total size of the matrix (and hence volume of data read) is at least 13.907\(\times 10^9\) bytes. In the inner loop, the processor must continually access M rows of the matrix Z. As the resultant volume of data (103,200 bytes) easily fits in cache, we need only read each \(Z_i\) once (data movement is well proxies by compulsory cache misses). The size of the matrix \(W_{XY}\) is \((N-M)\times M\), where \(M=100\). As each double-precision element is written once, we can bound write data movement as \((N-M)\times M \times 8\) = \(10.78\times 10^9\) bytes. A similar calculation can be performed to calculate the requisite number of floating-point operations. In the optimized code, although there are dot products for \(<Z_j,Z_j>\) coupled with a reciprocal square root and one exponential per element of \(W_{XY}\), the DGEMM used for calculating \(X_{mat}\times Y_{submat}\) should dominate the flop count. The matrix \(X_{mat}\) is \(100\times 129\), the matrix \(Y_{submat}\) is on average \(64\times 129\), and there are roughly \(13,475,840/64 = 210560\) \(Y_{submat}\) matrices. Thus, the number of floating-point operations in the loop is about \(210560\times 2\times 64\times 129\times 100 = 347.68\times 10^9\) (ignoring any BLAS 2 operations, the dot products, and the exponential).

Table 1. Theoretical estimates (ignoring dual-socket nature of the machine) and Empirical measurements (using VTune and SDE) of data memory and floating-point operations for the Nyström loop.
Full size table

Table 1 presents our theoretical estimates and empirical measurements (using VTune and SDE) of data memory and floating-point operations for the Nyström loop. As expected, our rough theoretical model slightly underestimated each quantity. Multiple sockets (each with their own caches) may be required to read unique bytes, but in reality will access overlapping data due to the realities of large cache lines and hardware stream prefetchers. In terms of floating-point operations, it is clear DGEMM (the basis for our theoretical model) constitutes over 90 % of the total flop count with the remainder likely arising from exponentials and dot products. Overall, with a run time of about 1.28 s, the optimized code attains about 300GFlop/s of performance and 23GB/s of DRAM bandwidth at an arithmetic intensity of just over 13 flops per byte. At such a high arithmetic intensity, Fig. 6 suggests the full node DRAM bandwidth will not be the ultimate limiting factor. However, as we have not included any NUMA optimizations in the implementation, we expect the single socket’s DRAM bandwidth (slightly less than 54 GB/s) to be a substantial performance impediment. Additional data movement in the cache hierarchy coupled with performance challenges associated with transcendental operations such as reciprocal-square-root and exponential likely impede our ability to fully saturate even a single socket’s bandwidth.

5 Conclusion and Future Work

In this paper, we present a parallel implementation of two novel classification algorithms using OpenMP. We show OpenMP parallel and SIMD regions in combination with optimized library routines achieve almost ideal scaling and significant speedup over serial implementations. Although, we attain roughly 50 % of the Roofline bound (no NUMA), we expect future optimizations for the transcendentals, the cache hierarchy, and NUMA to substantially improve performance. We also expect more performance optimization results on KNL “white boxes” (pre-release hardware) and the future Cori Phase II.