Keywords

1 Introduction

Moving robotic arms requires typically forward as well as inverse kinematic control and planning. Planning trajectories of robotic arms in high dimensional configuration space is nontrivial. This planning process gets even more difficult under the objective to obtain feasible, smooth and collision free trajectories or if one includes orientation constraints, for example moving a cup of coffee without spilling. Consequently, in some cases planners fail to find a solution for given problem. State-of-the-art algorithms like Rapid Exploring Random Trees [5] or the Covariant Hamiltonian Optimization Motion Planner [12] need several hundred milliseconds to several seconds to plan trajectories, depending on the complexity of the planning task.

In this research we investigate Recurrent Neural Networks (RNNs), particularly Dynamic Cortex Memorys (DCMs) [7, 8], for computing inverse kinematics of robot arms, particularly with many joints. More concretely, we learned to estimate poses for given arm configurations with RNNs, which match the sequential nature of computing kinematic forward-chains. Back-Propagation Through Time (BPTT) is used to to generate the inverse mapping. We show that the presented approach can handle arms even with up to 120 articulated degrees of freedom (DoF) and that it also works on real robot arms. Handling robot arms with many DoF have studied, e.g., by Rolf et al. in [9] in which the inverse kinematics of a bionic elephant trunk was learned, making use of known (explored) mappings from target space to configuration space.

2 Methodology

Our first step towards gaining inverse kinematics is to train a recurrent forward model. Particularly, the neural network must first learn to estimate end-effector poses based on configuration vectors, i.e. joint angles. Therefore, a set of configuration vector and pose pairs is required. When the mathematical forward model of the arm is known, samples can be computed directly. Otherwise, another feedback mechanism providing end-effector poses is required, for instance, a tracking system. The starting point is a general arm model with universal joints, each providing a yaw-pitch-roll rotation at once with three DoF. Note that this procedure can later be applied to realistic and more specific arms, which usually have only one DoF per joint. On the other hand, the configuration commands must not necessarily be angles, but can also be, for instance, muscular contraction forces, as used in octopus-arms [11].

2.1 Dynamic Cortex Memory Networks

A DCM [7, 8] is in principle an LSTM with forget gate [2] and peephole connections [3], but additionally provides a communication infrastructure that enables the gates to share information. This infrastructure is established through two connection schemes. The first scheme is called cortex and connects each gate with every other gate. The second scheme equips each gate with a self-recurrent connection providing a local gate-state. In the original study [7] it was pointed out, that these two schemes used in combination lead to a synergy effect. In comparison with an LSTM block, a DCM block has nine additional connections that are all weighted and, hence, trainable.

Beyond the structural modification, DCMs are used exactly like LSTMs and are trained in the same manner. In this paper all recurrent networks are trained using gradient descent with momentum term, whereas the gradients are computed with Back Propagation Through Time (BPTT) [10]. The presented experiments were performed using the JANNLab neural network framework [6].

2.2 Learning the Forward Model

Let us consider an arm with n universal joints. The three angles for the j-th joint are given by a vector \(\varvec{\upvarphi }^{(j)} \in [-\pi , \pi ]^{3}\). We refer to the entire sequence for all joints here as configuration state denoted by \(\varvec{\Upphi }\). Let now M be the forward model of the robot arm, which maps a configuration state to the corresponding end-effector frame (denoted by N) relative to the base frame (denoted by 0)

$$\begin{aligned} \varvec{\Upphi }= \left( \varvec{\upvarphi }^{(1)}, \ldots ,\varvec{\upvarphi }^{(n)}\right) \mathop {\longmapsto }\limits ^{\text {M}} {}_{N}^{0}\mathbf {A} =\begin{bmatrix} {}_{N}^{0}\mathbf {R}&{}_{N}^{0}\mathbf {p} \\ \mathbf {0}&1 \end{bmatrix}, \end{aligned}$$
(1)

where \({}_{N}^{0}\mathbf {A} \in \mathbb {R}^{4\times 4}\) can be decomposed into the rotation, i.e., the orientation of the end-effector, given by an orthonormal base \({}_{N}^{0}\mathbf {R} \in SO(3) \subset \mathbb {R}^{3\times 3}\) and the translation, i.e., the position of end-effector, given by \({}_{N}^{0}{\mathbf {p}} \in \mathbb {R}^{3}\). It is important to mention that M also considers the lenghts of the segments and other possible offsets. They are, however, left out in the formulation, because they are constant and, moreover, the neural networks do not need them for learning the forward model. Preliminary experiments indicated that constant translations (joints offsets etc.) can be deduced by the networks using trainable biases. Given such an observable model, our first objective is to train an RNN to become a neural approximation of M, able to produce pose estimates \({}_{N}^{0}\tilde{\mathbf {A}}\) for given configuration states. In the case of universal joints there are three variables per joint. At this point, the key aspect of the recurrent forward model comes into play: each joint transformation is considered as a “computing time-step” in the RNN. Accordingly, the RNN requires then only three input neurons, fully independently from the number of joints. The angle triples are presented to the network in a sequential manner. Due to this, the network is forced to use its recurrence to handle the repetitive character of computing chains of mostly very similar transformations. This forward computing procedure is illustrated in Fig. 1.

Fig. 1.
figure 1

The RNN based forward computation. The angle-triples of the joints are interpreted as a sequence. One computation step in the RNN is associated with a certain joint (3 rotations) and, implicitly, with its corresponding segment (translation). Thus, each hidden state \(\mathbf {x}_{h}^{(j)}\) of the RNN at time step j is computed based on the associated angle triple \(\varvec{\upvarphi }^{(j)}\) and the previous hidden state \(\mathbf {x}_{h}^{(j-1)}\) with \(\mathbf {x}_{h}^{(0)}\,{=}\,\mathbf {0}\). The output of the RNN after n time steps is the pose estimate with regard to the given angles.

Full size image

While the position can be represented directly using three output neurons, there are several options to represent the orientation. For this proof-of-concept we used a vector-based representation of the two base axes z and x, which worked significantly better than, e.g., 3 rotation angles. Thus, the orientation requires six output neurons such that the RNNs have overall nine linear output neurons, whereas we denote the final output vector (after n computing steps) of an RNN by \(\mathbf {y} \in \mathbb {R}^{9}\) in which the first three components encode the position estimate \({}_{N}^{0}\tilde{\mathbf {p}}\) and the last six components encode the orientation estimate \({}_{N}^{0}\tilde{\mathbf {R}}\). In the long run, however, it could make sense to use a quaternion-based representation in combination with a special output layer providing normalized outputs directly.

2.3 Inverse Recurrent Model

During training of the forward model, the network learned to encode and decode the kinematic behavior of the robot arm using an internal representation – a recursive superimposition of sigmoidals – that is possibly a simplification of the “real” kinematic relationships. To gain the inverse mapping, we utilize the backward-pass of the network, namely, we back-propagate through time a change in the output space. Note that a similar idea was used earlier for inverting feed-forward networks in [4]. This allows us to yield a direction in the input space in which the input must be adapted such that the output gets closer to the desired output, i.e., the target pose. In an iterative process, starting from any possible configuration state, when following the negative gradient through the configuration space, we can obtain a possible solution for the inverse kinematics. Let \(\varvec{\Upphi }\) be the current configuration state from which we start computing the inverse kinematic and let \({}_{N}^{0}\overset{_*}{\mathbf {A}}\) be the target pose. First, we perform a forward pass with the RNN, yielding a pose estimate \({}_{N}^{0}\tilde{\mathbf {A}}\) with respect to \(\varvec{\Upphi }\). Second, we present the target pose \({}_{N}^{0}\overset{_*}{\mathbf {A}}\) as the desired output, like in a regular training step, and perform the backward pass, which propagates the influence to the output discrepancy (loss) \(\mathcal {L}\) reversely in “time” though the recurrent network. Third, we need to derive the influence of each input to \(\mathcal {L}\). Since all \(\varvec{\updelta }_{h}^{(j)}\) are known we can apply the chain rule as a step upon BPTT to yield

$$\begin{aligned} \frac{ \partial \mathcal {L}}{ \partial \upvarphi _{i}^{(j)} }= & {} \sum _{h = 1}^{H} \left[ \frac{ \partial net_{h}^{(j)} }{ \partial \upvarphi _{i}^{(j)} } \frac{ \partial \mathcal {L}}{ \partial net_{h}^{(j)} } \right] \sum _{h = 1}^{H} w_{ih} \delta _{h}^{(j)}. \end{aligned}$$
(2)

This procedure of computing the input gradient joint-wise is illustrated in Fig. 2. In LSTM-like networks the gradient can be kept more stable over time during back-propagation, which plays obviously a major role for the proposed method, particularly for arms with many joints, since traditional RNNs were not able to learn the forward model precisely. Fourth, we update \(\varvec{\Upphi }\) by simply applying the rule

$$\begin{aligned} \varvec{\Upphi }(\tau + 1) \longleftarrow \varvec{\Upphi }(\tau ) - \eta \nabla _{\varvec{\Upphi }(\tau )}\mathcal {L} + \mu \left[ \varvec{\Upphi }(\tau ) - \varvec{\Upphi }(\tau - 1)\right] \end{aligned}$$
(3)
Fig. 2.
figure 2

Inverse computing using BPTT. After an input sequence (the current state of the arm) is presented, the discrepancy between the output and the desired pose is back-propagated through the network.

Full size image

where \(\tau \) denotes the current iteration step, \(\eta \in \mathbb {R}\) is a gradient scale factor (cf. learning rate in gradient descent learning). Note that large step size \(\eta > 0.5\) may cause oscillations during this process. Optionally, we added the last update step as momentum scaled with the rate \(\mu \in \mathbb {R}\) (i.e., \(\mu \approx 0.5\)), which results in a faster convergence. The entire procedure is repeated until the current pose estimate is sufficiently close to \({}_{N}^{0}\overset{_*}{\mathbf {A}}\). The proposed method can be applied offline, where a full solution is searched first and then the controller interpolates towards it, or online, where the search process is (partially) synchronized with the arm movement, whereas the motion-trajectory basically represents the gradient-guided trajectory in configuration space.

A drawback of the approach is that the accuracy of potential solutions is limited to the accuracy of the neural forward model. However, this can be compensated if the “real” pose of the robot arm with respect to a given \(\varvec{\Upphi }\) is accessible either via the exact mathematical forward model or another feedback provided. The idea is as follows: Instead of presenting the desired target, encoded as a vector \(\mathbf {z} \in \mathbb {R}^{9}\) analogously to \(\mathbf {y}\) in Sect. 2.2, we present a “modified” version \(\tilde{\mathbf {z}}\). Let \(\mathbf {u} \in \mathbb {R}^{9}\) be the true current pose, which encodes \({}_{N}^{0}\mathbf {p}\) in the same manner, we compute \(\tilde{\mathbf {z}}\) with respect to a given \(\varvec{\Upphi }\) through

$$\begin{aligned} \tilde{\mathbf {z}} = \begin{bmatrix} \left[ y_{i} + \gamma _{1}(z_{i} - u_{i}) \right] _{1\le i \le 3} \\ \left[ y_{j} + \gamma _{2}(z_{j} - u_{j}) \right] _{4\le j \le 9} \end{bmatrix}^{\top }, \end{aligned}$$
(4)

where \(\gamma _{1},\gamma _{2} \in [0, 1]\) are additional scaling factors weighting the influence of the position discrepancy and the orientation discrepancy respectively. The modification causes the networks to converge towards the real target pose.

3 Exerimental Results

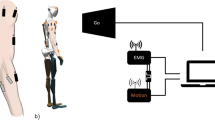
The results presented in this section are based on four different simulated arms with 5, 10, 20, and 40 universal joints. The rotations along the segment axis z are restricted to angle range , whereas both orthogonal rotations (x, y) are restricted to the angle range . A larger angle range for the z rotation caused problems during earlier experiments and we hence limited the range as stated above for the moment. To learn these arms 20, 000 random configurations and associated poses are used. To show that the approach also works on a real robot arm, we additionally included a CrustCrawler manipulator in our experiments. This is a light-weight, low budget manipulator with 9 Robotis Dynamixel servomotors, which we used in a four articulated DoF setup. For training also 20, 000 random poses were computed using the Trac-IK kinematic plugin [1] for ROS MoveItFootnote 1. Note, that only one parameter per computation step is required, whereby we do not have to distinguish the rotation axis – the correct association is ensured by the trained network – such that we can directly use the angles given in DH (Denavit-Hartenberg) notation. It should be mentioned that the position values in all experiments were normalized such that each arm has a unit-less length of 1.

Fig. 3.
figure 3

Convergence (average MSE over 100 random samples) towards target poses for different arm models during 500 iterations.

Full size image
Fig. 4.
figure 4

The first two rows show the movement towards the target pose (blue) for a 20-joint arm (top) and a 40-joint arm (middle). In the bottom row it is shown that inverse kinematics can be produced even under difficult conditions (from left to right): Unreachable poses, heavily screwed, locked joints.(Color figure online)

Full size image

The experiments are based on RNNs with two hidden layers, each consisting of 24 DCM blocks for the universal arms and 20 DCM block for the CrustCrawler, respectively. In both architectures each hidden block contains 3 inner cells and has variable biases for cells and gates. Further, each hidden layer is not recurrently connected to itself, but both hidden layers are mutually fully connected. This was the best architecture we discovered in preliminary investigations. During training, the learning rate was repeatedly decreased every 20 epochs (from 0.01 over \(5{\cdot }10^{-3}\), \(10^{-3}\), \(5{\cdot }10^{-4}\), \(10^{-4}\), \(5{\cdot }10^{-5}\) to \(10^{-5}\)) and the momentum rate was fixed to 0.95. However, with 10, 20, and 40 joints there was an issue concerning the covered angle ranges within the training samples. With increasing the number of joints, the learnable angle ranges descreased. We figured out that for those arms the forward model can be significantly improved, if the network is pretrained either on an arm with less joints or with limited angles. For these retraining procedures we performed similarly as described above but skipped the first two largest learning rates.

To analyze whether target poses can be reached reliably, we computed random configurations for which we then determined their corresponding poses using the known forward model. For the resulting poses we generated the inverse kinematics with the RNNs. Based on this configurations we computed again the pose using the forward model and finally compared both poses. Figure 3 shows the the average convergence of the pose error (MSE) over 100 random poses within 500 iterations on different arms.

Fig. 5.
figure 5

In the top row the MoveIT rviz plug-in is displayed. The current configuration of the arm is rendered in black and the goal in orange. A movement of the marker changes the arm’s goal pose. The kinematics solver is called and the goal configuration is rendered. In images from left to right the transition to the goal state is illustrated. Note that for this image series, we use one of MoveIT’s planning algorithms for the real arm’s trajectory generation in order to exclude self-collisions – nonetheless each particular call of the inverse kinematics is solved with the RNN.(Color figure online)

Full size image

As can be seen, on all arms the approach shows a relatively similar convergence behavior. Already after 50 iterations the end-effector poses are sufficiently close to the target poses. The results clearly indicate that for all arms, even for the one with 40 universal joints, precise solutions could be found consistently. Note that on the CrustCrawler for some random poses (\({{\approx }\,{10}\,\%}\)) the process got stuck in a local minimum. These cases were left out for computing the average curve. Figures 4 and 5 visually confirm the success of our approach, since the desired target poses are reached exactly. Figure 4 also demonstrates that good solutions can be found even under difficult conditions. If a target pose is unreachable the network drives the arm towards a close plausible pose. But also in the case when an arm is heavily screwed, the target can be reached robustly. Furthermore, entirely locked joints can also be easily compensated on the fly.

4 Conclusion

In this paper we introduced an approach for computing inverse kinematics of many-joint robot arms with inverse recurrent forward models. First, we learned to estimate poses for given arm configurations with RNNs. While the RNNs match the sequential nature of computing forward-chains, Back-Propagation Through Time (BPTT) is used to to generate the inverse mapping.

We verified our method on complex simulated 3D arms with multi-axis spherical joints. It was shown that the approach scales well, since we could effectively control arms with 5-joint, 10-joint, 20-joints, and even with 40-joints (the latter has 120 DoF). It is also shown that the approach can produce inverse kinematics precisely for a real robot arm. This research is to be regarded as a proof-of-concept and a first step towards a novel perspective on neural arm-control.