Feature Selection for High Dimensional Steganalysis

Abstract

In today’s digital image steganalysis, the dimensionality of the feature vector is relatively high. This may result in much redundancy and high computational complexity. In this paper, a novel feature selection method is proposed from a new perspective. The main idea of our proposed feature selection method is that the element in the extracted feature vector should consistently increase or decrease with the increase of embedding rate for a given steganographic scheme. Various experimental results tested on 10000 grayscale images demonstrate that our feature selection method can reduce the dimensionality of the high dimensional feature vector efficiently, and meanwhile the detection accuracy can be well preserved.

1 Introduction

Steganography is the art and science of concealing secret messages [11]. Currently, adaptive embedding is one of the major research directions. Some spatial domain adaptive steganographic schemes have been proposed in recent years, such as WOW (Wavelet Obtained Weights) [5] and EAMR (Edge adaptive image steganography based on LSB matching revisited algorithm) [8]. The basic idea of adaptive steganographic schemes is to preferentially modify some elements (pixels/coefficients) in complex textural regions that are difficult to model, and keep the elements in the smooth regions unchanged. Generally, adaptive steganographic schemes are more secure than non-adaptive steganography, such as LSB (Least Significant Bit) based [2, 10] algorithms, especially when the embedding rate is high.

In order to accurately detect adaptive steganographic schemes in the spatial domain, the higher and higher dimensional feature representation of image is required in steganalysis. For example, the dimensionality of the feature vector extracted by SRM (Spatial Rich Model) [4] is higher than thirty thousand. Although the high dimensional feature vector may perform better in detecting secret messages, some limitations may exist in practical applications because of the high computational complexity. Thus proper dimensionality reduction for the high dimensional feature vector is necessary. In this paper, according to some specific characteristics in the field of steganography/steganalysis, a novel feature selection method is proposed. For the ease of explanation, the elements in the feature vector are called features in the following. The main idea of our proposed novel feature selection method is that the values of effective feature (belonging to the high dimensional feature vector) should consistently increase or decrease with the increase of embedding rate, and thus the feature that does not have this characteristic should be removed from the original high dimensional feature vector. Various experimental results demonstrate that the dimensionality of the high dimensional feature vector can be reduced efficiently via using our proposed new feature selection method, and meanwhile the detection accuracy of the corresponding steganalytic algorithm can be well preserved.

The rest of this paper is arranged as follows. Section 2 provides a brief description of three high dimensional steganalytic algorithms. The characteristic of stego images with different embedding rates are described in Sect. 3. Our new feature selection method is proposed in Sect. 4. The experimental results are shown in Sect. 5 and we draw the conclusion in Sect. 6.

2 Overview of Three High Dimensional Steganalytic Algorithms

In this section, we give a brief overview of three high dimensional steganalytic algorithms, i.e., Spatial Rich Model (SRM) [4], maxSRM [3] and maxSRMd2 [3], which are used for testing our proposed feature selection method.

2.1 SRM

In order to capture a large number of different types of dependencies among neighboring pixels, the SRM model is formed by merging multiple diverse and smaller submodels to produce a better detection result. There are mainly three steps for explaining how to form the SRM submodels.

• (1) Computing residuals: The submodels are formed from noise residuals, $R=R_{ij}{\in }R^{n1\times {n2}}$, computed using high-pass filters of the following form:

  $$\begin{aligned} R_{ij}=\widehat{X_{ij}}(N_{ij})-cX_{ij}, \end{aligned}$$

  (1)

  where $c{\in }\mathbb {N}$ is the residual order, the $\mathbb {N}$ represents the set of all integers. $X_{ij}$ represents pixel values located at (i, j) of 8-bits grayscale cover images. $N_{ij}$ is a local neighborhood of pixel $X_{ij}$, $X_{ij}{\notin }N_{ij}$, and $\widehat{(X_{ij})}(.)$ is a predictor of $cX_{ij}$ defined on $N_{ij}$. The set $\left\{ X_{ij}+N_{ij}\right\}$ is called the support of the residual.

• (2) Truncation and quantization: Each submodel is formed from a quantized and truncated version of the residual:

  $$\begin{aligned} R_{ij}{\leftarrow }trunc_T(round(\frac{R_{ij}}{q})), \end{aligned}$$

  (2)

  where $q>0$ is a quantization step. The operation of rounding to an integer is denoted by round(x). The truncation function with threshold $\,T>0$ is defined for any $x{\in }\mathbb {R}$ as $trunc_T(x)=x$ for $x{\in }\left[ {-T,T}\right]$ and $trunc_T (x)=Tsign(x)$ otherwise. The symbol $\mathbb {R}$ is used to represent the set of all real numbers.

• (3) Co-occurrences: Submodels will be constructed from horizontal and vertical co-occurrences of four consecutive residual samples processed using (2) with $T=2$. Formally, each co-occurrence matrix C is a four-dimensional array indexed with $d=(d_1,d_2,d_3,d_4 ){\in }T_4{\triangleq }\left\{ {-T,{\dots },T}\right\} ^4$. The $d^{th}$ element of the horizontal co-occurrence for residual $R=(R_{ij})$ is formally defined as the normalized number of groups of four neighboring residual samples with values equal to $d_1,d_2,d_3,d_4$:

  $$\begin{aligned} C_{d}^{(h)}={\frac{1}{Z}}{\vert }\left\{ (R_{ij},R_{i,j+1},R_{i,j+2},R_{i,j+3}){\vert }R_{i,j+k-1}=d_k,k=1,{\dots },4\right\} {\vert }, \end{aligned}$$

  (3)

  where Z is the normalization factor ensuring that $\sum _{d{\in }T_4}{C_{d}^{(h)}}=1$. The vertical co-occurrence, $C^{(v)}$, is defined analogically (please refer to [4] for more details). For a finite set $\chi$, the ${\vert }\chi {\vert }$ denotes the number of its elements.

2.2 maxSRM

The maxSRM is a variant of the SRM (Spatial Rich Model), and it is built in the same manner as the SRM, but the process of forming the co-occurrence matrices is modified to consider the embedding change probabilities $\widehat{\beta _{ij}}$ estimated from the analyzed image. The SRM uses the 4D co-occurrences, where 4D arrays are defined as

$$\begin{aligned} C_{d_0d_1d_2d_3}=\sum _{i,j=1}^{n_1,n_2-3}\left[ \widehat{\beta _{ij}}=d_k,\forall {k=0,\dots ,3}\right] , \end{aligned}$$

(4)

This is an example of a horizontal co-occurrence. The (i, j) denotes the location of pixel in the image.

In maxSRM, this definition is modified to

$$\begin{aligned} \tilde{C}_{d_0d_1d_2d_3}=\sum _{i,j=1}^{n_1,n_2-3}{\max \limits _{k=0,\dots ,3}}\widehat{\beta _{i,j+k}}\left[ \widehat{\beta _{ij}}=d_k,\forall {k=0,\dots ,3}\right] , \end{aligned}$$

(5)

That is, instead of adding a 1 to the corresponding co-occurrence bin, the maximum of the embedding change probabilities taken across the four residuals will be added. The rest of the process of forming the SRM stays the same, including the symmetrization by sign and direction and merging into SRM submodels.

2.3 maxSRMd2

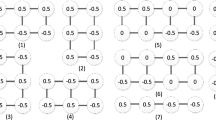
Both the original SRM and maxSRM use horizontal and vertical scans (see the case (a) in Fig. 1). However, the version of the maxSRM with all co-occurrence scan directions is replaced with the oblique direction ‘d2’ (see the case (b) in Fig. 1), and this version of the rich model is called the maxSRMd2.

Fig. 1.

Two types of co-occurrence scan direction

In principle, the three high dimensional steganalytic algorithms are similar in the process of catching distortions, and they are frequently used to detect the existence of secret messages in the spatial images. The feature vectors extracted by the three steganalytic algorithms all have the dimension of 34671.

Fig. 2.

Stego images of the WOW algorithm with different embedding rates. (a) The cover image. (b) The stego image with the embedding rate of 0.1 bpp(bits per pixel). (c) The stego image with the embedding rate of 0.2 bpp. (d) The stego image with the embedding rate of 0.3 bpp. (e) The stego image with the embedding rate of 0.4 bpp.

3 The Characteristic of Stego Images with Different Embedding Rates

For any steganographic scheme, the detectable distortions that may be introduced to the carrier image will increase with the increase of embedding rate, which may also influence the value of extracted features. Some experimental results corresponding to the steganographic scheme WOW are illustrated in Fig. 2. The cover image is shown in Figs. 2(a) and (b–e) show the positions of those pixels changed by using the WOW algorithm with different embedding rates. The white points indicate that in these positions the pixels have been modified after embedding secret messages.

From Fig. 2, it is observed that even if embedding rates are different, the modifications are in the same area generally. As seen in Fig. 2, most of the modifications are made in the edge areas and those smooth areas are kept unchanged, such as the region in the sky. However, with the increase of embedding rate, the difference between the cover and stego images will be more clearly visible. As we all know, the features in steganalysis are extracted to discriminate the difference between cover and stego images. In general, the value of each effective feature should consistently increase or decrease with the increase of embedding rate. Some examples are shown in Table 1.

Table 1. Values of the same feature with different embedding rates

The values of three features (i.e., 1$^{th}$, 4$^{th}$ and 27$^{th}$) extracted by SRM from an image with different embedding rates are shown in Table 1. It is observed from Table 1 that values of the 1$^{th}$ (27$^{th}$) feature consistently decrease (increase) with the increase of embedding rate. Whereas for the 4$^{th}$ feature, it may decrease or increase randomly with the increase of embedding rate. According to our opinion, these kinds of features (e.g., 1$^{th}$ and 27$^{th}$) may be effective and should be selected in the steganalytic process. However, those kinds of features (e.g., 4$^{th}$) may confuse the classifier and can be excluded from the high dimensional feature vector in the steganalytic process.

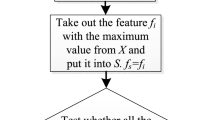
4 Proposed Feature Selection Method

Based on the characteristic described in Table 1, the detailed realization of our proposed feature selection method in the experiments is given in the following. Assume that $f^{\beta }_{i,j}\,(1\le i\le M,1\le j\le N,{\beta }{\ge }0)$ denotes the value of $j^{th}$ feature of the $i^{th}$ image with the embedding rate $\beta$, where M denotes the number of images in the image set, N denotes the total number of features extracted from the $i^{th}$ image, and j denotes the $j^{th}$ feature extracted from the $i^{th}$ image. The parameter $\beta$ represents the embedding rate. In this paper, we have selected $\beta$ as 0.1, 0.2, 0.3 and 0.4 in all our testing, that is, the embedding rate is 0.1 bits per pixel (bpp), 0.2 bpp, 0.3 bpp and 0.4 bpp, respectively. Note that $\beta =0$ represents that the embedding rate is 0 bpp. The $A^{\beta }_{i,j}$ is defined as

$$\begin{aligned} A^{\beta }_{i,j}=\left\{ \begin{array}{ll} 1, &{} if (f^{\beta }_{i,j}-f^{0}_{i,j})>0\\ 0, &{} otherwise\\ \end{array} \,\,\,\,\,\,\,(1\le i \le M,1\le j \le N,\beta >0), \right. \end{aligned}$$

(6)

where the $f_{i,j}^0$ represents the value of the $j^{th}$ feature extracted from the $i^{th}$ cover image, and the $f_{i,j}^\beta$ denotes the value of the $j^{th}$ feature extracted from the $i^{th}$ stego image with the embedding rate $\beta$. Then the $S_j^{\beta }$ is defined as

$$\begin{aligned} S_{j}^{\beta }=\sum _{i=1}^{i=M}A^{\beta }_{i,j}\qquad (1\le j \le N, \beta >0), \end{aligned}$$

(7)

In Eq. (7), for a given embedding rate $\beta$, if the value of $S_j^\beta$ is a big value (e.g., nearly the value M), it represents that for most of the images in the testing image data set the value of $j^{th}$ feature may increase with the increase of embedding rate. On the contrary, if the value of $S_j^\beta$ is a small value (e.g., nearly the value of 0), it represents that for most of the images in the testing image data set the value of $j^{th}$ feature may decrease with the increase of embedding rate. In both of these two cases, the $j^{th}$ feature is considered as an effective feature. However, if the value of $S_j^\beta$ is around M / 2, it represents that for about half of the images in testing image data set the value of $j^{th}$ feature may increase whereas for the remaining half of the images in testing image data set the value of $j^{th}$ feature may decrease with the increase of embedding rate. In this case, the $j^{th}$ is considered as the non-effective feature and should be excluded from the original high dimensional feature vector. Thus, in our proposed method, the extracted feature may be selected as an effective feature in these two cases.

In the first case, the extracted feature from the original high dimensional feature vector must satisfy the following two conditions.

• (1) For any given embedding rate, e.g., $\beta _{1},\dots ,\beta _{k}\,(k{\in }\mathbb {N})$, the following inequality Eq. (8) must be satisfied.

  $$\begin{aligned} M\times (1-{P/2})\le S_j^{\left\{ {\beta _1,\beta _2,\dots ,\beta _k}\right\} }\le M\,\,\,\,\,\,\,\,\,(1\le j \le N, k\in \mathbb {N}), \end{aligned}$$

  (8)

  where $P\,(0<P<1)$ is a control parameter which is used to control the number of features that may be excluded from the original high dimensional feature vector. Generally, we can select $P=0.7\sim 0.9$, which means that for most of the images in the testing image data set, and the value of the $j^{th}$ feature may increase with the increase of embedding rate.

• (2) For any embedding rate, e.g., for different embedding rates $\beta _1$ and $\beta _2$, if $\beta _1<\beta _2$, then $S_j^{\beta _1 }<S_j^{\beta _2}$ must be satisfied. In the same way, when there are k embedding rates, such as $\beta _1,\dots ,\beta _k\, (k\in \mathbb {N})$, if $\beta _1<\beta _2<\dots <\beta _k$, the inequality $S_j^{\beta _1}<S_j^{\beta _2}<\dots <S_j^{\beta _k}$ must be satisfied.

In the same way, in the second case the extracted feature from the original high dimensional feature vector must satisfy the following feature two conditions.

• (1) For any given embedding rate, e.g., $\beta _1,\dots ,\beta _k\,(k\in \mathbb {N})$, the following inequality Eq. (9) must be satisfied.

  $$\begin{aligned} 0< S_j^{\left\{ {\beta _1,\beta _2,\dots ,\beta _k}\right\} }\le P\times \left\lfloor \frac{M}{2} \right\rfloor \,\,\,\,\,\,\,\,\,(1\le j \le N). \end{aligned}$$

  (9)

  where for any value of M, the largest integer smaller than or equal to M is $\left\lfloor {M}\right\rfloor$. Similarly, we can choose $P=0.7\sim 0.9$ in general, which means that for most of images in the testing image data set, and the value of $j^{th}$ feature may decrease with the increase of embedding rate.

• (2) For any embedding rate, e.g., for different embedding rates $\beta _1$ and $\beta _2$, if $\beta _1<\beta _2$, then $S_j^{\beta _1 }>S_j^{\beta _2}$ must be satisfied. In the same way, when there are k embedding rates, such as $\beta _1,\dots ,\beta _k \,(k\in \mathbb {N})$, if $\beta _1<\beta _2<\dots <\beta _k$, the inequality $S_j^{\beta _1}>S_j^{\beta _2}>\dots >S_j^{\beta _k}$ must be satisfied.

Table 2. Features dimension and E$_{OOB}$ for four different embedding rates, i.e., 0.1 bpp, 0.2 bpp, 0.3 bpp and 0.4 bpp. $'$Original$'$ denotes the feature vector without undergoing feature selection.

5 Experimental Results

In this paper, all experimental results are obtained on BOSSbase ver. 1.01 [1], which consists of 10000 gray-scale cover images with the size 512$\times$512. Four different embedding rates, i.e., 0.1 bpp, 0.2 bpp, 0.3 bpp and 0.4 bpp, are selected in our testing. The ensemble classifier [7] is used for classification. We randomly select 5000 images for training and the remaining 5000 images are used for testing. In the training process, the effective features are selected according to the control parameter P (P is selected as 0.9, 0.8 or 0.7 in our testing) and a series of classifiers can be obtained. Then these obtained classifiers are used for testing.

5.1 Experiment #1

The efficiency of our proposed feature selection method for dimensionality reduction regarding to the steganalytic algorithm (SRM) is shown in the Table 2. In this case, three steganographic schemes, i.e., WOW [5], HUGO [9] and S-UNIWARD [6] and four different embedding rates, i.e., 0.1 bpp, 0.2 bpp, 0.3 bpp, 0.4 bpp are tested.

Table 3. Features dimension and E$_{OOB}$ for three high dimensional steganalytic algorithms and three steganographic schemes with the embedding rate of 0.4 bpp.

From the Table 2, it is obvious that the dimensionality of the original high dimensional feature vector (dimension of 34671) can be reduced efficiently by using our proposed feature selection method. For example, when the steganographic scheme is selected as the WOW algorithm and the embedding rate is 0.4 bpp, the testing error E$_{OOB}$ is 0.2105 with the feature dimension of 34671. However, when $P=0.7$, the testing error is 0.2116 with the feature dimension of 9507 by using our feature selection method (please refer to the Table 2 for more details).

5.2 Experiment #2

The efficiency of our feature reduction method regarding to three different high dimensional steganalytic algorithms, i.e., SRM [4], maxSRM [3] and maxSRMd2 [3] is shown in the Table 3. In this case, three different adaptive steganographic schemes, i.e., WOW, HUGO and S-UNIWARD and one embedding rate, i.e., 0.4 bpp, are tested.

From the Table 3, it is obvious that our proposed feature selection method can be applied to various high dimensional steganalytic algorithms for dimensionality reduction. For example, when the steganographic scheme is HUGO with the embedding rate 0.4 bpp and the steganalytic algorithm is maxSRMd2, the original feature dimension of 34671 can be reduced to 2670, namely the dimension is reduced by more than ten times. However, the testing error almost keeps the same as before (please refer to the Table 3 for more details).

6 Conclusions

In this paper, we firstly point out that the element in the extracted feature vector should consistently increase or decrease with the increase of embedding rate for a given steganographic scheme. Moreover, this new finding can be utilized to achieve the dimensionality reduction for various steganalytic algorithms with high dimensional feature vector. The realization of our feature selection method can not only eliminate the redundancy in the high dimensional feature vector, but may also improve the overall classification efficiency. We will further optimize our proposed feature selection method and extend it to other pattern classification fields, not limit to the field of image steganalysis.