Shearography

Abstract

This chapter provides a review of the developments of shearography and its applications in nondestructive testing (NDT) and evaluation (NDE). Shearography, or speckle pattern shearing interferometry, is an interferometric technique for full-field, non-contact measurement of the first derivative of surface deformation, which is strain information. It was originally developed to overcome several limitations of holography by eliminating the reference beam. Consequently, shearography is an interferometric technique that has very high measurement sensitivity but, through its direct measurement of strain information, is less sensitive to environmental disturbances. Therefore, it is a practical tool which can be used in field/factory settings. Furthermore, the self-reference system has a simple optical layout and balanced optical paths, which enables the construction of a very compact and practical shearographic sensor using a cost-economical diode-laser. In NDT, shearography reveals defects in an object by identifying defect-induced deformation anomalies through the display of strain concentrations (i.e., first derivatives of surface deformation). Shearography has already received considerable industry acceptance, in particular for nondestructive testing of such materials as composites and honeycomb structures. Another application of shearography is for strain measurement. This chapter focuses on the digital version of shearography for NDT. After discussion of the fundamentals of shearography, the recent developments and applications of shearography, as well as its potential and limitations, will be demonstrated through examples of NDT for different applications.

Introduction

Nondestructive testing (NDT) is a group of techniques used to evaluate the properties of a structure or product without causing damage (Cartz 1995). It is a highly valuable technique in product evaluation, troubleshooting, and research since it does not alter the object being inspected. Recently, a requirement has arisen for a better NDT technique, due to a demand for greater product performance and reliability, especially for online inspection. To meet this requirement, the new NDT technique should contain such advantages as real-time inspection, whole-field test, non-contact measurement, and high-sensitivity. Most optical NDT techniques, such as holographic interferometry (Vest 1979), electronic speckle pattern interferometry (ESPI) (Løkberg 1987), shearography (Steinchen and Yang 2003), thermography (Clark et al. 2003), profilometry (Targowski et al. 2004), digital image correlation (DIC) (Li et al. 2017a), etc., have the virtues mentioned above. Of these techniques, shearography has already been applied in the field of NDT for decades and been proven to be a practical tool for online inspection due to its simple setup, direct measurement of strain information and relatively insensitive to environment interruptions. It is gaining more and more acceptance and applications in the automotive and aerospace industries for NDT/NDT, strain measurement, and vibration analysis.

Shearography, sometimes called speckle pattern shearing interferometry, is a laser-based optical interferometric method that is similar to ESPI. Unlike ESPI, which measures deformation, shearography directly measures the gradient of the deformation, e.g., strain information, using a special shearing device. Since object defects induce strain concentrations during loading, shearography is much more sensitive for detection of defects with strain anomalies than for deformation anomalies. Also, shearography is insensitive to environmental disturbances, such as environmental vibration and motion, because the rigid-body movement does not induce strain. Moreover, shearography uses the self-reference technique, which does not require a reference beam and leads to a much more compact and stable optical setup. The self-reference also reduces the coherent length requirement of the laser and enables to use simple and cheap diode lasers for illumination.

The development of shearography can be divided into three stages: photographic shearography, electronic shearography, and digital shearography. In the early decades of the development of shearography, image recording was restricted to dry plate photography, and photographic emulsion was used as the recording media to obtain very high-quality images (Hung 1982; Sirohi 1984). However, traditional photographic shearography requires a slow and complicated wet photographic process, limiting its industrial applications. To address this limitation, a reusable thermoplastic plate was adopted to replace the traditional dry plate, enabling the image to be instantly obtained after recording (Hung and Hovanesian 1982). An initial attempt to achieve real-time inspection using shearography, the thermoplastic-based photographic shearography partially solves the existing problem of slow processing, but the inconsistent quality and the high price of the thermoplastic plate deterred its further application. The slow processing problem for real-time shearographic inspection was not fully solved until the electronic technique was introduced to shearography, known as electronic shearography (Steinchen et al. 1994). The electronic sensor allowed the interferogram to be captured electronically and then displayed on a TV monitor, enabling real-time display of the shearographic measurement result. However, the spatial resolution was much lower compared to photographic shearography due to the low resolution of the video camera.

Digital shearography as the latest version of shearography and the successor to electronic shearography, uncovered the full capability of shearography in many aspects (Hung 1999). Digital shearography utilizes a digital camera to capture information and create the digital photograph. There are two primary types of image sensors in a digital camera − complementary metal-oxide semiconductor (CMOS) and charge-coupled device (CCD) − and each has its advantages. The utilization of the digital camera provides good image resolution and quality to shearography, as well as the capability to display the result instantly. More importantly, the digitized image can be processed using multiple digital image processing algorithms as well as the phase shifting technique, which increases the measurement sensitivity of shearography by tens of times. Today, digital shearography with phase shifting technique has become the most favorable shearography version due to its ease of use, fast evaluation, high sensitivity, and versatility. Based on the phase shifting technique, digital shearography can be cataloged as either temporal phase shift digital shearography (TPS-DS) or spatial phase shift digital shearography (SPS-DS) TPS-DS is usually suitable for static or quasi-static tests, whereas the SPS-DS is preferable for dynamic tests.. Although the application of TPS-DS is limited to quasi-static applications, it provides a higher quality phase map compared to the SPS-DS. In recent decades, both the dynamic range of the TPS-DS and the phase map quality of SPS-DS has been greatly improved with the rapid development of the electronic technique.

At the same time, with the development of phase shift digital shearography, the application of digital shearography has been greatly extended, and the setup has been optimized for various new applications. All these efforts have greatly enhanced the diversity of the NDT applications of shearography. For instance, the rubber industry evaluates the quality of tires using shearography (Hung 1996; Krivtsov et al. 2002; Baldwin and Bauer 2008; Zhang et al. 2013), and the aerospace industry utilizes shearography to examine the structure of aircraft (Yang and Hung 2004; Ibrahim et al. 2004; Lobanov et al. 2009; Růžek and Běhal 2009). In addition to these two areas, many types of research related to the NDT of composites using shearography have also been investigated and published in the same period (Toh et al. 1990; Hung 1996; Burleigh 2002; Gryzagoridis and Findeis 2008; De Angelis et al. 2012). As the NDT of composites using shearography reaches its mature stage, ASTM has published a standard for NDT of polymer matrix composites and sandwich core materials using shearography (ASTM E2581-14 2014). Furthermore, other applications of shearography includes: strain measurement (Hung 1982; Hung and Wang 1996; Steinchen et al. 1998a; Kästle et al. 1999), residual stress (Hung and Hovanesian 1990; Hathaway et al. 1997; Hung et al. 1997; Dıaz et al. 2000), material properties (Lee et al. 2004, 2008; Huang et al. 2009; Taillade et al. 2011), 3D shape (Shang et al. 2000; Groves et al. 2004), vibration (Sim et al. 1995; Toh et al. 1995; Steinchen et al. 1996; Yang et al. 1998), and leak detection (Hung and Shi 1998).

Principles of Digital Shearography

Schematic Setups of Shearography

Several basic setups of shearography are illustrated in this section to introduce the fundamentals of shearography as well as some basic concepts, such as the shearing device, shearing amount, intensity equation, and fringe generation. The schematic of shearography is shown in Fig. 1. The test object is illuminated by an expanded laser point, and the object image is captured by the digital camera connected to a computer for fringe evaluation. A required special shearing device is placed in front of the camera to introduce image shearing. The shearing device brings two non-parallel light beams that reflected from two different object points to interfere with each other on the camera sensor. The usage of the shearing device allows shearography to be a self-referenced interferometric system, which provides a distinguishing feature compared to the other interferometric systems. Three different practical shearing devices will be described, corresponding to three well-known shearography setups.

Fig. 1

Schematic of the shearographic system

The schematic arrangement of a very early shearography setup is shown in Fig. 2. An optical wedge is used as the shearing device in this shearographic setup (Hung 1982). The glass wedge is a small-angle (~0.75°) prism that deflects rays passing through it. The wedge is placed in front of the lens of a camera, covering one-half of the lens, and induces the image from two different points on the object surface to coincide together. The magnitude of the shearing, known as the shearing amount, is determined by the wedge angle of the shearing device, while the orientation of the wedge determines the direction of the shearing, known as the shearing direction. The shearing effect introduced by the wedge can be explained using the same figure. The shearing direction is in the x-direction, and the shearing amount is δx on the object surface (distance between P1 and P2). The rays from two different points (P1 and P2) meets at the same location $\left({P}_{12}^{\prime}\right)$ on the image plane.

Fig. 2

Schematic of the shearographic setup with an optical wedge

Figure 3 shows another popular shearographic setup, which uses a modified Michelson interferometer as the shearing device (Hung 1974; Leendertz and Butters 1973). Shearing is created by tilting mirror 2 of the Michelson interferometer a very small angle. The tilting of mirror 2 brings laser rays from two different points on the object surface to one point on the sensor plane. These laser rays interfere with each other and produce the speckle pattern in the interferogram. This setup has the advantages of a simple structure and adjustable shearing direction and shearing amount. Due to these merits, this setup is widely used in the TPS-DS system and can also be used in the SPS-DS system with some limitations.

Fig. 3

Schematic of the shearographic setup with the modified Michelson interferometer

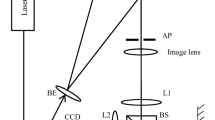
The third schematic shearographic setup, shown in Fig. 4, is based on a Mach-Zehnder interferometer. It is the first frequency carrier SPS-DS system, proposed by G. Pedrini in 1996 (Pedrini et al. 1996). The carrier frequency and the shearing amount is introduced by tilting mirror 2 in the Mach-Zehnder interferometer. Additionally, a slit aperture (AP) is placed in front of the imaging lens to control the spectral bandwidth in the spatial frequency domain. The sheared speckle pattern created by the shearing device is recorded and processed by the digital camera.

Fig. 4

Schematic of the shearographic setup with the Mach-Zehnder interferometer

Formation of Fringes in Digital Shearography

No matter what kind of shearing devices is used, the fundamental of shearography is to bring light waves reflected from two points (P₁ and P₂) from the object surface to meet at the same point P’₁₂ in the image plane due to the shearing device as shown in Fig. 2, where they interfere each other. Following the explanation in the previous section, the light waves reflected from two different points can be described using the exponential functions:

$$ {\displaystyle \begin{array}{l}{U}_1={a}_1{e}^{i{\theta}_1}\\ {}{U}_2={a}_2{e}^{i{\theta}_2}\end{array}} $$

(1)

Where θ₁ and θ₂ represent the random phase angle of the two points, and a₁ and a₂ are the amplitude of the two lights. The total light field U_t at the point ${P}_{12}^{\prime }$ on the image plane can be expressed:

$$ {U}_t={U}_1+{U}_2={a}_1{e}^{i{\theta}_1}+{a}_2{e}^{i{\theta}_2} $$

(2)

The intensity of the captured image, i.e., the speckle pattern, at the point ${P}_{12}^{\prime }$ can be obtained by the following equation:

$$ {\displaystyle \begin{array}{l}I={U}_t{U_t}^{\ast }=\left({a}_1{e}^{i{\theta}_1}+{a}_2{e}^{i{\theta}_2}\right)\left({a}_1{e}^{-i{\theta}_1}+{a}_2{e}^{-i{\theta}_2}\right)\\ {}\quad =\left({a_1}^2+{a_2}^2\right)+{a}_1{a}_2\left[{e}^{i\left({\theta}_1-{\theta}_2\right)}+{e}^{-i\left({\theta}_1-{\theta}_2\right)}\right]\\ {}\quad =\left({a_1}^2+{a_2}^2\right)+2{a}_1{a}_2\cos \left({\theta}_1-{\theta}_2\right)\\ {}\quad ={I}_0\left(1+\gamma \cos \phi \right)\end{array}} $$

(3)

Where U_t^∗ is the complex conjugate of U_t; I₀ = a₁² + a₂², is the background; γ = 2a₁a₂/(a₁² + a₂²), is the contrast; and ϕ = θ₁ − θ₂, is the phase difference between the rays from the two points. Figure 5a shows the intensity image of the speckle pattern before loading.

Fig. 5

Intensity images of speckle pattern (a) before loading, (b) after loading, and (c) Shearographic fringe pattern

After the object is loaded, the phase difference between the two points can be expressed as ϕ^′ = ϕ + Δ, where Δ is the relative phase change before and after loading between the two waves from P₁ to P₂ and it results from the relative deformation between the two points. The intensity of the speckle pattern after loading, as shown in Fig. 5b, then can be expressed:

$$ {\displaystyle \begin{array}{l}{I}^{\prime }={I}_0\left[1+\gamma \cos \left({\phi}^{\prime}\right)\right]\\ {}\, ={I}_0\left[1+\gamma \cos \left(\phi +\Delta \right)\right]\end{array}} $$

(4)

The subtraction between loaded and unloaded intensity images generated a fringe pattern, called shearogram. Because intensity cannot be negative, the absolute value of intensity change is displayed:

$$ \left|{I}_s\right|=\left|{I}^{\prime }-I\right|={I}_0\gamma \left|\cos \left(\phi +\Delta \right)-\cos \left(\phi \right)\right| $$

(5)

The dark fringe, which results when |I_s| = 0, occurs at the location where Δ = 2nπ, where n is the fringe order. A visible bright-dark fringe can be observed with this simple process. It is the fastest and most concise method to format the fringe without any further processing. It achieves real-time measurement and displays on a monitor controlled by a computer. Figure 5c shows a typical shearographic fringe pattern (x-direction shearing), generated using the method mentioned above, for a center-loaded square plate. The shearographic fringe pattern is butterfly-shaped and commonly called a butterfly pattern. Since the relative phase difference between two adjacent fringes is Δ = 2π, the phase at each fringe can be determined by counting the fringe order.

Relationship Between Relative Phase Change Δ and Deformation Derivatives

As explained in the previous section, the relative phase change at each fringe can be obtained by counting the fringe order. Once the relationship between the relative phase change and the relative surface deformation between the two interferometric points is established, the derivative of the deformation can be determined based on the measured relative phase change.

Assuming the two points P₁(x, y, z) and P₂(x + δx, y, z) on the object surface meets at the same point ${P}_{12}^{\prime}\left({x}_c,{y}_c,{z}_c\right)$ on the sensor plane due to the shearing device, the schematic of the system is shown in Fig. 6. The relative phase change Δ before and after loading of P₁ and P₂ can be expressed using the typical equation in holography (Vest 1976; Steinchen and Yang 2003), assuming the observation direction is perpendicular to the object surface, and the illumination angle lying on the XOZ plane is α:

$$ {\displaystyle \begin{array}{l}{\Delta}_x={\Delta}_{P1}-{\Delta}_{P2}\\ {}\, =\frac{2\pi }{\lambda}\left\{\left[{u}_{P1}\sin \alpha +{w}_{P1}\left(1+\cos \alpha \right)\right]-\left[{u}_{P2}\sin \alpha +{w}_{P2}\left(1+\cos \alpha \right)\right]\right\}\\ {}\, =\frac{2\pi }{\lambda}\left[\left({u}_{P1}-{u}_{P2}\right)\sin \alpha +\left({w}_{P1}-{w}_{P2}\right)\left(1+\cos \alpha \right)\right]\\ {}\, =\frac{2\pi }{\lambda}\left[\delta u\sin \alpha +\delta w\left(1+\cos \alpha \right)\right]\end{array}} $$

(6)

where u_P1, w_P1, u_P2, and w_P2 are the displacement of P₁ and P₂ in the x-direction and z-direction, respectively. If the shearing direction is in the x-direction and the distance between the two points is relatively small, the equation can be represented as:

$$ {\Delta}_x=\frac{2\pi }{\lambda}\left[\frac{\partial u}{\partial x}\sin \alpha +\left(1+\cos \alpha \right)\frac{\partial w}{\partial x}\right]\delta x $$

(7)

Fig. 6

Schematic of the interferometric effect of the shearography

Keeping the same illumination plane, and changing shearing direction in the y-direction, the equation becomes:

$$ {\Delta}_y=\frac{2\pi }{\lambda}\left[\frac{\partial u}{\partial y}\sin \alpha +\left(1+\cos \alpha \right)\frac{\partial w}{\partial y}\right]\delta y $$

(8)

Similarly, when the illumination plane is in YOZ plane, Eqs. 7 (x-shearing direction) and 8 (y-shearing direction) become:

$$ {\Delta}_x=\frac{2\pi }{\lambda}\left[\frac{\partial v}{\partial x}\sin \alpha +\left(1+\cos \alpha \right)\frac{\partial w}{\partial x}\right]\delta x $$

(9)

$$ {\Delta}_y=\frac{2\pi }{\lambda}\left[\frac{\partial v}{\partial y}\sin \alpha +\left(1+\cos \alpha \right)\frac{\partial w}{\partial y}\right]\delta y $$

(10)

Equations 7, 8, 9, and 10 are the fundamental equations of shearography. Different shearographic setups use a different method to evaluate the relative phase change, but all of them use these four equations to calculate the derivative of deformation. For NDT, a very small or close to zero illumination angle is usually selected; under this condition, Eqs. 7, 8, 9, and 10 are simplified into two equations:

$$ {\Delta}_x=\frac{4\pi }{\lambda}\cdot \frac{\partial w}{\partial x}\cdot \delta x $$

(11)

$$ {\Delta}_y=\frac{4\pi }{\lambda}\cdot \frac{\partial w}{\partial y}\cdot \delta y $$

(12)

Equations 11 and 12 are usually used to interpret shearographic test results in NDT.

Fringe Interpretation

Based on the derivation of the previous section, the measured relative phase change using shearography is directly related to the deformation gradient. In this section, the result measured by shearography will be interpreted in another aspect. Since the interpretation of holography for NDT is well-known, a comparison between holographic and shearographic measurement is presented. Figure 7 shows the results from the same NDT test measured using both holography and shearography. For this example, assume a void or delamination exists in the composite plate as the defect, and the plate is loaded by a thermal load or vacuum. The plate surface would exhibit slight buckling due to the inconsistency of material. Holography detects the flaw by detecting the deformation anomalies, and the anomaly area has a circular fringe pattern. In contrast, shearography discovers the flaw by looking for the anomalies of the first derivative of the deformation, and the defected area shows a butterfly pattern.

Fig. 7

Schematic of the NDT result between Holography and Shearography

Figure 8 shows the different NDT results, using the phase shift technique introduced in the next section, between holography and shearography to demonstrate the concept described above. A composite plate with three de-laminated defects is inspected using the two techniques simultaneously. The holographic measurement result shows the defect with several circular anomalous fringes, and the Shearographic measurement result displays several butterfly patterns at the de-bond locations.

Fig. 8

(a) NDT result obtained by Holography. (b) NDT result obtained by Shearography

Evaluation of Shearogram by Phase Shift Technique

Temporal Phase Shift Shearography

4 + 4 Phase Shift Algorithm

The real-time subtraction version of digital shearography is reviewed in section “Formation of Fringes in Digital Shearography.” The fringe pattern is generated by the numerical subtraction of the interferograms captured before and after loading. The relative phase change is calculated based on counting the fringes. However, the sensitivity of this method is limited to one fringe order, meaning that the maximum phase measurement sensitivity of real-time subtraction shearography is only 2π. Additionally, the information between the fringes cannot be obtained, which limits the application of real-time subtraction shearography.

To increase the phase measurement sensitivity, the phase shift technique was introduced to digital shearography. A higher phase measurement sensitivity can be achieved with the phase shift technique based digital shearography, commonly called phase shift digital shearography. The phase is directly measured in this technique rather than by counting the fringes. Phase shift digital shearography can be divided into two categories: temporal phase shift digital shearography (TPS-DS), which has the higher interferogram quality, and spatial phase shift digital shearography (SPS-DS), which has the higher dynamic range. A comparison between shearography with and without phase shift technique is shown in Fig. 9.

Fig. 9

The comparison between the (a) intensity fringe pattern and (b) phase map

A typical TPS-DS setup based on the modified Michelson interferometer was shown in Fig. 3. To solve for the phase (ϕ or ϕ^′) using Eq. 3 or Eq. 4, at least three equations are required because there are three unknowns: I₀, γ, and ϕ (or ϕ^′). The temporal phase shift is to record 3–4 images in a time series, and a phase shift is introduced between two images which is achieved by a piezoelectric crystal (PZT) driven mirror (Mirror 1), and the driven mirror can be moved with precise displacement to generate a known phase shift.

Though 3 equations can already solve the phase ϕ, 4 equations phase shift algorithm is the most widely used in the temporal phase shift method (Steinchen and Yang 2003; Yang et al. 1995). This algorithm is fast and simple with a high phase extraction accuracy. Usually, it is called a 4 + 4 algorithm, i.e., 4 equations to solve ϕ (phase before loading) and the other 4 to solve ϕ’ (phase after loading). A total of eight images are taken to calculate the phase change Δ. Before loading, four intensity images with a phase shift increment of π/2 are captured, based on Eq. 3, they can be expressed as the following:

$$ {\displaystyle \begin{array}{l}{I}_1={I}_0\left[1+\gamma \cos \left(\phi +0\right)\right]\\ {}{I}_2={I}_0\left[1+\gamma \cos \left(\phi +\pi /2\right)\right]\\ {}{I}_3={I}_0\left[1+\gamma \cos \left(\phi +\pi \right)\right]\\ {}{I}_4={I}_0\left[1+\gamma \cos \left(\phi +3\pi /2\right)\right]\end{array}} $$

(13)

The random phase ϕ can be calculated using Eq. (14):

$$ \phi =\arctan \frac{\left({I}_4-{I}_2\right)}{\left({I}_1-{I}_3\right)} $$

(14)

Similarity, the same process can be performed to calculate the random phase after loading using Eq. 4:

$$ {\phi}^{\prime }=\phi +\Delta =\arctan \frac{\left({I}_4^{\prime }-{I}_2^{\prime}\right)}{\left({I}_1^{\prime }-{I}_3^{\prime}\right)} $$

(15)

where ${I}_1^{\prime }$, ${I}_2^{\prime }$, ${I}_3^{\prime }$_, and ${I}_4^{\prime }$ are the intensity of 4 images after loading, respectively. Then the phase change Δ can be determined by subtracting ϕ from ϕ^′:

$$ \Delta =\left\{\begin{array}{l}{\phi}^{\prime }-\phi; \, if\ {\phi}^{\prime }>\phi \\ {}{\phi}^{\prime }-\phi +2\pi; \, \mathrm{else}\end{array}\right. $$

(16)

4 + 1 Phase Shift Algorithm

Since the 4 + 4 temporal phase shift algorithm requires four images at each loading condition, it is not suitable for dynamic tests (except for harmonic excitation with stroboscopic illumination (Steinchen and Yang 2003)). The 4 + 1 fast temporal phase shift algorithm was proposed to fulfill the dynamic measurement capability (Yang and Siebert 2008). Four images are taken using the same procedure described in the last section before loading. During loading, the camera only records a single image at each load, and no phase shift is needed.

The image captured using the four-step phase shift method before loading can be written using Eq. 13, and the recorded image during loading can be expressed as:

$$ {I}^{\prime }={I}_0\left[1+\gamma \cos \left(\phi +\Delta \right)\right] $$

(17)

Subtracting Eq. 17 from each equation in Eq. 13, then taking the square of the difference results in the following equations:

$$ {\displaystyle \begin{array}{l}{\tilde{I}}_1^2={\left\{{I}_0\left[1+\gamma \cos \left(\phi \right)\right]-{I}_0\left[1+\gamma \cos \left(\phi +\Delta \right)\right]\right\}}^2\\ {}\, ={\left[2{I}_0\gamma \sin \left(\phi +\frac{\Delta}{2}\right)\sin \left(\frac{\Delta}{2}\right)\right]}^2\\ {}{\tilde{I}}_2^2={\left\{{I}_0\left[1+\gamma \cos \left(\phi +\frac{\pi }{2}\right)\right]-{I}_0\left[1+\gamma \cos \left(\phi +\Delta \right)\right]\right\}}^2\\ {}\, ={\left[-2{I}_0\gamma \cos \left(\phi +\frac{\Delta}{2}-\frac{\pi }{4}\right)\sin \left(\frac{\pi }{4}-\frac{\Delta}{2}\right)\right]}^2\\ {}{\tilde{I}}_3^2={\left\{{I}_0\left[1+\gamma \cos \left(\phi +\pi \right)\right]-{I}_0\left[1+\gamma \cos \left(\phi +\Delta \right)\right]\right\}}^2\\ {}\, ={\left[-2{I}_0\gamma \cos \left(\phi +\frac{\Delta}{2}\right)\cos \left(\frac{\Delta}{2}\right)\right]}^2\\ {}{\tilde{I}}_4^2={\left\{{I}_0\left[1+\gamma \cos \left(\phi +\frac{3\pi }{2}\right)\right]-{I}_0\left[1+\gamma \cos \left(\phi +\Delta \right)\right]\right\}}^2\\ {}\, ={\left[2{I}_0\gamma \sin \left(\phi +\frac{\Delta}{2}-\frac{\pi }{4}\right)\cos \left(\frac{\pi }{4}-\frac{\Delta}{2}\right)\right]}^2\end{array}} $$

(18)

Though Δ/2 is a low-frequency component (induced by loading), the phase ϕ (phase difference between two points P1 and P2, see Eq. 3) is the high-frequency component due to surface roughness, and also the terms (ϕ + Δ/2), and (ϕ + Δ/2 + π/4) are high-frequency components too. For the high-frequency term, a detector captures an average value of the term within each speckle (Yang and Siebert 2008). With this assumption, we have the following result:

$$ {\left[\sin \left(\phi +\frac{\Delta}{2}\right)\right]}^2\approx \frac{1}{2 n\pi}{\int}_0^{2 n\pi}{\left[\sin \left(\phi +\frac{\Delta}{2}\right)\right]}^2d\left(\phi +\frac{\Delta}{2}\right)=\frac{1}{2} $$

(19)

Similarly, [sin(ϕ + Δ/2 + π/4)]², [cos(ϕ + Δ/2)]², and [cos(ϕ +Δ/2 + π/4)]² are equal 1/2 too. Therefore, the Eqs. 18 can be simplified to:

$$ {\displaystyle \begin{array}{l}{\tilde{I}}_1^2=2{\left({I}_0\gamma \right)}^2\sin {\left(\frac{\Delta}{2}\right)}^2={\left({I}_0\gamma \right)}^2\left[1-\cos \left(\Delta \right)\right]\\ {}{\tilde{I}}_2^2=2{\left({I}_0\gamma \right)}^2\sin {\left(\frac{\pi }{4}-\frac{\Delta}{2}\right)}^2={\left({I}_0\gamma \right)}^2\left[1-\cos \left(\Delta +\frac{\pi }{2}\right)\right]\\ {}{\tilde{I}}_3^2=2{\left({I}_0\gamma \right)}^2\cos {\left(\frac{\Delta}{2}\right)}^2={\left({I}_0\gamma \right)}^2\left[1-\cos \left(\Delta +\pi \right)\right]\\ {}{\tilde{I}}_4^2=2{\left({I}_0\gamma \right)}^2\cos {\left(\frac{\pi }{4}-\frac{\Delta}{2}\right)}^2={\left({I}_0\gamma \right)}^2\left[1-\cos \left(\Delta +\frac{3\pi }{2}\right)\right]\end{array}} $$

(20)

The relative phase change Δ can now be solved by:

$$ \Delta =\arctan \frac{\left({\tilde{I}}_4^2-{\tilde{I}}_2^2\right)}{\left({\tilde{I}}_1^2-{\tilde{I}}_3^2\right)} $$

(21)

The 4 + 1 phase shift algorithm provides the capability to realize dynamic shearographic measurement using the temporal phase shift technique. However, the phase map quality is not as good as 4 + 4 method due to the assumption in Eq. 19. Therefore, the 4 + 1 algorithm is not widely used in high-accuracy quantitative measurement but can be adopted in some NDT applications.

Other Temporal Phase Shift Algorithms

Besides the two algorithms mentioned in the previous two sections, there are other temporal phase shift algorithms (Creath 1990; Macy 1983; Wu et al. 2012). Some of them will be briefly introduced in this section.

The first one is the 3 + 3 temporal phase shift algorithm . As described in the previous section, three unknowns (I₀, γ, and ϕ) exists in the intensity equation; thus at least three equations are required to solve for the phase ϕ. In the 3 + 3 temporal phase shift algorithm, three interferograms with an increment 2π/3 phase shift are captured at each loading condition, and the phase map ϕ at the loading condition can be calculated. The 3 + 3 temporal phase shift algorithm provides similar phase map quality as the 4 + 4 temporal phase shift algorithm with fewer captured images. However, the algorithm for calculating phase is not simpler than the 4 + 4 algorithm.

Like the 4 + 1 fast temporal phase shift algorithm, a 3 + 1 fast temporal phase shift algorithm was developed to achieve dynamic measurement using shearography. In the 3 + 1 temporal phase shift algorithm, three interferograms are taken using the same procedure as the 3 + 3 phase shift algorithm before loading, and only one image is required during the loading. Similar to the 4 + 1 temporal phase shift algorithm, the phase map quality of the 3 + 1 temporal phase shift algorithm is usually adequate for NDT applications.

Other than the N + N (4 + 4 or 3 + 3) temporal phase shift algorithms and the N + 1 (4 + 1 or 3 + 1) fast temporal phase shift algorithms, an N + 2 temporal phase shift algorithm also exists. The N + 2 temporal phase shift uses two phase shifted images during each loading condition to calculate the relative phase change during the test. The phase map quality of these algorithms is better than the N + 1 temporal phase shift algorithms, but they are not as good as N + N methods. A comparison between these algorithms is shown in Fig. 10.

Fig. 10

Phase Map obtained by (a) 3 + 1 fast algorithm; (b) 3 + 2 algorithm; (c) 3 + 3 algorithm

Spatial Phase Shift Shearography

Multi-channel Spatial Phase Shift Shearography

With a Known Phase Shift

The temporal phase shift technique digital shearography (TPS-DS) achieves a high sensitivity measurement and is very suitable for static tests. Although some of the fast temporal phase shift algorithms can be used for dynamic tests, the quality of the acquired phase map is not good enough for many applications. Spatial phase shift digital shearography (SPS-DS) was proposed to overcome this drawback. Spatial phase shift digital shearography uses only a single image to create the phase map, making this technique extremely suitable for dynamic tests. The SPS-DS can be categorized into two types: multi-channel spatial phase shift shearography and carrier-frequency spatial phase shift shearography.

The multi-channel approach determines the phase distribution using the intensity data of three adjacent pixels in a single interferogram (Yamaguchi 2006; Hettwer et al. 2000). Figure 11 shows a schematic of this approach. If the phase difference δ between the pixels is fixed, the equations described in section “4 + 4 Phase Shift Algorithm” with four equations or with three equations can be used to solve the phase map using the single interferogram. If δ = 90°, with the above arrangement, the intensity of four adjacent pixels can be described using the following equations:

$$ {\displaystyle \begin{array}{l}{I}_1={I}_0\left[1+\gamma \cos \left(\phi \right)\right]\\ {}{I}_2={I}_0\left[1+\gamma \cos \left(\phi +\delta \right)\right]\\ {}{I}_3={I}_0\left[1+\gamma \cos \left(\phi +2\delta \right)\right]\\ {}{I}_4={I}_0\left[1+\gamma \cos \left(\phi +3\delta \right)\right]\end{array}} $$

(22)

Fig. 11

Schematic of multi-channel approach spatial phase shift technique

The random phase ϕ can be calculated by the Eq. (14) used in the four-step temporal phase shift algorithm.

The introduced phase difference δ can be calculated based on the relation shown in Eqs. 23. The optical path difference between adjacent pixels ΔL can be controlled by setting the reference beam at an appropriate angle α: ΔL = S ⋅  sin α, where S is the pixel size. The relationship between the phase difference and the angle is given:

$$ \delta =2\pi \cdot \frac{\Delta L}{\lambda }=2\pi \cdot \left(S\cdot \frac{\sin \alpha }{\lambda}\right) $$

(23)

where λ is the laser wavelength. For given wavelength and pixel size, the phase difference δ can be determined by setting an appropriate reference beam angle α. After the object is loaded, the same procedure can be used to calculate the phase distribution ϕ^′ at the loaded condition.

With an Unknown Phase Shift

The multi-channel SPS-DS algorithm described in section “With a Known Phase Shift” by using 3 or 4 pixels method requires a very accurately known incident angle α. As a result, the measurement result of the described method is limited to the accuracy of the incident angle α. Because of the difficulty to set a known incident angle, a more flexible multi-channel SPS-DS algorithm was proposed to solve this problem (Lassahn et al. 1994). In this method, the same experimental setup is used to induce the incident angle. The difference is that the incident angle is regarded as an unknown constant rather than the known constant. In this case, since the introduced phase difference δ becomes an unknown, at least four equations are required to solve the random phase ϕ. A well-known five-step phase shift algorithm is used for this case. The equations are described in the following: assuming the introduced phase difference between pixels is constant, the intensity of the five adjacent pixels can be expressed as:

$$ {\displaystyle \begin{array}{l}{I}_1={I}_0\left[1+\gamma \cos \left(\phi \right)\right]\\ {}{I}_2={I}_0\left[1+\gamma \cos \left(\phi +\delta \right)\right]\\ {}{I}_3={I}_0\left[1+\gamma \cos \left(\phi +2\delta \right)\right]\\ {}{I}_4={I}_0\left[1+\gamma \cos \left(\phi +3\delta \right)\right]\\ {}{I}_5={I}_0\left[1+\gamma \cos \left(\phi +4\delta \right)\right]\end{array}} $$

(24)

The random phase ϕ can be calculated using the following equation:

$$ \phi =\arctan \left\{\frac{2\left({I}_2-{I}_4\right)}{2{I}_3-{I}_1-{I}_5}\cdot \frac{1}{\sqrt{1-{\left[\frac{I_1-{I}_5}{2\left({I}_2-{I}_4\right)}\right]}^2}}\right\} $$

(25)

It should be emphasized that the background (I₀), the contrast (γ), and the phase (ϕ) of the intensity equations at these adjacent pixels must keep identical. This is the necessary condition for the multi-channel spatial phase shift methods. To maintain this necessary condition, the speckle size should be controlled so that it can cover 3, or 4 or 5 adjacent pixels depending on the algorithms utilized. This can be achieved by adjusting the aperture of the camera used. However, too big speckle size (to cover more pixels) needs very small aperture which will result in need of high power laser and low measuring resolution.

Carrier-Frequency Spatial Phase Shift Shearography

Method Based on Mach-Zehnder Interferometer

The carrier-frequency technique is widely used in many applications, such as in the telecommunication area. The carrier signal is modulated by a high-frequency carrier, and this technique can also be used to solve the phase from a single interferogram (Bhaduri et al. 2006, 2007; Xie et al. 2013a, b). A typical carrier-frequency spatial phase shift shearography can be explained by the Mach-Zehnder interferometer-based shearography setup. This setup has been shown in Fig. 4. The carrier frequency is introduced by tilting one mirror in the Mach-Zehnder interferometer.

After passing the shearing device, the light is divided into a sheared part and an un-sheared part. The wavefront can be expressed as:

$$ {\displaystyle \begin{array}{l}{u}_1\left(x,y\right)=\left|{u}_1\left(x,y\right)\right|\exp \left[ i\phi \left(x,y\right)\right]\\ {}{u}_2\left(x,y\right)=\left|{u}_2\left(x+\Delta x,y+\Delta y\right)\right|\exp \left[ i\phi \left(x+\Delta x,y+\Delta y\right)-2\pi i\cdot {f}_c\cdot x\right]\end{array}} $$

(26)

Where u₁ and u₂ are the two components with and without shearing. Δx and Δy represent the shearing distance in the x and y-direction, respectively. The carrier frequency f_c, which is introduced by the tilting angle β, can be expressed as:

$$ {f}_c=\frac{\sin \beta }{\lambda } $$

(27)

Thus, the intensity recorded by the digital camera can be represented as:

$$ {\displaystyle \begin{array}{l}I=\left({u}_1+{u}_2\right)\left({u}_1^{\ast }+{u}_2^{\ast}\right)\\ {}\, ={u}_1{u}_1^{\ast }+{u}_1{u}_2^{\ast }+{u}_2{u}_1^{\ast }+{u}_2{u}_2^{\ast}\end{array}} $$

(28)

Where the ^∗ denotes the complex conjugate of the light beams. To extract the phase ϕ from the above equations, a Fourier transform is performed, and the recorded information can be expressed in the frequency domain using the Fourier transform:

$$ {\displaystyle \begin{array}{l}F(I)={U}_1\left({f}_x,{f}_y\right)\otimes {U}_1^{\ast}\left({f}_x,{f}_y\right)\\ {}\, +{U}_2\left({f}_x+{f}_c,{f}_y\right)\otimes {U}_2^{\ast}\left({f}_x+{f}_c,{f}_y\right)\\ {}\, +{U}_1\left({f}_x,{f}_y\right)\otimes {U}_2^{\ast}\left({f}_x+{f}_c,{f}_y\right)\\ {}\, +{U}_2\left({f}_x+{f}_c,{f}_y\right)\otimes {U}_1^{\ast}\left({f}_x,{f}_y\right)\end{array}} $$

(29)

Where ⊗ is the convolution operation. Three spectra can be observed in the frequency domain, as shown in Fig. 12. The center spectrum is the low-frequency term $F\left({u}_1{u}_1^{\ast }+{u}_1{u}_2^{\ast}\right)$, and contains the information from the background. The two side spectra are the terms with the carrier frequency $F\left({u}_2{u}_1^{\ast}\right)$ and $F\left({u}_1{u}_2^{\ast}\right)$. These two terms are shifted to the location (f_c, 0) and (−f_c, 0). The spectral width is determined by the size of the aperture (AP).

Fig. 12

Schematic of the frequency domain using the carrier frequency spatial phase shift technique

The phase can be extracted by applying a windowed inverse Fourier transform on the area located at (−f_c, 0), and it can be expressed as:

$$ \phi +2\pi \cdot {f}_c\cdot x=\arctan \frac{\operatorname{Im}\left[F\left({u}_1{u}_2^{\ast}\right)\right]}{\operatorname{Re}\left[F\left({u}_1{u}_2^{\ast}\right)\right]} $$

(30)

Where the Im and Re denote the imaginary and real component of the complex number. The phase after loading can be calculated using the same method:

$$ {\phi}^{\prime }+2\pi \cdot {f}_c\cdot x=\arctan \frac{\operatorname{Im}\left[F\left({u}_1^{\prime }{u^{\prime}}_2^{\ast}\right)\right]}{\operatorname{Re}\left[F\left({u}_1^{\prime }{u^{\prime}}_2^{\ast}\right)\right]} $$

(31)

The relative phase change due to the loading can be calculated as:

$$ \Delta ={\phi}^{\prime }+2\pi \cdot {f}_c\cdot x-\left(\phi +2\pi \cdot {f}_c\cdot x\right)={\phi}^{\prime }-\phi $$

(32)

In this way, the phase map is evaluated using a single image at each loading condition, and the acquisition rate is no longer limited by the phase shift procedure.

Method Based on Michelson Interferometer

Another popular carrier-frequency spatial phase shift digital shearography setup is based on the 4f-system embedded Michelson interferometer. This setup is shown in Fig. 13. The fundamental of this setup is similar to the conventional modified Michelson interferometer-based digital shearography setup, which is described in the previous section. The 4f-system embedded Michelson interferometer-based SPS-DS has the following changes: (1) a 4f-system is embedded; and (2) an aperture is placed in front of the imaging lens. The 4f-system allows the field of view of the measurement system to be adjusted and enlarged, and the aperture is used to limit the spatial frequency of the light. The procedure of the phase evaluation of this setup is the same as the carrier-frequency SPS-DS based on Mach-Zehnder Interferometer.

Fig. 13

Schematic of the 4f-system embedded carrier frequency spatial phase shift shearographic setup

The Michelson interferometer-based spatial phase shift shearography has a simpler setup than Mach-Zehnder Interferometer based spatial phase shift shearography. However, the Michelson interferometer-based system usually needs a large shearing amount so that the two side spectra can be separated from the central spectrum whereas the Mach-Zehnder based setup can do it easily either in small or large shearing amount.

Comparison and Discussion

Spatial phase shift digital shearography (SPS-DS) was proposed to achieve dynamic measurement. SPS-DS can be categorized into two types: multi-channel spatial phase shift shearography and the carrier-frequency spatial phase shift shearography. The multi-channel approach determines the phase distribution using the intensity data of three or four adjacent pixels in a single interferogram; while the carrier-frequency approach extracts the phase distribution from the frequency domain via Fourier transform. The algorithm complexity of the multi-channel approach is much lower than that of the carrier-frequency approach. However, the phase map quality of the carrier-frequency approach is much better than the multi-channel approach.

Practical Applications of Digital Shearography for NDT

Introduction

Shearography, as a laser-based optical method, has been widely used in the automotive and aerospace industries for NDT. Its advantages include its high sensitivity, robustness for rigid-body motion, and high measurement accuracy with the phase shift technique. However, a successful application of digital shearography for NDT still depends on many factors, including the depth and type of defect, the type of material, the correct shearing amount and direction, and the illumination and loading. In this section, the effects of these parameters will be analyzed and discussed.

Instrumentation

The schematic setup has been described in detail in the previous sections; this section will summarize the hardware of digital shearography. The hardware for digital shearography consists of three parts: a digital camera, a shearing unit, and a laser device for illumination.

The digital camera records intensity through the use of gray levels. Various digital cameras are available commercially. The main specification of a digital camera is sensor type, sensor size, resolution, and frame rate (Li et al. 2017a and b). The sensor of the digital camera can be categorized into two types: complementary metal-oxide semiconductor (CMOS) and charge-coupled device (CCD). CCD cameras used to dominate the area of industrial application; however, the CMOS camera has started to become the more favorable type due to the high development of the CMOS technique. The sensor size is another important parameter for the digital camera. Sensor sizes commonly used for the industrial camera range from half an inch to 1 inch. A larger sensor size camera always provides better digital image quality. Corresponding to the sensor size, another important parameter of the digital camera is the resolution. Currently, the resolution of the most common industrial cameras is between 2 megapixels and 8 megapixels. A higher resolution camera can record a more detailed image and provide a more detailed phase map for shearography. The last important parameter is the frame rate. The frame rate of the digital camera determines the upper limit of the dynamic range of the test system. The frame rate for the current standard industrial camera is between 10 Hz and 100 Hz. If the dynamic range of the test is high, a high-speed digital camera is required.

The shearing device is the key component of digital shearography. It brings lights scattered from two points on the test object surface to a single point on the image plane. Different devices can be used as the shearing device, such as an optical glass wedge (Hung 1982), a bi-angle prism (Ettemeyer 1991), a double-refractive prism (Hung et al. 2003), a modified Michelson interferometer (Yang et al. 1995), and a modified Mach-Zehnder interferometer (Pedrini et al. 1996). Furthermore, it is important to select a shearing device that is compatible with the phase shift technique being utilized. The methodology of the different shearing devices and the phase shift technique has been introduced in detail in the previous section and will not be repeated here.

The laser device for illumination is the third important part of digital shearography in the aspect of hardware. A strong laser source is required to perform a whole-field test. Traditional high-powered laser sources, such as a He-Ne laser and Nd:YAG laser, are too big, fragile, and expensive for the NDT applications. Based on the fundamentals of shearography, the interference phenomenon in shearography is formed by two waves from two different points, and the optical path difference between them is very small. Therefore, the coherence length requirement for the laser device is relaxed. This characteristic of shearography allows the laser diode to be used as the laser source for illumination. The laser diode does not have a long coherent length, but it is compact in size and cheap in price. A portable digital shearography setup can be built utilizing of the laser diode in the shearography system. Also, multiple laser diodes can be used at the same time for large area illumination in some NDT applications, as shown in Fig. 14 (Yang 1998; Kalms and Osten 2003; Jackson 2004).

Fig. 14

Illustration of the shearographic system with two diodes

Measuring Sensitivity

Sensitivity for Phase Measurement

As displayed by Eqs. 11 and 12, digital shearography measures the gradient of deformation by determining the relative phase change. Therefore, the sensitivity of the shearography system depends on the sensitivity of the phase measurement. The measuring sensitivity of the phase for the shearography without using the phase shift technique is around 2π. However, the measuring sensitivity can be increased dramatically using the phase shift technique. Theoretically, the phase shift technique can reach a sensitivity of 2π/256 for the phase measurement, if the depth resolution of the camera is 8 bits. Practically, the sensitivity of the phase measurement is from 2π/30 to 2π/10, depending on the level of the speckle noises and the application of the phase shift technique.

Sensitivity for Shearing Amount

Another parameter that impacts the measuring sensitivity of shearography is the shearing amount. The gradient of deformation is obtained by calculating the deformation difference between two points with a separation of the shearing amount. Obviously, the measuring sensitivity depends on the shearing amount (Steinchen et al. 1998).

A small shearing amount leads to a low measuring sensitivity since the relative deformation between two points with small separation is low. However, the measuring result is close to the first derivative. For strain measurement, a small shearing amount is desirable. However, in NDT for measuring small defects, a relatively large shearing amount is required to reach a high measuring sensitivity.

Thus, in one respect, a small shearing amount is favorable to obtain the accurate strain information; on the other hand, a large shearing amount leads to high measuring sensitivity. Therefore, a critical shearing amount exists which provides the maximum sensitivity of the system. If the shearing amount is larger than the critical shearing amount, the sensitivity of the system will not increase anymore. To explain this concept, a relationship among deformation, relative deformation, and the shearing amount over the defect area is shown in Fig. 15. The relative deformation between two points increases with the shearing amount; however, the relative deformation no longer increases after the shearing amount reaches one-half of the area of deformation. Therefore, the critical shearing amount should be equal to one-half of the defect diameter. Usually, one knows what is the smallest defect size to be inspected, the critical shearing amount should be the one-half of the smallest defect size.

Fig. 15

The relation among the deformation, the relative deformation, and the shearing amount at the defect location

Sensitivity for Shearing Direction

The shearing direction can also affect the sensitivity of shearography. If the defect is a circular form, the shearing direction won’t affect the sensitivity of the measurement result since the anomaly of the relative deformation shows a uniform appearance in all directions. However, if the defect is a narrow slot form, the shearing direction plays an important role in flaw detection because the anomaly of the relative deformation is sensitive to the direction. To demonstrate this effect, a square plate with one round groove and three narrow slits oriented in different directions on the plate’s back side, as shown in Fig. 16, is tested with different shearing directions (x and y-direction). The slit oriented in the horizontal direction cannot be detected properly using the horizontal shearing direction, whereas the vertical notch can only be detected using the horizontal shearing direction.

Fig. 16

NDT result with different shearing direction. (a) Location and the shape of the defect (left). (b) NDT result with the x-direction shearing (middle). (c) NDT result with the y-direction shearing

Shearographic setup with double shearing direction has been developed for both the temporal phase shift (TPS) technique and spatial phase shift (SPS) technique to solve the above problem. A TPS technique based dual-shearing direction shearography system using two modified Michelson interferometers has been reported in the literature (Yang et al. 2004). The schematic of the system is shown in Fig. 17. Two beam splitters are stacked on top of each other. The two mirrors (1a and 1b) are arranged on one side of the beam splitters. On the other side of the beam splitters, a PZT driven mirror (2) is used to induce the temporal phase shift. Two cameras (3 and 4) are also stacked on top of each other and correspond to the two beam splitters. The different shearing directions for the upper and lower system are produced by tilting the upper (1a) and lower (1b) mirrors in different directions. Thus, two interferograms can be taken with the different shearing directions, and the dual-shearing direction TPS-DS is achieved.

Fig. 17

A TPS technique based shearography with two shearing directions

Figure 18 shows the TPS technique based shearographic system with two shearing directions for NDT of a micro-crack in a glass fiber-reinforced composite tube with loading by internal pressure. Two shearograms were obtained simultaneously under the same loading. The micro-crack was demonstrated more clearly in the shearogram with y-shearing direction.

Fig. 18

TPS based shearography with two shearing directions for NDT of a micro-crack: (a) x-shearing, (b) y-shearing

The spatial phase shift technique based dual-shearing direction shearography has been developed recently. Unlike the temporal phase shift technique based system, only one camera is required using the carrier-frequency technique. The schematic of the system is shown in Fig. 19. Two lasers with different wavelengths are used to illuminate the object. The scattered light from the object passes the shearing device and forms the image on the digital camera. The shearing device is composed of two modified Michelson interferometers: one generates shearing in the vertical direction, and the other generates shearing in the horizontal direction. The carrier frequency is also generated at the same time during shearing. Due to the different shearing directions, the carrier frequency of the two interferometers is different. Thus, the phase map from the two interferometers can be separated in the frequency domain. Two band filters, corresponding to the wavelengths of the two lasers, are used to guarantee that only one laser wave passes to one modified Michelson interferometer. An aperture is placed in front of the 4f imaging system to reduce the spatial frequency of the wave, and a beam splitter is used to synthesize two beams from these two Michelson interferometers to a single digital camera. The details regarding the principle of developing spatial phase shift technique based dual-shearing direction shearography systems can be found in the literature (Xie et al. 2013a, b, 2015; Wang et al. 2016).

Fig. 19

Schematic of the dual-shearing direction spatial phase shift shearography

Figure 20 shows SPS technique based shearographic system with two shearing directions for NDT of a honeycomb structure under a continuous loading. A heat gun was used to load the honeycomb continuously for 2 s, which resulted in a temperature change on the surface. At the same time, the SPS technique based shearographic system captured the speckle pattern images at a frame rate of 10 fps. Then, the phase map history in the x and y directions during the 2 s was measured simultaneously. Because the SPS based shearography is particularly well suited for dynamic loading, the shearogram history along the 2 s loading, i.e., the growth of ∂w/∂x (x-shearing) and ∂w/∂y (y-direction) during the 2-s loading, can be clearly observed. This NDT example shows that with SPS technique based shearographic system is possible to do NDT measurements in dual-shearing directions simultaneously, continuously, and dynamically.

Fig. 20

SPS based shearography for NDT of a honeycomb structure under a continuous loading in two shearing directions simultaneously, continuously, and dynamically

Methods of Stressing

Various methods are currently used to induce the stress for NDT (Tesfamariam and Goda 2013). Though shearography is relatively insensitive to rigid-body motion, the stressing methods should not create intolerable (too large) rigid-body motion of the test object, but generate enough stress to detect the flaws. Internal pressure loading, vacuum loading, thermal loading, and dynamic loading are most common methods used to induce stress.

Pressure vessels, pipes, or other structures that can be pressurized internally can be loaded using the internal pressure. The internal pressure can be applied to the maximum value of the actual loading condition to represent actual stressing of the structure. Shearography would reveal the flaws that create strain concentrations. The revealed critical flaws would reduce the strength of the structure and lead to failure of the component. As an example, a plastic PVC pipe with two flaws is loaded by a 0.02 MPa internal pressure. The NDT result using shearography, overlapped on the object, is shown in Fig. 21. The stress concentration can be clearly detected by viewing the phase map.

Fig. 21

NDT result of an internal pressured pipe using shearography

Vacuum stressing is one of the most popular loading methods for revealing disbands and delaminations in the composite material. Vacuum stressing is equivalent to a uniform tensile force applied to the surface, pulling the surface outward. The flaws under the vacuum stressing would bulge out slightly, and the anomalies due to the bulge can be detected using digital shearography. Figure 22 shows the NDT result for a composite fuselage using the vacuum stressing method. The shearing direction is in the vertical direction, and the two de-laminations are clearly demonstrated.

Fig. 22

NDT result of the delamination on the fuselage under vacuum stressing

Thermal stressing , another popular loading method, is an alternative method to generate the stress. The developed temperature gradient, generated by the thermal stressing, induces thermal strain to the object. Heat causes disbonds or delaminations expand and causes strain anomalies on the surface. Figure 23 shows NDT results using 3 + 1 temporal phase shift shearography for real-time measurement under thermal loading. The sample, an aerospace honeycomb aluminum plate with delamination, was pre-heated to a certain temperature. A series of interferograms are taken during cooling of the plate using the procedure that was described in the previous section.

Fig. 23

NDT result of the delamination on the honeycomb structure plate under heating using the 3 + 1 fast temporal phase shift shearography

Dynamic stressing is also useful loading method in applications for inspecting bonding integrity and weld joints. Dynamic stressing is created by an excitation source. The excitation source can be divided into harmonic and non-harmonic excitation sources. The harmonic excitation is usually generated by the PZT or a shaker and is suitable for dynamic analysis. The non-harmonic excitation is typically generated by an impact loading, and it usually uses the double-exposure method, or if phase map is required, it should use the double-exposure SPS-shearography system. Figure 24 shows an example for NDT of welding condition of nuggets in an automotive battery. While the top surface of the battery is harmonically excited at 11 KHz, the nugget area where multi sheets are welded together starts to vibration, a fringe pattern can be observed in the nugget areas (the left and the middle nuggets), whereas no fringes can be observed in the good nugget area (right nugget). It indicated that the left two nuggets are detached since the fringe characteristic on the nuggets under vibration are similar to the free copper margin area. However, there are no fringes on the right nugget, which means it is perfectly welded.

Fig. 24

NDT result of the welding parts under dynamic stressing

Conclusions

Potentials

In comparison with other optical methods for NDT, shearography offers many advantages, such as:

• 1. Shearography directly measures the first derivative of deformation/displacement which is the strain information, defects in objects generate strain concentration. Thus, shearography reveals defects in an object by identifying strain anomalies through the display of strain concentrations, which is a more direct and clear way to reveal defects as shown in Fig. 8b.

• 2. Shearography is relatively insensitive to rigid-body movement because a rigid-body movement generates a displacement, but not the first derivative of displacement. Therefore, shearography is less sensitive to environmental disturbances and suited well for practical application in compared with other interferometric methods such as holography, electron speckle pattern interferometry, etc.

• 3. Shearography uses a self-reference interferometric system, which has a very simple optical layout. It is of benefit to building a very robust shearographic sensor for industrial applications.

• 4. The self-reference interferometric system has balanced optical paths. Thus, a high requirement of coherent length is greatly reduced, which enables the utilization of a cost-economical diode-laser for illumination. If a larger object surface is needed for inspection, multi-diode lasers can be applied.

In comparison with the early version of shearography (so-called electronic shearography), in which the intensity image is used as the measured result, the phase shift digital shearography offers many new possibilities for NDT, such as:

• 1. The measurement sensitivity of the temporal phase shift digital shearography for phase determination is much higher than the electronic version. The sensitivity of the electronic shearography for phase determination is 2π, however, the sensitivity of the digital shearography with phase shift technique could reach 2π/20 or higher, which enables inspection of smaller defect as shown in Fig. 9b.

• 2. Phase shift digital shearography with multi-shearing directions makes NDT of direction sensitive flaws, such as micro-cracks, narrow slot shape defects, easier.

• 3. Spatial phase shift digital shearography enables displaying shearograms under dynamic loading continuously and dynamically.

Limitations

Digital shearography is an experimental technique for surface measurement. Thus, some limitations still exist for NDT.

• 1. Shearography detects flaws by looking for anomalies of the surface under stress. However, flaws that lie far from the object surface are hard to detect, since the flaw cannot generate large enough surface anomalies to be detected by shearography.

• 2. The application of shearography for NDT is mainly limited to composite materials, honeycomb structures, and thin plates. High strength materials, such as metallic materials, are difficult to test using shearography.

• 3. Although shearography uses a “self-referencing” optical system and is relatively robust to environmental disturbance compared to the other laser technique, shearography is still sensitive to ambient noises such as large rigid-body motions and strong thermal airflow, because it is, after all, an interferometric method.

• 4. With the fast development of the digital technique, the resolution of the digital camera has increased dramatically. However, the spatial resolution of the digital camera is still much lower than the special film used in photographic shearography.

• 5. The phase map obtained by the phase shift technique still contains lots of noise, and the signal to noise ratio of current shearography, especially, in the spatial phase shift digital shearography, is not high enough to detect some minor flaws.

Summary

The fundamental of shearography for NDT and its applications have been presented in this chapter. The principles of digital shearography including optics, setups, and algorithms are detailed described and analyzed in the first part of the chapter. Phase-shift techniques including temporal and spatial phase-shift methods are then introduced which can be applied to improve the measuring sensitivity of shearography for NDT. Different NDT applications of shearography are discussed and investigated in the last part, along with the analysis of the measuring sensitivity, and the concept of the critical shearing amount etc. In addition, higher dynamic test range can be achieved using the recently developed spatial phase-shift digital shearography. Digital shearography is well suitable to detect the delamination, disbands, and microcracks in composite materials, honeycomb structures, and thin plates. It is expected that the digital shearography can be applied to a wider range of applications with the recent and future developments.