Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Reservoir Computing (RC) is a set of methods for designing and training artificial recurrent neural networks [9, 12]. A typical reservoir is a randomly connected fixed network, with random coupling coefficients between the input signal and the nodes. This reduces the training process to solving a system of linear equations and yields performances equal, or even greater than other algorithms [7, 11]. For instance the RC algorithm has been applied successfully to phoneme recognition [19], and won an international competition on prediction of future evolution of financial time series [1].

Reservoir Computing is well suited for analog implementations. The opto-electronic implementations [10, 13, 15] were the first fast enough for real time data processing. Since 2012, all-optical reservoir computers have been reported using a variety of approaches [5, 6, 20, 21].

The performance of a reservoir computer greatly relies on the training technique. Up to now offline learning methods have been used [3, 5, 6, 10, 15, 20]. In these approaches one first acquires a long sequence of training data, and then uses it to compute the readout weights. An alternative approach is to use online training in which the readout weights are progressively adapted in real time. To this end a variety of algorithms can be used, such as gradient descent or recursive least squares. Online training is well suited to solve non-stationary problems, as the weights can be adjusted while the task changes, and can also be applied to systems with complex nonlinear output, such as analog readout layers, proposed in [18].

Online training requires that the readout weights updates are computed in real time, as the reservoir is running. This cannot be achieved with a regular CPU and thus requires dedicated electronics. Field Programmable Gate Arrays (FPGAs) are particularly suited for such applications. Several RC implementations using an FPGA chip have been reported [2, 8, 17], but no interconnection between an FPGA and a physical reservoir computer has been reported so far.

In the present work we report the first online-trained experimental reservoir computer. It consists of an opto-electronic reservoir computer of the type reported in [10, 15], combined with an FPGA board that generates the input sequence, collects the reservoir states and computes optimal readout weights using a simple gradient descent algorithm [4]. We evaluate the performance of our implementation on an example of a real-world task: the equalisation of a nonlinear communication channel [14]. We consider situations where the communication channel changes in time, and show that the online training can deal with this time-varying problem, whereas it would be difficult or impossible to adapt offline training methods to such a task. Furthermore, the use of an FPGA chip allows our system to be trained and tested over an arbitrarily long input sequence and significantly reduces the experimental runtime. The results (measured by the symbol error rate after equalization) are comparable to those reported previously [15].

2 Basic Principles

2.1 Reservoir Computing

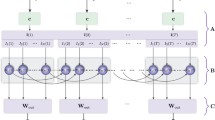
A typical reservoir computer is depicted in Fig. 1. The nonlinear function used here is \(f_{NL} = \sin (x)\), as in [10, 15]. To simplify the interconnection matrix \(a_{ij}\), we exploit the ring topology [16], so that only the first neighbour nodes are connected. The evolution equations thus become:

$$\begin{aligned} x_0(n+1)&= \sin \left( \alpha x_{N}(n-1) + \beta b_0 u(n) \right) \!, \end{aligned}$$
(1a)
$$\begin{aligned} \nonumber \\ x_i(n+1)&= \sin \left( \alpha x_{i-1}(n) + \beta b_i u(n) \right) \!, \end{aligned}$$
(1b)

with \(i=1,\ldots ,N-1\), where \(\alpha \) and \(\beta \) parameters are used to adjust the feedback and the input signals, respectively, and \(b_i\) is the input mask, drawn from a uniform distribution over the the interval \([-1, +1]\), as in [6, 15, 16].

Fig. 1.
figure 1

Schematic representation of a typical reservoir computer. It contains a large number N of internal variables \(x_i(n)\) evolving in discrete time \(n \in \mathbb {Z}\), \(f_{NL}\) is a nonlinear function, u(n) is an external signal that is injected into the system, \(a_{ij}\) and \(b_i\) are time-independent coefficients, drawn from a random distribution with zero mean and \(w_i\) are the readout weights, trained either offline (using standard linear regression methods), or online, as described in Sect. 2.3, in order to minimise the error between the output signal y(n) and some target signal d(n).

Full size image

2.2 Channel Equalisation Task

The performance of our implementation is evaluated on the channel equalisation task [9, 14, 16]. To demonstrate the benefits of the online learning, we investigated two variants of this task, a switching and a drifting channel, where some parameters of the channel vary during the experiment.

Constant Channel. An input signal \(d(n) \in \{-3, -1, 1, 3\}\) is transmitted through a noisy nonlinear wireless communication channel, producing an output signal u(n). The reservoir computer then has to recover the clean signal d(n) from the noisy distorted signal u(n). The channel is modelled by the following equations:

$$\begin{aligned} q(n) {}&= 0.08 d(n+2) - 0.120 d(n+1) + d(n) + 0.18 d(n-1) \nonumber \\&\quad - 0.10 d(n-2) + 0.091 d(n-3) - 0.05 d(n-4) + 0.04 d(n-5) \nonumber \\&\quad + 0.03 d(n-6) + 0.010 d(n-7), \end{aligned}$$
(2)
$$\begin{aligned} \nonumber \\ u(n) {}&= p_1 q(n) + 0.036 q^2(n) - 0.011q^3(n) + \nu (n), \end{aligned}$$
(3)

where the first equation stands for the symbol interference, the second represents the nonlinear distortion and \(\nu (n)\) is the noise, drawn from a uniform distribution over the interval \(\left[ -1,+1\right] \). The \(p_1 \in \left[ 0,1\right] \) parameter is used to tweak the nonlinearity of the channel. It is set to 1 for the constant channel, but varies in other cases. The performance of the reservoir computer is measured in terms of wrongly reconstructed symbols, given by the Symbol Error Rate (SER).

Switching Channel. In wireless communications, the properties of a channel are highly influenced by the environment. For better equalisation performance, it is crucial to be able to detect significant channel variations and adjust the RC readout weights in real time. We consider here the case of a “switching” channel, where \(p_1\) is regularly switched between three predefined values \(p_1 \in \{ 0.70, 0.85, 1.00 \}\). These variations occur at very slow rates, much slower than the time required to train the reservoir computer.

Drifting Channel. In the second variant the coefficient \(p_1\) varies faster than the equaliser learning rate, with the same values as for the switching channel. In this situation, the reservoir computer is trained over a “drifting” channel, that is, a channel whose parameters are changing during the computation of the optimal readout weights.

2.3 Gradient Descent Algorithm

The gradient, or steepest, descent method is an algorithm for finding a local minimum of a function using its gradient [4]. We use the following rule for updating the readout weights:

$$\begin{aligned} w_i (n+1) = w_i (n) + \lambda \left( d(n) - y(n) \right) x_i (n), \end{aligned}$$
(4)

where \(\lambda \) is the step size, used to control the learning rate. It starts with a high value \(\lambda (0)=\lambda _0\), and then gradually decreases to zero \(\lambda (n+1) = \gamma \lambda (n)\) at rate \(\gamma <1\).

3 Experimental Setup

Our experimental setup is depicted in Fig. 2. It contains three distinctive components: the optoelectronic reservoir, the FPGA board implementing the input and the readout layers and the computer used to control the experiment.

Fig. 2.
figure 2

Schematic representation of the experimental setup.

Full size image

Optoelectronic Reservoir. The optoelectronic reservoir is based on the same scheme as in [15]. The reservoir states are encoded into the intensity of the incoherent light signal, produced by a superluminiscent diode (SLED). The Mach Zehnder intensity modulator (MZ) implements the nonlinear function. A fraction of the signal is extracted from the loop by the 90/10 beam splitter and sent to the readout photodiode (\(\text {P}_\text {r}\)), the resulting voltage signal is sent to the FPGA. The optical attenuator (Att) is used to set the feedback gain \(\alpha \) of the system (see Eq. (1)). The fibre spool consists of about \(1.6 \; \text {km}\) single mode fibre, giving a round trip time of 8.4056 \(\upmu \text {s}\). The resistive combiner (Comb) sums the electrical feedback signal, produced by the feedback photodiode (\(\text {P}_\text {f}\)), with the input signal from the FPGA to drive the Mach Zehnder modulator, with an additional amplification stage of \(+27 \; \text {dB}\) to span the entire \(V_\pi \) interval of the modulator.

FPGA Board. For our implementation, we use the Xilinx ML605 board, powered by the Virtex 6 XC6VLX240T FPGA chip. The board is paired with a 4DSP FMC151 daughter card, containing one two-channel ADC (Analog-to-Digital converter) and one two-channel DAC (Digital-to-Analog converter). The synchronisation of the FPGA board with the reservoir delay loop is achieved by using an external clock signal, generated by a NI PXI-5422 AWG card. Its maximal output frequency of \(80 \; \text {MHz}\) limits the reservoir size of our implementation to 40 neurons.

The chip uses two Galois linear feedback shift registers with a total period of about \(10^9\) to generate pseudorandom symbols d(n), which are multiplied by the input mask and sent to the optoelectronic reservoir through the DAC. The resulting reservoir states are collected and digitised by the ADC, and used to compute readout weights and the output signal. The latter is compared to the input signal d(n) and the resulting SER is transmitted to the computer.

Personal Computer. The experiment is fully automated and controlled by a Matlab script, running on a computer. It is designed to run the experiment multiple times over a set of predefined values of parameters of interest and select the combination that yields the best results. For statistical purposes, each set of parameters is tested several times with different random input masks.

We scanned the following parameters: the input gain \(\beta \), the decay rate \(\gamma \), the channel signal-to-noise ratio and the feedback attenuation \(\alpha \). The other parameters were fixed during the experiments. Particularly, we used \(\lambda _0 = 0.4\) and \(\gamma = 0.999\) for the gradient descent algorithm.

4 Results

Constant Channel. Figure 3(a) presents the performance of our reservoir computer for different signal-to-noise ratios of the wireless channel (green squares). Each value is an average of the lowest rates obtained with different random input masks, and the error bars show the variations of the performance with these masks. We compare our results to those reported in [15], obtained with the same optoelectronic reservoir, trained offline (blue dots). For the lowest noise level (\(32 \; \text {dB}\)), our implementation produces an error rate of \(4.14\times 10^{-4}\), which is comparable to the \(1.3\times 10^{-4}\) SER of the optoelectronic setup. Note that the latter value is a rough estimation of the reservoir’s performance, due to the limited length of the input sequence (6 k symbols, see [15] for details), while in our case, the SER is estimated precisely over 100 k input symbols.

These results demonstrate that the online training algorithm works well, and is able to train an experimental reservoir computer. The obtained SERs are however somewhat worse than those reported in [15], sometimes with up to an order of magnitude. This may be due to the use of a smaller reservoir, with \(N=40\).

Fig. 3.
figure 3

(a) Comparison of experimental results for nonlinear channel equalisation. (b) Experimental results for switching channel task. After each switch, the SER goes up, the learning rate \(\lambda \) is reset to \(\lambda _0\), and then decreases while the SER gradually goes back to a low value. (c) Simulation results in the case of the drifting channel. Even though the channel is changing during training, the online training method is able to reach a low SER, that is evaluated during the last 15 k points.

Full size image

Switching Channel. Figure 3(b) shows the error rate produced by our experiment in case of a switching noiseless communication channel. The parameter \(p_1\) is programmed to switch every 150 k symbols. Every switch is followed by a steep increase of the SER, as the reservoir computer is no longer optimised for the channel it is equalising. The performance degradation is detected by the algorithm, causing the learning rate \(\lambda \) to be reset to the initial value \(\lambda _0\). The readout weights are then retrained to new optimal values, and the SER rate correspondingly goes down.

Drifting Channel. The reservoir computer is trained over a channel that gradually drifts from channel 3 (with \(p_1=0.70\)) to channel 1 (with \(p_1=1.0\)), and then tested over channel 1. Specifically, the system is presented with a sequence of 60 k input symbols: the first 15 k inputs are fed through channel 3, the next 15 k come out of channel 2, while the last 30 k are provided by channel 1. The reservoir is trained over the first 45 k inputs, while the channel is changing, and tested over the last 15 k inputs.

For simplicity, we simulate our implementation, which makes the reservoir states easily accessible. Figure 3(c) shows the simulation results. The SER gradually decreases during training. The average SER on the test sequence, when \(\lambda =0\), is \(1.41\times 10^{-3}\). For comparison, the same inputs were used for the offline training algorithm. We obtained a \(1.77\times 10^{-2}\) on the test set, that is, a performance ten times worse. Thus online training seems particularly adapted to the drifting channel, as it naturally takes into account the changing nature of the channel, whereas offline training is not able to cope with this feature.

5 Conclusion

We reported here the first physical reservoir computer with online training implemented on an FPGA chip. We demonstrated how online training could deal with a time-dependent channel. These results could not, or only with difficulty, be obtained with traditional online training methods. The results reported here thus significantly broaden the range of potential applications of experimental reservoir computers. In addition, interfacing physical reservoir computers with an FPGA chip should allow the investigation of many other questions, including the robust training of analog output layers, and using controlled feedback to enrich the dynamics of the system. The present work is thus the first step in what we hope should be a very fruitful line of investigation.