Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

15.1 Introduction

There is an extensive literature on the control, optimization and inverse design of partial differential equations. But, when dealing with nonlinear models, most often, the analysis requires to linearize the system under consideration. This is why most of the existing results do not apply to hyperbolic conservation laws since the shock discontinuities of solutions are an impediment to linearize the system under consideration in a classical manner.

This paper is devoted to analyze this issue for 1D scalar conservation laws. To complement previous related works by our group we consider the tracking problem in which the goal is to optimally choose the initial datum so that the solution is as close as possible to a prescribed trajectory. Our previous works are devoted to the problem of inverse design in which the goal is to determine the initial datum so that the solution achieves a given target at the final time (see, for instance, [9, 10] or the nonlinearity entering in the conservation law [8]).

To be more precise, given a finite time T > 0, a target function \(u^{d} \in L^{2}(\mathbb{R} \times (0,T))\), and a positive weight function \(\rho \in L^{\infty }(\mathbb{R} \times (0,T))\) with compact support in \(\mathbb{R} \times (0,T)\), we consider the functional cost to be minimized J, over a suitable class of initial data \(\mathcal{U}_{\mathit{ad}}\), defined by

$$\displaystyle{ J(u^{0}) = \frac{1} {2}\int _{0}^{T}\int _{ \mathbb{R}}\rho (x,t)\vert u(x,t) - u^{d}(x,t)\vert ^{2}\mathit{dx}\,\mathit{dt}, }$$
(15.1)

where \(u\,:\,\mathbb{R}_{x} \times \mathbb{R}_{t} \rightarrow \mathbb{R}\) is the unique entropy solution of the scalar conservation law

$$\displaystyle{ \partial _{t}u + \partial _{x}(f(u)) = 0,\;\text{in }\mathbb{R} \times (0,T);\;\;\;u(x,0) = u^{0}(x),\;x \in \mathbb{R}. }$$
(15.2)

Thus, the problem under consideration reads: To find \(u^{0,\mathit{min}} \in \mathcal{U}_{\mathit{ad}}\) such that

$$\displaystyle{ J(u^{0,\mathit{min}}) =\min _{ u^{0}\in \mathcal{U}_{\mathit{ab}}}J(u^{0}). }$$
(15.3)

Here the flux \(f: \mathbb{R} \rightarrow \mathbb{R}\) is assumed to be smooth: \(f \in C^{1}(\mathbb{R}, \mathbb{R})\). The initial datum u 0 will be assumed to belong to a suitable admissible class \(\mathcal{U}_{\mathit{ad}}\) to ensure the existence of a minimizer. As a preliminary fact we remind that for \(u^{0} \in L^{1}(\mathbb{R}) \cap L^{\infty }(\mathbb{R}) \cap BV (\mathbb{R})\), there exists an unique entropy solution in the sense of Kružkov (see [15]) in the class \(C^{0}([0,T];L^{1}(\mathbb{R})) \cap L^{\infty }(\mathbb{R} \times [0,T]) \cap L^{\infty }([0,T];BV (\mathbb{R}))\).

As we will see, the existence of minimizers can be established under some natural assumptions on the class of admissible data \(\mathcal{U}_{\mathit{ad}}\), using the well-posedness and compactness properties of solutions of the conservation law (15.2). The uniqueness of the minimizers is false, in general, due, in particular, to the possible presence of discontinuities in the solutions of (15.2).

One of our main goals in this paper is to compare how the discrete approach and the alternating descent methods perform in this new prototypical optimization problem. This alternating descent method was introduced and developed in the previous works by our group to deal with and exploit the sensitivity of shocks. In other words, the solutions of the conservation law are seen as a multi-physics object integrated by both the solution itself but also by the geometric location of the shock. Perturbing the initial datum of the conservation law produces perturbations on both components. Accordingly it is natural to analyze and employ both sensitivities to develop descent algorithms leading to an efficient computation of the minimizer. This is the basis of the alternating descent method [9].

As we shall see, in agreement with the results achieved in previously considered examples, the alternating descent method performs better than the classical discrete one which consists simply in applying a classical gradient descent algorithm to a discrete version of the functional and the conservation law.

This paper is limited to the one dimensional case but the alternating descent method can also be extended to the multi-dimensional frame, although this requires a much more careful geometric treatment of shocks since, for instance in 2 − d, these are curves evolving in time whose location has to be carefully determined and their motion and perturbation handled carefully to avoid numerical instabilities (see [16]).

There are other possible methods that could be employed to deal with these problems. In the present 1 − d setting, for instance, whenever the flux is convex, one could use the techniques developed in [1] based on the Lax-Oleinik representation formula of solutions. One could also employ the nudging method developed by J. Blum and coworkers [2, 3]. It would be interesting to compare in a systematic manner the results obtained in this article with those that could be achieved by these other methods.

The rest of this paper is organized as follows. In Sect. 15.2 we formulate the problem under consideration more precisely and prove the existence of minimizers.

In Sect. 15.3 we introduce the discrete approximation of the continuous optimal control problem. We prove the existence of minimizers for the discrete problem and their \(\Gamma \)-convergence towards the continuous ones as the mesh-size parameters tend to zero.

As we shall see, purely discrete approaches based on the minimization of the resulting discrete functionals by descent algorithms lead to very slow iterative processes. We thus need to introduce an alternated descent algorithm that takes into account the possible presence of shock discontinuities in solutions. For doing this the first step is to develop a careful sensitivity analysis. This is done in Sect. 15.4.

In Sect. 15.5 we present the alternating descent method which combines the advantages of both the discrete approach and the sensitivity analysis in the presence of shocks.

In Sect. 15.6 we explain how to implement both descent algorithms: The discrete approach consists mainly in applying a descent algorithm to the discrete version \(J_{\Delta }\) of the functional J, while the alternating descent method, by the contrary, is a continuous method based on the analysis of the previous section on the sensitivity of shocks.

In Sect. 15.7 we present some numerical experiments illustrating the overall efficiency of the alternating descent method. We conclude discussing some possible extensions of the results and methods presented in the paper.

15.2 Existence of Minimizers

In this section we prove that, under certain conditions on the set of admissible initial data \(\mathcal{U}_{\mathit{ad}}\), there exists at least one minimizer of the functional J, given in (15.1). To do this, we consider the class of admissible initial data \(\mathcal{U}_{\mathit{ad}}\) as:

$$\displaystyle{ \mathcal{U}_{\mathit{ad}} =\{ u^{0} \in L^{\infty }(\mathbb{R}) \cap \mathit{BV }(\mathbb{R}),\;\text{supp}(u^{0}) \subset K,\;\|u^{0}\|_{ L^{\infty }} + \mathit{TV }(u^{0}) \leq C\},\quad }$$
(15.4)

where \(K \subset \mathbb{R}\) is a given compact set and C > 0 a given constant. Note, however, that the same theoretical results and descent strategies we shall develop here can be applied to a much wider class of admissible sets.

Theorem 15.1.

Assume that \(u^{d} \in L^{2}(\mathbb{R} \times (0,T))\) , let \(\mathcal{U}_{\mathit{ad}}\) be defined in (15.4) and f be a C 1 function. Then the minimization problem,

$$\displaystyle{ \min _{u^{0}\in \mathcal{U}_{\mathit{ab}}}J(u^{0}), }$$
(15.5)

has at least one minimizer \(u^{0,\mathit{min}} \in \mathcal{U}_{\mathit{ad}}\). Moreover, uniqueness is false in general.

The proof follows the classical strategy of the Direct Method of the Calculus of Variations. We refer the reader to [9] for a similar proof in the case where the functional J is replaced by the one in which the distance to a given target at the final time t = T is minimized. Note that, in particular, for the class \(\mathcal{U}_{\mathit{ad}}\) of admissible initial data considered, solutions enjoy uniform BV bounds allowing to prove the needed compactness properties to pass to the limit. In the case of convex fluxes, using the well-known one-sided Lipschitz condition, the class of admissible initial data can be further extended.

We also observe that, as indicated in [9], the uniqueness of the minimizer is in general false for this type of optimization problems.

15.3 The Discrete Minimization Problem

The purpose of this section is to show that discrete minimizers obtained by a numerical approximation of (15.1) and (15.2), converge to a minimizer of the continuous problem as the mesh-size tends to zero. This justifies the usual engineering practice of replacing the continuous functional and model by discrete ones to compute an approximation of the continuous minimizer.

Let us introduce a mesh in \(\mathbb{R} \times [0,T]\) given by \((x_{i},t^{n}) = (i\Delta x,n\Delta t)\) (\(i = -\infty,\ldots,\infty;\;n = 0,\ldots,N + 1,\) so that \((N + 1)\Delta t = T\)), and let u i n be a numerical approximation of u(x i , t n) obtained as solution of a suitable discretization of Eq. (15.2).

Let us consider the following approximation of the functional J in (15.1):

$$\displaystyle{ J_{\Delta }(u_{\Delta }^{0}) = \frac{\Delta x\,\Delta t} {2} \sum \limits _{n=0}^{N}\sum \limits _{ i=-\infty }^{\infty }\rho _{ i}^{n}\left (u_{ i}^{n} - (u^{d})_{ i}^{n}\right )^{2}, }$$
(15.6)

where \(u_{\Delta }^{0} =\{ u_{i}^{0}\}\) is the discrete initial datum and \(u_{\Delta }^{d} =\{ (u^{d})_{i}^{n}\} = \Pi _{\Delta }u^{d}\) is the discretization of the target u d at (x i , t n), \(\Pi _{\Delta }\) being a discretization operator. A common choice consists in taking

$$\displaystyle{ \Pi _{\Delta }u^{d} = (u^{d})_{ i}^{n} = \frac{1} {\Delta x\Delta t}\int _{x_{i-1/2}}^{x_{i+1/2} }\int _{t^{n-1/2}}^{t^{n+1/2} }u^{d}(x,t)\,\mathit{dx}\,\mathit{dt}, }$$
(15.7)

where \(x_{i\pm 1/2} = x_{i} \pm \Delta x/2\) and \(t^{n\pm 1/2} = t^{n} \pm \Delta t/2\).

Moreover, we introduce an approximation of the class of admissible initial data \(\mathcal{U}_{\mathit{ad}}\) denoted by \(\mathcal{U}_{\mathit{ad},\Delta }\) and constituted by sequences \(\varphi _{\Delta } =\{\varphi _{i}\}_{i\in \mathbb{Z}}\) for which the associated piecewise constant interpolation function, that we still denote by \(\varphi _{\Delta }\), defined by

$$\displaystyle{\varphi _{\Delta }(x) =\varphi _{i},\;\;x \in (x_{i-1/2},x_{i+1/2}),}$$

satisfies \(\varphi _{\Delta } \in \mathcal{U}_{\mathit{ad}}\). Obviously, \(\mathcal{U}_{\mathit{ad},\Delta }\) coincides with the class of discrete vectors with support on those indices i such that x i  ∈ K and for which the discrete L ∞ and TV -norms are bounded above by the same constant C.

Let us consider \(S_{\Delta }: l^{1}(\mathbb{Z}) \rightarrow l^{1}(\mathbb{Z}),\) an explicit numerical scheme for (15.2), where

$$\displaystyle{ u_{\Delta }^{n} = S_{ \Delta }^{n}u_{ \Delta }^{0}, }$$
(15.8)

is the approximation of the entropy solution u(⋅ , t) = S(t)u 0 of (15.2), i.e. \(u_{\Delta }^{n} \simeq S(t)u^{0}\), with \(t = n\Delta t\). Here \(S: L^{1}(\mathbb{R}) \cap L^{\infty }(\mathbb{R}) \cap \mathit{BV }(\mathbb{R}) \rightarrow L^{1}(\mathbb{R}) \cap L^{\infty }(\mathbb{R}) \cap \mathit{BV }(\mathbb{R})\), is the semigroup (solution operator)

$$\displaystyle{S: u_{0} \rightarrow u = Su_{0},}$$

which associates to the initial condition \(u_{0} \in L^{1}(\mathbb{R}) \cap L^{\infty }(\mathbb{R}) \cap \mathit{BV }(\mathbb{R})\) the entropy solution u of (15.2).

For each \(\Delta = \Delta t\) (with \(\lambda = \Delta t/\Delta x\) fixed, typically given by the corresponding CFL-condition for explicit schemes), it is easy to see that the discrete analogue of Theorem 15.1 holds. In fact this is automatic in the present setting since \(\mathcal{U}_{\mathit{ad},\Delta }\) only involves a finite number of mesh-points. But passing to the limit as \(\Delta \rightarrow 0\) requires a more careful treatment. In fact, for that to be done, one needs to assume that the scheme under consideration, (15.8), is a contracting map in \(l^{1}(\mathbb{Z})\).

Thus, we consider the following discrete minimization problem: Find \(u_{\Delta }^{0,\mathit{min}}\) such that

$$\displaystyle{ J_{\Delta }(u_{\Delta }^{0,\mathit{min}}) =\min _{ u_{\Delta }^{0}\in \mathcal{U}_{\mathit{ad},\Delta }}J_{\Delta }(u_{\Delta }^{0}). }$$
(15.9)

The following holds

Theorem 15.2.

Assume that \(u_{\Delta }^{n}\) is obtained by a numerical scheme (15.8), which satisfies the following:

  • For a given \(u^{0} \in \mathcal{U}_{\mathit{ad}}\), \(u_{\Delta }^{n} = S_{\Delta }^{n}\Pi _{\Delta }u^{0}\) converges to u(x,t), the entropy solution of (15.2) . More precisely, if \(n\Delta t = t\) and T 0 > 0 is any given number,

    $$\displaystyle{ \max _{0\leq t\leq T_{0}}\|u_{\Delta }^{n} - u(\cdot,t)\|_{ L^{1}(\mathbb{R})} \rightarrow 0,\;\;\;\text{ as }\;\;\Delta \rightarrow 0. }$$
    (15.10)

  • The map \(S_{\Delta }\) is L ∞ -stable, i.e.

    $$\displaystyle{ \|S_{\Delta }u_{\Delta }^{0}\|_{ L^{\infty }} \leq \| u_{\Delta }^{0}\|_{ L^{\infty }}. }$$
    (15.11)

  • The map \(S_{\Delta }\) is a contracting map in \(l^{1}(\mathbb{Z})\) i.e.

    $$\displaystyle{ \|S_{\Delta }u_{\Delta }^{0} - S_{ \Delta }v_{\Delta }^{0}\|_{ L^{1}} \leq \| u_{\Delta }^{0} - v_{ \Delta }^{0}\|_{ L^{1}}. }$$
    (15.12)

Then:

  • For all \(\Delta \) , the discrete minimization problem (15.9) has at least one solution \(u_{\Delta }^{0,\mathit{min}} \in \mathcal{U}_{\mathit{ad},\Delta }\) .

  • Any accumulation point of \(u_{\Delta }^{0,\mathit{min}}\) with respect to the weak-∗ topology in L ∞ , as \(\Delta \rightarrow 0\) , is a minimizer of the continuous problem (15.5) .

The proof of this result can be developed as in [9]. We also refer to [16] for an extension to the multi-dimensional case.

This convergence result applies for 3-point conservative numerical approximation schemes, where \(S_{\Delta }\) is given by

$$\displaystyle{ \left (S_{\Delta }v_{\Delta }\right )_{i} = v_{i} - \frac{\Delta t} {\Delta x}\left (g(v_{i+1},v_{i}) - g(v_{i},v_{i-1})\right ), }$$
(15.13)

and g is the numerical flux. This scheme is consistent with the corresponding Eq. (15.2) when g(u, u) = f(u).

When the discrete semigroup \(S_{\Delta }(u,v,w) = v -\lambda (g(u,v) - g(v,w))\), with \(\lambda = \Delta t/\Delta x\) is monotonic increasing with respect to each argument, the scheme is also monotone. This ensures the convergence to the weak entropy solutions of the continuous conservation law, as the discretization parameters tend to zero, under a suitable CFL condition (see Ref. [12], Chap. 3, Th. 4.2).

All this analysis and results apply to the classical Godunov, Lax-Friedfrichs and Engquist-Osher schemes, the corresponding numerical flux being:

$$\displaystyle{ g^{G}(u,v) = \left \{\begin{array}{cc} \min _{w\in [u,v]}f(w),&\text{if }u \leq v, \\ \max _{w\in [u,v]}f(w),&\text{if }u \geq v, \end{array} \right. }$$
(15.14)
$$\displaystyle{ g^{\mathit{LF}}(u,v) = \frac{(f(u) + f(v))} {2} -\frac{(v - u)} {2\lambda ^{x}}, }$$
(15.15)
$$\displaystyle{ g^{\mathit{EO}}(u,v) = \frac{f(u) + f(v) -\int _{u}^{v}\vert f^{{\prime}}(\tau )\vert d\tau } {2}. }$$
(15.16)

See Chapter 3 in [12] for more details.

These 1D methods satisfy the conditions of Theorem 15.2.

15.4 Sensitivity Analysis: The Continuous Approach

We divide this section in three subsections. Specifically, in the first one we consider the case where the solution u of (15.2) has no shocks. In the second and third subsections we analyze the sensitivity of the solution and the functional in the presence of a single shock.

15.4.1 Sensitivity Without Shocks

In this subsection we give an expression for the sensitivity of the functional J with respect to the initial datum based on a classical adjoint calculus for smooth solutions. First we present a formal calculus and then we show how to justify it when dealing with a classical smooth solution for (15.2).

Let \(C_{0}^{1}(\mathbb{R})\) be the set of C 1 functions with compact support and let \(u^{0} \in C_{0}^{1}(\mathbb{R})\) be a given initial datum for which there exists a classical solution u(x, t) of (15.2) that can be extended to a classical solution in t ∈ [0, T +τ] for some τ > 0. Note that this imposes some restrictions on u 0 other than being smooth.

Let \(\delta u^{0} \in C_{0}^{1}(\mathbb{R})\) be any possible variation of the initial datum u 0. Due to the finite speed of propagation, this perturbation will only affect the solution in a bounded set of \(\mathbb{R} \times [0,T]\). This simplifies the argument below that applies in a much more general setting provided solutions are smooth enough.

Then, for \(\varepsilon > 0\) sufficiently small, the solution \(u^{\varepsilon }(x,t)\) corresponding to the initial datum

$$\displaystyle{ u^{\varepsilon,0}(x) = u^{0}(x) +\varepsilon \delta u^{0}(x), }$$
(15.17)

is also a classical solution in \((x,t) \in \mathbb{R} \times (0,T)\) and \(u^{\varepsilon } \in C^{1}(\mathbb{R} \times [0,T])\) can be written as

$$\displaystyle{ u^{\varepsilon } = u +\varepsilon \delta u + o(\varepsilon ),\mbox{ with respect to the $C^{1}$ topology,} }$$
(15.18)

where δ u is the solution of the linearized equation,

$$\displaystyle{ \partial _{t}\delta u + \partial _{x}(f^{{\prime}}(u)\delta u) = 0,\;\text{in }\mathbb{R} \times (0,T);\;\;\;\delta u(x,0) =\delta u^{0}(x),\;x \in \mathbb{R}. }$$
(15.19)

Let δ J be the Gateaux derivative of J at u 0 in the direction δ u 0. We have,

$$\displaystyle{ \delta J(u^{0})[\delta u^{0}] =\int _{ 0}^{T}\int _{ \mathbb{R}}\rho (x,t)(u(x,t) - u^{d}(x,t))\delta u(x,t)\,\mathit{dx}\,\mathit{dt} }$$
(15.20)

where δ u solves the linearized system above (15.19). Now, we introduce the adjoint system,

$$\displaystyle{ -\partial _{t}p - f^{{\prime}}(u)\partial _{ x}p =\rho \, (u - u^{d}),\;\text{in }\mathbb{R} \times (0,T);\;\;\;p(x,T) = 0,\;x \in \mathbb{R}.\quad }$$
(15.21)

Multiplying the equations satisfied by δ u by p, integrating by parts, and taking into account that p satisfies (15.21), we easily obtain

$$\displaystyle{ \int _{0}^{T}\int _{ \mathbb{R}}\rho (x,t)(u(x,t) - u^{d}(x,t))\delta u(x,t)\,\mathit{dx}\,\mathit{dt} =\int _{ \mathbb{R}}p(x,0)\delta u^{0}(x)\,\mathit{dx}. }$$
(15.22)

Thus, δ J in (15.20) can be written as,

$$\displaystyle{ \delta J(u^{0})[\delta u^{0}] =\int _{ \mathbb{R}}p(x,0)\delta u^{0}(x)\mathit{dx}. }$$
(15.23)

This expression provides an easy way to compute a descent direction for the continuous functional J, once we have computed the adjoint state. We just take:

$$\displaystyle{ \delta u^{0}(x) = -p(x,0). }$$
(15.24)

Under the assumptions above on u 0, u, δ u and p can be obtained from their data u 0(x), δ u 0(x) and ρ (u − u d) by using the characteristic curves associated to (15.2). For the sake of completeness we briefly explain this below.

The characteristic curves associated to (15.2) are defined by

$$\displaystyle{ x^{{\prime}}(t) = f^{{\prime}}(u(x(t),t)),\;\;\;t \in (0,T),\;\;\;x(0) = x^{0}. }$$
(15.25)

They are straight lines whose slopes depend on the initial data:

$$\displaystyle{x(t) = x^{0} + tf^{{\prime}}(u^{0}(x^{0})),\;\;\;t \in (0,T).}$$

As we are dealing with classical solutions, u is constant along such curves and, by assumption, two different characteristic curves do not meet each other in \(\mathbb{R} \times [0,T+\tau ]\). This allows to define u in \(\mathbb{R}\,\times \,[0,T+\tau ]\) in a unique way from the initial data.

For \(\varepsilon > 0\) sufficiently small, the solution \(u^{\varepsilon }(x,t)\) corresponding to the initial datum (15.17) has similar characteristics to those of u. This allows guaranteeing that two different characteristic lines do not intersect for 0 ≤ t ≤ T if \(\varepsilon > 0\) is small enough. Note that \(u^{\varepsilon }\) may possibly be discontinuous for t ∈ (T, T +τ] if u 0 generates a discontinuity at \(t = T+\tau\) but this is irrelevant for the analysis in [0, T] we are carrying out. Therefore \(u^{\varepsilon }(x,t)\) is also a classical solution in \((x,t) \in \mathbb{R} \times [0,T]\) and it is easy to see that the solution \(u^{\varepsilon }\) can be written as (15.18) where δ u satisfies (15.19).

System (15.19) can be solved again by the method of characteristics. In fact, as u is a regular function, the first equation in (15.19) can be written as

$$\displaystyle{ \partial _{t}\delta u + f^{{\prime}}(u)\partial _{ x}\delta u = -\partial _{x}(f^{{\prime}}(u))\,\delta u, }$$
(15.26)

i.e.

$$\displaystyle{ \frac{d} {\mathit{dt}}\delta u(x(t),t) = -\partial _{x}(f^{{\prime}}(u))\,\delta u, }$$
(15.27)

where x(t) are the characteristic curves defined by (15.25). Thus, the solution δ u along a characteristic line can be obtained from δ u 0 by solving this differential equation, i.e.

$$\displaystyle{\delta u(x(t),t) =\delta u^{0}(x^{0})\,\text{exp}\left (-\int _{ 0}^{t}\partial _{ x}(f^{{\prime}}(u))(x(s),s)\mathit{ds}\right ).}$$

Finally, the adjoint system (15.21) is also solved by characteristics, i.e.

$$\displaystyle{-\frac{d} {\mathit{dt}}p(x(t),t) =\rho (x(t),t)(u(x(t),t) - u^{d}(x(t),t)).}$$

This yields the steepest descent direction in (15.24) for the continuous functional:

$$\displaystyle{p(x^{0},0) = u^{0}(x^{0})\int _{ 0}^{T}\rho (x(s),s)\mathit{ds} -\int _{ 0}^{T}\rho (x(s),s)u^{d}(x(s),s)\mathit{ds}.}$$

Remark 15.1.

Note that for classical solutions the Gateaux derivative of J at u 0 is given by (15.23) and this provides an obvious descent direction for J at u 0, given by (15.24). However this fact is not very useful in practice since, even when we initialize the iterative descent algorithm with a smooth u 0, we cannot guarantee that the solution remains classical along the iterative process.

15.4.2 Sensitivity of the State in the Presence of Shocks

Inspired in several results on the sensitivity of solutions of conservation laws in the presence of shocks in one-dimension (see [4–7, 13, 17]), we focus on the particular case of solutions having a single shock. But the analysis can be extended to consider more general one-dimensional systems of conservation laws with a finite number of noninteracting shocks. We introduce the following hypothesis:

Hypothesis 15.1.

Assume that u(x,t) is a weak entropy solution of (15.2) with a discontinuity along a regular curve \(\Sigma =\{ (\varphi (t),t),\;t \in (0,T)\}\) , which is Lipschitz continuous outside \(\Sigma \). In particular, it satisfies the Rankine-Hugoniot condition on \(\Sigma \)

$$\displaystyle{\varphi ^{{\prime}}(t)[u]_{ \Sigma ^{t}} = [f(u)]_{\Sigma ^{t}}.}$$

Here we have used the notation: \([v]_{\Sigma ^{t}} =\lim \limits _{\varepsilon \searrow 0}v(\varphi (t)+\varepsilon,t) - v(\varphi (t)-\varepsilon,t)\) , for the jump at \(\Sigma ^{t} = (\varphi (t),t)\) of any piecewise continuous function v with a discontinuity at \(\Sigma ^{t}\) .

Note that \(\Sigma \) divides \(\mathbb{R} \times (0,T)\) into two parts: Q − and Q +, the sub-domains of \(\mathbb{R} \times (0,T)\) to the left and to the right of \(\Sigma \) respectively.

As we will see, in the presence of shocks, to deal correctly with optimal control and design problems, the state of the system needs to be viewed as constituted by the pair \((u,\varphi )\) combining the solution of (15.2) and the shock location \(\varphi\). This is relevant in the analysis of sensitivity of functions below and when applying descent algorithms.

We adopt the functional framework based on the generalized tangent vectors (see [7] and Definition 4.1 in [9]).

Let u 0 be the initial datum, that we assume to be Lipschitz continuous to both sides of a single discontinuity located at \(x =\varphi ^{0}\), and consider a generalized tangent vector \((\delta u^{0},\delta \varphi ^{0}) \in L^{1}(\mathbb{R}) \times \mathbb{R}\) for all 0 ≤ T. Let \(u^{0,\varepsilon }\) be a path which generates \((\delta u^{0},\delta \varphi ^{0})\). For \(\varepsilon\) sufficiently small, the solution \(u^{\varepsilon }(\cdot,t)\) of (15.2) is Lipschitz continuous with a single discontinuity at \(x =\varphi ^{\varepsilon }(t)\), for all t ∈ [0, T]. Therefore, \(u^{\varepsilon }(\cdot,t)\) generates a generalized tangent vector \((\delta u(\cdot,t),\delta \varphi (t)) \in L^{1}(\mathbb{R}) \times \mathbb{R}\). Moreover, in [9] it is proved that it satisfies the following linearized system:

$$\displaystyle{ \partial _{t}\delta u + \partial _{x}(f^{{\prime}}(u)\delta u) = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{in }Q_{ -}\cup Q_{+} }$$
(15.28)
$$\displaystyle{ \frac{d} {\mathit{dt}}\left ([u]_{\Sigma ^{t}}\delta \varphi \right ) = [f^{{\prime}}(u)\delta u]_{ \Sigma ^{t}} - [\delta u]_{\Sigma ^{t}} \frac{d} {\mathit{dt}}\varphi,\;\;t \in (0,T) }$$
(15.29)
$$\displaystyle{ \delta u(x,0) =\delta u^{0}(x),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\{x <\varphi ^{0}\} \cup \{ x >\varphi ^{0}\}\qquad \quad \;\; }$$
(15.30)
$$\displaystyle{ \delta \varphi (0) =\delta \varphi ^{0}. }$$
(15.31)

15.4.3 Sensitivity of the Cost in the Presence of Shocks

In this section we study the sensitivity of the functional J with respect to variations associated with the generalized tangent vectors defined in the previous section. We first define an appropriate generalization of the Gateaux derivative of J.

Definition 15.1.

Let \(J: L^{1}(\mathbb{R}) \rightarrow \mathbb{R}\) be a functional and \(u^{0} \in L^{1}(\mathbb{R})\) be Lipschitz continuous with a discontinuity in \(\Sigma ^{0}\), an initial datum for which the solution of (15.2) satisfies hypothesis (15.1). J is Gateaux differentiable at u 0 in a generalized sense if for any generalized tangent vector \((\delta u^{0},\delta \varphi ^{0})\) and any family \(u^{0,\varepsilon }\) associated to \((\delta u^{0},\delta \varphi ^{0})\) the following limit exists,

$$\displaystyle{\delta J =\lim _{\varepsilon \rightarrow 0}\frac{J(u^{0,\varepsilon }) - J(u^{0})} {\varepsilon },}$$

and it depends only on \((u^{0},\varphi ^{0})\) and \((\delta u^{0},\delta \varphi ^{0})\), i.e. it does not depend on the particular family \(u^{0,\varepsilon }\) which generates \((\delta u^{0},\delta \varphi ^{0})\). The limit is the generalized Gateux derivative of J in the direction \((\delta u^{0},\delta \varphi ^{0})\).

The following result easily provides a characterization of the generalized Gateaux derivative of J in terms of the solution of the associated adjoint system (15.33)–(15.38).

Proposition 15.1.

The Gateaux derivative of J can be written as follows

$$\displaystyle{ \delta J(u^{0})[\delta u^{0},\delta \varphi ^{0}] =\int _{ \mathbb{R}}p(x,0)\delta u^{0}(x)dx - q(0)[u]_{ \Sigma ^{0}}\delta \varphi ^{0}, }$$
(15.32)

where the adjoint state pair (p,q) satisfies the system

$$\displaystyle{ -\partial _{t}p - f^{{\prime}}(u)\partial _{ x}p =\rho \, (u - u^{d}),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{in }Q_{ -}\cup Q_{+} }$$
(15.33)
$$\displaystyle{ \,[p]_{\varSigma ^{t}} = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \in (0,T) }$$
(15.34)
$$\displaystyle{ q(t) = p(\varphi (t),t),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \in (0,T) }$$
(15.35)
$$\displaystyle{ -\frac{d} {dt}q = \frac{(1 + (\dot{\varphi })^{2})^{1/2}[\rho \,(u - u^{d})^{2}]_{\Sigma ^{t}}} {2[u]_{\Sigma ^{t}}},\;\;\;\;\;\;\;\;\;t \in (0,T)\qquad \qquad \qquad \qquad }$$
(15.36)
$$\displaystyle{ p(x,T) = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\{x <\varphi (T)\} \cup \{ x >\varphi (T)\} }$$
(15.37)
$$\displaystyle{ q(T) = 0. }$$
(15.38)

Let us briefly comment the result of Proposition 15.1 before giving its proof.

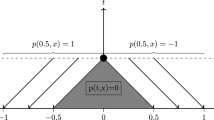
System (15.33)–(15.38) has a unique solution. In fact, to solve the backward system (15.33)–(15.38) we first define the solution q on the shock \(\Sigma \) from the conditions for q (15.36) and (15.38). This determines the value of p along the shock. We then propagate this information, together with (15.33) and (15.37), to both sides of \(\Sigma \), by characteristics (see Fig. 15.1 where we illustrate this construction).

Fig. 15.1
figure 1

Characteristic lines entering on a shock and how they may be used to build the solution of the adjoint system both away from the shock and on its region of influence

Full size image

Formula (15.32) provides an obvious way to compute a first descent direction of J at u 0. We just take

$$\displaystyle{ (\delta u^{0},\delta \varphi ^{0}) = (-p(\cdot,0),q(0)[u]_{ \Sigma ^{0}}). }$$
(15.39)

Here, the value of \(\delta \varphi ^{0}\) must be interpreted as the optimal infinitesimal displacement of the discontinuity of u 0.

In [9], when considering the inverse design problem, it was observed that the solution p of the corresponding adjoint system at t = 0 was discontinuous, with two discontinuities, one in each side of the original location of the discontinuity at \(\Sigma ^{0}\). This was a reason not to use this descent direction and for introducing the alternating descent method. In the present setting, however, the adjoint state p obtained is typically continuous. This is due to the fact that p at both side of the discontinuity is defined by the method of characteristics and that, on the region of influence of the characteristics emanating from the shock, the continuity is preserved by the fact that, on one hand, q = q(t) itself is continuous as the primitive of an integrable function and that the data for p and q at t = T are continuous too. Despite of this, as we shall see, the implementation of the alternating descent direction method is worth since it significantly improves the results obtained by the purely discrete approach.

We finish this section with the proof of Proposition 15.1.

Proof (of Proposition 15.1).

A straightforward computation shows that J is Gateaux differentiable in the generalized sense of Definition 15.1 and that the generalized Gateaux derivative of J in the direction of the generalized tangent vector \((\delta u^{0},\delta \varphi ^{0})\) is given by

$$\displaystyle\begin{array}{rcl} \delta J(u^{0})[\delta u^{0},\delta \varphi ^{0}]& =& \int _{ 0}^{T}\int \limits _{ \{x>\varphi (t)\}\cup \{x<\varphi (t)\}}\rho (x,t)(u(x,t) - u^{d}(x,t))\delta u(x,t)\,\mathit{dx}\,\mathit{dt} \\ & & \qquad \qquad \qquad \qquad -\int _{\Sigma }\left [\rho \frac{(u - u^{d})^{2}} {2} \right ]_{\Sigma ^{t}}\!\!\!\!\!\!\!\!\,\,\delta \varphi (t)\,d\Sigma (t), {}\end{array}$$
(15.40)

where the pair \((\delta u,\delta \varphi )\) solves the linearized problem (15.28)–(15.30) with initial data \((\delta u^{0},\delta \varphi ^{0})\).

Let us now introduce the adjoint system (15.33)–(15.38). Multiplying the equations of δ u by p, and integrating we get

$$\displaystyle\begin{array}{rcl} 0& =& \int _{0}^{T}\!\!\!\!\!\!\!\int \limits _{ \{x>\varphi (t)\}\cup \{x<\varphi (t)\}}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\left (\partial _{t}\delta u + \partial _{x}(f^{{\prime}}(u)\delta u)\right )p\,\mathit{dx}\,\mathit{dt} \\ & =& -\int _{0}^{T}\!\!\!\!\!\!\!\int \limits _{ \{x>\varphi (t)\}\cup \{x<\varphi (t)\}}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\delta u\left (\partial _{t}p + f^{{\prime}}(u)\partial _{ x}p\right )\,\mathit{dx}\,\mathit{dt} \\ & & \ +\int \limits _{\{x>\varphi (T)\}\cup \{x<\varphi (T)\}}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\delta u(x,T)p(x,T)\mathit{dx} -\int \limits _{\{x>\varphi ^{0}\}\cup \{x<\varphi ^{0}\}}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\delta u^{0}(x)p(x,0)\mathit{dx} \\ & & \ -\int _{\Sigma }\left ([\delta u\,p]_{\Sigma ^{t}}n_{\Sigma }^{t} + [f^{{\prime}}(u)\delta u\,p]_{ \Sigma ^{t}} \cdot n_{\Sigma }^{x}\right )d\Sigma (t), {}\end{array}$$
(15.41)

where (n x, n t) are the Cartesian components of the normal vector to the curve \(\Sigma \).

Therefore, since p satisfies the adjoint equation (15.33), (15.37), from (15.40) we obtain

$$\displaystyle\begin{array}{rcl} & & \ \ \delta J(u^{0})[\delta u^{0},\delta \varphi ^{0}] =\int \limits _{\{ x>\varphi ^{0}\}\cup \{x<\varphi ^{0}\}}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\delta u^{0}(x)p(x,0)\mathit{dx} \\ & & +\int _{\Sigma }\left ([\delta u\,p]_{\Sigma ^{t}}n_{\Sigma }^{t} + [f^{{\prime}}(u)\delta u\,p]_{ \Sigma ^{t}} \cdot n_{\Sigma }^{x}\right )d\Sigma (t) -\int _{ \Sigma }\left [\rho \frac{(u - u^{d})^{2}} {2} \right ]_{\Sigma ^{t}}\!\!\!\!\!\!\!\!\,\delta \varphi (t)\,d\Sigma (t).{}\end{array}$$
(15.42)

The last two terms in the right hand side of (15.42) will determine the conditions that p must satisfy on the shock.

Observe that for any functions f, g we have

$$\displaystyle{[fg]_{\Sigma ^{t}} = \overline{f}[g]_{\Sigma ^{t}} + \overline{g}[f]_{\Sigma ^{t}},}$$

where \(\overline{g}\) represents the average of g to both sides of the shock \(\Sigma ^{t}\), i.e.

$$\displaystyle{\overline{g}(t) = \frac{1} {2}\lim _{\varepsilon \searrow 0}\left (g(\varphi (t)+\varepsilon,t) + g(\varphi (t)-\varepsilon,t)\right ),\;\;\;\forall t \in (0,T).}$$

Thus we have

$$\displaystyle\begin{array}{rcl} \int _{\Sigma }\left ([\delta u\,p]_{\Sigma ^{t}}n_{\Sigma }^{t} + [f^{{\prime}}(u)\delta u\,p]_{ \Sigma ^{t}} \cdot n_{\Sigma }^{x}\right )d\Sigma & =& \int _{ \Sigma }[p]_{\Sigma ^{t}}\left (\overline{\delta u}n_{\Sigma }^{t} + \overline{f^{{\prime}}(u)\delta u} \cdot n_{ \Sigma }^{x}\right )d\Sigma \\ & & +\int _{\Sigma }\overline{p}\left ([\delta u]_{\Sigma ^{t}}n_{\Sigma }^{t} + [f^{{\prime}}(u)\delta u]_{ \Sigma ^{t}} \cdot n_{\Sigma }^{x}\right )d\Sigma.{}\end{array}$$
(15.43)

Now, we note that the Cartesian components of the normal vector to \(\Sigma \) are given by

$$\displaystyle{n^{t} = \frac{-\varphi ^{{\prime}}(t)} {\sqrt{1 + (\varphi ^{{\prime} } (t))^{2}}},\;\;\;n^{x} = \frac{1} {\sqrt{1 + (\varphi ^{{\prime} } (t))^{2}}},}$$

and \(d\Sigma (t) = \sqrt{1 + (\varphi ^{{\prime} } (t))^{2}}\mathit{dt}.\) Using (15.28), (15.34), we have

$$\displaystyle\begin{array}{rcl} \int _{\Sigma }\left ([\delta u\,p]_{\Sigma ^{t}}n_{\Sigma }^{t} + [f^{{\prime}}(u)\delta u\,p]_{ \Sigma ^{t}}n_{\Sigma }^{x}\right )d\Sigma & =& \int _{ 0}^{T}\overline{p}\,\left (-[\delta u]_{ \Sigma ^{t}}\varphi ^{{\prime}}(t) + [f^{{\prime}}(u)\delta u]_{ \Sigma ^{t}}\right )\mathit{dt} \\ & =& \int _{0}^{T}\overline{p}\, \frac{d} {\mathit{dt}}\left ([u]_{\Sigma ^{t}}\delta \varphi \right )\mathit{dt}. {}\end{array}$$
(15.44)

Therefore, replacing (15.35), (15.36), (15.38) and (15.44) in (15.42), we obtain (15.32).

This concludes the proof. □ 

15.5 The Alternating Descent Method

Here we explain how the alternating descent method introduced in [9] can be adapted to the present optimal control problem (15.3).

First let us introduce some notation. We consider two points

$$\displaystyle{ X^{-} =\varphi (T) - Tf^{{\prime}}(u^{-}(\varphi (T),T)),\;\;\;X^{+} =\varphi (T) - Tf^{{\prime}}(u^{+}(x,T)), }$$
(15.45)

(p, q) the solutions of (15.33)–(15.38) and

$$\displaystyle{p^{0,-} =\lim \limits _{ x\nearrow X^{-}}p(x,0),\;\;\;\;p^{0,+} =\lim \limits _{ x\searrow X^{+}}p(x,0).}$$

Now, we introduce the two classes of descent directions we shall use in our descent algorithm.

First directions: :

With this set of directions, we mainly modify the profile of u 0. We set the first directions \(d_{1} = (\delta u^{0},\delta \varphi ^{0})\), given by:

$$\displaystyle{ \begin{array}{l} \delta u^{0} = \left \{\begin{array}{ll} - p(x,0),&x < X^{-}, \\ - p^{0,-}, &x \in (X^{-},\varphi ^{0}), \\ - p^{0,+}, &x \in (\varphi ^{0},X^{+}), \\ - p(x,0),&x > X^{+}.\end{array} \right. \\ \\ \delta \varphi ^{0} = \left \{\begin{array}{ll} 0, &\text{if}\int \limits _{X^{-}}^{X^{+} }p(x,0)\delta u^{0}(x)\mathit{dx} \leq 0, \\ \frac{\int \limits _{X^{-}}^{X^{+} }p(x,0)\delta u^{0}(x)\mathit{dx}} {[u^{0}]_{\Sigma ^{0}}q(0)},&\text{if }\int \limits _{X^{-}}^{X^{+} }p(x,0)\delta u^{0}(x)\mathit{dx} > 0,\text{ and }q(0)\neq 0. \end{array} \right. \end{array} }$$
(15.46)

We note that, if q(0) = 0 and \(\int \limits _{X^{-}}^{X^{+} }p(x,0)\delta u^{0}(x)\mathit{dx} > 0,\) these directions are not defined.

Second directions: :

They are aimed to move the shock without changing the profile of the solution to both sides. Then \(d_{2} = (\delta u^{0},\delta \varphi ^{0})\), with:

$$\displaystyle{ \delta u^{0} \equiv 0,\;\;\;\;\delta \varphi ^{0}(x) = [u^{0}]_{ \Sigma ^{0}}q(0). }$$
(15.47)

We observe that d 1 given by (15.46) satisfies

$$\displaystyle\begin{array}{rcl} \delta J(u^{0})[d_{ 1}]& =& -\int _{x\notin [X^{-},X^{+}]}\vert p(x,0)\vert ^{2}\mathit{dx} \\ & & -p^{0,-}\int _{ X^{-}}^{\varphi ^{0} }p(x,0)\mathit{dx} - p^{0,+}\int _{ \varphi ^{0}}^{X^{+} }p(x,0)\mathit{dx} - [u^{0}]_{ \Sigma ^{0}}q(0)\delta \varphi ^{0} \leq 0.{}\end{array}$$
(15.48)

Note that in those cases where d 1 is not defined, as indicated above, this descent direction is simply not employed in the descent algorithm.

And for d 2 given by (15.47) we have

$$\displaystyle{ \delta J(u^{0})[d_{ 2}] = -([u^{0}]_{ \Sigma ^{0}}q(0))^{2} \leq 0. }$$
(15.49)

Thus, the two classes of descent directions under consideration have three important properties:

  1. 1.

    They are both descent directions.

  2. 2.

    They allow to split the design of the profile and the shock location.

  3. 3.

    They are true generalized gradients and therefore keep the structure of the data without increasing its complexity.

15.6 Numerical Approximation of the Descent Direction

We have computed the gradient of the continuous functional J in several cases (u smooth or having shock discontinuities) but, in practice, one has to work with discrete versions of the functional J. In this section we discuss two possible ways of searching discrete descent directions based either on the discrete or the continuous approaches and in the later on the alternating descent method.

The discrete approach consists mainly in applying directly a descent algorithm to the discrete version \(J_{\Delta }\) of the functional J by using its gradient. The alternating descent method, by the contrary, is a method inspired on the continuous analysis of the previous section in which the two main classes of descent directions that are, first, identified and later discretized.

Let us first discuss the discrete approach.

15.6.1 The Discrete Approach

Let us consider the approximation of the functional J by \(J_{\Delta }\) defined (15.1) and (15.6) respectively. We shall use the Engquist-Osher scheme which is a 3-point conservative numerical approximation scheme for (15.2). More explicitly we consider:

$$\displaystyle{ u_{i}^{n+1} = u_{ i}^{n} - \frac{\Delta t} {\Delta x}\left (g(u_{i+1}^{n},u_{ i}^{n}) - g(u_{ i}^{n},u_{ i-1}^{n})\right ),\;\;i \in \mathbb{Z},\;n = 0,\ldots,N, }$$
(15.50)

where g is the numerical flux defined in (15.16).

The gradient of the discrete functional \(J_{\Delta }\) requires computing one derivative of \(J_{\Delta }\) with respect to each node of the mesh. This can be done in a cheaper way using the discrete adjoint state. We illustrate it for the Engquist-Osher numerical scheme. However, as the discrete functionals \(J_{\Delta }\) are not necessarily convex the gradient methods could possibly provide sequences that do not converge to a global minimizer of \(J_{\Delta }\). But this drawback and difficulty appears in most applications of descent methods in optimal design and control problems.

As we will see, in the present context, the approximations obtained by discrete gradient methods are satisfactory, although convergence is slow due to unnecessary oscillations that the descent method introduces.

The gradient of \(J_{\Delta }\), rigorously speaking, requires the linearization of the numerical scheme (15.50) used to approximate Eq. (15.2). Then the linearization corresponds to

$$\displaystyle\begin{array}{rcl} \delta u_{i}^{n+1}& =& \delta u_{ i}^{n} - \frac{\Delta t} {\Delta x}\left (\partial _{a}g(u_{i+1}^{n},u_{ i}^{n})\delta u_{ i+1}^{n} - \partial _{ b}g(u_{i}^{n},u_{ i-1}^{n})\delta u_{ i-1}^{n}\right ) \\ & & -\frac{\Delta t} {\Delta x}\left (\partial _{b}g(u_{i+1}^{n},u_{ i}^{n}) - \partial _{ a}g(u_{i}^{n},u_{ i-1}^{n})\right )\delta u_{ i}^{n}, \\ & & i \in \mathbb{Z},\;\;n = 0,\ldots,N. {}\end{array}$$
(15.51)

In view of this, the discrete adjoint system of (15.51) can also be written for the differentiable flux functions:

$$\displaystyle\begin{array}{rcl} p_{i}^{N+1}& =& 0,\;\;i \in \mathbb{Z}, \\ p_{i}^{n}& =& p_{ i}^{n+1} + \frac{\Delta t} {\Delta x}\partial _{b}g(u_{i+1}^{n},u_{ i}^{n})\left (p_{ i+1}^{n+1} - p_{ i}^{n+1}\right ) \\ & & + \frac{\Delta t} {\Delta x}\partial _{a}g(u_{i}^{n},u_{ i-1}^{n})\left (p_{ i}^{n+1} - p_{ i-1}^{n+1}\right ) + F_{ i}^{n}, \\ & & i \in \mathbb{Z},\;\;n = 0,\ldots,N, {}\end{array}$$
(15.52)

where

$$\displaystyle{ F_{i}^{n} = \Delta t\rho _{ i}^{n}\left (u_{ i}^{n} - (u^{d})_{ i}^{n}\right ),\;\;i \in \mathbb{Z},\;\;n = 0,\ldots,N. }$$
(15.53)

In fact, when multiplying the equations in (15.51) by p i n+1 and adding in \(i \in \mathbb{Z}\) and n = 0, …, N, the following identity is easily obtained,

$$\displaystyle{ \Delta x\sum _{i\in \mathbb{Z}}p_{i}^{0}\delta u_{ i}^{0} = \Delta x\sum _{ n=0}^{N}\sum _{ i\in \mathbb{Z}}F_{i}^{n}\delta u_{ i}^{n}. }$$
(15.54)

This is the discrete version of formula (15.22) which allows us to simplify the derivative of the discrete cost functional.

Thus, for any variation \(\delta u_{\Delta }^{0},\) the Gateaux derivative of the cost functional defined in (15.6) is given by

$$\displaystyle{ \delta J_{\Delta } = \Delta x\Delta t\sum _{n=0}^{N}\sum _{ i\in \mathbb{Z}}\rho _{i}^{n}\left (u_{ i}^{n} - (u^{d})_{ i}^{n}\right )\delta u_{ i}^{n}, }$$
(15.55)

where δ u i, j n solves the linearized system (15.51). If we consider p i n the solution of (15.52) with (15.53), we obtain that \(\delta J_{\Delta }\) in (15.55) can be written as,

$$\displaystyle{\delta J_{\Delta } = \Delta x\sum _{i\in \mathbb{Z}}p_{i}^{0}\delta u_{ i}^{0},}$$

and this allows to obtain easily the steepest descent direction for \(J_{\Delta }\) by considering

$$\displaystyle{ \delta u_{\Delta }^{0} = -p_{ \Delta }^{0}. }$$
(15.56)

Remark 15.2.

We observe that for the Enquis-Osher’s flux (15.16), the system (15.52) is the upwind method for the continuous adjoint system. We do not address here the problem of the convergence of this adjoint scheme towards the solution of the continuous adjoint system. Of course, this is an easy matter when u is smooth but it is far from being trivial when u has shock discontinuities. Whether or not this discrete adjoint system, as \(\Delta \rightarrow 0\), allows reconstructing the complete adjoint system, with the inner Dirichlet condition along the shock (15.33)–(15.38), constitutes an interesting problem for future research. We refer to [14] and [18] for preliminary work on this direction in one-dimension.

15.6.2 The Alternating Descent Method

Now we describe the implementation of the alternating descent method.

The main idea is to approximate a minimizer of J alternating between two directions of descent: First we perturb the initial datum u 0 using the direction (15.46), which principally changes the profile of u 0. Second we move the shock curve without altering the profile of u 0 at both sides of \(\Sigma \), using the direction (15.47).

More precisely, for a given initialization \(u_{\Delta }^{0}\) and target function \(u_{\Delta }^{d}\), we compute \(\Sigma _{\Delta }^{0}\), the jump-point of \(u_{\Delta }^{0}\),\(u_{\Delta }\) and \(p_{\Delta }^{0}\) as the solutions of (15.51), (15.52) respectively.

As numerical approximation of the adjoint state q(0) we take the value of \(p_{\Delta }^{0}\) over the point \(\Sigma _{\Delta }^{0}\), i.e.

$$\displaystyle{q_{\Delta }^{0} = p_{ \Delta }^{0}(\Sigma _{ \Delta }^{0}) = p_{ i}^{0},\;\;\Sigma _{ \Delta }^{0} \in (x_{ i-1/2},x_{i+1/2}).}$$

The main advantage of this method introduced in [9] is that for an initial datum u 0 with a single discontinuity, the descent directions are generalized tangent vectors, i.e. they introduce Lipschitz continuous variations of u 0 at both sides of the discontinuity and a displacement of the shock position. In this way, the new datum obtained modifying the old one, in the direction of this generalized tangent vector, has again a single discontinuity. The method can be applied in a much more general context in which, for instance, the solution has various shocks since the method is able both to generate shocks and to destroy them, if any of these facts contributes to the decrease of the functional. This method is in some sense close to those employed in shape design in elasticity in which topological derivatives (that would correspond to controlling the location of the shock in our method) are combined with classical shape deformations (that would correspond to simply shaping the solution away from the shock in the present setting) [11].

As mentioned above, in the context of the tracking problem we are considering, the solutions of the adjoint system do not increase the number of shocks. Thus, a direct application of the continuous method, without employing this alternating variant, could make sense. Note that the purely discrete method is a limited version of the continuous one since one simply employs the descent direction indicated by p 0 without paying attention to the value q 0 corresponding to the shock sensitivity. However, the numerical experiments we have done with the full continuous method do not improve the results obtained by the discrete one since the definition of the location of the shocks is lost along the iterative process.

15.7 Numerical Experiments

In this section we present some numerical experiments which illustrate the results obtained in an optimization model problem with each one of the numerical methods described in the previous section.

We have chosen as computational domain the interval (−4, 4) and we have taken as boundary conditions in (15.50), at each time step t = t n, the value of the initial data at the boundary. This can be justified if we assume that the initial datum u 0 is constant in a sufficiently large inner neighborhood of the boundary x = ±4 (which depends on the size of the L ∞-norm of the data under consideration and the time horizon T), due to the finite speed of propagation. A similar procedure is employed for the adjoint equation.

We underline once more that the solutions obtained with each method may correspond to global minima or local ones since the gradient algorithm does not distinguish them.

In the experiments we consider the Burgers’ equation, i.e. \(f(z) = z^{2}/2\),

$$\displaystyle{ \partial _{t}u + \partial _{x}\left (\frac{u^{2}} {2} \right ) = 0,\;\;\;u(x,0) = u^{0}(x). }$$
(15.57)

The weight function ρ, under consideration in the experiments is given by

$$\displaystyle{\rho (x,t) = \left \{\begin{array}{cl} 1&t \in (T/2,T)\\ 0 &\text{otherwise.} \end{array} \right.}$$

And the time horizon T = 1.

To compare the efficiency of the different methods we consider a fixed \(\Delta x = 1/20,\lambda = \Delta t/\Delta x = 2/3\) (which satisfies the CFL condition). We then analyze the number of iterations that each method needs to attain a prescribed value of the functional.

15.7.1 Experiment 1

We first consider a piecewise constant target profile u d given by the solution of (15.57) with the initial condition (u d)0 given by

$$\displaystyle{ (u^{d})^{0}(x) = \left \{\begin{array}{cl} 0.7&x \in [-2,1] \\ 0 &\text{otherwise.} \end{array} \right. }$$
(15.58)

Note that, in this case, (15.58) yields a particular solution of the optimization problem and the minimum value of J vanishes.

We solve the optimization problem (15.3) with the above described different methods starting from the following initialization for u 0:

$$\displaystyle{ u^{0}(x) = \left \{\begin{array}{cl} 0.5 &x \leq 0 \\ - 0.1&x > 0, \end{array} \right. }$$
(15.59)

which also has a discontinuity but located on a different point.

In Fig. 15.2 we plot log(J) with respect to the number of iterations, for both, the purely discrete method and the alternating descent one. We see that the latter stabilizes in fewer iterations.

Fig. 15.2
figure 2

Experiment 1. log(J) versus the number of iterations in the descent algorithm for the discrete and the alternating descent methods

Full size image
Fig. 15.3
figure 3

Experiment 1: u 0, discrete method, iteration k = 999

Full size image
Fig. 15.4
figure 4

Experiment 1: u 0, alternating descent method, iteration k = 38

Full size image
Fig. 15.5
figure 5

Experiment 1: Solution u(x, t), discrete method, iteration k = 999

Full size image
Fig. 15.6
figure 6

Experiment 1: Solution u(x, t), alternating descent method, iteration k = 38

Full size image

In Figs. 15.3 and 15.4, we present the minimizers obtained by the methods above, and the associated solutions, Figs. 15.5 and 15.6.

The initial datum u 0 obtained by the alternating descent method (Fig. 15.4) is a good approximation of (15.58). The solution given by the discrete approach (Fig. 15.3) presents added spurious oscillations. Furthermore, the discrete method is much slower and does not achieve the same level of accuracy since the functional \(J_{\Delta }\) does not decrease so much.

15.7.2 Experiment 2

The previous experiment indicates that the alternating descent method performs significantly better. In order to show that this is a systematic fact, which arises independently of the initialization of the method, we consider the target u d given by the solution of (15.57) with the initial condition (u d)0 given by

$$\displaystyle{ (u^{d})^{0}(x) = \left \{\begin{array}{cl} 0.5&x \leq 0.5 \\ 0 &\text{otherwise,} \end{array} \right. }$$
(15.60)

but this time we compare the performance of both methods starting from different initializations.

The obtained numerical results are presented in Fig. 15.7.

Fig. 15.7
figure 7

Experiment 2. We present a comparison of the results obtained with both methods starting out of five different initialization configurations. In the left column we exhibit the results obtained with the discrete method. In the second one those achieved by the alternating descent method. In the last one we plot the evolution of the functional with both methods

Full size image

We see that, regardless the initialization considered, the alternating descent method performs significantly better.

We observe that in the five experiments the alternating descent method perfumes better ensuring the descent of the functional in much fewer iterations and yielding smoother, less oscillatory approximation of the minimizer.

Note also that the discrete method, rather than yielding discontinuous approximations of the minimizer as the alternating descent method does, it produces an initial datum with a Lipschitz front. Observe that these are two different configurations that can lead to the same evolution for the Burgers equation after some time, once the front develops the discontinuity. This is in agreement with the fact that the functional to be minimized is only active in the time-interval T∕2 ≤ t ≤ T.

15.8 Conclusions and Perspectives

In this paper we have adapted and presented the alternating descent method for a tracking problem for a 1 − d scalar conservation law, the goal being to identify an optimal initial datum so that the solution gets as close as possible to a given trajectory. We have exhibited in a number of examples the better performance of the alternating descent method with respect to the classical discrete method. Thus, the paper extends previous works on other optimization problems such as the inverse design or the optimization of the flux function.

The developments in this paper raise a number of interesting problems and questions that will deserve further investigation. We summarize here some of them:

  • The alternating descent method and the discrete one do not seem to yield the same minimizer. This should be further investigated in a more systematic manner in other experiments.

    The minimizer that the discrete method yields seems to replace the shock of the initial datum by a Lipschitz function which eventually develops the same dynamics within the time interval T∕2 ≤ t ≤ T in which the functional we have chosen is active. This is an agreement with the behavior of these methods in the context of the classical problem of inverse design in which one aims to find the initial datum so that the solution at the final time takes a given value. It would be interesting to prove analytically that the two methods may lead to different minimizers in some circumstances.

  • The experiments in this paper concern the case where the target u d is exactly reachable. It would be interesting to explore the performance of both methods in the case where the target u d is not a solution of the underlying dynamics.

  • It would be interesting to compare the performance of the methods presented in the paper with the direct continuous method, without introducing the alternating strategy. Our preliminary numerical experiments indicate that the continuous method, without implementing the alternating strategy, does not improve the results that the purely discrete strategy yields.

  • In [16] the problem of inverse design has been investigated adapting and extending the alternating descent method to the multi-dimensional case. It would be interesting to extend the analysis of this paper to the multidimensional case too.

  • It would worth to compare the results in this paper with those that could be achieved by the nudging method as in [2, 3].