Keywords

1 Introduction

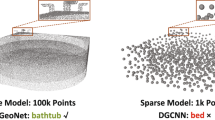
The progress in sensing technologies has significantly expedited the 3D data acquisition pipelines which in turn has increased the availability of large and diverse 3D datasets. With a single 3D sensing device [39], one can capture a target surface and represent it as a 3D object, with point clouds and meshes being the most popular representations. Several applications, ranging from virtual reality and 3D avatar generation [26, 46] to 3D printing and digitization of cultural heritage [43], depend from such representations. However, in general, a 3D capturing device generates thousands of points per second, making processing, visualization and storage of captured 3D objects a computationally daunting task. Often, raw point sets contain an enormous amount of redundant and putatively noisy points of points with low visual perceptual importance, which results into an unnecessary increase in the storage costs. Thus processing, rendering and editing applications require the development of efficient simplification methods that discard excessive details and reduce the size of the object, while preserving their significant visual characteristics. In particular, triangulation, registration and editing processes of real-world scans include an initial simplification step to achieve real-time meshing and rendering. In contrast to sampling methods that aim to preserve the overall point cloud structure, simplification methods attempt to solve the non-trival task of preserving the semantics of the input objects [8]. Visual semantics refer to the salient features of the object that mostly correlate with human perception and determine its visual appearance in terms of curvature and roughness characteristics of the shape [27, 33]. As can be easily observed in an indicative case shown in Fig. 1, effortless sampling techniques, such as FPS or uniform sampling, can easily preserve the structure of a point cloud. However, the preservation of perceptually visual characteristics, especially when combined with structural preservation, remains a challenging task.

Fig. 1.
figure 1

Point cloud simplified using FPS (left) smooths out facial characteristics of the input whereas our method preserves salient features of the input (right).

Full size image

Traditional simplification methods manage to retain the structural and the salient characteristics of large point clouds [15, 42, 49] by constructing a point importance queue that sorts points according to their scores at every iteration. However, apart from being very time demanding, such optimizations are non-convex with increased computational requirements and can not be generalized to different topologies. On the contrary, an end-to-end differentiable neural-based simplification method could leverage the parallel processing of neural networks and simplify batches of point clouds in one pass [45].

In this study, we tackle the limitations of the literature on the task of point cloud simplification and propose the first, to the best of our knowledge, learnable point cloud simplification method. Motivated by the works that showcase the importance of perceptual saliency, we propose a method that preserves both the salient features as well as the overall structure of the input and can be used for real-time point cloud simplification without any prior surface reconstruction. Given that our method is fully differentiable, it can be directly integrated to any learnable pipeline without any modification. Additionally, we introduce a fast latent space clustering using FPS that could benefit several fields (such as graph partitioning, generative models, shape interpolation, etc.), serving as a fast (non-iterative) alternative to differentiable clustering, in a way that the cluster center selection is guided by the loss function. Finally, we highlight the limitations of popular distance metrics, such as Chamfer, to capture salient details of the simplified models, and we propose several evaluation criteria, well-suited for simplification tasks. The proposed method is extensively evaluated in a series of wide range experiments.

2 Related Work

Mesh Simplification is a well studied field with long history of research. A mesh can be simplified progressively by two techniques, namely vertex decimation and edge collapse. Although the first approach is more interpretable, since it assigns importance scores to each vertex [36, 51, 52], it requires careful re-tessellation in order to fill the generated holes. Edge folding was first introduced in [18], where several transforms such as edge swap, edge split and edge collapse were introduced to minimize a simplification energy function. In the seminal works of [15, 50], the authors associated each vertex with the set of planes in its 1-hop neighborhood and defined a fundamental quadric matrix quantifying the distance of a point from its respective set of planes. A Quadric Error Metric (QEM) was proposed to measure the error introduced when an edge collapses, ensuring that edges with the minim error are folded first. Several modification of the QEM cost function have been proposed to incorporate curvature features [22, 23, 38, 62], mesh saliency [2, 40, 59] or to preserve boundary constrains [3] and spectral mesh properties [34, 37]. Recently, [17] proposed a learnable edge collapse method that learns the importance of each edge, for task-driven mesh simplification. However, the edges are contracted in an inefficient iterative way and the resulting mesh can only be decimated approximately by two.

Point Cloud Simplification and Sampling: Similar to mesh simplification, iterative point selection and clustering techniques have also been proposed for point clouds [16, 42, 49, 53, 64]. In particular, point cloud simplification can be addressed either via mesh simplification where the points are fitted to a surface and then simplified using traditional mesh simplification objectives [1, 14], or via direct optimization on the point cloud where the points are selected and decimated according to their estimated local properties [32, 42, 47, 53, 64]. However, similar to mesh simplification, computationally expensive iterative optimization is needed, making them inefficient for large scale point clouds. The point cloud simplification methodology presented in this paper attempts to address and overcome the inefficiencies of the aforementioned approaches using a learnable alternative that works with arbitrary, user-defined decimation factors.

In a different line of research, sampling methods rely on a point selection scheme that focuses on retaining either the overall structure of the object or specific components of the input. A huge difference between simplification and sampling is founded upon their point selection perspective. Sampling methods are usually utilized for hierarchical learning [48] in contrast to simplification methods that attempt to preserve as much of the visual appearance of the input even at very low resolutions. Farthest Point Sampling (FPS) [12], along with several modification of it, remains the most popular sampling choice and has been widely used as a building block in deep learning pipelines [47, 48, 61]. Nevertheless, as we experimentally showcase, FPS directly from the input xyz-space can not preserve sharp details of the input and thus is not suitable for simplification tasks. Recently, several methods [11, 25] have been proposed as a learnable alternative for task-driven sampling, optimized for downstream tasks. However, they require the input point clouds to have the same size which limits their usage to datasets with different topologies. In addition, they explicitly generate the sampled output using linear layers which is not scalable to large point clouds. Although the learnable sampling methods are closely related to ours, they only sample point clouds in a task-driven manner and as a result, the preservation of the high frequency details of the point cloud is not ensured.

Assessment of Perceptual Visual Quality: Processes such as simplification, lossy compression and watermarking inevitably introduce distortion to the 3D objects. Measuring the visual cost in rendered data is a long studied problem [9, 30]. Inspired by Image Quality Assessment measures, the objective of Perceptual Visual Quality (PVQ) assessment is to measure the distortion of an object in terms directly correlated with the Human Perceptual System (HPS). Several methods have been proposed, acting directly on 3D positions, to measure the PVQ using Laplacian distances [21], curvature statistics [24, 28, 54], dihedral angles [55] or per vertex roughness [9]. Several studies [10, 13, 29, 63] utilized crowdsourcing platforms and user subjective assessments to identify the most relevant geometric attributes that mostly correlate with human perception. The findings demonstrated that curvature related features along with dihedral angles and roughness indicate strong similarity with the HVS. In this work, motivated by the aforementioned studies we utilized curvature related losses and quality measures to train and assess the performance of the proposed model and we refer to them as perceptual measures.

3 Method

3.1 Preliminaries: Point Curvature Estimation

Calculating the local surface properties of an unstructured point cloud is a non-trivial problem. As demonstrated in [19, 42], covariance analysis can be an intuitive estimator of the surface normals and curvature. In particular, considering a neighborhood \(\mathcal {N}_i\) around the point \(\textbf{p}_i \in \mathcal {R}^3\) we can define the covariance matrix:

$$\begin{aligned} \textbf{C} = \frac{1}{k-1} \sum ^{k}_{i=1}{(\textbf{p}_{i_1}-\textbf{p}_i)^T(\textbf{p}_{i_1}-\textbf{p}_i)}, \quad \textbf{p}_{i_j} \in \mathcal {N}_i \end{aligned}$$
(1)

Solving the eigendecomposition of the covariance matrix \(\textbf{C}\) we can derive the eigenvectors corresponding to the principal eigenvalues that define an orthogonal frame at point \(\textbf{p}_i\). The eigenvalues \(\lambda _i\) measure the variation along the axis defined by their corresponding eigenvector. Intuitively, the eigenvectors that correspond to the largest eigenvalues span the tangent plane at point \(\textbf{p}_i\), whereas the eigenvector corresponding to the smallest eigenvalue can be used to approximate the surface normal \({\textbf {n}}_i\). Thus, given that the smallest eigenvalue \(\lambda _0\) measures the deviation of point \(\textbf{p}_i\) from the surface, it can be used as an estimate of point curvature. As shown in [42], we may define:

$$\begin{aligned} \kappa (\textbf{p}_i) = \frac{\lambda _0}{\lambda _0+\lambda _1+\lambda _2}, \quad \lambda _0<\lambda _1<\lambda _2 \end{aligned}$$
(2)

as the local curvature estimate at point \(\textbf{p}_i\) which is ideal for tasks such as point simplification. Using the previously estimated curvature at point \(\textbf{p}_i\) we can estimate the mean curvature as the Gaussian weighted average of the curvatures around the neighborhood \(\mathcal {N}_i\):

$$\begin{aligned} \bar{\mathcal {K}}(\textbf{p}_i) = \frac{\sum \limits _{j \in \mathcal {N}_i} \kappa (\textbf{p}_j) \exp {(-\Vert \textbf{p}_j - \textbf{p}_i\Vert ^2/h})}{\sum \limits _{j \in \mathcal {N}_i}\exp {(-\Vert \textbf{p}_j - \textbf{p}_i\Vert ^2/h}) } \end{aligned}$$
(3)

where h is a constant defining the neighborhood radius. Finally, we can define an estimation of the roughness as the difference between curvature and the mean curvature at point \(\textbf{p}_i\) as: \(\mathcal {R}(\textbf{p}_i)=|\kappa (\textbf{p}_i) -\bar{\mathcal {K}}(\textbf{p}_i)|\)

3.2 Model

The main building block of the proposed architecture is a graph neural network that receives at its input a point cloud (or a mesh) \(\mathcal {P}_1\) with N points \(\textbf{p}_i\) and outputs a simplified version \(\mathcal {P}_2\) with M points, \(M<<N\). It is important to note that the simplified point cloud \(\mathcal {P}_2\) does not need to be a subset of the original point set \(\mathcal {P}_1\). The proposed model is composed by three modules: the Projection Network, the Point Selector and the Refinement Network. Figure 2 illustrates the architecture of the proposed method.

Fig. 2.
figure 2

Overview of the proposed method. Initially a point cloud (or a mesh) is passed through a projection network (green) and embedded to a higher dimensional latent space. FPS is used to select points from the set of latent representations (blue) that can be conceived as cluster centers of the input. Finally, a k-NN graph is constructed between the cluster centers and the input points that is used to modify their positions using the refinement layer (purple). (Color figure online)

Full size image

Projection Network and Point Selector: In this study, we formulate sampling as a clustering problem. In particular, we aim to cluster points that share similar perceptual and structural features and express the simplified point cloud using the cluster centres. To do so, we designed a Projector Network that embeds (x, y, z) coordinates to a high dimensional space, where points with similar features are close in the latent space. In other words, instead of directly sampling from the Euclidean input space, we aim to sample points embedded to a high dimensional latent space that captures the perceptual characteristics of the input. Clustering the latent space will create clusters with latent vectors of points that share similar perceptual characteristics.

Based on the observations that Farthest Point Sampling (FPS) provides a simple and intuitive technique to select points covering the point cloud structure [48], we built a sampling module on top of this sampling strategy, where points are sampled from a high dimensional space instead of the input xyz-space. Although any clustering algorithm could be adequate, we utilized FPS module since it covers sufficiently the input space without solving any optimization problem. Intuitively, using this formulation we are allowed to interfere the selection process and transform it to a learnable module that is trained to select point embeddings that cover the perceptual latent space, enabling the preservation of both structural and perceptual salient features of the input.

Projector Network comprises of a multi-layer perceptron (MLP) applied to each point independently, followed by a Graph Neural Network (GNN) that captures the local geometric properties around each point. The update rule of the GNN layer is the following:

$$\begin{aligned} \textbf{f}_i' = {\textbf {W}}_c \textbf{f}_i +\frac{1}{\mathcal {N}_i} \sum _{j \in \mathcal {N}_i } {\textbf {W}}_n \textbf{f}_j \end{aligned}$$
(4)

where \(\textbf{f}_i\) denotes the output of the shared point-wise MLP for point \(\textbf{p}_i\) and \({\textbf {W}}_c, {\textbf {W}}_n\) represent learnable projection matrices. The connectivity between points can be given either by the mesh triangulation or by a k-nn query in the input space (we used a small neighborhood of \(k=7\) as in [44]). Following the Projector Network, Point Selector utilizes FPS to select points, i.e. cluster centers, based on their latent representations, in order to cover the latent space. Given the cluster centers selected by FPS, a k-nn graph is constructed that connects the center points with their k-nearest neighbours, based on their 3D positions.

Attention-Based Refinement Layer: Cluster centers, their neighboring point positions along with their respective embeddings from the projection networks are passed to the attention-based refinement layer (AttRef) that modifies the positions of the cluster centers. This layer can be considered as a rectification step that given a neighborhood and its corresponding latent features, displaces the cluster center points in order to minimize the visual perceptual error. Given that the latent embeddings of each point can be considered as its local descriptor, the refinement layer generates the new positions based on the vertex displacements along with the neighborhood local descriptors. The final positions of the points as predicted by AttRef are defined as follows:

$$\begin{aligned} \textbf{p}_{c_i}' = \textbf{p}_{c_i} + \gamma \left( \frac{1}{\mathcal {N}_{c_i}}\sum _{j \in \mathcal {N}_{c_i}} \alpha _{ij} \phi ( [\textbf{f}_j \Vert \textbf{p}_j - \textbf{p}_{c_i} ]) \right) \end{aligned}$$
(5)

where \(\gamma \) and \(\phi \) are MLPs, \(\mathcal {N}_{c_i}\) the k-nearest neighbors of point \(\textbf{p}_{c_i}\) (we used \(k=\) 15), \(\textbf{f}_j\) the latent features of point \(\textbf{p}_{j}\) and \(\alpha _{ij}\) the attention coefficients between center \(\textbf{p}_{c_i}\) and point \(\textbf{p}_{j}\). The attention coefficients \(\alpha _{ij}\) are computed using scaled dot-product [56], i.e. \(\alpha _{ij} = \) softmax\(\left( \frac{\mathbf {\theta }_q(\textbf{f}_j)^T \mathbf {\theta }_k(\textbf{f}_i)}{\sqrt{d}}\right) \), where \(\mathbf {\theta }_q, \mathbf {\theta }_k\) are linear transformations mapping features \(\textbf{f}\) to a d-dimensional space.

3.3 Loss Function

The selection of the loss function to be optimized is crucial for the task of simplification since we seek for a balance between the preservation of the object’s structure and its underlying salient features. A major barrier of most common distance metrics is the uniform weighting of points that can not reflect the perceptual differences between objects. As shown in many studies [20, 35, 58] the commonly used Chamfer distance (CD) between two point sets \(\mathcal {P}_1,\mathcal {P}_2\) defined as:

$$\begin{aligned} d_{\mathcal {P}_1, \mathcal {P}_2} = \sum _{x \in \mathcal {P}_1} \min _{y \in \mathcal {P}_2} \Vert x-y \Vert ^2 + \sum _{y \in \mathcal {P}_2} \min _{x \in \mathcal {P}_1} \Vert x-y \Vert ^2 \end{aligned}$$
(6)

can only describe the overall surface structure similarity between the two sets without taking into account the high frequency details of each point cloud. Figure 1 illustrates an example of such case. Similarly, the point to surface distance between points of a set \(\mathcal {P}\) and a surface \(\mathcal {M}\) as well as the Hausdorff distance can not preserve salient points of the object rather than its global appearance. To train our model task it is essential to devise a loss function that preserves both the salient features along with the structure of the point cloud.

Adaptive Chamfer Distance: As can be easily observed, the first term of Eq. (6) measures the preservation of the overall structure of \(\mathcal {P}_1\) by \(\mathcal {P}_2\), in a uniform way. To break the uniformity of the first term of CD we introduc a weighting factor \(w_x\) in Eq. 7 that penalizes the distances between the two sets at the points with high salient features ensuring that they will be preserved at the simplified point cloud. We define the modified adaptive Chamfer distance as:

$$\begin{aligned} d^{Adapt}_{\mathcal {P}_1, \mathcal {P}_2} = \sum _{x \in \mathcal {P}_1} w_{\bar{\mathcal {K}}(x)} \min _{y \in \mathcal {P}_2} \Vert x-y \Vert ^2 + \sum _{y \in \mathcal {P}_2} \min _{x \in \mathcal {P}_1} \Vert x-y \Vert ^2 \end{aligned}$$
(7)

where \(\mathcal {P}_1\) denotes the initial point cloud, \(\mathcal {P}_2\) the simplified one, and \(w_{\bar{\mathcal {K}}(x)}\) a weighting factor proportional to the mean curvature \(\bar{\mathcal {K}}\) at point xFootnote 1. Since we only aim to retain salient points of \(\mathcal {P}_1\), we avoid applying a similar weighting factor to the second term of Eq. (6) to prevent the optimization process from getting trapped at local minima.

Curvature Preservation: Additional to the adaptive CD, we make use of a loss term to reinforce the selection of high curvature points of the input. To quantify the preservation of salient features of the input we introduce an error to measure the average point-wise curvature distance between the two point clouds:

$$\begin{aligned} \mathcal {E}_c = \left( \frac{1}{|\mathcal {P}_1|}\sum _{ x \in \mathcal {P}_1} \Vert \bar{\mathcal {K}}_1(x) - \bar{\mathcal {K}}_2(\text {NN}(x,\mathcal {P}_2)) \Vert ^2 \right) ^{1/2} \end{aligned}$$
(8)

where \(\text {NN}(x,\mathcal {P}_2)\) denotes the nearest neighbour of x in set \(\mathcal {P}_2\), and \(\bar{\mathcal {K}}(\cdot )\) the mean curvature. We refer to this error as Curvature Error (CE).

Overall Objective: We used a combination of the two aforementioned losses as the total objective to be minimized:

$$\begin{aligned} \mathcal {L}(\mathcal {P}_1 ,\mathcal {P}_2) = d^{Adapt}_{\mathcal {P}_1, \mathcal {P}_2}+ \lambda \mathcal {E}_c , \end{aligned}$$
(9)

where \(\lambda \) is used as a scaling factor set to 0.1. The first term ensures that the selected points cover the surface of the input, while the latter enforces the selection of high curvature points.

4 Evaluation Criteria

To assess the performance of the simplified models generated by our method in terms of visual perception we define several metrics that measure the similarity between the two point cloud models.

Roughness Preservation: Roughness describes the deviation of a point from the surface defined by its neighbours and has been identified as a salient feature in many visual perception studies [33, 57]. Similar to the curvature preservation loss, we calculate the roughness preservation error by substituting the curvature values with roughness in Eq. (8). We refer to this error as RE.

Point Cloud Structural Distortion Measure: Additionally to curvature and roughness preservation metrics, we also calculate the structural similarity score between the two point clouds that has been shown to highly correlate with human perception [31]. In particular, the point cloud Structural Distortion Measure (SDM) can be defined as:

$$\begin{aligned} D(\mathcal {P}_1, \mathcal {P}_2) = \frac{\alpha \mathcal {L}(p_i, \hat{p}_i)+\beta \mathcal {C}(p_i, \hat{p}_i) +\gamma \mathcal {S}(p_i, \hat{p}_i)}{\alpha + \beta + \gamma } \end{aligned}$$
(10)
$$\begin{aligned} \mathcal {L}(p_i, \hat{p}_i) = \frac{||\bar{\mathcal {K}_1}(p_i) -\bar{\mathcal {K}_2}(\hat{p}_i) ||}{\max ( \bar{\mathcal {K}_1}(p_i),\bar{\mathcal {K}_2}(\hat{p}_i))} ,\quad \mathcal {C}(p_i, \hat{p}_i)= \frac{||\sigma _{\bar{\mathcal {K}_1}}(p_i) -\sigma _{\bar{\mathcal {K}_2}}(\hat{p}_i) ||}{\max ( \bar{\mathcal {K}_1}(p_i),\bar{\mathcal {K}_2}(\hat{p}_i))} \end{aligned}$$
(11)
$$\begin{aligned} \mathcal {S}(p_i, \hat{p}_i)= \frac{||\sigma _{\bar{\mathcal {K}_1}}(p_i)\sigma _{\bar{\mathcal {K}_2}}(\hat{p}_i) - \sigma _{\bar{\mathcal {K}}_{12}}(p_i,\hat{p}_i)^2 ||}{\sigma _{\bar{\mathcal {K}_1}}(p_i)\sigma _{\bar{\mathcal {K}_2}}(\hat{p}_i)} \end{aligned}$$
(12)

where \(\mathcal {K}_1\), \(\mathcal {K}_2, \sigma _{\bar{\mathcal {K}_1}}, \sigma _{\bar{\mathcal {K}_2}}, \sigma _{\bar{\mathcal {K}}_{12}}(p_i,\hat{p}_i)\) are the mean, the gaussian-weighted standard deviation and the covariance of the curvatures for point \(p_{i}\) in \(\mathcal {P}_1\) and its corresponding point \(\hat{p}_i\) in \(\mathcal {P}_2\), respectively. We establish the correspondence between the two point clouds using the 1-nearest neighbor for each point. The global similarity score is obtained using Minkowski pooling as suggested in [28].

Normals Consistency: Point normals are highly related to visual appearance as indicators of sharp and smooth areas. We measure the consistency of normals’ orientations between the two models using the cosine similarity loss:

$$\begin{aligned} \begin{aligned} \mathcal {E}_n =\frac{1}{|\mathcal {P}_1|}\sum _{\begin{array}{c} x \in \mathcal {P}_1 \\ y \in NN(x,\mathcal {P}_2) \end{array}}1 - {\mathbf {n_x} \cdot \mathbf {n_y} \over \Vert \mathbf {n_x} \Vert \Vert \mathbf {n_y} \Vert } + \frac{1}{|\mathcal {P}_2|}\sum _{\begin{array}{c} y \in \mathcal {P}_2 \\ x \in NN(y,\mathcal {P}_1) \end{array}}1 - {\mathbf {n_x} \cdot \mathbf {n_y} \over \Vert \mathbf {n_x} \Vert \Vert \mathbf {n_y} \Vert } \end{aligned} \end{aligned}$$
(13)

where \(\mathbf {n_x}\) denotes the normal at point x and \(NN(x,\mathcal {P}_2)\) the nearest neighbour of x in set \(\mathcal {P}_2\), calculated as described in Sect. 3.1.

5 Experiments

In this section we extensively evaluate the proposed method with both quantitative and qualitative experiments.

Baselines. We compare our approach against several sampling and simplification methods including: uniform sampling (random), FPS, PointASNL adaptive sampling method [61], quadric error metric (QEM) simplification [15], spectral mesh simplification [37], feature preserving point cloud simplification [49] along with a top curvature points sampling (TCP) where the top-k curvature points are selected from the input point cloud. We failed to compare with recent simplification methods [34, 41] that rely on the eigendecomposition of the Laplacian matrix, since they entail an overwhelmingly large processing run-time and memory consumption (\(\approx \) 15 min for a mesh with \(\approx \) 15K points).

Datasets. We evaluated the proposed method using several publicly available 3D datasets, with different characteristics. The simplification benchmark TOSCA [6] dataset comprises 80 synthetic high-resolution meshes with 9 different deformable objects. It is an excellent candidate to assess feature-preserving simplification, since most of its meshes are non-smooth consisting of high curvature regions. Additionally, we used the popular ModelNet10 dataset [60] and the fixed topology high-resolution MeIn3D face dataset [5]. All datasets used were randomly split in 80%–20% train-test sets, taking care that none of the identities/shapes used for training are present in the respective test set.

Evaluation. We quantitatively evaluate the quality of the simplified point clouds in three folds. Primarily, we measure the low-level structural and perceptual measures, as described in Sect. 4, in Sect. 5.1. We additionally use an pre-trained objective classifier to measure the preservation of high-level semantics along with a user-study that aims to access the conceivable human perceptual similarity between the input and the simplified models. Furthermore, we access the importance of the major components of the proposed method using ablations studies, as well as the performance of the proposed method under noisy conditions and real-world scans. Due to space limitations several of the aforementioned experiments are reported on the supplementary material along with additional qualitative results.

5.1 Point Cloud Simplification

In this section, we showcase the simplification performance of the proposed method. For each dataset, we report both structural (i.e. CD, NC) as well as perceptual metrics (i.e. CE, RE, SDM) for the proposed and the baseline methods. Table 1 indicates the superiority of the proposed method to maintain the perceptual features of the input (i.e. low SDM) without sacrificing the overall structure (i.e. low CD) of the shape at three indicative simplification ratios. Results for larger simplification ratios can be found in the supplementary material. In contrast to TPC method where the selection of high curvature points leads to an increased Chamfer distance, the proposed method achieves a fair balance between structure (CD and NC) and saliency (SDM and RE). Additionally, the proposed method exhibits lower perceptual error (SDM) compared to FPS and PointASNL [61] methods that sample points directly from the xyz-space. This may be also observed in Fig. 3 where sampling from the perceptual latent space can effectively induce the preservation of the details of the input cloud.

Table 1. Simplification performance tested on TOSCA (top), ModelNet10 (middle) and MeIn3d (bottom) datasets. Best approaches are highlighted in bold and second best in . We refer to the dataset used for training as “Proposed-Dataset”
Full size table
Fig. 3.
figure 3

Qualitative comparison between FPS (top row) and the proposed (bottom row) methods, at different simplification ratios. Differences between the two methods can be found at coarse and smooth areas, where the proposed model favours the preservation of high-frequency details of the input point cloud.

Full size image
Fig. 4.
figure 4

Curvature preservation error comparison for the TOSCA dataset at different simplification ratios. Curvature error scales linearly for the proposed method.

Full size image
Fig. 5.
figure 5

Colorcoded curvature error comparison between QEM and the proposed method. Blue color corresponds to larger error. (Color figure online)

Full size image

Significantly, it can be observed in Table 1 and Fig. 4, the proposed method outperforms recent methods [37, 49, 61] under all metrics, and QEM in terms of perceptual error. Figure 5, demonstrates the superiority of our method to remarkably retain the salient points of the input using just 1% of the input is retained, in contrast to QEM that performs poorly at coarse areas of high curvature. The selection of salient points of the input is demonstrated in Fig. 3, where the proposed method favours point selection around the chair’s arm, the face’s eyes and nose in contrast to points at smooth areas, such as the forehead. Intuitively, smooth areas require only a few points to describe their associated planes compared to coarse areas that demand many points in order to preserve their curvature.

We also experimented with a cross-dataset generalization scenario where different datasets were used for training and testing the model (bottom rows in Table 1). Interestingly, it is observed that the proposed model can generalize well to out-of-distribution shapes and topologies indicating that it can be applied directly to any point cloud without fine-tuning, especially when trained with TOSCA or ModelNet dataset. We argue that this is due to the diversity of shapes and topologies as well as the presence of many rough regions at the training sets of these datasets that enforce the model to favour salient features.

5.2 Computational Time

Inevitably, in addition to salient point preservation, a proper point cloud simplification method should confront real-time executions. Although time complexity is beyond the scope of this study, we assessed the time required for simplifying 80 high-resolution meshes from the TOSCA dataset. Since FPS, Uniform and TCP baseline methods do not require any significant computations, we compare the proposed method with the popular QEM approach using a highly optimized version from the MeshLab framework [7] and the official implementations of [49] and [37]. It is important to note that the code of the proposed method could be further optimized, using parallel programming. In particular, 80% of the computational time of the proposed method is acquired by k-NN search that could be further optimized whereas FPS takes 17 % and the rest 3% of the runtime is spent on the learnable modules. Figure 7 demonstrates that the required mean runtime of the proposed method decreases drastically across all experiments, as the desired simplification increases, requiring just a few seconds to simplify the input to 1% of its original size. In contrast, the methods of [49] and [37] require approximately a minute to simplify a single mesh which makes them impractical.

5.3 Mesh Simplification

As described in Sect. 2, mesh simplification is a long studied problem that has been tackled only by greedy algorithms. In this section, we will attempt to propose an alternative method that circumvents the greedy nature of simplification using the simplification technique proposed in Sect. 3. The proposed method, without the need of any particular modification, can be easily extended for the task of mesh simplification when combined with a triangulation algorithm to transform the simplified vertices into a mesh structure. The process unfolds in two steps. Initially, mesh vertices are simplified by treating them as a point cloud but, instead of using a k-nn, the mesh adjacency matrix is utilized in order to determine point connectivity. In a second step, the remaining vertices are re-triangulated using an off-the-self triangulation algorithm such as Ball Pivoting [4]. Other triangulation algorithms, such as Delaunay, alpha shapes or Voronoi diagrams, could be also used but we observed that Ball Pivoting algorithm produces better results for small point clouds. Figure 6 shows visual results for the extension of the proposed simplification method to triangular meshes (for various simplification ratios).

Fig. 6.
figure 6

Simplified meshes using the proposed method followed by Ball Pivoting Algorithm.

Full size image
Fig. 7.
figure 7

Average time of simplification for the proposed and the baseline methods.

Full size image
Table 2. User studies results of different methods. We average user preference scores (higher is better, results in %). Best results in bold.
Full size table

5.4 User-Study

To quantify the ability of the proposed method to select points that correlate with human perception we performed a user study, using the paired comparison protocol contrasting the proposed and one baseline method. In total, 50 participants were specifically asked to evaluate 18 point clouds and select one of the two simplified point clouds that mostly preserves the perceptual details of the reference one in terms of the overall shape and identity similarity. In average, as shown in Table 2, users selected 14 out of the 18 point clouds produced by the proposed method, as the ones preserving most of the visual features.

5.5 Simplification Under Noise Conditions

To both quantitatively and qualitatively evaluate the performance of the proposed method in the presence of noise we fed the pretrained model with point clouds distorted with Gaussian noise (\(\sigma = 1\)). Quantitative experimental result are summarized in Table 3, with the proposed method to exhibit the best performance for almost all metrics (NC, RE, SDM) across all simplification ratios, and even the best second for structure preservation (CD). Such findings reveal the anti-noising capabilities of latent space sampling that, compared to xyz-space sampling, is less affected by the outlier noisy points. For qualitative comparisons along with results on LiDAR scans we refer the reader to the Supplementary material.

Table 3. Simplification performance tested on TOSCA dataset with addition of Gaussian noise. Best approaches are highlighted in bold and second best in .
Full size table

6 Conclusion

Our work emphasises on the proposal of a learnable, neural-based simplification approach to overcome the inefficiencies of traditional greedy simplification methods. In this study we presented the first, to the best of our knowledge, learnable point cloud simplification method that aims at preserving salient features while at the same time retaining the global structural appearance of the input 3D object. Using three learnable modules we attain to simplify large-scale point clouds in real-time, addressing the literature limitations regarding computational complexity. As shown in an extensive series of both quantitative and qualitative experiments the proposed method not only outperforms its counterparts under most perceptual criteria but also exhibits zero-shot capabilities. Regarding future work, we plan to adapt the proposed method to mesh structures using a more sophisticated triangulation process. In particular, instead of using off-the-shelf triangulation algorithms on top of the point cloud simplification model, we aim to extend the proposed method to predict the triangulation of the simplified model utilizing the priors of the input mesh.