Abstract
The rebound attack was introduced by Mendel et al. at FSE 2009 to fulfill a heavy middle round of a differential path for free, utilizing the degree of freedom from states. The inbound phase was extended to 2 rounds by the Super-Sbox technique invented by Lamberger et al. at ASIACRYPT 2009 and Gilbert and Peyrin at FSE 2010. In ASIACRYPT 2010, Sasaki et al. further reduced the requirement of memory by introducing the non-full-active Super-Sbox. In this paper, we further develop this line of research by introducing Super-Inbound, which is able to connect multiple 1-round or 2-round (non-full-active) Super-Sbox inbound phases by utilizing fully the degrees of freedom from both states and key, yet without the use of large memory. This essentially extends the inbound phase by up to 3 rounds. We applied this technique to find classic or quantum collisions on several AES-like hash functions, and improved the attacked round number by 1 to 5 in targets including AES-128 and SKINNY hashing modes, Saturnin-Hash, and Grøstl-512. To demonstrate the correctness of our attacks, the semi-free-start collision on 6-round AES-128-MMO/MP with estimated time complexity \(2^{24}\) in classical setting was implemented and an example pair was found instantly on a standard PC.
The full version of the paper is available at https://eprint.iacr.org/2022/731.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Triangulating Rebound
- Quantum Attack
- Collision Attacks
- Rebound Attacks
- Triangulation Algorithm
- Super-Inbound
1 Introduction
Cryptographic hash function compresses a binary string of arbitrary length into a short fixed-length digest. It is one of the most fundamental cryptographic primitives that act as the underlying building blocks in various advanced cryptographic protocols, including digital signatures, authenticated encryption, secure multiparty computation and post-quantum public-key cryptography, etc. A cryptographic hash function must fulfill three basic security properties: collision resistance, preimage resistance, and second-preimage resistance. Due to the breakthroughs in collision attacks [74, 76, 77] on the hash functions MD5 and SHA-1, the academic communities advanced new hashing designs, including the best-known SHA-3 [10]. AES-like hashing, inspired by the elegant yet secure and efficient design strategies of Advanced Encryption Standard (AES) [21], is another new hashing design. It adopts block ciphers or permutations with similar features to AES as the underlying building blocks, such as Whirlpool [6], Grøstl [34], AES-MMO, Grindahl [52], ECHO [8], Haraka v2 [53], etc. These hash functions are commonly known as AES-like hashing.
Rebound Attacks [62], introduced by Mendel, Rechberger, Schläffer, and Thomsen at FSE 2009, is one of the most effective tools on the cryptanalysis of AES-like hash functions. It can be applied to both block cipher based and permutation based constructions. The idea of the rebound attack is to divide an attack into two phases, an inbound and an outbound phase. In the inbound phase, degrees of freedom are used to realize part of the differential characteristic deterministically. The remainder of the characteristic in the outbound phase is fulfilled in a probabilistic manner.
In order to penetrate more rounds, at ASIACRYPT 2009, Lamberger et al. [56] proposed the multiple inbound phases and connected them by leveraging the degrees of freedom of the key. Later, Gilbert and Peyrin [35] and Lamberger et al. [56] further extended the inbound phase by treating two consecutive AES-like rounds as the Super-Sbox [20]. At ASIACRYPT 2010, Sasaki et al. [70] reduced the memory cost by exploiting the differential property of non-full-active Super-Sboxes. At CRYPTO 2011, Naya-Plasencia [66] improved the rebound attack by introducing advanced algorithms for merging large lists. At CRYPTO 2012, Dinur et al. [26] further reduced the memory cost of the rebound attack by proposing the dissection technique. The rebound attack has since become a basic cryptanalysis tool to evaluate hash functions against collision attacks or distinguishing attacks [25, 32, 45, 46, 51, 59, 60, 63, 71]. Interestingly, the idea of the rebound attack was in turn used to improve the Demirci-Selçuk MITM attacks [24, 33] and biclique attack [11].
Quantum Cryptanalysis attracts more and more attention due to Shor’s quantum attacks [73] breaking the security of public-key crypto-systems RSA and ECC. For symmetric ciphers, the community has also witnessed many important quantum cryptanalysis results recently, such as quantum distinguisher on 3-round Feistel [54], key-recovery attack on Even-Mansour construction [55], key-recovery attacks or forgeries on MACs and authenticated encryption schemes [47], and more [13, 27, 57]. However, most attacks need to query the online quantum oracles with superposition states, which is believed to be an impractical projection for quantum physics. Thereafter, the quantum attacks [12, 14, 19, 36, 38, 48, 67] only using offline quantum computers are considered to be of more practical relevance.
Since hash functions can be implemented in offline quantum circuit, the attackers can freely make offline quantum superposition queries. There are several quantum generic (multi-target) preimage attacks [2, 19] and multicollision attacks [41, 42, 58]. For generic quantum collision attacks, three quantum generic algorithms exist under different assumptions of the availability of quantum and classical memory resources:
-
Condition 1: Exponentially large quantum random access memory (qRAM) is available. Brassard, Høyer, and Tapp [15] introduced the generic quantum collision attack (named as BHT algorithm) with \(2^{n/3}\) quantum time complexity and \(2^{n/3}\) qRAM.
-
Condition 2: Neither exponentially large qRAM nor classic RAM is available. The quantum version of parallel rho’s algorithm [9, 39, 75] achieves a time-space trade off of time \(\frac{2^{n/2}}{S}\) with S computers.
-
Condition 3: Exponentially large qRAM is not available but large classical RAM is. Chailloux, Naya-Plasencia, and Schrottenloher [19] introduced the CNS algorithm to find collision in time \(2^{2n/5}\) with classical RAM of size \(2^{n/5}\).
At EUROCRYPT 2020, Hosoyamada and Sasaki [39] introduced the first quantum dedicated collision attacks by converting the classical rebound attacks into quantum rebound attacks. This showed that, under their respective bounds of generic algorithms, quantum attacks are able to penetrate more rounds than classical attacks. At ASIACRYPT 2020, Dong et al. [30] reduced the requirement of qRAM in the quantum rebound attack by exploiting non-full-active Super-Sbox technique [70]. At CRYPTO 2021, Hosoyamada and Sasaki [40] introduced the quantum collision attacks on reduced SHA-2. At ASIACRYPT 2021, Dong et al. [31] studied the quantum free-start collision attacks.
1.1 Our Contributions
In order to extend the attacked round by the rebound attack, Lamberger et al. [56] connected two local inbound phases by consuming the degree of freedom in the key. Later, Super-Sbox [35, 56] and non-full-active Super-Sbox [70] were proposed. In this paper, we further generalize this idea by bridging multiple inbound phases with available degrees of freedom both from the key and the internal data path, to build the Super-Inbound. With the help of Khovratovich et al.’s [50] triangulation algorithm, we identify truncated differential trails for AES hashing modes with sound configurations on the positions of several local inbound parts, as well as relatively low complexity to bridge the multiple local inbound parts. We name this method as triangulating rebound attack. With this advanced method in hand, we achieve the following results:
AES-MMO. The MMO-mode (shown in Fig. 2) instantiated with AES [21] is a popular AES-like hashing design, which is standardized by Zigbee [1] and also suggested by ISO [43]. Many advanced cryptographic protocols, e.g., multi-party computation [37, 49], adopt AES-MMO due to its high efficiency when implemented with AES-IN. The best classical collision attacks are for 6 rounds [35, 56]. At EUROCRYPT 2020, Hosoyamda and Sasaki [39] introduced two 7-round quantum collision attacks better than BHT algorithm [15] or parallel rho’s algorithm [75]. At ASIACRYPT 2020, Dong et al. [30] introduced 7-round quantum collison better than CNS algorithm [19].
We extend the previous 2-round inbound phase into 3- or 4-round Super-Inbound for AES-128. Thereby, we build the first 7-round semi-free-start collision attack on AES-128-MMO/MP in classical setting, while the previous classical collision attack reaches 6 rounds [35, 56]. In addition, a 6-round practical instance of semi-free-start collision and an 8-round quantum semi-free-start collision attack are given. Moreover, the first 8-round quantum collision attack on AES-128-MMO/MP is given, with time complexity better than parallel rho’s algorithm [9, 39, 75].
Saturnin-Hash. It is the hash function among the post-quantum lightweight cipher family Saturnin designed by Canteaut et al. [17]. It is one of the round 2 candidates of the NIST lightweight cryptography competition. The designers of Saturnin introduced the 10-round related-key recovery attack on the Saturnin block cipher [16]. At ASIACRYPT 2021, Dong et al. [31] proposed several quantum and classical collision attacks on Saturnin-Hash and its compression function, including a 7-round semi-free-start quantum collision attack and an 8-round free-start quantum collision attack.
We extend the previous 2-round inbound phase to the 4-round Super-Inbound. Finally, the time complexity of the 8-round free-start quantum collision attack is significantly reduce from \(2^{122.5}\) to \(2^{89.65}\). Further, the first 10-round free-start quantum collision attack is derived with two more rounds than Dong et al.’s result [31].
SKINNY-128-384-MMO. As SKINNY [7] is running for ISO standard, it is natural to build lightweight hash with the ISO suggested hashing mode MMO. At ASIACRYPT 2021, Dong et al. [31] introduced the 16-round quantum free-start collision attack on SKINNY-128-384-MMO. In this paper, by exploring the large degrees of freedom of the key schedule for SKINNY-128-384-MMO, we extend the previous 2-round inbound phase into a 5-round Super-Inbound, and finally achieve 5 more rounds on the free-start quantum collision attack. In addition, a 19-round classical free start collision attack is given, which is even better than previous quantum attack.
Grøstl. Grøstl is one of the five finalists of SHA-3. In this paper, by bridging the differences with degrees of freedom from the states, we propose the memoryless method to solve the 3-round non-full-active inbound part for Grøstl-512. Thereafter, the improved semi-free-start collisions with one more round than before for both Grøstl-512 and its predecessor are derived. The results are summarized in Table 1.
1.2 Novelty and Comparison with Previous Works
Both rebound attack [62] and triangulation algorithm [50] are existing techniques. However, combining these two techniques together as one cryptanalysis tool has not appeared before. When using these two techniques together, we can exploit many more degrees of freedom (DoF) from the key schedule algorithm, which greatly extends the inbound part of our rebound attack. Therefore, the number of possible truncated differential trails for the rebound attack increases significantly than before. In previous rebound attacks on AES-MMO (including [30, 39]), the authors place a 2-round full/non-full active Super-Sbox in the inbound phase, and extend it forwards and backwards in the outbound phases to find a useful rebound-attack trail. However, in our attack, we have to use 3-/4-round truncated differentials as the multiple inbound phases, which have many more choices than a 2-round Super-Sbox before. Moreover, not all those 3-/4-round inbound can be solved efficiently by triangulation algorithm (actually, it is time consuming to compute a compatible pair for most 3-/4-round truncated differentials), and we have to pick a good trail from many choices.
Therefore, as another contribution, we introduce a heuristic automatic tool (CP-based) to identify good trails for our rebound attacks, which succeeds to find the 7-/8-round collision attacks on AES-MMO and gains 1-round improvement.
We note that the multiple inbound phases technique was already introduced and used many times before, see for instance the rebound attacks on the LANE [59], ECHO [44], JH [68], etc. The additional degrees of freedom were in these cases given by bigger states. The truncated differences affect both the number of rounds covered by the inbound phases, and the differential probabilities of the outbound phases. In the previous works, the choices of these truncated differences are made in ad hoc ways. In our paper, we introduce triangulation algorithm into the rebound attack, as well as the automated search of configuration for the rebound attack with multiple inbound phases, which is the main novelty comparing to previous ad hoc ways.
2 Preliminaries
2.1 AES-like Hashing
AES [21] operates on a \(4 \times 4\) column-major order array of bytes, whose round function contains four major transformations as illustrated in Fig. 1: SubBytes (SB), ShiftRows (SR), MixColumns (MC), and AddRoundKey (AK). By making changes to the numbers of rows and columns, the sizes of the cells, the order of the transformations, one can produce new designs named as AES-like round functions. Usually, the MixColumns is to multiply an MDS matrix to each column of the state. An exception is SKINNY [7], which uses the non-MDS matrix.
By using (keyed) permutations with AES-like round functions in certain hashing modes (like MD, MMO, and MP hashing modes [64, Section 9.4] in Fig. 2), compression functions (denoted as CF) can be constructed. Plugging such compression functions into the Merkle-Damgård construction [22, 65], one arrives at AES-like hashings. Concrete designs include AES-128-MMO, AES-128-MP, Saturnin-Hash [17], Whirlpool [6] Grøstl [34].
2.2 The Rebound Attack
The rebound attack was first introduced by Mendel et al. in [62]. It consists of an inbound phase and an outbound phase as shown in Fig. 3, where F is an internal block cipher or permutation which is split into three subparts, then \(F=F_{fw}\circ F_{in}\circ F_{bw}\).
-
Inbound phase. In the inbound phase, the attackers efficiently fulfill the low probability part in the middle of the differential trail with a meet-in-the-middle technique. The degree of freedom is the number of matched pairs in the inbound phase, which will act as the starting point for the outbound phase.
-
Outbound phase. In the outbound phase, the matched values of the inbound phase, i.e., starting points, are computed backward and forward through \(F_{bw}\) and \(F_{fw}\) to obtain a pair of values which satisfy the outbound differential trail in a bruteforce fashion.
Overall, the rebound attack is essentially a technique to efficiently generate a message pair fulfilling the inbound phase, which utilizes a truncated differential rather than a single differential characteristic. Suppose the probability of the outbound phase is p, then we have to prepare 1/p starting points in the inbound phase to expect one pair conforming to the differential trail of the outbound phase. Hence, the degree of freedom should be larger than 1/p.
2.3 The Super-Sbox Technique
The Super-Sbox technique proposed by Gilbert and Peyrin [35] and Lamberger et al. [56] extends Mendel et al.’s [62] inbound part into 2 S-box layers by regarding them as four Super-Sboxes as shown in Fig. 4 (a). In [70], Sasaki et al. further reduced the the memory complexity by considering non-full-active Super-Sboxes as shown in Fig. 4 (b). In both the two techniques, AK acts as a constant addition operation and does not provide any degree of freedom.
Super-Sbox Technique. For the jth Super-Sbox \(\texttt{SSB} _j\) and given input difference \(\Delta x_i^{(j)}\) (\(j=0\) in Fig. 4 (a)), compute \(\Delta y_{i+1}^{(j)}=\texttt{SSB} _j(x\oplus \Delta x_{i}^{(j)})\oplus \texttt{SSB} _j(x)\) for \(x \in \mathbb {F}^{32}\). Store the pair \((x,x\oplus \Delta x_i^{(j)})\) in a table \(\mathbb {L}^{(j)}[\Delta y_{i+1}^{(j)}]\). Given \(\Delta y_{i+1}^{(j)}\), we find a pair conforming the two-round differential with (\(\Delta x_{i}^{(j)}\), \(\Delta y_{i+1}^{(j)}\)) by assessing \(\mathbb {L}^{(j)}[\Delta y_{i+1}^{(j)}]\). The memory cost is about \(2^{32}\).
Non-full-active Super-Sbox. In Fig. 4 (b), the Property 1 of MDS in MC is used. Look at \(\Delta w_i=\texttt{MC} (\Delta z_i)\), by guessing the differences of one active byte, we can determine other differences according to Property 1. Then, for a fixed input-output differences (\(\Delta x_i^{(j)},\Delta y_{i+1}^{(j)}\)) of \(\texttt{SSB} _j\), we deduce all the input-output differences for the active cells of two S-box layers for each guess and then deduce their values by accessing the differential distribution table (DDT) of the S-box.
Property 1
Suppose MC is an \(n\times n\) MDS matrix and \(\texttt{MC} \cdot (z[1], \ldots , z[n])^T = (w[1], \ldots , w[n])^T\), the knowledge of any n out of 2n bytes of (z, w) is necessary and sufficient to determine the rest. (z, w) here can be either value or difference.
2.4 Triangulation Algorithm
At CT-RSA 2009, Khovratovich, Biryukov, and Nikolić [50] introduced the triangulation algorithm tool, an efficient Gaussian-based-algorithm to solve system of bijective equations, to automatically detect a way to solve the nonlinear system. The algorithm models an AES-like block cipher as a system of key schedule and round function equations, and the state bytes and key bytes as variables. At first, the system is determined by n initial state bytes and k initial key bytes. Therefore, when m bytes are fixed, the algorithm will return \(n+k-m\) “free variables” to form a basis of the system. The algorithm can output exactly the “free variables” when the system is deterministically solvable, and improve the guessing and checking the “free variables” when the system is probabilistically solvable. The idea of triangulation algorithm is roughly described following.
-
1.
Construct a system of equations whose variables are the bytes. The predefined values are fixed to constants.
-
2.
All variables and equations are marked as non-processed.
-
3.
Mark the variable which is involved in only one non-processed equation as processed. Also mark this equation as processed. If no such variable exist, exit.
-
4.
Return to Step 3 if still have non-processed equations.
-
5.
Return all non-processed variables as “free variables”.
After the “free variables” are identified, we randomly assign values for them and deduce a solution for the whole nonlinear system. For details, please refer to [50].
2.5 Collision Attacks and Its Variants
Given a hash function H, a standard collision message pair \((m, m')\) satisfies \(H(IV, m) = H(IV, m')\), where the initial vector IV is a fixed initial value. A semi-free-start collision is to find a pair (u, m) and \((u,m')\), such that \(H(u, m) = H(u, m')\) (\(u \ne IV\)). A free-start collision is to find a pair (v, m) and \((v',m')\), so that \(H(v, m) = H(v', m')\) \((v\ne v')\). When the hash function H is built by iterating the compression function (CF) with Merkle-Damgård construction, we can similarly define the semi-free-start collision and free-start collision attack on the compression function. Taking the MMO and MP hashing modes in Fig. 2 as examples, when considering the semi-free-start or free-start collision attack, the attackers can explore the degrees of freedom from the chaining value \(h_{i-1}\) through the key schedule algorithm, which may lead to better attacks such as [56, 71]. We would like to emphasize the importance of semi-free-start and free-start collision attacks: The Merkle-Damgård security reduction assumes that any type of collision for the compression function should be intractable for the attacker, including semi-free-start and free-start collisions.
3 Triangulating Rebound Attack
3.1 Solving Non-full-active Super-Sbox by Key Bytes
In previous collision attacks, both Super-Sbox [35, 56] and non-full-active Super-Sbox [70] techniques, the subkeys are prefixed in advance (as shown in Sect. 2.3). In other words, the degree of freedom of the subkeys was not be utilized. We observe that, by carefully choosing the values of subkeys, state pairs conforming the given differential can be obtained without additional computation only at a cost of memory for storing the differential distribution table (DDT). This observation enables utilization of the degrees of freedom from the corresponding subkeys and leads to collision attacks without the need of building large lists of compatible pairs for Super-Sboxes. Here we describe this new Super-Sbox technique through a concrete example in Fig. 5.
Given the pair of non-full difference of \((\Delta x_i, \Delta y_{i+1})\) and zero difference in key of an Super-Sbox (marked as red for the corresponding column), we are to generate state pairs and corresponding subkey \(k_{i+1}\) conforming to that difference. First, we randomly assign a difference \(\Delta \) compatible with \(\Delta y_{i+1}[0]\) to \(\Delta x_{i+1}[0]\) and asset to DDT to get an actual value for \(x_{i+1}[0]\) conforming the difference \((\Delta , \Delta y_{i+1}[0])\). Since there is no difference in the subkey \(k_{i+1}\), the difference \(\Delta w_i[0]\) is equal to \(\Delta \) as well. We use a simple property of maximum distance separable (MDS) matrix to determine all the rest bytes of \(\Delta w_{i}\) and \(\Delta z_{i}\).
With the knowledge of 4 bytes of \(\Delta z_i\) and \(\Delta w_i\) (\(\Delta z_{i}[0] = \Delta w_{i}[1,3]=0\) and \(\Delta w_{i}[0] = \Delta \)), all bytes of \(\Delta z_{i}\) and \(\Delta w_{i}\) are uniquely determined, and so for the entire differential characteristic (\(\Delta x_{i},\Delta z_{i},\Delta w_{i},\Delta x_{i+1},\Delta y_{i+1}\)) of the Super-Sbox. By looking up DDT, the byte values before and after the active Sboxes, e.g., \(x_{i}[5,10,15],z_i[1,2,3],x_{i+1}[0,2]\) and \(y_{i+1}[0,2]\), are determined as well. Next, we randomly assign a value to \(k_{i+1}[0]\), then \(w_i[0]\) can be calculated as \(w_i[0] = x_{i+1}[0] \oplus k_{i+1}[0]\). Again, Property 1 allows to determine the remaining bytes \(z_i[0]\) and \(w_i[1,2,3]\) since 4 bytes \(z_i[1,2,3]\) and \(w_i[0]\) are known. Finally, the key byte \(k_{i+1}[2]\) is determined as \(k_{i+1}[2] = w_i[2] \oplus x_{i+1}[2]\). In summary, after randomly assigning (compatible) values to \(\Delta x_{i+1}[0]\) and \(k_{i+1}[0]\), all the values and differences of the active bytes in the state as well as the subkey bytes corresponding to the active state bytes positions of AK are determined, with time complexity 1.
3.2 Connecting Multiple Inbound Phases by Key Bytes
In this section, we present a 3-round inbound phase by extending the Super-Sbox backward by one round. Since the Super-Sbox and the extended round are not solved in two inbound phases, this technique is also referred to as “multiple inbound phases”. These phases are connected by free bytes of the corresponding subkeys, and so one has to ensure the value assignments to the subkeys from different rounds are not over-defined through the key schedule algorithm. This new technique is illustrated through an example of 3-round truncated differential trail depicted in Fig. 6.
Given the differences \(\Delta x_{i-1}\), \(\Delta x_i\), \(\Delta y_{i+1}\) and zero difference in key, we are to generate state and key pairs conforming the differential path with low memory requirement by utilizing the degrees of freedom from subkeys \(k_i\) and \(k_{i+1}\). First, applying the Super-Sbox technique presented above to the given \(\Delta x_{i}\) and \(\Delta y_{i+1}\), both value and difference of \(\Delta x_{i}[5,10,15]\) and value of \(k_{i+1}[0,2]\) will be determined. Then, with fixed \(\Delta x_{i-1}\) and \(\Delta x_{i}\), standard inbound phase of the original rebound attack can be applied, i.e., lookup DDT with input/output differences \((\Delta x_{i-1}, \texttt{SR}^{-1}(\Delta z_{i-1} = \texttt{MC}^{-1}(\Delta x_{i})))\), values of the last three columns of \(z_{i-1}\) and so \(w_{i-1}\) are determined. Hence, \(\Delta k_{i}[5,10,15]\) can be calculated as \(\Delta w_{i-1}[5,10,15] \oplus \Delta x_{i}[5,10,15]\). Note, there is no direct implication between any assignment of \(k_{i}[5,10,15]\) and \(k_{i+1}[0,2]\) through the AES key schedule. The whole process costs 17 DDT lookups and memory hosting the DDT lookup table.
3.3 The Triangulating Rebound Attack
Generally speaking, the development of the rebound attack can be viewed as a continuous process to find as many degrees of freedom (DoF) as possible, to either reduce the overall inbound solving complexity, or to extend for more rounds. As shown in Fig. 7, the multiple local inbound parts form a Super-Inbound. Given the input/output differences \((\Delta _{in},\Delta _{out})\) of the super inbound phase, bridging the multiple local inbound parts is to find the conforming pair for \((\Delta _{in},\Delta _{out})\), while the exact differentials and values of the internal rounds are up to attacker’s control. Usually, \((\Delta _{in},\Delta _{out})\) are chosen from a truncated differential in the rebound attack. In summary, the source of DoF for the whole rebound attack can come from the choices of
-
S1
truncated differential of the internal rounds of the Super-Inbound,
-
S2
input/output differences and values of the active Sboxes of the state,
-
S3
values of the inactive Sboxes of the state,
-
S4
differences of key bytes,
-
S5
values of key bytes.
The differences and values of the active Sboxes of the state are listed together, as once differences are fixed, values can be derived from DDT, and vice versa. This is not the case for key bytes, as it is not necessarily for each of the key bytes to pass through Sbox depending on the key schedule algorithm. Then the Super-Sbox technique can be viewed as a way to connect two 1-round inbound parts by fully utilizing the DoF from S2, i.e., the output differences of first round and input differences of the second round. Our techniques presented in Sect. 3.1, 3.2 is from (S2,S5), (S2,S5), respectively. Under this generic view, connecting multiple inbound parts to form a Super-Inbound can be seen as a system of nonlinear equations, where all DoF serve as variables and DoF from subkeys are constrained by key schedule, and our goal is to find a procedure to solve this system, efficiently. There are two main considerations.
-
I.
The system of nonlinear equations must have solutions. In other words, the system should not be over-defined. Hence, the number DoF should be larger than the number of equations.
-
II.
The system must be solvable efficiently, which for most of the time can be translated into a procedure of consuming degrees of freedom by fixing certain variables involved, and the final complexity is determined by the number variables which can not be fixed and have to be brute-forced.
We adopt the triangulation algorithm [50] as shown in Sect. 2.4 to solve the nonlinear system and bridge the multiple inbound parts. The algorithm can output exactly the “free variables” when the system is deterministically solvable, and improve the guessing and checking the “free variables” when the system is probabilistically solvable. We name this method as triangulating rebound attack.
Heuristic Method to Determine a Trail. So far, we have not mentioned the use of DoF from S1 and S4 yet. While S4 determines whether difference is allowed in key hence resulting in semi-free-start or free-start collision for attacks against hash functions, S1 directly determines the system of nonlinear equations, hence the number of rounds covered by the Super-Inbound and complexity as well. For collision attack on n-bit hash, the overall steps to identify a rebound attack trail are as follows:
-
1.
Find a truncated differential trail following the Constrained Programming based search model from [5].
-
2.
Choose certain consecutive rounds as the Super-Inbound (i.e., S1), which includes several local inbound parts. For example, in Fig. 7 a Super-Inbound includes three local inbound parts. Usually, 2 to 4 consecutive rounds are chosen as possible Super-Inbound. Following this search, all the input/output differences of the active Sboxes are fixed, and therefore corresponding values are fixed.
-
3.
Build equation system that connects the inbound parts and through key schedule. Check if the system is solvable by triangulation algorithm.
Before checking the solvability of the system, a potential truncated trail must satisfy the condition that the number of active Sboxes in the Super-Inbound does not exceed the DoF from both key and state. This is because the system of state bytes and keys bytes are determined by the initial k key bytes and n plaintext bytes, then for any set of fixed bytes in advance, the system is potentially solvable if the number of fixed bytes is not larger than \(n+k\). Our observation shows that the ideal case is when the number of active bytes in the Super-Inbound equals to \(n+k-1\) and only 1 free byte is left, since the scenario without free byte is likely to form an over-defined system. Therefore, this constraint is also added to our model. For classical collision attacks, after the Super-Inbound is fixed, the probability of the outbound phase can be computed and denoted as Pr, which should meet \(Pr> 2^{-n/2}\). For quantum collision attacks, let PrFootnote 1 > \(2^{-n}\). Similarly to previous models [39], for the attacks based on the truncated differentials, \(P_r\) is the probability for the cancellation of MC operator in the backward and forward trunks, as well as the cancellation for the feed-forward operator of hashing modes. After checking the potential truncated trails satisfying the above conditions for inbound and outbound phases, the triangulation algorithm is applied to detect the free bytes left followed by the step to generate sufficient data pairs for the outbound phase.
4 Improved Collision Attacks on AES-128-MMO
In this section, by applying the triangulating rebound, we introduce a 7-round classical semi-free-start collision attack and an 8-round quantum semi-free-start collision attack on AES-MMO. Moreover, we identify the first 8-round quantum collision attack, which is better than parallel rho’s algorithm [75].
4.1 Semi-free-start Collision Attack on 7-Round AES-128
New 7-Round AES-128 Truncated Differential Trail. We introduce here our new differential trail in Fig. 8. Our Super-Inbound phase covers 3 middle rounds with 2 inbound phases (marked with red and blue dashed lines), which consumes 31 bytes of degree of freedom for the fixed state bytes, i.e., 16 active bytes in \(x_3\), 9 active bytes in \(x_4\), and 6 active bytes in \(x_5\). Since we have 32 bytes in total (16 bytes in key and 16 bytes in the state), only 1 free byte is left. By triangulating algorithm, the 1 free byte is identified to be \(k_5[12]\). The remaining outbound phase happens with probability \(p_{out} = 2^{-56}\) including the MC cancellation in round 1 and 4-byte cancellation for \(\Delta P=\Delta C\).
The Super-Inbound Phase. As shown in Fig. 8, the Super-Inbound phase divides into 2 parts, the Inbound II marked with blue dashed line makes use of \(k_5\) to link round 4 and round 5, and the Inbound I marked with red dashed line connects with Inbound II via \(k_4\). To generate a data pair conforming a given difference (\(\Delta z_2, \Delta w_3, \Delta w_5\)), assuming \(\Delta Z_5=\texttt{MC} ^{-1}(\Delta w_5)\) keeps the truncated differential in Fig. 8, we perform the following steps:
-
Perform the Inbound II:
-
1.
Randomly assign a difference to \(\Delta x_5[4,9,12]\). Then \(\Delta w_4[4,9,12]\) are known accordingly, implies all the differences at these active cells of \(z_4\) and the remaining active cells of \(w_4\) are determined as a result of the Property 1. From \(\Delta z_4\), we deduce \(\Delta y_4 = \texttt{SR} ^{-1}(\Delta z_4)\).
-
2.
Compute the difference \(\Delta y_5 = \texttt{SR} ^{-1}(\texttt{MC} ^{-1}(\Delta w_5))\). Next, we deduce the values of the active cells at \(x_4\) and \(x_5\) by assessing to the DDT for each cell of \((\Delta x_4, \Delta y_4)\) and \((\Delta x_5, \Delta y_5)\). The active byte values of \(y_4\) and \(y_5\) are determined respectively.
-
1.
-
Perform the Inbound I:
-
1.
Compute \(\Delta x_3 = \texttt{MC} (\Delta z_2)\) and \(\Delta y_3 = \texttt{SR} ^{-1}(\texttt{MC} ^{-1}(\Delta w_3))\).
-
2.
Deduce full state values \(x_3\) and \(y_3\) by assessing the DDT. We compute the full state values of \(w_3\) by the action \(w_3 = \texttt{MC} (\texttt{SR} (y_3))\).
-
1.
-
Connect the phases by the subkeys:
-
1.
Since the full state of \(w_3\) and the active bytes of \(x_4\) are known, we obtain \(k_4[1,3,6,7,8,9,11,13,14] = x_4[1,3,6,7,8,9,11,13,14] \oplus w_3[1,3,6,7,8,9,11,13,14]\) (marked as black dots).
-
2.
Add constrains on the related cells of \(k_5\) to the system of equations of the subkeys. We solve the constrains on \(k_4\) and \(k_5\) by triangulation algorithm and obtain a free byte \(k_5[12]\).
-
3.
The steps (shown in Fig. 9) to recover \(k_5\) and compute a starting point are shown as follows (equations are also given in Table 2):
-
(a)
As shown in Fig. 9(1), all the differences marked by ‘
 ’ are known. In Fig. 9(2), by assessing the DDT, we know the values of
’ are known. In Fig. 9(2), by assessing the DDT, we know the values of
 ,
,
 , and
, and
 . Then deduce
. Then deduce
 .
. -
(b)
In Fig. 9(3), randomly assign a value for \(k_5[12]\) marked by ‘
 ’, compute \(w_4[12]=k_5[12]\oplus x_5[12]\). According to Property 1, deduce all the bytes marked by ‘
’, compute \(w_4[12]=k_5[12]\oplus x_5[12]\). According to Property 1, deduce all the bytes marked by ‘
 ’ in \(z_4\) and \(w_4\). Then, \(k_5[14]=x_5[14]\oplus w_4[14]\). From
’ in \(z_4\) and \(w_4\). Then, \(k_5[14]=x_5[14]\oplus w_4[14]\). From
 , we get
, we get
 . Then
. Then
 is deduced.
is deduced. -
(c)
In Fig. 9(4), following the key schedule of AES-128, compute the
 : \(k_5[8]=k_4[12]\oplus k_5[12]\), \(k_5[10] = k_4[14] \oplus k_5[14]\), \(k_5[11]=k_4[11]\oplus k_5[7]\), \(k_5[4] = k_4[8] \oplus k_5[8]\), \(k_5[7] = k_5[3] \oplus k_4[7]\), \(k_5[1]=k_4[1]\oplus \texttt{SB} (k_4[14])\oplus r_c\), \(k_5[3] = k_4[3] \oplus \texttt{SB} (k_4[12]) \oplus r_{c}\).
: \(k_5[8]=k_4[12]\oplus k_5[12]\), \(k_5[10] = k_4[14] \oplus k_5[14]\), \(k_5[11]=k_4[11]\oplus k_5[7]\), \(k_5[4] = k_4[8] \oplus k_5[8]\), \(k_5[7] = k_5[3] \oplus k_4[7]\), \(k_5[1]=k_4[1]\oplus \texttt{SB} (k_4[14])\oplus r_c\), \(k_5[3] = k_4[3] \oplus \texttt{SB} (k_4[12]) \oplus r_{c}\). -
(d)
In Fig. 9(5), deduce \(w_4[4]=k_5[4]\oplus x_5[4]\) and \(w_4[11]=k_5[11]\oplus x_5[11]\), then according to Property 1, all the bytes in \(w_4\) and \(z_4\) marked by ‘
 ’ are deduced. Then, two bytes marked by ‘
’ are deduced. Then, two bytes marked by ‘
 ’ in \(k_5\) are deduced, i.e., \(k_5[6]=w_4[6]\oplus x_5[6]\) and \(k_5[9]=w_4[9]\oplus x_5[9]\). Moreover, compute two bytes marked by ‘
’ in \(k_5\) are deduced, i.e., \(k_5[6]=w_4[6]\oplus x_5[6]\) and \(k_5[9]=w_4[9]\oplus x_5[9]\). Moreover, compute two bytes marked by ‘
 ’ in \(k_4\), i.e., \(k_4[2]=x_4[2]\oplus w_3[2]\) and \(k_4[4]=x_4[4]\oplus w_3[4]\).
’ in \(k_4\), i.e., \(k_4[2]=x_4[2]\oplus w_3[2]\) and \(k_4[4]=x_4[4]\oplus w_3[4]\). -
(e)
In Fig. 9(6), following the key schedule, deduce the bytes marked by ‘
 ’ in \(k_5\), i.e., \(k_5[0]=k_4[4]\oplus k_5[4]\), \(k_5[2]=k_4[6]\oplus k_5[6]\), \(k_5[5]=k_4[9]\oplus k_5[9]\), \(k_5[13]=k_4[13]\oplus k_5[9]\), \(k_4[15]=\texttt{SB} ^{-1}(k_4[2]\oplus k_5[2])\), \(k_5[15]=k_4[15]\oplus k_5[11]\).
’ in \(k_5\), i.e., \(k_5[0]=k_4[4]\oplus k_5[4]\), \(k_5[2]=k_4[6]\oplus k_5[6]\), \(k_5[5]=k_4[9]\oplus k_5[9]\), \(k_5[13]=k_4[13]\oplus k_5[9]\), \(k_4[15]=\texttt{SB} ^{-1}(k_4[2]\oplus k_5[2])\), \(k_5[15]=k_4[15]\oplus k_5[11]\).
-
(a)
-
4.
Finally, full state \(w_3\) and full subkey \(k_5\) are obtained by using 34 DDT assesses.
-
1.
Due to the probability of the outbound phase is \(2^{-56}\), we need to check \(2^{56}\) starting points to find the collision. The final complexity is \(2^{56}\) and memory needed is \(2^{16}\) for DDT storing.
Remark. In a rebound attack [62], we typically have a probability \(\frac{1}{2}\) to have a solution for each active SBox, so that we have to repeat the attack with new differences, but when the differences are compatible we obtain many solutions and the amortized cost is close to 1. In our attack, when \((\Delta x_3,\Delta y_3)\), \((\Delta x_4,\Delta y_4)\) and \((\Delta x_5,\Delta y_5)\) are fixed, we have 31 active Sboxes. Therefore, one compatible differential characteristic is found in roughly \(2^{31}\) time, which leads to \(2^{31}\) solutions for the active bytes of \((x_3,x_4,x_5)\). Moreover, since we can randomly assign \(k_5[12]\) (Step 3 (b)), we totally have about \(2^{31+8}=2^{39}\) starting points, which is lower than the final time \(2^{56}\). Briefly, for a given \((\Delta x_3,\Delta y_3)\), \((\Delta x_4,\Delta y_4)\), \((\Delta x_5,\Delta y_5)\) and \(k_5[12]\), we find one starting point with time complexity of 1 on average.
4.2 Semi-free-start Collision Attack on 8-Round AES-128-MMO
As shown in Fig. 10, there are three inbound parts in the Super-Inbound phase. For given fixed differences of \(\Delta z_1\), \(\Delta z_2\), \(\Delta w_4\), and \(\Delta w_5\), assuming \(\Delta w_1=\texttt{MC} (\Delta z_1)\) and \(\Delta z_5=\texttt{MC} ^{-1}(\Delta w_5)\) keep the truncated differential of Fig. 10, we perform inbound part I, II, and III without the key information. Then, we connect the three inbound part by determining certain key values and get the starting point for the outbound phase. The probability of the outbound phase is \(2^{-64}\), including the condition \(\Delta P=\Delta C\).
Given fixed differences of \(\Delta z_1\), \(\Delta z_2\), \(\Delta w_4\), and \(\Delta w_5\), the procedures to get one starting point are as follows:
-
1.
Deduce values \((x_5[0,5,10],x'_5[0,5,10])\) with \(\Delta w_4\) and \(\Delta z_5=\texttt{MC} ^{-1}(\Delta w_5)\) by accessing the DDT.
-
2.
Deduce values \((x_2[0,1,2],x'_2[0,1,2])\) with \(\Delta w_1=\texttt{MC} (\Delta z_1)\) and \(\Delta z_2\) by accessing the DDT. Then \(z_2[0,10,13]\) are known as well.
-
3.
For \(\texttt{SSB} ^{(0)}\) in Inbound III (marked in red), we compute \(\Delta x_3 = \texttt{MC} (\Delta z_2)\) and \(\Delta y_4=\texttt{SR} ^{-1}(\texttt{MC} ^{-1}(\Delta w_4))\).
-
4.
Randomly choose \(\Delta w_3[0,2]\in \mathbb {F}_2^8\times \mathbb {F}_2^8\),
-
(a)
Compute other active differences \(\Delta z_3[0,2,3]\) and \(\Delta w_3[3]\) by Property 1
-
(b)
Deduce (\(z_3[0,2,3],z'_3[0,2,3]\)) and (\(x_4[0,2,3],x'_4[0,2,3]\)) by assessing DDT
-
(a)
-
5.
Repeat Step 4 for random differences \(\Delta w_3[4,5], \Delta w_3[8,9], \Delta w_3[13,14]\) to compute all active bytes of \(x_3\) and \(x_4\). Next, we compute \(w_4[0,5,10] = \texttt{MC} (\texttt{SR} (\texttt{SB} (x_4)))[0,5,10]\) and then \(k_5[0,5,10] = w_4[0,5,10] \oplus x_5[0,5,10]\).
-
6.
Assign random values to \(k_3[6]\), \(k_4[0]\), and \(k_4[4]\). We recover the full key \(k_5\) by the following steps in Table 3. There exists a filter of \(2^{-8}\) in the step to recover \(k_3[3]\).
Since Step 6 has a filter of \(2^{-8}\) to meet the condition “\(k_3[3]= w_2[3] \oplus x_3[3] \overset{?}{=}\ \texttt{SB} (k_3[12]) \oplus k_4[3] \oplus r_c\) ” in Table 3, the time complexity to find a starting point (including a data pair and a key value conforming the inbound parts from \(\Delta z_1\) to \(\Delta w_5\)) is \(2^{8}\). The probability of the outbound phase is \(2^{-64}\), we need \(2^{64}\) starting points to find one collision. In other words, given 21 bytes of \(\Delta z_1\), \(\Delta z_2\), \(\Delta w_4\), \(\Delta w_5\), \(\Delta w_3[0,2]\), \(\Delta w_3[4,5], \Delta w_3[8,9], \Delta w_3[13,14]\) and \(k_3[6]\) \(k_4[0]\), \(k_4[4]\), we get one collision with probability of \(2^{-72}\). Since \(21\times 8=168 > 72\), we have enough degrees of freedom to find one collision.
The Quantum Attack. Given input-output differences of the active Sbox, it is expected to find one pair on average, e.g. (\(x,x'\)), satisfying the differences. In inbound phase of the quantum rebound attacks, given a valid input-output differences of l active Sboxes, we obtain about \(2^{l}/2\) choices for starting points. To indicate which starting point to choose among \(2^{l}/2\) choices, Hosoyamda and Sasaki [39, Sect. 6.2, Page 22] introduce \(l-1\) auxiliary qubits. In Hosoyamda and Sasaki’s attack, l is usually small, e.g. \(l=4\), then the increased time complexity due to the \(l-1\) auxiliary qubits is marginal. However, in our 8-round attack of Fig. 10, we have to compute pairs for \(l=3+3+12+12=30\) active Sboxes with given input-output differences. If we follow Hosoyamda and Sasaki’s idea [39], we have to introduce \(l-1=29\) auxiliary qubits, which can not be ignored anymore. To deal with the problem, we introduce a trick in Supplementary Material A in our full version [28], which introduces the auxiliary qubits nearly for free. By our new trick, we perform the 8-round quantum semi-free-start collision attack. According to Equation 5 in [28], we have \(l=3+3+12+12=30\), and choose 9 bytes out of the 21 bytes to act as “\(|\Delta _{in}|+|\Delta _{out}|\)” to find the collision with time complexity roughly \(30\cdot 2^{72/2}/128\approx 2^{34}\) 8-round AES, which is roughly the square root of \(2^{72}\).
Practical Semi-free-start Collision Attack on 6-Round AES-128. To prove the correctness of the 8-round semi-free-start collision, we give a 6-round practical semi-free-start collision by cutting the differential characteristic depicted in Fig. 10 to 6 rounds (round 1 to 6). The total complexity to find the collision is \(2^{24}\), including \(2^{8}\) time for solving the Super-Inbound phase and \(2^{16}\) for the condition \(\Delta x_1=\Delta z_6\). We have verified the validity and complexity of the attack by implementing the 6-round attack. One such example collision is presented in Table 4 in Supplementary Material of the full version [28].
4.3 Quantum Collision Attack on 8-Round AES-128
Remove the Inbound I/II from Fig. 10, we get the trail for 8-round collision attack (also shown in Figure 15 in [28]). The inbound phase covers states \(z_2\) to \(w_4\). The probability of the outbound phase is \(2^{-96}\). For a random given \(\Delta z_2\), \(\Delta w_4\) and the master key, the steps to get one starting point are as follows:
-
1.
Deduce \(\Delta x_3\) and \(\Delta y_4\) from \(\Delta z_2\) and \(\Delta w_4\).
-
2.
For \(\texttt{SSB} ^{(0)}\) marked in red, randomly choose \(\Delta w_3[0,2]\in \mathbb {F}_2^{16}\),
-
(a)
Compute other active differences \(\Delta z_3[0,2,3]\) and \(\Delta w_3[3]\) by Property 1
-
(b)
Deduce the values for active bytes by accessing DDT to get (\(z_3[0,2,3],z'_3[0,2,3]\)) and (\(x_4[0,2,3],x'_4[0,2,3]\))
-
(c)
Deduce (\(w_4[0,2,3],w'_4[0,2,3]\)) by XORing (\(x_4[0,2,3],x'_4[0,2,3]\)) with \(k_4\)
-
(d)
Check if \(\texttt{MC} (z_3[0,2,3])\overset{?}{=}\ w_4[0,2,3]\), which is a 16-bit filter by Property 1
-
(a)
-
3.
Repeat Step 2 in parallel for \(\texttt{SSB} ^{(1)}\), \(\texttt{SSB} ^{(2)}\), and \(\texttt{SSB} ^{(3)}\) to get one starting point on average.
Hence, we need \(2^{16}\) time complexity to get one starting point for a random given a random given \(\Delta z_2\), \(\Delta w_4\) and the master key. Since the probability of the outbound phase is \(2^{-96}\), we need \(2^{96}\) starting points to get one collision. Since \(|\Delta z_2|\times |\Delta w_4|=2^{48}< 2^{96}\), we need two blocks as shown in Fig. 11 to get additional degrees of freedom from the first block. The overall time complexity of the classical time is \(2^{112}\). According to the quantum analysis by [30, 39], we apply Grover’s algorithm and get a quantum collision attack with roughly \(2^{56}\) quantum time complexity. Full paper [28] gives a very detailed quantum collision attack on 8-round AES, whose time complexity is \(2^{55.53}\) 8-round AES, which is very close to the estimated \(2^{56}\).
5 Improved Quantum Attacks on Saturnin-Hash
Saturnin is a block cipher with a 256-bit state and 256-bit key that was designed as the derivative of AES with efficient implementation by Canteaut et al. [17]. It is among the round 2 candidates of the NIST lightweight cryptography competition. The composition of two consecutive rounds starting from even round is called super-round, which is very similar to an AES round operating on 16-bit words except that the SR is replaced by a transposition. Saturnin-Hash is built on 16-super-round Saturnin block cipher with the MMO hashing mode.
5.1 Improved 8-Round Quantum Free-Start Collision
The differential trail we use here was found in [31]. As shown in Fig. 12, our new method extends the inbound phase by covering round 0 to round 4 in inbound phase, and the probability of the outbound phase becomes \(2^{-135.8}\).
Super-Inbound Phase. In Dong et al.’s [31] attack, the inbound phase covers states from \(y_0\) to \(x_3\). However, our Super-Inbound covers two more rounds from state \(y_0\) to \(x_5\). Hence, the probabilities \(Pr(\Delta x_3\mapsto \Delta y_3)=2^{-12}\) and \(Pr(\Delta x_4\mapsto \Delta z_4)=2^{-59.8}\) in Dong et al.’s attack are removed in ours.
To perform the 4-round Super-Inbound phase, we first randomly assign arbitrary differences for all unfixed differences in \(\Delta z_0 = \texttt{MR} (\Delta y_0)\), \(\Delta z_1\) and \(\Delta z_4\). Together with the prefixed differences of \(\Delta z_2\) and \(\Delta z_3\), we do the following steps to find a pair to confirm the given differences in the Super-Inbound phase.
-
1.
Deduce the differences of \(\Delta y_1\), \(\Delta y_4\). Compute all the active byte values of \((x_1, y_1), (x_2, y_2), (x_3, y_3)\) and \((x_4, y_4)\) by assessing the DDT. Then \(z_1\) is known.
As shown in Fig. 13, we pick out round 2 to round 4 to clarify the steps to compute a conforming pair for the inbound part. As shown Fig. 13 (2), compute
 . Compute
. Compute
 . Similarly, compute all other cells marked by “
. Similarly, compute all other cells marked by “
 ” and “
” and “
 ”.
”. -
2.
In Fig. 13 (3), deduce “
 ” and “
” and “
 ” cells by the “
” cells by the “
 ” cells. Guess \(z_3[0]\) to compute
” cells. Guess \(z_3[0]\) to compute
 and
and
 by Property 1. Compute
by Property 1. Compute
 . Guess \(z_2[9,10]\) to deduce
. Guess \(z_2[9,10]\) to deduce
 and
and
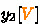 by Property 1. Then, compute
by Property 1. Then, compute
 and
and
 .
. -
3.
In Fig. 13 (4), guess \(z_2[0,1,2]\) to deduce
 and
and
 . Deduce
. Deduce
 and
and
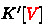 . Compute
. Compute
 .
. -
4.
In Fig. 13 (5), guess \(z_3[3]\) to deduce
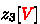 and
and
 . Compute
. Compute
 and
and
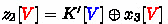 . Compute
. Compute
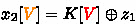 .
. -
5.
In Fig. 13 (6), compute
 and
and
 . Compute
. Compute
 . Compute
. Compute
 , so that the 2nd column and 3rd column of \(y_3\) and \(z_3\) form a filter of \(2^{-32}\).
, so that the 2nd column and 3rd column of \(y_3\) and \(z_3\) form a filter of \(2^{-32}\).
Totally, we guess 7-cell (\(z_3[0,3], z_2[9,10,0,1,2]\)) to deduce the conforming pair. In Step 5, there is a filter of \(2^{-32}\), together with the outbound probability \(2^{-135.8}\), we get a collision with total probability of \(2^{-32-135.8}=2^{167.8}\). We have \(2^{9\times 16}=2^{144}\) choices for \(\Delta z_0 = \texttt{MR} (\Delta y_0)\), \(\Delta z_1\) and \(\Delta z_4\). Together with the 7-cell (\(z_3[0,3], z_2[9,10,0,1,2]\)), the total degree of freedom is \(2^{144+16\times 7}=2^{256}>2^{167.8}\). Hence, we have enough degree of freedom to find the collision. Since we do not have the quantum circuit for the DDT of Saturnin like AES, we have to use Equation 4 in [28] to estimate the time complexity. With \(l=27\), the time is roughly \(27\cdot 2^{167.8/2+16/2}/(16\times 8)=2^{89.65}\) 8-round Saturnin-Hash.
5.2 Extend the Attack to 10-round Free-Start Collision
The 10-round differential trail is easily obtained by repeating the path of Fig. 12 round 5 and round 6 one more time before entering round 7. The figure for 10-round Saturnin-Hash is given in Figure 17 in our full version [28]. By this way, the probability of the outbound phase decreases by \(2^{-16-59.8} = 2^{-75.8}\) while the Super-Inbound phase maintains the same probability \(2^{-32}\). Finally, we obtain the free-start collision attack with probability \(2^{167.8-75.8} = 2^{-243.6}\). Since the number of degrees of freedom \(2^{256}\) is still larger than \(2^{243.6}\), so that we can find a collision. According to Equation 4 in [28], \(l=27\), the time is roughly \(27\cdot 2^{243.6/2+16/2}/(16\times 10)=2^{127.2}\) 10-round Saturnin-Hash. Additionally, we present an improved 7-round quantum semi-free-start collision in Supplementary Material D in [28].
6 Quantum Collision Attack on SKINNY-128-384-MMO
SKINNY is a family of lightweight block ciphers designed by Beierle et al. [7]. In this section, we focus on the hashing mode of SKINNY-128-384. Please find the structure of SKINNY-n-3n in [7]. The MC operation is non-MDS:
6.1 21-Round Quantum Free-Start Collision Attack
In quantum setting, we derive the free-start collision attack on hashing modes (MMO/MP) with 21-round SKINNY-128-384 using the differential characteristic shown in Figure 18 in Supplementary Material D in [28]. The new differential trail is found by using the automatic tool in [23]. The 5-round Super-Inbound covers from state \(w_9\) to \(x_{14}\). The outbound phase happens with probability \(2^{-103.4}\).
We pick out the 5-round Super-Inbound phase from the whole rebound attack trail of Figure 18 in [28] to get Fig. 14 (a). To launch the rebound attack, we first precompute a pair satisfying the 5-round inbound trail as shown in Fig. 14 (b). Then thanks to the large degrees of freedom from the tweakey, we get enough starting points by changing the 384-bit tweakey.
Precomputation in the Super-Inbound Phase. We build several steps to compute the conforming data pairs for the Super-Inbound phase.
-
1.
In Fig. 14(a), focusing on states \(z_{10}\) to \(x_{11}\), the values in \(z_{10}[8,12]=\texttt{SR} (x_{10}[10,13])\) and all active bytes of \(w_{10}\) are deduced by assessing DDT with fixed differences in Fig. 14(a). In the 1st column \(z_{10}\) and \(w_{10}\), i.e., \(z_{10}^{(0)}\) and \(w_{10}^{(0)}\), we have a condition “\(w_{10}[4]\oplus w_{10}[12]=z_{10}[8]\)” due to Eq. 1, which is a filter of \(2^{-8}\). In our trail, the differences are dedicatedly chosen, so that we have enough pairs to verify the filters for the given differences. For example, in the condition “\(w_{10}[4]\oplus w_{10}[12]=z_{10}[8]\)”, we choose \((w_{10}[4],w_{10}[12],z_{10}[8]) \in (\texttt{DDT} [\mathtt{b0_x}][ \mathtt{80_x}]\times \texttt{DDT} [\mathtt{21_x}][ \mathtt{a0_x}]\times \texttt{DDT} [\mathtt{2f_x}][ \mathtt{91_x}]) \), where \(\texttt{DDT} [\mathtt{b0_x}][ \mathtt{80_x}]\) is the subset of DDT with input-output differences (\(\mathtt{b0_x},\mathtt{80_x}\)). The size \(|\texttt{DDT} [\mathtt{b0_x}][ \mathtt{80_x}]\times \texttt{DDT} [\mathtt{21_x}][ \mathtt{a0_x}]\times \texttt{DDT} [\mathtt{2f_x}][ \mathtt{91_x}]|=48\cdot 2^5 \cdot 2^3 > 2^{8}\).
-
2.
With the choice of \(w_{10}[12], z_{11}[15]\) is known as well. \(z_{11}[8,9,10,12]\) and all active bytes of \(w_{11}\) are deduced by DDT. We have similar conditions to fulfill for the 1st column of \(z_{11}\) and \(w_{11}\) with \(w_{11}[0] \oplus w_{11}[12] = z_{11}[12]\), which act as a filter of \(2^{-8}\).
-
3.
Do similar steps from \(z_{10}\) to \(w_{13}\), we get a data and key pair as shown in Fig. 14(b) conforming the whole 5-round inbound trail.
An additional trick is used in our inbound phase. As only the first two rows of \(x_9\) are XORed with \(k_9\), the last two rows of \(x_9\) and \(w_8\) are fully determined by \(w_9\). Hence, in the inbound phase, we directly find the pair with \(\Delta w_8[8]=\mathtt{04_x}, \Delta w_8[13]=\mathtt{54_x}\), and \(\Delta w_8[14]=\mathtt{54_x}\), which increases the probability of the outbound phase from \(2^{-103.4}\) to \(2^{-92.4}\). The conforming pair for the Super-Inbound is given in Fig. 14(b), which is generated by the source code at https://www.dropbox.com/s/2n4d9zwufkpigqt/Find_inbound.7z
Generating Starting Points for Outbound Phase. Now we have the values of subkeys \(k_{10}, k_{11}, k_{12}, k_{13}\). Since the key schedule is linear and by solving a linear system on the 384-bit key with fixed values of subkeys \(k_{10}, k_{11}, k_{12}, k_{13}\) in Fig. 14 (b), we can derive at most \(2^{128}\) starting points for the outbound phase. We need only \(2^{92.4}\) starting points to get a collision. In quantum setting, the \(2^{92.4}\) starting points are traversed by Grover’s algorithm, which need roughly \(2^{46.2}\) time complexity to find the collision.
6.2 Classic Free-Start Collision Attack on 19-Round
The first classical free-start collision attack on 19-round SKINNY-128-384 hash mode is also given with the trail in Figure 19 in Supplementary Material F in [28]. The Super-Inbound covers 5 rounds from round 9 to round 13, and only one data pair, shown in Figure 20 in our full paper [28], is needed to confirm the inbound trail in the precomputation phase. Similar to the 21-round attack, the pre-computed pair of the inbound phase also satisfies the differential of the last two rows of \(x_8\) to \(w_7\). Since the outbound excluding the Sboxes in the last two rows of \(x_8\) happens with probability \(2^{-51.2}\), the final time complexity is \(2^{51.2}\).
7 Discussion and Conclusion
7.1 Possible Generalization of Triangulating Rebound
In Sect. 3, we have shown that the multiple inbound phases can be connected by the key bytes. We may describe the idea in a more generalized way. In fact, for active Sbox or Super-Sbox with fixed input/output differences, the values are fixed. For active Sbox without fixed input/output differences, or inactive Sbox, the values are not fixed and up to attacker’s control, which are the source of the degree of freedom (DoF). In order to identify a data pair conforming the truncated differential, we may consume the degree of freedom from the unfixed Sbox to bridge several fixed values due to active Sboxes or Super-Sboxes with fixed input/output differences. This intuitive idea implies that not only the key bytes are useful to connect the differences, but also the internal states. In Supplementary Material G in [28], we give an example to connect the differences with DoF from internal states and gain some improved collision attacks on Grøstl.
7.2 Conclusion
In this paper, we extended the number of attacked rounds by the rebound attack by introducing triangulating rebound attack. The core idea is to take full advantage of the available degrees of freedom from both the subkeys and the state to greatly extend the number of rounds covered by the inbound phase, which is named as Super-Inbound. As a consequence, multiple improved classic or quantum collision attacks on AES-like hashing were presented. Possible future works are to investigate more ciphers with our method, as well as to find more applications such as distinguishing attacks based the improved rebound attacks.
Notes
- 1.
As shown in the introduction, we consider three quantum attack conditions. \(Pr > 2^{-2n/3}\) is to be better than the BHT algorithm, \(Pr > 2^{-n}\) is to be better than quantum time-space tradeoff, \(Pr>2^{-4n/5}\) is to be better than CNS algorithm. So we let \(Pr > 2^{-n}\) to keep all characteristics that may lead to possible attacks.
References
Alliance, Z.: ZigBee 2007 specification (2007). http://www.zigbee.org/
Banegas, G., Bernstein, D.J.: Low-communication parallel quantum multi-target preimage search. In: Adams, C., Camenisch, J. (eds.) SAC 2017. LNCS, vol. 10719, pp. 325–335. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-72565-9_16
Bao, Z., Ding, L., Guo, J., Wang, H., Zhang, W.: Improved meet-in-the-middle preimage attacks against AES hashing modes. IACR Trans. Symmetric Cryptol. 2019(4), 318–347 (2019)
Bao, Z., et al.: Automatic search of meet-in-the-middle preimage attacks on AES-like hashing. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021, Part I. LNCS, vol. 12696, pp. 771–804. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77870-5_27
Bao, Z., Guo, J., Li, S., Pham, P.: Quantum multi-collision distinguishers. Cryptology ePrint Archive, Report 2021/703 (2021). https://ia.cr/2021/703
Barreto, P.S., Rijmen, V.: The Whirlpool hashing function. Submitted to NESSIE
Beierle, C., et al.: The SKINNY family of block ciphers and its low-latency variant MANTIS. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part II. LNCS, vol. 9815, pp. 123–153. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_5
Benadjila, R., et al: SHA-3 proposal: ECHO. Submission to NIST (updated), p. 113 (2009)
Bernstein, D.J.: Cost analysis of hash collisions: will quantum computers make SHARCS obsolete. In: SHARCS 2009, vol. 9, p. 105 (2009)
Bertoni, G., Daemen, J., Peeters, M., Assche, G.V.: Keccak sponge function family main document. Submission to NIST (Round 2), 3(30), 320–337 (2009)
Bogdanov, A., Khovratovich, D., Rechberger, C.: Biclique cryptanalysis of the full AES. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 344–371. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_19
Bonnetain, X., Hosoyamada, A., Naya-Plasencia, M., Sasaki, Yu., Schrottenloher, A.: Quantum attacks without superposition queries: the offline Simon’s algorithm. In: Galbraith, S.D., Moriai, S. (eds.) ASIACRYPT 2019, Part I. LNCS, vol. 11921, pp. 552–583. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34578-5_20
Bonnetain, X., Naya-Plasencia, M., Schrottenloher, A.: On quantum slide attacks. In: Paterson, K.G., Stebila, D. (eds.) SAC 2019. LNCS, vol. 11959, pp. 492–519. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-38471-5_20
Bonnetain, X., Naya-Plasencia, M., Schrottenloher, A.: Quantum security analysis of AES. IACR Trans. Symmetric Cryptol. 2019(2), 55–93 (2019)
Brassard, G., Høyer, P., Tapp, A.: Quantum cryptanalysis of hash and claw-free functions. In: Lucchesi, C.L., Moura, A.V. (eds.) LATIN 1998. LNCS, vol. 1380, pp. 163–169. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054319
Canteaut, A., et al.: A note on related-key attacks on Saturnin (2020). https://project.inria.fr/saturnin/files/2020/11/Note-RK-1.pdf
Canteaut, A., et al.: Saturnin: a suite of lightweight symmetric algorithms for post-quantum security. IACR Trans. Symmetric Cryptol. 2020(S1), 160–207 (2020)
Cauchois, V., Gomez, C., Lercier, R.: Grøstl distinguishing attack: a new rebound attack of an AES-like permutation. IACR Trans. Symmetric Cryptol. 2017(3), 1–23 (2017)
Chailloux, A., Naya-Plasencia, M., Schrottenloher, A.: An efficient quantum collision search algorithm and implications on symmetric cryptography. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part II. LNCS, vol. 10625, pp. 211–240. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70697-9_8
Daemen, J., Rijmen, V.: Understanding two-round differentials in AES. In: De Prisco, R., Yung, M. (eds.) SCN 2006. LNCS, vol. 4116, pp. 78–94. Springer, Heidelberg (2006). https://doi.org/10.1007/11832072_6
Daemen, J., Rijmen, V.: The Design of Rijndael: AES - The Advanced Encryption Standard. Information Security and Cryptography, Springer, Cham (2002). https://doi.org/10.1007/978-3-662-04722-4
Damgård, I.B.: A design principle for hash functions. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 416–427. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_39
Delaune, S., Derbez, P., Vavrille, M.: Catching the fastest boomerangs. IACR Trans. Symmetric Cryptol. 104–129 (2020)
Derbez, P., Fouque, P.-A., Jean, J.: Improved key recovery attacks on reduced-round AES in the single-key setting. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 371–387. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_23
Derbez, P., Huynh, P., Lallemand, V., Naya-Plasencia, M., Perrin, L., Schrottenloher, A.: Cryptanalysis results on Spook - bringing full-round Shadow-512 to the light. In: Micciancio, D., Ristenpart, T. (eds.) CRYPTO 2020, Part III. LNCS, vol. 12172, pp. 359–388. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56877-1_13
Dinur, I., Dunkelman, O., Keller, N., Shamir, A.: Efficient dissection of composite problems, with applications to cryptanalysis, knapsacks, and combinatorial search problems. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 719–740. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_42
Dong, X., Dong, B., Wang, X.: Quantum attacks on some Feistel block ciphers. Des. Codes Cryptogr. 88(6), 1179–1203 (2020). https://doi.org/10.1007/s10623-020-00741-y
Dong, X., Guo, J., Li, S., Pham, P.: Triangulating rebound attack on AES-like hashing. Cryptology ePrint Archive, Paper 2022/731 (2022). https://eprint.iacr.org/2022/731
Dong, X., Hua, J., Sun, S., Li, Z., Wang, X., Hu, L.: Meet-in-the-middle attacks revisited: key-recovery, collision, and preimage attacks. In: Malkin, T., Peikert, C. (eds.) CRYPTO 2021, Part III. LNCS, vol. 12827, pp. 278–308. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84252-9_10
Dong, X., Sun, S., Shi, D., Gao, F., Wang, X., Hu, L.: Quantum collision attacks on AES-like hashing with low quantum random access memories. In: Moriai, S., Wang, H. (eds.) ASIACRYPT 2020, Part II. LNCS, vol. 12492, pp. 727–757. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64834-3_25
Dong, X., Zhang, Z., Sun, S., Wei, C., Wang, X., Hu, L.: Automatic classical and quantum rebound attacks on AES-like hashing by exploiting related-key differentials. In: Tibouchi, M., Wang, H. (eds.) ASIACRYPT 2021, Part I. LNCS, vol. 13090, pp. 241–271. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-92062-3_9
Duc, A., Guo, J., Peyrin, T., Wei, L.: Unaligned rebound attack: application to Keccak. In: Canteaut, A. (ed.) FSE 2012. LNCS, vol. 7549, pp. 402–421. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34047-5_23
Dunkelman, O., Keller, N., Shamir, A.: Improved single-key attacks on 8-round AES-192 and AES-256. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 158–176. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_10
Gauravaram, P., et al.: Grøstl - a SHA-3 candidate. In: Symmetric Cryptography, 11–16 January 2009 (2009)
Gilbert, H., Peyrin, T.: Super-Sbox cryptanalysis: improved attacks for AES-like permutations. In: Hong, S., Iwata, T. (eds.) FSE 2010. LNCS, vol. 6147, pp. 365–383. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13858-4_21
Grassi, L., Naya-Plasencia, M., Schrottenloher, A.: Quantum algorithms for the \(k\)-xor problem. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018, Part I. LNCS, vol. 11272, pp. 527–559. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03326-2_18
Guo, C., Katz, J., Wang, X., Yu, Y.: Efficient and secure multiparty computation from fixed-key block ciphers. In: 2020 IEEE Symposium on Security and Privacy, San Francisco, CA, USA, 18–21 May 2020, pp. 825–841 (2020)
Hosoyamada, A., Sasaki, Yu.: Cryptanalysis against symmetric-key schemes with online classical queries and offline quantum computations. In: Smart, N.P. (ed.) CT-RSA 2018. LNCS, vol. 10808, pp. 198–218. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76953-0_11
Hosoyamada, A., Sasaki, Yu.: Finding hash collisions with quantum computers by using differential trails with smaller probability than birthday bound. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020, Part II. LNCS, vol. 12106, pp. 249–279. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45724-2_9
Hosoyamada, A., Sasaki, Yu.: Quantum collision attacks on reduced SHA-256 and SHA-512. In: Malkin, T., Peikert, C. (eds.) CRYPTO 2021. LNCS, vol. 12825, pp. 616–646. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84242-0_22
Hosoyamada, A., Sasaki, Yu., Tani, S., Xagawa, K.: Improved quantum multicollision-finding algorithm. In: Ding, J., Steinwandt, R. (eds.) PQCrypto 2019. LNCS, vol. 11505, pp. 350–367. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-25510-7_19
Hosoyamada, A., Sasaki, Yu., Xagawa, K.: Quantum multicollision-finding algorithm. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part II. LNCS, vol. 10625, pp. 179–210. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70697-9_7
ISO/IEC. 10118-2:2010 Information technology—Security techniques – Hash-functions – Part 2: Hash-functions using an \(n\)-bit block cipher. 3rd edn., International Organization for Standardization, Geneve, Switzerland, October 2010
Jean, J., Fouque, P.-A.: Practical near-collisions and collisions on round-reduced ECHO-256 compression function. In: Joux, A. (ed.) FSE 2011. LNCS, vol. 6733, pp. 107–127. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21702-9_7
Jean, J., Naya-Plasencia, M., Peyrin, T.: Improved rebound attack on the finalist Grøstl. In: Canteaut, A. (ed.) FSE 2012. LNCS, vol. 7549, pp. 110–126. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34047-5_7
Jean, J., Naya-Plasencia, M., Peyrin, T.: Multiple limited-birthday distinguishers and applications. In: Lange, T., Lauter, K., Lisoněk, P. (eds.) SAC 2013. LNCS, vol. 8282, pp. 533–550. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43414-7_27
Kaplan, M., Leurent, G., Leverrier, A., Naya-Plasencia, M.: Breaking symmetric cryptosystems using quantum period finding. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part II. LNCS, vol. 9815, pp. 207–237. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_8
Kaplan, M., Leurent, G., Leverrier, A., Naya-Plasencia, M.: Quantum differential and linear cryptanalysis. IACR Trans. Symmetric Cryptol. 2016(1), 71–94 (2016)
Keller, M., Orsini, E., Scholl, P.: MASCOT: faster malicious arithmetic secure computation with oblivious transfer. In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016, pp. 830–842 (2016)
Khovratovich, D., Biryukov, A., Nikolic, I.: Speeding up collision search for byte-oriented hash functions. In: Fischlin, M. (ed.) CT-RSA 2009. LNCS, vol. 5473, pp. 164–181. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00862-7_11
Khovratovich, D., Nikolic, I., Rechberger, C.: Rotational rebound attacks on reduced Skein. J. Cryptol. 27(3), 452–479 (2014)
Knudsen, L.R., Rechberger, C., Thomsen, S.S.: The Grindahl hash functions. In: Biryukov, A. (ed.) FSE 2007. LNCS, vol. 4593, pp. 39–57. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74619-5_3
Kölbl, S., Lauridsen, M.M., Mendel, F., Rechberger, C.: Haraka v2 - efficient short-input hashing for post-quantum applications. IACR Trans. Symmetric Cryptol. 2016(2), 1–29 (2016)
Kuwakado, H., Morii, M.: Quantum distinguisher between the 3-round Feistel cipher and the random permutation. In: Proceedings of ISIT 2010, Austin, Texas, USA, 13–18 June 2010, pp. 2682–2685 (2010)
Kuwakado, H., Morii, M.: Security on the quantum-type Even-Mansour cipher. In: ISITA 2012, Honolulu, HI, USA, 28–31 October 2012, pp. 312–316 (2012)
Lamberger, M., Mendel, F., Rechberger, C., Rijmen, V., Schläffer, M.: Rebound distinguishers: results on the full Whirlpool compression function. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 126–143. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_8
Leander, G., May, A.: Grover meets Simon – quantumly attacking the FX-construction. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part II. LNCS, vol. 10625, pp. 161–178. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70697-9_6
Liu, Q., Zhandry, M.: On finding quantum multi-collisions. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part III. LNCS, vol. 11478, pp. 189–218. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_7
Matusiewicz, K., Naya-Plasencia, M., Nikolić, I., Sasaki, Yu., Schläffer, M.: Rebound attack on the full Lane compression function. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 106–125. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_7
Mendel, F., Peyrin, T., Rechberger, C., Schläffer, M.: Improved cryptanalysis of the reduced Grøstl compression function, ECHO permutation and AES block cipher. In: Jacobson, M.J., Rijmen, V., Safavi-Naini, R. (eds.) SAC 2009. LNCS, vol. 5867, pp. 16–35. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-05445-7_2
Mendel, F., Rechberger, C., Schläffer, M., Thomsen, S.S.: Rebound attacks on the reduced Grøstl hash function. In: Pieprzyk, J. (ed.) CT-RSA 2010. LNCS, vol. 5985, pp. 350–365. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11925-5_24
Mendel, F., Rechberger, C., Schläffer, M., Thomsen, S.S.: The rebound attack: cryptanalysis of reduced Whirlpool and Grøstl. In: Dunkelman, O. (ed.) FSE 2009. LNCS, vol. 5665, pp. 260–276. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03317-9_16
Mendel, F., Rijmen, V., Schläffer, M.: Collision attack on 5 rounds of Grøstl. In: Cid, C., Rechberger, C. (eds.) FSE 2014. LNCS, vol. 8540, pp. 509–521. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46706-0_26
Menezes, A., van Oorschot, P.C., Vanstone, S.A.: Handbook of Applied Cryptography. CRC Press (1996)
Merkle, R.C.: A certified digital signature. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 218–238. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_21
Naya-Plasencia, M.: How to improve rebound attacks. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 188–205. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_11
Naya-Plasencia, M., Schrottenloher, A.: Optimal merging in quantum \(k\)-xor and k-sum algorithms. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020, Part II. LNCS, vol. 12106, pp. 311–340. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45724-2_11
Naya-Plasencia, M., Toz, D., Varici, K.: Rebound attack on JH42. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 252–269. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_14
Sasaki, Yu.: Meet-in-the-middle preimage attacks on AES hashing modes and an application to Whirlpool. In: Joux, A. (ed.) FSE 2011. LNCS, vol. 6733, pp. 378–396. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21702-9_22
Sasaki, Yu., Li, Y., Wang, L., Sakiyama, K., Ohta, K.: Non-full-active Super-Sbox analysis: applications to ECHO and Grøstl. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 38–55. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_3
Sasaki, Yu., Wang, L., Wu, S., Wu, W.: Investigating fundamental security requirements on Whirlpool: improved preimage and collision attacks. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 562–579. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_34
Schläffer, M.: Updated differential analysis of Grøstl. Grøstl website, January 2011 (2011)
Shor, P.W.: Algorithms for quantum computation: discrete logarithms and factoring. In: 35th Annual Symposium on Foundations of Computer Science, Santa Fe, New Mexico, USA, 20–22 November 1994, pp. 124–134 (1994)
Stevens, M., Bursztein, E., Karpman, P., Albertini, A., Markov, Y.: The first collision for full SHA-1. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 570–596. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_19
van Oorschot, P.C., Wiener, M.J.: Parallel collision search with cryptanalytic applications. J. Cryptol. 12(1), 1–28 (1999)
Wang, X., Yin, Y.L., Yu, H.: Finding collisions in the full SHA-1. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 17–36. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_2
Wang, X., Yu, H.: How to break MD5 and other hash functions. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 19–35. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_2
Acknowledgments
We would like to thank the anonymous reviewers from EUROCRYPT 2022 and CRYPTO 2022 for their valuable comments. This research is partially supported by Nanyang Technological University in Singapore under Grant 04INS000397C230, Ministry of Education in Singapore under Grants RG91/20 and MOE2019-T2-1-060, and National Natural Science Foundation of China (61961146004). Xiaoyang Dong is supported by National Key R &D Program of China (2018YFA0704701), the Major Program of Guangdong Basic and Applied Research (2019B030302008), Major Scientific and Technological Innovation Project of Shandong Province, China (2019JZZY010133), Natural Science Foundation of China (61902207).
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 International Association for Cryptologic Research
About this paper
Cite this paper
Dong, X., Guo, J., Li, S., Pham, P. (2022). Triangulating Rebound Attack on AES-like Hashing. In: Dodis, Y., Shrimpton, T. (eds) Advances in Cryptology – CRYPTO 2022. CRYPTO 2022. Lecture Notes in Computer Science, vol 13507. Springer, Cham. https://doi.org/10.1007/978-3-031-15802-5_4
Download citation
DOI: https://doi.org/10.1007/978-3-031-15802-5_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-15801-8
Online ISBN: 978-3-031-15802-5
eBook Packages: Computer ScienceComputer Science (R0)













 ’ are known. In Fig.
’ are known. In Fig.  ,
,
 , and
, and
 . Then deduce
. Then deduce
 .
. ’, compute
’, compute  ’ in
’ in  , we get
, we get
 . Then
. Then
 is deduced.
is deduced. :
:  ’ are deduced. Then, two bytes marked by ‘
’ are deduced. Then, two bytes marked by ‘
 ’ in
’ in  ’ in
’ in  ’ in
’ in 
 ’ are deduced from those marked by ‘
’ are deduced from those marked by ‘
 ’.
’.



 . Compute
. Compute
 . Similarly, compute all other cells marked by “
. Similarly, compute all other cells marked by “
 ” and “
” and “
 ”.
”. ” and “
” and “
 ” cells by the “
” cells by the “
 ” cells. Guess
” cells. Guess  and
and
 by Property
by Property  . Guess
. Guess  and
and
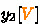 by Property
by Property  and
and
 .
. and
and
 . Deduce
. Deduce
 and
and
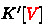 . Compute
. Compute
 .
.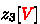 and
and
 . Compute
. Compute
 and
and
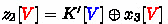 . Compute
. Compute
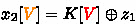 .
. and
and
 . Compute
. Compute
 . Compute
. Compute
 , so that the 2nd column and 3rd column of
, so that the 2nd column and 3rd column of 
