Keywords

1 Introduction

Laminated composite structures with superior properties such as high stiffness and high strength-to-weight ratio and light weight have been increasingly used in many advanced engineering structures [1]. In the automobile industry, the laminated composite structures have been increasingly used to replace the conventional metallic structures for saving weight and to increase the energy efficiency. The high-level vibrations can result in problems such as fatigue failure, destruction of mechanical system and high noise. There is a need for deeper understanding of vibration behaviour of laminated composite structures.

There have been a large number of studies on the free vibration behaviour of laminated composite panels based on several theories such as the classical laminate plate theory, first [2] and third-order shear deformation theory [3], and higher-order refined theory [4] to improve the accuracy of analytical methods. However, there have been much less studies reported on effects of the fiber orientations on vibration behaviour of the laminated composite panels subjected to complex dynamic loading. For instance, Dobyns [5] and Carvalho et al. [6] proposed a theoretical approach for vibration analysis of simply-supported rectangular laminated composite plate. Dynamic responses of laminated composite plates with respect to effects of various fiber orientations and stacking sequences were studied [7, 8]. The fibers could be tailored for vibration suppression designs [9, 10].

This paper presents an analytical approach and numerical FE method to examine the vibration behaviour of harmonically excited laminated composite panels with simply supported edges. Analytical method based on the first-order shear deformation theory (FSDT) can be used for special symmetric cross-ply laminated composite panel. For the laminated composite panels with various fiber orientations, the numerical ANSYS finite element (FE) method is used for investigation and validation of the analytical results. The dynamic responses are determined and compared with that of the steel panel. The effects of fiber orientations on the dynamic behaviour are examined.

2 Dynamic Analysis of Laminated Composite Panels

2.1 Model Description

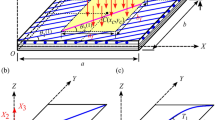
Figure 1 shows the schematic illustration of a four-layered laminated composite rectangular panel with length \(a\) and width \(b\) and thickness \(h\) in the directions of \(OX\), \(OY\) and \(OZ\), respectively. Its four edges are simply supported and a harmonic external excitation force with amplitude \({\tilde{f }}_{\mathrm{e}}\) and frequency \(\omega \) is applied at the point \({\text{A}}(x_e ,y_e )\). Also a general point \({\text{B}}(x_r ,y_r )\) is labelled in the Fig. 1 for which the response is of interest. The angle \({\theta }_{i}\) that is measured from the positive direction of \(OX\) to the principal material axis is used to indicate the fiber orientation of the i-th layer.

The constitutive equations for orthotropic lamina can be written as [1]:

$$ \left[ {\begin{array}{*{20}c} {\sigma _1 } \\ {\sigma _2 } \\ {\tau _{12} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{12} } & {Q_{22} } & 0 \\ 0 & 0 & {Q_{66} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon _1 } \\ {\varepsilon _2 } \\ {\gamma _{12} } \\ \end{array} } \right],\left[ {\begin{array}{*{20}c} {\tau _{23} } \\ {\tau _{13} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {Q_{44} } & 0 \\ 0 & {Q_{55} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\gamma _{23} } \\ {\gamma _{13} } \\ \end{array} } \right], $$
(1a-1b)

where \({Q}_{ij}(i,j=\mathrm{1,2},6)\) are the material constants in the material axes of the layer expressed by

$${Q}_{11}=\frac{{E}_{1}}{1-{\nu }_{12}{\nu }_{21}}, Q_{12} = \frac{{\nu _{12} E_2 }}{{1 - \nu _{12} \nu _{21} }} = \frac{{\nu _{12} E_1 }}{{1 - \nu _{12} \nu _{21} }},Q_{22} = \frac{{E_2 }}{{1 - \nu _{12} \nu _{21} }}, $$
$${Q}_{66}={G}_{12}, Q_{44} = G_{23} ,Q_{55}= G_{13} , $$

where \({E}_{11}\) and \({E}_{22}\) are the in-plane moduli of elasticity in local coordinate system, \({G}_{ij}\) are the shear moduli, while \({\nu }_{ij}\) are the Poisson’s coefficients of the orthotropic materials. The stress-strain relations for the i-th orthotropic layer in the local coordinate system are

$$\ \left[ {\begin{array}{*{20}c} {\sigma _x } \\ {\sigma _y } \\ {\tau _{xy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\bar{Q}_{11} } & {\bar{Q}_{12} } & 0 \\ {\bar{Q}_{12} } & {\bar{Q}_{22} } & 0 \\ 0 & 0 & {\bar{Q}_{66} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon _x } \\ {\varepsilon _y } \\ {\gamma _{xy} } \\ \end{array} } \right],\left[ {\begin{array}{*{20}c} {\tau _{yz} } \\ {\tau _{xz} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\bar{Q}_{44} } & 0 \\ 0 & {\bar{Q}_{55} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\gamma _{yz} } \\ {\gamma _{xz} } \\ \end{array} } \right]. $$
(2)

The constitutive relations can be transformed from the local coordinate system to the global coordinate system by using the following transformation matrix:

$$\left[{T}_{1}\right]=\left[\begin{array}{ccc}{\mathrm{cos}}^{2}\theta & {\mathrm{sin}}^{2}\theta & 2\mathrm{sin}\,\theta\, \mathrm{cos}\,\theta \\ {\mathrm{sin}}^{2}\theta & {\mathrm{cos}}^{2}\theta & -2\mathrm{sin}\,\theta \mathrm{cos}\,\theta \\ -\mathrm{sin}\,\theta\, \mathrm{cos}\,\theta & \mathrm{sin}\,\theta\, \mathrm{cos}\,\theta & {\mathrm{cos}}^{2}\theta -{\mathrm{sin}}^{2}\theta \end{array}\right], \left[{T}_{2}\right]=\left[\begin{array}{cc}\mathrm{cos}\,\theta & -\mathrm{sin}\,\theta \\ \mathrm{sin}\,\theta & \mathrm{cos}\,\theta \end{array}\right].$$
(3)

The stiffness matrix for the i-th layer in global coordinate system can be obtained from

$$\left[\bar{Q }\right]={\left({\left[T\right]}^{(i)}\right)}^{-1}{\left[Q\right]}^{(i)}{\left[T\right]}^{(i)}.$$
(4)
Fig. 1.
figure 1

Schematic illustrations of a laminated composite rectangular panel with simply supported (SS) edges.

Full size image

2.2 Vibration Analysis of Laminated Composite Panels

For a symmetric cross-ply orthotropic plate, some of stress stiffness coefficients can be assumed as zero, \({B}_{ij}=0, {A}_{16}={A}_{26}={D}_{16}={D}_{26}=0\). Hence, the equations of motion are

$$k{A}_{44}\left({{w}^{0}}_{,yy}+{\phi }_{y,y}\right)+k{A}_{55}\left({{w}^{0}}_{,xx}+{\phi }_{x,x}\right)+{p}_{z}=\rho h{\ddot{w}}^{0},$$
(5a)
$${D}_{11}{\phi }_{x,xx}+\left({D}_{12}+{D}_{66}\right){\phi }_{y,xy}+{D}_{66}{\phi }_{x,yy}-{kA}_{55}\left({{w}^{0}}_{,x}+{\phi }_{x}\right)=\frac{\rho {h}^{3}}{12}{\ddot{\phi }}_{x},$$
(5b)
$${D}_{66}{\phi }_{y,xx}+\left({D}_{12}+{D}_{66}\right){\phi }_{x,xy}+{D}_{22}{\phi }_{y,yy}-{kA}_{44}\left({{w}^{0}}_{,y}+{\phi }_{y}\right)=\frac{\rho {h}^{3}}{12}{\ddot{\phi }}_{y},$$
(5c)

where \(h\) is the plate thickness, \(\rho \) is material density, \(w\) is the plate displacement in the \(OZ\) direction at the plate midplane, \({\phi }_{x}\) and \({\phi }_{y}\) are the shear rotations on the \(OY\) and \(OX\) directions. \(k\) is used to account for the effect of shear deformation, which is normally taken as \(5/6\).

With simply supported edges, we have

$$ \begin{aligned} & w = \phi_{x,x} = 0,\,{\text{at}}\,x = 0,\,{\text{and}}\,x = a. \\ & w = \phi_{y,y} = 0,\,{\text{at}}\,y = 0,\,{\text{and}}\,y = b. \\ \end{aligned} $$

The solution of the dynamic response is based on expansions of the loads, displacement and rotations in double Fourier series. Each expression is the product of independent time coefficients by trigonometric functions, which satisfy the boundary condition:

$${\phi }_{x}\left(x,y,t\right)=\sum\nolimits_{m}\sum\nolimits_{n}{A}_{mn}(t)\mathrm{cos}\,\alpha x\,\mathrm{sin}\,\beta y,$$
(6a)
$${\phi }_{y}\left(x,y,t\right)=\sum\nolimits_{m}\sum\nolimits_{n}{B}_{mn}(t)\mathrm{sin}\,\alpha x\,\mathrm{cos}\,\beta y,$$
(6b)
$$w\left(x,y,t\right)=\sum\nolimits_{m}\sum\nolimits_{n}{W}_{mn}(t)\mathrm{sin}\,\alpha x\,\mathrm{sin}\,\beta y,$$
(6c)

where \(\alpha =m\pi /a\), \(\beta =n\pi /b\), \(m\) and \(n\) are integers, and \({A}_{mn}(t)\), \({B}_{mn}(t)\) and \({W}_{mn}(t)\) are the time-dependent coefficients. The load function is represented by

$$q\left(x,y,t\right)=\sum\nolimits_{m}\sum\nolimits_{n}{Q}_{mn}(t)\mathrm{sin}\,\alpha x\,\mathrm{sin}\,\beta y.$$
(7)

For a concentrated load located at the point A \(\left({x}_{e},{y}_{e}\right)\), we have

$${Q}_{mn}\left(t\right)=\frac{4F(t)}{ab}\mathrm{sin}\,\alpha {x}_{e}\,\mathrm{sin}\,\beta {y}_{e}.$$
(8)

A substitution of Eq. (6) into Eq. (5) leads to

$$\left[\begin{array}{ccc}{L}_{11}& {L}_{12}& {L}_{13}\\ {L}_{12}& {L}_{22}& {L}_{23}\\ {L}_{13}& {L}_{23}& {L}_{33}\end{array}\right]\left\{\begin{array}{c}{A}_{mn}(t)\\ {B}_{mn}(t)\\ {W}_{mn}(t)\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\\ {Q}_{mn}\left(t\right)-\mu {\ddot{W}}_{mn}(t)\end{array}\right\},$$
(9)

where \(\mu =\rho h\) is mass per unit area and the elements of the symmetric matrix \({L}_{ij}\) are

$${L}_{11}={D}_{11}{(\alpha )}^{2}+{D}_{66}{(\beta )}^{2}+\kappa {A}_{55}, L_{12} = \left( {D_{12} + D_{66} } \right)\alpha \beta ,L_{13} = \kappa A_{55} \alpha ,$$
$${L}_{22}={D}_{66}{(\alpha )}^{2}+{D}_{22}{(\beta )}^{2}+\kappa {A}_{44}, L_{33} = \kappa A_{55} \left( \alpha \right)^2 + \kappa A_{44} \left( \beta \right)^2 ,L_{23} = \kappa A_{44} \beta . $$

The Eq. (9) can be reduced to a single differential equation by the following transformation:

$${A}_{mn}\left(t\right)=\frac{{L}_{12}{L}_{23}-{L}_{13}{L}_{22}}{{L}_{11}{L}_{22}-{{L}_{12}}^{2}}{W}_{mn}(t),$$
(10a)
$${B}_{mn}\left(t\right)=\frac{{L}_{12}{L}_{13}-{L}_{11}{L}_{23}}{{L}_{11}{L}_{22}-{{L}_{12}}^{2}}{W}_{mn}(t).$$
(10b)

The equation of motion for a rectangular panel can be expressed as

$${\ddot{W}}_{mn}\left(t\right)+{{{\omega }_{mn}}^{2}W}_{mn}\left(t\right)=\frac{{Q}_{mn}\left(t\right)}{\mu },$$
(11)

where the natural frequency can be obtained from:

$${\omega }_{mn}=\sqrt{\frac{{L}_{13}{K}_{A}+{L}_{23}{K}_{B}+{L}_{33}}{\mu }}.$$
(12)

To solve the equation of motion, the modal displacement can be written as

$${W}_{mn}\left(t\right)=X{\mathrm{e}}^{\mathrm{i}(\omega t-\theta )}=\left(X{\mathrm{e}}^{-\mathrm{i}\theta }\right){\mathrm{e}}^{\mathrm{i}\omega t}={\overline{{W }_{mn}}}{\mathrm{e}}^{\mathrm{i}\omega t}.$$
(13)

In a damped system, the damping effect can be included by multiplying the stiffness term by a factor of \((1+\mathrm{i}\eta )\), where \(\eta \) denotes the structural damping. The displacement can be obtained and expressed as:

$$ \widetilde{w} \left(x,y,t\right)=\frac{4}{ab\mu }\sum\nolimits_{m}\sum\nolimits_{n}\mathrm{sin}\,\alpha {x}_{e}\,\mathrm{sin}\,\beta {y}_{e}\,\mathrm{sin}\,\alpha x\,\mathrm{sin}\,\beta y\times \frac{{\tilde{f }}_{\mathrm{e}}}{{{\omega }_{mn}}^{2}\left(1+\mathrm{i}\eta \right){-\omega }^{2}}{\mathrm{e}}^{\mathrm{i}\omega t}.$$
(14)

3 Results and Discussions

Here a rectangular panel with dimensions of 1 m by 0.5 m with total thickness of 0.005 m is considered. The material used for composite panel is T300/934 CFRP and the material properties are set as \({E}_{11}=120\) GPa, \({E}_{22}={E}_{33}=7.9\) GPa, \({G}_{12}={G}_{13}=5.5\) GPa, \({G}_{23}=1.58\) GPa, \({\nu }_{12}={\nu }_{13}=0.33\), \({\nu }_{23}=0.022\), \(\rho =1580\, \mathrm{kg}/{\mathrm{m}}^{3}\). The material properties used for the counterpart steel panel are listed as: \(E=205.8\) GPa, \(\rho =7800\, \mathrm{kg}/{\mathrm{m}}^{3}\) and \(\nu =0.3\). The structural damping coefficient \(\eta \) is \(0.01\). Both analytical and numerical ANSYS FE methods are employed for the free and forced vibration analysis of different types of panels. The free vibration analysis of a steel panel is carried out analytically based on the classical plate theory (CPT) and that of laminated composite panels with specific fiber orientation such as \({\left[{0}{^\circ }\right]}_{4}\) and \({\left[9{0}{^\circ }\right]}_{4}\) can be conducted by analytical method based on FSDT. The numerical FE method using element Shell 281 based on FSDT is used when the analytical method for the laminated composite panels with various fiber orientation is not available.

Table 1 shows first five natural frequencies (in Hz) of different steel and laminated composite panels. The numerical and analytical results show good agreement, verifying both methods. It is found that first five natural frequencies of the steel panel are larger than those of the \({\left[{0}{^\circ }\right]}_{4}\) laminated composite panel. It shows that the fundamental frequency of the steel panel is larger than that of the \({\left[{0}{^\circ }\right]}_{4}\), \({\left[{30}{^\circ }\right]}_{4}\) and \({\left[{45}{^\circ }\right]}_{4}\) laminated composite panels but lower than that of the \({\left[{60}{^\circ }\right]}_{4}\) and \({\left[{90}{^\circ }\right]}_{4}\) laminated composite panels. An increase in the fiber angle \(\theta \) leads to the increase of fundamental frequencies. It is found that the second natural frequencies decrease firstly and then increase when angle \(\theta \) changes from \({0}{^\circ }\) to \({90}{^\circ }\). The third, fourth and fifth natural frequencies are increased with fibre orientation with a maximum value being reached and then they are decreased.

Table 1. First five natural frequencies (in Hz) of different types of panels
Full size table

Figure 2 shows that dynamic responses of the steel panel and the \({\left[{0}{^\circ }\right]}_{4}\) panel at the forcing position (0.5 m, 0.25 m) in an examined frequency range of 0–500Hz. The solid and dashed lines represent the analytical results for steel and laminated composite panels, respectively and the corresponding numerical results from FE are denoted by circles and squares. It shows that the analytical results have a great agreement with FE results especially in the low-frequency range. It is found that at a lower excitation frequency, the laminated composite panel exhibits relatively high vibration responses. It is found that the peak amplitudes of laminated composite panel are higher than those of the considered steel panel. The steel panel with heavy weight has relatively lower dynamic responses when subjected to the excitation force.

Fig. 2.
figure 2

Dynamic responses at the centre point (0.5 m, 0.25 m) on the steel panel and the laminated composite \({\left[{0}{^\circ }\right]}_{4}\) panel with the excitation at the same point.

Full size image

Figure 3 shows the variations of the dynamic responses at the forcing position with the excitation frequency. In this case, the effects of fiber orientations such as \({0}{^\circ }\), \({30}{^\circ }\), \({45}{^\circ }\) and \({60}{^\circ }\) on the dynamic responses are examined. It is found that with the increase of fibre angles from \({0}{^\circ }\) to \({60}{^\circ }\), the first resonance peak is shifted to the higher frequency and the peak values are effectively reduced. The first resonance frequency of the \({\left[{60}{^\circ }\right]}_{4}\) panel is larger than that of steel panel. The frequency range between the first and the second peaks of the laminated composite panels are narrowed with the increase of the fiber angle. The frequency range between the first and second peaks of the \({\left[{0}{^\circ }\right]}_{4}\) panel is the widest. In the frequency band, the panel has relatively low dynamic response. In the frequency range approximately from 200 to 350 Hz, the vibration level of the steel panel is lower than that of laminated composite panels, whereas those of the laminated composite panels in the frequency range of 150 to 200 Hz are lowered. It demonstrates that reinforced composite laminates have an ability of reducing vibration levels in a described excitation frequency range and the peak values of dynamic response can be reduced by tailoring the fiber orientations.

In Fig. 4, the vibration transmission is investigated by examining the influences of fiber angles on the ratio \({R}_{\mathrm{t}}\) between the dynamic response amplitude of point B (0.75 m, 0.25 m) to that of the input point A (0.25 m, 0.25 m). In a lower frequency range of 0–55 Hz, it is found that the response amplitude ratio of the \({\left[{0}{^\circ }\right]}_{4}\) panel is larger than in other cases. With the increase of fiber angle, the first peak of \({R}_{\mathrm{t}}\) is moved to larger frequencies. The first peak value of the \({\left[{60}{^\circ }\right]}_{4}\) panel is the lowest, which indicates a low vibration transmission level. The first and second peak values of the \({\left[{0}{^\circ }\right]}_{4}\) panel and the steel panel are close with the same vibration transmission behaviour. The frequency range between the first and second peak can be narrowed by increasing the fiber angle from \({0}{^\circ }\) to \({60}{^\circ }\).

Fig. 3.
figure 3

Dynamic responses at the centre point (0.5 m, 0.25 m) on the steel panel and laminated composite panels with different fiber angles. —: the steel panel; ------: the \({\left[{0}{^\circ }\right]}_{4}\) panel; -·-·-·-: the \({\left[{30}{^\circ }\right]}_{4}\) panel; - - -: the \({\left[{45}{^\circ }\right]}_{4}\) panel; ······: the \({\left[{60}{^\circ }\right]}_{4}\) panel.

Full size image
Fig. 4.
figure 4

Ratio between response amplitudes at Points B (0.75m, 0.25m) and A (0.25 m, 0.25 m) of the steel panel and laminated composite panels with different fiber angles. —: the steel panel; ------: the \({\left[{0}{^\circ }\right]}_{4}\) panel; -·-·-·-: the \({\left[{30}{^\circ }\right]}_{4}\) panel; - - -: the \({\left[{45}{^\circ }\right]}_{4}\) panel; ······: the \({\left[{60}{^\circ }\right]}_{4}\) panel.

Full size image

4 Conclusions

This paper presented the free and forced vibration characteristics of rectangular laminated composite panels with various fiber orientations such as \({\left[{0}{^\circ }\right]}_{4}\), \({\left[{30}{^\circ }\right]}_{4}\), \({\left[{45}{^\circ }\right]}_{4}\) and \({\left[{60}{^\circ }\right]}_{4}\), with comparisons to vibration performance of a steel panel. The analytical method based on the FSDT has been shown to be accurate by verification with numerical ANSYS finite element results. This proposed method can be applied in investigation of forced vibration response at any designated positions. For panels with complex fiber orientations, the numerical FE method has been employed. The results showed that resonance peak values of dynamic responses of the steel panel are generally lower than that of laminated composite panels. The vibration responses and vibration transmission at a prescribed frequency can be reduced and designed by tailoring fiber orientation. The findings show the potential advantages of laminated composite panels with large design space to reduce the vibration level with reduced weight.