Abstract
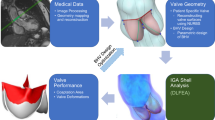
Volumetric meshes with hexahedral elements are generally best for stress analysis using finite element (FE) methods. With recent interests in finite element analysis (FEA) for Transcatheter Aortic Valve Replacement (TAVR) simulations, fast and accurate generation of patient-specific volumetric meshes of the aortic valve is highly desired. Yet, most existing automated image-to-mesh valve modeling strategies have either only produced surface meshes or relied on simple offset operations to obtain volumetric meshes, which can lead to undesirable artifacts. Furthermore, most recent advances in deep learning-based meshing techniques have focused on watertight surface meshes, not volumetric meshes. To fill this gap, we propose a novel volumetric mesh generation technique using template-preserving distortion energies under the deep learning-based deformation framework. Our model is trained end-to-end for image-to-mesh prediction, and our mesh outputs have good spatial accuracy and element quality. We check the FEA-suitability of our model-predicted meshes using a valve closure simulation. Our code is available at https://github.com/danpak94/Deep-Cardiac-Volumetric-Mesh.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
For stress analyses using finite element (FE) methods, volumetric meshes with hexahedral elements lead to most accurate results and better convergence [25]. With recent interests in finite element analysis (FEA) for Transcatheter Aortic Valve Replacement (TAVR) simulations [2, 28], fast and accurate generation of patient-specific volumetric meshes of the aortic valve is highly desired. Yet, most existing automated valve modeling strategies have only focused on voxel-wise segmentation [15], surface meshes, [7, 18] or volumetric meshes generated by simple offset operations [6, 12]. Although offsetting is viable for certain initial surface meshes, it quickly becomes ill-defined when combining multiple components or modeling structures with high curvature. Post-processing can mitigate some of these problems, but it limits usability by non-experts during test time. In this work, we aim to address this limitation by learning an image-to-mesh model that directly outputs optimized volumetric meshes.
Most existing valve modeling approaches have used template deformation strategies [4, 7, 12, 16]. We adopt a similar approach, as it ensures mesh correspondence between model predictions for easy application to downstream tasks (e.g. shape analysis or batch-wise FEA). Some previous works have used sequential localization + deformation-along-surface-normals and/or hand-crafted image features [7, 12], both of which limit the methods’ adaptability to image and template mesh variations. Instead, we focus on deep learning-based deformation methods [3, 16, 27, 30], which addresses both of these limitations by (1) not limiting the deformation to the surface normal directions and (2) learning image features via end-to-end training. Deep learning also has additional benefits such as fast inference and the ability to generate diffeomorphic deformation field [3].
Mesh deformation in computer graphics aims to match the user-defined locations of handle points while preserving the mesh’s geometric detail [1, 24]. Unfortunately, the same formulation is not ideal for valve modeling because it is difficult to define proper handle points and their desired locations on 3D images for the flexible valve components. Instead, we apply the idea of minimizing the mesh distortion energy into our deep learning pipeline, while enforcing spatial accuracy through surface distance metrics.
In summary, we propose a novel deep learning image-to-mesh model for volumetric aortic valve meshes. Our contributions include: (1) identifying two effective deformation strategies for this task, (2) incorporating distortion energy into both strategies for end-to-end learning, and (3) generating volumetric meshes from just the base surface training labels (i.e. surface before adding thickness).
2 Methods
2.1 Template Deformation-Based Mesh Generation
Template deformation strategies aim to find the optimal displacement vectors \(\delta \) for every vertex \(v_i \in V\) of a mesh M, where \(M = (V, \mathcal {E})\) is a graph with nodes V and edges \(\mathcal {E}\). Then, the optimization over a loss \(\mathcal {L}\) is:
where M and \(M_0\) are target and template meshes, respectively. We used deep learning models as our function approximator \(h_\theta (I; M_0) = \delta \), where I is the image and \(\theta \) is the network parameters. Thus, we ultimately solved for \(\theta \):
where \(\varOmega \) is the training set distribution. We experimented with two variations of \(h_{\theta }\), as detailed below. Both models are shown schematically in Fig. 1.
2.1.1 Space Deformation Field (U-Net)
For the first variation, we designed \(h_\theta \) to be a convolutional neural network (CNN) that predicts a space deforming field \(\phi \in \mathbb {R}^{H \times W \times D \times 3}\) for each \(I \in \mathbb {R}^{H \times W \times D}\). From \(\phi \), we trilinearly interpolated at \(V_0\) to obtain \(\delta \). To obtain a dense topology-preserving smooth field, we used the diffeomorphic B-spline transformation implemented by the Airlab library [22]. In this formulation, the loss typically consists of terms for task accuracy and field regularization [3, 21]:
where \(\mathcal {L}\) from Eq. 1 is modified to include \(\phi \), which fully defines \(\delta \). P is point sampling on the mesh surface, where for a volumetric mesh such as \(\phi (M_0)\), points are sampled on the extracted base surface. In this work, \(L_{acc}\) is fixed for all methods to be the symmetric Chamfer distance:
For baseline comparison, we used the bending energy for \(\mathcal {L}_{smooth}\) [11, 21]. For our final proposed method, however, we show that the proposed distortion energy is able to replace \(\mathcal {L}_{smooth}\) and produce better results.
2.1.2 Node-Specific Displacement Vectors (GCN)
For the second variation of \(h_\theta \), we directly predicted \(\delta \) using a combination of a CNN and a graph convolutional network (GCN), similar to [5, 27]. The intuition is to have the CNN extract useful imaging features and combine them with the GCN using the graph structure of \(M_0\). In this formulation, it is difficult to restrict node-specific displacements to be smooth or topology-preserving. Instead, the loss typically consists of metrics for task accuracy and mesh geometric quality:
where \(\mathcal {L}_{acc}\) is defined by Eq. 4. Similar to the space deformation method, we established the baseline with common \(\mathcal {L}_{geo}\) terms (\(\mathcal {L}_{normal}\), \(\mathcal {L}_{edge}\), \(\mathcal {L}_{lap}\) with uniform edge weights) [5, 10, 27, 30]. For our final proposed method, we show that the proposed distortion energy is able to replace \(\mathcal {L}_{geo}\) and produce better results.
2.2 Distortion Energy (\(\mathcal {L}_{arap})\)
Although \(\mathcal {L}_{smooth}\) and \(\mathcal {L}_{geo}\) have been effective in their proposed domains, they are not ideal for volumetric mesh generation, especially when we only use the base surface labels for training. To preserve the volumetric mesh quality of \(\delta (M_0)\), we used the deformation gradient \(\mathbf {F}\) to allow for the calculation of various distortion energies [8]. For each tetrahedral element with original nodes \(\bar{\mathbf {x}}_i\) and transformed nodes \(\mathbf {x}_i = \delta _i(\bar{\mathbf {x}}_i)\):
which can be broken down into rotation and stretch components using the polar decomposition: \(\mathbf {F} = \mathbf {RS}\). More specifically, we can use singular value decomposition (SVD) to obtain \(\mathbf {F} = \mathbf {U} \mathrm {\Sigma } \mathbf {V}^T\), from which we can calculate \(\mathbf {R} = \mathbf {U}\mathbf {V}^T\) and \(\mathbf {S} = \mathbf {V} \mathrm {\Sigma } \mathbf {V}^T\). Using these components, we can derive various task-related distortion energies [8, 24]. We used the as-rigid-as-possible (ARAP) energy, a widely used energy for geometry processing. The ARAP energy density for each \(i^\text {th}\) element can be expressed as:
where \(\mathbf {I}\) is the identity matrix and \(\left\Vert \cdot \right\Vert _F\) is the Frobenius norm. Assuming equal weighting, \(\mathcal {L}_{arap} = \frac{1}{N} \sum _{i=1}^\text {N} \varPsi _{arap}(i)\) for N elements. Note that all operations are fully differentiable and therefore suitable for end-to-end learning, as long as \(\mathbf {F}\) is full rank (i.e. no degenerate elements) and \(\mathrm {\Sigma }\) has distinct singular values (i.e. \(\mathbf {F} \ne \mathbf {I}\)). In our experiments, both conditions were satisfied as long as we initialized \(\delta \) with randomization. Computing \(\mathbf {F}\) for hexahedral elements involves using quadrature points, but we were able to obtain just as accurate results in less training time by simply splitting each hexahedron into 6 tetrahedra and using the above formulation.
2.3 Weighted \(\mathcal {L}_{arap}\) (\(\mathcal {L}_{warap}\))
Due to the large structural differences in the leaflets during valve opening and closing, imposing \(\mathcal {L}_{arap}\) with one template leads to suboptimal results. We addressed this with a simple weighting strategy:
where \(\alpha \) is the softmax of distances from the output to the closed and open templates: \(\alpha (i) = 1 - \exp (\mathcal {L}_{acc}(M_{0,i}, \delta (M_0))) / \sum _i \exp (\mathcal {L}_{acc}(M_{0,i}, \delta (M_0)))\). The final loss of our proposed method is then:
3 Experiments and Results
3.1 Data Acquisition and Preprocessing
We used a dataset of 88 CT scans from 74 different patients, all with tricuspid aortic valves. Of the 88 total scans, 73 were collected from IRB-approved TAVR patients at the Hartford hospital, all patients being 65–100 years old. The remaining 15 were from the training set of the MM-WHS public dataset [31]. For some Hartford scans, we included more than one time point. The splits for training, validation, and testing were 40, 10, 38, respectively, with no patient overlap between the training/validation and testing sets. We pre-processed all scans by thresholding the Hounsfield Units and renormalizing to [0, 1]. We resampled all images to a spatial resolution of \(1 \times 1 \times 1\) mm\(^3\), and cropped and rigidly aligned them using three manually annotated landmarks, resulting in final images with [64, 64, 64] voxels.
We focused on 4 aortic valve components: the aortic wall and the 3 leaflets. The ground truth mesh labels were obtained via a semi-automated process [12], which included manually annotating the component boundaries and points on the surface. Commissures and hinges were separately labeled to assess correspondence accuracy. Two mesh templates for open and closed valves were created using Solidworks and Hypermesh, with the representative anatomical parameters in [26]. Each template has 19086 nodes and 9792 linear hexahedral elements.
Mesh predictions using space deformation (U-net) and node-specific displacements (GCN), with baseline regularization terms vs. \(\mathcal {L}_{warap}\). The zoomed-in parts demonstrate the main advantage of our approach - good volumetric mesh quality throughout the entire mesh (shape closer to cube is better).
3.2 Implementation Details
We used Pytorch ver. 1.4.0 [17] to implement a variation of a 3D U-net for our CNN [20], and Pytorch3d ver. 0.2.0 [19] to implement the GCN. The basic CNN Conv unit was Conv3D-InstanceNorm-LeakyReLu, and the network had 4 encoding layers of ConvStride2-Conv with residual connections and dropout, and 4 decoding layers of Concatenation-Conv-Conv-Upsampling-Conv. The base number of filters was 16, and was doubled at each encoding layer and halved at each decoding layer. The GCN had 3 layers of graph convolution operations defined as \(ReLU(\mathbf {w}_0^T \mathbf {f}_i + \sum _{j \in \mathcal {N}(i)} \mathbf {w}_1^T \mathbf {f}_j)\) and a last layer without ReLU. The input to the initial GCN layer was concatenation of vertex positions and point-sampled features from the last 3 U-net decoding layers. The GCN feature sizes were 227 for input, 128 for hidden, and 3 for output layers. We found \(\lambda \) for every experiment with a grid search based on validation error, ranging 5 orders of magnitude. \(\lambda = 5\) for \(\mathcal {L}_{warap}\). The value of \(\lambda \) is crucial for all experiments, but results were generally not too sensitive within one order of magnitude. We used the Adam optimizer [9] with a fixed learning rate of 1e−4, batch size of 1, and 2000 training epochs. The models were trained with a B-spline deformation augmentation step, resulting in 80k training samples. All operations were performed on a single NVIDIA GTX 1080 Ti, with around \(\sim \)24 h of training time and maximum GPU memory usage of \(\sim \)1.2 GB. Inference takes \(\sim \)20 ms per image.
3.3 Spatial Accuracy and Volumetric Mesh Quality
We evaluated the mean and worst-case surface accuracy of our predicted meshes using the symmetric Chamfer distance (divided by 2 for scale) and Hausdorff distance, respectively. Note that the ground truth meshes are surface meshes, so we extracted the base surface of our predicted volumetric meshes for these calculations. For correspondence error, we measured the distance between hand-labeled landmarks (3 commissures and 3 hinges) and specific node positions on the predicted meshes. We also checked the predicted meshes’ geometric quality using the scaled Jacobian determinant (−1 to 1; 1 being an optimal cube) and skew metrics (0 to 1; 1 being a degenerate element) [23]. Statistical significance was evaluated with a paired Student’s t-test between our proposed method vs. the baseline/ablation experimental groups. The baseline was established with U-net + \(\mathcal {L}_{smooth}\) and GCN + \(\mathcal {L}_{geo}\), and the ablation study was for comparing against non-weighted \(\mathcal {L}_{arap}\).
For both deformation strategies, our proposed method with \(\mathcal {L}_{warap}\) holistically outperformed the baseline and non-weighted \(\mathcal {L}_{arap}\) (Table 1, Fig. 2, 3). As expected, the most significant improvement was in element quality, and our method also showed slight improvements in spatial accuracy. Our model was robust to the noisy TAVR CT scans riddled with low leaflet contrast and lots of calcification, and was applicable to various phases of the cardiac cycle.
3.4 FE Stress Analysis During Valve Closure
Figure 4 shows the results of FEA performed with volumetric meshes generated directly from our method (i.e. no post-processing). We used an established protocol [12, 29] with the static and nonlinear analysis type on Abaqus/Standard. Briefly, we simulated valve closure during diastole by applying an intraluminal pressure (P = 16 kPa) to the upper surface of the leaflets and coronary sinuses and a diastolic pressure (P = 10 kPa) to the lower portion of the leaflets and intervalvular fibrosa. The resulting maximum principal stresses in the aortic wall and leaflets were approximately 100–500 kPa (Fig. 4), consistent with previous studies [12, 29]. This demonstrates the predicted meshes’ viability for FEA, and thus potential clinical relevance in the form of biomechanics studies and TAVR planning.
Note that we can easily extend the analysis using the same predicted meshes, such as by using a material model that incorporates the strain energy function of fibrous and anisotropic structures. In this work, we evaluated the stresses based on the fact that the aortic valve is approximately statically determinate [13, 14].
3.5 Limitations and Future Works
There were no hard failure cases of our model, but in future works, we hope to enable expert-guided online updates for more rigorous quality control during test time. We will also aim to address our main limitation of requiring two well-defined volumetric mesh templates. Lastly, we will expand our framework to other important structures for TAVR simulations, such as calcification, myocardium, and ascending aorta.
4 Conclusion
We presented a novel approach for predicting aortic valve volumetric FE meshes from 3D patient images. Our method provides a principled end-to-end learnable way to optimize the volumetric element quality within a deep learning template deformation framework. Our model can predict meshes with good spatial accuracy, element quality, and FEA viability.
References
Botsch, M., Kobbelt, L., Pauly, M., Alliez, P., Lévy, B.: Polygon Mesh Processing. CRC Press, Boca Raton (2010)
Caballero, A., Mao, W., McKay, R., Sun, W.: The impact of balloon-expandable transcatheter aortic valve replacement on concomitant mitral regurgitation: a comprehensive computational analysis. J. Roy. Soc. Interface 16(157), 20190355 (2019)
Dalca, A.V., Balakrishnan, G., Guttag, J., Sabuncu, M.R.: Unsupervised learning of probabilistic diffeomorphic registration for images and surfaces. Med. Image Anal. 57, 226–236 (2019)
Ghesu, F.C., et al.: Marginal space deep learning: efficient architecture for volumetric image parsing. IEEE Trans. Med. Imaging 35(5), 1217–1228 (2016)
Gkioxari, G., Malik, J., Johnson, J.: Mesh R-CNN. In: Proceedings of the IEEE International Conference on Computer Vision, pp. 9785–9795 (2019)
Grbic, S., et al.: Image-based computational models for TAVI planning: from CT images to implant deployment. In: Mori, K., Sakuma, I., Sato, Y., Barillot, C., Navab, N. (eds.) MICCAI 2013. LNCS, vol. 8150, pp. 395–402. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40763-5_49
Ionasec, R.I., et al.: Patient-specific modeling and quantification of the aortic and mitral valves from 4-D cardiac CT and tee. IEEE Trans. Med. Imaging 29(9), 1636–1651 (2010)
Kim, T., Eberle, D.: Dynamic deformables: implementation and production practicalities. In: ACM SIGGRAPH 2020 Courses, pp. 1–182 (2020)
Kingma, D.P., Ba, J.: Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014)
Kong, F., Wilson, N., Shadden, S.C.: A deep-learning approach for direct whole-heart mesh reconstruction. arXiv preprint arXiv:2102.07899 (2021)
Lee, M.C.H., Petersen, K., Pawlowski, N., Glocker, B., Schaap, M.: TeTriS: template transformer networks for image segmentation with shape priors. IEEE Trans. Med. Imaging 38(11), 2596–2606 (2019)
Liang, L., et al.: Machine learning-based 3-D geometry reconstruction and modeling of aortic valve deformation using 3-D computed tomography images. Int. J. Numer. Methods Biomed. Eng. 33(5), e2827 (2017)
Liu, M., Liang, L., Liu, H., Zhang, M., Martin, C., Sun, W.: On the computation of in vivo transmural mean stress of patient-specific aortic wall. Biomech. Model. Mechanobiol. 18(2), 387–398 (2019). https://doi.org/10.1007/s10237-018-1089-5
Miller, K., Lu, J.: On the prospect of patient-specific biomechanics without patient-specific properties of tissues. J. Mech. Behav. Biomed. Mater. 27, 154–166 (2013)
Pak, D.H., Caballero, A., Sun, W., Duncan, J.S.: Efficient aortic valve multilabel segmentation using a spatial transformer network. In: 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI), pp. 1738–1742. IEEE (2020)
Pak, D.H., et al.: Weakly supervised deep learning for aortic valve finite element mesh generation from 3D CT images. In: Feragen, A., Sommer, S., Schnabel, J., Nielsen, M. (eds.) IPMI 2021. LNCS, vol. 12729, pp. 637–648. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-78191-0_49
Paszke, A., et al.: Automatic differentiation in PyTorch (2017)
Pouch, A.M., et al.: Medially constrained deformable modeling for segmentation of branching medial structures: application to aortic valve segmentation and morphometry. Med. Image Anal. 26(1), 217–231 (2015)
Ravi, N., et al.: Accelerating 3D deep learning with PyTorch3D. arXiv:2007.08501 (2020)
Ronneberger, O., Fischer, P., Brox, T.: U-Net: convolutional networks for biomedical image segmentation. In: Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F. (eds.) MICCAI 2015. LNCS, vol. 9351, pp. 234–241. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24574-4_28
Rueckert, D., Sonoda, L.I., Hayes, C., Hill, D.L., Leach, M.O., Hawkes, D.J.: Nonrigid registration using free-form deformations: application to breast MR images. IEEE Trans. Med. Imaging 18(8), 712–721 (1999)
Sandkühler, R., Jud, C., Andermatt, S., Cattin, P.C.: AirLab: autograd image registration laboratory. arXiv preprint arXiv:1806.09907 (2018)
Schroeder, W.J., Lorensen, B., Martin, K.: The visualization toolkit: an object-oriented approach to 3D graphics. Kitware (2004)
Smith, B., Goes, F.D., Kim, T.: Analytic eigensystems for isotropic distortion energies. ACM Trans. Graph. (TOG) 38(1), 1–15 (2019)
Smith, M.: ABAQUS/Standard User’s Manual, Version 6.9. Dassault Systèmes Simulia Corp, United States (2009)
Sun, W., Martin, C., Pham, T.: Computational modeling of cardiac valve function and intervention. Ann. Rev. Biomed. Eng. 16, 53–76 (2014)
Wang, N., Zhang, Y., Li, Z., Fu, Y., Liu, W., Jiang, Y.G.: Pixel2Mesh: generating 3D mesh models from single RGB images. In: Proceedings of the European Conference on Computer Vision (ECCV), pp. 52–67 (2018)
Wang, Q., Kodali, S., Primiano, C., Sun, W.: Simulations of transcatheter aortic valve implantation: implications for aortic root rupture. Biomech. Model. Mechanobiol. 14(1), 29–38 (2015). https://doi.org/10.1007/s10237-014-0583-7
Wang, Q., Primiano, C., McKay, R., Kodali, S., Sun, W.: CT image-based engineering analysis of transcatheter aortic valve replacement. JACC Cardiovasc. Imaging 7(5), 526–528 (2014)
Wickramasinghe, U., Remelli, E., Knott, G., Fua, P.: Voxel2Mesh: 3D mesh model generation from volumetric data. In: Martel, A.L., et al. (eds.) MICCAI 2020. LNCS, vol. 12264, pp. 299–308. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-59719-1_30
Zhuang, X., Shen, J.: Multi-scale patch and multi-modality atlases for whole heart segmentation of MRI. Med. Image Anal. 31, 77–87 (2016)
Acknowledgments and Conflict of Interest
This work was supported by the NIH R01HL142036 grant. Dr. Wei Sun is a co-founder and serves as the Chief Scientific Advisor of Dura Biotech. He has received compensation and owns equity in the company.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Pak, D.H. et al. (2021). Distortion Energy for Deep Learning-Based Volumetric Finite Element Mesh Generation for Aortic Valves. In: de Bruijne, M., et al. Medical Image Computing and Computer Assisted Intervention – MICCAI 2021. MICCAI 2021. Lecture Notes in Computer Science(), vol 12906. Springer, Cham. https://doi.org/10.1007/978-3-030-87231-1_47
Download citation
DOI: https://doi.org/10.1007/978-3-030-87231-1_47
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-87230-4
Online ISBN: 978-3-030-87231-1
eBook Packages: Computer ScienceComputer Science (R0)