The Search for Symmetry in Hohfeldian Modalities

Abstract

In this work we provide an analysis of some issues arising with geometrical representations of a family of deontic and potestative relations that can be classified as Hohfeldian modalities, traditionally illustrated on two diagrams, the Hohfeldian squares. Our main target is the lack of symmetry to be found in various formal accounts by drawing analogies with the square of opposition for alethic modalities. We argue that one should rather rely on an analogy with the alethic hexagon of opposition and exploit the notions of contingency and absoluteness in order to restore the symmetry of Hohfeldian modalities in accordance to the diagrams presented by Hohfeld. Interestingly, the investigation unveils three potestative squares defined at different levels of granularity (force, outcome and change) and allows us to further elaborate on the connections between deontic and potestative relations.

1 Introduction

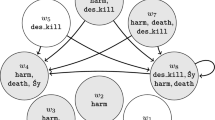
Diagrams are powerful tools for conceptual modelling, and powerful didactic tools. In the early XX century the legal scholar W. N. Hohfeld offered a systematic analysis of different uses of the word ‘right’ in the context of legal and judicial reasoning [5, 6], illustrating the resulting framework by two diagrams, consequently named Hohfeldian squares. Hohfeld’s theory of rights is based on a conceptual distinction between two families of normative relations: first-order relations (duty, claim, liberty, and no-claim), which can be also called deontic relations, and second-order relations (power, liability, disability, and immunity), also called potestative relations, which specify how first-order relations can be modified. Because of the focus on judiciary settings, Hohfeld’s investigation is about subjective rights: all the uses of the word ‘right’¹ express relations between two normative parties and a certain behaviour (a normative party can be taken to be either an individual or a collective; a behaviour can be equated with a type of action). The eight normative relations were illustrated by Hohfeld on two squares: the obligative (or deontic) square and the potestative square (Fig. 1). In a broader perspective, these relations can be conceived of as ternary modalities; for this reason we will speak of Hohfeldian modalities. A natural question is then the following: how can the diagrammatic representation offered by Hohfeld’s theory be transformed into a standard geometrical representation of modalities, such as an Aristotelian polygon of opposition?

Hohfeld’s squares have an important role in legal education; Aristotelian squares are instead used in linguistic, literary and semiotic studies, and have attracted a renewed interest in logic. The convergence to geometric constructs is plausibly not by chance: cognitive studies show that symmetries facilitate perception of structure, memorization and thus recall. Unveiling an underlying connection between the two representations would have in principle both a theoretical and practical value. Indeed, diagrams help in understanding relations between norms. Suppose a legal code includes two norms N1 and N2. N1 speaks of the duties of a normative party x, N2 speaks of the liberties of a party y and it is intended that N1 and N2 jointly describe the normative relation between x and y. Diagrams (and, in particular, Aristotelian polygons of opposition) provide hints on how to translate, e.g., statements about duties into statements about liberties (and vice versa). In the present work we will point out that the task of translating Hohfeldian squares into Aristotelian polygons is very challenging, due to an overlap of perspectives from which some fundamental notions, such as power and liberty, can be analysed.

Fig. 1.

The two Hohfeldian squares: (left) the deontic square, (also obligative or of the first-order), and (right) the potestative square (or of the second-order).

The paper proceeds as follows. Section 2 provides the background, with a brief overview of related works. Section 3 presents the notation upon which our proposal will be constructed, and introduces to the most common formalization of the normative concepts illustrated in Hohfeld’s framework. Section 4 investigates those concepts through the framing of squares of opposition, reorganizing, integrating, and extending several contributions presented in the literature. In particular, we unveil three squares of opposition associated to the potestative dimension, defined at different level of abstraction (force, outcome, and change). Section 5 argues that, in order to obtain a proper symmetric treatment of the two families of Hohfeldian modalities (in particular with respect to the notions of liberty and of power), one has to move from squares to hexagons of opposition. Finally, Sect. 6 elaborates shortly on the causal and logical connections between the deontic and potestative relations.

Fig. 2.

Aristotelian square of opposition for basic deontic modalities, with subaltern (green), contrary (orange), sub-contrary (blue) and contradictory (red) bindings, and the traditional labels associated to each node (A, E, I, O). (Color figure online)

2 Background and Related Works

A good starting point to build a geometrical representation of Hohfeldian modalities is the Aristotelian square of opposition for basic deontic modalities, that is, obligation, permission and forbiddance (prohibition),² reproduced in Fig. 2.³ Hohfeld did not refer to Aristotelian squares in his work; however, his diagrams were meant to clarify the logic of the relations at the basis of his theory.⁴

While Hohfeld’s notions have been long since analysed via formal logic (see, e.g., the seminal works of Lindahl [8] or Makinson [10], or, more recently, the work of Markovich [11] or our own proposal [17]), a full understanding of the meaning of his two squares has been regarded as problematic. No standard formalization exists today. Hohfeld’s framework suggests that the relations at its core are symmetric, but most used formalizations do not fully capture this feature. In contrast, O’Reilly [12] elaborated on reframing the two Hohfeldian squares in terms of Aristotelian polygons (focusing on what we will name here “change-centered” power), in order to provide a more systematic encoding of logical relations. However, the Aristotelian squares that he gets also encode problematic relations between, e.g., liberties and duties due to a lack of symmetry. He points out that a different sort of Aristotelian polygon is called for. Sileno [16], following Blanché’s insights [4], proposed to use triangles of opposition (focusing on a “force-centered” power). However, both works presented a semi-formal conceptualization only.

The present contribution aligns and extends both diagrammatic and formal characterizations. Hohfeldian squares are mapped to Aristotelian hexagons, to restore the symmetries on various levels. Additionally, we formalize change-, force-, and outcome-centered squares of power, visualizing their mutual relations.

3 Formalization

According to Lindahl [8], all relations in each of the deontic and potestative families of concepts analysed by Hohfeld are interdefinable, in the sense that one could take a single deontic relation and a single potestative relation as primitives and introduce all the others via logical operations. This idea will serve as a guide through our formal transposition of Hohfeld’s theory in the present section.

3.1 Language

In order to analyse the notions at stake, we can conveniently introduce a language of first-order logic. We will use two categories of variables: x, y etc. to denote normative parties and $\alpha$, $\beta$, etc. to denote action types. We will also have constants p, q, etc. for normative parties and constants A, B, etc. for action types. The symbol − (overline) will denote complementation on action types. Complementation will be the only operation that allows one to build complex action types: given an action type A, $\overline{A}$ will denote the complement of A, that is, the type of any action that does not instantiate A. We will work under the assumption that the Law of Double Complementation holds ($\overline{\overline{A}}=A$). Hohfeldian modalities will be represented via n-ary predicates (relations) and will be given an explicit name throughout the presentation. We will use a different font for relations not corresponding to Hohfeldian modalities (the only relation that is not a Hohfeldian modality in the rest of the exposition is Ability). In some cases the argument of a relation can be a statement involving another relation. However, no quantification on such statements will be employed; therefore, the language will remain at the level of first-order logic. Finally, we will employ standard symbols for logical connectives: $\lnot$ to denote Boolean negation, $\rightarrow$ to denote material implication, $\equiv$ to denote material equivalence, $\exists$ and $\forall$ as quantifiers, etc. For the sake of brevity, we will omit quantification over variables for normative parties, interpreting a formula of the form $\phi (x,y,...)$ as implicitly having the form $\forall x\forall y...\phi (x,y,...)$. Thus, while we will read an expression of the form $\mathsf {Claim}(x,y,A)$ as “for all x, for all y: x has a claim that A be performed by y”, we will read an expression of the form $\mathsf {Claim}(p,q,A)$ as “p has a claim that A be performed by q”. We divide our analysis into two parts, respectively dealing with first-order and second-order Hohfeldian relations.

3.2 First-Order Hohfeldian Relations

The formal renderings of the fundamental deontic relations identified in Hohfeld’s framework, for two normative parties p and q and an action type A, are the following: $\mathsf {Claim}(p,q,A)$, $\mathsf {Liberty}(p,q,A)$, $\mathsf {Duty}(p,q,A)$ and $\mathsf {NoClaim}(p,q,A)$. One can immediately notice that the last Hohfelidian modality in this list is, due to its name, just the negation of the first. Therefore, if one wants to take $\mathsf {Claim}$ as the primitive deontic concept, the definability of $\mathsf {NoClaim}$ with respect to a given action type A turns out to be obvious, thanks to Boolean negation:

$$\mathsf {NoClaim}(x,y,A) \equiv \lnot \mathsf {Claim}(x,y,A)$$

Furthermore, one can treat $\mathsf {Claim}$ and $\mathsf {Duty}$ as correlative notions, in the sense that they are two faces of the same modality, seen from the points of view of the two normative parties involved, (whence, $\mathsf {Duty}$ just results from a permutation of the two parties):

$$\mathsf {Duty}(y,x,A) \equiv \mathsf {Claim}(x,y,A)$$

Finally, one can define $\mathsf {Liberty}$ in terms of $\mathsf {Claim}$, Boolean negation, a permutation of normative parties and action complementation:

$$ \mathsf {Liberty}(y,x,A) \equiv \lnot \mathsf {Claim}(x,y,\overline{A}) $$

Note that the last two equations, together with the Law of Double Complementation, entail that:

$$\lnot \mathsf {Duty}(y,x,A) \equiv \mathsf {Liberty}(y,x,\overline{A})$$

that is, the negation of a duty of performance corresponds to the liberty of non-performance.

3.3 Second-Order Hohfeldian Relations

Relations of the potestative family concern actions that trigger changes of first-order or even second-order relations (although for most legal scholars legal power concerns only first-order relations), such as, for instance, an action B creating a duty for a party q to perform an action A to the advantage of a party p. A possible way of writing that p has such a power would be by means of a predicate expression Ability(p, B, R) (cf. the predicate $has\_ability$ investigated in [17]), where R is a Hohfeldian relation issued at B’s performance by p; for instance, $Ability(p, B, \mathsf {Claim}(p, q, A))$. Indeed, to simplify the notation, we may abstract the triggering action B, and focus on a common relation, e.g. $R = \mathsf {Claim}(p,q,A)$). In the following we denote this canonic⁵ power construct with reference to a given action type A by means of the expression $\mathsf {Power}(p,q,A)$, whose definition involves an existential quantification on the set of action types:

$$ \mathsf {Power}(x,y,A) \equiv \exists \beta : Ability(x, \beta , \mathsf {Claim}(x,y,A))$$

The four fundamental potestative relations identified by Hohfeld can then be encoded following the same syntactic pattern used in the case of first-order relations, namely as ternary relations whose first and second argument is a normative party and whose third argument is an action type (that is, as the equivalence above indicates, the action type mentioned in the relation affected): $\mathsf {Power}(p,q,A)$, $\mathsf {Liability}(p,q,A)$, $\mathsf {Disability}(p,q,A)$, $\mathsf {Immunity}(p,q,A)$.

Now, suppose we take $\mathsf {Power}$ as the primitive potestative notion. First, one can treat $\mathsf {Disability}$ as the negation of $\mathsf {Power}$ and thus define it with reference to a given action type A as follows:

$$ \mathsf {Disability}(x,y,A) \equiv \lnot \mathsf {Power}(x,y,A) $$

Then, also in this case, one can identify correlative statements involving $\mathsf {Liability}$ and $\mathsf {Power}$ via permutations of the normative parties:

$$\mathsf {Liability}(y,x,A) \equiv \mathsf {Power}(x,y,A) $$

Finally, one can define $\mathsf {Immunity}$ in terms of $\mathsf {Power}$, Boolean negation and a permutation of the normative parties:

$$\mathsf {Immunity}(y,x,A) \equiv \lnot \mathsf {Power}(x,y,A) $$

In this case, the last two equations entail a structurally different template:

$$\lnot \mathsf {Liability}(x,y,A) \equiv \mathsf {Immunity}(x, y, A)$$

that is, the negation of a liability (correlatively, power) towards performance corresponds to the immunity (disability) towards performance (whereas for the first square it was towards non-performance). Therefore, according to this formalization (or analogous proposals by most subsequent authors, e.g. [10, 11, 14]), the two Hohfeldian squares lose the symmetry suggested in Hohfeld’s diagrams.

4 Hohfeldian Squares and Aristotelian squares

The previous formalization makes clear that any of the four relations on each of the Hohfeldian squares can be defined in terms of any other relation belonging to the same family. Some authors, as e.g. O’Reilly [12] (in turn extending Sumner’s analysis [18]), observe that, for any choice of a primitive deontic and potestative modality, one can build two Aristotelian squares of opposition whose corners are labelled by a formula where only the primitive modality of the relevant family is mentioned. The four formulas needed as labels for a square are obtained by the possible combinations of Boolean negation and action complementation (either both present, or both absent, or one present and one absent).

4.1 Deontic Square of Opposition

Let us choose $\mathsf {Claim}$ as primitive for the square of opposition extracted from the first-order Hohfeldian diagram. This choice leads to the following set of labels $\mathsf {DR}$ (for “deontic relations”) with respect to a given action type A:

$$\mathsf {DR}=\{ \mathsf {Claim}(p,q,A), \mathsf {Claim}(p,q,\overline{A}), \lnot \mathsf {Claim}(p,q,\overline{A}), \lnot \mathsf {Claim}(p,q,A) \}$$

We will say that this is a $\mathsf {Claim}$-based description of $\mathsf {DR}$; exploiting the correlativity principles one could write, equivalently, a $\mathsf {Duty}$-based description. The same holds, relying on other principles, for $\mathsf {Right}$- and $\mathsf {NoClaim}$-based descriptions of $\mathsf {DR}$. The set $\mathsf {DR}$, together with the meaning of Boolean negation and action complementation, naturally gives rise to a deontic square of opposition. The only additional principle needed is the following, used to characterize subalternate statements:

$$\mathsf {Claim}(x,y,A) \rightarrow \lnot \mathsf {Claim}(x,y,\overline{A})$$

By substituting the (implicitly) quantified variables for normative parties x and y with constants p and q, this can be read as saying that if p has a claim towards q about the performance of A, then p does not have a claim towards q about its non-performance.

4.2 O’Reilly’s (or Change-Centered) Potestative Square of Opposition

O’Reilly applies a similar approach to the potestative relations. He first considers power as the ability of p to affect q with respect to a relation R. This can be rephrased in our formal setting by saying that there are triggering actions that produce a change w.r.t. R. More precisely, a change can occur when either R or its contrary or its contradictory is created. Therefore, this is a change-centered notion of power. Focusing on $R = \mathsf {Claim}(p, q, A)$, we can take a triggering action B and write the definitional equivalence for this O’Reillian notion of power as:

$$\begin{aligned}\mathsf {Power_{OReilly}}(x,y,B, A) \equiv&\; Ability(x, B, \mathsf {Claim}(x, y, A)) \\&\vee \; Ability(x, B, \mathsf {Claim}(x, y, \overline{A})) \\&\vee \; Ability(x, B, \lnot \mathsf {Claim}(x, y, A)) \end{aligned}$$

We can then use quantification over the set of possible action types and the O’Reillian notion of power to define a form of positive-change power ($\mathsf {Power}^+$), with respect to a given action type A, as below:

$$\mathsf {Power^+}(x, y, A) \equiv \exists \beta : \mathsf {Power_{OReilly}}(x, y, \beta , A) $$

Positive-change power corresponds to the ability of affecting (in any sense) a relation. O’Reilly then refers to a distinct form of internal negation, capturing the ability of a party p to not affect a party q with respect to a relation R. This will be said to represent a form of negative-change or no-change power ($\mathsf {Power}^-$). In other words, this means that p may choose an action that does not produce any change. In our formalization the resulting definitional equivalence would be:

$$\mathsf {Power^-}(x, y, A) \equiv \exists \beta : \lnot \mathsf {Power_{OReilly}}(x, y, \beta , A)$$

Starting from these concepts, we can define a set $\mathsf {PR^\pm }$ of potestative (change-centered) relations with the aim of building a square of opposition for second-order Hohfeldian relations. Here the four formulas needed are obtained via possible combinations of Boolean negation and of positive- vs. negative-change power:

$$ \mathsf {PR^\pm }= \{ \mathsf {Power}^+(p,q,A), \mathsf {Power}^-(p,q,A), \lnot \mathsf {Power}^-(p,q,A), \lnot \mathsf {Power}^+(p,q,A) \}$$

To build a square of opposition upon $\mathsf {PR^\pm }$, and follow O’Reilly’s approach, one has to add the principle below, which captures subalternation:

$$\lnot \mathsf {Power^-}(x,y,A)\rightarrow \mathsf {Power^+}(x,y,A)$$

However, in this case such a principle is not independent from the rest; the formalization proposed here, together with the plausible assumption that the set of action types is non-empty, already entails this principle. Note also that:

$$\mathsf {Power}(x, y , A) \rightarrow \mathsf {Power^+}(x, y , A) \qquad \mathsf {Power^-}(x, y , A) \not \rightarrow \lnot \mathsf {Power}(x, y, A) $$

The first implication above indicates that the canonic notion of power introduced in Sect. 3.3 has a narrower scope than the notion of positive-change power.

Fig. 3.

Deontic and potestative (change-centered, force-centered, and outcome-centered) Aristotelian squares of opposition constructed from the two Hohfeldian diagrams. The usual convention on the colour of bindings apply.

4.3 Force-Centered Potestative Square of Opposition

The notion of power considered by O’Reilly is rather complex: one may then wonder whether a square of opposition may be constructed starting instead from more primitive forms of power. As observed in [16], [15, Ch.4], power relations can be put in analogical correspondence to physical phenomena as attraction, repulsion, and absence of those (independence). To express such physical metaphor of “force”, we need to separate the stimulus component (a particular type of action, such as a verbal command) and the consequent target manifestation (a type of action that is due on the basis of the stimulus). If the latter is denoted by the action type symbol A, then, the former can be here conveniently represented via the symbol "A", rather than with a generic symbol for an action type B. In this way, one emphasizes the connection between stimulus and target manifestation. Relevant scenarios can be then identified on, e.g., whether stimulus and manifestation converge (A is always performed in correspondence to its stimulus) or diverge (A is never performed in correspondence to its stimulus). Using our notation, the definition of force-centered notions of power is:

$$\begin{aligned}\mathsf {\overset{\rightarrow \leftarrow }{Power}}(x,y,A)&\; \equiv Ability(x, \texttt {"A"}, \mathsf {Claim}(x, y, A)) \\ \mathsf {\overset{\leftarrow \rightarrow }{Power}}(x,y, A)&\; \equiv Ability(x, \texttt {"A"}, \mathsf {Claim}(x, y, \overline{A})) \end{aligned}$$

We will say that $\mathsf {\overset{\rightarrow \leftarrow }{Power}}$ represents positive-force power and that $\mathsf {\overset{\leftarrow \rightarrow }{Power}}$ represents negative-force power. (As an empirical confirmation, see e.g. the negative-force liability position found in the Dutch Act of Abjuration [15].)

From these concepts we can define a new set of potestative relations $\mathsf {PR}^{\overset{\leftarrow }{\rightarrow }}$ as labels for a force-centered potestative square of opposition. More precisely, here the four formulas needed for the square are obtained by taking into account all possible combinations of positive- vs. negative-force power and Boolean negation:

$$ {\mathsf {PR}^{\overset{\leftarrow }{\rightarrow }}} = \{ \mathsf {\overset{\rightarrow \leftarrow }{Power}}(p,q,A), \mathsf {\overset{\leftarrow \rightarrow }{Power}}(p,q,A), \lnot \mathsf {\overset{\leftarrow \rightarrow }{Power}}(p,q,A), \lnot \mathsf {\overset{\rightarrow \leftarrow }{Power}}(p,q,A) \}$$

The subalternity is here captured by the logical principle:

$$\mathsf {\overset{\rightarrow \leftarrow }{Power}}(x,y,A) \rightarrow \lnot \mathsf {{\overset{\leftarrow \rightarrow }{Power}}}(x,y,A)$$

which is acceptable because otherwise the same stimulus "A" could generate two conflicting first-order relations.

Note also that:

$$\mathsf {\overset{\rightarrow \leftarrow }{Power}}(x,y,A) \rightarrow \mathsf {{Power}}(x,y,A) \qquad \mathsf {\overset{\leftarrow \rightarrow }{Power}}(x,y,A) \rightarrow \mathsf {{Power}}(x,y,\overline{A})$$

As the first implication indicates, the notion of positive-force power has a narrower scope than the canonic notion of power, whence a fortiori, a narrower scope than the notion of positive-change power.

4.4 Outcome-Centered Potestative Square of Opposition

So far, we have presented an abstract notion of power (concerned by the possibility of change or not of the target relation), and an operational notion (concerned by the interaction between directive and performance). Strangely enough, we lack of a square of opposition centered around the canonic form of power captured by $\mathsf {Power}(p, q, A)$ (the power to issue a duty to A), that is, power centered around the outcome. For doing this, we also need to introduce the notion of power to release a duty. In this way we can distinguish between a positive-outcome notion of power (i.e., the canonic notion of power) and a negative-outcome notion of power. More formally, let us define the power to release a command as:

$$\mathsf {\overline{Power}}(x, y, A) \equiv \exists \beta : Ability(x, \beta , \lnot \mathsf {Claim}(x, y, A))$$

Thus, with respect to any action type A we can form a set $\mathsf {PR}$ of four powers:

• the power to issue a duty to A, or $\mathsf {Power}(p, q, A)$

• the power to issue a prohibition to A, or $\mathsf {Power}(p, q, \overline{A})$

• the power to release a duty to A, or $\mathsf {\overline{Power}}(p, q, A)$

• the power to release a prohibition to A, or $\mathsf {\overline{Power}}(p, q, \overline{A})$

Furthermore, we adopt the following logical principles, which provide conditions for the truth of statements involving outcome-centered notions of power:

$$\begin{aligned} \begin{aligned} \mathsf {Power}(x,y,A) \rightarrow \lnot \mathsf {Claim}(x,y,A)\\ \overline{\mathsf {Power}}(x,y,A) \rightarrow \mathsf {Claim}(x,y,A) \end{aligned} \end{aligned}$$

The rationale behind these formulas is that power captures a potential of a manifestation, and so the manifestation must not hold, for the potentiality to hold.

Thus, having a power to impose A on q entails that one does not already have a claim that A be performed by q. Analogously, having a power to release q from the performance of A entails that one has (until the power at issue will be exercised) a claim that A be performed by q. These principles shed light on the way in which an Aristotelian square of opposition for outcome-centered modalities should be built.

In fact, at a first glance one might be inclined to consider the statement $\mathsf {Power}(p, q, \overline{A})$ as contrary to the statement $\mathsf {Power}(p, q, A)$ (namely, the power to forbid A as contrary to the power to impose A), but this is not a valid choice: it may well be the case that p has the power to impose the duty to A, as well as to impose the prohibition to A. This intuition can be confirmed by analyzing their truth-conditions: $\mathsf {Power}(p, q, A)\wedge \mathsf {Power}(p, q, \overline{A})$ entails (according to the principles stated above and the Law of Double Complementation) $\lnot \mathsf {Claim}(p,q,A)\wedge \lnot \mathsf {Claim}(p,q,\overline{A})$. Looking at the $\mathsf {Claim}$-based deontic square of opposition in Fig. 3, the latter is a conjunction of subcontrary statements, whence it can be true.

By contrast, in order to find the appropriate contrary to the statement $\mathsf {Power}(p, q, A)$, one has to rely on the observation that, according to the logical principles on outcome-centered notions of power, for the same normative party it is not possible to have the power to create a claim that A be performed by q and the power to release q from the duty of performing A. Thus, it is not possible that $\mathsf {\overline{Power}}(p, q, A)$ is true at the same time of $\mathsf {Power}(p, q, A)$. This observation provides us with the sub-alternation principle

$$\mathsf {Power}(p, q, A) \rightarrow \lnot \mathsf {\overline{Power}}(p, q, A)$$

to construct a square of opposition by means of the set $\mathsf {PR}$.

Fig. 4.

Map of potestative relations defined in terms of triggering action (force-centered square of opposition, the left one), in terms of outcome (middle square), in terms of change or affecting outcomes (O’Reilly’s square of opposition, the right one). Notice that the leftmost square is vertically mirrored and the rightmost square underwent a $90^{\circ }$ clockwise rotation. The usual convention on the colour of bindings apply.

Comparison. It is interesting to check which corners of squares of oppositions are occupied by the notions of power discussed thus far. We will make reference to the four corners in a square with the labels A (upper left corner), E (upper right corner), I (lower left corner) and O (lower right corner) as in the tradition (see e.g. [3]). Looking at Fig. 4, one sees that $\mathsf {Power}^{\rightarrow \leftarrow }$ and $\mathsf {Power}$ occupy the A position in their respective squares, whereas $\mathsf {Power}^{\leftarrow \rightarrow }$ and $\mathsf {\overline{Power}}$ occupy the E position, $\mathsf {Power}^+$ occupies the I position and $\mathsf {Power}^-$ occupies the O position.

Fig. 5.

The two correlative hexagons of opposition for Hohfeld’s deontic relations.

5 Of Lost Symmetries

Here we return on the issue of the asymmetry between the analysis of first-order and second-order Hohfeldian diagrams. Symmetry is a desired property not only among relations belonging to the same square (given that these should be all interdefinable), but also between pairs of relations belonging to the deontic and to the potestative square, respectively. The reason for this will be clarified below.

5.1 Half-Liberties and Full-Liberties

According to the description of the deontic square that we have provided in Fig. 3, the formula $\mathsf {Liberty}(q,p,A)$ is logically equivalent to $\lnot \mathsf {Claim}(p,q,\overline{A})$. However, this captures a notion that does not match the ordinary meaning of ‘liberty’ (see, on similar lines, [12, 15]). The two statements $\lnot \mathsf {Claim}(p,q,\overline{A})$ and $\lnot \mathsf {Claim}(p,q,A)$—the latter is logically equivalent to $\mathsf {Liberty}(q,p,\overline{A})$—are sub-contraries, which means that they cannot be both false. But then, it may be that only one of $\mathsf {Liberty}(q,p,\overline{A})$ and $\mathsf {Liberty}(q,p,A)$ is true. In this case, speaking of a ‘liberty’ is misleading. In fact, suppose, without loss of generalization, that $\mathsf {Liberty}(q,p,A)$ is true and that $\mathsf {Liberty}(q,p,\overline{A})$ is false: then, $\lnot \mathsf {Liberty}(q,p,\overline{A})$ is true and so is $\mathsf {Claim}(p,q,A)$. The latter, in turn, is equivalent to $\mathsf {Duty}(q,p,A)$. Therefore, one gets that q is free to perform A with respect to p and, at the same time, has a duty to p to perform A. This is only a half-liberty, rather than a genuine one. By contrast, a full-liberty for q with respect to the performance of A obtains only when both formulas $\mathsf {Liberty}(q,p,A)$ and $\mathsf {Liberty}(q,p,\overline{A})$ are true:

$$\mathsf {{FullLiberty}}(y,x,A) \equiv \mathsf {Liberty}(y,x,A) \wedge \mathsf {Liberty}(y,x,\overline{A}) $$

We can define correlatively a full no-claim relation: $\mathsf {{FullNoClaim}}(x,y,A) \equiv$

$\lnot \mathsf {Claim}(x,y,A) \wedge \lnot \mathsf {Claim}(x,y,\overline{A})$.

5.2 Disjoint or Absolute Duty

Being moved by the aim of an overall symmetry of the geometrical construction of deontic modalities, one could argue that there must be a notion of duty associated with the combination of the two formulas $\mathsf {Duty}(q,p,A)$ and $\mathsf {Duty}(q,p,\overline{A})$, which correspond to $\mathsf {Claim}(p,q,A)$ and $\mathsf {Claim}(p,q,\overline{A})$ in the $\mathsf {Claim}$-based deontic square. However, as it is acknowledged by O’Reilly, such a combination cannot correspond to the joint truth of the two formulas. Indeed, if q were required both to perform A and to forbear from A, then there would be a conflict between norms, since q could not avoid doing something regarded as wrong. Here, we rather propose to further exploit the analogy between deontic and alethic modalities in order to find a more plausible solution. In fact, the notion of liberty is associated with the alethic notion of possibility; by contrast, the notion of claim and the correlative notion of duty are associated with the alethic notion of necessity. The square of opposition can thus be expanded to an hexagon of opposition, following the ideas in [4], in order to make room for two notions that respectively correspond with two-sided possibility and two-sided necessity. In the alethic case, the former notion is also known as contingency, the latter notion as non-contingency or absoluteness (see, e.g., [3], and [13].)

Fig. 6.

The two correlative hexagons of opposition for Hohfeld’s potestative relations (outcome-centered).

We can define, accordingly, an absolute duty, and a correlative absolute claim, confirming its duality with the full no-claim (see Fig. 5):

$$\begin{aligned} \mathsf {{AbsDuty}}(y,x,A)&\equiv \mathsf {Duty}(y,x,A) \vee \mathsf {Duty}(y,x,\overline{A}) \\ \mathsf {{AbsClaim}}(x,y,A)&\equiv \mathsf {Claim}(x,y,A) \vee \mathsf {Claim}(x,y,\overline{A}) \\ \mathsf {{FullNoClaim}}(x,y,A)&\equiv \lnot \mathsf {{AbsClaim}}(x,y,A) \end{aligned}$$

Similar considerations can be applied to the correspondent potestative concepts, resulting in the construction of full-disabilities, or absolute powers (see Fig. 6). As the two figures show, taking as descriptions of normative relations the top and bottom points of the hexagons, concepts of the first and second Hohfeldian square follow the same structure. Another possibility, that diagrammatically maintains the core structure, would be to construct Hohfeldian prisms made of triangles of opposition, i.e. the positions $\mathrm {A}$, E, and $I \wedge O$ of each hexagons [15].

Fig. 7.

Hohfeld’s cube: relations connecting the second-order Hohfeldian square constructed upon the canonic power $\mathsf {Power}(p, q, A)$ with relations of the first-order Hohfeldian square. The wavy arrows are causal relationships.

6 Prototypical Relations Between the Two Squares

As a second-order relation, power reifies the possibility of an agent to modify some normative relation (of the first-, or of the second-order). The most prototypical power is the one that, once enacted by an agent, creates a duty upon another agent, and thus a correlative claim upon the first one towards the second (e.g., a commander w.r.t. a soldier). Abstracting the internal workings of power (for a possible formalization, see [17]), we can still observe that power generally leads to a claim, or (using $\leadsto$ for the notion of a dynamic/causal entailment):

$$\mathsf {Power}(x,y,A) \leadsto \mathsf {Claim}(x,y,A)$$

As observed by Andrews [1], one can construct, following the same idea, similar patterns between the other notions, resulting into a Hohfeld’s cube (Andrews however does not consider the temporal/causal aspect we suggest here and reduces all relations to variations of composite deontic structures). Proceeding along this path, we observe that liability generally leads to a duty:

$$\mathsf {Liability}(x,y,A) \leadsto \mathsf {Duty}(x,y,A)$$

This approach has however a different interpretation on the other relations: “immunity generally leads to a liberty” and “disability generally leads to a no-claim”. Superficially, these sentences capture that a liberty becomes explicit only in the moment in which immunity is utilized against a supposed power. However, from a logical point of view, it is the very presence of immunity that makes the agent free of behaving how she prefers with respect to the holder of a disability, whereas the manifestation is only an epiphenomenon.

$$\begin{aligned} \begin{aligned} \mathsf {Immunity}(x,y,A) \rightarrow \mathsf {Liberty}(x,y,A) \\ \mathsf {Disability}(x,y,A) \rightarrow \mathsf {NoClaim}(x,y,A) \end{aligned} \end{aligned}$$

These four relations are illustrated in Fig. 7.

7 Conclusion

The paper revisits, reorganizes and extends several distinct contributions developed around the primitive normative relations expressed in the framework of Hohfeld, with the purpose of capturing underlying patterns. In contrast to most papers on this topic, we gave here precedence to the systematization of views that are generally lost when we look at more general logical constructs. The primary focus on a canonic form of power (the one creating a claim/duty) allowed us to make explicit three distinct levels of abstraction on which power can be defined (force, outcome and change). We showed in what sense contemporary formalizations were losing part of the appeal of Hohfeld’s proposal, and how this can be solved by making reference to concepts expressed on the deontic hexagon, as e.g. full-liberty and absolute duty. Finally, we illustrated the prototypical connections (causal, or logical) between the second-order (potestative) and first-order (deontic) relations by means of a cube. In this effort of systematization, diagrams have proven to us to be an effective method to discover gaps in the theoretical framework that were not evident from the syntactic view.

Furthermore, in a normative context, diagrams may be used to create user-friendly interfaces for the analysis of legal/contractual constructs. Rather than inspecting hundreds of sentences in the text of a contract, a subject may more easily figure out her normative relations (duties, rights, etc.) with the other parties by navigating or exploring a diagram-construed model.