An Equivalence Relation Between Morphological Dynamics and Persistent Homology in n-D

Abstract

In Mathematical Morphology (MM), dynamics are used to compute markers to proceed for example to watershed-based image decomposition. At the same time, persistence is a concept coming from Persistent Homology (PH) and Morse Theory (MT) and represents the stability of the extrema of a Morse function. Since these concepts are similar on Morse functions, we studied their relationship and we found, and proved, that they are equal on 1D Morse functions. Here, we propose to extend this proof to n-D, $n \ge 2$, showing that this equality can be applied to n-D images and not only to 1D functions. This is a step further to show how much MM and MT are related.

1 Introduction

Fig. 1.

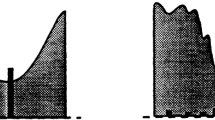
Low sensibility of dynamics to noise (extracted from [15]).

In Mathematical Morphology [21,22,23], dynamics [14, 15, 24], defined in terms of continuous paths and optimization problems, represents a very powerful tool to measure the significance of extrema in a gray-level image (see Fig. 1). Thanks to dynamics, we can construct efficient markers of objects belonging to an image which do not depend on the size or on the shape of the object we want to segment (to compute watershed transforms [20, 25] and proceed to image segmentation). This contrasts with convolution filters very often used in digital signal processing or morphological filters [21,22,23] where geometrical properties do matter. Selecting components of high dynamics in an image is a way to filter objects depending on their contrast, whatever the scale of the objects.

Fig. 2.

The dynamics of a minimum of a given function can be computed thanks to a flooding algorithm (extracted from [15]).

Note that there exists an interesting relation between flooding algorithms and the computation of dynamics (see Fig. 2). Indeed, when we flood a local minimum in the topographical view of the 1D function, we are able to know the dynamics of this local minimum when water reaches some point of the function where water is lower than the height of the initial local minimum.

In Persistent Homology [6, 10] well-known in Computational Topology [7], we can find the same paradigm: topological features whose persistence is high are “true” when the ones whose persistence is low are considered as sampling artifacts, whatever their scale. An example of application of persistence is the filtering of Morse-Smale complexes [8, 9, 16] used in Morse Theory [13, 19] where pairs of extrema of low persistence are canceled for simplification purpose. This way, we obtain simplified topological representations of Morse functions. A discrete counterpart of Morse theory, known as Discrete Morse Theory can be found in [11,12,13, 17].

As detailed in [5], pairing by persistence of critical values can be extended in a more general setting to pairing by interval persistence of critical points. The result is that they are able to do function matching based on their critical points and they are able to pair all the critical points of a given function (see Fig. 2 in [5]) where persistent homology does not succeed. However, due to the modification of the definition they introduce, this matching is not applicable when we consider usual threshold sets.

In this paper, we prove that the relation between Mathematical Morphology and Persistent Homology is strong in the sense that pairing by dynamics and pairing by persistence are equivalent (and then dynamics and persistence are equal) in n-D when we work with Morse functions. Note that this paper is the extension from 1D to n-D of [4].

The plan of the paper is the following: Sect. 2 recalls the mathematical background needed in this paper, Sect. 3 proves the equivalence between pairing by dynamics and pairing by persistence and Sect. 4 concludes the paper.

2 Mathematical Pre-requisites

We call path from $\mathbf {x}$ to $\mathbf {x} '$ both in $\mathbb {R} ^n$ a continuous mapping from [0, 1] to $\mathbb {R} ^n$. Let $\varPi _1$, $\varPi _2$ be two paths satisfying $\varPi _1(1) = \varPi _2(0)$, then we denote by $\varPi _1 <> \varPi _2$ the join between these two paths. For any two points $\mathbf {x} ^1,\mathbf {x} ^2 \in \mathbb {R} ^n$, we denote by $[\mathbf {x} ^1,\mathbf {x} ^2]$ the path:

$$\lambda \in [0,1] \rightarrow (1-\lambda ) . \mathbf {x} ^1 + \lambda . \mathbf {x} ^2.$$

Also, we work with $\mathbb {R} ^n$ supplied with the Euclidean norm $\Vert .\Vert _2 : \mathbf {x} \rightarrow \Vert \mathbf {x} \Vert _2 = \sqrt{\sum _{i = 1}^n \mathbf {x} _i^2}$.

We will use lower threshold sets coming from cross-section topology [2, 3, 18] of a function f defined for some real value $\lambda \in \mathbb {R}$ by:

$$[f< \lambda ] = \left\{ x \in \mathbb {R} ^n \ \Big | \ f(x) < \lambda \right\} ,$$

and

$$[f \le \lambda ] = \left\{ x \in \mathbb {R} ^n \ \Big | \ f(x) \le \lambda \right\} .$$

2.1 Morse Functions

We call Morse functions the real functions in $\mathcal {C}^{\infty }(\mathbb {R} ^n)$ whose Hessian is not degenerated at critical values, that is, where their gradient vanishes. A strong property of Morse functions is that their critical values are isolated.

Lemma 1

(Morse Lemma  [1]). Let $f : \mathcal {C}^{\infty }(\mathbb {R} ^n) \rightarrow \mathbb {R}$ be a Morse function. When $x^* \in \mathbb {R} ^n$ is a critical point of f, then there exists some neighborhood V of $x^*$ and some diffeomorphism $\varphi : V \rightarrow \mathbb {R} ^n$ such that f is equal to a second order polynomial function of $\mathbf {x} = (x_1,\dots ,x_n)$ on V:

$$ \forall \; \mathbf {x} \in V, \ f \circ \varphi ^{-1} (\mathbf {x}) = f(x^*) - x_1^2 - x_2^2 - \dots - x_k^2 + x_{k+1}^2 + \dots + x_n^2,$$

We call k-saddle of a Morse function a point $x \in \mathbb {R} ^n$ such that the Hessian matrix has exactly k strictly negative eigenvalues (and then $(n-k)$ strictly positive eigenvalues); in this case, k is sometimes called the index of f at x. We say that a Morse function has unique critical values when for any two different critical values $x_1,x_2 \in \mathbb {R} ^n$ of f, we have $f(x_1) \ne f(x_2)$.

Fig. 3.

Pairing by dynamics on a Morse function: the red and blue paths are both in $(D_{\mathbf {x^{min}}})$ but only the blue one reaches a point $\mathbf {x_{<}}$ whose height is lower than $f(\mathbf {x^{min}})$ with a minimal effort. (Color figure online)

2.2 Dynamics

From now on, $f : \mathbb {R} ^n \rightarrow \mathbb {R}$ is a Morse function with unique critical values.

Let $\mathbf {x^{min}}$ be a local minimum of f. Then we call set of descending paths starting from $\mathbf {x^{min}}$ (shortly $(D_{\mathbf {x^{min}}})$) the set of paths going from $\mathbf {x^{min}}$ to some element $\mathbf {x_{<}} \in \mathbb {R} ^n$ satisfying $f(\mathbf {x_{<}}) < f(\mathbf {x^{min}})$.

The effort of a path $\varPi : [0,1] \rightarrow \mathbb {R} ^n$ (relatively to f) is equal to:

$$ \max _{\ell \in [0,1], \ell ' \in [0,1]} (f(\varPi (\ell )) - f(\varPi (\ell '))).$$

A local minimum $\mathbf {x^{min}}$ of f is said to be matchable if there exists some $\mathbf {x_{<}} \in \mathbb {R} ^n$ such that $f(\mathbf {x_{<}}) < f(\mathbf {x^{min}})$. We call dynamics of a matchable local minimum $\mathbf {x^{min}}$ of f the value:

$$\mathrm {dyn} (\mathbf {x^{min}}) = \min _{\varPi \in (D_{\mathbf {x^{min}}})} \max _{\ell \in [0,1]} \left( f(\varPi (\ell )) - f(\mathbf {x^{min}}) \right) ,$$

and we say that $\mathbf {x^{min}}$ is paired by dynamics (see Fig. 3) with some 1-saddle $\mathbf {x^{\mathrm {sad}}} \in \mathbb {R} ^n$ of f when:

$$\mathrm {dyn} (\mathbf {x^{min}}) = f(\mathbf {x^{\mathrm {sad}}}) - f(\mathbf {x^{min}}).$$

An optimal path $\varPi ^{\mathrm {opt}}$ is an element of $(D_{\mathbf {x^{min}}})$ whose effort is equal to $\min _{\varPi \in (D_{\mathbf {x^{min}}})}(\mathrm {Effort} (\varPi ))$. Note that for any local minimum $\mathbf {x^{min}}$ of f, there always exists some optimal path $\varPi ^{\mathrm {opt}}$ such that $\mathrm {Effort} (\varPi ^{\mathrm {opt}}) = \mathrm {dyn} (\mathbf {x^{min}})$.

Thanks to the uniqueness of critical values of f, there exists only one critical point of f which can be paired with $\mathbf {x^{min}}$ by dynamics.

Dynamics are always positive, and the dynamics of an absolute minimum of f is set at $+\infty$ (by convention).

Fig. 4.

Pairing by persistence on a Morse function: we compute the plane whose height is reaching $f(\mathbf {x^{\mathrm {sad}}})$ (see the left side), which allows us to compute $C^{\mathrm {sad}}$, to deduce the components $C^I_i$ whose closure contains $\mathbf {x^{\mathrm {sad}}}$, and to decide which representative is paired with $\mathbf {x^{\mathrm {sad}}}$ by persistence by choosing the one whose height is the greatest. We can also observe (see the right side) the merge phase where the two components merge and where the component whose representative is paired with $\mathbf {x^{\mathrm {sad}}}$ dies. (Color figure online)

2.3 Topological Persistence

Let us denote by $\mathrm {clo}$ the closure operator, which adds to a subset of $\mathbb {R} ^n$ all its accumulation points, and by $\mathcal {CC} (X)$ the connected components of a subset X of $\mathbb {R} ^n$. We also define the representative of a subset X of $\mathbb {R} ^n$ relatively to a Morse function f the point which minimizes f on X:

$$\mathrm {rep} (X) = {\arg \min }_{\mathbf {x} \in X} f(\mathbf {x}).$$

Definition 1

Let f be some Morse function with unique critical values, and let $\mathbf {x^{\mathrm {sad}}}$ be the abscissa of some 1-saddle point of f. Now we define the following expressions. First,

$$C^{\mathrm {sad}} = \mathcal {CC} ([f \le f(\mathbf {x^{\mathrm {sad}}})],\mathbf {x^{\mathrm {sad}}})$$

denotes the component of the set $[f \le f(\mathbf {x^{\mathrm {sad}}})]$ which contains $\mathbf {x^{\mathrm {sad}}}$. Second, we denote by:

$$\{C^I_i \}_{i \in I} = \mathcal {CC} ([f < f(\mathbf {x^{\mathrm {sad}}})])$$

the connected components of the open set $[f < f(\mathbf {x^{\mathrm {sad}}})]$. Third, we define

$$\{C_i^{\mathrm {sad}} \}_{i \in I^{\mathrm {sad}}} = \left\{ C^I_i\ |\ \mathbf {x^{\mathrm {sad}}} \in \mathrm {clo} (C^I_i) \right\} $$

the subset of components $C^I_i$ whose closure contains $\mathbf {x^{\mathrm {sad}}}$. Fourth, for each $i \in I^{\mathrm {sad}}$, we denote

$$\mathrm {rep} _i = {\arg \min }_{x \in C_i^{\mathrm {sad}}} f(x)$$

the representative of $C_i^{\mathrm {sad}}$. Fifth, we define the abscissa

$$\mathbf {x^{min}} = \mathrm {rep} _{i_{\mathrm {paired}}}$$

with

$$i_{\mathrm {paired}} = {\arg \max }_{i \in I^{\mathrm {sad}}} f(\mathrm {rep} _i),$$

thus $\mathbf {x^{min}}$ is the representative of the component $C_i^{\mathrm {sad}}$ of minimal depth. In this context, we say that $\mathbf {x^{\mathrm {sad}}}$ is paired by persistence to $\mathbf {x^{min}}$ (Fig. 4). Then, the persistence of $\mathbf {x^{\mathrm {sad}}}$ is equal to:

$$\mathrm {Per} (\mathbf {x^{\mathrm {sad}}}) = f(\mathbf {x^{\mathrm {sad}}}) - f(\mathbf {x^{min}}).$$

3 The n-D Equivalence

Let us make two important remarks that will help us in the sequel.

Fig. 5.

Every optimal descending path goes through a 1-saddle. Observe the path in blue coming from the left side and decreasing when following the topographical view of the Morse function f. The effort of this path to reach the minimum of f is minimal thanks to the fact that it goes through the saddle point at the middle of the image. (Color figure online)

Lemma 2

Let $f : \mathbb {R} ^n \rightarrow \mathbb {R}$ be a Morse function and let $\mathbf {x^{min}}$ be a local minimum of f. Then for any optimal path $\varPi ^{\mathrm {opt}}$ in $(D_{\mathbf {x^{min}}})$, there exists some $\ell ^* \in ]0,1[$ such that it is a maximum of $f \circ \varPi ^{\mathrm {opt}}$ and at the same time $\varPi ^{\mathrm {opt}} (\ell ^*)$ is the abscissa of a 1-saddle point of f.

Fig. 6.

How to compute descending paths of lower efforts. The initial path going through $x^*$ (the little grey ball) is in red, the new path of lower effort is in green (the non-zero gradient case is on the left side, the zero-gradient case is on the right side). (Color figure online)

Proof: This proof is depicted in Fig. 5. Let us proceed by counterposition, and let us prove that when a path $\varPi$ in $(D_{\mathbf {x^{min}}})$ does not go through a 1-saddle of f, it cannot be optimal.

Let $\varPi$ be a path in $(D_{\mathbf {x^{min}}})$. Let us define $\ell ^* \in [0,1]$ as one of the positions where the mapping $f \circ \varPi$ is maximal:

$$\ell ^* \in {\arg \max }_{\ell \in [0,1]} f( \varPi (\ell )),$$

and $x^* = \varPi (\ell ^*)$. Let us prove that we can find another path $\varPi '$ in $(D_{\mathbf {x^{min}}})$ whose effort is lower than the one of $\varPi$.

At $x^*$, f can satisfy three possibilities:

• When we have $\nabla f (x^*) \ne 0$ (see the left side of Fig. 6), then locally f is a plane of slope $\Vert \nabla f (x^*)\Vert$, and then we can easily find some path $\varPi '$ in $(D_{\mathbf {x^{min}}})$ with a lower effort than $\mathrm {Effort} (\varPi )$. More precisely, let us fix some arbitrary small value $\varepsilon > 0$ and draw the closed topological ball $\bar{B}(x^*,\varepsilon )$, we can define three points:

  $$\begin{aligned} \ell _{min}&= \min \{\ell \ |\ \varPi (\ell ) \in \bar{B}(x^*,\varepsilon ) \},\\ \ell _{max}&= \max \{\ell \ |\ \varPi (\ell ) \in \bar{B}(x^*,\varepsilon ) \},\\ x_B&= x^*- \varepsilon . \frac{\nabla f (x^*)}{\Vert \nabla f (x^*)\Vert }. \end{aligned}$$

  Thanks to these points, we can define a new path $\varPi '$:

  $$\varPi |_{[0,\ell _{min} ]}<> [\varPi (\ell _{min}),x_B]<> [x_B,\varPi (\ell _{max})] <> \varPi |_{[\ell _{max},1]}.$$

  By doing this procedure at every point in [0, 1] where $f\, \circ \, \varPi$ reaches its maximal value, we obtain a new path whose effort is lower than the one of $\varPi$.

• When we have $\nabla f (x^*) = 0$, then we are at a critical point of f. It cannot be a 0-saddle, that is, a local minimum, due to the existence of the descending path going through $x^*$. It cannot be a 1-saddle neither (by hypothesis). It is then a k-saddle point with $k \in [2,n]$ (see the right side of Fig. 6). Using Lemma 1, f is locally equal to a second order polynomial function (up to a change of coordinates $\varphi$ s.t. $\varphi (x^*) = \mathbf {0}$):

  $$ \ f \circ \varphi ^{-1} (\mathbf {x}) = f(x^*) - x_1^2 - x_2^2 - \dots - x_k^2 + x_{k+1}^2 + \dots + x_n^2.$$

  Now, let us define for some arbitrary small value $\varepsilon > 0$:

  $$\begin{aligned} \ell _{min}&= \min \{\ell \ |\ \varPi (\ell ) \in \bar{B}(\mathbf {0},\varepsilon ) \},\\ \ell _{max}&= \max \{\ell \ |\ \varPi (\ell ) \in \bar{B}(\mathbf {0},\varepsilon ) \},\\ \mathfrak {B}&= \left\{ \mathbf {x}\ \Big | \ \sum _{i \in [1,k]} x_i^2 \le \varepsilon ^2 \ \mathbf{and} \forall j \in [k+1,n], x_j = 0\right\} \setminus \{\mathbf {0} \}. \end{aligned}$$

  This last set is connected since it is equal to a k-manifold (with $k \ge 2$) minus a point. Let us assume without constraints that $\varPi (\ell _{min})$ and $\varPi (\ell _{max})$ belong to $\mathfrak {B}$ (otherwise we can consider their orthogonal projections on the hyperplane of lower dimension containing $\mathfrak {B}$ but the reasoning is the same). Thus, there exists some path $\varPi _\mathfrak {B}$ joining $\varPi (\ell _{min})$ to $\varPi (\ell _{max})$ in $\mathfrak {B}$, from which we can deduce the path $\varPi ' = \varPi |_{[0,\ell _{min} ]}<> \varPi _\mathfrak {B} <> \varPi |_{[\ell _{max},1]}$ whose effort is lower than the one of $\varPi$ since its image is inside $[f < f(x^*)]$.

Since we have seen that, in any possible case, $\varPi$ is not optimal, it concludes the proof.    $\square$

Fig. 7.

A 1-saddle point leads to two open connected components. At a 1-saddle point whose abscissa is $\mathbf {x^{\mathrm {sad}}}$ (at the center of the image), the component $[f \le f(\mathbf {x^{\mathrm {sad}}})]$ is locally the merge of the closure of two connected components (in orange) of $[f < f(\mathbf {x^{\mathrm {sad}}})]$ when f is a Morse function. (Color figure omline)

Proposition 1

Let f be a Morse function from $\mathbb {R} ^n$ to $\mathbb {R}$ with $n \ge 1$. When $x^*$ is a critical point of index 1, then there exists $\varepsilon > 0$ such that:

$$\mathrm {Card} \left( \mathcal {CC} (B(x^*,\varepsilon ) \cap [f < f(x^*)])\right) = 2,$$

where $\mathrm {Card}$ is the cardinality operator.

Proof: The case $n = 1$ is obvious, let us then treat the case $n \ge 2$ (see Fig. 7). Thanks to Lemma 1 and thanks to the fact that $\mathbf {x^{\mathrm {sad}}}$ is the abscissa of a 1-saddle, we can say that (up to a change of coordinates and in a small neighborhood around $\mathbf {x^{\mathrm {sad}}}$) for any $\mathbf {x}$:

$$f(x) = f(\mathbf {x^{\mathrm {sad}}}) + \mathbf {x} ^T . \begin{bmatrix} -1 &{} \mathbf {0} \\ \mathbf {0} &{} \mathbb {I}_{n-1} \\ \end{bmatrix} . \mathbf {x},$$

where $\mathbb {I}_{n-1}$ is the identity matrix of dimension $(n-1) \times (n-1)$. In other words, around $\mathbf {x^{\mathrm {sad}}}$, we obtain that:

$$[f< f(\mathbf {x^{\mathrm {sad}}})] = \left\{ \mathbf {x}\ \Big | \ - x_1^2 + \sum _{i = 2}^n x_i^2 < 0 \right\} = C_+ \cup C_-,$$

with:

$$C_+ = \left\{ \mathbf {x}\ \Big | \ x_1 > \sqrt{\sum _{i = 2}^n x_i^2} \right\} ,\quad C_- = \left\{ \mathbf {x}\ \Big | \ x_1 < - \sqrt{\sum _{i = 2}^n x_i^2} \right\} ,$$

where $C_+$ and $C_-$ are two open connected components of $\mathbb {R} ^n$. Indeed, for any pair $(M,M')$ of $C_+$, we have $x_1^M > \sqrt{\sum _{i = 2}^n (x_i^M) ^2}$ and $x_1^{M'} > \sqrt{\sum _{i = 2}^n (x_i^{M'}) ^2}$, from which we define $N = (x_1^M,0,\dots ,0)^T \in C_+$ and $N' = (x_1^{M'},0,\dots ,0)^T \in C_+$ from which we deduce the path $[M,N]<> [N,N'] <> [N',M']$ joining M to $M'$ in $C_+$. The reasoning with $C_-$ is the same. Since $C_+$ and $C_-$ are two connected (separated) disjoint sets, the proof is done.    $\square$

3.1 Pairing by Persistence Implies Pairing by Dynamics in n-D

Theorem 1

Let f be a Morse function from $\mathbb {R} ^n$ to $\mathbb {R}$. We assume that the 1-saddle point of f whose abscissa is $\mathbf {x^{\mathrm {sad}}}$ is paired by persistence to a local minimum $\mathbf {x^{min}}$ of f. Then, $\mathbf {x^{min}}$ is paired by dynamics to $\mathbf {x^{\mathrm {sad}}}$.

Proof: Let us assume that $\mathbf {x^{\mathrm {sad}}}$ is paired by persistence to $\mathbf {x^{min}}$, then we have the hypotheses described in Definition 1. Let us denote by $C^{\mathrm {min}}$ the connected component in $\{C_i\}_{i \in I^{\mathrm {sad}}}$ satisfying that $\mathbf {x^{min}} = \mathrm {rep} (C_{i_{\mathrm {min}}})$.

Since $\mathbf {x^{\mathrm {sad}}}$ is the abscissa of a 1-saddle, by Proposition 1, we know that $\mathrm {Card} (I^{\mathrm {sad}}) = 2$, then there exists: $\mathbf {x_{<}} = \mathrm {rep} (C^<)$ with $C^<$ the component $C_i$ with $i \in I \setminus \{i_{\mathrm {min}} \}$, then $\mathbf {x^{min}}$ is matchable. Let us assume that the dynamics of $\mathbf {x^{min}}$ satisfies:

$$\mathrm {dyn} (\mathbf {x^{min}}) < f(\mathbf {x^{\mathrm {sad}}}) - f(\mathbf {x^{min}}). \ \ \ (\mathrm {HYP})$$

This means that there exists a path $\varPi _<$ in $(D_{\mathbf {x^{min}}})$ such that:

$$\max _{\ell \in [0,1]} f(\varPi _< (\ell )) - f(\mathbf {x^{min}}) < f(\mathbf {x^{\mathrm {sad}}}) - f(\mathbf {x^{min}}),$$

that is, for any $\ell \in [0,1]$, $f(\varPi _< (\ell )) < f(\mathbf {x^{\mathrm {sad}}})$, and then by continuity in space of $\varPi _<$, the image of [0, 1] by $\varPi _<$ is in $C^{\mathrm {min}}$. Because $\varPi _<$ belongs to $(D_{\mathbf {x^{min}}})$, there exists then some $\mathbf {x_{<}} \in C^{\mathrm {min}}$ satisfying $f(\mathbf {x_{<}}) < f(\mathbf {x^{min}})$. We obtain a contradiction, $(\mathrm {HYP})$ is then false. Then, we have $\mathrm {dyn} (\mathbf {x^{min}}) \ge f(\mathbf {x^{\mathrm {sad}}}) - f(\mathbf {x^{min}}).$

Because for any $i \in I^{\mathrm {sad}}$, $\mathbf {x^{\mathrm {sad}}}$ is an accumulation point of $C_i$ in $\mathbb {R} ^n$, there exist a path $\varPi _m$ from $\mathbf {x^{min}}$ to $\mathbf {x^{\mathrm {sad}}}$ such that:

$$\begin{aligned} \forall \ell \in [0,1],&\varPi _m(\ell ) \in C^{\mathrm {sad}},\\ \forall \ell \in [0,1[,&\varPi _m(\ell ) \in C^{\mathrm {min}}. \end{aligned}$$

In the same way, there exists a path $\varPi _M$ from $\mathbf {x_{<}}$ to $\mathbf {x^{\mathrm {sad}}}$ such that:

$$\begin{aligned} \forall \ell \in [0,1],&\varPi _M(\ell ) \in C^{\mathrm {sad}},\\ \forall \ell \in [0,1[,&\varPi _M(\ell ) \in C^<. \end{aligned}$$

We can then build a path $\varPi$ which is the concatenation of $\varPi _m$ and $\ell \rightarrow \varPi _M(1-\ell )$, which goes from $\mathbf {x^{min}}$ to $\mathbf {x_{<}}$ and goes through $\mathbf {x^{\mathrm {sad}}}$. Since this path stays inside $C^{\mathrm {sad}}$, we know that $\mathrm {Effort} (\varPi ) \le f(\mathbf {x^{\mathrm {sad}}}) - f(\mathbf {x^{min}})$, and then $\mathrm {dyn} (\mathbf {x^{min}}) \le f(\mathbf {x^{\mathrm {sad}}}) - f(\mathbf {x^{min}})$.

By grouping the two inequalities, we obtain that $\mathrm {dyn} (\mathbf {x^{min}}) = f(\mathbf {x^{\mathrm {sad}}}) - f(\mathbf {x^{min}})$, and then by uniqueness of the critical values of f, $\mathbf {x^{min}}$ is then paired by dynamics to $\mathbf {x^{\mathrm {sad}}}$.    $\square$

3.2 Pairing by Dynamics Implies Pairing by Persistence in n-D

Theorem 2

Let f be a Morse function from $\mathbb {R} ^n$ to $\mathbb {R}$. We assume that the local minimum $\mathbf {x^{min}}$ of f is paired by dynamics to a 1-saddle of f of abscissa $\mathbf {x^{\mathrm {sad}}}$. Then, $\mathbf {x^{\mathrm {sad}}}$ is paired by persistence to $\mathbf {x^{min}}$.

Proof: Let us assume that $\mathbf {x^{min}}$ is paired to $\mathbf {x^{\mathrm {sad}}}$ by dynamics. Let us recall the usual framework relative to persistence:

$$\begin{aligned} C^{\mathrm {sad}}&= \mathcal {CC} ([f \le f(\mathbf {x^{\mathrm {sad}}})],\mathbf {x^{\mathrm {sad}}}),\end{aligned}$$

(1)

$$\begin{aligned} \{C^I_i \}_{i \in I}&= \mathcal {CC} ([f < f(\mathbf {x^{\mathrm {sad}}})]),\end{aligned}$$

(2)

$$\begin{aligned} \{C_i^{\mathrm {sad}} \}_{i \in I^{\mathrm {sad}}}&= \left\{ C^I_i | \mathbf {x^{\mathrm {sad}}} \in \mathrm {clo} (C^I_i) \right\} ,\end{aligned}$$

(3)

$$\begin{aligned} \forall i \in I^{\mathrm {sad}}, \ \mathrm {rep} _i&= {\arg \min }_{x \in C_i^{\mathrm {sad}}} f(x). \end{aligned}$$

(4)

By Definition 1, $\mathbf {x^{\mathrm {sad}}}$ will be paired to the representative $\mathrm {rep} _i$ of $C_i^{\mathrm {sad}}$ which maximizes $f(\mathrm {rep} _i)$.

• 1. Let us show that there exists $i_{\mathrm {min}}$ such that $\mathbf {x^{min}}$ is the representative of a component $C_{i_{\mathrm {min}}}^{\mathrm {sad}}$ of $\{C_i^{\mathrm {sad}} \}_{i \in I^{\mathrm {sad}}}$.

  • (a) First, $\mathbf {x^{min}}$ is paired by dynamics with $\mathbf {x^{\mathrm {sad}}}$ and $\mathrm {dyn} (\mathbf {x^{min}})$ is greater than zero, then $f(\mathbf {x^{\mathrm {sad}}}) > f(\mathbf {x^{min}})$, then $\mathbf {x^{min}}$ belongs to $[f < f(\mathbf {x^{\mathrm {sad}}})]$, then there exists some $i_{\mathrm {min}} \in I$ such that $\mathbf {x^{min}} \in C_{i_{\mathrm {min}}}$ (see Eq. (2) above).

  • (b) Now, if we assume that $\mathbf {x^{min}}$ is not the representative of $C_{i_{\mathrm {min}}}$, there exists then some $\mathbf {x_{<}}$ in $C_{i_{\mathrm {min}}}$ satisfying that $f(\mathbf {x_{<}}) < f(\mathbf {x^{min}})$, and then there exists some $\varPi$ in $(D_{\mathbf {x^{min}}})$ whose image is contained in $C_{i_{\mathrm {min}}}$. In other words,

    $$\mathrm {dyn} (\mathbf {x^{min}}) \le \mathrm {Effort} (\varPi ) < f(\mathbf {x^{\mathrm {sad}}}) - f(\mathbf {x^{min}}),$$

    which contradicts the hypothesis that $\mathbf {x^{min}}$ is paired with $\mathbf {x^{\mathrm {sad}}}$ by dynamics.

  • (c) Let us show that $i_{\mathrm {min}}$ belongs to $I^{\mathrm {sad}}$, that is, $\mathbf {x^{\mathrm {sad}}} \in \mathrm {clo} (C_{i_{\mathrm {min}}})$. Let us assume that:

    $$\mathbf {x^{\mathrm {sad}}} \not \in \mathrm {clo} (C_{i_{\mathrm {min}}}). \ \ \ (\mathrm {HYP2})$$

    Every path in $(D_{\mathbf {x^{min}}})$ goes outside of $C_{i_{\mathrm {min}}}$ to reach some point whose image by f is lower than $f(\mathbf {x^{min}})$ since $\mathbf {x^{min}}$ has been proven to be the representative of $C_{i_{\mathrm {min}}}$. Then this path will intersect the boundary $\partial$ of $C_{i_{\mathrm {min}}}$. Since by $(\mathrm {HYP2})$, $\mathbf {x^{\mathrm {sad}}}$ does not belong to the boundary $\partial$ of $C_{i_{\mathrm {min}}}$, any optimal path $\varPi ^*$ in $(D_{\mathbf {x^{min}}})$ will go through one 1-saddle $\mathbf {x^{\mathrm {sad}}} _2 = {\arg \max }_{\ell \in [0,1]} f(\varPi ^* (\ell ))$ (by Lemma 2) different from $\mathbf {x^{\mathrm {sad}}}$ and verifying then $f(\mathbf {x^{\mathrm {sad}}} _2) > f(\mathbf {x^{\mathrm {sad}}})$. Thus, $\mathrm {dyn} (\mathbf {x^{min}}) > f(\mathbf {x^{\mathrm {sad}}}) - f(\mathbf {x^{min}})$, which contradicts the hypothesis that $\mathbf {x^{min}}$ is paired with $\mathbf {x^{\mathrm {sad}}}$ by dynamics. Then, we have:

    $$\mathbf {x^{\mathrm {sad}}} \in \mathrm {clo} (C_{i_{\mathrm {min}}}).$$

• 2. Now let us show that $f(\mathbf {x^{min}}) > f(\mathrm {rep} (C_i^{\mathrm {sad}}))$ for any $i \in I^{\mathrm {sad}} \setminus \{i_{\mathrm {min}} \}$. For this aim, we will prove that there exists some $i \in I^{\mathrm {sad}}$ such that $f(\mathrm {rep} (C_i^{\mathrm {sad}})) < f(\mathbf {x^{min}})$ and we will conclude with Proposition 1. Let us assume that the representative r of each component $C_i^{\mathrm {sad}}$ except $C^{\mathrm {min}}$ satisfies $f(r) > f(\mathbf {x^{min}})$, then any path $\varPi$ of $(D_{\mathbf {x^{min}}})$ will have to go outside $C^{\mathrm {sad}}$ to reach some point whose image by f is lower than $f(\mathbf {x^{min}})$. We obtain the same situation as before (see (1.c)), and then we obtain that the effort of $\varPi$ will be greater than $f(\mathbf {x^{\mathrm {sad}}}) - f(\mathbf {x^{min}})$, which leads to a contradiction with the hypothesis that $\mathbf {x^{min}}$ is paired with $\mathbf {x^{\mathrm {sad}}}$ by dynamics. We have then that there exists $i \in I^{\mathrm {sad}}$ such that $f(\mathrm {rep} (C_i^{\mathrm {sad}})) < f(\mathbf {x^{min}})$. Thanks to Proposition 1, we know then that $\mathbf {x^{min}}$ is the representative of the components of $[f < f(\mathbf {x^{\mathrm {sad}}})]$ whose image by f is the greatest.

• 3. It follows that $\mathbf {x^{\mathrm {sad}}}$ is paired with $\mathbf {x^{min}}$ by persistence.

4 Conclusion

We have proved that persistence and dynamics lead to same pairings in n-D, $n \ge 1$, which implies that they are equal whatever the dimension. Concerning the future works, we propose to investigate the relationship between persistence and dynamics in the discrete case [12] (that is, on complexes). We will also check under which conditions pairings by persistence and by dynamics are equivalent for functions that are not Morse. Furthermore, we will examine if the fast algorithms used in MM like watershed cuts, Betti numbers computations or attribute-based filtering are applicable to PH. Conversely, we will study if some PH concepts can be seen as the generalization of some MM concepts (for example, dynamics seems to be a particular case of persistence).

A Ambiguities occurring when values are not unique

As depicted in Fig. 8, the abscissa of the blue point can be paired by persistence to the abscissas of the orange and/or the red points. The same thing appears when we want to pair the abscissa of the pink point to the abscissas of the green and/or blue points. This shows how much it is important to have unique critical values on Morse functions.

Fig. 8.

Ambiguities can occur when critical values are not unique for pairing by dynamics and for pairing by persistence. (Color figure online)