Keywords

1 Introduction

The deformation history plays an important role in soil constitutive modelling, as a change in the deformation direction yields an increased stiffness. Several material models as hypoplastic models (e.g. von Wolffersdorff 1996; Mašín 2013) or barodetic models (e.g. Kolymbas 2015; Medicus and Fellin 2017) use only the void ratio and the stress state as state variables for the calculation, but those state variables do not contain enough information to consider the deformation history (Herle 2008). To consider memory effects in hypoplastic models, Niemunis and Herle (1997) developed the intergranular strain concept (IS) by introducing the so-called intergranular strain \( \varvec{\delta} \), an additional tensorial state variable. This concept was developed and widely used for simulations with hypoplastic models. Bode et al. (2019) recently presented an approach to apply the original intergranular strain concept also directly on non-hypoplastic models. In the following sections we briefly explain the implementation of the IS approach with barodesy and employ barodesy, extended by the IS concept, in finite element simulations.

2 Barodesy

We use barodesy (Medicus and Fellin 2017) to show the application of the recently developed small-strain extension using the intergranular strain concept. Barodesy, introduced by Kolymbas (2009), is a material model which has similarities to hypoplasticity. As in hypoplasticity, the objective stress rate is formulated as a function of the effective stress \( \varvec{T} \), stretching \( \varvec{D } \) and void ratio \( e \). The model also includes concepts from critical state soil mechanics as a stress-dependent critical void ratio. Critical stress states in barodesy almost coincide with predictions by Matsuoka-Nakai (Fellin and Ostermann 2013). In contrast to elastoplastic models, barodesy and hypoplasticity do not distinguish between elastic and plastic strain which leads to simple numerical implementation. Since the void ratio and the actual stress state are not sufficient to capture the deformation history (Herle 2008), the material model needs a small-strain extension.

3 Extension to Small-Strain Behaviour

To introduce the deformation history in barodesy we use a modified version of the original IS concept (Bode et al. 2019). The formulation is based on the original concept and uses the basic features as an elastic strain range and a stiffness increase for small-strains and changes of the deformation direction. In the following we give a brief introduction in the extension of the IS concept to barodesy, for more details we refer to Bode et al. (2019).

For a simple formulation, which is independent from the mathematical structure of the large-strain model, we use a formulation in stress rates. We need the stress rate of the large-strain model , which is in our case the stress rate of barodesy. Additionally, we need an elastic model for the small strain range. For this model we calculate first the stress rate for the given stretching \( \varvec{D} \) and secondly the elastic stress rate in direction of intergranular strain for the directional interpolation between the elastic model and barodesy. The objective stress rate using the intergranular strain concept can be calculated by

with the stiffness interpolation factors \( f_{A} = \left[ {\rho^{\chi } m_{T} + \left( {1 - \rho^{\chi } } \right)m_{R} } \right] ,\, f_{A} = \left[ {\rho^{\chi } m_{T} + \left( {1 - \rho^{\chi } } \right)m_{R} } \right] \,and\, f_{B2} = \rho^{\chi } \left( {m_{R} - m_{T} } \right) . \) Here, we use the magnitude of the intergranular strain \( \rho = \frac{{\left|\varvec{\delta}\right|}}{R} \) and the material parameters \( R,m_{R} , m_{T} \) and \( \chi . \) The functions \( \eta_{1} \) and \( \eta_{2} \) depend on of the angle between \( \varvec{\delta}^{0} \) and \( \varvec{D}^{0} \). The tensor of intergranular strain follows the evolution equation of Niemunis and Herle (Niemunis and Herle 1997) dependent on the deformation rate \( \varvec{D} \) and the material parameter \( \beta_{r} \).

Additional to the stress rate of barodesy , we need an elastic model to calculate the stress rates and . We can use a hypoelastic model employing the stiffness matrix

with a pressure dependent shear modulus \( G \) and the Poisson’s ratio \( \nu \). The additional elastic material parameters can automatically be calibrated to approximate the material behaviour of the large-strain model (Bode et al. 2019) to be consistent. We obtain and .

With the proposed approach it is possible to calculate an increased stiffness and an incrementally elastic response within the small-strain range. The additional elastic model can be a simple hypoelastic model as shown here but it is also possible to use any other sophisticated approach. It is possible to uncouple the models used for large-strain and for small-strain, but it is also possible to calculate an elastic response directly from barodesy (Bode et al. 2019).

4 Numerical Implementation

4.1 Basic Intergranular Strain Concept

The formulation of the applied small-strain approach allows a simple finite element implementation as an overlay model which can easily be adapted for any kind of models formulated as rate equations. For a calculation using the proposed IS approach we need to calculate the three different stress rates . Using the interpolation scheme in Eq. (1), we directly obtain the objective stress rate for the intergranular strain concept. The models for large-strain and for small-strain can be implemented independently in the finite element subroutine and are afterwards combined in one single equation. The time integration to obtain the new stress state can be performed by an explicit Euler procedure. For a better performance, we use a Richardson extrapolation scheme with substepping and error control (Fellin and Ostermann 2002).

Parallel to the integration of the stress rate and the void ratio, we perform the integration of the evolution equation for the intergranular strain tensor .

4.2 Reduction of Overshooting Effects

The original IS concept (Niemunis and Herle 1997) is widely accepted as small-strain extension for hypoplastic models but has also some shortcomings. As the small-strain range is defined by the material parameter \( R \), for a specific range of strain cycles the model shows a clear improvement of the cyclic behaviour. In several cases, for small-strain cycles the model may lead to so-called overshooting effects and thus inadmissible states are reached. This effect can be seen in Fig. 1. The simulations of a small reloading cycle in an undrained triaxial test and an oedometric compression test overshoot the critical state line (CSL) and the oedometric normal consolidation line (oedNCL), respectively. The overshooting effects produce in both cases an unrealistic behaviour or even to an overestimation of the shear strength.

Fig. 1.
figure 1

Simulation of an oedometric test and an undrained triaxial test with and without the ASBS-cut. The starting point of each test is marked with x.

Full size image

These effects appear because the intergranular strain is not yet completely mobilised when the limit states are reached, and the elastic model does not contain any information about the asymptotic behaviour of the large-strain model.

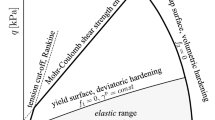
To overcome this shortcoming and to reduce the overshooting effects of the IS model we combine this model with some features of barodesy. Although the material behaviour is not explicitly defined by yield surfaces as with elastoplastic models, it is possible to derive an explicit formulation of the asymptotic states in the stress-void ratio space which defines the so-called asymptotic state boundary surface (ASBS) (Medicus 2020). The ASBS is defined by the states which are asymptotically reached by ongoing constant stretching independently of the initial state. For axisymmetric conditions and by normalizing the stress state by the Hvorslev’s equivalent pressure \( p_{e} = e^{{\left( {\frac{{N - \ln \left( {1 + e} \right)}}{{\lambda^{*} }}} \right)}} \) the ASBS can be plotted in the \( \frac{p}{{p_{e} }} \) − \( \frac{q}{{p_{e} }} \) - space, Fig. 1(a).

We use a combination of the IS concept with the ASBS of barodesy as limit surface assuming that the intergranular strain must be completely mobilized on the asymptotic state boundary surface. To obtain a completely mobilized state with \( \rho = 1 \) and \( \varvec{\delta}^{0} = \varvec{D}^{0} \) we introduce an ASBS-cut and set \( \varvec{\delta}= R\varvec{D}^{0} \varvec{ } \) when the ASBS is reached. According to Eq. (1) only barodesy is activated with these settings. Using the ASBS-cut for the simulations shown in Fig. 1, the stress paths do not pass the ASBS anymore.

4.3 Strength Reduction Procedure

It is possible to perform a safety calculation by reducing the material parameters using finite element calculations (Zienkiewicz et al. 1975). A similar procedure is possible for barodesy (Schneider-Muntau et al. 2018). For the following simulations, the critical friction angle \( \varphi_{c} \) is reduced to obtain a factor of safety \( FoS = \frac{{\tan \varphi_{c} }}{{\tan \varphi_{c,red} }} \).

For a material model of the rate type, a change of the material parameters without changing the stress state does not produce any deformations. Thus, no failure can occur. In elastoplastic models, a state which violates the failure criteria is mapped return to the yield surface. For barodesy, a reduction of the critical friction angle \( \varphi_{c} \) yields a shrinking of the ASBS’ to ASBS in Fig. 2. This may result a stress state \( \varvec{\sigma}^{*} \) that lies outside the ASBS. A stress state in barodesy can be uniquely defined with the mean pressure \( p \), the Lode angle \( \theta \) and the equivalent Matsuoka-Nakai mobilized friction angle \( \varphi_{mob} \) (Medicus et al. 2016). The states outside the ASBS can be identified by the fact that the mobilized friction angle of the state \( \varphi_{mob}^{*} \) is larger than the according asymptotic friction angle, Fig. 2(b).

Fig. 2.
figure 2

Schematic illustration of the radial return-mapping scheme on the ASBS in a normalized p-q-plane (a) and a deviatoric plane (b).

Full size image

To avoid inadmissible states and to induce a stress redistribution during the strength reduction, we use a return-mapping scheme with a radial projection. The mean pressure and the Lode angle stay constant and we search a stress state with \( {\varphi }_{mob} = {\varphi }_{ASBS} \). The new stress state can be found by a scalar scaling of the deviatoric stress tensor \( \varvec{s} \). Starting with the stress state \( \varvec{\sigma}^{*} = - p\varvec{I} + \varvec{s}^{*} \), we get the corrected stress tensor

$$ {\varvec{\upsigma}} = - p\varvec{I} + \mu \varvec{s}^{\varvec{*}} = \left( {\mu - 1} \right)p\varvec{I} + \mu {\varvec{\upsigma}}^{*} $$
(3)

with the scaling factor \( \upmu \). To find the solution for \( \upmu \) we employ a one-dimensional Newton iteration using the condition \( \varphi_{mob} = \varphi_{ASBS} \). For a detailed derivation and the equations of the ASBS we refer to (Medicus 2020).

During the strength reduction process, the redistribution of the stress causes deformations until the failure state is reached. As those deformations do not have any physical meaning, we do not use the intergranular strain concept when the safety calculation is performed. Thus, the intergranular strain concept only influences the initial stress and state and the void ratio before the safety calculation.

5 Simulations

We investigate the influence of the IS concept on barodesy and the here presented numerical implementation on finite element simulations. The model is implemented in a user subroutine for the finite element software PLAXIS.

For the verification of the model performance we calculate the construction of an \( 7\,{\text{m}} \) deep excavation, supported by a 0.3 m thick and \( 12\,{\text{m}} \) deep concrete diaphragm wall, Fig. 3(a). The wall is tied back by \( 11.5\,{\text{m}} \) long pre-stressed ground anchors, which are installed after the first excavation step of \( 3\,{\text{m}} \). A strength reduction computation is performed as final step to calculate the overall factor of safety. The plain strain FE-model is \( 50\,{\text{m}} \) wide, \( 30\,{\text{m}} \) high and consists of 5928 15-noded elements. For numerical stabilisation a load of \( 1\,{\text{kPa}} \) is applied to the free surfaces.

Fig. 3.
figure 3

Results of the FE simulation. (a) Detail of the FE-model and the shear bands resulting from the strength reduction presented by the deviatoric shear strain for the calculation using the IS concept. (b) Horizontal displacement and bending moment of the diaphragm wall for the first (dashed lines) and second (solid lines) excavation stage.

Full size image

We employ barodesy for clay (Medicus and Fellin 2017) with the parameters for Dortmund clay (Mašín 2013) and default parameters for the IS concept (Bode et al. 2019), Table 1. We use an oedometrically normal consolidated soil and an initial \( K_{0} \) stress field with \( \upsigma_{h} = (1 - \sin {\upvarphi }_{c} )\upsigma_{v} \).

Table 1. Parameters for barodesy of Dortmund clay and for the IS extension.
Full size table

The IS concept considers the deformation history. Thus, we must assume the deformation direction of the soil that occurred before the start of the computation, i.e. we have to set an initial value for \( {\varvec{\updelta}} \). Here, we initialise the IS with the common assumption \( {\varvec{\updelta}} = 0 \). Without the ASBS-cut any following compression would go along with overshooting effects, which sometimes yield numerical problems. The presented ASBS-cut reduces this problem.

The results of the calculations are summarized in Table 2. The small-strain stiffness modelled by the IS concept leads to smaller deflections of the diaphragm wall in the first excavation step than those computed without the IS concept, Fig. 3(b).

Table 2. Calculation results with and without the IS concept
Full size table

The second excavation step, after the installation of the anchor, causes a strong change of the deformation behavior of the diaphragm wall. This yields a change of the deformation direction in the soil and therefore a stiffness increase by the IS concept, which reduces the additional horizontal displacement \( u_{x} \) of the wall compared to the computations without the IS concept, Fig. 3(b). The stiffness increase reduces the anchor force \( A \) and the bending Moment \( M \), too. Thus, the consideration of the deformation history and therefore the more realistic stiffness of the soil influences the degree of utilization of the excavation support. A good prediction of the wall deformation is also important for the monitoring of the construction process using the observational method.

Although the strength reduction starts with different internal forces and a different resulting stress state in both calculations, here represented by the resulting active and passive horizontal earth pressures \( E_{a,h} \) and \( E_{p,h} \), we obtain almost the same overall factor of safety. The reduction of the friction angle yields a localization of the shear strain in thin shear bands and both computations show the same failure mechanism, Fig. 3(a). For the here considered, normally consolidated soil the mobilized friction angle is bounded by the critical friction angle which is reduced by the same factor in both computations during the strength reduction. In the limit state, when failure occurs, the mobilized friction angle along the shear bands is everywhere equal to the critical friction angle. In this case the IS concept does not influence the overall stability.

6 Conclusions

The intergranular strain concept has been applied to barodesy and implemented into finite element simulations. It is possible to reduce the overshooting effects of the IS model using the asymptotic state boundary surface of barodesy. The results of the simulation of the construction of a supported excavation show the influence of the IS concept on the deformations of the construction. The increased stiffness causes a decreased anchor force and bending moment of the wall which also decreases the degree of utilization of the construction support. Additionally, the factor of safety is calculated, performing a strength reduction using a radial projection scheme. In this case of a normally consolidated soil there is no influence of the IS concept on the factor of safety. Future research will focus on heavily overconsolidated problems, where the mobilized friction angle can be larger than the critical one.