Abstract
We adapt existing approaches for privacy-preserving publishing of linked data to a setting where the data are given as Description Logic (DL) ABoxes with possibly anonymised (formally: existentially quantified) individuals and the privacy policies are expressed using sets of concepts of the DL \(\mathcal {EL} \). We provide a chacterization of compliance of such ABoxes w.r.t. \(\mathcal {EL} \) policies, and show how optimal compliant anonymisations of ABoxes that are non-compliant can be computed. This work extends previous work on privacy-preserving ontology publishing, in which a very restricted form of ABoxes, called instance stores, had been considered, but restricts the attention to compliance. The approach developed here can easily be adapted to the problem of computing optimal repairs of quantified ABoxes.
Funded by the Deutsche Forschungsgemeinschaft (DFG) – 430150274.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Before publishing data concerned with persons, one may want to or be legally required to hide certain private information [15]. For example, a shady politician may not want the public to know that he is not only a politician, but also a businessman, and that he is additionally related to someone who is both a politician and a businessman. Before they publish data about their boss, his aids thus need to remove or modify certain information, but being honest themselves, they want to keep the changes minimal, and they do not want to invent incorrect information. This poses the question of how to change a given data set in a minimal way such that all the information to be published follows from the original one, but certain privacy constraints are satisfied. Basically the same question is asked in ontology repair [4], with the difference that the information to be removed is deemed to be erroneous rather than private.
A survey on privacy-preserving data publishing in general is given in [15]. In the context of ontologies, two different approaches for preserving privacy constraints have been investigated. In the controlled query evaluation framework, the source data are left unchanged, but an additional layer, called censor, is introduced, which decides whether and how queries are answered [9, 11, 16]. In contrast, anonymisation approaches modify the source data in a minimal way such that secrets that should be preserved can no longer be derived [3, 12,13,14]. We use the approach for privacy-preserving publishing of linked data introduced in [12, 13] as a starting point, where the information to be published is a relational dataset, possibly with (labelled) null values, and the privacy constraints (called policy) are formulated as conjunctive queries. A dataset is compliant with such a policy if the queries have no answers. In our example, the dataset consists of
and the policy of the two conjunctive queries \( Politician (x)\wedge Businessman (x)\) and \(\exists {y}.{ related (x,y)\wedge Politician (y)\wedge Businessman (y)}\). Since the first query has d and g, and the second has d as answers, the dataset does not comply with this policy. The only anonymisation operation provided in [12, 13] for making the given dataset compliant is to replace constants (naming known individuals, like d and g) or null values by new null values. In our example, we can achieve compliance by renaming one occurrence of d and one occurrence of g:
Basically, this has the effect of removing \( Businessman (d)\) and \( Politician (g)\) from the dataset. While this is one of the optimal anonymisations (w.r.t. minimal loss of information) that can be obtained with the anonymisation operation allowed in [12, 13], it is not optimal without this restriction. In fact, if we add \( related (d,n_2)\) to this anonymisation, then the resulting dataset is still compliant, and it retains the information that d is related to some politician. The main difference of our approach to the one in [12, 13] is that there only certain operations are available for anonymising ABoxes, whereas we consider all possible ABoxes that are implied by the given one. Optimality in [12, 13] looks only at the range of ABoxes that can be obtained using the anonymisation operations defined there. Thus, optimal anonymisations obtained by the approach in [12, 13] may not be optimal in our sense, as illustrated by the example above.
The aim of this paper is to determine a setting where optimal compliant anonymisations exist and can effectively be computed. To this purpose, we restrict the datasets with labelled null values of [12, 13] to unary and binary relations, as usually done in DL ABoxes. In order to express the labelled null values, we consider an extension of ABoxes, called quantified ABoxes, in which some of the object names occurring in the ABox are existentially quantified. The main restriction is, however, that policies are expressed as concepts of the DL \(\mathcal {EL}\), which can be seen as restricted form of conjunctive queries. The policy in our example can be expressed by the \(\mathcal {EL}\) concepts \( Politician \sqcap Businessman \) and \(\exists { related }.{( Politician \sqcap Businessman )}\).
In this setting, we characterise compliance of quantified ABoxes, and use this characterisation to show how to compute the set of all optimal compliant anonymisations of a non-compliant quantified ABox by a deterministic algorithm with access to an NP oracle that runs in exponential time. We also show that a certain (non-empty) subset of this set can be computed in deterministic exponential time without oracle. If we are only interested in answers to instance queries (i.e., which instance relationships follow from the given ABox), we can replace classical logical entailment by IQ-entailment when defining the notion of an optimal compliant anonymisation. In this case, the full set of all optimal compliant anonymisations can be computed in deterministic exponential time, and the sizes of the anonymisations can be reduced as well.
These results improve on the ones in [3], where a severely restricted form of ABoxes, called instance stores, was investigated. The ABox in our example is not an instance store, due to the role assertion between the individuals d and g. Note that, even in this restricted case, the set of optimal compliant anonymisations may be exponentially large, which demonstrates that the exponential complexity of our algorithms cannot be avoided.
In [12, 13] and [3], safety is introduced as a strengthening of compliance. Basically, safety means that the hidden facts should not be derivable even if additional compliant information is added. The compliant anonymisation in the above example is not safe since adding \( Businessman (d)\) would make it non-compliant. Due to the space restrictions, we cannot present results for safety here, though the methods developed in this paper can be extended to deal also with safety [6].
2 Formal Preliminaries
In this section, we first introduce the logical formalisms considered in this paper, and then recall some definitions and known results for them.
From a logical point of view, we consider only formulas in the so-called primitive positive (pp) fragment of first-order logic (FO) [20], which consists of existentially quantified conjunctions of atomic relational formulas. Atomic relational formulas are of the form \(R(x_1,\ldots ,x_n)\), where R is an n-ary relation symbol and the \(x_i\) are variables. Not all variables occurring in the conjunction need to be existentially quantified, i.e., a pp formula may contain both quantified and free variables. We say that the pp formula \(\exists \vec {x}.\varphi _1(\vec {x},\vec {z_1})\) entails \(\exists \vec {y}.\varphi _2(\vec {y},\vec {z_2})\) if the following is a valid FO formula: \( \forall \vec {z_1}.\forall \vec {z_2}.(\exists \vec {x}.\varphi _1(\vec {x},\vec {z_1})\rightarrow \exists \vec {y}.\varphi _2(\vec {y},\vec {z_2})). \)
From a database point of view, pp formulas are conjunctive queries (CQs), where the free variables are usually called answer variables [1]. Entailment of pp formulas corresponds to CQ containment, which is a well-known NP-complete problem [10].Footnote 1 The relational datasets with labelled null values (which generalize RDF graphs) considered in [12, 13] can also be viewed as pp formulas, where the quantified variables are the labelled null values.
Following the tradition in DL, we consider a signature that contains only unary and binary relation symbols, respectively called concept names and role names. Basically, a quantified ABox is just a pp formula over such a signature, but defined in line with the notation usually employed in the DL community.
Definition 1
Let \(\varSigma \) be a signature, given by pairwise disjoint, countably infinite sets \(\varSigma _{\mathsf{O}}\), \(\varSigma _{\mathsf{C}}\), and \(\varSigma _{\mathsf{R}}\) of object-, concept-, and role names, respectively. A quantified ABox \(\exists {X}.{\mathcal {A}}\) consists of
-
the quantifier prefix \(\exists {X}.\), where X is a finite subset of \(\varSigma _{\mathsf{O}} \) whose elements are called variables, and
-
the matrix \(\mathcal {A}\), which is a set of assertions of the form A(u) (concept assertions) and r(u, v) (role assertions), for \(A\in \varSigma _{\mathsf{C}} \), \(r\in \varSigma _{\mathsf{R}} \), and \(u, v\in \varSigma _{\mathsf{O}} \).
We denote the set of elements of \(\varSigma _{\mathsf{O}} \setminus X\) occurring in \(\mathcal {A}\) as \(\varSigma _{\mathsf{I}} (\exists {X}.{\mathcal {A}})\), and call them individual names.
An interpretation \(\mathcal {I}= (\varDelta ^\mathcal {I},\cdot ^\mathcal {I})\) of \(\varSigma \) consists of a non-empty set \(\varDelta ^\mathcal {I}\), called the domain, and an interpretation function mapping each object name \(u\in \varSigma _{\mathsf{O}} \) to an element \(u^\mathcal {I}\in \varDelta ^\mathcal {I}\), each concept name \(A\in \varSigma _{\mathsf{C}} \) to a subset \(A^\mathcal {I}\subseteq \varDelta ^\mathcal {I}\), and each role name \(r\in \varSigma _{\mathsf{R}} \) to a binary relation \(r^\mathcal {I}\) over \(\varDelta ^\mathcal {I}\). It is a model of the quantified ABox \(\exists {X}.{\mathcal {A}}\) if there is an interpretation \(\mathcal {J}= (\varDelta ^\mathcal {I},\cdot ^\mathcal {J})\) such that
-
\(\cdot ^\mathcal {J}\) coincides with \(\cdot ^\mathcal {I}\) on \(\varSigma _{\mathsf{C}} \), \(\varSigma _{\mathsf{R}} \), and \(\varSigma _{\mathsf{O}} \setminus X\), and
-
\(u^\mathcal {J}\in A^\mathcal {J}\) for all \(A(u)\in \mathcal {A}\) and \((u^\mathcal {J},v^\mathcal {J}) \in r^\mathcal {J}\) for all \(r(u,v)\in \mathcal {A}\).
Given two quantified ABoxes \(\exists {X}.{\mathcal {A}}\) and \(\exists {Y}.{\mathcal {B}}\), we say that \(\exists {X}.{\mathcal {A}}\) entails \(\exists {Y}.{\mathcal {B}}\) (written \(\exists {X}.{\mathcal {A}}\models \exists {Y}.{\mathcal {B}}\)) if every model of \(\exists {X}.{\mathcal {A}}\) is a model of \(\exists {Y}.{\mathcal {B}}\). Two quantified ABoxes are equivalent if they entail each other.
Any quantified ABox \(\exists {X}.{\mathcal {A}}\) can be expressed by a pp formula, which existentially quantifies (in arbitrary order) over the variables in X and conjoins all the assertions from \(\mathcal {A}\). The individual names in \(\varSigma _{\mathsf{I}} (\exists {X}.{\mathcal {A}})\) are the free variables of this pp formula and the variables in X are the quantified variables. Entailment of quantified ABoxes corresponds to entailment of the corresponding pp formulas, and thus to containment of conjunctive queries. Consequently, the entailment problem for quantified ABoxes is NP-complete. It is well known [1, 10] that containment of conjunctive queries can be characterised using homomorphisms. This characterisation can be adapted to quantified ABoxes as follows.
Henceforth, when considering two quantified ABoxes, say \(\exists {X}.{\mathcal {A}}\) and \(\exists {Y}.{\mathcal {B}}\), we assume without loss of generality that they are renamed apart in the sense that X is disjoint with \(Y\cup \varSigma _{\mathsf{I}} (\exists {Y}.{\mathcal {B}})\) and Y is disjoint with \(X\cup \varSigma _{\mathsf{I}} (\exists {X}.{\mathcal {A}})\). This also allows us to assume that the two ABoxes are built over the same set of individuals  . A homomorphism from \(\exists {X}.{\mathcal {A}}\) to \(\exists {Y}.{\mathcal {B}}\) is a mapping
. A homomorphism from \(\exists {X}.{\mathcal {A}}\) to \(\exists {Y}.{\mathcal {B}}\) is a mapping  that satisfies the following conditions:
that satisfies the following conditions:
-
1.
\(h(a)=a\) for each individual name \(a\in \varSigma _{\mathsf{I}} \);
-
2.
\(A(h(u))\in \mathcal {B}\) if \(A(u)\in \mathcal {A}\) and \(r(h(u),h(v))\in \mathcal {B}\) if \(r(u,v)\in \mathcal {A}\).
Proposition 2
Let \(\exists {X}.{\mathcal {A}}, \exists {Y}.{\mathcal {B}}\) be quantified ABoxes that are renamed apart. Then, \(\exists {X}.{\mathcal {A}}\models \exists {Y}.{\mathcal {B}}\) iff there exists a homomorphism from \(\exists {Y}.{\mathcal {B}}\) to \(\exists {X}.{\mathcal {A}}\).
Traditional DL ABoxes are not quantified. Thus, an ABox is a quantified ABox where the quantifier prefix is empty. Instead of \(\exists {\emptyset }.{\mathcal {A}}\) we simply write \(\mathcal {A}\). The matrix \(\mathcal {A}\) of a quantified ABox \(\exists {X}.{\mathcal {A}}\) is such a traditional ABox. Note, however, that one can draw fewer consequences from \(\exists {X}.{\mathcal {A}}\) than from its matrix \(\mathcal {A}\).
Example 3
Consider the ABox  which entails A(x) (where we view A(x) as a singleton ABox). In contrast, the quantified ABox \(\exists {\{x\}}.{\mathcal {A}}\) does not entail A(x) since, due to the existential quantification, the x in \(\exists {\{x\}}.{\mathcal {A}}\) stands for an arbitrary object instead of a specific one with name x. This shows that the quantification allows us to hide information about certain individuals. We can, however, still derive from \(\exists {\{x\}}.{\mathcal {A}}\) that a (which is not quantified) is related with some individual that belongs to A.
which entails A(x) (where we view A(x) as a singleton ABox). In contrast, the quantified ABox \(\exists {\{x\}}.{\mathcal {A}}\) does not entail A(x) since, due to the existential quantification, the x in \(\exists {\{x\}}.{\mathcal {A}}\) stands for an arbitrary object instead of a specific one with name x. This shows that the quantification allows us to hide information about certain individuals. We can, however, still derive from \(\exists {\{x\}}.{\mathcal {A}}\) that a (which is not quantified) is related with some individual that belongs to A.
Such properties of individuals can be expressed using concept descriptions of the DL \(\mathcal {EL}\).
Definition 4
Given two pairwise disjoint, countably infinite sets \(\varSigma _{\mathsf{C}}\) and \(\varSigma _{\mathsf{R}}\) of concept and role names, we define \(\mathcal {EL}\) atoms and \(\mathcal {EL}\) concept descriptions by simultaneous induction as follows.
-
An \(\mathcal {EL}\) atom is either a concept name \(A\in \varSigma _{\mathsf{C}} \) or an existential restriction \(\exists {r}.{C}\), where \(r\in \varSigma _{\mathsf{R}} \) and C is an \(\mathcal {EL}\) concept description.
-
An \(\mathcal {EL}\) concept description is a conjunction \(\sqcap \mathcal {C}\), where \(\mathcal {C}\) is a finite set of \(\mathcal {EL}\) atoms.
Given an interpretation \(\mathcal {I}= (\varDelta ^\mathcal {I},\cdot ^\mathcal {I})\) of a signature \(\varSigma \) containing \(\varSigma _{\mathsf{C}}\) and \(\varSigma _{\mathsf{R}}\) (see Definition 1), we extend the interpretation function \(\cdot ^\mathcal {I}\) to \(\mathcal {EL}\) atoms and concept descriptions as follows:
-
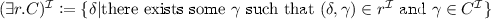 ,
, -
 , where the intersection over the empty set \(\mathcal {C}= \emptyset \) is \(\varDelta ^\mathcal {I}\).
, where the intersection over the empty set \(\mathcal {C}= \emptyset \) is \(\varDelta ^\mathcal {I}\).
Given \(\mathcal {EL}\) concept descriptions C, D and a quantified ABox \(\exists {X}.{\mathcal {A}}\), we say that
-
C is subsumed by D (written \(C\sqsubseteq _{\emptyset }D\)) if \(C^\mathcal {I}\subseteq D^\mathcal {I}\) holds for all interpretations \(\mathcal {I}\), and C is equivalent to D (written \(C\equiv _\emptyset D\)) if \(C\sqsubseteq _{\emptyset }D\) and \(D\sqsubseteq _{\emptyset }C\). We write \(C\sqsubset _{\emptyset }D\) to express that \(C\sqsubseteq _{\emptyset }D\), but \(C\not \equiv _\emptyset D\).
-
the object \(u\in \varSigma _{\mathsf{O}} \) is an instance of C w.r.t. \(\exists {X}.{\mathcal {A}}\) (written \(\exists {X}.{\mathcal {A}} \models C(u)\)) if \(u^\mathcal {I}\in C^\mathcal {I}\) holds for all models \(\mathcal {I}\) of \(\exists {X}.{\mathcal {A}}\).
To make the syntax introduced above more akin to the one usually employed for \(\mathcal {EL}\), we denote the empty conjunction \(\sqcap \emptyset \) as \(\top \) (top concept), singleton conjunctions \(\sqcap \{C\}\) as C, and conjunctions \(\sqcap \mathcal {C}\) for \(|\mathcal {C}|\ge 2\) as \(C_1\sqcap \ldots \sqcap C_n\), where \(C_1,\ldots ,C_n\) is an enumeration of the elements of \(\mathcal {C}\) in an arbitrary order. Given an \(\mathcal {EL}\) concept description \(C = \sqcap \mathcal {C}\), we sometimes denote the set of atoms \(\mathcal {C}\) as \(\mathsf{Conj}(C)\). The set \(\mathsf{Sub}(C)\) of subconcepts of an \(\mathcal {EL}\) concept description C is defined in the usual way, i.e.,  ,
,  , and
, and  . We denote the set of atoms occurring in \(\mathsf{Sub}(C)\) with \(\mathsf{Atoms}(C)\). The subscript \(\emptyset \) in \(\sqsubseteq _{\emptyset }\) indicates that no terminological axioms are available, i.e., we consider subsumption w.r.t. the empty TBox.
. We denote the set of atoms occurring in \(\mathsf{Sub}(C)\) with \(\mathsf{Atoms}(C)\). The subscript \(\emptyset \) in \(\sqsubseteq _{\emptyset }\) indicates that no terminological axioms are available, i.e., we consider subsumption w.r.t. the empty TBox.
It is well-known that \(\mathcal {EL}\) concept descriptions C can be translated into semantically equivalent pp formulas \(\phi _C(x)\) with one free variable x. For example, the \(\mathcal {EL}\) concept description  , which we can also write as \(A\sqcap \exists {r}.{(B\sqcap \exists {r}.{(A\sqcap B)})}\), translates into the pp formula \(\phi _C(x) = \exists y.\exists z.(A(x)\wedge r(x,y) \wedge B(y)\wedge r(y,z)\wedge A(z)\wedge B(z))\). The subsumption and the instance problems thus reduce to entailment of pp formulas:
, which we can also write as \(A\sqcap \exists {r}.{(B\sqcap \exists {r}.{(A\sqcap B)})}\), translates into the pp formula \(\phi _C(x) = \exists y.\exists z.(A(x)\wedge r(x,y) \wedge B(y)\wedge r(y,z)\wedge A(z)\wedge B(z))\). The subsumption and the instance problems thus reduce to entailment of pp formulas:
Thus, the homomorphism characterisation of entailment applies to subsumptions and instances as well. However, since the pp formulas obtained from \(\mathcal {EL}\) concept descriptions are tree-shaped, the existence of a homomorphism can be checked in polynomial time. Thus, the subsumption and the instance problem are in P [7, 19]. The fact that \(\mathcal {EL}\) concept descriptions can be translated into pp formulas (and thus quantified ABoxes) also shows that quantified ABoxes can express \(\mathcal {EL}\) ABoxes with concept assertions of the form C(u) for complex \(\mathcal {EL}\) concepts C.
The homomorphism characterisation of subsumption also yields the following recursive characterisation of subsumption [8].
Lemma 5
Let C, D be \(\mathcal {EL}\) concept descriptions. Then \(C\sqsubseteq _{\emptyset }D\) holds iff the following two statements are satisfied:
-
1.
\(A\in \mathsf{Conj}(D)\) implies \(A\in \mathsf{Conj}(C)\) for each concept name A;
-
2.
for each existential restriction \(\exists {r}.{F}\in \mathsf{Conj}(D)\), there is an existential restriction \(\exists {r}.{E}\in \mathsf{Conj}(C)\) such that \(E\sqsubseteq _{\emptyset }F\).
An analogous characterisation can be given for the instance problem w.r.t. (unquantified) ABoxes.
Lemma 6
Let \(\mathcal {A}\) be an ABox, D an \(\mathcal {EL}\) concept description, and \(u\in \varSigma _{\mathsf{O}} \). Then \(\mathcal {A}\models D(u)\) holds iff the following two statements are satisfied:
-
1.
for each concept name \(A\in \mathsf{Conj}(D)\), the ABox \(\mathcal {A}\) contains A(u),
-
2.
for each existential restriction \(\exists {r}.{E}\in \mathsf{Conj}(D)\), the ABox \(\mathcal {A}\) contains a role assertion r(u, v) such that \(\mathcal {A}\models E(v)\).
Regarding the effect that the existential quantification in quantified ABoxes has on the instance problem, we generalise the observations made in Example 3.
Lemma 7
If \(\exists {X}.{\mathcal {A}}\) be a quantified ABox, C an \(\mathcal {EL}\) concept description, \(x\in X\), and \(a\in \varSigma _{\mathsf{I}} (\exists {X}.{\mathcal {A}})\), then \(\exists {X}.{\mathcal {A}}\models C(a)\) iff \(\mathcal {A}\models C(a)\), and \(\exists {X}.{\mathcal {A}}\models C(x)\) iff \(C = \top \).
Note that, according to our definition of the syntax of \(\mathcal {EL}\), the only \(\mathcal {EL}\) concept description equivalent to \(\top = \sqcap \emptyset \) is \(\top \) itself. We also need the reduced form \(C^r\) of an \(\mathcal {EL}\) concept description C [18], which is defined inductively as follows.
-
For atoms, we set
 for \(A\in \varSigma _{\mathsf{C}} \) and
for \(A\in \varSigma _{\mathsf{C}} \) and  .
. -
To obtain the reduced form of \(\sqcap \mathcal {C}\), we first reduce the elements of \(\mathcal {C}\), i.e., construct the set
 . Then we build \(\mathsf{Min}(\mathcal {C}^r)\) by removing all elements D that are not subsumption minimal, i.e., for which there is an E in the set such that \(E\sqsubset _{\emptyset }D\). We then set
. Then we build \(\mathsf{Min}(\mathcal {C}^r)\) by removing all elements D that are not subsumption minimal, i.e., for which there is an E in the set such that \(E\sqsubset _{\emptyset }D\). We then set  .
.
Adapting the results in [18], one can show that \(C \equiv _\emptyset C^r\) and that \(C \equiv _\emptyset D\) implies \(C^r=D^r\). In particular, this implies that, on reduced \(\mathcal {EL}\) concept descriptions, subsumption is a partial order and not just a pre-order.
3 Compliant Anonymisations w.r.t. Classical Entailment
A policy is a finite set of \(\mathcal {EL}\) concept descriptions. Intuitively, a policy says that one should not be able to derive that any of the individuals of a quantified ABox belongs to a policy concept.
Definition 8
Let \(\exists {X}.{\mathcal {A}}, \exists {Y}.{\mathcal {B}}\) be quantified ABoxes and \(\mathcal {P}\) a policy. Then
-
1.
\(\exists {X}.{\mathcal {A}}\) is compliant with \(\mathcal {P}\) at object \(u\in \varSigma _{\mathsf{O}} \) if \(\mathcal {A}\not \models P(u)\) for each \(P\in \mathcal {P}\);
-
2.
\(\exists {X}.{\mathcal {A}}\) is compliant with \(\mathcal {P}\) if it is compliant with \(\mathcal {P}\) at each element of \(\varSigma _{\mathsf{I}} = \varSigma _{\mathsf{I}} (\exists {X}.{\mathcal {A}})\);
-
3.
\(\exists {Y}.{\mathcal {B}}\) is a \(\mathcal {P}\)-compliant anonymisation of \(\exists {X}.{\mathcal {A}}\) if \(\exists {X}.{\mathcal {A}} \models \exists {Y}.{\mathcal {B}}\) and \(\exists {Y}.{\mathcal {B}}\) is compliant with \(\mathcal {P}\);
-
4.
\(\exists {Y}.{\mathcal {B}}\) is an optimal \(\mathcal {P}\)-compliant anonymisation of \(\exists {X}.{\mathcal {A}}\) if it is a \(\mathcal {P}\)-compliant anonymisation of \(\exists {X}.{\mathcal {A}}\), and \(\exists {X}.{\mathcal {A}} \models \exists {Z}.{\mathcal {C}} \models \exists {Y}.{\mathcal {B}}\) implies \(\exists {Y}.{\mathcal {B}}\models \exists {Z}.{\mathcal {C}}\) for every \(\mathcal {P}\)-compliant anonymisation \(\exists {Z}.{\mathcal {C}}\) of \(\exists {X}.{\mathcal {A}}\).
We require that an anonymisation of a quantified ABox is entailed by it, and also compare different anonymisations using entailment. Later on, we will look at a setting where a weaker notion than classical entailment is employed. In the following we assume without loss of generality that all concepts in a given policy are reduced and incomparable w.r.t. subsumption. In fact, given a policy \(\mathcal {P}\), we can first reduce the elements of \(\mathcal {P}\), i.e., construct the set  , and then build \(\mathsf{Max}(\mathcal {P}^r)\) by removing all elements that are not subsumption maximal. Any quantified ABox is compliant with \(\mathcal {P}\) iff it is compliant with \(\mathsf{Max}(\mathcal {P}^r)\). We call such a policy reduced.
, and then build \(\mathsf{Max}(\mathcal {P}^r)\) by removing all elements that are not subsumption maximal. Any quantified ABox is compliant with \(\mathcal {P}\) iff it is compliant with \(\mathsf{Max}(\mathcal {P}^r)\). We call such a policy reduced.
Since the instance problem in \(\mathcal {EL}\) is in P, compliance can obviously be tested in polynomial time. However, our main purpose is not to test for compliance of a given quantified ABox, but to compute compliant anonymisations of it in case it is not compliant. For this purpose, we need an appropriate characterisation of compliance. The following lemma is an easy consequence of Lemma 6. Its formulation uses the notion of a hitting set. Given a set of sets \(\{\mathcal {P}_1,\ldots ,\mathcal {P}_n\}\), a hitting set of this set is a set \(\mathcal {H}\) such that \(\mathcal {H}\cap \mathcal {P}_i \ne \emptyset \) for \(i\in \{1,\ldots ,n\}\).
Lemma 9
The quantified ABox \(\exists {X}.{\mathcal {A}}\) is compliant with the policy \(\mathcal {P}\) at \(u\in \varSigma _{\mathsf{O}} \) iff there is a hitting set \(\mathcal {H}\) of \(\{\mathsf{Conj}(P)|P\in \mathcal {P}\}\) such that
-
\(\exists {X}.{\mathcal {A}}\) is compliant with \(\mathcal {H}\cap \varSigma _{\mathsf{C}} \) at u, i.e., \(A\not \in \mathcal {H}\) for each concept assertion A(u) in \(\mathcal {A}\), and
-
\(\exists {X}.{\mathcal {A}}\) is compliant with \(\{Q|\exists {r}.{Q}\in \mathcal {H}\}\) at v for each role assertion r(u, v) in \(\mathcal {A}\).
Computing Compliant Anonymisations. We assume that \(\varSigma _{\mathsf{I}} (\exists {X}.{\mathcal {A}})\ne \emptyset \) since otherwise \(\exists {X}.{\mathcal {A}}\) is trivially compliant, and additionally that the policy \(\mathcal {P}\) does not contain \(\top \) since otherwise no compliant anonymisation exists.
If a quantified ABox is not compliant with \(\mathcal {P}\), then the characterisation of compliance in Lemma 9 tells us that, for some of the individuals \(a\in \varSigma _{\mathsf{I}} \), the required hitting sets do not exist. To overcome this problem, one needs to remove some of the (implied) instance relationships for these individuals. Compliance seed functions tell us which ones to remove.
Definition 10
A compliance seed function (abbrv. csf) on \(\exists {X}.{\mathcal {A}}\) for \(\mathcal {P}\) is a mapping  such that the following holds for each \(a\in \varSigma _{\mathsf{I}} \):
such that the following holds for each \(a\in \varSigma _{\mathsf{I}} \):
-
1.
the set s(a) contains only atoms C where \(\mathcal {A}\models C(a)\),
-
2.
for each \(P\in \mathcal {P}\) with \(\mathcal {A}\models P(a)\), the set s(a) contains an atom subsuming P, i.e., there is some \(C\in s(a)\) such that \(P\sqsubseteq _\emptyset C\), and
-
3.
the set s(a) does not contain \(\sqsubseteq _\emptyset \)-comparable atoms.
Assuming that \(\top \not \in \mathcal {P}\), a compliance seed function always exists because \(\mathsf{Conj}(P)\) is non-empty for every \(P\in \mathcal {P}\); thus one can take as atom C an arbitrary element of \(\mathsf{Conj}(P)\) to satisfy Property 2. Property 3 avoids redundancies in seed functions, and thus reduces their overall number. If it does not hold for the set of atoms chosen to satisfy Property 2, we can simply remove the atoms that are not subsumption-maximal from this set.
We show that each compliance seed function induces a compliant anonymisation. For concept names \(A\in s(a)\), we simply remove the concept assertion A(a) from \(\mathcal {A}\). For atoms of the form \(\exists {r}.{C}\in s(a)\), we need to modify the role successors of a such that \(\exists {r}.{C}(a)\) is no longer entailed. To avoid losing more information than required, we will not just remove assertions from the objects in \(\mathcal {A}\), but also split such objects into several objects by introducing new variables, as motivated by the simple example in the introduction.
To be more precise, we will use the elements of the following set as variables.

For \(a\in \varSigma _{\mathsf{I}} \), there is no variable \(y_{a,s(a)}\) in Y. To simplify the following definition, we will, however, use \(y_{a,s(a)}\) as a synonym for the individual a, i.e., in this definition the object names \(y_{u,\mathcal {K}}\) and \(y_{v,\mathcal {L}}\) range over the elements of Y and these synonyms for individual names.
Definition 11
Consider a quantified ABox \(\exists {X}.{\mathcal {A}}\) that is not compliant with the policy \(\mathcal {P}\), a compliance seed function s on \(\exists {X}.{\mathcal {A}}\) for \(\mathcal {P}\), and Y as defined above. The canonical compliant anonymisation \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\) of \(\exists {X}.{\mathcal {A}}\) induced by s is the quantified ABox \(\exists {Y}.{\mathcal {B}}\), where \(\mathcal {B}\) consists of the following assertions:
-
1.
\(A(y_{u,\mathcal {K}})\in \mathcal {B}\) if \(A(u)\in \mathcal {A}\) and \(A\not \in \mathcal {K}\);
-
2.
\(r(y_{u,\mathcal {K}},y_{v,\mathcal {L}})\in \mathcal {B}\) if \(r(u,v)\in \mathcal {A}\) and, for each existential restriction \(\exists {r}.{Q}\in \mathcal {K}\) with \(\mathcal {A}\models Q(v)\), the set \(\mathcal {L}\) contains an atom subsuming Q, i.e., there is \(D\in \mathcal {L}\) such that \(Q\sqsubseteq _\emptyset D\).
We illustrate this definition by an abstract and slightly modified version of the example from the introduction.
Canonical anonymisation induced by the seed function s in Example 12.
Example 12
The ABox
is not compliant with the policy  . In fact, it entails both \((A\sqcap B)(a)\) and \((\exists {r}.{(A\sqcap B)})(a)\). There exist only two csfs s and t, where \(s(a)=\{A,\exists {r}.{(A\sqcap B)}\}\) and \(t(a)=\{B,\exists {r}.{(A\sqcap B)}\}\). Figure 1 shows the canonical anonymisation induced by s. The gray node represents the individual a, and all other nodes are variables introduced by the construction. Since there is only one role name r, we did not label the edges connecting objects with it. The canonical anonymisation induced by t differs from the one shown in Fig. 1 in that a then corresponds to \(y_{a,\{B,\exists {r}.{(A\sqcap B)}\}}\).
. In fact, it entails both \((A\sqcap B)(a)\) and \((\exists {r}.{(A\sqcap B)})(a)\). There exist only two csfs s and t, where \(s(a)=\{A,\exists {r}.{(A\sqcap B)}\}\) and \(t(a)=\{B,\exists {r}.{(A\sqcap B)}\}\). Figure 1 shows the canonical anonymisation induced by s. The gray node represents the individual a, and all other nodes are variables introduced by the construction. Since there is only one role name r, we did not label the edges connecting objects with it. The canonical anonymisation induced by t differs from the one shown in Fig. 1 in that a then corresponds to \(y_{a,\{B,\exists {r}.{(A\sqcap B)}\}}\).
We want to show that \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\) is a compliant anonymisation of \(\exists {X}.{\mathcal {A}}\). This is an easy consequence of the following lemma.
Lemma 13
Let \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s) = \exists {Y}.{\mathcal {B}}\) be the canonical compliant anonymisation of \(\exists {X}.{\mathcal {A}}\) induced by the compliance seed function s, and consider an \(\mathcal {EL}\) concept description Q and an \(\mathcal {EL}\) atom C. The following properties hold:
-
1.
The mapping \(h:\varSigma _{\mathsf{I}} \cup Y \rightarrow \varSigma _{\mathsf{I}} \cup X :y_{u,\mathcal {K}}\mapsto u\) is a homomorphism from \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\) to \(\exists {X}.{\mathcal {A}}\).
-
2.
If \(\mathcal {A}\not \models Q(u)\), then \(\mathcal {B}\not \models Q(y_{u,\mathcal {K}})\) for all objects \(u\in \varSigma _{\mathsf{I}} \cup X\) and \(y_{u,\mathcal {K}}\in \varSigma _{\mathsf{I}} \cup Y\).
-
3.
If \(C\in \mathcal {K}\), then \(\mathcal {B}\not \models C(y_{u,\mathcal {K}})\) for all objects \(y_{u,\mathcal {K}}\in \varSigma _{\mathsf{I}} \cup Y\).
Proof
1. It is easy to verify that the mapping h defined in the formulation of the lemma is a homomorphism. In particular, since \(y_{a,s(a)}\) is synonym for a, this mapping maps every individual \(a\in \varSigma _{\mathsf{I}} \) to itself.
2. It is an easy consequence of the homomorphism characterization of the instance problem that \(\mathcal {B}\models C(y_{u,\mathcal {K}})\) implies \(\mathcal {A}\models C(h(y_{u,\mathcal {K}}))\). Since \(h(y_{u,\mathcal {K}}) = u\), the second property stated in the lemma is the contrapositive of this fact.
3. The third property can be shown by induction on the role depth of C, using the definition of \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\) and Property 2. If \(C = A\in \varSigma _{\mathsf{C}} \), then \(A\in \mathcal {K}\) implies \(A(y_{u,\mathcal {K}})\not \in \mathcal {B}\), and thus \(\mathcal {B}\not \models A(y_{u,\mathcal {K}})\). Now, assume that \(C =\exists {r}.{Q}\) and that \(r(y_{u,\mathcal {K}},y_{v,\mathcal {L}})\in \mathcal {B}\). We must show that \(\mathcal {B}\not \models Q(y_{v,\mathcal {L}})\). If \(\mathcal {A}\not \models Q(v)\), then this is a consequence of Property 2. If \(\mathcal {A}\models Q(v)\), then the definition of \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\) yields an atom \(D\in \mathcal {L}\) such that \(Q\sqsubseteq _\emptyset D\). Since the homomorphism characterisation of subsumption implies that the role depth of D is then bounded by the role depth of Q, induction yields \(\mathcal {B}\not \models D(y_{v,\mathcal {L}})\), and thus \(\mathcal {B}\not \models Q(y_{v,\mathcal {L}})\). \(\square \)
Proposition 14
Let \(\exists {X}.{\mathcal {A}}\) be a quantified ABox that does not comply with the policy \(\mathcal {P}\), and s a compliance seed function on \(\exists {X}.{\mathcal {A}}\) for \(\mathcal {P}\). Then \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\) is entailed by \(\exists {X}.{\mathcal {A}}\) and complies with \(\mathcal {P}\).
Proof
Property 1 of Lemma 13 and Proposition 2 yield \(\exists {X}.{\mathcal {A}}\models \mathsf{ca}(\exists {X}.{\mathcal {A}},s)\). For compliance of \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s) = \exists {Y}.{\mathcal {B}}\) with \(\mathcal {P}\), let \(P\in \mathcal {P}\) and \(a = y_{a,s(a)}\in \varSigma _{\mathsf{I}} \). If \(\mathcal {A}\not \models P(a)\), then Property 2 of Lemma 13 yields \(\mathcal {B}\not \models P(a)\). Otherwise, there is an atom \(C\in s(a)\) such that \(P\sqsubseteq _\emptyset C\), by the definition of a csf. Then Property 3 of Lemma 13 yields \(\mathcal {B}\not \models C(a)\), and thus \(\mathcal {B}\not \models P(a)\). \(\square \)
This proposition shows that the set

contains only compliant anonymisations of \(\exists {X}.{\mathcal {A}}\). This set actually covers all compliant anonymisations of \(\exists {X}.{\mathcal {A}}\) in the following sense.
Proposition 15
If \(\exists {Z}.{\mathcal {C}}\) is a \(\mathcal {P}\)-compliant anonymisation of \(\exists {X}.{\mathcal {A}}\), then there exists a csf s such that \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\models \exists {Z}.{\mathcal {C}}\).
Proof
Since \(\exists {X}.{\mathcal {A}}\models \exists {Z}.{\mathcal {C}}\), Proposition 2 implies the existence of a homomorphism h from \(\exists {Z}.{\mathcal {C}}\) to \(\exists {X}.{\mathcal {A}}\). We define the mapping  :
:

We claim that the restriction s of f to \(\varSigma _{\mathsf{I}} \) is a csf. Assume that \(a\in \varSigma _{\mathsf{I}} \) and \(P\in \mathcal {P}\) with \(\mathcal {A}\models P(a)\). Since \(\exists {Z}.{\mathcal {C}}\) complies with \(\mathcal {P}\), there is an atom \(C\in \mathsf{Conj}(P)\) such that \(\mathcal {C}\not \models C(a)\). Thus, \(h(a) = a\) yields that either \(C\in f(a)\) or there is \(C'\in f(a)\) with \(C\sqsubseteq _{\emptyset }C'\). In both cases, Property 2 of Definition 10 is satisfied. Since the subsumption-maximal elements of a set of reduced atoms are incomparable w.r.t. subsumption,Footnote 2 Property 3 is satisfied as well.
Let  . To show that \(\exists {Y}.{\mathcal {B}}\models \exists {Z}.{\mathcal {C}}\), we prove that the mapping \(k:\varSigma _{\mathsf{I}} \cup Z\rightarrow \varSigma _{\mathsf{I}} \cup Y\) where
. To show that \(\exists {Y}.{\mathcal {B}}\models \exists {Z}.{\mathcal {C}}\), we prove that the mapping \(k:\varSigma _{\mathsf{I}} \cup Z\rightarrow \varSigma _{\mathsf{I}} \cup Y\) where  is a homomorphism. If \(A(u)\in \mathcal {C}\), then \(A(h(u))\in \mathcal {A}\) since h is a homomorphism, but \(A\not \in f(u)\). Thus \(A(y_{h(u),f(u)})\in \mathcal {B}\). If \(r(u,v)\in \mathcal {C}\), we must show that \(r(y_{h(u),f(u)},y_{h(v),f(v)})\in \mathcal {B}\). Assume that \(\exists {r}.{Q}\in f(u)\) and \(\mathcal {A}\models Q(h(v))\). The former yields \(\mathcal {C}\not \models (\exists {r}.{Q})(u)\), and thus \(\mathcal {C}\not \models Q(v)\). Thus, there is an atom \(D\in \mathsf{Conj}(Q)\) with \(\mathcal {A}\models D(h(v))\) and \(\mathcal {C}\not \models D(v)\). This implies that either D itself or an atom subsuming D belongs to f(v). In both cases, we obtain \(r(y_{h(u),f(u)},y_{h(v),f(v)})\in \mathcal {B}\). \(\square \)
is a homomorphism. If \(A(u)\in \mathcal {C}\), then \(A(h(u))\in \mathcal {A}\) since h is a homomorphism, but \(A\not \in f(u)\). Thus \(A(y_{h(u),f(u)})\in \mathcal {B}\). If \(r(u,v)\in \mathcal {C}\), we must show that \(r(y_{h(u),f(u)},y_{h(v),f(v)})\in \mathcal {B}\). Assume that \(\exists {r}.{Q}\in f(u)\) and \(\mathcal {A}\models Q(h(v))\). The former yields \(\mathcal {C}\not \models (\exists {r}.{Q})(u)\), and thus \(\mathcal {C}\not \models Q(v)\). Thus, there is an atom \(D\in \mathsf{Conj}(Q)\) with \(\mathcal {A}\models D(h(v))\) and \(\mathcal {C}\not \models D(v)\). This implies that either D itself or an atom subsuming D belongs to f(v). In both cases, we obtain \(r(y_{h(u),f(u)},y_{h(v),f(v)})\in \mathcal {B}\). \(\square \)
The next theorem is a straightforward consequence of the last two propositions.
Theorem 16
The set \(\mathsf{CA}(\exists {X}.{\mathcal {A}},\mathcal {P})\) is a set of \(\mathcal {P}\)-compliant anonymisations of \(\exists {X}.{\mathcal {A}}\) that contains (up to equivalence) all optimal \(\mathcal {P}\)-compliant anonymisations of \(\exists {X}.{\mathcal {A}}\). It can be computed in (deterministic) exponential time. There is a (deterministic) algorithm with access to an NP oracle that computes the set of all optimal \(\mathcal {P}\)-compliant anonymisations of \(\exists {X}.{\mathcal {A}}\) and runs in exponential time.
Proof
There are exponentially many csfs, which can be computed in exponential time. For each csf, the canonical anonymisation induced by it can also be computed in exponential time. Assume now that \(\exists {Z}.{\mathcal {C}}\) is an optimal \(\mathcal {P}\)-compliant anonymisation of \(\exists {X}.{\mathcal {A}}\). By Proposition 15, there exists a csf s such that \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\models \exists {Z}.{\mathcal {C}}\). Since \(\exists {Z}.{\mathcal {C}}\) is optimal, \(\exists {Z}.{\mathcal {C}}\) and \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\) are equivalent. The non-optimal elements of \(\mathsf{CA}(\exists {X}.{\mathcal {A}},\mathcal {P})\) can be removed from this set by applying entailment tests. These tests can be realised using an NP oracle. \(\square \)
Note that this complexity result considers combined complexity, where the policy \(\mathcal {P}\) is assumed to be part of the input. For data complexity, where the policy is assumed to be fixed, our approach shows that all optimal compliant anonymisations can be computed in polynomial time with an NP oracle.
At the moment, it is not clear whether the set of optimal compliant anonymisations of a quantified ABox can be computed in exponential time. The reason why our approach does not run in exponential time without an NP oracle is that the elements of \(\mathsf{CA}(\exists {X}.{\mathcal {A}},\mathcal {P})\) to which the oracle is applied may be exponentially large in the size of \(\exists {X}.{\mathcal {A}}\). Thus, one may ask whether one can design an approach that only generates optimal compliant anonymisations. We answer this question affirmatively in the rest of this section, but unfortunately the approach we introduce does not produce all of them.
Computing Optimal Compliant Anonymisations. The main idea underlying our approach is to define an appropriate partial order on csfs.
Definition 17
Let \(\exists {X}.{\mathcal {A}}\) be a quantified ABox that does not comply with the policy \(\mathcal {P}\), and s, t csfs on \(\exists {X}.{\mathcal {A}}\) for \(\mathcal {P}\). We say that s is covered by t (written \(s\le t\)) if for each \(a\in \varSigma \) and \(C\in s(a)\) there is an atom \(D\in t(a)\) s.t. \(C\sqsubseteq _\emptyset D\).
It is easy to see that this relation is a partial order. Reflexivity and transitivity are trivial. To show anti-symmetry, assume that \(s\le t\) and \(t\le s\). It suffices to prove that \(s(a)\subseteq t(a)\) holds for all \(a\in \varSigma _{\mathsf{I}} \); the inclusion in the other direction can be shown symmetrically. Assume that \(C\in s(a)\). Since \(s\le t\), this implies that there is an atom \(D\in t(a)\) with \(C\sqsubseteq _\emptyset D\). But then \(t\le s\) yields an atom \(C'\in s(a)\) such that \(D\sqsubseteq _\emptyset C'\). Since the elements of s(a) are incomparable w.r.t. subsumption, this yields \(C = C'\), and thus \(C\equiv _\emptyset D\). Since both atoms are assumed to be reduced, we obtain \(C = D\), which yields \(C\in t(a)\).
To show that entailment between canonical anonymisations implies covering for the compliance seed functions inducing them, we need the following lemma.
Lemma 18
Let \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s) = \exists {Y}.{\mathcal {B}}\) be the canonical compliant anonymisation of \(\exists {X}.{\mathcal {A}}\) induced by the csf s, \(C\in \mathsf{Atoms}(\mathcal {P})\), and \(y_{u,\mathcal {K}}\in Y\) a variable. If \(\mathcal {A}\models C(u)\) and \(\mathcal {B}\not \models C(y_{u,\mathcal {K}})\), then \(\mathcal {K}\) contains an atom subsuming C.
Proof
We prove the lemma by induction on the role depth of C. In the base case, \(C = A\in \varSigma _{\mathsf{C}} \). Thus, \(\mathcal {A}\models C(u)\) implies that \(A(u)\in \mathcal {A}\), and thus \(A\not \in \mathcal {K}\) would yield \(A(y_{u,\mathcal {K}})\in \mathcal {B}\), contradicting the assumption that \(\mathcal {B}\not \models C(y_{u,\mathcal {K}})\).
Induction step: if \(C = \exists {r}.{D}\), then \(\mathcal {A}\models C(u)\) implies that there is an object v such that \(r(u,v)\in \mathcal {A}\) and \(\mathcal {A}\models D(v)\). Assume that \(\mathcal {K}\) does not contain an atom subsuming \(\exists {r}.{D}\). We claim that this implies the existence of a variable \(y_{v,\mathcal {L}}\in Y\) such that \(r(y_{u,\mathcal {K}},y_{v,\mathcal {L}})\in \mathcal {B}\). Since \(\mathcal {K}\) does not contain an atom subsuming \(\exists {r}.{D}\), we know that, for every existential restriction \(\exists {r}.{Q}\in \mathcal {K}\), we have \(D\not \sqsubseteq _{\emptyset }Q\), and thus \(\mathsf{Conj}(Q)\) must contain an atom \(C_Q\) such that \(D\not \sqsubseteq _{\emptyset }C_Q\). Let \(\mathcal {L}\) consist of the subsumption-maximal elements of the set \( \{C_Q|\exists {r}.{Q}\in \mathcal {K}\ \text {and}\ \mathcal {A}\models Q(v)\}. \) Then we have \(y_{v,\mathcal {L}}\in Y\) and \(r(y_{u,\mathcal {K}},y_{v,\mathcal {L}})\in \mathcal {B}\). Since \(\mathcal {B}\not \models C(y_{u,\mathcal {K}})\), this implies that \(\mathcal {B}\not \models D(y_{v,\mathcal {L}})\), and thus there is an atom \(C'\in \mathsf{Conj}(D)\) with \(\mathcal {A}\models C'(v)\) and \(\mathcal {B}\not \models C'(y_{v,\mathcal {L}})\). Induction yields an atom \(C''\in \mathcal {L}\) such that \(C'\sqsubseteq _{\emptyset }C''\). Together with \(C'\in \mathsf{Conj}(D)\), this shows that \(D\sqsubseteq _{\emptyset }C''\). However, by construction, \(\mathcal {L}\) contains only atoms \(C_Q\) such that \(D\not \sqsubseteq _{\emptyset }C_Q\). This contradiction shows that our assumption that \(\mathcal {K}\) does not contain an atom subsuming \(C=\exists {r}.{D}\) cannot hold. \(\square \)
Proposition 19
Let s and t be csfs on \(\exists {X}.{\mathcal {A}}\) for \(\mathcal {P}\). Then the entailment \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\models \mathsf{ca}(\exists {X}.{\mathcal {A}},t)\) implies that \(s\le t\).
Proof
Let \(\exists {Y}.{\mathcal {B}} = \mathsf{ca}(\exists {X}.{\mathcal {A}},s)\) and \(\exists {Z}.{\mathcal {C}} = \mathsf{ca}(\exists {X}.{\mathcal {A}},t)\), and assume that \(\exists {Y}.{\mathcal {B}}\models \exists {Z}.{\mathcal {C}}\). We must show for all \(a\in \varSigma _{\mathsf{I}} \) that \(C\in s(a)\) implies the existence of an atom \(D\in t(a)\) with \(C\sqsubseteq _{\emptyset }D\). By the definition of csfs and Property 3 of Lemma 13, \(C\in s(a)\) implies \(\mathcal {A}\models C(a)\) and \(\mathcal {B}\not \models C(a)\). Since \(\exists {Y}.{\mathcal {B}}\models \exists {Z}.{\mathcal {C}}\), the latter yields \(\mathcal {C}\not \models C(a)\). By Lemma 18, t(a) contains an atom subsuming C. \(\square \)
As an easy consequence, this proposition shows that the set

contains only optimal compliant anonymisations of \(\exists {X}.{\mathcal {A}}\).
Theorem 20
The set \(\mathsf{CA}_{ min }(\exists {X}.{\mathcal {A}},\mathcal {P})\) is non-empty, contains only optimal \(\mathcal {P}\)-compliant anonymisation of \(\exists {X}.{\mathcal {A}}\), and can be computed in exponential time.
Proof
Since policies are assumed not to contain \(\top \), the set of all csfs is non-empty. Since it is a finite set, it must contain minimal elements w.r.t. the partial order \(\le \). Assume the \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\in \mathsf{CA}_{ min }(\exists {X}.{\mathcal {A}},\mathcal {P})\) is not optimal. Then there is a compliant anonymisation \(\exists {Z}.{\mathcal {C}}\) of \(\exists {X}.{\mathcal {A}}\) such that \(\exists {Z}.{\mathcal {C}}\models \mathsf{ca}(\exists {X}.{\mathcal {A}},s)\), but \(\exists {Z}.{\mathcal {C}}\) and \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\) are not equivalent. By Proposition 15, there exists a csf t such that \(\mathsf{ca}(\exists {X}.{\mathcal {A}},t)\models \exists {Z}.{\mathcal {C}}\). But then we have \(\mathsf{ca}(\exists {X}.{\mathcal {A}},t)\models \mathsf{ca}(\exists {X}.{\mathcal {A}},s)\), which yields \(t\le s\) by Proposition 19. Since \(s=t\) would imply that \(\exists {Z}.{\mathcal {C}}\) and \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\) are equivalent, we actually have \(t<s\), which contradicts the minimality of s. The set \(\mathsf{CA}_{ min }(\exists {X}.{\mathcal {A}},\mathcal {P})\) can be computed in exponential time, by first generating all csfs, then removing the non-minimal ones, and finally generating the induced canonical anonymisations. \(\square \)
A simple consequence of this theorem is that one optimal compliant anonymisation can always be computed in exponential time w.r.t. combined complexity, and polynomial time w.r.t. data complexity. One simply needs to compute a minimal csf s, and then build \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\). In contrast to computing all optimal compliant anonymisations, this process does not need an NP oracle. In general, however, not all optimal compliant anonymisations of \(\exists {X}.{\mathcal {A}}\) are contained in \(\mathsf{CA}_{ min }(\exists {X}.{\mathcal {A}},\mathcal {P})\). Technically, the reason is that the converse of Proposition 19 need not hold. The following gives a concrete example where \(\mathsf{CA}_{ min }(\exists {X}.{\mathcal {A}},\mathcal {P})\) is not complete.
Example 21
Consider the policy  and the non-compliant ABox \(\exists {\emptyset }.{\mathcal {A}}\), with
and the non-compliant ABox \(\exists {\emptyset }.{\mathcal {A}}\), with  . The only minimal csf is the function s defined as
. The only minimal csf is the function s defined as  and
and  . In \(\mathsf{ca}(\exists {\emptyset }.{\mathcal {A}},s)\), the individual b still belongs to A, but the role assertions r(a, b) is no longer there.
. In \(\mathsf{ca}(\exists {\emptyset }.{\mathcal {A}},s)\), the individual b still belongs to A, but the role assertions r(a, b) is no longer there.
Consider the (non-minimal) csf t defined as  and
and  . In \(\mathsf{ca}(\exists {\emptyset }.{\mathcal {A}},t)\), the individual b does not belong to A, but the role assertions r(a, b) is still there. Thus, \(\mathsf{ca}(\exists {\emptyset }.{\mathcal {A}},s)\) and \(\mathsf{ca}(\exists {\emptyset }.{\mathcal {A}},t)\) are incomparable w.r.t. entailment, although \(s < t\). We claim that \(\mathsf{ca}(\exists {\emptyset }.{\mathcal {A}},t)\) is optimal. Otherwise, we can use Proposition 15 to obtain a csf \(t'<t\) such that \(\mathsf{ca}(\exists {\emptyset }.{\mathcal {A}},t')\models \mathsf{ca}(\exists {\emptyset }.{\mathcal {A}},t)\). However, the only csf smaller than t is s, which yields a contradiction.
. In \(\mathsf{ca}(\exists {\emptyset }.{\mathcal {A}},t)\), the individual b does not belong to A, but the role assertions r(a, b) is still there. Thus, \(\mathsf{ca}(\exists {\emptyset }.{\mathcal {A}},s)\) and \(\mathsf{ca}(\exists {\emptyset }.{\mathcal {A}},t)\) are incomparable w.r.t. entailment, although \(s < t\). We claim that \(\mathsf{ca}(\exists {\emptyset }.{\mathcal {A}},t)\) is optimal. Otherwise, we can use Proposition 15 to obtain a csf \(t'<t\) such that \(\mathsf{ca}(\exists {\emptyset }.{\mathcal {A}},t')\models \mathsf{ca}(\exists {\emptyset }.{\mathcal {A}},t)\). However, the only csf smaller than t is s, which yields a contradiction.
4 Compliant Anonymisations w.r.t IQ-Entailment
Since we are only interested in instance queries (i.e., checking which instance relationships C(a) hold for individuals a in a quantified ABox), it makes sense to consider a different notion of entailment and equivalence based on which instance relationships are implied by the ABox. Switching to this alternative notion of entailment allows us to improve on the results shown in the previous section.
Definition 22
Let \(\exists {X}.{\mathcal {A}}\) and \(\exists {Y}.{\mathcal {B}}\) be quantified ABoxes. We say that \(\exists {X}.{\mathcal {A}}\) IQ-entails \(\exists {Y}.{\mathcal {B}}\) (written \(\exists {X}.{\mathcal {A}}\models _{\mathsf{IQ}}\exists {Y}.{\mathcal {B}}\)) if \(\exists {Y}.{\mathcal {B}}\models C(a)\) implies \(\exists {X}.{\mathcal {A}}\models C(a)\) for all \(\mathcal {EL}\) concept descriptions C and all \(a\in \varSigma _{\mathsf{I}} \). Two quantified ABoxes are IQ-equivalent if they IQ-entail each other.
Obviously, \(\exists {X}.{\mathcal {A}}\models \exists {Y}.{\mathcal {B}}\) implies \(\exists {X}.{\mathcal {A}}\models _{\mathsf{IQ}}\exists {Y}.{\mathcal {B}}\), but the converse need not be true. Whereas entailment can be characterised using homomorphisms, IQ-entailment is characterised using simulations. Similar results have been shown in the context of interpolation and separability, but for interpretations rather than ABoxes (see, e.g., Lemma 4 in
[21]). A simulation from \(\exists {X}.{\mathcal {A}}\) to \(\exists {Y}.{\mathcal {B}}\) is a relation  that satisfies the following properties:
that satisfies the following properties:
-
1.
 for each individual name \(a\in \varSigma _{\mathsf{I}} \);
for each individual name \(a\in \varSigma _{\mathsf{I}} \); -
2.
if
 and \(A(u)\in \mathcal {A}\), then \(A(v)\in \mathcal {B}\);
and \(A(u)\in \mathcal {A}\), then \(A(v)\in \mathcal {B}\); -
3.
if
 and \(r(u,u')\in \mathcal {A}\), then there exists an object \(v'\in \varSigma _{\mathsf{I}} \cup Y\) such that
and \(r(u,u')\in \mathcal {A}\), then there exists an object \(v'\in \varSigma _{\mathsf{I}} \cup Y\) such that  .
.
Proposition 23
Let \(\exists {X}.{\mathcal {A}}\) and \(\exists {Y}.{\mathcal {B}}\) be quantified ABoxes that are renamed apart. Then, \(\exists {Y}.{\mathcal {B}}\models _{\mathsf{IQ}}\exists {X}.{\mathcal {A}}\) iff there exists a simulation from \(\exists {X}.{\mathcal {A}}\) to \(\exists {Y}.{\mathcal {B}}\).
Proof
To prove the only-if direction, we define an appropriate relation  and show that it is a simulation:
and show that it is a simulation:

-
1.
Since \(\exists {Y}.{\mathcal {B}}\) IQ-entails \(\exists {X}.{\mathcal {A}}\),
 contains the pair (a, a) for each \(a\in \varSigma _{\mathsf{I}} \).
contains the pair (a, a) for each \(a\in \varSigma _{\mathsf{I}} \). -
2.
Let
 and \(A(u)\in \mathcal {A}\). Then \(\mathcal {A}\models A(u)\), which yields \(\mathcal {B}\models A(v)\) by the definition of
and \(A(u)\in \mathcal {A}\). Then \(\mathcal {A}\models A(u)\), which yields \(\mathcal {B}\models A(v)\) by the definition of  . By Lemma 6, this implies that \(\mathcal {B}\) contains A(v).
. By Lemma 6, this implies that \(\mathcal {B}\) contains A(v). -
3.
Let
 and consider a role assertion \(r(u,u')\in \mathcal {A}\). It follows that \(\mathcal {A}\) entails \(\exists {r}.{\top }(u)\) and so \(\mathcal {B}\) entails \(\exists {r}.{\top }(v)\), i.e., v has at least one r-successor in \(\mathcal {B}\). Since \(\mathcal {B}\) is finite, v can only have finite number of r-successors in \(\mathcal {B}\). We use a diagonalization argument. Assume that, for each \(r(v,v')\in \mathcal {B}\), there is an \(\mathcal {EL}\) concept description \(C_{v'}\) such that \(\mathcal {A}\models C_{v'}(u')\) and \(\mathcal {B}\not \models C_{v'}(v')\). Define
and consider a role assertion \(r(u,u')\in \mathcal {A}\). It follows that \(\mathcal {A}\) entails \(\exists {r}.{\top }(u)\) and so \(\mathcal {B}\) entails \(\exists {r}.{\top }(v)\), i.e., v has at least one r-successor in \(\mathcal {B}\). Since \(\mathcal {B}\) is finite, v can only have finite number of r-successors in \(\mathcal {B}\). We use a diagonalization argument. Assume that, for each \(r(v,v')\in \mathcal {B}\), there is an \(\mathcal {EL}\) concept description \(C_{v'}\) such that \(\mathcal {A}\models C_{v'}(u')\) and \(\mathcal {B}\not \models C_{v'}(v')\). Define  , which is a well-defined \(\mathcal {EL}\) concept description since v has only finitely many r-successors. Then \(\mathcal {A}\models C(u')\), and so \(\mathcal {A}\models \exists {r}.{C}(u)\). We conclude that \(\mathcal {B}\models \exists {r}.{C}(v)\), and so there must exist \(r(v,v')\in \mathcal {B}\) such that \(\mathcal {B}\models C(v')\), which contradicts our construction of C. It follows that there must exist an r-successor \(v'\) of v in \(\mathcal {B}\) such that \(\mathcal {A}\models C(u')\) implies \(\mathcal {B}\models C(v')\) for all \(\mathcal {EL}\) concept descriptions C, and thus the pair \((v,v')\) is in
, which is a well-defined \(\mathcal {EL}\) concept description since v has only finitely many r-successors. Then \(\mathcal {A}\models C(u')\), and so \(\mathcal {A}\models \exists {r}.{C}(u)\). We conclude that \(\mathcal {B}\models \exists {r}.{C}(v)\), and so there must exist \(r(v,v')\in \mathcal {B}\) such that \(\mathcal {B}\models C(v')\), which contradicts our construction of C. It follows that there must exist an r-successor \(v'\) of v in \(\mathcal {B}\) such that \(\mathcal {A}\models C(u')\) implies \(\mathcal {B}\models C(v')\) for all \(\mathcal {EL}\) concept descriptions C, and thus the pair \((v,v')\) is in  and the role assertion \(r(u',v')\) is in \(\mathcal {B}\).
and the role assertion \(r(u',v')\) is in \(\mathcal {B}\).
For the if direction, assume that  is a simulation from \(\exists {X}.{\mathcal {A}}\) to \(\exists {Y}.{\mathcal {B}}\). If \(\exists {X}.{\mathcal {A}}\models C(a)\), then there is a homomorphism from the pp formula \(\phi _C(a)\) corresponding to C(a) to \(\exists {X}.{\mathcal {A}}\) such that a is mapped to a. The composition of this homomorphism with
is a simulation from \(\exists {X}.{\mathcal {A}}\) to \(\exists {Y}.{\mathcal {B}}\). If \(\exists {X}.{\mathcal {A}}\models C(a)\), then there is a homomorphism from the pp formula \(\phi _C(a)\) corresponding to C(a) to \(\exists {X}.{\mathcal {A}}\) such that a is mapped to a. The composition of this homomorphism with  yields a simulation from \(\phi _C(a)\) to \(\exists {Y}.{\mathcal {B}}\). Since \(\phi _C(a)\) is tree-shaped, the existence of such a simulation implies the existence of a homomorphism from \(\phi _C(a)\) to \(\exists {Y}.{\mathcal {B}}\), which yields \(\exists {Y}.{\mathcal {B}}\models C(a)\). \(\square \)
yields a simulation from \(\phi _C(a)\) to \(\exists {Y}.{\mathcal {B}}\). Since \(\phi _C(a)\) is tree-shaped, the existence of such a simulation implies the existence of a homomorphism from \(\phi _C(a)\) to \(\exists {Y}.{\mathcal {B}}\), which yields \(\exists {Y}.{\mathcal {B}}\models C(a)\). \(\square \)
Since the existence of a simulation can be decided in polynomial time [17], this proposition implies that IQ-entailment can be decided in polynomial time. We redefine the notions “compliant anonymisation” and “optimal compliant anonymisation” by using IQ-entailment rather than entailment.
Definition 24
Let \(\exists {X}.{\mathcal {A}}, \exists {Y}.{\mathcal {B}}\) be quantified ABoxes and \(\mathcal {P}\) a policy. Then
-
1.
\(\exists {Y}.{\mathcal {B}}\) is a \(\mathcal {P}\) -compliant IQ-anonymisation of \(\exists {X}.{\mathcal {A}}\) if \(\exists {X}.{\mathcal {A}} \models _{\mathsf{IQ}}\exists {Y}.{\mathcal {B}}\) and \(\exists {Y}.{\mathcal {B}}\) is compliant with \(\mathcal {P}\);
-
2.
\(\exists {Y}.{\mathcal {B}}\) is an optimal \(\mathcal {P}\) -compliant IQ-anonymisation of \(\exists {X}.{\mathcal {A}}\) if it is a \(\mathcal {P}\)-compliant IQ-anonymisation of \(\exists {X}.{\mathcal {A}}\), and \(\exists {X}.{\mathcal {A}} \models _{\mathsf{IQ}}\exists {Z}.{\mathcal {C}} \models _{\mathsf{IQ}}\exists {Y}.{\mathcal {B}}\) implies \(\exists {Y}.{\mathcal {B}}\models _{\mathsf{IQ}}\exists {Z}.{\mathcal {C}}\) for every \(\mathcal {P}\)-compliant IQ-anonymisation \(\exists {Z}.{\mathcal {C}}\) of \(\exists {X}.{\mathcal {A}}\).
We can show that \(\mathsf{CA}(\exists {X}.{\mathcal {A}},\mathcal {P})\) covers all compliant IQ-anonymisations of \(\exists {X}.{\mathcal {A}}\) w.r.t. IQ-entailment. The proof of this result is similar to the proof of Proposition 15 (see [5] for an explicit proof).
Proposition 25
If \(\exists {Z}.{\mathcal {C}}\) is a \(\mathcal {P}\)-compliant IQ-anonymisation of \(\exists {X}.{\mathcal {A}}\), then there exists a csf s such that \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\models _{\mathsf{IQ}}\exists {Z}.{\mathcal {C}}\).
As in Sect. 3, this implies that \(\mathsf{CA}(\exists {X}.{\mathcal {A}},\mathcal {P})\) contains (up to IQ-equivalence) all optimal compliant IQ-anonymisations. Since IQ-entailment can be decided in polynomial time, removing non-optimal elements from \(\mathsf{CA}(\exists {X}.{\mathcal {A}},\mathcal {P})\) can now be realised in exponential time without NP oracle.
Theorem 26
Up to IQ-equivalence, the set of all optimal \(\mathcal {P}\)-compliant IQ-anonymisations of \(\exists {X}.{\mathcal {A}}\) can be computed in exponential time.
This theorem shows that using IQ-entailment improves the complexity of our algorithm for computing optimal compliant anonymisations. For data complexity, it is even in P. Moreover, in the setting of IQ-entailment the set \(\mathsf{CA}_{ min }(\exists {X}.{\mathcal {A}},\mathcal {P})\) turns out to be complete. Indeed, the converse of Proposition 19 holds as well in this setting (see [5] for a detailed proof).
Proposition 27
Let s and t be compliance seed functions on \(\exists {X}.{\mathcal {A}}\) for \(\mathcal {P}\). Then we have \(\mathsf{ca}(\exists {X}.{\mathcal {A}},s)\models _{\mathsf{IQ}}\mathsf{ca}(\exists {X}.{\mathcal {A}},t)\) iff \(s\le t\).
Proof sketch
The only-if direction is analogous to the proof of Proposition 19. Conversely, we can show that the relation  consisting of the pairs \((y_{u,\mathcal {K}},y_{u,\mathcal {L}})\) such that, for each \(C\in \mathcal {L}\), there is some \(D\in \mathcal {K}\) with \(C\sqsubseteq _\emptyset D\), is a simulation (see
[5] for details). \(\square \)
consisting of the pairs \((y_{u,\mathcal {K}},y_{u,\mathcal {L}})\) such that, for each \(C\in \mathcal {L}\), there is some \(D\in \mathcal {K}\) with \(C\sqsubseteq _\emptyset D\), is a simulation (see
[5] for details). \(\square \)
As a consequence, we obtain the following improvement over Theorem 26.
Theorem 28
Up to IQ-equivalence, the set \(\mathsf{CA}_{ min }(\exists {X}.{\mathcal {A}},\mathcal {P})\) consists of all optimal \(\mathcal {P}\)-compliant IQ-anonymisations of \(\exists {X}.{\mathcal {A}}\), and it can be computed in exponential time.
Thus, it is not necessary to compute the whole set \(\mathsf{CA}(\exists {X}.{\mathcal {A}},\mathcal {P})\) first and then remove non-optimal elements. One can directly compute the set \(\mathsf{CA}_{ min }(\exists {X}.{\mathcal {A}},\mathcal {P})\). Using IQ-entailment also allows us to reduce the sizes of the elements of this set. In fact, it is easy to see that removing variables not reachable by a role path from an individual results in a quantified ABox that is IQ-equivalent to the original one. For the canonical anonymisation depicted in Fig. 1, this yields an ABox that, in addition to the individual a (i.e., the grey node) contains only the three variables \(y_{x,\{B\}}\), \(y_{x,\{A\}}\), and \(y_{x,\{A,B\}}\) that are directly reachable from a. In practice, one would not first generate all variables and then remove the unreachable ones, but generate only the reachable ones in the first place.
5 Conclusions
We have developed methods to hide private information (as expressed by a policy \(\mathcal {P}\)) while modifying the knowledge base (given by a quantified ABox \(\exists {X}.{\mathcal {A}}\)) in a minimal way. More formally, we have shown how to compute the set of all optimal \(\mathcal {P}\)-compliant anonymisations of \(\exists {X}.{\mathcal {A}}\). In general, this set contains exponentially many anonymisations that may be of exponential size. As already shown in [3] for the restricted case of an \(\mathcal {EL}\) instance store, this exponential blow-up cannot be avoided in the worst case, both regarding the number and the size of the anonymisations. These exponential lower bounds hold both for the case of classical entailment and of IQ-entailment (since for instance stores this does not make a difference). Nevertheless, we have shown that using IQ-entailment leads to a more efficient algorithm (exponential time instead of exponential time with NP oracle), and may result in considerably smaller anonymisations. One may ask why we did not restrict our attention to IQ-entailment altogether. The reason is that, even if one considers only policies expressed by \(\mathcal {EL}\) concepts, one may still want to query the ABoxes using general conjunctive queries. ABoxes that are IQ-equivalent, but not equivalent, may yield different answers to CQs. An interesting topic for future research is to see whether our approach can be extended to policies expressed by CQs rather than \(\mathcal {EL}\) concepts. A first step in this direction could be to extend the policy language to \(\mathcal {ELI}\) or acyclic CQs.
There is a close connection between computing a compliant anonymisation of and repairing an ABox [4]. Basically, if \(C\in \mathcal {P}\), then we want to avoid conclusions of the form C(a) for all individuals a, whereas repairs want to get rid of conclusions C(a) for a specific individual a. It is easy to see how to adapt our notion of a compliance seed function to the repair setting. By making small modifications to our framework, we can thus also compute optimal repairs [5].
As mentioned in the introduction, achieving compliance of a knowledge base is not always sufficient. Instead, one sometimes wants to ensure the more stringent requirement of safety [3, 12, 13]. Currently, we investigate how to extend the results presented in this paper from compliance to safety. Although adapting our approach to deal with the case of safety is not trivial, and requires the development of new methods, the basic formal setup for both problems remains unchanged. In particular, the results for compliance presented here are important stepping-stones since our approach basically reduces safety to compliance w.r.t. a modified policy [6]. Another interesting topic for future research is to consider compliance and safety of ABoxes w.r.t. terminological knowledge. Without additional restrictions, optimal compliant anonymisations (repairs) need no longer exist [4], but we conjecture that our methods can still be applied if the terminological knowledge is cycle-restricted in the sense introduced in [2].
Notes
- 1.
NP-hardness holds even if only unary and binary relation symbols are available.
- 2.
Recall that we assume that policies are reduced, which implies that the elements of \(\mathsf{Atoms}(\mathcal {P})\) are reduced, and thus subsumption is a partial order on them.
References
Abiteboul, S., Hull, R., Vianu, V.: Foundations of Databases. Addison Wesley Publ. Co., Massachussetts (1995)
Baader, F., Borgwardt, S., Morawska, B.: Extending unification in \(\cal{EL}\) towards general TBoxes. In: Proceedings of KR 2012, pp. 568–572. AAAI Press (2012)
Baader, F., Kriegel, F., Nuradiansyah, A.: Privacy-preserving ontology publishing for \(\cal{EL} \) instance stores. In: Calimeri, F., Leone, N., Manna, M. (eds.) JELIA 2019. LNCS (LNAI), vol. 11468, pp. 323–338. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-19570-0_21
Baader, F., Kriegel, F., Nuradiansyah, A., Peñaloza, R.: Making repairs in description logics more gentle. In: Proceedings of KR 2018, pp. 319–328. AAAI Press (2018)
Baader, F., Kriegel, F., Nuradiansyah, A., Peñaloza, R.: Computing compliant anonymisations of quantified ABoxes w.r.t. \(\cal{EL}\) policies (Extended Version). LTCS-Report 20–08, TU Dresden, Germany (2020)
Baader, F., Kriegel, F., Nuradiansyah, A., Peñaloza, R.: Computing safe anonymisations of quantified ABoxes w.r.t. \(\cal{EL}\) policies (Extended Version). LTCS-Report 20–09, TU Dresden, Germany (2020)
Baader, F., Küsters, R., Molitor, R.: Computing least common subsumers in description logics with existential restrictions. In: Proceedings of IJCAI 1999, pp. 96–101. Morgan Kaufmann (1999)
Baader, F., Morawska, B.: Unification in the description logic \(\cal{EL}\). Logical Methods Comput. Sci. 6(3) (2010). https://doi.org/10.2168/LMCS-6(3:17)2010
Bonatti, P.A., Sauro, L.: A confidentiality model for ontologies. In: Alani, H., Kagal, L., Fokoue, A., Groth, P., Biemann, C., Parreira, J.X., Aroyo, L., Noy, N., Welty, C., Janowicz, K. (eds.) ISWC 2013. LNCS, vol. 8218, pp. 17–32. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-41335-3_2
Chandra, A.K., Merlin, P.M.: Optimal implementation of conjunctive queries in relational data bases. In: Proceedings of STOC 1977, pp. 77–90. ACM (1977)
Cima, G., Lembo, D., Rosati, R., Savo, D.F.: Controlled query evaluation in description logics through instance indistinguishability. In: Proceedings of IJCAI 2020, pp. 1791–1797. ijcai.org (2020)
Grau, B.C., Kostylev, E.V.: Logical foundations of privacy-preserving publishing of linked data. In: Proceedings of AAAI 2016, pp. 943–949. AAAI Press (2016)
Grau, B.C., Kostylev, E.V.: Logical foundations of linked data anonymisation. J. Artif. Intell. Res. 64, 253–314 (2019)
Delanaux, R., Bonifati, A., Rousset, M.-C., Thion, R.: Query-based linked data anonymization. In: Vrandečić, D., Bontcheva, K., Suárez-Figueroa, M.C., Presutti, V., Celino, I., Sabou, M., Kaffee, L.-A., Simperl, E. (eds.) ISWC 2018. LNCS, vol. 11136, pp. 530–546. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-00671-6_31
Fung, B.C.M., Wang, K., Chen, R., Yu, P.S.: Privacy-preserving data publishing: a survey of recent developments. ACM Comput. Surv. 42(4), 14:1–14:53 (2010)
Grau, B.C., Kharlamov, E., Kostylev, E.V., Zheleznyakov, D.: Controlled query evaluation for datalog and OWL 2 profile ontologies. In: Proceedings of IJCAI 2015, pp. 2883–2889. AAAI Press (2015)
Henzinger, M.R., Henzinger, T.A., Kopke, P.W.: Computing simulations on finite and infinite graphs. In: FOCS 1995, pp. 453–462. IEEE Computer Society Press (1995)
Küsters, R. (ed.): Non-Standard Inferences in Description Logics. LNCS (LNAI), vol. 2100. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44613-3
Küsters, R., Molitor, R.: Approximating most specific concepts in description logics with existential restrictions. In: Baader, F., Brewka, G., Eiter, T. (eds.) KI 2001. LNCS (LNAI), vol. 2174, pp. 33–47. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45422-5_4
Libkin, L.: Elements of Finite Model Theory. Texts in Theoretical Computer Science. An EATCS Series. Springer (2004)
Lutz, C., Seylan, I., Wolter, F.: An automata-theoretic approach to uniform interpolation and approximation in the description logic \(\cal{EL}\). In: Proceedings of KR 2012, pp. 286–296. AAAI Press (2012)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Baader, F., Kriegel, F., Nuradiansyah, A., Peñaloza, R. (2020). Computing Compliant Anonymisations of Quantified ABoxes w.r.t. \(\mathcal {EL} \) Policies. In: Pan, J.Z., et al. The Semantic Web – ISWC 2020. ISWC 2020. Lecture Notes in Computer Science(), vol 12506. Springer, Cham. https://doi.org/10.1007/978-3-030-62419-4_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-62419-4_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-62418-7
Online ISBN: 978-3-030-62419-4
eBook Packages: Computer ScienceComputer Science (R0)





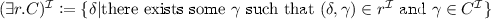 ,
, , where the intersection over the empty set
, where the intersection over the empty set  for
for  .
. . Then we build
. Then we build  .
.
 for each individual name
for each individual name  and
and  and
and  .
. contains the pair (a, a) for each
contains the pair (a, a) for each  and
and  . By Lemma
. By Lemma  and consider a role assertion
and consider a role assertion  , which is a well-defined
, which is a well-defined  and the role assertion
and the role assertion