Keywords

1 Introduction

Mathematical modelling of biological systems is a daunting challenge. In order to cope realistically with the biochemistry of cells, tissues and organisms, both in fundamental and applied biological research, systems biology models use hundreds and thousands of variables structured as biochemical networks  [1, 16, 38]. Nonlinear, large scale network models are also used in neuroscience to model brain activity  [7, 29]. Ecological and epidemiological modelling cope with population dynamics of species organized in networks and interacting on multiple spatial and temporal scales  [2, 28]. Mathematical models of complex diseases such as cancer combine molecular networks with population dynamics  [5].

Denis Noble, a pioneer of multi-cellular modelling of human physiology, advocated the use of middle-out approaches in biological modelling  [23]. Middle-out is an alternative to bottom-up, that tries to explain everything from detailed first principles, and to top-down, that uses strongly simplified representations of reality. A middle-out model uses just enough details to render the essence of the overall system organization. Although this is potentially a very powerful principle, the general mathematical methods to put it into practice are still awaited.

Recently, we have used tropical geometry to extract the essence of biological systems and to simplify complex biological models  [24, 25, 30, 32, 33]. Tropical geometry methods exploit a feature of biological systems called multiscaleness  [11, 35], summarized by two properties: i) the orders of magnitude of variables and timescales are widely distributed; and ii) at a given timescale, only a small number of variables or components play a driving role, whereas large parts of the system have passive roles and can be reduced.

Modellers and engineers reduce models by introducing ad hoc small parameters in their equations. After scaling of variables and parameters, singular perturbations techniques such as asymptotic approximations, boundary layers, invariant manifolds, etc. can be used to cope with multiple time scales. These techniques, invented at the beginning of the 20\(^{th}\) century for problems in aerodynamics and fluid mechanics  [26] are also known in biochemistry under the name of quasi-equilibrium and quasi-steady state approximations   [10, 12, 13, 36]. The reduction of the model in a singular perturbation framework is traditionally based on a two time scales (slow and fast) decomposition: fast variables are slaved by the slow ones and can therefore be eliminated. Geometrically, this corresponds to fast relaxation of the system to a low dimensional invariant manifold. The mathematical bases of the slow/fast decomposition were set in  [14, 39, 40] for the elimination of the fast variables, and in  [8] for the existence of a low dimensional, slow invariant manifold. However, the slow/fast decomposition is neither unique, nor constant; it depends on model parameters and can also change with the phase space position on a trajectory. Despite of several attempts to automatically determine small parameters and slow/fast decompositions, the problem of finding a reduced model remains open. We can mention numerical approaches such as Computational Singular Perturbations  [18], or Intrinsic Low Dimensional Manifold  [21] that perform a reduction locally, in each point of the trajectory. Notwithstanding their many applications in reactive flow and combustion, these methods are simulation based and may not provide all the possible reductions. Furthermore, explicit reductions obtained by post-processing of the data generated by these numerical methods may be in conflict with more robust approaches  [33]. A computer algebra approach to determine small parameters for the quasi-steady state reduction of biochemical models was proposed, based on Gröbner bases calculations, but this approach is limited to models of small dimension  [9].

Perturbation approaches, both regular and singular, operate with orders of magnitude. In such approaches, some terms are much smaller than others and can, under some conditions, be neglected. Computations with orders of magnitudes follow maxplus (or, depending on the definition of orders, minplus) algebraic rules. The same rules apply to valuations, that are building blocks for tropical geometry  [22]. We developed tropical geometry methods to identify sub-systems that are dominant in certain regions of the phase- and/or parameter-space of dynamical systems  [30, 32]. Moreover, tropical geometry is a natural approach to find the scalings needed for slow/fast decompositions and perform model order reduction in the framework of geometric singular perturbation theory. Scaling calculations are based on finding solutions of the tropical equilibration problem, which is very similar to computing tropical prevarieties  [25]. For such a problem we have effective algorithms that work well for medium size biochemical models (10–100 species)  [20, 33, 37].

Tropical approaches provide a timescale for each biochemical species or relaxation process and one generally has not only two but multiple timescales. This situation is the rule rather than the exception in biology. For instance, cells or organisms use multiple mechanisms to adapt to changes of their environment. These mechanisms involve rapid metabolic or electrophysiological changes (seconds, minutes), slower changes of gene expression (hours), and even slower mutational genetic changes (days, months). Within each category, sub-mechanism timescales spread over several log scale decades. We are using tropical approaches also to cover such situations and obtain reductions for systems with more than two timescales  [17].

Interestingly, the dominance relations unravelled by tropical geometry can highlight approximate conservation laws of biological systems, i.e. conservation laws satisfied by a dominant subsystem and not satisfied by the full system. These approximate conservations are exploited for the simplification of biological models  [6]. Beyond their importance for model reduction, approximate conservations and tropical equilibrations can be used for computing metastable states of biochemical models, defined as regions of very slow dynamics in phase space  [32, 34, 35]. Metastable states represent a generalization of the stable steady states commonly used in analyzing biological networks  [29]. A dynamical system spends an infinite time in the neighbourhood of stable steady state, and a large but finite time in the neighborhood of metastable states. In biology, both steady and metastable states are important. The existence of metastable states leads to a property of biological systems called itinerancy, meaning that the system can pass from one metastable state to another one during its dynamics [15, 29]. From a biological point of view itinerancy explains plasticity during adaptation, occurring in numerous situations: brain functioning, embryo development, cellular metabolic changes induced by changes of the environment. The study of the relation between the network structure and the metastable states is also a possible way to design dynamical systems with given properties. This is related to the direction suggested by O.Viro at the 3\(^{rd}\) European Congress of Mathematics to use tropical geometry for constructing real algebraic varieties with prescribed properties in the sense of Hilbert’s 16\(^{th}\) problem  [41, 42].

2 Models of Biological Systems and Their Reductions

Chemical reaction networks (CRN) are bipartite graphs such as those represented in Fig. 1, where one type of node stands for chemical species and the other for reactions. Although mainly designed for modelling cell biochemistry, CRNs can also be used to describe interactions of the cell with its microenvironment in tissue models and also the population dynamics in compartment models in ecology and epidemiology. When the copy numbers of all molecular species are large, CRN dynamics is given by systems of ordinary differential equations, usually with polynomial or rational right hand side. For instance, in the Michaelis–Menten model, an archetype of enzymatic reactions, the differential equations for the concentrations of relevant chemical species (substrate and enzyme-substrate complex) have the form

$$\begin{aligned} \frac{\mathrm {d} x_1 }{\mathrm {d} t }= & {} - k_1 x_1 + k_2 x_1 x_2 + k_3 x_2 \nonumber \\ \frac{\mathrm {d} x_2 }{\mathrm {d} t }= & {} k_1 x_1 - k_2 x_1 x_2 - (k_3 + k_4) x_2, \end{aligned}$$
(1)

where \(k_1,\ldots ,k_4\) are kinetic parameters.

The Michaelis–Menten model is already quite simple, however comprehensive models of cell biochemistry can be very large. By model reduction one transforms the system of differential equations into a system with less equations and variables that have approximately the same solutions. The variables of the full model missing in the reduced model should be also computable, for instance as functions of the reduced model variables. For applications it is handy when not only the full model but also the reduced model is a CRN, like in Fig. 1.

3 Tropical Geometry Approaches

In order to “tropicalize” biochemical networks, one replaces parameters and species with orders of magnitude. This is performed by the change of variables

$$ x \mapsto a = \log (x) / \log \epsilon , $$

where \(\epsilon \) is a small, positive parameter.

This logarithmic change of variables defines a map \(V_{\epsilon } : {\mathbb {R}}_+ \rightarrow {\mathbb {R}}\cup \{-\infty \}\). It is easy to check that when \(\epsilon \rightarrow 0\),

$$\begin{aligned} V_{\epsilon } (x y)= & {} V_{\epsilon } (x) + V_{\epsilon }(y), \\ V_{\epsilon } (x + y)= & {} \min (V_{\epsilon } (x) , V_{\epsilon }(y)). \end{aligned}$$

This mapping transforms the semifield \({\mathbb {R}}_+\) into the semifield \({\mathbb {R}}_{min}\) (or min-plus algebra) where multiplication, addition, \(\mathbf{0}\) and \(\mathbf{1}\) become addition, multiplication, \(-\infty \) and 0, respectively. Furthermore, \(V_{\epsilon }(x)\) represents the order of magnitude of x and can express dominance relations, because when \(\epsilon \rightarrow 0\)

$$V_{\epsilon }(x) < V_{\epsilon }(y) \implies x>> y.$$

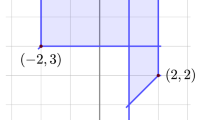
Tropicalizing a biochemical model consists of keeping in the r.h.s. of the ODEs only the dominant terms and eliminating the other terms  [24]. As can be seen in the Fig. 2 for the Michaelis–Menten model, generically there is only one dominant term, but there are special situations when more than two dominant terms exist. We called tropical equilibration the situation when at least two dominant terms, one positive and one negative exist  [24]. Heuristically, the tropical equilibration corresponds to compensation of dominant terms and to slow dynamics, whereas the dynamics with uncompensated dominant terms is fast.

Fig. 1.
figure 1

Modified from  [30, 31].

Reduction of a biochemical network. A model M(n, r, p) has n species, r reactions and p parameters. In the Systems Biology Graphical Notation, molecular species are represented by rectangles and reactions by dots  [19]. Oriented edges (arrows) leave reactant species, enter reactions, and leave reactions, enter reaction products. After reduction, a network has less species, reactions and parameters.

Full size image
Fig. 2.
figure 2

Analysis of dominant terms in the tropicalized Michaelis–Menten model for \(k_4<< k_3\). Each ODE corresponds to a tripod (tropical curve) made of three half-lines. The lines where two monomial terms are dominant in each ODE form the tropical prevariety (intersection of the two tropical curves). The solid half-lines of the tropical prevariety form the tropical equilibrations.

Full size image

4 Scaling and Singular Perturbation Schemes

In singular perturbation problems it is considered that both parameters and species concentrations depend on some small parameter. In practice we consider that the parameters of the model can be written as \(k=\bar{k} (\epsilon ^*)^{\gamma }\) where \(\epsilon ^*\) is a small positive parameterFootnote 1. Next, we replace k by \(k(\epsilon ) = \bar{k} \epsilon ^\gamma \) and we study the asymptotic solutions in the limit \(\epsilon \rightarrow 0\). If \(\epsilon ^*\) is small enough, then the asymptotic solutions are close to the solutions of the model.

The tropical geometry approaches allow to find the appropriate scalings. To this end, we use valuations of parameters and species concentrations defined as \(V(x(\epsilon )) = \lim _{\epsilon \rightarrow 0} V_\epsilon (x(\epsilon )) ,\, V(k(\epsilon )) = \lim _{\epsilon \rightarrow 0} V_\epsilon (k(\epsilon )) \). It follows, at lowest order that

$$\begin{aligned} x(\epsilon ) = \bar{x} \epsilon ^{V(x)}, k(\epsilon ) = \bar{k} \epsilon ^{V(k)}. \end{aligned}$$
(2)

The valuations of the parameters can be obtained by rounding from their actual numeric values \(V(k) = \mathrm {round}(V_{\epsilon ^*} (k))\), where \(\epsilon ^*\) can be any small positive number. Different choices of \(\epsilon ^*\) are only approximately equivalent and in practice one tries several values and selects a robust choice. We showed in  [32] that the valuations of the concentrations V(x) have to satisfy tropical equilibrations.

Let us illustrate how this can be used to define slow/fast decompositions and reduce the Michaelis–Menten model. Consider the case when \(k_3<< k_4\) corresponding to the quasi-steady state approximation. In this case we have

$$\begin{aligned} \frac{\mathrm {d} \bar{x}_1 }{\mathrm {d} t }= & {} - \epsilon ^{\gamma _1} \bar{k}_1 \bar{x}_1 + \epsilon ^{\gamma _2 + a_2} \bar{k}_2 \bar{x}_1 \bar{x}_2 + \epsilon ^{\gamma _3 + a_2 - a_1} \bar{k}_3 \bar{x}_2, \nonumber \\ \frac{\mathrm {d} \bar{x}_2 }{\mathrm {d} t }= & {} \epsilon ^{\gamma _1 + a_1 - a_2} \bar{k}_1 \bar{x}_1 - \epsilon ^{\gamma _2 + a_1} \bar{k}_2 \bar{x}_1 \bar{x}_2 - \epsilon ^{\gamma _4} \bar{k}_4 \bar{x}_2 - \epsilon ^{\gamma _3} \bar{k}_3 \bar{x}_2, \end{aligned}$$
(3)

where \(\gamma _i = V(k_i), 1\le i \le 4,\, a_j = V(x_j), 1\le j \le 2 \).

Each tropical equilibration leads to a scaling and to a candidate reduced model. For instance, the tropical equilibration \(\gamma _1 + a_1 - a_2 = \gamma _2 + a_1 = \gamma _4\) leads to

$$\begin{aligned} \bar{x}_1'= & {} - \bar{k}_1 \bar{x}_1 + \bar{k}_2 \bar{x}_1 \bar{x}_2 + \epsilon ^{\gamma _3 - \gamma _4} \bar{k}_3 \bar{x}_2, \nonumber \\ \epsilon ^{\gamma _1-\gamma _4} \bar{x}_2'= & {} \bar{k}_1 \bar{x}_1 - \bar{k}_2 \bar{x}_1 \bar{x}_2 - \bar{k}_4 \bar{x}_2 - \epsilon ^{\gamma _3 - \gamma _4} \bar{k}_3 \bar{x}_2 , \end{aligned}$$
(4)

where the derivatives are with respect to the rescaled time \(\tau = \epsilon ^{\gamma _1}\) and \(\gamma _3 - \gamma _4>0\) (because \(k_3<< k_4)\).

The case \(\gamma _1-\gamma _4>0\) is typically a singular perturbation case and the solution of (4) converges to the solution of

$$\begin{aligned} \bar{x}_1'= & {} - \bar{k}_1 \bar{x}_1 + \bar{k}_2 \bar{x}_1 \bar{x}_2, \nonumber \\ 0= & {} \bar{k}_1 \bar{x}_1 - \bar{k}_2 \bar{x}_1 \bar{x}_2 - \bar{k}_4 \bar{x}_2, \end{aligned}$$
(5)

as \(\epsilon \rightarrow 0\).

The justification of the convergence lies outside tropical geometry considerations and uses singular perturbations results; in this simple case it follows from  [39]. Some general results of convergence can be found in  [32] for the two time scale case and in  [17] for the multiple timescale case.

The second equation of (5) is called quasi-steady state condition. Using this condition to eliminate \(\bar{x}_2\), we obtain the reduced model

$$\begin{aligned} \bar{x}_1' = - \frac{V_{max} \bar{x}_1}{ \bar{x}_1 + K_m}, \end{aligned}$$
(6)

that is the Briggs-Haldane approximation to the Michaelis–Menten model, with \(V_{max}=\bar{k}_1 \bar{k}_4 / \bar{k}_2\), \(K_m = \bar{k}_4/\bar{k}_2\).

By this procedure a model of two differential equations and four parameters was reduced to a model of one differential equation and two parameters.

5 Approximate Conservation Laws

In the case when \(k_3>> k_4\) using the same procedure as in the preceding section for the tropical equilibration \(\gamma _1 + a_1 - a_2 = \gamma _2 + a_1 = \gamma _3\) leads to

$$\begin{aligned} 0= & {} - \bar{k}_1 \bar{x}_1 + \bar{k}_2 \bar{x}_1 \bar{x}_2 + \bar{k}_3 \bar{x}_2, \nonumber \\ 0= & {} \bar{k}_1 \bar{x}_1 - \bar{k}_2 \bar{x}_1 \bar{x}_2 - \bar{k}_3 \bar{x}_2, \end{aligned}$$
(7)

as \(\epsilon \rightarrow 0\).

The quasi-steady state equations are indeterminate and one can not eliminate both fast variables \(x_1\) and \(x_2\) as usual in the quasi-steady state approximation. Furthermore, the slow variables whose dynamics have to be retained in the asymptotic limit are not explicit.

This degenerate case occurs quite often in practice. In order to obtain a reduction, we exploit approximate conservations. When \(k_3>> k_4\), the fast dynamics of the Michaelis–Menten model can be approximated by

$$\begin{aligned} \frac{\mathrm {d} x_1 }{\mathrm {d} t }= & {} - k_1 x_1 + k_2 x_1 x_2 + k_3 x_2, \nonumber \\ \frac{\mathrm {d} x_2 }{\mathrm {d} t }= & {} k_1 x_1 - k_2 x_1 x_2 - k_3 x_2. \end{aligned}$$
(8)

It can be easily checked that this system has a first integral \( \frac{\mathrm {d} (x_1+x_2) }{\mathrm {d} t } =0\). \(x_1+x_2\) is called an approximate conservation law because it is conserved by the fast approximated system and is not conserved by the full system.

By introducing the new variable \(x_3 = x_1 + x_2 = \bar{x}_3 \epsilon ^{\min (a_1,a_2)}\) we get

$$\begin{aligned} \frac{\mathrm {d} \bar{x}_1 }{\mathrm {d} t }= & {} \epsilon ^{\gamma _3+a_2-a_1} ( -\bar{k}_1 \bar{x}_1 + \bar{k}_2 \bar{x}_1 \bar{x}_2 + \bar{k}_3 \bar{x}_2), \nonumber \\ \frac{\mathrm {d} \bar{x}_2 }{\mathrm {d} t }= & {} \epsilon ^{\gamma _3} ( \bar{k}_1 \bar{x}_1 - \bar{k}_2 \bar{x}_1 \bar{x}_2 - \bar{k}_3 \bar{x}_2 - \epsilon ^{\gamma _4-\gamma _3} \bar{k}_4 \bar{x}_2), \nonumber \\ \frac{\mathrm {d} \bar{x}_3 }{\mathrm {d} t }= & {} -\epsilon ^{\gamma _4+a_2-\min (a_1,a_2)} \bar{k}_4 \bar{x}_2. \end{aligned}$$
(9)

As \(\gamma _4+a_2-\min (a_1,a_2) > \gamma _3\) and \(\gamma _4+a_2-\min (a_1,a_2) > \gamma _3\), it follows that the variable \(x_3\) is slower than both \(x_1\) and \(x_2\), with no condition on the valuations of parameters and variables.

More generally, approximate conservations can be defined each time a scaling of the system by powers of \(\epsilon \) is known. We proved, for polynomial ODEs, that any approximate linear or polynomial conservation law is a slow variable  [6]. This result can be used for model reduction in the degenerate situation when the quasi-steady state equations are indeterminate.

6 Metastability

A typical trajectory of a multiscale system consists in a succession of qualitatively different slow segments separated by fast transitions (see Fig. 3). The slow segments, corresponding to metastable states or regimes, can be of several types such as attractive slow invariant manifolds, Milnor attractors, saddle connections, etc.

According to the famous conjecture of Jacob Palis, smooth dynamical systems on compact spaces should have a finite number of attractors whose basins cover the entire ambient space  [27]. These conditions apply to biochemical reaction networks whose ambient space is compact because of conservation, or dissipativity. The conjecture could be extended to metastable states where smoothness of the vector fields and compactness of the ambient space should lead to a finite number of such states. In this case, symbolic descriptions of the trajectories as sequences of symbols, representing the metastable states that are visited, are possible.

Tropical equilibrations are natural candidates for slow attractive invariant manifolds and metastable states. Beyond the purely geometric conditions, hyperbolicity conditions are needed for the stability of such states  [17, 32]. The set of tropical equilibrations is a polyhedral complex. The maximal dimension faces of such a complex are called branches (Fig. 4).

Because it is much easier to make calculations in polyhedral geometry than with high dimensional smooth dynamical systems, the computation of tropical branches represents a useful tool for understanding complex dynamical systems. Moreover, many dynamical properties such as timescales, are linear functions of parameter and species concentrations orders after tropicalization. Thus, polyhedral geometry can be used for expressing conditions for particular model behaviors. This opens fascinating directions for the synthesis of systems with desired properties.

Fig. 3.
figure 3

From   [35].

Dynamics of multiscale systems can be represented as itinerant trajectory in a patchy phase space landscape made of slow attractive invariant manifolds. The term crazy-quilt was coined to describe such a patchy landscape  [11]. In the terminology of the singular perturbations theory slow dynamics takes place on these slow manifolds, while fast transitions (layers) occur by following the flow of the fast vectorfield (long arrows) away from the slow manifolds.

Full size image
Fig. 4.
figure 4

Left: Polyhedral tropical branches for a model of MAPK cellular signaling in projection on directions of variation of three chemical species; a real trajectory spans several such branches in a well defined sequence, from alpha (initial condition) to omega (steady state). Right: The adjacency relations of the branches in the polyhedral complex are represented as a graph.

Full size image

7 Conclusion

Tropical geometry has promising applications in the field of analysis of biological models.

The calculation of tropical equilibrations is a first important step in algorithms for automatic reduction of complex biological models. By model reduction, complex models are transformed into simpler models that can be more easily analyzed, simulated and learned from data.

Tropical geometry methods are possible ways to symbolic characterization of dynamics in high dimension, also to synthesis of dynamical systems with desired features. This may have important practical applications but can also provide at least partial answers to open questions in mathematics.

Several tools for tropical simplification of biological systems are currently being developed within the French-German Symbiont consortium  [3, 4] and will be made available to the computer algebra and computational biology communities.