Keywords

1 Introduction

Chest X-ray has been widely adopted for annual medical screening, where the main purpose is to check whether the lung is healthy or not. Considering the huge amount of regular medical tests worldwide, it would be desirable if there exists an intelligent system helping clinicians automatically detect potential abnormality in chest X-ray images. Here we consider such a specific task of abnormality detection, for which there is only normal (i.e., healthy) data available during model training. Compared to diagnosis with supervised learning, the key challenge of the task is the lack of abnormal data for training an abnormality detector.

For medical image analysis, the approaches thus far proposed for abnormality detection include parametric and non-parametric statistical models, one-class SVM, and deep learning models like generative adversarial networks (GANs). Parametric models usually refer to Gaussian and Gaussian mixture models, which estimate the density distribution of normal data from training set to predict the abnormality of a test sample  [17]. Parametric models often assume that the normal data distribution is a Gaussian or a mixture of Gaussian distributions. In comparison, non-parametric statistical models, such as Gaussian process, are more capable of modelling complex distributions but have more computational loads  [20]. Both parametric and non-parametric models are bottom-up generative approaches. In contrast, one-class SVM is a top-down classification-based method for abnormality detection, which constructs a hyperplane as a decision boundary that best separates normal data and the origin point, and meanwhile maximises the distance between the origin and the hyperplane  [15]. It has been applied to abnormal detection based on fMRI and retinal OCT images  [11, 16]. While the above conventional approaches have been widely used in the medical domain, there is one serious drawback to restrict their performance, i.e., the feature representation of images need to be manually designed in advance. Without the need to extract hand-crafted features, generative adversarial networks (GANs)  [8] and autoencoders are recently becoming popular for medical abnormality detection due to their capability of implicitly modelling more complex data distribution than the conventional approaches. The early GAN-based approach for anomaly detection, called AnoGAN, was proposed for abnormality detection in retinal OCT images  [14]. The basic idea is to train a generator in the AnoGAN which can generate only normal image patches, such that any abnormal patch would not be well reconstructed by the generator. A fast version of the AnoGAN called f-AnoGAN  [13] was recently proposed with an additional encoder included to make the generator become an autoencoder. More autoencoder models which are often combined with GANs have also been recently developed for abnormality detection in medical image analysis  [1,2,3,4, 18] and natural image analysis  [7, 12]. One issue in most GAN and autoencoder models is about the relative large reconstruction errors particularly at region boundaries although the regions are normal, which would cause false detection of abnormality in normal images.

This paper for the first time applies an autoencoder model to not only reconstruct the corresponding normal version of any input image, but also estimate the uncertainty of reconstruction at each pixel  [5, 6] to enhance the performance of anomaly detection. Higher uncertainty often appears at normal region boundaries with relatively larger reconstruction errors, but not at potential abnormal regions in the lung area. As a result, the normalized reconstruction error by the uncertainty can then be used to better detect potential abnormality. Our approach obtains state-of-the-art performance on two chest X-ray datasets.

Fig. 1.
figure 1

Autoencoder with both reconstruction \(\varvec{\mu }(\mathbf {x})\) and predicted pixel-wise uncertainty \(\varvec{\sigma }^2(\mathbf {x})\) as outputs.

Full size image

2 Method

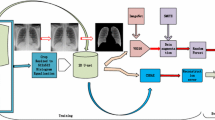
The problem of interest is to automatically determine whether any new chest X-ray image is abnormal (‘unhealthy’) or not, only based on a collection of normal (‘healthy’) images. Since abnormality in X-ray images could be due to small area of lesions or unexpected change in subtle contrast between local regions, extracting an image-level feature representation may suppress such small-scale features, while extracting features for each local image patch may fail to detect the contrast-based abnormalities, both resulting in the failing of abnormality detection. In comparison, reconstruction error based on pixel-level differences between the original image and its reconstructed version by an autoencoder model may be a more appropriate measure to detection abnormality in X-ray images, because both local and global features have been implicitly considered to reconstruct each pixel by the autoencoder. However, it has been observed that there often exists relatively large reconstruction errors around the boundaries between different regions (e.g., lung vs. the others, foreground vs. background, Fig. 2) even in normal images. Such large errors could result in false positive detection, i.e., considering a normal image as abnormal. Therefore, it would be desirable to automatically suppress the contribution of such reconstruction errors in anomaly detection. Simply detecting edges and removing their contributions in reconstruction error may not work well due to the difficulty in detecting low-contrast boundaries in X-ray images and due to possibly larger reconstruction errors close to region boundaries. In this paper, we applied a probabilistic approach to automatically downgrade the contribution of normal regions with larger reconstruction errors. The basic idea is to train an autoencoder to simultaneously reconstruct the input image and estimate the pixel-wise uncertainty in reconstruction (Fig. 1), where larger uncertainties often appear at normal regions with larger reconstruction errors. On the other hand, there are often relatively large reconstruction errors with small reconstruction uncertainties at abnormal regions in the lung area. All together, normal images would be more easily separated from abnormal images based on the uncertainty-weighted reconstruction errors.

2.1 Autoencoder with Pixel-Wise Uncertainty Prediction

In order to reconstruct the input image and estimate pixel-wise uncertainty for the reconstruction, the autoencoder needs to somehow automatically learn to find where the reconstruction is more uncertain without ground-truth uncertainty available. As in the related work for estimation of uncertainty  [5, 6, 9, 10], here we formulate the reconstruction uncertainty prediction problem by a probabilistic model, with the special (unusual) property that each variance element in the model is not fixed but varies depending on input data. Formally, given a collection of N normal images \(\{\mathbf {x}_i, i=1,\ldots ,N\}\), where \(\mathbf {x}_i \in \mathbb {R}^D\) is the vectorized representation of the corresponding i-th original image, an autoencoder can be trained to make each reconstructed image \(\varvec{\mu }(\mathbf {x}_i)\) as similar to the corresponding input image \(\mathbf {x}_i\) as possible. In general, there are always more or less pixel-wise differences between the autoencoder’s expected output \(\mathbf {y}_i\) (i.e., same as the input \(\mathbf {x}_i\)) and the real output \(\varvec{\mu }(\mathbf {x}_i)\). Suppose such differences are noise sampled from an input-dependent (note traditionally noise is assumed input-independent) multivariate Gaussian distribution \(\mathcal {N}(\textit{\textbf{0}}, \varvec{\mathrm{\Sigma }}(\mathbf {x}_i))\), i.e., \(\mathbf {y}_i = \varvec{\mu }(\mathbf {x}_i) + \varvec{\epsilon }(\mathbf {x}_i)\), where \(\varvec{\epsilon }(\mathbf {x}_i) \sim \mathcal {N}(\textit{\textbf{0}}, \varvec{\mathrm{\Sigma }}(\mathbf {x}_i))\). Then the conditional probability density of the ideal output \(\mathbf {y}_i\) (same as the input \(\mathbf {x}_i\)) given the input to the autoencoder is

$$\begin{aligned} p(\mathbf {y}_i | \mathbf {x}_i, \varvec{\theta }) = \frac{1}{(2\pi )^{\frac{D}{2}} |\varvec{\mathrm{\Sigma }}(\mathbf {x}_i)|^{\frac{1}{2}}} \exp \left\{ -\frac{1}{2} (\mathbf {y}_i-\varvec{\mu }(\mathbf {x}_i))^{\mathsf {T}} \varvec{\mathrm{\Sigma }}^{-1}(\mathbf {x}_i) (\mathbf {y}_i-\varvec{\mu }(\mathbf {x}_i)) \right\} {\!,} \end{aligned}$$
(1)

where \(\varvec{\theta }\) denotes the parameters of the model which can output both the reconstructed image \(\varvec{\mu }(\mathbf {x}_i)\) and the covariance matrix \(\varvec{\mathrm{\Sigma }}(\mathbf {x}_i)\). By simplfying \(\varvec{\mathrm{\Sigma }}(\mathbf {x}_i)\) to a diagnonal matrix \(\varvec{\mathrm{\Sigma }}(\mathbf {x}_i) = \mathrm{diag} (\sigma ^2_1(\mathbf {x}_i),\sigma ^2_2(\mathbf {x}_i),...,\sigma ^2_D(\mathbf {x}_i))\), the negative logarithm of Eq. (1) gives

$$\begin{aligned} -\log p(\mathbf {y}_i | \mathbf {x}_i, \varvec{\theta }) = \frac{1}{D}\sum _{k=1}^D \left\{ \frac{(x_{i,k}-\mu _{k}(\mathbf {x}_i))^2}{\sigma ^2_{k}(\mathbf {x}_i)} + \log \sigma _{k}^2(\mathbf {x}_i) \right\} + \frac{D}{2} \log (2\pi ), \end{aligned}$$
(2)

where \(x_{i,k}\) is the k-th element of the expected output \(\mathbf {y}_i\) (i.e., the input \(\mathbf {x}_i\)), and \(\mu _{k}(\mathbf {x}_i)\) is the k-th element of the real output \(\varvec{\mu }(\mathbf {x}_i)\). Then the autoencoder can be optimized by maximizing the log-likelihood over all the normal (training) images, i.e., by minimizing the negative log-likelihood function \(\mathcal {L}(\varvec{\theta })\),

$$\begin{aligned} \mathcal {L}(\varvec{\theta }) = \frac{1}{N D} \sum _{i=1}^N \sum _{k=1}^D \left\{ \frac{(x_{i,k}-\mu _{k}(\mathbf {x}_i))^2}{\sigma ^2_{k}(\mathbf {x}_i)} + \log \sigma _{k}^2(\mathbf {x}_i) \right\} {\!.} \end{aligned}$$
(3)

Equation (3) would be simplified to the mean squared error (MSE) loss based on either Mahalanobis distance or Euclidean distance, when the variance elements \(\sigma _{k}^2(\mathbf {x}_i)\)’s are fixed and not dependent on the input \(\mathbf {x}_i\) or when they are not only fixed but also equivalent.

Note that for each input image \(\mathbf {x}_i\), the model generates two outputs, the reconstruction \(\varvec{\mu }(\mathbf {x}_i)\) and the noise variance \(\varvec{\sigma }^2(\mathbf {x}_i) = (\sigma ^2_1(\mathbf {x}_i),\sigma ^2_2(\mathbf {x}_i),..., \sigma ^2_D(\mathbf {x}_i))^{\mathsf {T}}\) (Fig. 1). Interestingly, while \(\varvec{\mu }(\mathbf {x}_i)\) is supervised to approach to \(\mathbf {x}_i\), \(\varvec{\sigma }(\mathbf {x}_i)\) is totally unsupervised during model training, only based on minimization of the objective function \(\mathcal {L}(\varvec{\theta })\). From the definition of the noise variance (above Eq. (1)), each element \(\sigma ^2_{k}(\mathbf {x}_i)\) of the noise variance represents not the reconstruction error but the degree of uncertainty for the i-th element of the reconstruction \(\varvec{\mu }(\mathbf {x}_i)\). This uncertainty is used to naturally normalize the reconstruction error for the i-th element of the reconstruction (first loss term in Eq. (3)). During model training, the first loss term discourages the autoencoder from predicting very small uncertainty values for those pixels with higher reconstruction errors, because smaller \(\sigma ^2_{k}(\mathbf {x}_i)\) will enlarge the contribution of the already large reconstruction errors by the first loss term. Therefore, the autoencoder will automatically learn to generate relatively larger uncertainties for those pixels (e.g., around region boundaries) with relatively larger reconstruction errors in normal images. On the other hand, the second loss term \(\log \sigma _{k}^2(\mathbf {x}_i)\) in Eq. (3) will prevent the autoencoder from predicting larger uncertainty for all reconstructed pixels. Therefore, the two loss terms together will help train an autoencoder such that the predicted uncertainty will be smaller at those regions where the model can reconstruct well and relatively larger otherwise in normal images.

It is worth noting that the positive correlation between the uncertainty prediction and the reconstruction error may hold mainly for normal image pixels or regions. For anomaly in the lung area which has not been seen during model training, the uncertainty prediction is often small (see Sect. 3.2), probably because the model has learned to reconstruct well (with smaller uncertainty) inside the lung area during model training and therefore often predicts low uncertainty for lung area for any new image, no matter whether there exists anomaly in the area or not. On the other hand, the reconstruction errors at abnormal regions in the lung area are often relatively large because the well-trained autoencoder learns to just reconstruct normal lung by removing any potential noise or abnormal signals in this area. As a result, anomaly with larger reconstruction errors and small uncertainty would become distinctive from normal regions which have positive correlation between reconstruction errors and predicted uncertainties.

2.2 Abnormality Detection

Based on the above analysis, for any new image \(\mathbf {x}\), it is natural to use the pixel-wise normalized reconstruction error (as first term in Eq. (3)) to represents the degree of abnormality for each pixel \(x_k\), and the average of such errors over all pixels for the abnormality \( \mathcal {A}(\mathbf {x})\) of the image, i.e.,

$$\begin{aligned} \mathcal {A}(\mathbf {x})=\frac{1}{D}\sum _{k=1}^D\frac{(x_k-\mu _{k}(\mathbf {x}))^2}{\sigma ^2_{k}(\mathbf {x})}. \end{aligned}$$
(4)

Since the pixel-wise uncertainties \(\sigma ^2_{k}(\mathbf {x})\) depend on the input \(\mathbf {x}\), it is not as easily estimated as for fixed variance. As far as we know, it is the first time to apply such pixel-wise input-dependent uncertainty to estimate of abnormality. If the image \(\mathbf {x}\) is normal, pixels or regions with larger reconstruction errors are often accompanied with larger uncertainties, therefore often resulting in the overall smaller abnormality score \(\mathcal {A}(\mathbf {x})\). In contrast, if there is certain anomaly in the image, the relatively larger reconstruction errors still with small uncertainties at the abnormal region would lead to a relatively larger abnormality score \(\mathcal {A}(\mathbf {x})\).

3 Experiments

3.1 Experimental Setup

Datasets. Our method is tested on two publicly available chest X-ray datasets: 1) RSNA Pneumonia Detection Challenge datasetFootnote 1 and 2) pediatric chest X-ray datasetFootnote 2. The RSNA dataset is a subset of ChestXray14 [19]; it contains 26,684 X-rays with 8,851 normal, 11,821 no lung opacity/not normal and 6,012 lung opacity. The pediatric dataset consists of 5,856 X-rays from normal children and patients with pneumonia.

Protocol. For the RSNA dataset, we used 6,851 normal images for training, 1,000 normal and 1,000 abnormal images for testing. On this dataset, our method was tested on three different settings: 1) normal vs. lung opacity; 2)normal vs. not normal and 3) normal vs. all (lung opacity and not normal). For the pediatric dataset, 1,249 normal images were used for training, and the original author-provided test set was used to evaluate the performance. The test set contains 234 normal images and 390 abnormal images. All images were resized to 64 \(\times \) 64 pixels and pixel values of each image were normalized to [-1,1]. The area under the ROC curve (AUC) is used to evaluate the performance, together with equal error rate (EER), F1-score (at EER) reported.

Implementation. The backbone of our method is a convolutional autoencoder. The network is symmetric containing an encoder and a decoder. The encoder contains four layers (each with one 4 \(\times \) 4 convolution with a stride 2), which is then followed by two fully connected layers whose output sizes are 2048 and 16 respectively. The decoder is connected by two fully connected layers and four transposed convolutions, which constitute the encoder. The channel sizes are 16-32-64-64 for encoder and 64-64-32-16 for decoder. All convolutions and transposed convolutions are followed by batch normalization and ReLU nonlinearity except for the last output layer. We trained our model for 250 epochs. The optimization was done using the Adam optimizer with a learning rate 0.0005. For numerical stability we did not directly predict \(\varvec{\sigma }^2\) in Eq. (3). Instead, the uncertainty output by the model is the log variance (i.e., \(\log \varvec{\sigma }^2\)).

3.2 Evaluations

Baselines. Our method is compared with three baselines as well as state-of-the-art methods for anomaly detection. Below summarizes the methods compared.

  • Autoencoder (AE). A vanilla autoencoder is the most relevant baseline. For a fair comparison, the backbone of the vanilla AE is designed exactly the same as ours. We use the \(L_2\) reconstruction error as anomaly score for this method.

  • OC-SVM. The one-class support vector machine (OC-SVM) [15] is a traditional model for one-class learning. For OC-SVM, we use the feature representations (i.e., the output of the encoder) learned from a vanilla AE and ours as the input to SVM respectively, resulting in two versions OC-SVM-1 and OC-SVM-2.

  • f-AnoGAN. It is a state-of-the-art anomaly detection method in medical imaging [13]. During inference in this model, we fed an image into the encoder-generator to acquire an reconstructed image. A hybrid score combining pixel-level and feature reconstruction error is used to measure abnormality.

Comparison and analysis. The abnormality detection performance with different methods was summarized in Table 1. The state-of-the-art method f-AnoGAN clearly outperforms the other baselines, but performs worse than ours. OC-SVM-2 (with our encoder) is consistently better than OC-SVM-1, suggesting that the encoder in our approach may have mapped normal data into a more compact region in the latent feature space, which can be easily learned by one-class SVM. The superior performance of our method is probably due to the suppression of larger reconstruction error at normal region boundaries by the predicted pixel-wise uncertainties. As Fig. 2 (columns 3, 5, 7) demonstrated, while the reconstruction errors are relatively large at some normal region boundaries for all methods, only our method can estimate the pixel-wise uncertainty (column 8), by which the pixel-wise normalized reconstruction errors at normal region boundaries has been largely reduced (column 9). On the other hand, larger reconstruction errors in abnormal regions in the lung area often do not correspond to larger uncertainties.

Table 1. Comparison with others with different metrics. Bold face indicates the best, and italic face for the second best.
Full size table
Fig. 2.
figure 2

Exemplar reconstructions of normal (rows 1–2) and abnormal (rows 3–4) test images. \(\mathbf {x}\) is input; \(\mathbf {x}'\), \(\mathbf {x}''\), and \(\varvec{\mu }(\mathbf {x})\) are reconstructions from AE, f-AnoGAN, and our method; operators are pixel-wise. Green bounding boxes for abnormal regions.

Full size image

As a result, the uncertainty normalized abnormality score can help separate abnormal images from normal ones, as confirmed in Fig. 3 (right). In comparison, the two histograms are largely overlapped when using the vanilla reconstruction error (Fig. 3, left). In addition, it is worth noting that, as in other autoencoder and GAN based image reconstruction methods, our method can also provide the pixel-level localization of potential abnormalities (Fig. 2, last column), which could be helpful for clinicians to check and analyze the abnormality details in practice.

Fig. 3.
figure 3

Histograms of abnormality score for normal (blue) and abnormal (red) images in the test set (RSNA Setting-1). Left: without uncertainty normalization. Right: with uncertainty normalization. Scores are normalized to [0, 1] in each subfigure. (Color figure online)

Full size image
Table 2. Ablation study on RSNA Setting-1. ‘U’ denotes uncertainty output. ‘0’–‘4’: number of skip connections between encoder and decoder convolutional layers, with ‘1’ for the connection between encoder’s last and decoder’s first convolutional layers.
Full size table

Ablation Study. Table 2 shows that only incorporating uncertainty loss with autoencoder (i.e., without uncertainty normalization) doesn’t improve the performance (Table 2, ‘without-U’, AUC = 0.68 which is similar to that of vanilla AE). In contrast, uncertainty normalized abnormality score (‘with-U’) largely improves the performance. Interestingly, adding skip connections downgraded performance. This is probably because skip connections prevents the encoder learning the true low-dimensional distribution of normal data.

4 Conclusion

We proposed an uncertainty normalized abnormality detection method which is capable of reconstructing the image with the pixel-wise prediction uncertainty. Experiments on two chest X-ray datasets shows that the uncertainty can well suppress the adversarial effect of larger reconstruction errors around normal region boundaries, and consequently state-of-the-art performance was obtained.