Keywords

1 Introduction

Blade vibrations of turbomachine impellers are the subject of research by many authors. The dependences of the vibration characteristics (displacement, stress, frequency) on geometric parameters can appear as the main function for the construction of energy and transport turbomachines. As an example, we can indicate the rotor blades of turbomachine impellers. Due to the cantilever design, the characteristics of these vibration blades are very sensitive to changes in geometric parameters. Using the sensitivity functions in the analysis of the natural frequencies blades provides a qualitative improvement in resonance mistuning. Many authors use numerical methods to analyze the dynamics and durability of rotor turbomachines [1,2,3,4,5,6,7,8]. In publications [3, 9,10,11,12,13], authors describe the development of research methods with using sensitivity functions on the field of the turbomachine.

Analysis of dynamic characteristics of impeller blades with sensitivity functions to location of mistuning zones can be useful for design of blades and new design of such structures. A numerical analysis of sensitivity allows to create effective models of mistuning and reduce the levels of arising stresses in the blades, and therefore increases their life. This paper proposes an effective methods for analyzing the sensitivity blades of the turbomachine impellers to determine the locations of mistuning zones with additional masses with their maximum influence on the dynamic response of the structure.

2 Fundamentals

Currently, finite element method is most widely used to solve problems of statics, dynamics, and durability calculation of various technical systems, including turbine impellers. There are many works devoted to the theory and application of this method in calculating the characteristics of vibrations, the durability of the turbomachine impellers. In particular, the works [14,15,16] can be noted.

In finite element method, the statics equation in case of constant speed of rotation and temperature by linear formulation (1) and nonlinear formulation (2) is:

$$K\delta = F_{l} ,$$
(1)
$$(K + K_{G} + K_{R} )\delta = F_{l} ,$$
(2)

where K is stiffness matrix, \(K_{G}\) is stiffness matrix of a geometrical, \(K_{R}\) is supplementary stiffness matrix arising from rotation, \(\delta\) is node displacements, \(F_{l}\) is vector of loads.

The dynamic equation in case of the free vibration without damping [10] by linear formulation (3) and nonlinear formulation (4) is:

$$M\ddot{\delta } + K\delta = 0,$$
(3)
$$M\ddot{\delta } + M_{C} \dot{\delta } + (K + K_{G} + K_{R} )\delta = 0,$$
(4)

where \(M_{C}\) is Coriolis matrix.

The solution of Eq. (3) takes the form of harmonic vibration:

$$\delta = y\cos (\omega - \beta )\,,$$
(5)

substituting this expression in Eq. (3), we obtain the following result:

$$(\omega^{2} M + K)y\cos (\omega t - \beta ) = 0\,\,\,or\,\,(K - \lambda M)y = 0\,,$$
(6)

where \(\omega\) is angular frequency. \(\lambda\) is eigenvalue.

This equation makes sense when the determinant is equaled to zero. By linear formulation (7) and nonlinear formulation (8):

$$\det (K - \lambda M) = 0\,,$$
(7)
$$\det (K + K_{G} + K_{R} ) - \lambda M = 0\,,$$
(8)

Solving Eq. (8) in the linear formulation, we can define eigenvalues:

$$\lambda = \left\{ {\lambda_{1} ,\lambda_{2} , \ldots .,\lambda_{N} } \right\}^{T} ,$$
(9)

or modal displacements (mode shapes):

$$y^{(i)} = \delta^{{(i)^{T} }} = \left\{ {\delta_{i1} ,\delta_{i2} , \ldots ,\delta_{iN} } \right\}^{T} ,\quad i = 1,2, \ldots ,N,$$
(10)

and vibration frequencies:

$$f = \frac{1}{2\pi }\sqrt \lambda = \left\{ {f_{1} ,f_{2} , \ldots ,f_{N} } \right\}^{T} ,$$
(11)

The values of the mistuning parameters of the blades are defined as:

$$\Delta f_{n} = \frac{{f_{m,n} - \bar{f}_{m} }}{{\bar{f}_{m} }},$$
(12)

where \(\bar{f}_{m}\)—is the arithmetic value of the fundamental frequencies; \(f_{m,n}\)—the value of the frequency mth form vibration of blades, \(n = 1, \ldots ,N\) (N—number blade).

The value of the sensitivity is positive when function gets a maximum value in the upper range of design parameters variations and negative when the function gets a maximum value in the lower range of design parameters variations.

A large absolute sensitivity value means a greater degree of changes in the experimental parameters (e.g., frequency) when changing the design parameters (e.g., mass). Mistuning values are random variables. Using experimental methods to evaluate the effect of random mistuning on the dynamics of impellers is a difficult task, because it is necessary to analyze a large number of mistuning options during the experiment. In these cases, authors can use such numerical methods for studying random processes as the Monte Carlo method [17] and others [13, 18, 19].

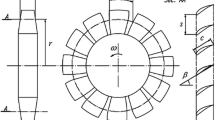
As an example of the research, the mistuning of an academic impeller with 10 blades is considered at the Brandenburg Technical University (Germany). The measurement system for analyzing the excitation of vibration disks with 10 blades (laser scanning vibrometer) is shown in Fig. 1a. In the work [20,21,22], authors demonstrated an approach to determine experimentally blade individual eigenfrequency. Therefore, a bladed disk is excited by a miniature modal hammer while the vibration response is measured non-intrusively by a laser vibrometer. Summarizing, all blades except the excited one are mistuned with additional masses to decouple one blade from the already disturbed cyclic symmetry. The miniature modal hammer excites sequentially all blades. Figure 1b presents the schematic of the experimental setup for research vibration and mistuning parameters [20]. In this paper, the illustrated bladed disk is not the investigated bladed disk.

Fig. 1
figure 1

An experiment for research mistuning parameters of the turbomachine impellers with using sensitivity functions. a Measurement system; b schematic of the experimental setup

Full size image

3 Numerical Results

An academic impeller with 10 blades was chosen as the object research. Material of the impeller-steel, Young’s modulus—\(2.1 \cdot 10^{5} \,{\text{N}}/{\text{mm}}^{2}\), density—\(7.85 \cdot 10^{ - 6} \,{\text{kg}}/{\text{mm}}^{3}\), Poisson’s ratio—0.3. Figure 2a, b shows general view of an academic impeller (3D model blade disk and one sector model).

Fig. 2
figure 2

An academic impeller with 10 blades. a 3D model blade disk; b one sector model; c finite element model of the blade

Full size image

The numerical research in this work is based on the ANSYS MECHANICAL APDL software packages. Figure 2c shows a finite element model of the blade using quadrilateral shell element SHELL 63 from the ANSYS program, which is defined by four nodes and six degrees of freedom at each node. If the speed of rotation of the blades and flow pressure and temperature are constant, then we can say that the rotor of the engine is in stationary mode. In our example, speed of the rotor is 100 s−1.

Table 1 presents the calculation of the frequency vibration blade of the impeller without and with rotation 100 s−1. By researching sensitivity, it is possible to determine the areas of the greatest influence of changes mass on natural frequencies and displacements at resonances. A topical continuation of this work is the sensitivity analysis and the optimal location of the mistuning in the form of additional masses for a single blade and blades impeller disks without and with rotation 100 s−1 (Figs. 3 and 4). The sensitivity for the first 10 modes of vibration is calculated and shown to the feather blades of the impeller, which show points of maximum and minimum influence on the place of additional masses for researching each mode of vibration. The blue zone means the maximum decrease in the frequency with additional masses in a particular place of the blade. And the red zone indicates the minimum decrease in the frequency of vibrations with the location of the mass on the blade.

Table 1 Calculation of the vibration frequencies blade of the impeller without the corresponding sensitivity without and with rotation 100 s−1
Full size table
Fig. 3
figure 3

Sensitivity analysis of an academic impeller blades turbomachines without rotation

Full size image
Fig. 4
figure 4

Sensitivity analysis of an academic impeller blades turbomachines with rotation 100 s−1

Full size image

Table 2 presents the calculation of the vibration frequency blades with the corresponding sensitivities without and with rotation 100 s−1 with additional mass 5.0 g. As can be seen from Table 2 in the zone of maximum sensitivity, the maximum value of the effect mistuning parameter is observed (about 17% for the fifth mode of blade vibration), while the results for the zone of minimum sensitivity show that the values of the natural frequencies of the vibration of the impeller blade do not change (the maximum value of reducing vibration frequencies is only 0.3% for the fourth mode of blade vibration).

Table 2 Calculation of the vibration frequency blades with the corresponding sensitivity without and with rotation 100 s−1 (additional mass 5.0 g)
Full size table

4 Conclusion

This paper presents the results of a numerical analysis sensitivity of the natural frequencies vibration blade of the turbomachine impellers with mistuning parameter blades and also shows the zones of maximum and minimum response to the introduction of additional masses. From the results described in this work, we can conclude that the proposed results of the analysis natural frequencies vibrations of the impeller blades taking into account the sensitivity functions and can be used for new design and refinement of existing structures with the highest efficiency.