Abstract
In this paper, we propose a subclass of single-occurrence regular expressions with counting (cSOREs) and give a learning algorithm of cSOREs. First, we learn a SORE. Then, we construct a countable finite automaton (CFA) by traversing the syntax tree of the obtained SORE. Next, the CFA runs on the given finite sample to obtain the minimum and maximum number of repetitions of the subexpressions under the iteration operators. Finally we obtain a cSORE by traversing the syntax tree and introducing the counting operators. Our algorithm not only can learn a cSORE, which is expressive enough to cover more XML data, but also has better generalization ability for smaller sample.
Work supported by National Natural Science Foundation of China under Grant No. 61472405.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The eXtensible Markup Language (XML), which has been widely used on the Web, is the lingua franca for data exchange [1]. The schema languages (such as DTD (Document Type Definitions) and XSD (XML Schema Definitions) recommended by W3C (World Wide Web Consortium) [24]) have advantages for diverse applications such as data processing, automatic data integration, and static analysis of transformations [12, 21, 22]. However, many XML documents on the Web are not accompanied by a schema [3, 23], or valid schema [6, 7], therefore, schema inference becomes an essential work.
Schema inference can be reduced to learning regular expressions from sets of positive samples. Using techniques from Gold [16], the class of regular expressions cannot be learned only from positive data. Even Bex et al. proved in [5] that the class of deterministic regular expressions cannot be learned from positive data. Therefore for practical purposes many researchers turned to focus on learning subclasses of deterministic regular expressions [4, 5, 8, 9, 13, 14, 25].
Deterministic regular expressions [11] require that each symbol in the input word can unambiguously be matched to a position in the regular expression without looking ahead in the word. In practice, there are many applications of the subclass of deterministic regular expressions on the Web, including that of single-occurrence regular expressions (SOREs) [8, 9]. However, SOREs, which do not support counting, are defined on standard regular expressions. Regular expressions with counting, which are used in XML Schema [10, 15, 17,18,19,20, 25], are extended from standard regular expressions by adding counting [15]. In this paper, we propose a subclass of single-occurrence regular expressions with counting (cSOREs). Our experiments (see Table 1) showed that the proportion of cSOREs is 94.16% for 32,750 real-world XSD files grabbed from Google, Maven, and GitHub, where 378,558 regular expressions were extracted. This indicates the practicability of cSORE. Therefore, it is necessary to study a learning algorithm for cSORE.
For learning regular expressions with counting, we have proposed the class ECsores [25], and the corresponding learning algorithm InfECsore [25]. However, although the ECsore learnt by InfECsore is a precise representation of any given finite sample, the algorithm InfECsore has less generalization ability such that, in some cases, the learnt ECsore covers relatively less XML dataFootnote 1. Therefore, a new subclass cSORE and a new method for learning cSORE are proposed. Although the defined cSOREs have more constrains than ECsores, compared with the algorithm InfECsore, our algorithm not only can learn a cSORE, which is expressive enough to cover more XML data, but also has better generalization ability (higher precision and recall) for smaller sample.
The main contributions of this paper are as follows. First, we infer a SORE. Then, we present a learning algorithm for cSOREs, where the main steps are as follows: (1) Construct a countable finite automaton (CFA) [25] from the syntax tree of the learnt SORE; (2) The CFA runs on the given finite sample to obtain the minimum and maximum number of repetitions of the subexpressions under the iteration operators; and (3) Generate the cSORE by traversing the syntax tree and introducing the counting operators. Finally, we provide the evaluations in generalization ability about our algorithm.
The paper is structured as follows. Section 2 gives the basic definitions. Section 3 presents the learning algorithm of the cSORE, Sect. 4 presents experiments. Section 5 concludes the paper.
2 Preliminaries
2.1 Regular Expression with Counting
Let \(\varSigma \) be a finite alphabet of symbols. The class of standard regular expressions over \(\varSigma \) is defined in the standard way: \(\varepsilon \), \(a \!\in \! \varSigma \) are regular expressions. For any regular expressions \(r_1\) and \(r_2\), the disjunction \((r_1|r_2)\), the concatenate \((r_1\cdot r_2)\), and the Kleene-star \(r_1^{*}\) are also regular expressions. Usually, we omit concatenation operators in examples. The regular expressions with counting are extended from standard regular expressions by adding the counting [15]: \(r^{[m,n]}\) is a regular expression for regular expression r, where \(m \!\in \! \mathbb {N}\), \(n \!\in \! \mathbb {N}_{/1}\), \(\mathbb {N}\!=\!\{1,2,3,\cdots \}\), \(\mathbb {N}_{/1}\!=\!\{2,3,4,...\} \cup \{+\infty \}\), and \(m \!\le \! n\). \(\mathcal {L}(r^{[m,n]})\!=\!\{w_1\cdots w_i|w_1,\cdots ,w_i\!\in \! \mathcal {L}(r),m\!\le \! i\!\le \! n\}\). Note that \(r^{+}\), r?, and \(r^{*}\) are used as abbreviations of \(r^{[1,+\infty ]}\), \(r|\varepsilon \), and \(r^{[1,+\infty ]}|\varepsilon \), respectively.
2.2 SORE, ECsore and cSORE
SORE is defined as follows.
Definition 1
(SORE [8, 9]). Let \(\varSigma \) be a finite alphabet. A single-occurrence regular expression (SORE) is a standard regular expression over \(\varSigma \) in which every terminal symbol occurs at most once.
In this paper, for a SORE r, since \(\mathcal {L}(r^*)\!=\!\mathcal {L}((r^+)?)\), a SORE does not use the Kleene-star operation, and forbids the expressions of forms (r?)?, \((r^+)^+\), and \((r?)^+\).
Example 1
\((ab)^+\) is a SORE, while \((ab)^{+}a\) is not. The expressions (a?)?, \((a^+)^+\), and \((a?)^+\) are forbidden.
Definition 2
(ECsore [25]). Let \(\varSigma \) be a finite alphabet. An ECsore is a regular expression with counting over \(\varSigma \) in which every terminal symbol occurs at most once. For a regular expression r, an ECsore forbids immediately nested counters, expressions of form (r?)? and \((r?)^{[m,n]}\).
ECsore does not use the Kleene-star and the iteration operations. And ECsores are deterministic by definition.
Definition 3
(cSORE). Let \(\varSigma \) be a finite alphabet. A cSORE is an ECsore over \(\varSigma \). For regular expressions \(r_1\), \(r_2\), \(\cdots \), \(r_k\) (\(k\ge 2\)), a cSORE forbids expressions of form \((r_1r_2^{[m_1,n_1]}r_3)^{[m_2,n_2]}\) and \((r_1(r_2^{[m_1,n_1]})?r_3)^{[m_2,n_2]}\) where \(\varepsilon \in \mathcal {L}(r_1)\) and \(\varepsilon \in \mathcal {L}(r_3)\), and expressions of form \((r_1?r_2?\cdots r_k?)^{[m,n]}\).
According to the definition, cSOREs are a subclass of ECsores. ECsores are deterministic regular expressions, so are the cSOREs.
Example 2
\(a?b^{[1,2]}(c|d)^{[1,+\infty ]}\), \(((c|d)^{[1,2]})?\), and a?b(c|d)e are cSOREs, also ECsores, while \(a (b|c)^{+}a\) is not a SORE, therefore neither a cSORE nor an ECsore. \((a^{[3,4]}|b)^{[1,2]}\) and \((a^{[3,4]}b)^{[1,2]}\) are cSOREs, also ECsores. However, the expressions \((a?b^{[1,2]}c?)^{[3,4]}\), \((a?(b^{[1,2]})?c?)^{[3,4]}\) are ECsores, not cSOREs.
Definition 4
(Countable Finite Automaton [25]). A Countable Finite Automaton (CFA) is a tuple \((Q,Q_c,\varSigma ,\mathcal {C},q_0,\) \(q_f,\varPhi ,\mathsf {U},\mathsf {L})\). The members of the tuple are described as follows:
-
\(\varSigma \) is a finite and non-empty alphabet.
-
\(q_0\) and \(q_f:\) \(q_0\) is the initial state, \(q_f\) is the unique final state.
-
Q is a finite set of states. \(Q=\varSigma \cup \{q_0,q_f\} \cup \{+_i\}_{i \in \mathbb {N}}\).
-
\(Q_c\subset Q\) is a finite set of counter states. Counter state is a state q (\(q\in \varSigma \)) that can directly transit to itself, or a state \(+_i\). For each subexpression (excluding single symbol \(a\in \varSigma \)) under the iteration operator, we associate a unique counter state \(+_i\) to count the minimum and maximum number of repetitions of the subexpression, respectively.
-
\(\mathcal {C}\) is finite set of counter variables that are used for counting the number of repetitions of the subexpressions under the iteration operators. \(\mathcal {C}=\{c_{q}|q\in Q_c\}\), for each counter state q, we also associate a counter variable \(c_{q}\).
-
\(\mathsf {U}\!=\!\{u(q)|q\in Q_c\}\), \(\mathsf {L}\!=\!\{l(q)|q\in Q_c\}\). For each subexpression under the iteration operator, we associate a unique counter state q such that l(q) and u(q) are the minimum and maximum number of repetitions of the subexpression, respectively.
-
\(\varPhi \) maps each state \(q\!\in \! Q\) to a set of tuples consisting of a state \(p\!\in \! Q\) and two update instructions. \(\varPhi \):
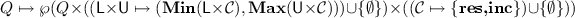 . (\(\emptyset \) denotes empty instruction.)
. (\(\emptyset \) denotes empty instruction.)
Definition 5
(Transition Function of a CFA [25]). The transition function \(\delta \) of a CFA \((Q,Q_c,\varSigma \), \(\mathcal {C},q_0,q_f,\varPhi ,\mathsf {U},\mathsf {L})\) is defined for any configuration \((q,\gamma ,\theta )\) and the letter \(y \in \varSigma \cup \{\dashv \}\)
-
(1)
\(y\!\in \! \varSigma :\) \(\delta ((q,\gamma ,\theta ), y)\) \(=\!\{(z,f_{\alpha }(\gamma , \theta ),g_{\beta }(\theta ))|(z,\alpha ,\beta ) \!\in \! \varPhi (q) \wedge (z=y \vee ((y,\alpha ,\beta )\not \in \varPhi (q) \wedge z\!\in \! \{+_i\}_{i\in \mathbb {N}})) \}\).
-
(2)
\(y= \dashv :\) \(\delta ((q,\gamma ,\theta ), \dashv )\) \(=\{(z,f_{\alpha }(\gamma , \theta ),g_{\beta }(\theta ))|(z,\alpha ,\beta ) \in \varPhi (q) \wedge (z=q_f \vee z\in \{+_i\}_{i\in \mathbb {N}}) \}\).
3 Inference of cSOREs
Our learning algorithm works in the following steps.
Step 1: We infer a SORE for a given finite sample, and the SORE is obtained by post-processing the result of the algorithm Soa2Sore [14].
The post processes for the SORE derived from algorithm Soa2Sore are as follows. Let \(r_0\) denote the SORE inferred by Soa2Sore. Every possibly repeated subexpression of \(r_0\) is rewritten to be under iteration \((^+)\), and for regular expressions \(r_1\), \(r_2\), \(\cdots \), \(r_k\) (\(k\!\ge \! 2\)), the expressions of forms \((r_1r_2^+r_3)^+\) and \((r_1(r_2^+)?r_3)^+\) (\(\varepsilon \!\in \!\mathcal {L}(r_1)\) and \(\varepsilon \!\in \!\mathcal {L}(r_3)\)) are forbidden. And the expressions of form \((r_1?r_2?\cdots r_k?)^+\) are also forbidden.
Step 2: A CFA is constructed by traversing the syntax tree of the SORE obtained from step 1.
First, the state-transition diagram G of a CFA is constructed by traversing the syntax tree of the SORE obtained from step 1. The entire process is similar to the preorder traversal of the binary tree. Then, the detailed descriptions of the CFA are presented such as like in [25]. Note that, the parameter \(\varPhi (q)\) in transition function of a CFA can be obtained from G.
Step 3: The CFA derived from step 2 runs on the same finite sample used in step 1 to obtain the minimum and maximum number of repetitions of the subexpressions under the iteration operators.
The CFA counts the minimum and maximum number of repetitions of the subexpressions under the iteration operators. Counting rules are given by transition functions of the CFA. We use the algorithm Counting proposed in [25] to run the CFA. Let \(\mathcal {A}\) denote the constructed CFA and S denote the given finite sample. Let \(\mathsf {C}\!=\!Counting(\mathcal {A},S)\), where \(\mathsf {C}=\{(l(q),u(q))|q\in \mathcal {A}.Q_c\}\).
Step 4: We obtain a cSORE by traversing the syntax tree constructed in step 2 and replace the iteration operators with corresponding counting operators where the values of the lower bound and upper bound are obtained in step 3.
Note that, \(\mathsf {C}\) is the set of pairs of the lower bound and upper bound values.
4 Experiments
In this section, first, we present the practical analysis of cSOREs. Then, we provide the evaluations in generalization ability about our algorithm. And all experiments were conducted on a ThinkCentre M8600t-D065 with an Intel core i7-6700 CPU (3.4 GHz) and 8G memory. All codes were written in C++.
4.1 Practicability
The 32,750 real-world XSD files were grabbed from Google, Maven, and GitHub. Table 1 shows that the proportion of cSOREs is 94.16% for the 378,558 regular expressions that were extracted from these XSD files. This indicates the significant practicability of cSOREs.
4.2 Generalization Abilities
We evaluate the algorithms InfECsore and InfcSORE by computing the precision and recall according to the given sample. We specify that, the learnt expression with higher precision and recall has better generalization ability. The average precision and average recall, which are as functions of sample size, respectively, are averaged over 1000 expressions.
We randomly extracted the 1000 expressions from XSDs, which were grabbed from Google, Maven, and GitHub. Each one of the 1000 expressions does not contain the iteration operators (\(^+\)), but contains the counters, where the upper bounds are less than 10. To learn each extracted expression \(e_0\), we randomly generated corresponding XML data by using ToXgene [2], the samples are extracted from the XML data, each sample size is that listed in Fig. 1. And we define precision (p) and recall (r). Let positive sample (\(S_+\)) be the set of the all strings accepted by \(e_0\), and let negative sample (\(S_-\)) be the set of the all strings not accepted by \(e_0\). Let \(e_1\) be the expression derived by InfECsore or InfcSORE. A true positive sample (\(S_{tp}\)) is the set of the strings, which are in \(S_+\) and accepted by \(e_1\). While a false negative sample (\(S_{fn}\)) is the set of the strings, which are in \(S_+\) and rejected by \(e_1\). Similarly, a false positive sample (\(S_{fp}\)) is the set of the strings, which are in \(S_-\) and accepted by \(e_1\). While a true negative sample (\(S_{tn}\)) is the set of the strings, which are in \(S_-\) and rejected by \(e_1\). Then, let \(p=\frac{|S_{tp}|}{|S_{tp}|+|S_{fp}|}\) and \(r=\frac{|S_{tp}|}{|S_{tp}|+|S_{fn}|}\). Note that \(\mathcal {L}(e_0)\) and \(\mathcal {L}(e_1)\) are finite languages, and we can construct counter automata [15] (receptors) for \(e_0\) and \(e_1\), respectively. Then we can obtain \(|S_{tp}|\), \(|S_{fp}|\) and \(|S_{fn}|\).
The plots in Fig. 1(a) show that, for a smaller sample (sample size \(\le 500\)), the precision for the expression derived by InfcSORE is higher than that for the expression learnt by InfECsore. But for a larger sample (sample size \(\ge 600\)), the precision for the expression derived by InfcSORE is lower than that for the expression learnt by InfECsore. However, the plots in Fig. 1(b) illustrate that, the recall for the expression derived by InfcSORE is consistently higher than that for the expression learnt by InfECsore. The reason is that, although the cSOREs are a subclass of the ECsores, for the same sample, the learnt cSORE can have more constrains than the learnt ECsore such that some subexpressions without numerical constrains in the learnt cSORE. This will lead to that the learnt cSORE is expressive enough to cover more XML data. In general, for a smaller sample, InfcSORE has better generalization ability such that its result has higher precision and recall.
5 Conclusion
This paper proposed an inference algorithm for learning a subclass of deterministic regular expressions: cSOREs. The main strategies include: (1) Construct a CFA from the syntax tree of the learnt SORE; (2) The CFA runs on the given finite sample to obtain the counting operators; and (3) Generate the cSORE by traversing the syntax tree and introducing the counting operators. Compared with previous work, for any given finite language, our algorithm not only can learn a cSORE, which is expressive enough to cover more XML data, but also has better generalization ability for smaller sample. A future work is extending the SORE with counting and interleaving, studying the practical issues and the learning algorithms.
Notes
- 1.
For instance, the original schema in XSD can be denoted by \(r_0=(a|b)^+\), given sample \(S=\{ba,aa,baabaa\}\), the ECsore learnt by InfECsore is \(r_1=(b?a^{[1,2]})^{[1,2]}\). However, an learnt cSORE can be \(r_2=(b?a)^{[1,4]}\), \(|\mathcal {L}(r_1)|=16<|\mathcal {L}(r_2)|=30\). Note that \(\mathcal {L}(r_0)\supseteq \mathcal {L}(r_2)\supseteq S\) and \(\mathcal {L}(r_0)\supseteq \mathcal {L}(r_1)\supseteq S\).
References
Abiteboul, S., Buneman, P., Suciu, D.: Data on the Web: From Relations to Semistructured Data and XML. Morgan Kaufmann, Burlington (2000)
Barbosa, D., Mendelzon, A.O., Keenleyside, J., Lyons, K.: ToXgene: an extensible template-based data generator for XML. In: WebDB (2002)
Barbosa, D., Mignet, L., Veltri, P.: Studying the XML web: gathering statistics from an XML sample. World Wide Web 9(2), 187–212 (2006)
Bex, G.J., Gelade, W., Neven, F., Vansummeren, S.: Learning deterministic regular expressions for the inference of schemas from XML data. In: Proceedings of the 17th International Conference on World Wide Web, pp. 825–834. ACM (2008)
Bex, G.J., Gelade, W., Neven, F., Vansummeren, S.: Learning deterministic regular expressions for the inference of schemas from XML data. ACM Trans. Web 4(4), 1–32 (2010)
Bex, G.J., Martens, W., Neven, F., Schwentick, T.: Expressiveness of XSDs: from practice to theory, there and back again. In: Proceedings of the 14th International Conference on World Wide Web, pp. 712–721. ACM (2005)
Bex, G.J., Neven, F., Van den Bussche, J.: DTDs versus XML schema: a practical study. In: Proceedings of the 7th International Workshop on the Web and Databases: Colocated with ACM SIGMOD/PODS 2004, pp. 79–84. ACM (2004)
Bex, G.J., Neven, F., Schwentick, T., Tuyls, K.: Inference of concise DTDs from XML data. In: International Conference on Very Large Data Bases, Seoul, Korea, pp. 115–126, September 2006
Bex, G.J., Neven, F., Schwentick, T., Vansummeren, S.: Inference of concise regular expressions and DTDs. ACM Trans. Database Syst. 35(2), 1–47 (2010)
Boneva, I., Ciucanu, R., Staworko, S.: Schemas for unordered XML on a DIME. Theor. Comput. Syst. 57(2), 337–376 (2015)
Brüggemann-Klein, A., Wood, D.: One-unambiguous regular languages. Inf. Comput. 142(2), 182–206 (1998)
Che, D., Aberer, K., Özsu, M.T.: Query optimization in XML structured-document databases. VLDB J. 15(3), 263–289 (2006)
Freydenberger, D.D., Kötzing, T.: Fast learning of restricted regular expressions and DTDs. In: Proceedings of the 16th International Conference on Database Theory, pp. 45–56. ACM (2013)
Freydenberger, D.D., Kötzing, T.: Fast learning of restricted regular expressions and DTDs. Theor. Comput. Syst. 57(4), 1114–1158 (2015)
Gelade, W., Gyssens, M., Martens, W.: Regular expressions with counting: weak versus strong determinism. SIAM J. Comput. 41(1), 160–190 (2012)
Gold, E.M.: Language identification in the limit. Inf. Control 10(5), 447–474 (1967)
Hovland, D.: Regular expressions with numerical constraints and automata with counters. In: Leucker, M., Morgan, C. (eds.) ICTAC 2009. LNCS, vol. 5684, pp. 231–245. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03466-4_15
Kilpeläinen, P., Tuhkanen, R.: Towards efficient implementation of XML schema content models. In: Proceedings of the 2004 ACM Symposium on Document Engineering, pp. 239–241. ACM (2004)
Kilpeläinen, P., Tuhkanen, R.: One-unambiguity of regular expressions with numeric occurrence indicators. Inf. Comput. 205(6), 890–916 (2007)
Latte, M., Niewerth, M.: Definability by weakly deterministic regular expressions with counters is decidable. In: Italiano, G.F., Pighizzini, G., Sannella, D.T. (eds.) MFCS 2015. LNCS, vol. 9234, pp. 369–381. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48057-1_29
Manolescu, I., Florescu, D., Kossmann, D.: Answering XML queries on heterogeneous data sources. In: VLDB, vol. 1, pp. 241–250 (2001)
Martens, W., Neven, F.: Typechecking top-down uniform unranked tree transducers. In: Calvanese, D., Lenzerini, M., Motwani, R. (eds.) ICDT 2003. LNCS, vol. 2572, pp. 64–78. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36285-1_5
Mignet, L., Barbosa, D., Veltri, P.: The XML web: a first study. In: Proceedings of the 12th International Conference on World Wide Web, pp. 500–510. ACM (2003)
Thompson, H., Beech, D., Maloney, M., Mendelsohn, N.: XML Schema Part 1: Structures, 2nd edn. W3C Recommendation (2004)
Wang, X., Chen, H.: Inferring deterministic regular expression with counting. In: Trujillo, J.C., et al. (eds.) ER 2018. LNCS, vol. 11157, pp. 184–199. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-00847-5_15
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Wang, X., Chen, H. (2019). Learning a Subclass of Deterministic Regular Expression with Counting. In: Douligeris, C., Karagiannis, D., Apostolou, D. (eds) Knowledge Science, Engineering and Management. KSEM 2019. Lecture Notes in Computer Science(), vol 11775. Springer, Cham. https://doi.org/10.1007/978-3-030-29551-6_29
Download citation
DOI: https://doi.org/10.1007/978-3-030-29551-6_29
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29550-9
Online ISBN: 978-3-030-29551-6
eBook Packages: Computer ScienceComputer Science (R0)





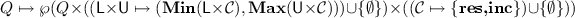 . (
. (