1 Introduction

Healthcare is moving from a population-based model, in which the decision making process is targeted to the “average” patient, to an individual-based model, in which each diagnosis is based on the features characterizing the given patient. This process has been boosted by the recent developments in the Deep Learning field, which has been proven to not only get impressive results in its traditional areas, but also to perform very well in medical tasks.

In particular, in the medical field, the study of the time-to-event, i.e., the expected duration of time until one or more events happen, such as death or recurrence of a disease, is of vital importance. Nevertheless, it is often made more complicated by the presence of censored data, i.e., data in which the information about the time-to-event is incomplete, as it happens, e.g., when a patient drops a clinical trial. Traditionally, these issues are tackled in a field called Survival Analysis, a branch of statistics in which special models have been proposed to predict the time-to-event exploiting censored data, while only a few deep learning approaches have such an ability (e.g., [13, 28]). About the latter, it is interesting to note that most of the encountered deep learning approaches are based on feedforward neural networks and, at least so far, there does not seem to exist published results deploying recurrent neural networks despite the sequential nature of the problem.

In this paper we present a new recurrent neural network model handling censored data and computing, for each patient, both a survival function and a unique risk score. The survival function is computed by considering a series of binary classifications problems each leading to the estimation of the survival probability in a given interval of time, while the risk score is obtained through the linear combination of the estimates. rnn-surv three main features are:

  1. 1.

    its ability to model the possible time-variant effects of the covariates,

  2. 2.

    its ability to model the fact that the survival probability estimate at time t is function of each survival probability estimate at \(t': t' < t\), and

  3. 3.

    its ability to compute a highly interpretable risk score.

The first two are given by the recurrent structure, while the last is given by the linear combination of the estimates.

rnn-surv is tested on three small publicly available datasets and on two large heart transplantation datasets. On these datasets rnn-surv performs significantly better than the state of the art models, always resulting in a higher C-index than the state of the art models (up to 28.4%). We further show that if we simplify the model we always get worse performances, hence showing the significance of rnn-surv different features.

This paper is structured as follows. We start with the analysis of the related work (Sect. 2), followed by the background about Survival Analysis (Sect. 3). Then, we present of our model (Sect. 4), followed by the experimental analysis (Sect. 5), and finally the conclusions (Sect. 6).

2 Related Work

The problem of survival analysis has attracted the attention of many machine learning scientists, giving birth to models such as random survival forest [11], dependent logistic regressors [26], multi-task learning model for survival analysis [17], semi-proportional hazard model [27] and support vector regressor for censored data [21], all of which not based on neural networks.

Considering the works that have been done in the field of Survival Analysis using Deep Learning techniques, these can be divided in three main subcategories, that stemmed from just as many seminal papers:

  1. (1)

    Faraggi and Simon [7] generalized Cox Proportional Hazards model (CPH) [5] allowing non-linear functions instead of the traditional linear combinations of covariates by modeling the relationship between the input covariates and the corresponding risk with a single hidden layer feedforward neural network. This work has been later resumed in [13] and [28]. Contrarily to rnn-surv, CPH and the models [13] and [28] assume time-invariant effects of the covariates.

  2. (2)

    Liestbl, Andersen and Andersen [18] subdivided time into K intervals, assumed the hazard to be constant in each interval and proposed a feedforward neural network with a single hidden layer that for each patient outputs the conditional event probabilities \(p_k = P(T \ge t_k | T \ge t_{k-1})\) for \(k = 1,...,K\), T being the time-to-event of the given patient. This work was then expanded in [2], but even in this later work the value of the estimate \(p_{k-1}\) for a given patient is not exploited for the computation of the estimate \(p_k\) for the same patient. On the contrary, rnn-surv, thanks to the presence of recurrent layers, is able to capture the intrinsic sequential nature of the problem.

  3. (3)

    Buckley and James [4] developed a linear regression model that deals with each censored data by computing its most likely value on the basis of the available data. This approach was then generalized using neural networks in various ways (e.g., [6]). Unlike rnn-surv, in [4] and in the following ones, estimated and known data are treated in the same way during the regression phase.

3 Background on Survival Analysis

Consider a patient i, we are interested in estimating the duration \(T_i\) of the interval in between the event of interest for i and the time \(t_0\) at which we start to measure time for i. We allow for right censored data, namely, data for which we do not know when the event occurred, but only that it did not occur before a censoring time \(C_i\). The observed time \(Y_i\) is defined as \(Y_i = \text {min}(T_i,C_i)\), and each datapoint corresponds to the pair \((Y_i,\delta _i)\) where \(\delta _i = 0\) if the event is censored (in which case \(Y_i = C_i\)) and \(\delta _i = 1\) otherwise.

In Survival Analysis, the standard functions used to describe \(T_i\) are the survival function and the hazard function [15].

  1. 1.

    The survival function \(S_i(t)\) is defined as:

    $$\begin{aligned} S_i(t) = Pr (T_i > t) \end{aligned}$$
    (1)

    with \(S_i(t_0) = 1\).

  2. 2.

    The hazard function \(h_i(t)\) is defined as:

    $$\begin{aligned} h_i(t) = \lim _{dt \rightarrow 0}\frac{Pr(t \le T_i < t + dt \mid T_i \ge t)}{dt}. \end{aligned}$$
    (2)

Further, in order to offer a fast understanding of the conditions of the patient, a common practice of the field is to create a risk score \(r_i\) for each patient i: the higher the score the higher the risk of the occurrence of the event of interest.

Fig. 1.
figure 1

rnn-surv with \(N_1=2\) feedforward layers, followed by \(N_2=2\) recurrent layers.

Full size image

4 RNN-SURV

In order to transform the survival analysis problem in a series of binary decision problems, we assume that the maximal observed time is divided into K intervals \((t_0 , t_1], \ldots , (t_{K -1} , t_K]\) and that the characteristic function modeling \(T_i\) is constant within each interval \((t_{k-1},t_k]\) with \(k = 1,\ldots ,K\). Given a patient i, the purpose of our model is to output both an estimate \(\hat{y}_i^{(k)}\) of the survival probability \(S_i\) for the kth time interval and a risk score \(r_i\).

4.1 The Structure of the Model

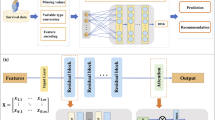
The overall structure of rnn-surv is represented in Fig. 1 and is described and motivated below:

  1. 1.

    the input of each layer is given by the features \(\mathbf {x}_i\) of each patient i together with the time interval identifier k. Thanks to this input, rnn-surv is able to capture the time-variant effect of each feature over time,

  2. 2.

    taking the idea from the natural language processing field, the input is then elaborated by \(N_1\) embedding layers. Thanks to the embeddings we are able to create a more meaningful representation of our data, and

  3. 3.

    the output of the embedding layers is then passed through \(N_2\) recurrent layers and a sigmoid non-linearity. This generates the estimates \(\hat{y}_i^{(1)}, \ldots , \hat{y}_i^{(K)}\) from which we can compute the risk score with the following equation:

    $$\begin{aligned} \hat{r}_i = \sum _{k=1}^K w_k \hat{y}_i^{(k)} \end{aligned}$$
    (3)

    where \(w_k\) for \(k = 1, \ldots , K\) are the parameters of the last layer of rnn-surv. Thanks to the linear combination, the risk score, whose quality is evaluated with the C-index [9], is highly interpretable.

Further, in order to handle the vanishing gradient problem, the feedforward layers use the ReLU non-linearity [19], while the recurrent layers are constituted of LSTM cells [10], which are defined as:

(4)

4.2 Training

Since the neural network predicts both the discrete survival function and the risk score for each datapoint, it is trained to jointly minimize two different loss functions:

  1. 1.

    The first one is a modified cross-entropy function able to take into account the censored data, defined as:

    (5)

    where \(U_k = \{i \mid \delta _i=1 \,\,\text{ or } \,\, C_i > t_k\}\) represents the set of individuals that are uncensored throughout the entire observation time or for which censoring has not yet happened at the end of the kth time interval.

  2. 2.

    The second one is an upper bound of the negative C-index [23] defined as:

    $$\begin{aligned} \mathcal {L}_2 = - \frac{1}{\mathcal {|C|}} \sum _{(i,j) \in \mathcal {C}} \bigg [ 1 + \bigg (\frac{\log \sigma (\hat{r}_j - \hat{r}_i) }{\log 2} \bigg )\bigg ] \end{aligned}$$
    (6)

    where \(\mathcal {C}\) is the set of pairs \(\{(i,j) \mid \delta _i = 1 \text {~and~} (Y_i \le Y_j) \}\). The advantage of minimizing (6) instead of the negative C-index is that the former still leads to good results [23], and the latter is far more expensive to compute and would have made the experimental evaluation impractical.

The two losses \(\mathcal {L}_1\) and \(\mathcal {L}_2\) are then linearly combined, with the hyperparameters of the sum optimized during the validation phase.

In order to avoid overfitting, we apply dropout to both the feedforward layers [22] and to the recurrent layers [8], together with a holdout-based early stopping as described in [20]. Further, we add L2-regularization to the linear combination of the losses. The entire neural network is trained using mini-batching and Adam optimizer [14].

5 Experimental Analysis

All our experiments are conducted on two large datasets, UNOS Transplant and UNOS Waitlist, from the United Network for Organ Sharing (UNOS)Footnote 1 and on three publicly available, small datasets, AIDS2, FLCHAIN, NWTCO.Footnote 2 In each experiment we deploy 60/20/20 division into training, validation and test sets and the early stopping is configured as a no validation gain for 25 consecutive epochs. The main characteristics of these datasets are shown in Table 1, while the structure of rnn-surv for each dataset is shown in Table 2. The performances of our model are measured using the C-index [9].Footnote 3

Table 1. Datasets description
Full size table
Table 2. Structure of the model for each experiment.
Full size table

5.1 Preprocessing

Our datasets present missing data and thus they require a preprocessing phase. UNOS Transplant and UNOS Waitlist contain data about patients that registered in order to undergo heart transplantation during the years from 1985 to 2015. In particular UNOS Transplant contains data about patients who have already undergone the surgery, while UNOS Waitlist contains data about patients who are still waitlisted. From the complete datasets, we discard 12 features that can be obtained only after transplantation and all the features for which more than 10% of the patients have missing information. In order to deal with the missing data on the remaining 53 and 27 features, we conduct 10 multiple imputations using Multiple Imputation by Chained Equations (MICE) [24].

The three small datasets contain data about:

  1. 1.

    NWTCO: contains data from the National Wilm’s Tumor Study [3],

  2. 2.

    FLCHAIN: contains half of the data collected during a study [16] about the possible relationship between serum FLC and mortality, and

  3. 3.

    AIDS2: contains data on patients diagnosed with AIDS in Australia [25].

For these datasets, we complete the missing data using the mean value for the continuous features and using the most recurrent value for the categorical ones. Once complete the missing data, we then use one-hot encoding for the categorical features and we standardize each feature so that each has mean \(\mu = 0\) and variance \(\sigma = 1\).

5.2 Comparison with Other Models

We have compared rnn-surv with the two traditional Survival Analysis models, CPH and Aalen Additive Hazards model (AAH) [1], and with three recent models that try to conjugate Machine Learning with Survival Analysis: rfs [11], deep-surv [13] and mtlsa [17]. Both CPH and AAH have been implemented using the lifelines packageFootnote 4, while we deployed the randomForestSRC packageFootnote 5 for rfs, the deepsurv packageFootnote 6 for deep-surv and the mtlsa packageFootnote 7 for mtlsa. The results shown in Table 3 are obtained using k-fold cross validation (with \(k = 5\)). As it can be seen from the table, rnn-surv outperforms the other models in all the datasets. In particular, the biggest improvements are obtained with respect to mtlsa, with a peak of 28.4% on the FLCHAIN dataset.

Table 3. Performances, in terms of C-index, of rnn-surv, CPH, AAH, deep-surv, rfs and mtlsa together with the 95% confidence interval for the mean C-index. The * indicates a p-value \(< 0.05\) while ** \(<0.01\).
Full size table

5.3 Estimating the Survival Curves

To further demonstrate the good results obtained by rnn-surv, in Fig. 2 we show some of the survival curves obtained in largest dataset available, the UNOS Transplant dataset.

Figure 2 shows that our model is able to capture the average trend of the survival curves, both for the whole population and for subsets of it. Further, rnn-surv demonstrates to have a great discriminative power: it is able to plot a unique survival function for each patient and, as it is shown in Fig. 2(c), the survival curves can be very different one from another and from the average survival curve.

Fig. 2.
figure 2

Performances of rnn-surv on UNOS Transplant dataset on a 36 months horizon on the test set. (a) average Survival Function obtained with rnn-surv and Kaplan-Meier curve [12]. (b) average Survival Functions obtained with rnn-surv and Kaplan-Meier curves for two subgroups of patients: patients who experienced an infection and patients who did not. (c) Kaplan-Meier curve together with the survival curves of two different patients (P1: Patient 1, P2: Patient 2).

Full size image

5.4 Analysis of the Model

We now analyze how the different main components of rnn-surv contribute to its good performances. In particular, we consider the model without the three main features of the model:

  1. 1.

    We first consider the case in which we do not have the feedforward layers, i.e., with \(N_1 = 0\);

  2. 2.

    Then the case in which the interval identifier k as input to the feedforward layer is always set to 1;

  3. 3.

    Finally the case in which the model has only one likelihood, i.e., \(\mathcal {L}_2\).

The C-index of the various versions and of the complete model on the different datasets are shown in Table 4. In the Table the best results are in bold, while the worst results are underlined. As it can be seen, the best performances are always obtained by the complete model, meaning that all the different components have a positive contribution. Interestingly, the worst performances are obtained when we disable the \(\mathcal {L}_1\) score on the large datasets and the feedforward layers in the small ones. The explanation for the very positive contribution of using both the \(\mathcal {L}_1\) and \(\mathcal {L}_2\) scores on the two large datasets is that \(\mathcal {L}_1\) allows to take into account the intermediate performances of the network when computing \(\hat{y}^{(1)}_i,\ldots ,\hat{y}^{(K)}_i\). On the other hand, for the small datasets, the positive contribution of using the two scores is superseded by the feedforward layers and this can be explained by the characteristics of the datasets presenting a majority of discrete features.

Table 4. Performances, in terms of C-index, of the complete model compared with its incomplete versions.
Full size table

6 Conclusions

In this paper we have presented rnn-surv: a new recurrent neural network model for predicting a personalized risk score and survival probability function for each patient in presence of censored data. The proposed model has three main distinguishing features, each having a positive impact on the performances on two large and three small, publicly available datasets. Our experiments show that rnn-surv always performs much better than competing approaches when considering the C-index, improving the state of the art up to 28.4%.