EMS Planning and Management

Abstract

In this chapter I survey research on planning and management for emergency medical services, emphasizing four topics: forecasting demand, response times, and workload; measuring performance; choosing station locations; and allocating ambulances to stations, based on predictable and unpredictable changes in demand and travel times. I focus on empirical work and the use of analytical stochastic models.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 EMS Scope and Scale

Emergency medical services (EMS) refers to the provision of out-of-hospital acute medical care and the transport of patients to hospitals for definitive care. In 1792, Dominique Jean Larrey, a surgeon in Napoleon Bonaparte’s Imperial Guard, was the first to develop ambulances [54], in the modern sense of specially equipped vehicles for carrying sick or injured people, usually to hospital. In the 220 years since, EMS has evolved and expanded to become a significant component of modern health-care systems.

Table 6.1 provides a sense of the scale of EMS, with statistics on call volumes, resources, and operating expenses in Canada [25,  2,  9]; London, England [38]; the United States [17]; and rural Iceland, Scotland, and Sweden [23]. These statistics suggest that a person in any one of these jurisdictions calls EMS an average of once every 5 to 12 years and that the cost of providing EMS (financed through a combination of public funding and user fees) ranges from US$40 to US$90 per capita, per year.

Table 6.1 EMS statistics

EMS planning and management are challenging, because the volume, location, and severity of EMS calls are highly variable, making it difficult to decide where to position ambulances and their crews while they wait for their next call. Planning is facilitated, however, by the ever-increasing quantity and quality of data collected by modern EMS agencies, through computer-aided dispatch (CAD) and global positioning system (GPS) technologies. CAD systems typically collect times tamps for all the events associated with a typical EMS call that are shown in Fig. 6.1 (from [5]), for the geographical coordinates of the ambulance at the time of dispatch and for the call address. In addition to improving the real-time information available to dispatchers, these data make it possible to model and predict call volumes and response times more realistically. Partly because of the increased availability of data, perhaps, the number of publications in the operations research and management science (OR/MS) literature that includes “emergency medical services” or “ambulances” as keywords has grown rapidly during the last decade, as demonstrated in Fig. 6.2 (data obtained from the ISI Web of Science).

Fig. 6.1

Events and time intervals for an EMS call, with median minutes (coefficients of variation) for each interval, based on 2003 Calgary EMS data

Fig. 6.2

Number of OR/MS publications with keywords “emergency medical service” or “ambulances”

This chapter summarizes recent OR/MS contributions to EMS planning and management. Several related survey articles have been published during the last four decades, including general surveys on emergency response planning for EMS, fire, and police [6, 56, 21]; a survey of OR/MS methods aimed at EMS practitioners [20]; surveys that focus on optimal facility location models [3, 37]; and surveys focusing on the use of simulation [28]. In comparison, this chapter places greater emphasis on forecasting EMS demand, response times, and workload; EMS performance measures; and the use of stochastic models to predict the performance of EMS systems.

The remainder of this chapter is organized as follows. Section 6.2 addresses the prediction of demand, response times, and workload. Section 6.3 summarizes EMS performance measures, and Sect. 6.4 outlines stochastic models to predict the performance of EMS systems. Section 6.5 discusses optimization models for station planning and allocation of ambulances to stations.

2 Predicting Demand, Response Times, and Workload

Mathematical models of EMS systems require three components as input information: (1) demand—how call volumes vary over time and space; (2) response times—how the response time to a call varies with the distance that the ambulance must travel and perhaps other factors; and (3) workload—how long an ambulance and its crew will be occupied with a call. Researchers have started to use the call-by-call data that modern EMS systems collect, together with road network information, in order to investigate each of these components in detail.

2.1 Demand

EMS call volumes vary predictably by month, day of the week, and hour of the day. Figure 6.3 shows a typical weekly pattern for average call volumes, revealing a regular diurnal cycle each weekday, higher volumes on Friday and Saturday night (which carry on into early Saturday and Sunday morning), and lower volumes on Sundays. This weekly pattern is crucial for planning purposes, particularly for shift scheduling. Figure 6.4 displays the annual cycle for Calgary, Canada. Other predictable patterns include higher-than-average volumes on certain holidays (e.g., New Year’s Day) and during certain annual festivals or other special events. See [7] for time series models that incorporate both seasonal patterns and special events. Extreme weather events and natural or human-caused disasters are other special events for which timing is more difficult to predict, but the impact on call volume can be predicted to some extent [43].

Fig. 6.3

Average hourly call volume as a percentage of weekly volume, with 95% confidence intervals (2000–2004 Calgary EMS data, adapted from [7])

Fig. 6.4

Average monthly call volume as a percentage of annual volume, with 95% confidence intervals (2000–2004 Calgary EMS data, adapted from [7])

It is commonly assumed in planning models that call volumes follow a stationary or time-varying Poisson process. This assumption is supported by theoretical arguments [27] and empirical evidence [22,  61]. It is often appropriate, however, to view the Poisson arrival rate as a random variable, with a distribution that is narrower for time periods closer to the present. To be more precise, suppose that the call volume on day t + n (where call volumes are known up to and including day t and n is the forecast horizon) is Y _t + n , that the arrival rate for day t + n is ${\Lambda }_{t+n} = {B}_{t+n}{\lambda }_{t+n}$ (where B _t + n has a mean of 1 and a standard deviation ${\sigma }_{{B}_{t+n}}$), and that conditional on ${\Lambda }_{t+n} = \lambda$, Y _t + n is Poisson-distributed with mean λ. One can interpret λ _t + n as a long-term average call volume for day t + n and B _t + n as a “busyness factor” that perturbs the average call volume away from its long-term value, because of such factors as the weather. To the extent that these factors persist from one day to the next, one would expect that information on the actual call volume on day t should make it possible to forecast the call volume on day t + 1 with greater accuracy.

As an example, Fig. 6.5 shows the root-mean-square forecast error (RMSE—the square root of the average of the squared forecast errors) for daily EMS call volumes in Calgary using five time series methods described in [7]. We focus on Models 1 and 4. The average daily call volume was 174. If daily call volumes were Poisson distributed with a mean of 174/day, then the standard deviation of the daily call volumes, estimated by the RMSE, should be approximately $\sqrt{ 174} = 13.2$. This estimate is likely to represent a lower bound on the achievable forecast accuracy for two reasons: average call volumes are not constant but have seasonality and trend and because, as alluded to above, such factors as the weather tend to increase call volume variability. Model 4 in Fig. 6.5 comes close to this lower bound, however, with an RMSE of 14, which corresponds to an estimate of 0.027 for ${\sigma }_{{B}_{t+1}}$; thus, the busyness factor for “tomorrow” has a standard deviation of 2.7%. Put differently, call arrivals for tomorrow can be modeled as following a Poisson process, the arrival rate of which is almost deterministic (and can be forecast using Model 4) and conditional on call volumes up to and including today. In contrast, when forecasting 14 days into the future, the RMSEs for Models 1 and 4 are both 18, corresponding to an estimate of 0.07 for ${\sigma }_{{B}_{t+14}}$. Model 1 is a linear regression model with an intercept and trend term and dummy variables for month of the year, hour of the week, New Year’s Day, and a special event that occurs every year in Calgary (the Calgary Stampede). Model 4 is a time series regression model, with the same independent variables as Model 1, some interaction terms added, and error terms that are modeled as an autoregressive process. (Models 2 and 3 are similar to Model 4, differing only in which interaction terms are included. Model 5 is a seasonal ARIMA model).

Fig. 6.5

Root-mean-square forecast error for daily call volume forecasts from 1 to 21 days into the future. (2000–2004 Calgary EMS data, from [7])

See Matteson et al. [40] and Vile et al. [58] for additional research on forecasting the evolution of EMS call volumes over time. The spatial distribution of EMS calls, which is also important for planning, has not been studied as much as call volume forecasting has. See [53] for recent work on forecasting the spatial distribution of EMS calls.

Each EMS call has an associated response time (R, the sum of the pre-travel delay and the travel time in Fig. 6.1) and service time (S, the sum of the travel, scene, transport, and hospital time in Fig. 6.1—the time interval during which an ambulance and its crew are occupied with a call). These time intervals are important for different reasons: the response time is the basis for most EMS performance measures, and the service times determine the workload on the EMS system.

Response and service times potentially depend on all of the following factors:

• The time when the call arrived

• The location of the call (i) and the location of the responding ambulance (j)

• The system load, which I will consider to be the number of busy ambulances when the call arrived

• The urgency of the call

In the remainder of this section, I summarize some of the available evidence on whether and how response and service times depend on these factors, but there is much that we have yet to learn about this issue. To illustrate the potential benefits of further research, consider that average service times appear to increase with system load, as discussed later in this section. Future research could address three types of questions:

Fundamental knowledge: Does average service time vary with system load? If so, why? Does the strength and nature of the relationship vary among geographic regions or depend on the way EMS service is organized?

Modeling: How can load-dependent average service times be incorporated into mathematical models of EMS systems? How do the validity, tractability, and scalability of different modeling approaches compare?

Implications for planning: How do the recommended number of ambulances and the predicted system performance differ as a function of the incorporation of load-dependent average service times?

2.2 Response Times

Travel time is usually the largest component of response time. Statistical analysis of EMS travel times has focused either on predicting travel time based on the characteristics of the links in a transport network that are included in the trip (e.g., the length and the road type for each link) [59] or on predicting travel time based only on the distance between the responding ambulance and the call location [34, 5]. Both of these approaches incorporate dependence of travel time on locations of the responding ambulance and call address. The latter approach is more parsimonious, and the calculations needed to predict travel times are simpler and require fewer data (e.g., Euclidean distance can be used instead of road network distance, if desired). Focusing on the latter approach, Fig. 6.6 shows how estimated medians and coefficients of variation of travel time vary with distance, based on 2003 Calgary data [5]. The median travel time curve is concave because average speeds are typically higher for longer trips.

Fig. 6.6

Parametric estimates of median and coefficient of variation of travel time functions with nonparametric 95% confidence limits (2003 Calgary EMS data, from [5])

EMS travel speeds tend to be higher for urgent calls [5, 59] and lower during rush hours, but the rush-hour effect is less pronounced for urgent “lights-and-siren” calls [59].

The pretravel delay can be decomposed into evaluation and dispatch time and chute time (the time from dispatch until the dispatched ambulance starts its travel toward the call address). Evaluation and dispatch times are shorter for urgent calls [1], and there is some evidence (left panel of Fig. 6.7) that they depend on the system load for nonurgent calls, perhaps indicating that dispatching is delayed for nonurgent calls when the system is congested. Chute times tend to be shorter when the system is more highly loaded (right panel of Fig. 6.7), because the responding ambulance is more likely to be traveling rather than to waiting at a station.

Fig. 6.7

Means and 95% confidence intervals for evaluation and dispatch time and for chute time (2008 Edmonton EMS data, from [1])

If one can predict the response-time distribution for a representative set of combinations of ambulance locations and call addresses, then one can plot probability of coverage maps, as shown in Fig. 6.8. Coverage refers to the proportion of calls with response time below a time standard, such as 9 min (see Sect. 6.3 for further discussion). The map on the right of Fig. 6.8 is based on the assumption that all stations have an available ambulance, whereas the map on the left incorporates the probability that an ambulance is available at each station, as calculated using the Hypercube Queueing Model (a Markov chain model with a state variable for the status of every ambulance; see Sect. 6.4 for further information). A visual comparison of these two maps can help planners diagnose which regions of a city require additional stations and which regions could benefit from more ambulances. The lack of coverage in the northwest area of the city that is apparent on map (a), for example, could be attributable to an inadequate number of stations in the area or an inadequate number of ambulances allocated to those stations. Map (b), which is based on the assumption of unlimited ambulance availability, indicates that coverage in the northwest could be increased considerably by allocating more ambulances to the stations already in that area, without building any new stations. In contrast, having unlimited ambulance availability appears not to address the lack of coverage in the northeast, suggesting that it is necessary to build new stations in order to improve coverage in that area.

Fig. 6.8

Probability-of-coverage map. Locations of ambulance stations are depicted as black squares. The colors of the other locations (neighborhoods aggregated to a single point) indicate the probability of coverage. Unshaded regions represent areas with sparse or no population. (a) Closest available ambulance responds. (b) Closest station responds (2003 Calgary EMS data, from [5])

2.3 Workload

The most obvious reason for EMS service times to depend on the location of the responding ambulance and the call address is that travel time, which depends on travel distance, is part of service time. This dependence has driven generalizations of the Hypercube Queueing Model [31], for example. The dependence of travel times on travel distances should induce a dependence of travel times on the system load, because, when the system is more highly loaded, the average distance from a call address to the closest available ambulance should be higher. Considerably less attention has been devoted to the study of service time components other than travel time, but these other components also appear to depend on the system load. I have already discussed how chute time appears to decrease with load, as shown in Fig. 6.7. Hospital time is the component that appears to be most strongly influenced by system load, as the right panel of Fig. 6.9 shows, revealing average hospital times that are approximately 30 min longer when the system is most highly loaded [1], likely because emergency departments (EDs) tend to be highly loaded when an EMS system is highly loaded. In contrast, average length of stay in at least some hospital wards has been found to be shorter under heavier load [32]. It is not clear why average hospital times decrease at extreme loads, but the effect may be linked to protocols that operate in EDs when the number of patients is deemed to have exceeded capacity.

Fig. 6.9

Means and 95% confidence intervals for on-scene time and hospital time (2008 Edmonton EMS data, from [1]). On-scene times are shown separately for patients who were transported to hospital (PT) and those who were not (PT ^C)

I believe that further study should seek to determine if EMS service times depend more on the locations of the responding ambulance (i) and the call address (j) than they do on the system load and if the dependence on (i, j) can be captured via the load (as is done in the repositioning model proposed in [1]). These issues have modeling implications, because models with a single state variable for the system load are likely to be more scalable than are models that keep track of the address and the identity of the responding ambulance for every call in progress.

3 Performance Measures

Where EMS systems are publicly funded, their operations should presumably aim to deliver maximum benefit to the public, given their budget. But measuring the benefits that EMS systems provide is no straightforward matter. Ideally, the benefit would be measured in such concrete and easily interpreted units as lives saved—units that facilitate comparisons between competing uses of funds [15]. But this is typically not the case. Most EMS systems use such system-wide response-time statistics as the proportion of urgent calls with a response time within a certain time standard. The US National Fire Protection Association, for instance, recommends a target of 90% within 4 min for the first response to an urgent EMS call, followed by an Advanced Life Support (ALS) response within 8 min [46, Sects. 5.3.3.4.2-3]. Reaching 90% of urgent urban EMS calls in 9 min is a common target in North America [19]. The National Health Service in the UK sets targets of 75% in 8 min and 95% in 19 min for urgent urban EMS calls [12]. The advantage of response-time performance targets is the fact that response-time data are relatively easy to collect and understand. There are disadvantages, however: the link between response-times and medical outcomes is not clear, and response time standards and percentages are necessarily arbitrary.

Optimization models for EMS station location and ambulance allocation (discussed in Sect. 6.5) typically aim to maximize coverage, which corresponds to the EMS response time being within a time standard. For the sake of simplicity, some models assume a deterministic relationship between distance and response time, implying that all call locations within a given distance from an available ambulance are covered and that all locations that are further away are not covered. Other models use a probability of coverage, p _ij , of a call location i by an available ambulance at location j, where p _ij is estimated using such methods as the estimated travel time distributions discussed in [5].

Planners must answer a variety of questions when recommending appropriate EMS performance measures, including:

• Should one report response-time statistics or medical outcome statistics?

• When reporting response times, should one report averages, quantiles (such as medians or 90th percentiles), or fractiles (the proportion of response times within a time standard)?

• Should one use different standards for different call priorities?

• Should one use different standards for urban and rural areas?

• Should one report system-wide measures or separate measures for different geographical regions?

The last two questions concern equity. Economies of scale typically make it more difficult to achieve a response-time standard in city suburbs than in the more densely populated downtown core and more difficult still in rural areas. As Felder and Brinkmann [18] point out, the objectives of providing equal access to EMS versus minimizing system-wide response times lead to different deployment patterns. Response-time standards and actual performance typically differ for urban and rural areas in the USA, UK, and Germany [18, 19], indicating that the standard setters have decided against equal access. As Felder and Brinkmann [18] note, although a policy of equal access may appear difficult to criticize, such a policy does imply that lives are valued more highly in more sparsely populated areas.

As two examples of the political issues involved with access to medical care in remote areas, the cities of Edmonton, Canada and Reykjavik, Iceland both have two airports—an international airport that is relatively far from the city center and a smaller domestic airport close to the center. In Edmonton, the decision has been made to close the City Centre Airport, and in Reykjavik, there is a continuing debate about whether to close all or part of its domestic airport. In both cases [26, 60], advocates for rural areas have raised the issue of longer transport times to hospital for patients that are flown to the city by air ambulance, pitting urban interest in reducing sprawl against rural concerns about access to medical care.

Although the link between EMS response times and medical outcomes is not always clear, this issue has been studied extensively for patients experiencing cardiac arrest. A study by Valenzuela et al. [57] illustrates the type of knowledge generated by medical researchers. They used data from Tucson, AZ, and King County, WA, to fit logistic regression models that predict the probability of survival as a function of various factors. One of their prediction equations was:

$$s({I}_{\mathrm{ CPR}},{I}_{\mathrm{ Defib}}) = 1/\left (1 +\exp \left (-0.260 + 0.106{I}_{\mathrm{ CPR}} + 0.139{I}_{\mathrm{ Defib}}\right )\right )\;,$$

where s(. ) is the survival probability, I _CPR is the duration from collapse to cardiopulmonary resuscitation (CPR), and I _Defib is the duration from collapse to defibrillation. By combining this survival function with assumptions about such factors as the proportion of cardiac arrests witnessed, the proportion of cardiac arrest patients that receive CPR from a bystander, and estimates of the distribution of EMS response time as a function of distance, Erkut et al. [15] estimated the relationship between distance and survival probability shown in Fig. 6.10. They found that replacing coverage with a survival probability did not greatly complicate optimization models for EMS station location and ambulance allocation. They also found that coverage-maximizing models in which the relationship between distance and coverage is probabilistic are much better proxies for maximizing the expected number of survivors than are deterministic coverage models. Figure 6.10 compares the shape of a survival probability function and a probabilistic coverage function. Although the two functions have different shapes, they share two characteristics that may explain why one is a good proxy for the other: (1) the benefit decays gradually with distance from the closest ambulance, in contrast to a deterministic coverage function that drops from one to zero at the coverage distance standard, and (2) the benefit approaches and remains close to zero after a certain distance, in contrast to a linear decrease in benefit that continues indefinitely, as implied by minimization of average distance.

Fig. 6.10

Estimated survival probability and coverage probability as a function of distance for cardiac arrest patients (adapted from [15])

Work continues on the incorporation of survival probabilities in EMS planning models (see, e.g., [47, 42, 44, 33]). Although a shift of focus from coverage to medical outcomes appears to be relatively straightforward from the point of view of mathematical modeling, shifting the focus of EMS planners to outcome-based measures will likely involve challenges. One of these challenges is the collection of information about events prior to the arrival of an ambulance at the scene (for a cardiac arrest patient, e.g., was CPR administered and how long ago did the cardiac arrest occur?), about medical outcomes after EMS has transferred care of the patient to a hospital, and the linking of both types of information to the response-time data that EMS agencies typically collect.

4 Performance Evaluation

In this section, I focus on the use of stochastic models to predict how EMS system performance changes as the deployment of ambulances changes. To compute EMS system performance measures, it is often convenient to condition on the call location (j) and the location of the ambulance that responds to the call (i). One first requires an estimate of the performance measure of interest for calls from j that are responded to from i, which I will denote with p _ij . I leave the interpretation of p _ij open, but it could, for example, represent average response time, proportion of calls with a response time under 9 min, or the probability of survival. Second, one requires the dispatch probability, f _ij , that an ambulance from location i responds, given that the call is from location j.

I focus on stochastic models that can be solved analytically rather than simulation models. Simulation models of EMS systems have been discussed by [30, 28, 39], among others. Both simulation models and analytical models have their uses, and they can be utilized to complement each other. A primary advantage of analytical models is their short computation time, which is important when using such a model as a component in a procedure to search for optimal or near-optimal deployment plans or as a component in a decision support system that allows EMS planners to experiment with deployment policies and to (almost) immediately see the likely consequences for system performance. Such a system would be frustrating to use if one had to wait several minutes each time a change was made.

To simplify the discussion in this section, I assume that the model parameters do not vary with time or with the system state. Some of the models that I discuss, however, can incorporate time- or state-dependent parameters. For further information, please refer to the references that I cite for each model.

To illustrate the models, I use an example with two single-vehicle ambulance stations and two demand nodes (ambulance call locations), shown in Fig. 6.11. (The figure shows all the input parameters that I use, but the simpler models do not require all the parameters.) In this example, the demand nodes correspond to the catchment areas around the two stations. I assume throughout that the closest available ambulance responds to every incoming call. When both ambulances are busy, with probability B, incoming calls are responded to by backup systems—for example, by EMS supervisors or the fire service. The situation when all ambulances are busy is sometimes referred to as “code red.”

Fig. 6.11

Performance evaluation example

The simplest model assumes that both stations have an available ambulance at all times, which implies that ${f}_{11} = {f}_{22} = 1$, ${f}_{12} = {f}_{21} = 0$, and B = 0. This is the model implicitly used in such optimal facility location models as the maximal covering location problem (MCLP) [8]. The simplest model that accounts for ambulance unavailability is based on the assumption that at any given time, each ambulance is unavailable with probability p (the “average busy fraction,” assumed equal to 0.4 in our example) and available with probability 1 − p, independent of all other ambulances. This binomial model is implicit in the maximum expected covering location model (MEXCLP) [10] and implies that ${f}_{11} = {f}_{22} = 1 - p = 0.6$, ${f}_{12} = {f}_{21} = p(1 - p) = 0.24$, and $B = {p}^{2} = 0.16$.

Up to this point, the only input parameter that I have used is the busy fraction p. Next, suppose that we model the system as an Erlang B (i.e., $M/M/2/2$) loss system, with arrival rate λ = 1 per hour and service rate μ = 1 per hour. Standard calculations reveal that B = 0. 2, the average ambulance utilization is 0.4 (I chose λ and μ so as to obtain an average ambulance utilization equal to p), the probability of both ambulances being free is 0.4, and the probability of one ambulance being free is 0.4. We calculate the dispatch probabilities for demand node 1 as follows:

$$\begin{array}{lll}{ f}_{11}&= \Pr \{\text{both\ ambulances\ free}\} \\& \quad+\Pr \{\text{Ambulance1 free}\;\vert \text{ one ambulance free}\}\Pr \{\text{one ambulance free}\} \\&= 0.4 + 0.5 \times 0.4 = 0.6 \\{f}_{21}&= \Pr \{\text{Ambulance 2 free}\;\vert \; \text{one ambulance free}\}\Pr \{\text{one ambulance free}\} \\&= 0.5 \times 0.4 \end{array}$$

(0.2)

By symmetry, f ₁₁ = f ₂₂ and f ₁₂ = f ₂₁. Observe that the probability of the closest ambulance responding is the same (1 − p) as in the binomial model, but the probability of the second-closest ambulance responding is different, because the Erlang B model incorporates dependence—essentially, given that Ambulance 1 is busy, the probability that Ambulance 2 is busy (0.2/(0.2 + 0.2) = 0.5) is higher than the average busy fraction (p = 0. 4).

Next, I use the Hypercube Queueing Model (HQM, [35]) to compute the dispatch probabilities. Unlike the models I have considered so far, the HQM views the two ambulances as distinguishable, taking into account that 80% of the arrivals are to the Station 2 catchment area and that Ambulance 2 is therefore likely to be busier than Ambulance 1. The HQM dispatch probabilities are obtained by computing the steady-state probabilities for the Markov chain shown in Fig. 6.12; they are shown, together with the dispatch probabilities from all the models, in Table 6.2.

Fig. 6.12

Transition diagram for the Hypercube Queueing Model

Table 6.2 Dispatch probabilities

The HQM assumes that every ambulance returns to its home station at the conclusion of every call. The final model that I discuss (introduced in [1]) assumes instead that ambulances are repositioned based on the compliance table shown in Fig. 6.13, which indicates that when only one of the two ambulance is free, that ambulance should ideally be located at Station 2 (because Station 2’s catchment area has a higher call rate). This Markov chain model, the transition diagram of which is shown in Fig. 6.13, has one state variable for the number of busy ambulances and another state variable indicating if the system is “in compliance.” When the system is out of compliance, I assume that an ambulance is moved to another station, an action that takes 6 min on average, implying that the “rate of reaching compliance” is γ = 10 per hour.

Fig. 6.13

Transition diagram for the repositioning model

Table 6.2 shows the dispatch probabilities and the code red probabilities B, as computed with each of the five performance evaluation models. The bottom row of the table also shows a possible performance measure, which could be thought of as the probability that the response time R is within some time standard—that is,

$${p}_{ij} =\Pr \{ R \leq \text{ time standard }\vert \text{ station }i\text{ responds, call from location }j\}.$$

I show the conditional performance estimate for each combination of call location and ambulance location at the bottom of the table, and display the system-wide expected performance in the rightmost column. The system-wide performance is computed using

$$\mathrm{ Performance} ={ \sum \limits_{j=1}^{2}}\frac{{\lambda }_{j}} {\lambda } {\sum \limits_{i=1}^{2}}{f}_{ ij}{p}_{ij}\;.$$

The optimistic “always available” model provides an upper bound on performance. The Erlang B model predicts lower performance than the binomial model does, because the dependence between the statuses of Ambulances 1 and 2 leads to a higher code red probability. The HQM predicts lower performance than the Erlang B model does because the HQM incorporates the inefficiencies that result from the demand imbalance between the catchment areas for Stations 1 and 2, which leads to better performance for the low-demand Station 1 region and worse performance for the high-demand Station 2 region. The repositioning strategy is intended to address this imbalance by favoring Station 2 when only one ambulance is available. We see that repositioning is predicted to increase the performance by 5 percentage points, compared to the “return to home station” that is implicit in the HQM.

The operation of the system is held constant in the first four rows of Table 6.2, and changes in estimated performance are therefore attributable to improved model realism as one moves down the rows in the table. In contrast, the performance estimates for the last two rows show the impact of changing the way the system operates, by repositioning ambulances based on the system state. The first four models represent different trade-offs between model tractability and accuracy. The HQM has a state space the size of which increases exponentially with the number of ambulances, rendering that model intractable for systems with more than 36 ambulances [4, online supplement], based on typical computer storage capacities available in 2009, but approximate versions of the HQM [36, 31, 4] improve its scalability. The simpler “always available” and binomial models have been used in station planning and ambulance allocation optimization models, in order to make it possible to formulate and solve the models as mathematical programs. Incorporating the HQM into a mathematical program is difficult, but the HQM can be incorporated into optimization heuristics, such as the tabu search heuristic discussed in [13]. The “always available” model remains relevant because it facilitates decoupling station planning models from ambulance allocation models, as discussed in Sec. 6.5.1.

The repositioning model is more scalable than the HQM, with a state space that grows only linearly with the number of ambulances. As an example of the benefits of repositioning policies in a real system, a simulation study of the Edmonton, Canada EMS system [14] estimated that the use of repositioning increased the percentage of urgent calls reached in 9 min or less from 77% to 85%. Repositioning policies do increase workload for EMS staff, which may lead to back problems [45] and increased fatigue, but these potential impacts require further investigation. Studnek et al. [55] linked back pain among EMS professionals to various factors, but failed to find a statistically significant relationship with call volume.

5 Station Planning and Ambulance Allocation

Having discussed the prediction of EMS model inputs, EMS performance measures, and models to predict performance, I now turn to optimization models designed to help planners decide where ambulance stations should be located and how to assign ambulances and their crews to stations. The choice of locations for ambulance stations is a long-term decision, but the assignment of ambulances to stations can change over time to provide a better match for supply and demand on a timescale of days and hours.

5.1 Station Planning

By ambulance station, I mean a structure in which ambulances can be stored, cleaned, and restocked with medical supplies. Ambulance crews typically begin and end their shifts at an ambulance station and return to an ambulance station between calls. There are exceptions, however. In some systems, ambulance crews wait for their next call in locations with no dedicated infrastructure. Other systems have a single start station [30, 48], in order to increase efficiency in maintenance and inventory.

I choose to focus on the typical situation, in which planners must decide where to build ambulance stations. Perhaps the best-known model for this purpose is the MCLP [8], which selects locations for q stations so as to maximize the proportion of demand within a coverage distance standard of the closest station. This model is based on several assumptions, including:

• A coverage distance standard is an adequate proxy for a coverage time standard. This assumption is relatively easy to relax—see the MCLP with probabilistic response times (MCLP + PR) [11, 16].

• The system is to be designed from scratch. This assumption is also easy to relax, by adding constraints to the MCLP or MCLP + PR integer program to account for preexisting stations.

• Every station has an available ambulance at all times. This assumption implies that the coverage values obtained from the MCLP and the MCLP + PR are upper bounds on the coverage that can be achieved with a finite number of ambulances. Such models as the MEXCLP [10], which relax this assumption, can be seen as combining station planning and the allocation of ambulances to stations.

• All ambulance responses start from a station. In reality, however, ambulances often respond while in transit.

Using the MCLP, the MCLP + PR, or other similar optimization problem formulations to inform EMS station planning requires not only reliable data but also good judgment [24]. How does one choose the potential station locations, for example? If a municipality-operated EMS service constrains itself to locations with publicly owned land where current zoning allows the building of EMS stations, then the list of possible sites could be very short. It could be worthwhile to include more potential sites and use the model to quantify the amount by which EMS response times could be reduced by relaxing zoning regulations. Conversely, when EMS operates separately from fire services, but the fire service provides first response to EMS calls, one should perhaps include the current fire station locations and use the model to find a set of EMS station locations that complement the fire stations in a way that minimizes first response times.

Station planning and ambulance allocation are closely linked: on the one hand, station locations constrain the way in which ambulances can be deployed. On the other hand, the way in which ambulances are deployed determines the performance of a plan that indicates where stations should be located. According to one point of view, one should therefore develop models that simultaneously optimize station locations and ambulance allocation. Another point of view is that it is natural and appropriate to separate the two, given that station planning is a strategic issue, whereas ambulance allocation is a tactical and operational issue. Furthermore, integrated models may oversimplify ambulance allocation, because they do not take into consideration how the allocation should change as a function of day of the week and hour of the day in order to match demand patterns, for example.

5.2 Ambulance Allocation

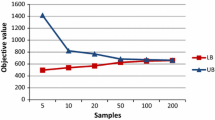
Notwithstanding the need to consider how ambulance allocation should vary with time to match daily and weekly demand patterns, I begin by discussing optimization models for allocating ambulances to stations in a static situation. These models are based on the assumption that every ambulance will return to the station to which it has been assigned at the conclusion of every call. Several such models are compared in [16] the MCLP, the MCLP + PR, the MEXCLP, and variations of MEXLCP that incorporate probabilistic response times and busy probabilities that vary by station. Figure 6.14 shows how expected coverage, as evaluated using the approximate hypercube model and incorporating stochastic response times, varies as the number of ambulances that are allocated to a set of 16 stations increases from 1 to 25. The more realistic models result in expected coverage that is considerably higher, especially when the number of ambulances is larger than the number of stations.

Fig. 6.14

Expected coverage for various ambulance allocation models, evaluated using the approximate hypercube model. MCLP, maximum coverage location problem; MEXCLP, maximum expected coverage location problem; PR, probabilistic response times; SSBP, station-specific busy probabilities (from [16])

All the models that [16] compare are formulated as mathematical programs, and such formulations require some simplifications. Alternatively, one can formulate the problem more directly, as follows:

$$\begin{array}{lll} P\text{ : maximize}\ & \text{cov}({z}_{1},\ldots,{z}_{n}), \\\text{ subject to}\ & {\sum \limits _{i=1}^{n}}{z}_{ j} = q;\ {z}_{j} \in \{ 0,\ldots,{c}_{j}\}\;, \\\end{array}$$

where cov(. ) is the expected coverage, evaluated with the approximate hypercube model, for example; c _j and z _j are the capacity and the number of ambulances assigned to station j, respectively; n is the number of stations; and q is the number of ambulances to be allocated. Erdogan et al. [13] describe a tabu search heuristic to solve this problem, and report that the tabu search finds better solutions in less time than does the mathematical programming-based heuristic discussed in [16].

Erdogan et al. [13] present one way of planning ambulance deployment over a weekly time horizon. First, solve problem P repeatedly, for each hour of the week and for every possible total number of ambulances, in order to generate expected coverage curves like those shown in Fig. 6.15. Note that the input data for the instances of P that are solved at this stage will reflect differences in average call volume by hour of the week, and can also reflect other predictable changes in the spatial distribution of calls or in travel speeds, for example. Second, incorporate the maximum expected coverage values from the first stage into a linear integer program that simultaneously determines how many ambulances to assign for each hour of the week and weekly shifts for the ambulance crews. The solutions to P for each hour of the week specify the way to allocate the ambulances to stations. This procedure is an example of preplanned repositioning. Other examples of models for preplanned repositioning include [50, 49, 52].

Fig. 6.15

Expected number of covered calls as a function of number of ambulances (based on [16]

Finally, I mention the currently active research topic of repositioning based on the system state, or real-time repositioning, which involves EMS dispatchers moving ambulances in real time to fill “holes” in coverage. In Sect. 6.4, I mentioned compliance table policies for real-time repositioning and a Markov chain model to analyze the performance of these policies. Other researchers have investigated the use of approximate dynamic programming to find optimal repositioning policies—see [41, 51], for example.

Some of the issues regarding repositioning that could benefit from further study include:

• If and how to integrate preplanned and real-time repositioning: All the work done so far focuses on either preplanned or real-time repositioning (although the approximate dynamic programming approach used in [41] could, in principle, incorporate both types of repositioning).

• Trade-off between improvement in performance and increase in workload: Workload is increased by repositioning, especially when done in real time for ambulance crews that are currently idle at a station. Empirical work could clarify whether the increased workload increases fatigue, back pain, job satisfaction, or has other undesirable consequences. Further modeling work could lead to tools to help dispatchers decide if the increase in coverage resulting from a potential ambulance move outweighs the increased workload.

• Suboptimality of compliance table policies: Compliance tables are already used in practice for real-time repositioning, and they are simple to explain and to use. Approximate dynamic programming approaches, which do not restrict the form of real-time repositioning policies, could be used to investigate the performance loss resulting from the use of a compliance table policy and to determine if compliance table policies are optimal in some situations.

6 Conclusions and Policy Implications

The amount and scope of OR/MS research on EMS planning and management have grown rapidly in recent years, perhaps fueled by the increased availability of detailed EMS call data and persistent pressure on EMS providers to operate more efficiently. Availability of EMS call data makes it possible to investigate the accuracy of modeling assumptions used in the past and to improve understanding of the way EMS systems operate. Although it is valuable to question modeling assumptions and although computing power continues to increase, modelers should not forget about parsimony and tractability. An ideal model is one that is no more complicated than necessary to shed light on the health-care decisions or issues that prompted the development or use of the model. A more realistic model is not always a more useful model.

Although EMS data are more readily available than ever, the data collected are not always the ideal data for informing the decisions of EMS planners. EMS call data reports the journey of a patient from the moment the EMS agency receives a call until EMS staff complete their care or until they transfer care to another part of the health-care system. Linking EMS data to information about what happened to the patient before and after the EMS call is necessary in order to develop and track performance measures that emphasize medical outcomes rather than response times. A greater focus on medical outcomes could help planners and policy makers compare the consequences of competing uses of funds, particularly in jurisdictions where EMS is part of a publicly funded health-care system. Measures of medical outcomes, such as survival probabilities, can typically be incorporated into existing EMS planning models without greatly complicating them, so the challenge lies in collecting and analyzing the appropriate data—not in model formulation and solution. Linking patient data collected by different agencies also presents challenges in safeguarding patient privacy and confidentiality. In the absence of reliable information about outcome measures, models that incorporate response-time variability appear to provide better proxies for outcome measures than do models based on deterministic distance-based coverage.