Keywords

58.1 Introduction

Building an effective method to capture shock waves that has been an important part of the study in computational fluid dynamics (CFD) field [1]. John Von Neumann first proposed the use of artificial viscosity method to capture shock,and the method of artificial viscosity is still one of the core in the CFD. The emergence of artificial viscosity means losting the part of information, and lowering the computational accuracy. For the non-physical oscillations problems generated near the shock wave, Harten [2–4] proposed the total variation difference scheme- the concept of TVD scheme, which the total variation is decreasing,and constructed the specifical TVD scheme with second order accuracy. meanwhile, Steger and Warming [5] proposed a new class of upwind scheme—vector splitting scheme (FVS scheme). Steger-Warming splitting method are often used by other schemes to better capture the shock wave for its characteristics of high efficiency and easy to program. The difference method that can automatically capture the shock wave is proposed based on the combination of improved Steger-Warming splitting method and NND scheme. The algorithm maintained the characteristics of high efficiency and easy to program that Steger-Warming splitting method have had, and overcomed the numerical oscillation near the shock wave that in Steger-Warming splitting method, and had accuracy and maneuverability. Method proposed in this paper have some reference value to the calculation of vector splitting.

58.2 The FVS Split of Euler Equations

58.2.1 Euler Equations

Conservation form of two-dimensional Euler equations [6] are:

$$ \frac{\partial U}{\partial t} + \frac{\partial F}{\partial x} + \frac{\partial G}{\partial y} = 0 $$
(58.1)

Which \( U = \left( \begin{gathered} \rho \hfill \\ \rho u \hfill \\ \rho v \hfill \\ E \hfill \\ \end{gathered} \right),F = \left( \begin{array}{c} \rho u \\ \rho u^{2} + p \\ \rho uv \\ (E + p)u \\ \end{array} \right),G = \left( \begin{array}{c} \rho v \\ \rho vu \\ \rho v^{2} + p \\ (E + p)v \\ \end{array} \right), \) Therein \( E = \frac{p}{\gamma - 1} + \frac{1}{2}\rho (u^{2} + v^{2} ),a = \sqrt {\frac{\gamma p}{\rho }} ,H = \frac{E + p}{\rho } = \frac{1}{2}(u^{2} + v^{2} ) + \frac{{a^{2} }}{\gamma - 1} = \frac{1}{2}(u^{2} + v^{2} ) + \frac{\gamma p}{(\gamma - 1)\rho } \).

58.2.2 Flux Vector Splitting Technique

Jacobian matrix is

$$ A = \frac{\partial F}{\partial U} = \left( {\begin{array}{*{20}c} 0 & 1 & 0 & 0 \\ {\frac{1}{2}(\gamma - 3)u^{2} + \frac{1}{2}(\gamma - 1)v^{2} } & {(3 - \gamma )u} & {(1 - \gamma )v} & {\gamma - 1} \\ { - uv} & v & u & 0 \\ {\frac{1}{2}(\gamma - 2)(u^{3} + uv^{2} ) - \frac{{a^{2} u}}{(\gamma - 1)}} & {\frac{1}{2}(3 - 2\gamma )u^{2} + \frac{1}{2}v^{2} + \frac{{a^{2} }}{(\gamma - 1)}} & {(1 - \gamma )uv} & {\gamma u} \\ \end{array} } \right)\,\,,B = \frac{\partial G}{\partial U} = \left( {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ {uv} & v & u & 0 \\ {\frac{1}{2}(\gamma - 1)u^{2} - \frac{1}{2}(\gamma - 3)v^{2} } & {(1 - \gamma )u} & {(3 - \gamma )v} & {\gamma - 1} \\ {\frac{1}{2}(\gamma - 2)(v^{3} + u^{2} v) - \frac{{a^{2} v}}{(\gamma - 1)}} & {(1 - \gamma )uv} & {\frac{1}{2}(3 - 2\gamma )v^{2} + \frac{1}{2}u^{2} + \frac{{a^{2} }}{(\gamma - 1)}} & {\gamma v} \\ \end{array} } \right) $$
(58.4)

Matrix A and B were similarly transformed respectively as follows:

$$ A = M\Uplambda_{1} M^{ - 1} ,B = N\Uplambda_{2} N^{ - 1} $$
(58.5)

Therein, the expressions of eigenvalues matrices is respectively:

$$ \Uplambda_{1} = diag[u, \, u,{\text{ u + a, u}}\text{a} -\text{a}],\Uplambda_{2} = diag[v,{\text{ v}},{\text{ v + a, v}} -\text{a}] $$
(58.6)

Therein \( \lambda_{1}^{(1)} = \lambda_{1}^{(2)} = u,\lambda_{1}^{(3)} = u + a,\lambda_{1}^{(4)} = u - a;\lambda_{2}^{(1)} = \lambda_{2}^{(2)} = v,\lambda_{2}^{(3)} = v + a,\lambda_{2}^{(4)} = v - a \)

The left and right eigenvector matrices of A and B are respectively:

$$ M = \left( {\begin{array}{*{20}c} 1 & 0 & {\frac{\rho }{\sqrt 2 a}} & {\frac{\rho }{\sqrt 2 a}} \\ u & 0 & {\frac{\rho }{\sqrt 2 a}(u + a)} & {\frac{\rho }{\sqrt 2 a}(u - a)} \\ v & { - \rho } & {\frac{\rho v}{\sqrt 2 a}} & {\frac{\rho v}{\sqrt 2 a}} \\ {\frac{1}{2}(u^{2} + v^{2} )} & { - \rho v} & {\frac{\rho }{2\sqrt 2 a}(u^{2} + v^{2} ) + \frac{\rho a + \rho u(\gamma - 1)}{\sqrt 2 (\gamma - 1)}} & {\frac{\rho }{2\sqrt 2 a}(u^{2} + v^{2} ) + \frac{\rho a - \rho u(\gamma - 1)}{\sqrt 2 (\gamma - 1)}} \\ \end{array} } \right)\,\,\,\,M^{ - 1} = \left( {\begin{array}{*{20}c} {1 - \frac{(\gamma - 1)}{{2a^{2} }}(u^{2} + v^{2} )} & {\frac{(\gamma - 1)u}{{a^{2} }}} & {\frac{(\gamma - 1)v}{{a^{2} }}} & {\frac{(1 - \gamma )}{{a^{2} }}} \\ {\frac{v}{\rho }} & 0 & { - \frac{1}{\rho }} & 0 \\ {\frac{(\gamma - 1)}{2\sqrt 2 \rho a}(u^{2} + v^{2} ) - \frac{u}{\sqrt 2 \rho }} & {\frac{1}{\sqrt 2 \rho } - \frac{(\gamma - 1)u}{\sqrt 2 \rho a}} & { - \frac{(\gamma - 1)v}{\sqrt 2 \rho a}} & {\frac{(\gamma - 1)}{\sqrt 2 \rho a}} \\ {\frac{(\gamma - 1)}{2\sqrt 2 \rho a}(u^{2} + v^{2} ) + \frac{u}{\sqrt 2 \rho }} & { - \frac{1}{\sqrt 2 \rho } - \frac{(\gamma - 1)u}{\sqrt 2 \rho a}} & { - \frac{(\gamma - 1)v}{\sqrt 2 \rho a}} & {\frac{(\gamma - 1)}{\sqrt 2 \rho a}} \\ \end{array} } \right) $$
(58.7)
$$ N^{ - 1} = \left( {\begin{array}{*{20}c} {1 - \frac{(\gamma - 1)}{{2a^{2} }}(u^{2} + v^{2} )} & {\frac{(\gamma - 1)u}{{a^{2} }}} & {\frac{(\gamma - 1)v}{{a^{2} }}} & {\frac{(1 - \gamma )}{{a^{2} }}} \\ { - \frac{u}{\rho }} & {\frac{1}{\rho }} & 0 & 0 \\ {\frac{(\gamma - 1)}{2\sqrt 2 \rho a}(u^{2} + v^{2} ) - \frac{v}{\sqrt 2 \rho }} & {\frac{(1 - \gamma )u}{\sqrt 2 \rho a}} & {\frac{1}{\sqrt 2 \rho } - \frac{(\gamma - 1)v}{\sqrt 2 \rho a}} & {\frac{(\gamma - 1)}{\sqrt 2 \rho a}} \\ {\frac{(\gamma - 1)}{2\sqrt 2 \rho a}(u^{2} + v^{2} ) + \frac{v}{\sqrt 2 \rho }} & {\frac{(1 - \gamma )u}{\sqrt 2 \rho a}} & { - \frac{1}{\sqrt 2 \rho } - \frac{(\gamma - 1)v}{\sqrt 2 \rho a}} & {\frac{(\gamma - 1)}{\sqrt 2 \rho a}} \\ \end{array} } \right)\,\,\,\,\,\,N = \left( {\begin{array}{*{20}c} 1 & 0 & {\frac{\rho }{\sqrt 2 a}} & {\frac{\rho }{\sqrt 2 a}} \\ u & \rho & {\frac{\rho }{\sqrt 2 a}u} & {\frac{\rho }{\sqrt 2 a}u} \\ v & 0 & {\frac{\rho }{\sqrt 2 a}(v + a)} & {\frac{\rho }{\sqrt 2 a}(v - a)} \\ {\frac{1}{2}(u^{2} + v^{2} )} & {\rho u} & {\frac{\rho }{2\sqrt 2 a}(u^{2} + v^{2} ) + \frac{\rho a + \rho v(\gamma - 1)}{\sqrt 2 (\gamma - 1)}} & {\frac{\rho }{2\sqrt 2 a}(u^{2} + v^{2} ) + \frac{\rho a - \rho v(\gamma - 1)}{\sqrt 2 (\gamma - 1)}} \\ \end{array} } \right) $$
(58.8)

There are the following relationships between the matrix M and N

$$ C = M^{ - 1} N = \left( {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 0 & { - 1/\sqrt 2 } & {1/\sqrt 2 } \\ 0 & {1/\sqrt 2 } & {1/2} & {1/2} \\ 0 & { - 1/\sqrt 2 } & {1/2} & {1/2} \\ \end{array} } \right),C^{ - 1} = N^{ - 1} M = \left( {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 0 & {1/\sqrt 2 } & { - 1/\sqrt 2 } \\ 0 & { - 1/\sqrt 2 } & {1/2} & {1/2} \\ 0 & {1/\sqrt 2 } & {1/2} & {1/2} \\ \end{array} } \right) $$
(58.9)

From formular (58.12) a can be seen that matrix C and \( C^{ - 1} \) has nothing to do with flow variables.

Now splitting the flux vector,and first, the eigenvalues of Jacobian matrix,that are \( \lambda_{1}^{(l)} ,\,\lambda_{2}^{(l)} , \) split the sum form of two:

$$ \lambda_{1}^{(l)} = \lambda_{1}^{(l) + } + \lambda_{1}^{(l) - } { ; }\lambda_{1}^{(l) + } \ge 0{ , }\lambda_{1}^{(l) - } \le 0;\lambda_{2}^{(l)} = \lambda_{2}^{(l) + } + \lambda_{2}^{(l) - } { ; }\lambda_{2}^{(l) + } \ge 0{ , }\lambda_{2}^{(l) - } \le 0\,\,\,\,\,\,\,\,\,l = 1, 2 , 3 , 4 $$
(58.10)

According to flux vector splitting method

$$ \lambda_{1}^{(l) \pm } = (\lambda_{1}^{(l)} \pm |\lambda_{1}^{(l)} |)/2;\lambda_{2}^{(l) \pm } = (\lambda_{2}^{(l)} \pm |\lambda_{2}^{(l)} |)/2 $$
(58.11)

Thus, the eigenvalues matrix after splitting are respectively:

$$ \Uplambda_{1}^{ \pm } = diag[\lambda_{1}^{(1) \pm } , \, \lambda_{1}^{(2) \pm } , \, \lambda_{1}^{(3) \pm } , \, \lambda_{1}^{(4) \pm } ];\Uplambda_{2}^{ \pm } = diag[\lambda_{2}^{(1) \pm } , \, \lambda_{2}^{(2) \pm } , \, \lambda_{2}^{(3) \pm } , \, \lambda_{2}^{(4) \pm } ] $$
(58.12)

And the corresponding Jacobian matrices after splitting are respectively:

$$ A^{ \pm } = M\Uplambda_{1}^{ \pm } M^{ - 1} ,B^{ \pm } = N\Uplambda_{2}^{ \pm } N^{ - 1} $$
(58.13)

The corresponding flux vector can be obstained in the end after splitting

$$ F^{ \pm } = A^{ \pm } U,G^{ \pm } = B^{ \pm } U $$
(58.14)

The expressions as follows:

$$ F^{ + } = \frac{\rho }{2\gamma }\left( \begin{gathered} \lambda_{1}^{(4) + } + 2(\gamma - 1)\lambda_{1}^{(2) + } + \lambda_{1}^{(3) + } \hfill \\ (u - a)\lambda_{1}^{(4) + } + 2(\gamma - 1)u\lambda_{1}^{(2) + } + (u + a)\lambda_{1}^{(3) + } \hfill \\ v\lambda_{1}^{(4) + } + 2(\gamma - 1)v\lambda_{1}^{(2) + } + v\lambda_{1}^{(3) + } \hfill \\ (H - ua)\lambda_{1}^{(4) + } + (\gamma - 1)(u^{2} + v^{2} )\lambda_{1}^{(2) + } + (H + ua)\lambda_{1}^{(3) + } \hfill \\ \end{gathered} \right)\,\,\,\,\,F^{ - } = \frac{\rho }{2\gamma }\left( \begin{gathered} \lambda_{1}^{(4) - } + 2(\gamma - 1)\lambda_{1}^{(2) - } + \lambda_{1}^{(3) - } \hfill \\ (u - a)\lambda_{1}^{(4) - } + 2(\gamma - 1)u\lambda_{1}^{(2) - } + (u + a)\lambda_{1}^{(3) - } \hfill \\ v\lambda_{1}^{(4) - } + 2(\gamma - 1)v\lambda_{1}^{(2) - } + v\lambda_{1}^{(3) - } \hfill \\ (H - ua)\lambda_{1}^{(4) - } + (\gamma - 1)(u^{2} + v^{2} )\lambda_{1}^{(2) - } + (H + ua)\lambda_{1}^{(3) - } \hfill \\ \end{gathered} \right) $$
(58.15)
$$ G^{ + } = \frac{\rho }{2\gamma }\left( \begin{gathered} \lambda_{2}^{(4) + } + 2(\gamma - 1)\lambda_{2}^{(2) + } + \lambda_{2}^{(3) + } \hfill \\ u\lambda_{2}^{(4) + } + 2(\gamma - 1)u\lambda_{2}^{(2) + } + u\lambda_{2}^{(3) + } \hfill \\ (v - a)\lambda_{2}^{(4) + } + 2(\gamma - 1)v\lambda_{2}^{(2) + } + (v + a)\lambda_{2}^{(3) + } \hfill \\ (H - va)\lambda_{2}^{(4) + } + (\gamma - 1)(u^{2} + v^{2} )\lambda_{2}^{(2) + } + (H + va)\lambda_{2}^{(3) + } \hfill \\ \end{gathered} \right)\,\,\,\,\,G^{ - } = \frac{\rho }{2\gamma }\left( \begin{gathered} \lambda_{2}^{(4) - } + 2(\gamma - 1)\lambda_{2}^{(2) - } + \lambda_{2}^{(3) - } \hfill \\ u\lambda_{2}^{(4) - } + 2(\gamma - 1)u\lambda_{2}^{(2) - } + u\lambda_{2}^{(3) - } \hfill \\ (v - a)\lambda_{2}^{(4) - } + 2(\gamma - 1)v\lambda_{2}^{(2) - } + (v + a)\lambda_{2}^{(3) - } \hfill \\ (H - va)\lambda_{2}^{(4) - } + (\gamma - 1)(u^{2} + v^{2} )\lambda_{2}^{(2) - } + (H + va)\lambda_{2}^{(3) - } \hfill \\ \end{gathered} \right) $$
(58.16)

The derivative of positive and negative flux is noncontinuous near the sign reversal point of Eigenvalue [5], and leading the flux vector splitting methods not to be transited smoothly. Therefore, turn flux F, G into continuous function of \( \lambda_{1}^{(3)} ,\,\lambda_{1}^{(4)} ,\,\lambda_{1}^{(3)} \) and \( \lambda_{2}^{(4)} . \)

$$ {\text{Assumed}}\,\,\lambda_{1}^{(2) \pm } = (\lambda_{1}^{(3) \pm } + \lambda_{1}^{(4) \pm } )/2;\lambda_{2}^{(2) \pm } = (\lambda_{2}^{(3) \pm } + \lambda_{2}^{(4) \pm } )/2 $$
(58.17)

So far,we have been completed splitting the flux F, G.

58.3 NND Scheme in Two-Demensional and New Scheme

The NND scheme [7] is a computational scheme that has a non-volatile, no free parameters characeristics, and can effectively suppress numerical calculation oscillation. From the modified equation in the scheme, different schemes were used according to the location of relative break points, and physical meaning is clear. For Eq. (58.1), Explicit scheme of NND scheme can be expressed as follows:

$$ U_{i,j}^{n + 1} = U_{i,j}^{n} - \frac{\Updelta t}{\Updelta x}(\overline{F}_{i + 1/2}^{n} - \overline{F}_{i - 1/2}^{n} ) - \frac{\Updelta t}{\Updelta y}(\overline{G}_{j + 1/2}^{n} - \overline{G}_{j - 1/2}^{n} ) $$
(58.18)

Therein

$$ \begin{gathered} \overline{F}_{i + 1/2} = F_{i + 1/2,L}^{ + } + F_{i + 1/2,R}^{ - } ,F_{i + 1/2,L}^{ + } = F_{i,j}^{ + } + \frac{1}{2}\min \bmod (\Updelta F_{i - 1/2,j}^{ + } , \, \Updelta F_{i + 1/2,j}^{ + } ) \hfill \\ F_{i + 1/2,R}^{ - } = F_{i + 1,j}^{ - } - \frac{1}{2}\min \bmod (\Updelta F_{i + 1/2,j}^{ - } , \, \Updelta F_{i + 3/2,j}^{ - } ),\Updelta F_{i + 1/2,j}^{ + } = F_{i + 1,j}^{ + } - F_{i,j}^{ + } ,\Updelta F_{i + 1/2,j}^{ - } = F_{i + 1,j}^{ - } - F_{i,j}^{ - } \hfill \\ \overline{G}_{j + 1/2} = G_{L,j + 1/2}^{ + } + G_{R,j + 1/2}^{ - } ,G_{L,j + 1/2}^{ + } = G_{i,j}^{ + } + \frac{1}{2}\min \bmod (\Updelta G_{i,j - 1/2}^{ + } , \, \Updelta G_{i,j + 1/2}^{ + } ),G_{R,j + 1/2}^{ - } = G_{i,j + 1}^{ - } - \frac{1}{2}\min \bmod (\Updelta G_{i,j + 1/2}^{ - } , \, \Updelta G_{i,j + 3/2}^{ - } ) \hfill \\ \Updelta G_{i,j + 1/2}^{ + } = G_{i,j + 1}^{ + } - G_{i,j}^{ + } ,\Updelta G_{i,j + 1/2}^{ - } = G_{i,j + 1}^{ - } - G_{i,j}^{ - } \hfill \\ \end{gathered} $$
$$ \min \bmod (x,y) = \left\{ \begin{gathered} 0{\text{ x}} \cdot {\text{y}} \le 0\hfill \\ {\text{sign(x)}} \cdot {\text{min(|x|,|y|) x}} \cdot {\text{y}} > 0 \hfill \\ \end{gathered} \right. $$

In summary, formular (58.15, 58.16) and (58.18) are the difference method combining the improved Steger-Warming flux vector splitting.

58.4 Numerical Experiments

The calculation of the flow field in shock wave Pipe is the common example to test ability in capturing the shock wave. The answer to this problem can compare to the Riemann’s analytical solution [8]. The initial equation is 2-dimensional unconstant Euler equations (58.1), the initial conditions are uniform flow field.

Inlet conditions: the inlet density \( \rho = 1.0, \) mach number \( Ma = 2.9, \) inlet angle \( \beta_{1} = 29, \) inlet total pressure \( p = 1.0, \) air specific heat ratio \( \gamma = 1.4. \) Outlet condition:

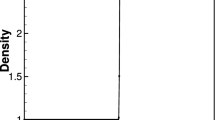
$$ \frac{\partial p}{\partial x} = \frac{\partial \rho }{\partial x} = \frac{\partial u}{\partial x} = \frac{\partial v}{\partial x} = 0 $$

The pressure distribution of \( y = 0.5 \) is shown in Fig. 58.1. From Fig. 58.1 can be seen that: The computational scheme that constructed by combination of Steger-Warming splitting vector method and the NND scheme has good ability in capturing shock wave,the calculated results and the theoretical values are in good agreement, and there is no calculated value oscillation appeared near shock wave.

Fig. 1
figure 1

The pressure distribution of \( y = 0.5 \)

Full size image

58.5 Conclusion

Steger-Warming flux vector splitting scheme is becoming the first choice in CFD calculations because of its high precision and efficiency in for numerical calculation of Euler equations, the Steger-Warming flux vector splitting scheme is improved in this paper and make the scheme transit smoothly near the sign reversal point of Eigenvalue. A differential algorithm is constituted by combined the improved Steger-Warming flux vector splitting scheme and the NND scheme, the flux decomposition term in NND scheme is processed by Steger-Warming flux vector splitting method,so that algorithm has higher efficiency. By solving the two-dimensional Euler equations, numerical experiment results can be verified that differentiate scheme can inhibit oscillations and maintain precision and stability, ensure that the shock wave in flow field is captured effectively. Method used in this paper has some reference value about the calculation of flux vector splitting.