Perspectives on Children’s Fraction Knowledge

Abstract

The separation of the study of whole numbers and fractions is historical and contributes to the legendary difficulty children experience in the learning of fractions that inspired Davis et al. (1993) to comment that “the learning of fractions is not only very hard, it is, in the broader scheme of things, a dismal failure” (p. 63). I cite Davis et al. not because I believe that the teaching and learning of fractions is by necessity a dismal failure, but rather to accentuate the historical difficulties children experience in learning fractions in mathematics education. These difficulties are quite unsettling because they have been known for a long time. For example, in his famous study on the grade placement of arithmetical topics, Washburne (1930, p. 669) reported that a mental age level of 9 years should be attained by children if at least three out of four of them are to make the very modest mastery represented by a retention test score of 80% on the meaning of “nongrouping” fractions. But, in the case of “grouping” fractions, the analogous mental age was 11 years 7 months.¹

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

The separation of the study of whole numbers and fractions is historical and contributes to the legendary difficulty children experience in the learning of fractions that inspired Davis et al. (1993) to comment that “the learning of fractions is not only very hard, it is, in the broader scheme of things, a dismal failure” (p. 63). I cite Davis et al. not because I believe that the teaching and learning of fractions is by necessity a dismal failure, but rather to accentuate the historical difficulties children experience in learning fractions in mathematics education. These difficulties are quite unsettling because they have been known for a long time. For example, in his famous study on the grade placement of arithmetical topics, Washburne (1930, p. 669) reported that a mental age level of 9 years should be attained by children if at least three out of four of them are to make the very modest mastery represented by a retention test score of 80% on the meaning of “nongrouping” fractions. But, in the case of “grouping” fractions, the analogous mental age was 11 years 7 months.¹

An assessment of children’s mathematical development conducted 50 years later in England and Wales (Foxman et al. 1980) also indicates the difficulty children experience when learning fractions. In their Primary Survey Report, it is reported that only 42% of the 11-year-olds of the study could say that one-fourth of one-half of a piece of string was one-eighth of the whole string. And only 61% could make a reasonable estimate of what fraction of the pegs in a bag were white, where 15 where white and 45 colored. Any estimate between and including one-tenth and one-half was accepted. Moreover, Kerslake (1986) found that 13 and 14-year old students in England had a good idea of fractions as part of a whole, which is compatible with Washburne’s findings concerning “nongrouping fractions,” but only a fragile notion of fraction equivalence, which is compatible with Washburne’s findings concerning “grouping” fractions and with the findings from the Primary Survey Report (Foxman et al. 1980).

In spite of Kerslake’s findings that the concept of fractional equivalence is fragile even for 13 and 14-year olds, Smith’s (1987) mathematically appropriate belief that the equivalence class is the central concept in the mathematics of rational number unproblematically drives not only what is taught about fractions in the elementary school, but also what is taught about fractions in mathematics courses designed for elementary school teachers (Long and DeTemple 1996, p. 374). Believing that children’s mathematical knowledge corresponds to and can be explained by conventional mathematical concepts and operations, mathematics educators traditionally have regarded the content of children’s mathematical knowledge as fixed and a priori. In our view, this belief constitutes what Stolzenberg (1984) called a trap. According to Stolzenberg, a trap is a:

Closed system of attitudes, beliefs, and habits of thought for which one can give an objective demonstration that certain of the beliefs are incorrect and that certain of the attitudes and habits of thought prevent this from being recognized (p. 260).

Because children’s mathematical learning in school occurs in the specific context of teaching, it might seem to be reasonable to regard the content of children’s mathematical knowledge to be explained by conventional mathematical concepts such as fractional equivalence. However, several researchers working within a constructivist view of knowledge and reality have found it necessary to explain what students learn using constructs that differ significantly from standard mathematical concepts and operations (e.g., Confrey 1994; Kieren 1993; Thompson 1982, 1994; Steffe and Cobb 1988). I therefore seriously question the belief that school instruction should be based on concepts such as fractional equivalence.

On Opening the Trap

According to Stolzenberg (1984), it is indisputable that the contemporary mathematician operates within a belief system whose core belief is that mathematics is discovered rather than created or invented by human beings. This belief is equivalent to believing, as did Erdös, in a transfinite Book that contains the best proofs of all mathematical theorems (Hoffman 1987). Of course, this is a “mathematicians’ book,” and a belief in its existence apparently supports and sustains mathematical research for those who believe in it: “Mathematics is there. It’s beautiful. It’s the jewel we uncover” (p. 66).

Stolzenberg’s (1984) contention that mathematics is not discovered but invented is according to Watzlawick (1984), “one of the most fascinating aspects of Stolzenberg’s essay” (p. 254). It constitutes a shift in belief that is needed to open the trap because mathematicians’ belief in the Book is reenacted by mathematics educators concerning the books of contemporary school mathematics. The mathematics that is recorded in these books is usually regarded as a priori and as constituting what children are to learn. This assumption places the mathematics of schooling outside of the minds of the children who are to learn it, and it is manifest in the practice of separating the study of whole numbers and fractions between the discrete and the continuous as well as in the acceptance of concepts such as equivalent fractions as what children are to learn in school mathematics. School mathematics is regarded as a fixed nucleus, and one searches the school mathematics books in vain for mathematics of children.

Invention or Construction?

Stolzenberg’s view is compatible with an assumption I make in our work with children, but it is not identical. The first difference resides in the meaning of the terms “invented” and “constructed.” “To invent” implies the production of something unknown by the use of ingenuity or imagination. An invention certainly falls within the scope of what is meant by a construction, but the latter term implies conceptual productions within or as a result of interactions that I would not want to call inventions. Although any construction implies the production of a novelty, I would hesitate to call, for example, an association between two contiguous perceptual items (Guthrie 1942), an invention if for no other reason than many such associations are formed without forethought and sometimes even without the awareness of the associating individual. But I do regard associations as constructions regardless of the conditions of their formation (Steffe and Wiegel 1996). The boundary between the meanings of “to invent” and “to construct” is quite fuzzy, and it would certainly be counterproductive to insist that creative acts within this fuzzy boundary are exclusively one or the other. Nevertheless, making a distinction between the two provides a basis for a critique of the following rather restricted interpretation of constructivist learning.

In promulgating an active, constructive and creative view of learning, however, the constructivists painted the learner in close-up as a solo player, a lone scientist, a solitary observer, a meaning-maker in a vacuum.

(Renshaw 1992, p. 91)

Renshaw’s interpretation of constructivist learning is based almost exclusively on the interaction of constructs within the individual. Social interaction seems excluded, so his characterization of constructivist learning is more or less compatible with the perhaps restricted view that mathematicians invent mathematics without the benefit of interacting with other mathematicians. In contrast, I emphasize the constructing individual as a socially interactive being² as well as a self-organizing and maturing being (Steffe 1996).

First-Order and Second-Order Mathematical Knowledge

The second difference between Stolzenberg’s view and the constructivist view is apparent in Stolzenberg’s comment that “when I stress the importance of standpoint, I am not preaching any brand of relativism. I do not say that there is your truth and my truth and never the twain shall meet” (p. 260). In taking this position, Stolzenberg seemed to be saying that the mathematics produced by one mathematician could be judged by other mathematicians concerning its fallibility or viability. That is, he was basically concerned with first-order mathematical knowledge – the models an individual construct to organize, comprehend, and control his or her experience, i.e., their own mathematical knowledge. In our work, we are mainly concerned with second-order mathematical knowledge – the models observers may construct of the observed person’s knowledge (Steffe et al. 1983, p. xvi).

Distinguishing between first- and second-order mathematical knowledge (or models) is critical in avoiding a conflation between children’s mathematical concepts and operations and what has been established as conventional school mathematics. Traditionally, there has been little distinction between these two kinds of knowledge, and school mathematics is considered as first-order mathematical knowledge. In our framework, we regard “school mathematics” as a second-order mathematical knowledge – a model of children’s mathematics – rather than as the first-order model constituted by conventional school mathematics. Second-order models are constructed through social processes and I thereby refer to them as social knowledge. Regarding school mathematics as social knowledge is a fundamental shift in belief that is yet to be fully appreciated.

Mathematics of Children

We, as constructivist researchers, attribute mathematical knowledge to children that is independent of our own mathematical knowledge (Kieren 1993; Steffe and Cobb 1988; Steffe and Thompson 2000). Although the attribution of such knowledge to children is essential in their mathematical education, the first-order knowledge that constitutes children’s mathematics is essentially inaccessible to us as observers. By saying this, we do not mean that we do not try to construct children’s mathematical knowledge. Quite to the contrary, we spend a substantial part of our time, during and after teaching children, analyzing the mathematical knowledge that they bring to the learning situation as well as their evolving mathematical knowledge within the learning situation. What we do mean is that regardless of what the results of those analyses might be, we make no claim that the first-order models that constitute the children’s mathematics correspond piece-by-piece to what we have established as second-order models.

We will use the phrase “children’s mathematics” for whatever constitutes children’s first-order mathematical knowledge and “mathematics of children” to mean our second-order models of children’s mathematics. We regard the mathematics of children as legitimate mathematics to the extent that we find rational grounds for what children say and do mathematically. A shift in the belief of what should constitute school mathematics from conventional school mathematics to the mathematics that children do construct is foundational in opening the trap that has contributed to the historical difficulty in children’s learning of fractions. In fact, a primary goal of our work is to construct second-order models of children’s fractional knowledge that we are able to bring forth, sustain, and modify.

Mathematics for Children

I usually find it inappropriate to attribute even my most fundamental mathematical concepts and operations to children. For example, a set of elements arranged in order is a basic element in ordinal number theory. For a given number word, although children might establish a unit of units that they associate with that number word, I have not found sufficient warrant to infer that children constitute these composite units as ordered sets in the way I understand ordered sets (Steffe 1994a). The observer might regard the composite units that are attributed to the children as an early form of ordered sets, but to regard them as ordered sets would be a serious conflation of the conventional idea of an ordered set and our idea of a composite unit, which I have found useful in understanding children’s mathematics. Conventional mathematics, such as ordinal number theory, can be orienting, but it is not explanatory; it alone cannot be used to account for children’s numerical concepts and operations.

It might seem that the mathematics adults intend for children to learn remains unspecified. However, I regard mathematics for children as consisting of those concepts and operations that children might learn (Steffe 1988). But rather than regard these concepts as being a part of my own mathematical knowledge, I base mathematics for children on the mathematics that I have observed children actually learn. Essentially, mathematics for children cannot be specified a priori and must be experientially abstracted from the observed modifications children make in their mathematical activity. That is, mathematics for children can be known only through interpreting changes in children’s mathematical activity. Specifically, the mathematics for a group of children is initially determined by the modifications that other children have been observed to make whose mathematical behavior is like the current children. I call these observed modifications zones of potential construction for the children whom I am currently teaching.

A teacher may not have constructed zones of potential construction suitable for the children he or she is currently teaching. Even in that case, a hypothetical zone of potential construction can be posited by the teacher to serve as a guide in the selection of learning situations. As a result of actually interacting with the particular children, the hypothetical zone of potential construction is reconstituted to form a zone of actual construction. The two zones usually diverge, because in the course of actually interacting with the children, they may make unanticipated contributions and new situations of learning may need to be formulated. Through establishing actual zones of construction, new possibilities may arise and a new zone of potential construction may be posited.³ It is through such experimentation in teaching that children’s mathematics may emerge in the experience of the teacher. In short, we recognize the necessity to modify our models of children’s mathematics according to the children’s work. Teaching mathematics is adaptive: It is the responsibility of the teacher to construct mathematics of and for children in the teaching context.

Our own first-order mathematical knowledge does play fundamental roles in formulating the second-order models that we call the mathematics of children. Perhaps the most fundamental of these roles is in orienting us as we formulate mathematics for children and decide how to interact with them. Rather than elaborate on these roles here, we discuss them throughout the remainder of the book because the discussion is concentrated and content specific. My focus in the next sections of this chapter is on developing a central conceptual construct – scheme – that I use in building models of children’s mathematics.

Fractions as Schemes

Our use of the concept of scheme in building models of children’s fractional knowledge is essential if Freudenthal’s (1983) distinction between fractions and rational numbers is taken seriously.

Fractions are the phenomenological source of the rational number – a source that never dries up. “Fraction” – or what corresponds to it in other languages – is the word by which the rational number enters, and in all languages that I know it is related to breaking: fracture. (p. 134)

Freudenthal’s emphasis on fractions as the phenomenological source of the rational number is similar to Kieren’s (1993) idea that ethnomathematical know-ledge is at the center of mathematical knowledge building. In Kieren’s (1993) words, ethnomathematical knowledge is that kind of knowledge that children possess “because they have lived in a particular environment. For example, children have shared continuous quantities and described such shares; they have seen measurements being made using fractional numbers” (pp. 67–68).

I believe that ethnomathematical knowledge includes Freudenthal’s idea of fractions as the phenomenological source of rational number because, as Kieren emphasizes, it is a kind of knowing. In other words, to construct meaning for the term “fraction,” we look to what children say and do as a source of our construction of such meaning. We bring Freudenthal’s and Kieren’s emphases together through the notion of the scheme, which is a conceptual tool that we use to analyze children’s language and actions as they interact with us. That is, in our view, the evolving fractional knowledge of children consists of the construction of schemes of action and operation in their environments.

We describe schemes through observing children recurrently engage in goal-directed activity on several different occasions in what to us are related situations.⁴ These descriptions are usually interesting and often contain insightful behavior on the part of the child. For example, Kieren (1993) described three 7-year-old girls as characterizing one of seven children’s share of four pizzas in Fig. 2.1 as “a half and a bite.”

Fig. 2.1.

A sharing situation.

As researchers, it is our intention to go beyond this description in an attempt to understand and formulate plausible conceptual operations used by the children as they established one child’s share as “a half and a bite.” In this, I infer that the children’s assimilated situation, which involved a question of how much pizza one child would get as well as the picture of the seven children and the four pizzas, constitutes what I interpret as a sharing situation. This inference is based on the result of the children’s activity – “a half and a bite.” I infer that the children would need to establish a goal and engage in a sharing activity to reply as they did.

This intuitive understanding of the mental operations involved in sharing is enough to qualify the sharing activity as a scheme in the Piagetian sense if I could observe the three children engage in similar sharing activity in other situations. The necessity of inferring schemes based on repeatable and generalized action is based on Piaget’s (1980) definition of scheme as action “that is repeatable or generalized through application to new objects” (p. 24). Focusing only on the activity of sharing, however, does not provide a full account of the concept of scheme. von Glasersfeld (1980), in a reformulation of Piaget’s concept of scheme, described a scheme as an instrument of interaction and elaborated the concept in a way that opens the possibility of focusing on what may go on prior to observable action. It also opens the possibility that the action of a scheme is not sensory-motor action, but interiorized action that is executed with only the most minimal sensory-motor indication. Finally, it opens the possibility to focus on the results of the scheme’s action and how those results might close the child’s use of the scheme.

The Parts of a Scheme

According to von Glasersfeld (1980), a scheme consists of three parts. First, there is an experiential situation; an activating situation as perceived or conceived by the child, with which an activity has been associated. Second, there is the child’s specific activity or procedure associated with the situation. Third, there is a result of the activity produced by the child.⁵

“Schemes” are basic sequences of events that consist of three parts. An initial part that serves as trigger or occasion. In schemes of action, this roughly corresponds to what behaviorists would call “stimulus,” i.e., a sensory motor pattern. The second part, that follows upon it, is an action (“response”)… or an operation (conceptual or internalized activity). … The third part is … what I call the result or sequel of the activity (and here, again, there is a rough and only superficial correspondence to what behaviorists call “reinforcement”). (p. 81)

Unlike the stimulus in the stimulus-response theory, then, the situation of a scheme is an experiential situation as perceived or conceived by the child rather than by the observer. In Piaget’s (1964) view, a stimulus:

Is a stimulus only to the extent that it is significant, and it becomes significant only to the extent that there is a structure which permits its assimilation, a structure which can integrate this stimulus but which at the same time sets off the response. (p. 18)

For Piaget (1964), assimilation rather than association constituted the fundamental relation involved in learning, and he defined it as follows:

I shall define assimilation as the integration of any sort of reality into a structure, and it is this assimilation which seems to me fundamental in learning, and which seems to me the fundamental relation from the point of view of pedagogical or didactic applications. … Learning is possible only when there is active assimilation. (p. 18)

When I speak of assimilation, I do not assume that an experiential situation “exists” a priori somewhere in the mind in its totality as an object that a child retrieves. Rather, I assume that records of operations used in past activity are activated in assimilation. I further assume that the activated operations produce a “recognition template,” which is used in creating an “experiential situation” that may have been experienced before.

So, in the first part of a scheme, records of operations from past activity, when activated, produce a “recognition template” that is used in establishing an experiential situation. When it is clear from context, I refer to the recognition template as an assimilating structure and to the operations that produce it as operations of assimilation. The experiential situation may be created by means of visualized imagination as well as perception. It may in turn activate the scheme’s activity, which, in the case of a cognitive scheme, may consist of an implementation of the assimilating operations in the context of the experiential situation. The result of the cognitive scheme consists of whatever modification of the experiential situation is induced by the activity.

Learning as Accommodation

In Piaget’s quotation concerning assimilation, he commented that “learning is possible only when there is active assimilation.” Learning, however, is not to be equated with assimilation. Rather, when there is an irregularity or disturbance in the functioning of an established scheme, only then can accommodation take place, and not otherwise (von Glasersfeld 1980, p. 82). In our work, learning is construed as accommodation, that is, the modification of schemes.

This feature of the Piagetian model, as I see it, constitutes its main basis as a constructivist theory of cognition in which “knowledge’ is no longer a true or false representation of reality but simply the schemes of action and the schemes of operating that are functioning reliably and effectively

(von Glasersfeld 1980, p. 83)

There is indeed interaction between schemes and experiential events, but as von Glasersfeld points out, the child does not get to know the observer’s situations; in the sense that its schemes come to match or in any sense reflect structures as they might be to the observer in his or her situations. So, although an observer may have the observed child and the child’s environment in his or her experiential field, and observe the child using schemes while interacting with events, perhaps including other people, the interaction from the point of view of the interacting child is between schemes and experiential events within the system that constitutes the child.

The Sucking Scheme

Glasersfeld uses the sucking scheme in illustrating his idea of scheme. He uses it not only because of its essentiality in the survival of Homo sapiens, but also because of its importance in the construction of object concepts (Piaget 1937) and, thus, eventually in the construction of numerical concepts and schemes (Steffe and Cobb 1988). I have chosen the sucking scheme of newborn infants to illustrate the possibility of nonlinearity among the parts of a scheme in that the parts do not always proceed one way from the scheme’s situation to activity to result. One may regard the activity of the sucking scheme as being involved in assimilating objects in that case where the sucking action is driven by a sensation of hunger rather than by some sensory experience like touching the infant’s cheek. In the case of the sensation of hunger, the activity of sucking is activated and the baby searches for something on which to suck, and often it is a part of the baby’s hand. Here, the baby establishes a possible situation of the scheme by means of the activity that is driven by the gnawing sensation of hunger.

The possibility that a scheme’s activity can be the primary operation of assimilation solidly differentiates a scheme from the classical S → R schema. In the latter, it is the observer’s stimulus that sets off a response. In the former, the activity of the scheme may be triggered by disequilibria internal to the scheme and only then is a situation created by the actions of the child. I interpret Piaget’s (1964) comment that “the response was there first” (p. 15) as meaning that the activity of a scheme can be involved in establishing a situation of the scheme as well as the other way around, which is an important consideration in self-generated mathematical activity.

In the case of the sharing scheme, I can imagine the sharing operations as being activated by the question of how much pizza one person gets and by being involved in establishing the situation as a sharing situation. In the case of the sucking scheme, the sucking activity (activated by a sensation of hunger) can be involved in establishing a situation of the scheme. In that case where the baby sucks its hand, the situation may be the only result of the scheme’s activity. Unlike the sharing scheme, which is closed by implementing the sharing operations within the situation of sharing, the sensation of hunger would not be reduced in intensity by the activity of sucking. And yet, the infant may achieve some sense of satisfaction by implementing the activity of the scheme – the infant is temporarily “pacified.”

In other cases, the recognition template may be used in assimilation without the scheme’s activity being implemented. An example is where one observes the people in a large stadium. The question of how many people are in the stadium could be answered by counting the people as they exit the stadium or by counting them by counting the number of tickets sold. But as one sits in the stadium without recourse to either possibility, the activity of counting usually remains only minimally implemented, even though it may be evoked. The question of how many people are in the stadium is meaningful in that the activity of counting could be implemented given an appropriate situation. But the constraints in implementing the counting activity leave the individual without an activity, so the individual has a goal but no activity to reach the goal. In such cases, I would say that the individual has established a problem.

The Structure of a Scheme

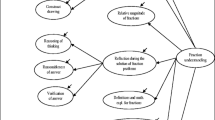
Fig. 2.2 is a diagram of the idea of a scheme. This diagram is static and as such it can be grossly misleading in interpretation. But it does help to highlight the essential aspects of a scheme. The Generated Goal can be regarded as the apex of a tetrahedron. The vertices of the base of the tetrahedron constitute the three components of a scheme. The double arrows linking the three components are to be interpreted as meaning that it is possible for any one of them to be in some way compared or related to either of the two others. The dashed arrow is to be interpreted as an expectation of the scheme’s result.

Fig. 2.2.

A diagram for the structure of a scheme.

In the case of the sucking scheme, I have already indicated how the scheme’s activity can lead to an establishment of a situation of the scheme. This situation along with the activity can in turn lead to a full stomach as a result. The result in turn can engender a feeling of satisfaction usually manifest as a sleeping baby and the scheme’s activity is discontinued, which is indicated by the double arrow between the scheme’s result and the generated goal.

Given a generated goal and a result of a scheme, in some cases, it is possible for a child to establish a situation of the scheme if the scheme’s activity is reversible. For example, a basic reason why 58% of the 11-year-old children in the study of mathematical development conducted by the National Foundation for Educational Research in England and Wales (Foxman et al. 1980) could not say that one-fourth of one-half is one-eighth is understandable when considering the possibility that their fractional schemes were not reversible schemes.⁶ The children were first given a piece of string and then were asked to cut it in half. The children were then presented with one of the halves and were asked to “cut off one-fourth of this piece.” The question “what fraction of the whole string that you started with is that little piece”? was then asked.

The children who were successful in cutting off one-fourth of one-half of the whole string had produced a result of their fractional scheme and their goal of making one-fourth had been satisfied. When the last question of the series of three was asked, this would serve to establish a new goal and a new situation using the results of the old scheme. To find one-eighth, the children might first reassemble the four pieces in thought and see them as one-half of the string partitioned into four equal pieces. The children could then produce another one-half of the string in thought also partitioned into four equal pieces, which would produce the whole string as two equal pieces each partitioned into four equal pieces. To do this, the children would need a fractional scheme that is reversible, in that they would be able to start from a result and reestablish the situation using inverse operations. So, in the case a scheme is reversible, its result can be used in establishing a situation of the scheme via the scheme’s reversible activity. I stress, however, that these relations are only possible for some schemes. They are not a necessary aspect of all schemes. Some schemes are entirely “one-way” schemes that proceed from situation to activity to result.

The diagram also indicates that the goal of a scheme can be generated in the process of assimilation. In Fig. 2.1, a child may see the picture of the stick figures, but form no immediate goal for further action. The child may simply recognize the stick figures as indicating people. In this sense, there is an assimilation using concepts constructed at an earlier time. In the process of assimilation, the child may form a goal of finding how many stick figures because it may establish an awareness of more than one figure – an awareness of plurality – which in turn may activate counting activity. The arrows between the scheme’s situation and goal and between the scheme’s activity and goal indicate these possibilities.

It would be unlikely, in the process of assimilation, for the child to form the goal of finding how much of one pizza each stick figure would have if the pizzas were shared equally. But if another person were to ask an appropriate sharing question about an assimilated situation, the activated sharing operations would constitute a reinterpretation – a further assimilation – of the situation as originally established by the child. The resulting goal to find the share for one of the seven stick figures drives the sharing activity during the activity. One might say the goal frames the activity. Partial results (partial from the point of view of the goal) feed back into the goal and I assume that they are compared with the generated goal. The connecting line between the generated goal and the activity indicates this feedback system.

The connecting line between the scheme’s activity and the scheme’s results indicates that the results or partial results may modify the activity, which in turn may modify the results. Likewise, a modification of either of the scheme’s activity or results may lead to a modification of the recognition template. In further uses of the scheme, the latter modification may in turn lead to a change in the scheme’s activity. Of course, the generated goal may also change as the scheme is being used.

Seriation and Anticipatory Schemes

Operations of a scheme are basic in our construction of children’s fraction schemes. For Piaget (1964), “An operation is … the essence of knowledge: it is an interiorized action which modifies the object of knowledge” (p. 8). An operation, for Piaget, was always a part of a structure of operations. A key example of such a structure is seriation, the setting of elements in order. Piaget wrote that “an asymmetrical relation does not exist in isolation. Seriation is the natural, basic operational structure” (pp. 9–10). Seriation should be regarded as a basic mechanism of intelligence and as a product of spontaneous development, and it can be profitably considered as a scheme in von Glasersfeld’s terms.

The seriation scheme can be used to portray what I mean by an anticipatory scheme. A child might form a goal of placing a collection of sticks in order from the shortest to the longest upon recognizing a collection of sticks. Prior to the activity of ordering the sticks the child might imagine the activity by imagining several sticks aligned in order. In this case, I say that the scheme is anticipatory as well as operative because the child can imagine the scheme’s activity or result without carrying out the activity.

An ordering of the sticks is contributed to the collection of sticks by the seriating child. By activating the conceptual structure of seriation, a child can formulate an expectation that a collection of sticks be ordered. The child does not abstract seriation from the sticks; rather, the child contributes it to the collection of sticks.

Mathematics of Living Rather Than Being

Scheme is an observer’s concept and, in the case of schemes that are mathematical, it refers to children’s mathematical language and actions. As observers, we can make a distinction between our concept of scheme and the children’s mathematical activity to which it refers, just as we can make a distinction between our concept of tree, and something “out there” to which we can point. One may object because the goal-directed activity of children is of a different nature than a tree. I agree they are of a different nature, but our concept, tree, can go beyond the concept that we initially constructed using the sensory material that was available to us. It can include our understanding of a tree as a dynamic living system and include such properties as photosynthesis.

Like our concept of tree, we also have a concept of children as physical objects. But that is only a beginning. We form the goal to understand children’s mathematics as a constitutive part of a living conceptual system. This way of understanding their mathematics has great advantages for mathematics education and puts us in education, we think, in an appropriate frame of reference. No longer is the sole focus on the abstracted adult concepts and operations, and no longer is children’s mathematical development conflated with those abstracted concepts and operations. Rather, the focus is on the living systems that children comprise and the problem is to understand how to bring the subsystems called mathematics of these living systems forth, and how to bring modifications in these subsystems forth. In this way, we may escape from Stolzenberg’s trap.