Data Sampling in Multidimensional NMR: Fundamentals and Strategies

Abstract

Beginning with the introduction of Fourier Transform NMR by Ernst and Anderson in 1966, time domain measurement of the impulse response (free induction decay) consisted of sampling the signal at a series of discrete intervals. For compatibility with the discrete Fourier transform, the intervals are kept uniform, and the Nyquist theorem dictates the largest value of the interval sufficient to avoid aliasing. With the proposal by Jeener of parametric sampling along an indirect time dimension, extension to multidimensional experiments employed the same sampling techniques used in one dimension, similarly subject to the Nyquist condition and suitable for processing via the discrete Fourier transform. The challenges of obtaining high-resolution spectral estimates from short data records were already well understood, and despite techniques such as linear prediction extrapolation, the achievable resolution in the indirect dimensions is limited by practical constraints on measuring time. The advent of methods of spectrum analysis capable of processing nonuniformly sampled data has led to an explosion in the development of novel sampling strategies that avoid the limits on resolution and measurement time imposed by uniform sampling. In this chapter we review the fundamentals of uniform and nonuniform sampling methods in one- and multidimensional NMR.

An erratum to this chapter is available at http://dx.doi.org/10.1007/211822_1_En_291

An erratum to this chapter can be found at http://dx.doi.org/10.1007/128_2011_291

1 Introduction

Since the introduction of Fourier Transform NMR by Richard Ernst and Weston Anderson in 1966, the measurement of NMR spectra has principally involved the measurement of the free induction decay (FID) following the application of a broad-band RF pulse to the sample [1]. The FID is measured at regular intervals, and the spectrum obtained by computing the discrete Fourier transform (DFT). The accuracy of the spectrum obtained by this approach depends critically on how the data are sampled. In the application of this approach to multidimensional NMR experiments, the constraint of uniform sampling interval imposed by the DFT incurs substantial sampling burdens. The advent of non-Fourier methods of spectrum analysis that do not require data sampled at uniform intervals has enabled the development of a host of nonuniform sampling (NUS) strategies. In this chapter we review the fundamentals of sampling, both uniform and nonuniform, in one and multiple dimensions. We then survey recently developed NUS methods that have been applied to multidimensional NMR, and consider prospects for new developments. While non-Fourier methods of spectrum analysis are indispensible for nonuniformly sampled data, they have been reviewed elsewhere.

2 Fundamentals: Sampling in One Dimension

Implicit in the definition of the complex DFT,

$$ {f_n} = \frac{1}{{\sqrt {N} }}\sum\limits_{k = 0}^{N - 1} {{d_k}} {{\text{e}}^{ - 2\pi ikn/N}} $$

(1)

is the periodicity of the spectrum, which is apparent by setting k to N in (1). Thus the component at frequency nΔt/N is equivalent to (and indistinguishable from) the components at (n/NΔt) +/− (m/Δt), m = 1, 2, …. This periodicity makes it possible to consider the DFT spectrum as containing all positive frequencies with zero frequency at one edge, or containing both positive and negative frequencies with zero frequency at (actually near) the middle. The equivalence of frequencies in the DFT spectrum that differ by a multiple of 1/Δt is a manifestation of the Nyquist sampling theorem, which states that, in order to determine unambiguously the frequency of an oscillating signal from a set of uniformly spaced samples, the sampling interval must be at least 1/Δt. (For additional details of the DFT and its application in NMR, see [2].)

In the description of the DFT given by (1) it is assumed that the data samples and DFT spectrum are both complex. Implicit in this description is that two orthogonal components of the signal are sampled at the same time, referred to as simultaneous quadrature detection. Most modern NMR spectrometers are capable of simultaneous quadrature detection, but early instruments had a single detector, so only a single component of the signal could be sampled at any one time. With so-called single-phase detection, the sign of the frequency is indeterminate. Consequently the carrier frequency must be placed at one edge of the spectral region and the data must be sampled at 1/2Δt to determine unambiguously the frequencies of signals spanning a bandwidth (or spectral width, SW) 1/Δt.

The detection of two orthogonal components permits the sign ambiguity to be resolved while sampling at a rate of 1/Δt. This approach, called phase sensitive or quadrature detection, enables the carrier to be placed at the center of the spectrum. Simultaneous quadrature detection is commonly achieved by mixing a detected signal with a fixed-frequency reference signal and the same reference signal phase shifted by 90°, or a cosinusoidal reference. The output of the phase-sensitive detector is two signals, differing in phase by 90°, containing frequency components of the original signal oscillating at the sum and difference of the reference frequency with the original frequencies. The sum frequencies are typically filtered out using a low-pass filter. While quadrature detection enables the sign of frequencies to be determined unambiguously, while sampling at 1/Δt, it requires just as many data samples as single-phase detection since it samples the signal twice at each 1/Δt interval, while single-phase detection samples once at each 1/2Δt interval.

2.1 Oversampling

The Nyquist theorem places a lower bound on the sampling rate, but what about sampling faster? It turns out that sampling faster than the reciprocal of the spectral width, called oversampling, can provide some benefits. One is that the oversampling increases the dynamic range, the ratio between the largest and smallest (non-zero) signals that can be detected [3, 4]. Analog-to-digital (A/D) converters employed in most NMR spectrometers represent the converted signal with fixed binary precision, e.g., 14 or 16 bits. A 16-bit A/D converter can represent signed integers between −32,768 and +32,767. Oversampling by a factor of n effectively increases the dynamic range by sqrt(n). Another benefit of oversampling is that it prevents certain sources of noise that are NOT band-limited to the same extent as the systematic (NMR) signals from being aliased into the spectral window.

2.2 How Long Should One Sample?

For signals that are stationary, that is their behavior doesn’t change with time, the longer you sample the better the sensitivity and accuracy. For normally distributed random noise, the signal-to-noise (S/N) ratio improves with the square root of the number of samples. NMR signals are rarely stationary, however, and the signal envelope typically decays exponentially in time. For decaying signals, there invariably comes a time when collecting additional samples is counter-productive, because the amplitude of the signal has diminished below the amplitude of the noise, and additional sampling only serves to reduce S/N. The time 1.3 × R ₂, where R ₂ is the decay rate of the signal, is the point of diminishing returns, beyond which additional data collection results in reduced sensitivity [5]. It makes sense to sample at least this long in order to optimize the sensitivity per unit time of an experiment. However, limiting sampling to 1.3 × R ₂ results in a compromise. That’s because the ability to distinguish signals that have similar frequencies increases the longer one samples. Intuitively this makes sense because the longer two signals with different frequencies evolve, the greater the difference in their values at a specific time. Thus resolution, the ability to distinguish closely-spaced frequency components, is largely related to the longest time sample.

3 Sampling in Multiple Dimensions

While the FTNMR experiment of Ernst and Anderson was the seminal development behind all of modern NMR spectroscopy, it wasn’t until 1971 that Jean Jeener proposed a strategy for parametric sampling of a virtual or indirect time dimension that formed the basis for modern multidimensional NMR [6], including applications to magnetic resonance imaging (MRI). In the simplest realization, an indirect time dimension can be defined as the time between two RF pulses applied in an NMR experiment. The FID is recorded subsequent to the second pulse, and because it evolves in real time its evolution is said to occur in the acquisition dimension. A given experiment can only be conducted using a single value of the time interval between pulses, but the indirect time dimension can be explored by repeating the experiment using different values of the time delay. When the values of the time delay are systematically varied using a fixed sampling interval, the resulting spectrum as a function of the time interval can be computed using the DFT along the columns of the two-dimensional data matrix, with rows corresponding to samples in the acquisition dimension and columns the indirect dimension. Generalization of the Jeener principle to an arbitrary number of dimensions is straightforward, limited only by the imagination of the spectroscopist and the ability of the spin system to maintain coherence over an increasingly lengthy sequence of RF pulses and indirect evolution times.

3.1 Quadrature Detection in Multiple Dimensions

Left ambiguous in the discussion above of multidimensional NMR experiments is the problem of frequency sign discrimination in the indirect dimensions. Because the indirect dimensions are sampled parametrically, i.e., each indirect evolution time is sampled via a separate experiment, the possibility of simultaneous quadrature detection is not available. Quadrature detection in the indirect dimension of a two-dimensional experiment nonetheless can be accomplished by using two experiments for each indirect evolution time to determine two orthogonal responses. This approach was first described by States, Haberkorn, and Ruben, and is frequently referred to as the States method [7]. Alternatively, oversampling could be used by sampling at twice the Nyquist frequency while rotating the detector phase through 0°, 90°, 180°, and 270°, an approach called time-proportional phase incrementation (TPPI). A hybrid approach is referred to as States-TPPI. Processing of States-TPPI sampling is performed using a complex DFT, just as for States sampling, while TPPI employs a real-only DFT.

3.2 Sampling Limited Regime

An implication of the Jeener strategy for multidimensional experiments is that the length of time required to conduct a multidimensional experiment is directly proportional to the total number of indirect time samples (times two for each indirect dimension if States or States-TPPI sampling is used). In experiments that permit the spin system to return close to equilibrium by waiting on the order of T ₁ before performing another experiment, sampling along the acquisition dimension effectively incurs no time cost. Sampling to the Rovnyak limit (1.3 × R ₂) in the indirect dimensions places a substantial burden on data collection, even for experiments on proteins with relatively short relaxation times. Thus a three dimensional experiment for a 20-kDa protein at 14 T (600 MHz for ¹H) exploring ¹³C and ¹⁵N frequencies in the indirect dimensions would require 2.6 days in order to sample to 1.3 × R ₂ in both indirect dimensions. A comparable four-dimensional experiment with two ¹³C (aliphatic and carbonyl) and one ¹⁵N indirect dimensions would require 137 days. As a practical matter, multidimensional NMR experiments rarely exceed a week, as superconducting magnets typically require cryogen refill on a weekly basis. Thus multidimensional experiments rarely achieve the full potential of the resolution afforded by superconducting magnets. The problem becomes more acute with very high magnetic fields. The time required for data collection in a multidimensional experiment to fixed maximum evolution times in the indirect dimensions increases with the increase in magnetic field raised to the power of the number of indirect dimensions. The same four-dimensional protein NMR experiment performed at 21.2 T (900 MHz for ¹H), sampled to 1.3 × R ₂, would require about 320 days. NUS approaches have made it possible to conduct high resolution 4D experiments that would otherwise be impractical [45].

While methods of spectrum analysis capable of super-resolution exist, that is, methods that can achieve resolution greater than 1/t _max, the most common of these, linear prediction (LP) extrapolation, has substantial drawbacks. LP extrapolation is used to extrapolate signals beyond the measured interval. While this can dramatically suppress truncation artifacts associated with zero-filling as well as improve resolution, because LP extrapolation implicitly assumes exponential decay it can lead to subtle frequency bias when the signal decay is not perfectly exponential [8]. This bias can have detrimental consequences for applications that require the determination of small frequency differences, such as measurement of residual dipolar couplings (RDCs).

4 Non-Fourier Methods of Spectrum Analysis

The DFT, strictly speaking, requires data sampled at uniform intervals. Thus the development of NUS methods to avoid the sampling limited regime in multidimensional NMR closely parallels the development of non-Fourier methods of spectrum analysis capable of treating data that have been collected at nonuniform intervals. One of the first methods to be employed in NMR in conjunction with NUS is maximum entropy (MaxEnt) reconstruction [9, 10]. MaxEnt reconstruction seeks that spectrum containing the least amount of information that is still consistent with the measured data. It makes no assumption regarding the nature of the signal, and thus is suitable for application to signals characterized by non-exponential decay (non-Lorentzian line shapes). A host of similar methods employ functionals other than the entropy to regularize the spectrum, for example the l₁-norm [11, 12]. Another class of methods that can reconstruct frequency spectra from data that are sampled nonuniformly assume a model for the data. Bayesian [13] and maximum likelihood [14, 15] (MLM) methods both assume the signal can be described as a sum of exponentially decaying sinusoids, and can be used either to reconstruct a frequency spectrum or to determine a list of frequency components and their characteristics; for this reason these methods are often described as being parametric. A method that is intermediate between the parametric methods that assume a model for the signal and regularization methods that do not is a method called multidimensional decomposition [16] (MDD). It assumes that frequency components in multidimensional spectra can be decomposed into a vector product of one-dimensional lineshapes. The approach is related to principle component analysis, and has been utilized in the field of analytical chemistry and chemometrics (where it is called PARAFAC [17]); a unique decomposition exists only for spectra that have three or more dimensions.

4.1 “DFT” of NUS Data and the Point-Spread Function

From the definition of the DFT, it is clear that the Fourier sum can be modified by evaluating the summand at arbitrary frequencies rather than uniformly spaced frequencies. Kozminksi and colleagues have proposed utilizing this approach for computing frequency spectra of NUS data [18]; however, strictly speaking it is no longer properly called a Fourier transformation of the NUS data. Consider the special case where the summand in (1) is evaluated for a subset of the normal regularly-spaced time intervals. An important characteristic of the DFT is the orthogonality of the basic functions (the complex exponentials),

$$ \sum\limits_{n = 0}^{N - 1} {{{\text{e}}^{ - 2\pi i(k - k\prime )n/{\rm N}}}} = 0,\quad k \ne k^\prime, $$

(2)

when the summation is carried out over a subset of the time intervals. Some of the values of n indicated by the sum in (2) are left out, and the complex exponentials are no longer orthogonal. An implication is that frequency components in the signal interfere with one another when the sampling is nonuniform.

Consider now NUS data sampled at the same subset of uniformly spaced times, but supplemented by the value zero for those times not sampled. Clearly the DFT can be applied to this augmented data, but it is not the same as “applying the DFT to NUS data.” It is a subtle distinction but an important one. What is frequently referred to as the DFT spectrum of NUS data is not the spectrum of the NUS data but the spectrum of the zero-augmented data. The differences between the DFT of the zero-augmented data and the spectrum of the signal are mainly the result of the choice of sampled times, and are called sampling artifacts. While the DFT of zero-augmented data is not the spectrum we seek, it can sometimes be a useful approximation if the sampled times are chosen carefully to diminish the sampling artifacts.

The application of the DFT to NUS data has parallels in the problem of numerical quadrature on an irregular mesh, or evaluating an integral on a set of irregularly-spaced points [19]. The accuracy of the integral estimated from discrete samples is typically improved by judicious choice of the sample points, or pivots, and by weighting the value of the function being integrated at each of the pivots. For pivots (sampling schedules) that can be described analytically, the weights correspond to the Jacobian for the transformation between coordinate systems (as for the polar FT, discussed below). For sampling schemes that cannot be described analytically, for example those given with a random distribution, the Voronoi area (in two dimensions; volume in three dimensions, etc.) provides a useful set of weights [20]. The Voronoi area is the area occupied by the set of points around each pivot that are closer to that pivot than to any other pivot in the NUS set.

Under certain conditions the relationship between the DFT of the zero-augmented NUS data and the true spectrum has a particularly simple form. If the sampling is restricted to the uniformly-spaced Nyquist grid (also referred to as the Cartesian sampling grid) and there exists a real-valued sampling function with the property that when it multiplies a uniformly sampled data vector, element-wise, the result is the zero-augmented NUS data vector, then the DFT of the zero-augmented NUS data is the convolution of the DFT spectrum of the uniformly sampled data with the DFT of the sampling function. The sampling function has the value 1 for times that are sampled and zero for times that are not. The DFT of the sampling function is variously called the point-spread function (PSF), the impulse response, or the sampling spectrum.

The PSF provides insight into the locations and magnitudes of sampling artifacts that result from NUS, and it can have an arbitrary number of dimensions, corresponding to the number of dimensions in which NUS is applied. The PSF typically consists of a main central component at zero frequency, with smaller non-zero frequency components. Because the PSF enters into the DFT of the zero-augmented spectrum through convolution, each non-zero frequency component of the PSF will give rise to a sampling artifact for each component in the signal spectrum, with positions relative to the signal components that are the same as the relationship of the satellite peaks in the PSF. The amplitudes of the sampling artifacts will be proportional to the amplitude of the signal component and the relative height of the satellite peaks in the PSF. Thus the largest sampling artifacts will arise from the largest-amplitude components of the signal spectrum. The effective dynamic range (ratio between the magnitude of the largest and smallest signal component that can be unambiguously identified) of the DFT spectrum of the zero-augmented data can be directly estimated from the PSF for a sampling scheme as the ratio between the amplitude of the largest non-zero frequency component and the amplitude of the zero-frequency component.

Using NUS approaches to reconstruct a fully-dimensional spectrum invariably introduces sampling artifacts that are characteristic of the NUS strategy employed. Characteristic ridge artifacts emanating from peaks in back-projection reconstruction (BPR) spectra (described below) that were initially believed to be artifacts of back projection were instead demonstrated to be characteristic of radial sampling by using MaxEnt reconstruction to process radially-sampled data: the MaxEnt spectrum contained essentially identical ridge artifacts [44]. While spectral reconstruction methods attempt to diminish sampling artifacts in the reconstructed spectrum, their ability to suppress sampling artifacts is limited by the presence of noise. It is thus important to have an understanding of the nature of sampling artifacts that is independent of the method used to reconstruct the spectrum. Provided that sampling is restricted to a uniform Cartesian grid (arbitrary sampling schemes can be treated using successively fine grids) and one can define a real-valued sampling function that has the value one when a sample is collected and zero when it is not collected, sampling artifacts arise from the convolution of the impulse response or PSF with the true spectrum. The PSF is simply given by the DFT of the sampling function. PSFs typically exhibit a major peak at zero frequency, with satellite peaks of varying intensity at non-zero frequencies. Using the DFT to process NUS data, the resulting spectrum corresponds exactly to the convolution of the PSF with the true spectrum (Fig. 1). Methods such as MaxEnt reconstruction suppress the magnitude of sampling artifacts, but they appear at the same locations as found in the DFT spectrum (Fig. 2).

Fig. 1

The DFT of a decaying sinusoid (a, b) and a sampling function (c, d) and their multiplication in the time domain (e) resulting in their convolution in the frequency domain (f). The DFT of the sampling function (f) is the PSF

Fig. 2

(a) nuDFT vs (b) MaxEnt reconstruction applied to the same data. The inset in B shows a tenfold expansion of the baseline

In addition to helping to specify the frequencies of sampling artifacts (which will depend on the frequencies contained in the signal being sampled as well as the sampling scheme), the PSF helps to specify the magnitudes of the sampling artifacts, as discussed above. While MaxEnt or other methods of spectrum analysis that attempt to deconvolve the PSF can improve the dynamic range, sampling schemes with PSFs containing smaller satellite peaks (relative to the central component) will give rise to smaller sampling artifacts.

An implication of restricting the sampling function to being a real vector is that if quadrature detection is employed in the indirect dimensions, e.g., States-Haberkorn-Ruben, then all quadrature components must be sampled for a given set of indirect evolution times. If they are not all sampled, the sampling function is complex, and the relationship between the DFT of the NUS data, the DFT of the sampling function, and the true spectrum is no longer a simple convolution.

5 Nonuniform Sampling: A Brief History

5.1 The Accordion

It was recognized soon after the development of FT NMR that one way to avoid the sampling limited regime in multidimensional situations is to avoid collecting the entire Nyquist grid in the indirect time dimensions. The principal challenge to this idea was that methods for computing the multidimensional spectrum from nonuniformly sampled data were not widely available. In 1981 Bodenhausen and Ernst introduced a means of avoiding the sampling constraints associated with uniform parametric sampling of two indirect dimensions of three-dimensional experiments, while also avoiding the need to compute a multidimensional spectrum from an incomplete data matrix, by coupling the two indirect evolution times [21]. By incrementing the evolution times in concert, sampling occurs along a radial vector in t ₁−t ₂, with a slope given by the ratio of the increments applied along each dimension. This effectively creates an aggregate evolution time t = t ₁ + α*t ₂ that is sampled uniformly, and thus the DFT can be applied to determine the frequency spectrum. According to the projection-cross-section theorem, this spectrum is the projection of the full t ₁−t ₂ spectrum onto a vector with angle α in the f ₁−f ₂ plane. Bodenhausen and Ernst referred to this as an “accordion” experiment. Although they did not propose reconstruction of the full f ₁−f ₂ spectrum from multiple projections, they did discuss the use of multiple projections for characterizing the corresponding f ₁−f ₂ spectrum, and thus the accordion experiment is the precursor to more recent radial sampling methods that are discussed below. Because the coupling of evolution times effectively combines time (and the corresponding frequency) dimensions, the accordion experiment is an example of a reduced dimensionality (RD) experiment.

5.2 Random Sampling

The 3D accordion experiment has much lower sampling requirements because it avoids sampling the Cartesian grid of (t ₁, t ₂) values that must be sampled in order to utilize the DFT to compute the spectrum along both t ₁ and t ₂. A more general approach than the accordion experiment is to eschew regular sampling altogether. A consequence of this approach is that one cannot utilize the DFT to compute the spectrum, so some alternative method capable of utilizing nonuniformly sampled data must be employed. In seminal work, Laue and collaborators introduced the use of MaxEnt reconstruction to compute the frequency spectrum from nonuniformly sampled data [22]. In analogy with the concept of matched filter apodization for maximizing signal-to-noise ratio (S/N), Barna et al. utilized random sampling that was exponentially biased to short times, so that the sampling distribution matched the decay of the signal envelope. The concept of biased random sampling was further generalized to J-modulated experiments (cosine-modulated exponential decay) and constant-time experiments (no decay) by Schmieder et al. [32, 33] While the combination of biased random sampling and MaxEnt reconstruction provided high resolution spectra with dramatic reductions in experiment time compared to conventional uniform sampling because it employs samples collected at long evolution times without the need to sample all uniformly-spaced shorter times, the approach was not widely adopted, no doubt because neither MaxEnt reconstruction nor NUS was highly intuitive. Nevertheless a small cadre of investigators continued to explore novel NUS schemes in conjunction with MaxEnt reconstruction throughout the 1990s.

5.3 RD, Redux

The first RD experiment was the accordion experiment. In the original accordion experiment one indirect dimension represented chemical shift evolution while the second indirect dimension encoded a mixing time designed to measure chemical exchange. Although this experiment established the foundation for a host of subsequent RD experiments, most of which deal exclusively with chemical shift evolution, its utility for measuring relaxation rates and other applications is still being developed [23, 24]. Even though it was clear from the initial description of the accordion experiment that the method was applicable to any 3D experiment, it was nearly a decade before it was applied to a 3D experiment where both indirect dimensions represented chemical shifts [25, 26]. This application emerged as a consequence of newly-developed methods for isotopic labeling of proteins that enabled multinuclear, multidimensional experiments, with reasonable sensitivity, for sequential resonance assignment and structure determination of proteins. The acquisition of two coupled frequency dimensions, however, introduces some difficulties. The main problem is that the two dimensions being co-evolved are mixed and must be deconvoluted before any useful information can be extracted. Since the evolution linearly combines the two dimensions, their frequencies are “mixed” in the spectrum in a linear manner as well. The number of resonances observed in the lower dimensional spectrum depends on the number of linked dimensions. Thus, if two dimensions are linked, the RD spectrum will contain two peaks per resonance of the higher dimensional spectrum, whereas if three dimensions are coupled, each of the above two peaks will be split by the second frequency resulting in four resonances and so on. The position of the peaks in the spectrum can be used to extract the true frequency of the resonances in the spectrum. The problem obviously becomes more complicated as the number of resonances is increased. If overlap can be avoided, however, it is possible to reduce experimental time drastically. Among the weaknesses of this approach are sensitivity losses, associated with both peak splitting and relaxation losses, which effectively limit the number of dimensions that can be coupled for a given molecular size.

An extension of RD was presented by Kim and Szyperski [27] in 2003 in which they used a “G-matrix” to combine appropriately the hypercomplex data of arbitrary dimensionality to produce “basic spectra.” These spectra are much less complicated than the RD projections and the known relationship between the various patterns can be used to extract true chemical shifts (via nonlinear least-squares fitting). Combination of the hypercomplex planes enables recovery of some sensitivity that is otherwise lost in RD approaches due to peak splitting. A disadvantage is that the data are not combined in a higher dimensional spectrum so that the sensitivity is related to that of each of the lower dimensional projections rather than the entire dataset. GFT-NMR was developed contemporaneously with advances in sensitivity delivered by higher magnetic fields and cryogenically cooled probes, providing sufficient sensitivity to make GFT experiments feasible for the first time, albeit using very concentrated protein samples (the GFT method was demonstrated on a 2 mM sample of ubiquitin).

Broader appreciation for NUS was stimulated by a series of papers by Kupce and Freeman, in which they utilized BPR from a series of experiments employing radial sampling in t ₁/t ₂ to reconstruct the fully-dimensional f ₁/f ₂/f ₃ spectrum [28–32]. While the data sampling was equivalent to that employed by the accordion, GFT, and RD experiments, the use of back-projection (by analogy to computerized tomography) demonstrated the connection with the 3D spectrum conventionally obtained by uniform sampling and DFT. Despite some drawbacks to radial sampling (discussed below), the BPR approach was important because it provided a useful heuristic for more general NUS approaches.

The principle underlying radial sampling in 3D experiments generalizes to higher dimensions. For example, coupling of three indirect evolution times results in a projection of three dimensions onto a vector with one angle specifying the orientation with respect to the t ₁/t ₂ plane, and one specifying the angle with respect to the t ₂/t ₃ plane. Two very similar approaches for circumventing sampling limitations associated with uniform sampling in higher-dimensional experiments have been introduced to achieve high resolution while employing prior knowledge to design sampling angles. Chemical shift distributions expected for proteins can be used to determine a set of radial sampling angles (projection angles) that will optimally resolve potential overlap. Identification of frequencies in the projected spectra, together with knowledge of the projection angles, can be used to determine the (unprojected) frequencies in the orthogonal coordinate system of the fully-dimensional experiment.

In addition to GFT and BPR, a host of other methods can be applied to radially-sampled data; like BPR, these methods reconstruct the fully-dimensional spectrum. Zhou and colleagues employed radial FT [28] to process data collected along concentric rings in t ₁/t ₂ [29]. MLM methods that fit a model (typically consisting of a sum of exponentially-damped sinusoids) can also be used to analyze radially sampled data, as can regularization methods that do not model the signal (e.g., l₁-norm, MaxEnt).

5.4 The NUS Explosion

Since the turn of the twenty-first century, there has been a great deal of effort devoted to developing novel NUS strategies for multidimensional NMR. A recurring theme has been the importance of irregularity or randomness. Approaches involving various analytic sampling schemes (triangular, concentric rings, spirals) as well as novel random distributions (Poisson gap) have been described.

6 General Aspects of Nonuniform Sampling

We will contrast different approaches to NUS that have been applied to multidimensional NMR in a moment, but we first discuss some characteristics of NUS that are general and apply to all NUS approaches.

6.1 On-Grid vs Off-Grid Sampling

NUS schemes are sometimes characterized as on-grid or off-grid. Schemes that sample a subset of the evolution times normally sampled using uniform sampling at the Nyquist rate (or faster) are called on-grid. In schemes such as radial, spiral, or concentric ring, the samples do not fall on the same Cartesian grid. However, one can define a Cartesian grid with spacing determined by the precision with which evolution times are specified (discussed below). Alternatively, “off grid” sampling schemes can be approximated by “aliasing” (this time in the computer graphics sense) the evolution times onto a Nyquist grid, without greatly impacting the sampling artifacts (Fig. 3).

Fig. 3

(a) Radial sampling (left) on-grid and (right) off-grid. Dots represent the Nyquist grid, circles represent sampled data points. The solid lines indicate the angle of the radial vector (projection axis). (b) Reconstruction of radially sampled data; on-grid sampling reconstructed using MaxEnt (left) and off-grid sampled data reconstructed using PR (right)

6.2 Bandwidth and Aliasing

Bretthorst was the first to consider carefully the implications of NUS for bandwidth and aliasing [30, 31]; his important contribution was published in a rather obscure proceedings volume, but more recently a version has been published in a more widely-accessible publication. Among the major points Bretthorst raises is that sampling artifacts accompanying NUS can be viewed as aliases. This is demonstrated in Fig. 4, where the spectrum obtained using uniform but deliberate undersampling is contrasted with the DFT spectrum for NUS data of the same signal.

Fig. 4

Examples of aliasing using uniform (a, b) and nonuniform (c, d) sampling. (a, b) DFT spectrum using uniform sampling for a single synthetic sinusoid; (a) at the Nyquist rate, (b) at one-half the Nyquist rate. (c, d) nuDFT (DFT in which samples not measured are set to zero) for the same synthetic signal using nonuniform sampling from the Nyquist grid. In (c) an alias appears at the frequency expected using deliberate undersampling by a factor of 2, but with a height slightly less than the true (unaliased) peak. In (d) the alias is greatly diminished, a result of the greater number of samples in the NUS set spaced at the Nyquist interval

6.3 Sampling Artifacts Are Spectral Aliases

However, as Bretthorst has pointed out, when the sampling (evolution) times are specified with finite precision (as they are in all commercial instruments), one can always define a uniform grid on which all the samples will fall. This grid spacing will generally be finer than the Nyquist grid. The largest grid spacing sufficient to encompass fully an arbitrary NUS scheme is given by the greatest common divisor (GCD) of the sampled times, which is at least as large as the precision and may be larger, depending on the sampling scheme. As the samples are not uniform, the Nyquist sampling theorem does not apply, so strictly speaking there is not a bandwidth limiting the frequencies that can be unambiguously determined.

NUS artifacts are a form of aliasing, which can be appreciated by considering uniform undersampling as a form of NUS. Figure 4 illustrates a one-dimensional spectrum computed by applying the DFT to a synthetic signal sampled at the Nyquist interval (Fig. 4a) and twice the Nyquist interval (Fig. 4b). The signal sampled at twice the Nyquist interval has one alias of the true signal. Figure 4c depicts the DFT spectrum of a signal sampled nonuniformly. Note the strongest sampling artifact occurs precisely at the location of the undersampling artifact. Higher order sampling artifacts can be ascribed to aliases due to undersampling by greater degrees.

Since sampling artifacts are aliases, they can be diminished by increasing the effective bandwidth. One way to do this is to decrease the GCD. As shown above the GCD need not correspond to the spacing of the underlying grid. Introducing irregularity is one way to decrease the GCD to the size of the grid, and this helps to explain the usefulness of randomness for reducing artifacts from NUS schemes [46]. The ability of randomness to reduce NUS aliasing artifacts is depicted in Fig. 5. The left panels depict a two-dimensional sampling scheme (top) in which the data are undersampled by a factor of four in each dimension, leading to multiple instances of each true peak in the DFT spectrum (bottom). The middle and right panels illustrate the effect of increasing amounts of randomness incorporated into the sampling scheme on the spectral aliases. The incorporation of randomness can suppress artifacts in otherwise regular sampling schemes, such as radial sampling, as shown in Fig. 6.

Fig. 5

MaxEnt spectra for synthetic two-dimensional data consisting of five exponentially decaying sinusoids plus noise. The left-most panels depict deliberate undersampling selecting every fourth point along both dimensions. The center and right panels depict blurred undersampling, RMS 0.625 and 1.25, respectively. White contour levels are plotted at multiples of 1.4 starting with 3% of the height of the highest peak

Fig. 6

¹H/¹³C plane (¹⁵N chemical shift 121.96 ppm) from the HNCO spectrum of Ubiquitin, using data collected at 9.4 T (400 MHz for ¹H) on a Varian Inova instrument. Spectra were computed using MaxEnt reconstruction and radial sampling using five projections with different amounts of random “blurring” of the sampling schedule (RMS zero (none), 0.625 and 1.25, left to right). Top: sampling schedules. Bottom: MaxEnt spectra. Contour levels are chosen as in Fig. 5

Another way to increase the effective bandwidth is to sample from an oversampled grid. We saw earlier that oversampling can benefit uniform sampling approaches by increasing the dynamic range. When employed with NUS, oversampling has the effect of shifting sampling artifacts out of the original spectral window [47]. This effect is shown in Fig. 7.

Fig. 7

Effect of oversampling. The top panel shows the two peaks and their associated sampling artifacts and the middle and lower panels show the same peaks using 4× and 8× SW. The sampling artifacts are shifted to extreme frequencies at the cost of line broadening

7 A Menagerie of Sampling Schemes

While the efficacy of a particular sampling scheme depends on a host of factors, including the nature of the signal being sampled, the PSF provides a useful first-order tool for comparing sampling schedules. Figure 8 illustrates examples of several common two-dimensional NUS schemes, together with PSFs computed for varying levels of coverage (30%, 10%, and 5%) of the underlying uniform grid. Some of the schemes are off-grid schemes, but they are approximated here by mapping onto a uniform grid. As noted previously, on-grid approximation of off-grid sampling schemes coupled with reconstruction methods such as MaxEnt gives results that are very similar to off-grid sampling. The PSF gives an indication of the distribution and magnitude of sampling artifacts for a given sampling scheme; schemes with PSFs that have very low values other than the central component give rise to weaker artifacts. Of course the PSF alone does not tell the whole story, because it does not address relative sensitivity. For example, while the random schedule has a PSF with very weak side-lobes, and gives rise to fewer artifacts than a radial sampling scheme for the same level of coverage, it has lower sensitivity for exponentially decaying sinusoids than a radial scheme (which concentrates more samples at short evolution times where the signal is strongest). Thus more than one metric is needed to assess the relative performance of different sampling schemes.

Fig. 8

A menagerie of sampling schemes. The first column depicts examples of two-dimensional sampling schemes that have been employed in NMR, for 30% coverage of a 128 × 128 uniform grid (i.e., approx. 4915 samples out of 16,384). Successive columns depict the PSF for 30%, 10%, and 5% coverage. The PSFs are normalized to the value of the central component, and the color coding is depicted on the far right. Sampling schedules depicted include (c) circular shell, (cr) randomized circular, (r) radial, (Poisson) Poisson gap, (rand) random, (EMS) envelope-matched, (BMS) beat-matched, (burst) bursty, and (triangle) triangular

7.1 Random and Biased Random Sampling

Exponentially-biased random sampling was the first general NUS approach applied to multidimensional NMR [22]. By analogy with matched filter apodization (which was first applied in NMR by Ernst, and maximizes the S/N of the uniformly-sampled DFT spectrum), Laue and colleagues reasoned that tailoring NUS so that the signal is sampled more frequently at short times, where the signal is strong, and less frequently when the signal is weak, would similarly improve S/N. They applied an exponential bias to match the decay rate of the signal envelope; we refer to this as envelope-matched sampling (EMS). Generalizations of the approach to sine-modulated signals, where the signal is small at the beginning, and constant-time experiments, where the signal envelope does not decay, were described by Schmieder et al. [32, 33].

7.2 Triangular

Somewhat analogous to the rationale behind exponentially-biased sampling, Delsuc and colleagues employed triangular sampling in two time dimensions to capture the strongest part of a two-dimensional signal [34]. The approach is easily generalized to arbitrary dimension.

7.3 Radial

Radial sampling results when the incrementation of evolution times is coupled, and is the approach employed by GFT, RD, and back-project reconstruction methods. Radial sampling has also found application in MRI. When a fully-dimensional spectrum is computed from a set of radial samples (e.g., BPR, radial FT, MaxEnt), the radial sampling vectors are typically chosen to somewhat uniformly span the orientations from 0° to 90°. When the fully-dimensional spectrum is not reconstructed, but instead the individual one-dimensional spectra (corresponding to projected cross sections through the fully-dimensional spectrum) are analyzed separately, the sampling angles are typically determined using a knowledge-based approach (HIFI, APSY [35, 36]). Prior knowledge about chemical shift distributions in proteins is employed to select sequentially radial vectors to minimize the likelihood of overlap in the projected cross section.

The successes of methods like RD, GFT, and BPR notwithstanding, when the aim is to reconstruct the fully-dimensional spectrum, radial sampling is a rather poor approach compared to less regular sampling schemes. When the aim is not to reconstruct the fully dimensional spectrum, but to analyze projections separately, a complete separate and dedicated infrastructure for the analysis is required (which comprises much of the effort behind GFT, HIFI, and APSY approaches). The advantage of reconstructing the fully dimensional spectrum is that the data are isomorphic with spectra computed using conventional uniform sampling methods, and the abundance of graphical and analysis tools that exist for multidimensional NMR data can be used to visualize and quantify the spectra. This includes XEASY [37], NMRDraw [38], NMRViewJ [39], Sparky [40], and a host of automated scripts for “strip” plots and sequential assignment of proteins. Figure 9 compares the use of radial sampling with exponentially biased random sampling in two indirect dimensions, using MaxEnt reconstruction to compute the 3D spectrum. The top panels depict contour plots using one, two, and three radial sampling vectors (from left to right). Below each panel are shown contour plots for spectra computed using biased random sampling using the same number of samples as the radial sampling example given directly above. The accuracy of the reconstruction of the 3D spectrum from a set of sparse samples is dramatically better when biased random sampling is used instead of radial sampling.

Fig. 9

HNCO spectra of ubiquitin. Top panels show the addition of 0°, 90°, and 30° projections of the two jointly sampled indirect dimensions at a proton chemical shift of 8.14 ppm, reconstructed using back projection reconstruction. Each projection contains 52 complex points; thus the total number of complex points sampled from left to right is 52, 104, and 156. The lower panel shows MaxEnt reconstruction using the same number of complex data points, distributed randomly along the nitrogen dimension (constant time) and with an exponentially decreasing sampling density decay rate corresponding to 15 Hz in the carbon dimension. A 1D trace at the position of the weakest peak present in the spectrum is shown at the top of each spectrum (indicated by a dashed line). The insets depict the sampling scheme

7.4 Concentric Rings

Coggins and Zhou introduced the concept of concentric ring sampling (CRS), and showed that radial sampling is a special case of CRS [29]. They showed that the DFT could be adapted to CRS (and radial sampling) by changing to polar coordinates from Cartesian coordinates (essentially by introducing the Jacobian for the coordinate transformation as weighting factors). Optimized CRS that linearly increases the number of samples in a ring as the radius increases and incorporates randomness were shown to provide resolution comparable to uniform sampling for the same measurement time, but with fewer sampling artifacts than radial sampling. They also showed that the discrete polar FT is equivalent to the result from weighted back projection reconstruction.

7.5 Spiral

Spiral sampling is used mainly in MRI, where it permits reduced exploration of k-space (and thus a reduction of scan time).

7.6 Beat-Matched Sampling

The concept of matching the sampling density to the signal envelope, in order to sample most frequently when the signal is strong and less frequently when it is weak, can be extended to match finer details of the signal. For example, a signal containing two strong frequency components will exhibit beats in the time domain signal separated by the reciprocal of the frequency difference between the components. As the signal becomes more complex, with more frequency components, more beats will occur corresponding to frequency differences between the various components. If one knows a priori the expected frequencies of the signal components, one can predict the location of the beats (and nulls, or zero-crossings), and tailor sampling accordingly. The procedure is entirely analogous to EMS, except that the sampling density is matched to the fine detail of predicted time-domain data, not just the signal envelope. We refer to this approach as beat-matched sampling (BMS). Possible applications where the frequencies are known a priori include relaxation experiments or multidimensional experiments in which scout scans or complementary experiments provide knowledge of the frequencies. In practice, BMS sampling schedules appear similar to EMS (e.g., exponentially biased) schedules; however, they tend not to be as robust, as small difference in noise level or small frequency shifts can have pronounced effects on the location of beats or nulls in the signal.

7.7 Poisson Gap Sampling

Hyberts and Wagner [41] noted empirically that the distribution of the gaps in a sampling schedule are also important. Long gaps near the beginning or end of a sample schedule were particularly detrimental. They adapted an idea employed in computer graphics, Poisson gap sampling, to generate sampling schedules that avoid long gaps while ensuring the samples are randomly distributed. Similar distributions can be generated using other approaches, for example quasi-random (e.g., Sobolev) sequences. In addition to being robust, Poisson gap sampling schedules show less variation with the random deviate than other sampling schemes. A potential weakness of Poisson gap sampling, however, is that the minimum distance between samples must not be too small, otherwise aliasing can become significant.

7.8 Burst Sampling

In burst or burst-mode sampling, short high-rate bursts are separated by stretches with no sampling. It effectively minimizes the number of large gaps, while ensuring that samples are spaced at the minimal spacing when sub-sampling from a grid. Burst sampling has found application in commercial spectrum analyzers and communications gear. In contrast to Poisson gap sampling, burst sampling ensures that most samples are separated by the grid spacing to suppress aliasing [42].

7.9 Nonuniform Averaging

The concept underlying EMS or BMS can be applied to the amount of signal averaging performed, in contexts where a significant number of transients are averaged to obtain sufficient sensitivity. In this sensitivity-limited regime, varying the number of transients in proportion to the signal envelope could be utilized in conjunction with uniform or nonuniform sampling in the time domain. An early application of this idea in NMR employed uniform sampling with nonuniform averaging, and computed the multidimensional DFT spectrum after first normalizing each FID by dividing by the number of transients summed at each indirect evolution time [43]. Although the results of this approach are qualitatively reasonable provided that the S/N is not too low, a flaw in the approach is that noise will not be properly weighted. A solution is to employ a method where appropriate statistical weights can be applied to each FID, e.g., MaxEnt or MLM reconstruction.

7.10 Random Phase Detection

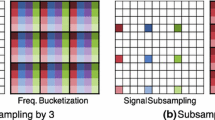
We’ve seen how NUS artifacts are a manifestation of aliasing, and how randomization can mitigate the extent of aliasing. There is another context in which aliasing appears in NMR, and that is determining the sign of frequency components (i.e., the direction of rotation of the magnetization). An approach widely used in NMR to resolve this ambiguity is to detect simultaneously two orthogonal phases (simultaneous quadrature detection). When simultaneous quadrature detection is not feasible, for example in the indirect dimensions of a multidimensional experiment, oversampling by a factor of two together with placing the detector reference frequency outside the spectral window spanned by the signal can resolve the ambiguity (TPPI). Alternatively, two orthogonal phases can be detected sequentially (sequential quadrature detection). The total number of samples required to resolve the sign ambiguity is the same whether quadrature detection or oversampling is employed. Single-phase detection using uniform sampling with random phase (random phase detection, RPD) is able to resolve the frequency sign ambiguity without oversampling, as shown in Fig. 10. This results in a factor of two reduction in the number of samples required, compared to quadrature or TPPI detection methods, for each indirect dimension of a multidimensional experiment. For experiments not employing quadrature or TPPI detection, it provides a factor of two increase in resolution for each dimension.

7.11 Optimal Sampling?

Any sampling scheme, whether uniform or nonuniform, can be characterized by its effective bandwidth, dynamic range, resolution, sensitivity, and number of samples. Some of these metrics are closely related, and it is not possible to optimize all of them simultaneously. For example, minimizing the total number of samples (and thus the experiment time) invariably increases the magnitude of sampling artifacts. Furthermore, a sampling scheme that is optimal for one signal will not necessarily be optimal for a signal containing frequency components with different characteristics. Thus the design of efficient sampling schemes involves tradeoffs. Simply put, no single NUS scheme will be best suited for all experiments.

Fig. 10

Two-dimensional f ₁/f ₂ cross-sections from four-dimensional N,C-NOESY data for the DH1 domain of Kalirin. One dimensional cross sections parallel to the f ₁ axis at the f₂ frequencies indicated by the colored lines are shown above each panel. Panel A is the real/real component of the two dimensional DFT spectrum using quadrature detection in all dimensions. Panel B is the DFT spectrum obtained using only the real/real/real component from the three indirect time dimensions of the time domain data. Panel C is the maximum entropy spectrum obtained using random phase detection. Panels B and C employ 1/8th the number of samples used in panel A

8 Concluding Remarks

The use of NUS in all its guises is transforming the practice of multidimensional NMR, most importantly by lifting the sampling limited obstacle to obtaining the potential resolution in indirect dimensions afforded by ultra high-field magnets. NUS is also beginning to have tremendous impact in MRI, where even small reductions in the time required to collect an image can have tremendous clinical impact. For all the successes using NUS, our understanding of how to design optimal sampling schemes remains incomplete. A major limitation is that we lack a comprehensive theory able to predict the performance of a given NUS scheme a priori. This in turn is related to the absence of a consensus on performance metrics, i.e., measures of spectral quality. Ask any three NMR spectroscopists to quantify the quality of a spectrum and you are likely to get three different answers. Further advances in NUS will be enabled by the development of robust, shared metrics. An additional hurdle has been the absence of a common set of test or reference data, which is necessary for critical comparison of competing approaches. Once shared metrics and reference data are established, we anticipate rapid additional improvements in the design and application of NUS to multidimensional NMR spectroscopy.