Concepts in Projection-Reconstruction

Abstract

The Achilles heel of conventional multidimensional NMR spectroscopy is the long duration of the measurements, set by the Nyquist sampling condition and the resolution requirements in the evolution dimensions. Projection-reconstruction solves this problem by radial sampling of the evolution-domain signals, relying on Bracewell’s Fourier transform slice/projection theorem to generate a set of projections at different inclinations. Reconstruction is implemented by one of three possible deterministic back-projection schemes (additive, lowest-value, or algebraic), or by a statistical model-fitting program. For simplicity the treatment focuses principally on the three-dimensional case, and then extends the analysis to four dimensions. The concept of hyperdimensional spectroscopy is described for dealing with even higher dimensions.

1 Introduction

We live in a three-dimensional world. Survival has ensured that our brains have evolved a remarkable capacity to reconstruct a three-dimensional image based on a pair of slightly different two-dimensional views of our environment. While we take this apparent instance of projection-reconstruction entirely for granted, the complexity of the general problem soon becomes apparent in the science of robotics, when we attempt to teach a machine to construct a reliable visual model of its surroundings. What for humans is an entirely automatic process needs to be derived again from first principles for a perambulating robot. Concepts like parallax and occultation have to be re-examined.

Art presents similar challenges. It was quite some time before artists discovered perspective – the key to depicting a plausible representation of three dimensions on a plane canvas. Nowhere is this challenge more critical than in sculpture, the creation of three-dimensional artefacts that reconcile the visual and tactile senses. It is reported that the famous French sculptor Auguste Rodin employed an unusual stratagem – he placed his model on a turntable with strong back-lighting, concentrating his attention on the changing silhouettes as he rotated the table in small steps. This scheme was certainly effective; his sculptures of the human form are so life-like that his critics accused him of cheating by taking plaster casts of his subjects. A good case can be made that Rodin was the true father of projection-reconstruction.

Present-day computers greatly facilitate this transformation of two-dimensional raw data into a three-dimensional image. Artefacts in a museum collection are often irreplaceable, so that worldwide dissemination is quite impractical. However, if a sequence of digital photographs is taken from several different points of view, a program can be written to reconstruct an image that can be rotated about an axis to give a lifelike representation of three spatial dimensions [1]. The resulting digital archive is readily transferable to any desired location and can be scaled if necessary. A more mundane application is to offer some article for sale on a popular website in a form that conveys a three-dimensional impression. Google Earth offers street views of many cities that give the perception of three-dimensional reality, while more recent research [1] creates a true three-dimensional reconstruction of the local street environment. Lost in a strange city, a person could in principle use a mobile phone to photograph an adjacent building, pass on the information to a distant computer, and receive confirmation of his present location (within a metre) and also his orientation, followed by detailed directions for proceeding to his intended destination. Face-recognition software employs related procedures to track a person in a crowd.

X-Ray tomography [2] makes use of the same principles. A set of pictures of X-ray absorption is taken at different angles of incidence around a circle. The software uses this information to reconstruct an image of the internal organs of the patient. Whereas traditional X-ray studies gave only a two-dimensional image on a sheet of photographic film, tomography allows the surgeon to examine the internal structure as if in three spatial dimensions. At about the same time, and completely independently, Paul Lauterbur [3] hit on the idea of medical imaging by recording nuclear magnetic resonance absorption in an applied magnetic field gradient. By combining the results of measurements at different inclinations of the magnetic field gradient, he was able to reconstruct a map of the distribution of protons within the sample. Soon the ‘sample’ became a human patient and the exciting science of MRI was born.

Projection-reconstruction is not therefore a new phenomenon. Recently it has become of particular interest to high-resolution NMR spectroscopists with the realization [4] that a three-dimensional spectrum can be treated as a candidate for reconstruction in just the same manner as a physiological sample, but with the advantage that the ‘object’ is now a sparse distribution of discrete resonances, like the stars in the night sky, not a continuous absorption medium. (Interestingly, projection-reconstruction borrows at least two data processing schemes from earlier work in radio astronomy.) Sparse sampling assumes particular importance as spectra are recorded in higher and higher dimensions in order to study larger and larger biomolecules, often with isotopic enrichment in both carbon-13 and nitrogen-15. The prime concern is speed. This review focuses on data-sampling methodology rather than the actual spectroscopic applications.

2 Three-Dimensional NMR

The basic principles of projection-reconstruction are most easily understood by reference to the simplest case – three dimensional spectroscopy. Early experiments in NMR were preoccupied with the inherently poor sensitivity. The duration of a measurement was often dictated by the need for appreciable multiscan averaging. On the other hand, multidimensional spectra must normally satisfy the Nyquist sampling condition and the resolution requirements in each and every evolution dimension, so the number of scans is inevitably large. In modern spectrometers, particularly those equipped with a cryogenically cooled probe (receiver coil and preamplifier), this usually ensures a satisfactory signal-to-noise ratio long before all the evolution dimensions have been explored on a full Cartesian matrix. The measurement duration is said to be ‘sampling-limited’ rather than ‘sensitivity-limited’. The obvious remedy is to resort to some form of sparse sampling of evolution space.

Sacrifices must therefore be made. All sparse sampling regimes come at the expense of spectral artefacts. Some introduce an element of randomness in the selection of sampling co-ordinates, but although this can reduce the mean intensity of artefacts, it does so at the expense of widespread proliferation. Better the devil you know. Of the many possible schemes, radial sampling appears to offer the most acceptable solution. Because the resulting artefacts are well defined, effective suppression schemes can be devised. More important is the fact that radial sampling in the time domain gives rise to a particularly simple observable result – projections of the target spectrum in the frequency domain.

The key ‘slice/projection’ theorem was first formulated in a radio astronomy context by Bracewell [5] and later exploited in NMR by Nagayama et al. [6] and Bodenhausen and Ernst [7, 8]. Consider the case of a typical plane S(F ₁ ,F ₂) from a three-dimensional NMR spectrum S(F ₁ ,F ₂ ,F ₃). In order to obtain a projection at some angle α, the theorem postulates that the time domain response should be sampled along a slice through the origin at this same angle α. This requires that the evolution parameters t ₁ and t ₂ be varied jointly [7–13]:

$$ {t_1} = t\ { \cos }\alpha, $$

(1)

$$ {t_2} = t\ { \sin }\alpha. $$

(2)

Fourier transformation of this skew slice through two-dimensional evolution space provides the required projection (Fig. 1).

Fig. 1

The Bracewell slice/projection theorem. The Fourier transform of a slice through the evolution dimension at an inclination α (left) is the projection of the corresponding frequency-domain spectrum at the same angle α (right)

Suppose that the NMR signal from a typical chemical site evolves at a frequency Ω _A in t ₁, and one from a second correlated site evolves at Ω _B during t ₂. The signal component that is observed after the second evolution stage is modulated as cos(Ω _A t ₁) cos(Ω _B t ₂). As in the standard practice, quadrature detection is employed in both evolution intervals, generating four signal components:

$$ {{\text{S}}_1} = { \cos }({\Omega_{\text{A}}}\ {t_1})\,{ \cos }({\Omega_{\text{B}}}\ {t_2}), $$

(3)

$$ {{\text{S}}_2} = { \sin }({\Omega_{\text{A}}}\ {t_1})\,{ \cos }({\Omega_{\text{B}}}\ {t_2}), $$

(4)

$$ {{\text{S}}_3} = { \cos }({\Omega_{\text{A}}}\ {t_1}){ \,\sin }({\Omega_{\text{B}}}\ {t_2}), $$

(5)

$$ {{\text{S}}_4} = { \sin }({\Omega_{\text{A}}}\ {t_1})\,{ \sin }({\Omega_{\text{B}}}\ {t_2}). $$

(6)

After substitution of (1) and (2) the appropriate combinations of these terms creates the four signals:

$$ {{\text{S}}_1} - {{\text{S}}_4} = { \cos }({\Omega_{\text{A}}}t{ \cos }\alpha + {\Omega_{\text{B}}}t{ \sin }\alpha ), $$

(7)

$$ {{\text{S}}_2} + {{\text{S}}_3} = { \sin }({\Omega_{\text{A}}}t{ \cos }\alpha + {\Omega_{\text{B}}}t{ \sin }\alpha ), $$

(8)

$$ {{\text{S}}_1} + {{\text{S}}_4} = { \cos }({\Omega_{\text{A}}}t{ \cos }\alpha - {\Omega_{\text{B}}}t{ \sin }\alpha ), $$

(9)

$$ {{\text{S}}_2} - {{\text{S}}_3} = { \sin }({\Omega_{\text{A}}}t{ \cos }\alpha - {\Omega_{\text{B}}}t{ \sin }\alpha ). $$

(10)

Hypercomplex Fourier transformation gives the sum and difference frequencies (scaled accordingly) given by (Ω _Acosα + Ω _Bsinα) and (Ω _Acosα − Ω _Bsinα). Consequently each measurement produces a pair of projections inclined at ±α. Figure 2 shows five projections of a simulated two-dimensional spectrum containing seven peaks. They were calculated as integrals of the intensities along rays perpendicular to the projected trace. In the time domain the angle α must be positive whereas in the frequency domain α can take on all angles 0° to 360°, although the projections at α and α ± 180° are of course identical.

Fig. 2

A set of five integral projections of a simulated two-dimensional spectrum containing seven responses. Note the situation (upper right) where two responses are eclipsed, giving a projected response with an increased integral in that particular direction

Because the number of time-domain slices (and hence the number of recorded projections) is relatively small, the density of sampling points is far lower than the density used in the conventional experiment, which must examine every point on the complete Cartesian grid while satisfying the Nyquist condition and the requirement for adequate resolution. This is where the critical time saving occurs. With this limited radial sampling [13], the speed advantage increases by an order of magnitude for each new evolution dimension beyond the first. This opens up the possibility of studying unstable molecules, or chemically exchanging systems, or even some protein folding applications. Naturally the sensitivity falls off as the measurement duration is reduced, but it is assumed here that sensitivity is not a limiting factor.

3 Reconstruction

Projections are therefore relatively easily obtained, but the following reconstruction stage is more challenging. Formally this involves the inverse Radon transform [14, 15] – computing the three-dimensional spectrum S(F ₁ ,F ₂ ,F ₃) starting from all the recorded projections. Inverse problems of this kind are notoriously tricky to solve but an NMR spectrum is a favourable case because the target spectrum comprises discrete resonances sparsely distributed in three dimensions rather than a continuum of absorption. There are two general approaches to this problem – deterministic and statistical [16].

3.1 Deterministic Reconstruction

The full three-dimensional spectrum S(F ₁ ,F ₂ ,F ₃) is built up by assembling individual reconstructed planes S(F ₁ ,F ₂) as a function of the directly detected dimension F ₃. The basic procedure for reconstructing S(F ₁ ,F ₂) is best described as ‘back-projection’. Suppose that there are n one-dimensional projection traces available for the reconstruction. Consider a typical trace P ₁, recorded at some arbitrary angle α. Every peak in P ₁ is extended at right angles to the trace to form a set of parallel ridges running across the plane S(F ₁ ,F ₂). These ridges have cross-sections defined by the resonance lineshapes in P ₁. Another set of ridges from a differently oriented projection trace P ₂ intersect with those from P ₁, and the point of intersection defines the location of a potential correlation peak of the target spectrum. If the signals are added there is a peak at the point of intersection (Fig. 3). A set of P _n back-projections is measured. Usually these include α = 0° and α = 90° projections, obtained by Fourier transformation of time-domain signals recorded with t ₂ = 0 or t ₁ = 0, because they have a relatively high sensitivity [17]. When all the projections are combined, the genuine correlation peaks become better defined in comparison with the artefacts.

Fig. 3

The intersection of two back-projected ridges in the additive mode creates a correlation peak but leaves undesirable ridges

The ambiguity between genuine and false correlations can normally be resolved in terms of the number of back-projected ridges that intersect at the same location. A genuine correlation peak involves the intersection of n ridges – one from each and every trace P _n . Intersections involving less than n ridges can normally be taken to indicate false correlations, although in practice this criterion may not be entirely clear cut, notably in situations where some projections contain very weak or missing resonances. Exactly how the intersecting ridges are combined is determined by the back-projection algorithm used [18]. There are three principal methods for reconstructing the two-dimensional spectrum S(F ₁ ,F ₂) by combining back-projections. Each approach has strengths and disadvantages, and the choice is mainly determined by the nature of the available experimental projection data.

3.1.1 The Additive Algorithm

Consider a typical pixel in the S(F ₁ ,F ₂) plane. If it corresponds to a genuine correlation response there are n signal-bearing rays intersecting at that point, one from each of the n projections. The simplest procedure is to add these n contributions to signal intensity of this pixel (or alternatively, calculate the arithmetic mean). This has the advantage that all n traces contribute to the final signal-to-noise ratio, just as in multiscan averaging. Figure 4 illustrates the improvement in spectral quality as the number of measured projections n is increased from 6 through 18. Not only does the signal-to-noise ratio increase, but artefacts also become less apparent, indicating that increasing n is to be preferred over time-averaging identical traces. One advantage is that the additive algorithm allows for the possibility that some projection traces may be missing a particular resonance through poor sensitivity; genuine correlation peaks then occur at lower-order (<n) intersections. Even in the case where there is a very noisy projection trace with no detectable signals, the additive reconstruction remains valid.

Fig. 4

Reconstructed spectra using the additive back-projection algorithm, showing the effect of increasing the number of projections, (a) n = 6, (b) n = 12, (c) n = 18. Six responses are detected as the signal-to-noise ratio increases and the artefacts become less obtrusive. Residual ridges are apparent in (a) but not in (c)

The additive algorithm has the advantage of being linear. The correct relative intensities are normally preserved, and there is no spurious ‘improvement’ in the signal-to-noise ratio in the reconstructed spectrum; the noise floor increases as the square root of n. This algorithm proves to be most useful when n is relatively large, for then the intensities of residual ridges and false cross-peaks are weak in comparison with the genuine correlation peaks, and may fall below the general level of the noise. However, the presence of many vestigial ridges in the skirts of a reconstructed resonance distorts and broadens the derived line-shape. This can be corrected by the application of a resolution enhancement function to the projection traces [19] – a procedure known as filtered back-projection.

If necessary, a reprocessing program can be written to filter out artefacts on the grounds that each true correlation peak carries with it a known, well-defined pattern of back-projection ridges. One such program, ‘CLEAN’, has been adapted from a procedure first introduced in radio astronomy [20, 21] and later applied in NMR spectroscopy [22, 23]. It presupposes that the line shapes in the reconstructed spectrum are known, or can be measured. Then an iterative search selects the tallest response in the reconstructed S(F ₁ ,F ₂) plane and subtracts it, along with its associated back-projection ridges, storing the appropriate intensity and frequency co-ordinates in a table. The next iteration stage is slightly less burdened with artefactual ridges, and the next-tallest response is located and removed, along with its associated ridges. The procedure continues until the detection threshold is just above the base-plane noise, where further iteration becomes unproductive. The only remaining danger is that extremely weak NMR responses, comparable with the baseline noise, could be overlooked. The spectroscopist may then make direct use of the correlation information stored in the table, or alternatively, reconstruct a processed version of the spectrum.

3.1.2 The Lowest-Value Algorithm

In situations where artefacts are of more serious concern than any sensitivity considerations, a more appropriate approach is to superimpose all n back-projection rays, but retain only the lowest amplitude at each pixel [24, 25]. (More specifically, the program selects the lowest absolute magnitude response and then reinstates the original sign.) Then the only intersections that give rise to correlation peaks are those involving one ridge from each trace. Intersections of less than n ridges necessarily overlap with noise from a back-projection that carries no NMR signal, causing any potential false correlation peak to be replaced by the base-plane noise. A similar suppression occurs for all the extraneous ridges. For this reason the lowest-value algorithm generates a very clean reconstruction, because each additional back-projection operation constrains the artefacts more effectively. Sensitivity does not improve with n; indeed it is determined by the signal-to-noise ratio of the weakest resonance in one of the projections. Consequently the reconstruction process breaks down if one of the n traces has a missing resonance, unless this eventuality is recognized and that particular projection is deliberately eliminated from the reconstruction. The lowest-value algorithm is most useful when n is small. Its inherent non-linearity has two consequences. First, the skirts of the reconstructed peaks are clipped; instead of circular (or elliptical) intensity contours, some polyhedral character is imposed, with 2n edges. Second, the character of the base-plane noise is changed, because the algorithm selects the lowest noise amplitude at each pixel.

However, the principal restriction of the lowest-value algorithm is to experiments where all projections have an acceptable signal-to-noise ratio. Otherwise problems arise because the algorithm discriminates against very weak signals comparable with the noise. One bad apple spoils the whole barrel. At any given pixel, the intensity is set by the one particular back-projected ray that just happens to contribute a near-zero noise fluctuation. In this situation the degree of signal suppression may vary from pixel to pixel across the region where a weak correlation peak is expected, leading to break up of the peak profile.

3.1.3 Hybrid Schemes

One solution is to devise a methodology that combines the advantages of the additive and lowest value procedures while avoiding the pitfalls of each. These hybrid schemes seek to balance the advantages of accumulation and purging. An initial accumulation stage combines the reconstructed spectra in the additive mode to improve sensitivity, and then any artefacts are purged by the lowest-value algorithm. The n experimental projections are divided into p independent batches, usually of equal size k. These subsets are used to reconstruct p different versions of the desired S(F ₁ ,F ₂) spectrum, enhanced in signal-to-noise ratio by applying the additive algorithm to each batch in turn. Then the resulting p reconstructions are combined pixel-by-pixel according to the lowest-value algorithm in order to minimize the artefacts. The ratio k:p determines the balance between the conflicting demands of sensitivity and artefact suppression. In the limit that k = n this regime reduces to pure accumulation; at the opposite extreme where p = n this scheme reduces to pure purging. This simple hybrid algorithm is effective, but is not necessarily the optimum scheme.

In an attempt to improve on this hybrid scheme, a combinatorial approach has been suggested [26]. Instead of accumulating p independent batches, this procedure examines a much larger number of batches $^n{C_k} = n!/(n - k)!k!$, representing the sums of all possible combinations of k amplitudes chosen from the available total n. The perceived rationale for this combinatorial method is that processing an extremely high number of batches should deliver a substantial sensitivity advantage as the lowest-value operation is applied to all ⁿ C _k sums. Since these calculations must be repeated for every pixel in the S(F ₁ ,F ₂) plane, and for every plane as a function of F ₃, the method is very computationally intensive.

Mandelshtam [27] has suggested a fast and very effective simplification. When all possible combinations of n signals in batches of k have been examined to search for the batch with the lowest sum, all these low-intensity items must necessarily be found in one particular batch, so the result is simply the sum of the k lowest-amplitude signals. The slow combinatorial calculation can therefore be replaced by a single, fast summation. All n back-projected rays that intersect at a given pixel are examined, and the subset with the k lowest amplitudes is retained. As before, the adjustable parameter k serves to define the desired balance between sensitivity and artefact suppression. Clearly this is the most effective hybrid scheme discovered so far.

3.1.4 The Algebraic Algorithm

When the aim is to study the very crowded spectra characteristic of large biomolecules such as proteins, the overriding concern is to reduce the amount of data to be processed. Then it makes sense to simplify the information in the raw projection traces by eliminating all except the frequency information, ignoring intensities and line shapes. Each projection trace is processed with a peak-picking routine and all further processing is based solely on frequency information. The n projection traces are replaced by n lists of frequencies, each list from a different projection at a specific projection angle α. Here lies the real danger – peak-picking can miss a resonance because it is lying on the shoulder of a stronger response, or simply because a weak resonance lies below the arbitrary intensity threshold assumed by the peak-picking program. Then the criterion for recognizing a genuine correlation peak (n intersections) is compromised.

Apart from these caveats, the algorithm is an exercise in simple algebra [15, 28]. It selects one frequency from each of the n lists, thus defining n intersecting straight lines running across the reconstruction plane S(F ₁ ,F ₂) at various inclinations α. By solving the resulting n simultaneous equations, the algorithm determines whether or not all these straight lines intersect at a point. In practice a certain degree of leeway is allowed, based on the expected accuracy of the frequency measurements. The process is continued until a positive outcome is detected – all n straight lines meet within a small, predefined ‘area of uncertainty’. The ‘centre of gravity’ is taken as the location of a genuine correlation peak. The frequency co-ordinates used in these n-fold solutions are then saved, and the corresponding frequencies removed from the frequency lists.

Problems arise because there may still be further genuine correlations that involve less than n intersecting lines, owing to the shortcomings of the peak-picking routine. An iterative scheme is contrived [29] which relaxes the requirement that there be n intersections. The next stage examines combinations of frequencies from the depleted projection lists, accepting all (n−1)-fold intersections as genuine correlations, and transferring the corresponding frequency co-ordinates to the ‘accepted’ list. There is no absolute guarantee that these new solutions do not contain an occasional false correlation, but the probability is minimized because a large number of resonance frequencies associated with n-fold solutions has already been removed from the list. A third level of iteration may then be initiated, searching for possible genuine solutions of the order (n−2) and so on, until the operator terminates the search.

The power of this algebraic algorithm stems from the very high degree of data reduction achieved in the peak-picking stage, something that is indispensable when dealing with spectra of very high complexity. A possible disadvantage is the lack of a cast-iron criterion for identifying false correlations, but the saving grace is that for large biomolecules an absolutely complete solution may not be necessary. Note that although this mode of operation is correctly categorized as back-projection, it does not involve ‘reconstruction’ in the spectroscopic sense. Correlations appear as frequency co-ordinates in the ‘accepted’ list, with no opportunity for viewing a reconstructed spectrum to make a judgement about reliability. This apparently clean end-result is illusory because information about signal intensities compared with levels of artefacts and noise has been intentionally disregarded. The method has been applied successfully to multidimensional spectra of proteins [29].

3.1.5 Eclipsed Resonances

Complications arise whenever two responses are eclipsed – where the projection has been recorded at an inclination α that happens to catch two peaks in the S(F ₁ ,F ₂) plane in exact alignment. Consider first of all the common case where all responses are positive. One example is illustrated in Fig. 2 (upper right). In the additive algorithm, back-projection then makes a twofold contribution to the intensities at both locations, distorting the relative intensities in the final reconstruction. Fortunately the severity of this intensity error decreases with n. One remedy is to discard the highest and lowest back-projected contributions to the intensity of a given pixel on the grounds that they could be unreliable, then sum the rest. By its very nature the lowest-value algorithm is more forgiving when there are eclipsed peaks; an abnormally intense response in one projection is unlikely to affect the corresponding pixel. Because the algebraic algorithm retains no intensity information but relies solely on frequencies, it is essentially unaffected by eclipsed back-projection.

There is a far more serious problem when the S(F ₁ ,F ₂) spectrum is composed of both positive and negative resonances, since the eclipsed condition can lead to cancellation (or severe attenuation) of the corresponding projected signal. This interference between signals of opposite phase affects the three back-projection algorithms in quite different ways. The additive scheme (with n large) should tolerate occasional cancellation effects reasonably well, since if one direction of back-projection proves ineffective this does little to falsify the overall reconstruction. The lowest-value algorithm is far more sensitive to accidental cancellation because destructive interference can seriously degrade the reconstruction.

A comprehensive solution to interference between eclipsed resonances is provided by a subroutine that sets up the radial sampling in such a way as to avoid all those projection directions α that would lead to eclipsed peaks [18]. It is based on initial sampling with t ₂ = 0 or t ₁ = 0, generating the 0° and 90° projections after Fourier transformation. Two-dimensional convolution of the responses along these axes produces a preliminary test map containing both genuine and false correlation peaks. Projections that record not the integral, but the tallest signal on the projection ray are known as ‘skyline projections’. These are computed at all possible angles α, and the integral over each projection trace is plotted as a function of α. This graph displays a constant integral except at inclinations where two or more responses are eclipsed, when there is a sudden dip. The graph overestimates the danger that genuine peaks are eclipsed because false correlation peaks make contributions to the projections, but it can nevertheless be used to predict those projection angles that avoid all possible cases of overlap.

There are alternative strategies for treating spectra with positive and negative responses. They work best if the projection angles are chosen to avoid eclipsed peaks. One method divides the projection information into two independent sets – one with positive signals and the other with negative signals. These plus and minus sets are used separately to reconstruct plus and minus S(F ₁ ,F ₂) planes, which are then recombined. Another scheme converts all the resonances in the projections into positive peaks, thereby limiting the reconstruction to the absolute magnitude mode.

Mandelshtam [27] has proposed a histogram-based algorithm for reconstructing spectra with both positive and negative peaks, and it does not rely on avoiding the eclipsed case. It retains only the most-likely contribution to the intensity at a given pixel. An artificially broadened amplitude distribution function is derived from the histogram representing all the intensity contributions. Although loosely related to the sum of the individual amplitudes, the maximum of this function is quite insensitive to cancellation effects. This scheme works better at higher values of n. It has been successfully tested on simulated two-dimensional spectra.

3.1.6 Projected Linewidths

In a three-dimensional experiment it is quite likely that the nuclei evolving in t ₁ and t ₂ have different spin–spin relaxation times ${T_2}^{\text{A}}$ and ${T_2}^{\text{B}}$. This means that a response in the S(F ₁ ,F ₂) plane may have very different natural linewidths in the two frequency dimensions. With a skew slice through evolution space at an angle α, Fourier transformation generates a projected response with a Lorentzian width given by

$$ \Delta \nu = {{{{ \cos }\alpha }} \left/ {{(\pi {T_2}^{\text{A}})}} \right.} + {{{{ \sin }\alpha }} \left/ {{(\pi {T_2}^{\text{B}})}} \right.}. $$

(11)

This response is broader than at least one of the parent lines in F ₁ or F _2. This may suggest a choice of projection angle α that favours a narrower projected line if good resolution is an important consideration.

3.2 Statistical Methods

An entirely different approach to reconstruction [16] is to find a model of the two-dimensional spectrum S(F ₁ ,F ₂) that is compatible with all the measured projection traces. In principle the iteration could start with an arbitrary or completely featureless model (zero intensity at every pixel), but usually it is better to employ some ‘prior knowledge’. In the vicinity of a correlation peak it is clear that there must be some correlation between the intensities of adjacent pixels. Prior knowledge may take the form of assumptions about lineshapes or the expected number of resonances in the two-dimensional spectrum, or it might exploit hard evidence from an earlier deterministic scheme. At the most primitive level, where each pixel in the S(F ₁ ,F ₂) plane is fitted independently, these statistical programs converge very slowly, but there is much to be gained by restricting the variable parameters to a number of discrete resonances with appropriate line-shapes, for example two-dimensional Gaussians. There is an inherent danger in these assumptions because a spurious spike in the noise could be ‘promoted’ to the status of a genuine correlation peak – this particular wolf has been provided with sheep’s clothing. A standard least-squares procedure may be used, but convergence to a global solution is faster if the more sophisticated simulated annealing routine [30] is employed. The ‘maximum likelihood’ estimate [31], loosely related to least-squares fitting, seeks to maximize the probability of observing the set of experimental projections P _n given the current proposed S(F ₁ ,F ₂) map.

Maximum entropy reconstruction [32] is claimed to return a ‘maximally non-committal’ solution. It calculates a small set of proposed S(F ₁ ,F ₂) maps that are compatible with the measured projections within the experimental errors, and selects the one with the least information content. For this reason it suppresses all noise and artefacts in the reconstruction and is therefore prone to be misleading. In another terminology, it rejects ‘false positives’ but is likely to return ‘false negatives’. This particular feature suggests that the maximum entropy solution could prove to be a useful starting point for more sophisticated statistical programs.

3.2.1 Bayesian Inference [33]

This is a learning system that tests the degree to which the suggested model ‘M’ is consistent with the experimental data ‘D’, and any prior knowledge about the problem ‘C’. It proposes an initial model two-dimensional spectrum S(F ₁ ,F ₂) in the light of any prior assumptions, for example the expected lineshapes. This defines a conditional prior probability P(M|C) that the model is correct based only on the initial assumptions. The next stage updates P(M|C) in the light of the experimental projection data D to give the posterior probability P(M|DC) reflecting how well the proposed model is justified based on both D and C. The next parameter is the likelihood P(D|MC) that the experimental data D is consistent with the model M and the prior assumptions C. Bayes’ theorem can be expressed as

$$ P\left( {M|DC} \right) \propto P\left( {M|C} \right){ }P\left( {D|MC} \right). $$

(12)

It is now possible to maximize the posterior probability P(M|DC) to give the most probable model for the two-dimensional spectrum S(F ₁ ,F ₂). There are many methods available for such a computation, including the Markov chain Monte-Carlo algorithm.

3.2.2 The Markov Chain Monte-Carlo Method

Monte Carlo methods originated in an ingenious approach to the complex problem of evaluating the probability that a hand of Solitaire would come out successfully. The solution was to set out several Solitaire hands at random and count the proportion of successful hands. A Markov chain defines a sequence of states where the ‘transition probability’ from the current state of a system to its next state is dependent only on the value of the current state. The starting point can be arbitrary but the chain must eventually reach a stationary distribution. It should not get trapped in a loop, and must also retain some probability of jumping to the next state. To avoid bias in the choice of starting conditions the initial set of results is usually discarded, a procedure known as ‘burn in’. Confirmation of convergence of the Markov chain is achieved by inspection of the trajectories to check that there is no obvious remaining trend, or by running several independent simulations to verify that the various solutions lie within a reasonable range.

One example of the NMR reconstruction problem employs the reversible-jump Markov chain Monte-Carlo method [16]. It assumes that the model spectrum S(F ₁ ,F ₂) is made up of a limited number m of two-dimensional Gaussian resonance lines. Then m, the linewidths, intensities, and frequency co-ordinates are varied until the Markov chain reaches convergence. The allowed transitions between the current map M and the new map M’ comprise movement, merging or splitting of resonance lines, and ‘birth’ or ‘death’ of component responses. Compatibility with the experimental traces is checked by projecting M’ at the appropriate angles. The procedure has been found to be stable and reproducible [16].

Some measure of the reliability of all these statistical methods can be obtained by rerunning the programs with different initial conditions. It emerges that in general the location of peaks in the reconstruction is well reproduced, but relative intensities can sometimes vary appreciably. The possibility of false or missing correlations suggests that, in principle, the aforementioned deterministic schemes may be preferable.

4 Four-Dimensional Spectroscopy

When there is ambiguity in the three-dimensional spectrum, or where global isotopic enrichment in ¹³C and ¹⁵N has been employed, a further evolution dimension may be introduced [18]. The problem can still be visualized as a cube in three-dimensional evolution space, neglecting any representation of the real-time direct acquisition dimension t ₄. The three evolution parameters are defined by

$$ {t_1} = t\,{ \cos }\alpha \,{ \cos }\beta, $$

(13)

$$ {t_2} = t\,{ \sin }\alpha \,{ \cos }\beta, $$

(14)

$$ {t_3} = t\,{ \sin }\beta. $$

(15)

(These reduce to the expressions for three-dimensional spectra if β = 0°.) After Fourier transformation a cube that represents the evolution subspace S(F ₁ F ₂ F ₃) is created, with the fourth frequency dimension F ₄ left to the imagination. In this representation the simplest projections are the three ‘first planes’ F ₁ F ₄ (where t ₂ = t ₃ = 0), F ₂ F ₄ (where t ₁ = t ₃ = 0), and F ₃ F ₄ (where t ₁ = t ₂ = 0). Resonance locations in one such plane are independent of peak positions in one of the other planes. Normally these first planes do not provide enough information to solve the reconstruction problem unambiguously. However they do generate accurate values of the chemical shifts, they tend to have relatively good sensitivity, and they can be ‘borrowed’ from related NMR experiments if necessary. A second category of projections is generated by varying two evolution parameters (say t ₁ and t ₂) in step, while holding the third (t ₃) at zero. There are three such kinds of tilted projections, at angles ±α with β = 0°, at ±β with α = 0°, and at ±β with α = 90°.

The third category comprises doubly-tilted projections (involving simultaneous tilting through α and β) recorded when t ₁, t ₂, and t ₃ are incremented jointly. The observed NMR signals are modulated as functions of the evolving chemical shifts (Ω _A, Ω _B, and Ω _C). There are now eight relevant time-domain expressions:

$$ {{\text{S}}_1} = { \cos }({\Omega_{\text{A}}}t\,{ \cos }\alpha { \cos }\beta )\ { \cos }({\Omega_{\text{B}}}t\,{ \sin }\alpha { \cos }\beta )\ { \cos }({\Omega_{\text{C}}}t\,{ \sin }\beta ), $$

(16)

$$ {{\text{S}}_2} = { \cos }({\Omega_{\text{A}}}t\,{ \cos }\alpha { \cos }\beta )\ { \cos }({\Omega_{\text{B}}}t\,{ \sin }\alpha { \cos }\beta )\ { \sin }({\Omega_{\text{C}}}t\,{ \sin }\beta ), $$

(17)

$$ {{\text{S}}_3} = { \cos }({\Omega_{\text{A}}}t\,{ \cos }\alpha { \cos }\beta )\ { \sin }({\Omega_{\text{B}}}t\,{ \sin }\alpha { \cos }\beta )\ { \cos }({\Omega_{\text{C}}}t\,{ \sin }\beta ), $$

(18)

$$ {{\text{S}}_4} = { \cos }({\Omega_{\text{A}}}t\,{ \cos }\alpha { \cos }\beta ){ \ \sin }({\Omega_{\text{B}}}t\,{ \sin }\alpha { \cos }\beta )\ { \sin }({\Omega_{\text{C}}}t\,{ \sin }\beta ), $$

(19)

$$ {{\text{S}}_5} = { \sin }({\Omega_{\text{A}}}t\,{ \cos }\alpha { \cos }\beta )\ { \cos }({\Omega_{\text{B}}}t\,{ \sin }\alpha { \cos }\beta )\ { \cos }({\Omega_{\text{C}}}t\,{ \sin }\beta ), $$

(20)

$$ {{\text{S}}_6} = { \sin }\left( {{\Omega_{\text{A}}}t\,{ \cos }\alpha { \cos }\beta } \right)\ { \cos }\left( {{\Omega_{\text{B}}}t\,{ \sin }\alpha { \cos }\beta } \right)\ { \sin }\left( {{\Omega_{\text{C}}}t\,{ \sin }\beta } \right), $$

(21)

$$ {{\text{S}}_7} = { \sin }\left( {{\Omega_{\text{A}}}t\,{ \cos }\alpha { \cos }\beta } \right){ \ \sin }\left( {{\Omega_{\text{B}}}t\,{ \sin }\alpha { \cos }\beta } \right)\ { \cos }\left( {{\Omega_{\text{C}}}t\,{ \sin }\beta } \right), $$

(22)

$$ {{\text{S}}_8} = { \sin }\left( {{\Omega_{\text{A}}}t\,{ \cos }\alpha { \cos }\beta } \right)\ { \sin }\left( {{\Omega_{\text{B}}}t\,{ \sin }\alpha { \cos }\beta } \right){ \ \sin }\left( {{\Omega_{\text{C}}}t\,{ \sin }\beta } \right). $$

(23)

The treatment is a straightforward extension of the three-dimensional case outlined in Sect. 2. There are four independent projections of the four-dimensional spectrum S(F ₁ F ₂ F ₃ F ₄), giving the frequencies of a typical peak symmetrically related in two pairs:

$$ {\Omega_{\text{A}}}{ \cos }\alpha { \cos }\beta + {\Omega_{\text{B}}}t\,{ \sin }\alpha { \cos }\beta + {\Omega_{\text{C}}}t\,{ \sin }\beta, $$

(24)

$$ {\Omega_{\text{A}}}{ \cos }\alpha { \cos }\beta - {\Omega_{\text{B}}}t\,{ \sin }\alpha { \cos }\beta + {\Omega_{\text{C}}}t\,{ \sin }\beta, $$

(25)

$$ {\Omega_{\text{A}}}{ \cos }\alpha { \cos }\beta + {\Omega_{\text{B}}}t\,{ \sin }\alpha { \cos }\beta - {\Omega_{\text{C}}}t\,{ \sin }\beta, $$

(26)

$$ {\Omega_{\text{A}}}{ \cos }\alpha { \cos }\beta - {\Omega_{\text{B}}}t\,{ \sin }\alpha { \cos }\beta - {\Omega_{\text{C}}}t\,{ \sin }\beta. $$

(27)

5 Hyperdimensional Spectroscopy

The treatment in Sect. 4 is readily extended to five dimensions [18, 34], but the time factor begins to be critical for actual measurements. Drastic economies in digitization must be made in all four evolution intervals before the experiment becomes practically feasible. A five-dimensional experiment that employs only 16 complex time-domain samples in each of the four evolution periods, with 1 s allowed for (complex) signal acquisition and relaxation, would require 12 days to complete. Furthermore, there would be cumulative losses of magnetization due to relaxation and pulse imperfections, and a fourfold overall signal loss attributable to the √2 attenuation between successive stages. Even the processing and storage of high-dimensional data begins to make excessive demands on present-day computers. Although such an experiment is feasible in practice, it is far better to consider an alternative mode for higher dimensional spectra.

The new concept is called hyperdimensional NMR [35, 36]. Consider the case of a ten-dimensional experiment, as might be contemplated for a ten-spin system representing two adjacent aminoacids in a large biomolecule. Imagine the corresponding virtual matrix comprising all ten orthogonal frequency dimensions. There is no point in attempting to construct this matrix by means of an actual ten-dimensional experiment, but it can be used as a conceptual framework for combining lower-dimensional results. The key point is that (say) a three-dimensional spectrum and a four-dimensional spectrum can be combined into a six-dimensional spectrum provided they share one common frequency axis. (A minor assignment problem arises if there are degenerate chemical shifts in the common dimension, but there are relatively simple solutions to this difficulty [37]). Tacking together the appropriate low-dimensional spectra on this imaginary framework allows any one of the ten chemical sites to be correlated with any other; there are 45 pairwise correlations of this kind. Note the irony that the results for a ten-dimensional problem are only easily visualized as plane projections of this monster matrix. The conventional procedure has always been manual cross-referencing of peaks in the two independent low-dimensional spectra. In contrast, hyperdimensional NMR combines these spectra directly, and then relates them to a virtual high-dimensional matrix.

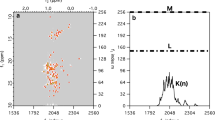
As a practical illustration, Fig. 5 shows 4 typical two-dimensional projections of the ten-dimensional spectrum of a small 39-residue protein agitoxin, globally enriched in ¹³C and ¹⁵N. All these spectra were obtained by combining three- and four-dimensional experiments that were completed in a reasonably short time, whereas the duration of the full ten-dimensional experiment would have been completely unacceptable. These four planes have been selected from the full complement of 45 possible projections. Each of these spectra contains many cross-peaks because there are many different pairs of adjacent amino acids.

Fig. 5

Four typical planes chosen from 45 possible projections of a virtual ten-dimensional matrix, representing the ten-dimensional spin systems in adjacent aminoacid residues of a small protein, agitoxin. They show the correlations (a) N(i−1) to NH(i), (b) CH(i−1) to NH(i), (c) N(i) to Cα(i), (d) Cα(i) to CO(i)

6 Conclusions

Projection-reconstruction is not a new idea. The brain performs hundreds of related operations every second by constructing mental three-dimensional images based on two slightly shifted two-dimensional views of the outside world. Applications in other scientific fields – magnetic resonance imaging and X-ray tomography – are well known. This review focuses on the data-sampling methods required to implement projection-reconstruction schemes designed to speed up multidimensional NMR spectroscopy. Radial sampling of time-domain data is clearly an effective sparse sampling route for this purpose. It relies on a well-proven theorem that the Fourier transform of a skew slice through a two-dimensional time-domain function is the projection of the corresponding frequency-domain function viewed at the same angle. Although, as with all sparse sampling protocols, this scheme introduces artefacts, these are well defined and can be suppressed very effectively. There are basically four deterministic schemes to implement the reconstruction stage. It is essential to match the mode of reconstruction to the appropriate experimental situation – the additive scheme for sensitivity, the lowest-value program for artefact suppression, the Mandelshtam hybrid algorithm for balancing the accumulation and purging features, or the algebraic algorithm for complicated biochemical spectra. On the whole the deterministic schemes are to be preferred over statistical model-fitting procedures. Finally the review describes an effective way to deal with very high dimensional cases – hyperdimensional spectroscopy. Note that the term is not merely a codeword for experiments in higher dimensions, but a conceptual framework for dealing with such systems and for extracting the appropriate information.