Keywords

1 Introduction

Quasicrystals (QCs), which possess a structure between crystalline and amorphous, were first discovered by Shechtman et al. [1] in 1984. It represents an important accomplishment in materials science and condensed matter physics [2]. Due to the unique atomic arrangement structure, QCs possess outstanding properties such as high hardness, high thermal stability, high wear resistance, low surface energy, low friction coefficient, and low heat conductivity [3]. As a result, the vast majority of practical applications of QCs have been applied in the coating industry, including the coating of cookware utensils and effective thermal insulation coatings [4]. QCs can be classified via the number of quasiperiodic directions, such as one-, two-, and three-dimensional QCs, which have one, two, and three quasiperiodic directions, respectively [2]. Most studies related to QCs focus on the one- and two-dimensional form, because of the simplicity of modeling and solution procedures. 1D-QCs with only one direction are quasiperiodic, and two other directions are periodic as conventional crystal materials. Wang et al. [5] derived all possible point groups of 1D-QCs. The general solution in the framework of linear elasticity of 1D-QCs was proposed by Wang [6] through the introduction of two displacement functions following the theory of transversely isotropic materials. The general solutions for other specific systems of 1D-QCs, such as hexagonal and orthorhombic, were also established. For instance, Chen et al. [7] developed the general theory of three-dimensional (3D) elastic problems for 1D-hexagonal QCs and obtained the fundamental solution for the concentrated phonon and phason forces. Liu et al. [8] applied a technique based on the potential theory to derive the general solution for plane problems of 1D-QCs.

In recent years, in-depth research in the coating-substrate area has been a popular issue. In particular, Hou et al. [9, 10] proposed 3D fundamental solutions for the 1D-hexagonal QC layer coating. Huang and his research group [11,12,13] have conducted a series of studies on the coating of 1D-hexagonal piezoelectric QCs with various substrates by using the Fourier transform method. With a similar procedure, Ma et al. [14] studied the problem for the 1D-hexagonal QC coating substrate, considering the thermal effect.

The present study aims to propose a mathematical formulation based on the linear elastic theory of 1D-hexagonal QCs to model the response of a single-layer coating under surface loads. In a layer-substrate system with perfect interface conditions, the substrate is treated mathematically as either a rigid substrate or an elastic half-plane. The governing equations, in terms of the phonon and phason displacements, for both layer and substrate are derived from the linear elasticity theory for 1D-hexagonal QC materials and then solved by the Fourier transform and direct stiffness technique. An efficient and accurate numerical quadrature is then implemented to evaluate all involved integrals resulting from the Fourier transform inversion. The model results are presented for some benchmark cases to verify both the implemented scheme and the obtained solutions.

2 Problem Formulation

2.1 Problem Description

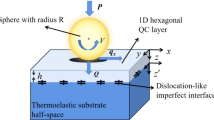
Consider a two-dimensional elastic medium consisting of a single layer resting on the infinite elastic substrate or the rigid substrate, as illustrated in Fig. 1a, b. The interaction between the single layer and the infinite elastic substrate (half-plane) is assumed to be perfectly bonded along their interfaces. The reference Cartesian coordinate system \(\left\{ {x,y,z,O} \right\}\) are taken such that the origin O is located at the top of the surface; the x- and z-axes direct in the rightward and downward directions, respectively; and the y-axis follows the right handed rule. Referring to the chosen coordinate systems, the elastic coasting layer is made of a 1D-hexagonal QC with a constant thickness \(h\). In the present study, the medium is assumed to be free of body forces and subjected only to the arbitrarily distributed loads within the finite range \(x \in \left[ { - a,a} \right]\) on the top surface of the medium. Specifically, these surface loads include the distributed phonon normal traction \(p_{u} (x)\), the distributed phonon shear traction \(q_{u} (x)\), and the distributed phason normal traction \(p_{w} (x)\). Note that the boundary value problems with the considered settings should serve as a mathematical model suitable for simulating the near-surface mechanical behavior of an object coated by a 1D-Hexagonal QC layer.

Fig. 1.
figure 1

Schematic of single-layered elastic medium resting on: a elastic substrate; b rigid substrate under arbitrary distributed surface loadings

Full size image

2.2 Basic Field Equations

Basic field equations for 1D-hexagonal QCs are taken from the work of Wang et al. [5]. For a body undergoing the plane strain deformation in the x-z plane, there are only three non-zero components including the horizontal phonon displacement \(u_{x}\), the vertical phonon displacement \(u_{z}\), and the vertical phason displacement \(w_{z}\). The corresponding phonon and phason strain fields for the 1D-hexagonal QCs are given by

$$ \begin{aligned} & \varepsilon _{{xx}} = \frac{{\partial u_{x} }}{{\partial x}};{\text{ }}\varepsilon _{{zz}} = \frac{{\partial u_{z} }}{{\partial z}};{\text{ }}\varepsilon _{{xz}} = \varepsilon _{{zx}} = \frac{1}{2}\left( {\frac{{\partial u_{z} }}{{\partial x}} + \frac{{\partial u_{x} }}{{\partial z}}} \right); \\ & W_{{zx}} = \frac{{\partial w_{z} }}{{\partial x}};{\text{ }}W_{{zz}} = \frac{{\partial w_{z} }}{{\partial z}} \\ \end{aligned} $$
(1)

where \(\{ \varepsilon_{xx} ,\varepsilon_{zz} ,\varepsilon_{xz} ,\varepsilon_{zx} \}\) are non-zero components of the phonon strain and \(\{ W_{zx} ,W_{zz} \}\) are non-zero components of the phason strain. The generalized Hooke’s law for 1D-QCs is expressed as [5]

$$ \begin{aligned} & \sigma _{{xx}} = C_{{11}} \varepsilon _{{xx}} + C_{{13}} \varepsilon _{{zz}} + R_{1} W_{{zz}} ;{\text{ }}\sigma _{{zz}} = C_{{13}} \varepsilon _{{xx}} + C_{{33}} \varepsilon _{{zz}} + R_{2} W_{{zz}} ; \\ & \sigma _{{xz}} = \sigma _{{zx}} = 2C_{{44}} \varepsilon _{{xz}} + R_{3} W_{{zx}} \\ \end{aligned} $$
(2)
$$ H_{zz} = R_{1} \varepsilon_{xx} + R_{2} \varepsilon_{zz} + K_{1} W_{zz} ; \, H_{zx} = 2R_{3} \varepsilon_{xz} + K_{2} W_{zx} $$
(3)

where \(\{ \sigma_{xx} ,\sigma_{zz} ,\sigma_{xz} ,\sigma_{zx} \}\) are non-zero components of the phonon stress; \(\{ H_{zz} ,H_{xz} \}\) are non-zero components of the phason stress; \(\{ C_{11} ,C_{13} ,C_{33} ,C_{44} \}\) are phonon elastic constants; \(\{ K_{1} ,K_{2} \}\) are phason elastic constants; and \(\{ R_{1} ,R_{2} ,R_{3} \}\) are coupling phonon-phason elastic constants. In the absence of body forces, equilibrium equations governing the phonon and phason stress field are given as

$$ \frac{{\partial \sigma_{xx} }}{\partial x} + \frac{{\partial \sigma_{xz} }}{\partial z} = 0; \, \frac{{\partial \sigma_{zx} }}{\partial x} + \frac{{\partial \sigma_{zz} }}{\partial z} = 0; \, \frac{{\partial H_{zx} }}{\partial x} + \frac{{\partial H_{zz} }}{\partial z} = 0 $$
(4)

By combining Eqs. (1)–(4), it leads to the generalized Navier-Cauchy equations governing the phonon and phason displacement fields:

$$ \left( {C_{11} \frac{{\partial^{2} }}{{\partial x^{2} }} + C_{44} \frac{{\partial^{2} }}{{\partial z^{2} }}} \right)u_{x} + \left( {C_{13} + C_{44} } \right)\frac{{\partial^{2} }}{\partial x\partial z}u_{z} + \left( {R_{1} + R_{3} } \right)\frac{{\partial^{2} }}{\partial x\partial z}w_{z} = 0 $$
(5)
$$ \left( {C_{13} + C_{44} } \right)\frac{{\partial^{2} }}{\partial x\partial z}u_{x} + \left( {C_{44} \frac{{\partial^{2} }}{{\partial x^{2} }} + C_{33} \frac{{\partial^{2} }}{{\partial z^{2} }}} \right)u_{z} + \left( {R_{3} \frac{{\partial^{2} }}{{\partial x^{2} }} + R_{2} \frac{{\partial^{2} }}{{\partial z^{2} }}} \right)w_{z} = 0 $$
(6)
$$ \left( {R_{1} + R_{3} } \right)\frac{{\partial^{2} }}{\partial x\partial z}u_{x} + \left( {R_{3} \frac{{\partial^{2} }}{{\partial x^{2} }} + R_{2} \frac{{\partial^{2} }}{{\partial z^{2} }}} \right)u_{z} + \left( {K_{2} \frac{{\partial^{2} }}{{\partial x^{2} }} + K_{1} \frac{{\partial^{2} }}{{\partial z^{2} }}} \right)w_{z} = 0 $$
(7)

Note that by setting the coupling constants \(R_{1} ,R_{2} ,R_{3} = 0\), Eqs. (5)–(6) reduce to those for the case of periodic or crystal materials with transverse isotropy.

2.3 Solution Procedure

The Fourier integral transform method [15] is utilized to establish a pair of linear ordinary differential equations (ODEs) governing the phonon and phason displacements of the generic layer in the transform space. A standard technique in the theory of differential equations is adopted to obtain a general solution of the ODEs in the transform space. Subsequently, the general solution for other elastic fields, such as phonon and phason stress in the transform space, is obtained via direct substitution in the involved field equations. A stiffness equation for the generic layer in the transform space is also established in explicit form from the established general solution for the displacements and stresses. The direct stiffness method is employed together with the stiffness equation of the coating layer and elastic substrate, the boundary conditions, and the continuity conditions along the material interfaces to form a set of linear algebraic equations governing the displacement unknowns on the boundary and interfaces of the coated-substrate system. Finally, an efficient and accurate numerical quadrature is implemented to evaluate all involved integrals resulting from Fourier transform inversion in the expressions of the phonon and phason displacement and stress fields.

3 Numerical Results

3.1 Material Constants Used in Numerical Study

In the numerical study, a 1D-hexagonal QC with the material constants shown in Table 1 [16] is chosen as a representative material for the coating layer, whereas the elastic substrate (representing the coated component) is made of steel with its properties shown in Table 2. To simulate an elastic substrate made of a periodic or crystal material, the phonon-phason coupling constants are taken as zero, whereas the phason field is fully ignored.

Table 1. Material constants of the coating layer
Full size table
Table 2. Material constants of the elastic substrate. The phonon constants are obtained directly from Young’s modulus and Poisson’s ratio.
Full size table

3.2 Verification

To verify the solution procedure and obtained results, a problem of an isotropic half plane subjected to a uniformly distributed normal phonon traction \(p_{u0}\) over the interval \([ - a,a]\) (i.e., \(p_{u} (x) = p_{u0} ,q_{u} (x) = 0,p_{w} (x) = 0\) for \(x \in [ - a,a]\)) is considered. The exact solution for this particular case can be readily obtained from the results of classical elastic half plane made of isotropic material. To convert from 1D-hexagonal QCs layer to isotropic layer, the phonon-phason coupling constants of 1D-hexagonal QCs are set equal to zero. Additionally, the transition between elastic constant of isotropic materials to the phonon elastic constants following relationship as

$$ C_{11} = C_{33} = \frac{{E\left( {1 - v} \right)}}{(1 - 2v)(1 + v)};C_{12} = C_{13} = \frac{Ev}{{(1 - 2v)(1 + v)}};C_{44} = \frac{E}{2(1 + v)} $$
(8)

where \(E\) and \(v\) are known as Young’s modulus and Poisson ratio, respectively.

To simulate the half plane within the current setting, the thickness of the layer is taken to be sufficiently large. Results for the normalized phonon vertical stress \(\sigma_{zz} /p_{u0}\) and the normalized phonon shear stress \(\sigma_{zx} /p_{u0}\) for three normalized depths \(z/a = 0.1,\,0.5,\,1.0\) with \(a\) denoting a range of loading applied, are reported in Fig. 2 along with the benchmark solutions of classical elaticity. It is seen that the two solutions are in excellent agreement and this therefore confirms the correctness of the proposed scheme.

Fig. 2.
figure 2

Results for a normalized phonon vertical stress \(\sigma_{zz} /p_{u0}\) and b normalized phonon shear stress \(\sigma_{zx} /p_{u0}\) at three different normalized depths \(z/l = 0.1,0.5,1.0\)

Full size image

3.3 Effect of Coating Thickness and Type of Substrate

To investigate the effect of the 1D-hexagonal QC coating layer thickness h and the type of substrate (either rigid or elastic) used in the modeling on the stress transferring to the surface of the substrate, let us consider the coated substrate subjected to a uniformly distributed, phonon normal traction \(p_{u0}\) over the interval \([ - a,a]\) (i.e., \(p_{u} (x) = p_{u0} ,q_{u} (x) = 0,p_{w} (x) = 0\) for \(x \in [ - a,a]\)).

Fig. 3.
figure 3

Results for a normalized phonon vertical stress \(\sigma_{zz} /p_{u0}\) at the bottom of the coating layer and b normalized maximum phonon vertical stress \(\sigma_{zz} (\max )/p_{u0}\) at the bottom of the coating layer versus the normalized coating thickness \(h/a\)

Full size image

The distribution of normalized phonon vertical stress \(\sigma_{zz} /p_{u0}\) at the bottom of the coating layer is reported in Fig. 3a for three values of the normalized thickness \(h/a = 0.5,\,1,\,2\). Results obtained from both rigid and elastic substrates are compared. It is seen that as the normalized coating thickness increases, the maximum phonon vertical stress (attained at \(x = 0,z = h\)) significantly decreases with the transferring stress tending to spread in a wider region over the surface of the substrate. In addition, there is no significant difference of the transferring vertical stress to the substrate predicted by both models (i.e., rigid and elastic substrates). This observation suggests that the simulation of the surface coating by modeling the coated object as a rigid substrate is sufficient for this particular case and can yield comparable results to those with an elastic substrate.

The maximum normalized phonon vertical stress at the bottom of the coating layer versus the normalized coating thickness is also illustrated in Fig. 3b. It is seen that the reduction of the maximum transferring stress is quite rapid for \(h/a \le 3\) and starts to decay in rate as the normalized coating thickness becomes larger than 3. Again, both rigid and elastic substrate models predict almost identical results for the entire range of coating thickness considered. Note also that results reported in Fig. 3b can be potentially useful in the selection of the coating thickness to meet the target of reducing the transfering stress at the surface of coated objects.

4 Conclusion

The elastic response of a plane-strain, surface loaded layer of 1D-hexagonal QCs resting on either a rigid or elastic substrate was investigated. A set of governing differential equations was formulated in terms of phonon and phason displacements from a linear elasticity theory for QCs and then solved analytically by the method of Fourier transform and the stiffness approach. An efficient quadrature was implemented to evaluate all involved integrals in the final expression of all field quantities. The correctness of established results was confirmed by benchmarking with available reference solutions. Verified results and schemes can be further utilized not only in the investigation of the near-surface response of surface coated objects but also to generate essential fundamental solutions sufficient for handling contact problems.