Keywords

1 Introduction

Precise point positioning, as a GNSS high-precision positioning technology, is widely used in Marine, precision timing, disaster monitoring, and other fields because of its advantages such as not being limited by distance in a single operation and without distance limitation [1]. However, low-cost receivers have poor carrier tracking loop performance and multipath under the influence of ionospheric activity and satellite signal occlusion, the receiver loses the lock of satellite signal more frequently, which leads to the re-initialization of the carrier phase ambiguity, so that PPP will experience the same convergence time as the start-up initialization, and high-precision positioning results cannot be obtained for a long time, which seriously restricts the practical engineering application of low-cost receiver PPP [2, 3].

In general, the hardware delay at the satellite changes slowly and can be ignored within a short period time. Therefore, the change of carrier phase ambiguity caused by signal interruption and other reasons can be treated as an integer cycle [4]. Accurate post-interruption ambiguity parameters can be obtained through cycle slip fixing and repair, and rapid re-initialization of PPP can be realized [5]. Therefore, the key to PPP re-initialization is cycle slip fixing.

Precision point positioning usually adopts linear combination methods to deal with cycle slips. Linear combinations of observations can eliminate geometric distance, ionospheric delay, and other parameters. Many scholars have proposed a variety of linear combination cycle slip fixing methods for triple-frequency carrier phase observations [6, 7]. However, most low-cost receivers can only receive single-frequency or dual-frequency observations, so the above methods cannot be used. Joint Doppler observations or inertial navigation methods are usually adopted to deal with cycle slips. Chen et al. proposed an INS (initial navigation system) assisted cycle slip detection and repair method [8]. Li et al. proposed a method to use Doppler observation and inertial combined to assist cycle slip detection and repair [9]. The above methods combined with Doppler observations or INS assistance have achieved excellent results, but the effect will be significantly reduced without the above assistance.

On the other hand, Banville et al. and Zhang et al. proposed a cycle slip repair method based on the time-differenced model [4, 10]. Xiao et al. and Zhao et al. based on the time-differenced model, use quality control to detect the cycle slip and estimate the cycle slip based on the time-differenced model [11, 12]. The method of estimating cycle slip as an unknown parameter by using the geometric time-differenced model is not limited by the frequency number of observations, and the single-frequency, dual-frequency, and triple-frequency observations can be processed. The model also takes into account the correlation of each observation quantity in the geometric position, which can enhance the reliability of cycle slip estimation.

Although the cyclic slip detection and repair method of the high-precision receiver is relatively mature, the research on the cycle slip processing of low-cost receivers with poor observation quality is not perfect, and it is necessary to study the content of cycle slip fixing and repair of low-cost receivers. Therefore, this paper proposes a partial cycle slip fixing method suitable for low-cost receivers, and deals with artificially introduced cycle slips. Through partial cycle slip fixing and repair, the rapid re-initialization of PPP based on a low-cost receiver is realized. Firstly, based on the original observation model, the time-differenced model is derived, and its related error-processing strategy is introduced. Then, the method of selecting part of the cycle slip subset by quality control based on the time-differenced model is introduced in detail, and the model and method of cycle slip estimation and testing are given. Finally, based on the data collected by a u-blox low-cost receiver and the processing of artificially introduced cycle slips, it is verified that the proposed method can fix cycle slips correctly and achieve rapid re-initialization of PPP.

2 Mathematical Model

2.1 Undifferenced and Uncombined Model

The expression of the original undifferenced pseudo-range and carrier phase raw observations is as follows [11]:

$$ P_{r,j}^{s} = \rho_{r}^{s} + c\left( {dt_{r} - dt^{s} } \right) + a_{j} I_{r,1}^{s} + T_{r}^{s} + \left( {D_{r,j} - D_{j}^{s} } \right) + \varepsilon_{{P_{r,j}^{s} }} $$
(1)
$$ L_{r,j}^{s} = \rho_{r}^{s} + c\left( {dt_{r} - dt^{s} } \right) - a_{j} I_{r,1}^{s} + T_{r}^{s} + \lambda_{j} \left( {N_{j}^{s} + d_{r,j} - d_{j}^{s} } \right) + \varepsilon_{{L_{r,j}^{s} }} $$
(2)

In Eqs. (1) and (2), the superscript \(s\) refers to a specific satellite, subscript \(r\) and \(j\) refer to receiver and a specific frequency, respectively; \(P_{r,j}^{s}\) and \(L_{r,j}^{s}\) denote pseudo-range and carrier phase raw observations in meters, respectively; \(\rho_{r}^{s}\) denotes the range between receiver antenna and the phase center of satellite in meters; \(dt_{r}\) denotes the clock offsets of receiver \(r\) in seconds; \(dt^{s}\) denotes the clock offsets of satellite \(s\) in seconds; \(c\) is the speed of light in vacuum, meters per second; \(a_{j}\) is a constant \({{f_{1}^{2} } \mathord{\left/ {\vphantom {{f_{1}^{2} } {f_{j}^{2} }}} \right. \kern-0pt} {f_{j}^{2} }}\), \(I_{r,1}^{s}\) is the slant ionospheric delay on the first frequency of satellite \(s\) in meters; \(T_{r}^{s}\) is the slant tropospheric delay in meters; \(D_{r,j}\) is receiver hardware code delay in meters; \(D_{j}^{s}\) is satellite hardware code delay in meters; \(\lambda_{j}\) and \(N_{j}^{s}\) are the wavelength of the signal in meters and the integer ambiguity in cycles; \(d_{r,j}\) and \(d_{j}^{s}\) are the receiver and satellite uncalibrated hardware phase delays at frequency \(j\) and satellite \(s\) in cycles; \(\varepsilon_{{P_{r,j}^{s} }}\) and \(\varepsilon_{{L_{r,j}^{s} }}\) are the pseudo-range and carrier phase measurement noise.

Among the Eqs. (1) and (2), the effects of phase center offsets (PCO) and phase center variations (PCV) at satellite and receiver antenna, as well as phase wind-up, earth tides, ocean loading, and relativistic effects, can be calculated using existing correction models [11].

2.2 Time-Differenced Model

For epoch \(k\) and \(k + 1\), time-differenced model is formulated as:

$$\Delta P_{r,j}^{s} =\Delta \rho_{r}^{s} + c\left( {\Delta dt_{r} -\Delta dt^{s} } \right) + a_{j}\Delta I_{r,1}^{s} +\Delta T_{r}^{s} + \left( {\Delta D_{r,j} -\Delta D_{j}^{s} } \right) + \varepsilon_{{\Delta P_{r,j}^{s} }} $$
(3)
$$\begin{aligned} {\Delta }L_{{r,j}}^{s} = & {\Delta }\rho _{r}^{s} + c\left( { {\Delta }dt_{r} - {\Delta }dt^{s} } \right) - a_{j} {\Delta }I_{{r,1}}^{s} + {\Delta }T_{r}^{s} \\ & + \lambda _{j} \left( { {\Delta }N_{j}^{s} + {\Delta }d_{{r,j}} - {\Delta }d_{j}^{s} } \right) + \varepsilon _{{ {\Delta }L_{{r,j}}^{s} }} \\ \end{aligned} $$
(4)

where \(\Delta \) is the symbol of time difference, the other parameters with \(\Delta \) denote their variation in two adjacent epochs. The variation of the ambiguity parameter \(\Delta N_{j}^{s}\) is zero for continuous observations, which is an integer number when cycle slip occurs.

In Eqs. (3) and (4), the effects of satellite position and clock offset can be eliminated by external products [11]. Since code hardware delay, uncalibrated hardware phase delay, and the tropospheric delay change slowly with time, the time-differencing can eliminate the influence of relatively stable parameters in a short time. Therefore, the time-differenced model can be simplified as [11, 13]:

$$\Delta P_{r,j}^{s} =\Delta \rho_{r}^{s} + c\Delta dt_{r} + a_{j}\Delta I_{r,1}^{s} + \varepsilon_{{\Delta P_{r,j}^{s} }} $$
(5)
$$\Delta L_{r,j}^{s} =\Delta \rho_{r}^{s} + c\Delta dt_{r} - a_{j}\Delta I_{r,1}^{s} + \lambda_{j}\Delta N_{j}^{s} + \varepsilon_{{\Delta L_{r,j}^{s} }} $$
(6)

3 Partial Cycle Slip Fixing

Based on Eqs. (3) and (4), the cycle slip detection can be divided into linear combination method and quality control-based method, the linear combination method mainly includes wide lane combination (also known as MW combination) and GF combination two linear combinations [14]. The linear combination method only conducts cycle slip detection without cycle slip fixing and repair, etc., which is a common method of conventional PPP. When most satellites cycle slip, it will lead to the re-initialization of PPP, while the cycle slip fixing and repair can significantly accelerate or avoid the re-initialization process. Next, it mainly introduces the partial cycle slip subset method based on quality control and the relevant content of cycle slip estimation and test.

3.1 Partial Cycle Slip Subset Filtering

First, linearize Eqs. (5) and (6), ignoring noise, and get [13]:

$$\Delta P_{r,j}^{s} =\Delta \rho_{0,r}^{s} +\Delta \left( {\varvec{Gx}} \right) + c\Delta dt_{r} + a_{j}\Delta I_{r,1}^{s} $$
(7)
$$\Delta L_{r,j}^{s} =\Delta \rho_{0,r}^{s} +\Delta \left( {\varvec{Gx}} \right) + c\Delta dt_{r} - a_{j}\Delta I_{r,1}^{s} + \lambda_{j}\Delta N_{j}^{s} $$
(8)

where \(\Delta \rho_{0,r}^{s}\) denotes geometry distance variation between satellite position of epoch \(k\), \(k + 1\) and receiver position of epoch \(k\).

The time-differenced geometric change between epochs can be expressed as:

$$ \begin{gathered}\Delta \left( {\varvec{Gx}} \right) = \varvec{G}_{k + 1} \varvec{x}_{k + 1} - \varvec{G}_{k} \varvec{x}_{k} \\ = \frac{{\varvec{G}_{k + 1} \varvec{ + G}_{k} }}{2}\varvec{b} + \frac{{\varvec{G}_{k + 1} - \varvec{G}_{k} }}{2}\left( {\varvec{x}_{k + 1} + \varvec{x}_{k} } \right) \\ \end{gathered} $$
(9)

where \(\varvec{G}\) denotes the direction vector between the receiver position and the satellite position, \(\varvec{x}\) denotes the receiver position parameter; \(\varvec{b} = \varvec{x}_{k + 1} - \varvec{x}_{k}\) is the receiver position variation parameter.

In a short period, the receiver position changes very little compared with the satellite position variation, so the direction vector changes very slowly with time. To illustrate \({{\left( {\varvec{G}_{k + 1} - \varvec{G}_{k} } \right)} \mathord{\left/ {\vphantom {{\left( {\varvec{G}_{k + 1} - \varvec{G}_{k} } \right)} 2}} \right. \kern-0pt} 2}\) with time, the MEO of GPS, MEO, GEO, and IGSO of BDS is analyzed using the 24-h JFNG station data with interval of 30 s. The analysis results of directional vector changes of satellites are shown in Figs. 1 and 2.

Since the high orbit of GNSS satellites, the direction vector changes very slowly with time, it can be seen from Figs. 1, 2, 3 and 4 that when the epoch interval is 30 s, the amplitude is of the magnitude \({{\left( {\varvec{G}_{k + 1} - \varvec{G}_{k} } \right)} \mathord{\left/ {\vphantom {{\left( {\varvec{G}_{k + 1} - \varvec{G}_{k} } \right)} 2}} \right. \kern-0pt} 2}\) or even smaller, as the sampling interval becomes smaller, its value will become smaller, so the data with a sampling interval of 1 s is analyzed subsequently, \({{\left( {\varvec{G}_{k + 1} - \varvec{G}_{k} } \right)\left( {\varvec{x}_{k + 1} + \varvec{x}_{k} } \right)} \mathord{\left/ {\vphantom {{\left( {\varvec{G}_{k + 1} - \varvec{G}_{k} } \right)\left( {\varvec{x}_{k + 1} + \varvec{x}_{k} } \right)} 2}} \right. \kern-0pt} 2}\) in Eq. (9) can be ignored, and then:

$$\Delta \left( {\varvec{Gx}} \right) = \frac{{\left( {\varvec{G}_{k + 1} \varvec{ + G}_{k} } \right)\left( {\varvec{x}_{k + 1} - \varvec{x}_{k} } \right)}}{2} = \overline{\varvec{G}}\varvec{b} $$
(10)
Fig. 1.
figure 1

The time series of \({{\left( {G_{k + 1} - G_{k} } \right)} \mathord{\left/ {\vphantom {{\left( {G_{k + 1} - G_{k} } \right)} 2}} \right. \kern-0pt} 2}\) for MEO satellites of GPS (left) and BDS (right)

Full size image
Fig. 2.
figure 2

The time series of \({{\left( {G_{k + 1} - G_{k} } \right)} \mathord{\left/ {\vphantom {{\left( {G_{k + 1} - G_{k} } \right)} 2}} \right. \kern-0pt} 2}\) for GEO (left) and IGSO (right) satellites of BDS

Full size image

Equations (7) and (8) can be further simplified as:

$$\Delta \tilde{P}_{r,j}^{s} =\Delta P_{r,j}^{s} { - \Delta }\rho_{0,r}^{s} = \overline{\varvec{G}}\varvec{b} + c\Delta dt_{r} + a_{j}\Delta I_{r,1}^{s} $$
(11)
$$\Delta \tilde{L}_{r,j}^{s} =\Delta L_{r,j}^{s} { - \Delta }\rho_{0,r}^{s} = \overline{\varvec{G}}\varvec{b} + c\Delta dt_{r} - a_{j}\Delta I_{r,1}^{s} + \lambda_{j}\Delta N_{j}^{s} $$
(12)

According to Eqs. (11) and (12), a cycle slip detection method based on quality control can be obtained. The ionospheric delay changes little when the epoch interval is small, and can be ignored compared with the cycle slip value [15]. Assuming that there is no cycle slip in all observations, the mathematical model in the form of a matrix is given as follows:

$$ E\left( y \right) = Ax,Q_{y} $$
(13)

where \(y = \left[ {\Delta \tilde{P}_{r,1}^{1} , \ldots ,\Delta \tilde{P}_{r,2}^{n} ,\Delta \tilde{L}_{r,1}^{1} , \ldots ,\Delta \tilde{L}_{r,2}^{n} } \right]^{T}\) is measurement, \(Q_{y}\) is covariance matrix of measurement given by priori pseudo-range and carrier phase accuracy weighted by satellite elevation angle [13], \(x = \left[ {\delta x,\delta y,\delta z,\delta dt_{r} } \right]^{T}\) is estimated parameters.

For the above model, the least squares parameter estimation is performed:

$$ \hat{x} = \left( {A^{T} Q_{y}^{ - 1} A} \right)^{ - 1} A^{T} Q_{y}^{ - 1} y $$
(14)
$$ Q_{{\hat{x}}} = \left( {A^{T} Q_{y}^{ - 1} A} \right)^{ - 1} $$
(15)

Calculate the posterior residual and its covariance matrix:

$$ \hat{v} = y - A\hat{x} $$
(16)
$$ Q_{{\hat{v}}} = Q_{y} - A\left( {A^{T} Q_{y}^{ - 1} A} \right)^{ - 1} A^{T} $$
(17)

According to the estimated result, testing statistics of ith carrier phase residual \(\hat{v}_{i}\) is as follows:

$$ T_{i} = \left| {\frac{{\hat{v}_{i} }}{{\hat{\sigma }_{0} \sqrt {Q_{{\hat{v}_{i} }} } }}} \right| > t_{{\tfrac{\alpha }{2}}} , \, \hat{\sigma }_{0} = \frac{{\hat{v}Q_{y}^{ - 1} \hat{v}^{T} }}{r} $$
(18)

where \(\hat{\sigma }_{0}\) is the estimated value of variance factor \(\sigma_{0}\); \(r\) is the redundancy of design matrix \(A\), which is the difference between the number of rows and the number of columns; \(t_{{{\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0pt} 2}}}\) denotes the test threshold of the two-tail t distribution with degrees of freedom \(r\) and the significance level \(\alpha\), the specific calculation method of threshold value can be referred to in literature [11] and [12]. If the max testing statistics \(\left( {T_{i} } \right)_{\max }\) is satisfied with the inequality in Eq. (18), ith carrier phase measurement is judged existing cycle slip.

Fig. 3.
figure 3

Flowchart of quality control method

Full size image

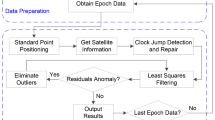
The overall process of quality control is shown in Fig. 3. The maximum value in the carrier phase test statistics is tested through the weighted least square estimation. If it is larger than the test threshold, the corresponding carrier phase observation value is removed and re-estimated, and tested until it passes the test.

3.2 Cycle Slip Estimate and Testing

According to the cycle slip detection results of the quality control method, taking the dual-frequency observation value as an example, it is assumed that the carrier phase value of the first frequency band of the first satellite has cycle slip, and the time-differenced cycle slip estimation model based on geometry is as follows [11, 13]:

$$ y = Ax + Bz $$
(19)
$$ A = \left[ {\begin{array}{*{20}c} {\overline{\varvec{G}}} & {e_{2n}^{T} } \\ {\overline{\varvec{G}}} & {e_{2n}^{T} } \\ \end{array} } \right], \, B = \left[ {\begin{array}{*{20}c} {0_{2n \times 1} } \\ {\lambda_{1} } \\ {0_{{\left( {2n - 1} \right) \times 1}} } \\ \end{array} } \right] $$
(20)

where define \(e_{k}\) as \(1 \times k\) dimension matrix \(\left[ {1, \ldots ,1} \right]_{k}\), \(0_{a \times b}\) as \(a \times b\) dimension zero matrix. In static mode, \(x = \left[ {\delta dt_{r} } \right]^{T}\), matrix \(A\) only contains the coefficients associated with the change in the receiver clock variation. In kinematic mode, \(x = \left[ {\delta x, \delta y{,}\delta z{,}\delta dt_{r} } \right]^{T}\), \(z = \left[ {z_{1}^{1} } \right]^{T}\). If there are other detected cycle slips, the wavelength coefficient and 0 can be added to the corresponding rows and columns of the matrix \(B\).

According to the model described in Eqs. (19) and (20), the least square estimation is carried out, and the float solution of the receiver position change, the receiver clock difference change, and the cycle slip float value and the covariance matrix are obtained. The cycle slip float value and its covariance matrix are brought into the LAMBDA algorithm to fix, and the reliability of the cycle slip fix solution is judged by the R ratio test. The specific expression of the test value is as follows:

$$ \frac{{F\left( {\overline{a}} \right)}}{{F\left( {\overline{a}^{\prime}} \right)}} \le \mu , \, F\left( z \right) = \left( {\hat{z} - z} \right)^{T} Q_{{\hat{z}\hat{z}}}^{ - 1} \left( {\hat{z} - z} \right) $$
(21)

where \(\mu\) is the testing threshold, usually \(\mu = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}\) or \(\mu = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}\); \(\overline{a}\) is the best fixed value; \(\overline{a}^{\prime}\) is the second best fixed value; \(\hat{z}\) is the float value of cycle slip. \(Q_{{\hat{z}\hat{z}}}\) is the covariance matrix of the cycle slip float value. If Eq. (21) is satisfied, the optimal solution is considered to be reliably fixed, and the optimal solution is taken as the fixed solution of the cycle slip.

4 Experimental Results and Analysis

In order to verify whether the method used in this paper can achieve rapid re-initialization of precise point positioning, a simulation experiment is conducted using static data, which is verified by processing artificially introduced cycle slips. The static data collected by the u-blox low-cost receiver is analysed.

4.1 Processing Strategy

The data processing strategy for PPP is shown in Table 1, which processes static data collected by the u-blox C099-f9p low-cost receiver in kinematic mode.

Table 1. Processing Strategy of PPP
Full size table

4.2 Experimental Analysis

The experimental data is the static data collected by the u-blox C099-f9p low-cost receiver in the 16th apartment of Harbin Engineering University, and the reference position high-precision receiver is given. The observation time of the data is October 26, 2020 (DOY: 300), and the data duration is about 3 h 10 min. The experimental scenario, the number of satellites, and PDOP are shown in Fig. 4. The number of satellites ranges from 11 to 14, and the PDOP value ranges from 1.5 to 3, which can see that the geometry of the satellites is better.

Cycle slips were artificially introduced to all satellites every 3000 epochs on the raw carrier phase observation quantity, and the processing analysis was carried out based on conventional PPP and PPP after cycle slip fixing and repair.

The processing results of conventional PPP and repaired PPP are shown in Fig. 5. In the positioning error figure, an obvious re-initialization process existed in conventional PPP, the re-initialization time is the almost same as the first convergence time. The repaired PPP after cycle slip fixing and repair has no re-initialization process, which realizes the rapid re-initialization of PPP. In addition, according to the RMS comparison of Positioning errors between conventional PPP and cycle slip repaired PPP, compared with conventional PPP, after cycle slip fixing and repair, the RMS of positioning errors is significantly reduced because there is no reconvergence.

Fig. 4.
figure 4

Experiment scenario (left), Number of satellites and PDOP (right)

Full size image
Fig. 5.
figure 5

Positioning error of conventional PPP and Repaired PPP (left), RMS of Positioning error between conventional PPP and cycle slip repaired PPP (right)

Full size image

5 Conclusions

To solve the problem of long re-initialization time of PPP due to frequent cycle slips in low-cost receivers, this paper proposes a partial cycle slip fixing method for low-cost receivers with the time-differenced model, which is based on the quality control method to filter a subset of partial cycle slips, and on the time-differenced model and LAMBDA algorithm to estimate and fix cycle slips for rapid re-initialization of PPP. The performance of the proposed algorithm is verified based on static data measured with the u-blox C099-f9p low-cost receiver and artificially introduced cycle slips. The results show that the adopted partial cycle slip fixing method can correctly fix cycle slips and make the PPP essentially free of re-convergence time after repairing cycle slips, with a significantly reduced RMS of positioning error compared to the conventional PPP. The situation will be more severe in real kinematic environments, and subsequent research will focus on how low-cost receivers can handle cycle slips to achieve rapid re-initialization of the PPP in kinematic or partially occluded environments.