Keywords

1 Introduction

Perovskite, which occurs naturally and artificially, is used in our references as an example of how research throughout the world has made truly important strides toward the effective utilization of every attribute of every element categorization. As a platform for broad study on the electronic states and physical characteristics of transition metal oxides (TMOs) for human needs, perovskite oxides (ABO3) have been intensively studied by researchers. For the First-principles investigation, we considered A = Sr and B = Nb, respectively, where A and B correspond to different cations. Similar to SrVO3 perovskite TMOs with a d1 electronic configuration is strontium niobium oxide (SNO). When compared to 4d TMOs, a large range of studies have been conducted on 3d TMOs; however, Oka et al study on 4d TMOs [1] has described the high conductivity of stoichiometric SNO. The fact that bulk samples display metallic electrical conduction, as well as photocatalytic activity for both UV and visible windows, has received significant interest in the scientific community. Mathieu Mirjolet et al. [2, 3] examined the Sr-deficient powder of Sr1-xNbO3, a material that's metallic and exhibits lovely red color indicating an optical absorption process, and found that TMOs based on 3d and 4d metals have great potential for plasmonic applications. In the study of the SNO band diagram, Suresh Thapa et al. discovered that Nbt2g band crosses the Fermi level and suggests metallic nature [4]. To demonstrate the potential of SNO as a UV transparent conduction medium, Yoonsang Park et al. presented a combined DFT and experimental study [5, 6].

With the above inspiration and the great utility of such metal perovskite, material, our present research is also focused on the cubic system of bulk SNO for the understanding of metallic character and optical properties using DFT, keeping in mind the framework discussed above from various literature. This is because the behavior of perovskite oxides holding 4d TM ions is expected to be quite different in comparison to similar and more extensively studied 3d compounds [7,8,9]. Due to their dynamic (electron mobility, carrier density, and electrical resistivity) and static (absorption, refractive index, and loss function) properties at room temperature, the family of SNO has attracted major attention for optoelectronic device applications. Since d1-type TMOs have potential applications as the next generation of transparent electrode materials and are a leading contender to displace traditional TCOs like tin-doped indium oxide (ITO) [8], there is a vital need for us to research the electrical and optical behavior of SNO, as already suggested by our objective. Due to hybridization with the surrounding oxygen ions in the crystal and a reduction in on-site Coulomb interaction, SNO has a higher electrical conductivity. This is also due to its longer 4d electronic states, which give it a more metallic character and diminishing electronic correlation.

2 Theoretical Details

For a clear vision of the present research work, the theoretical details are divided into the following categories:

2.1 Material Details

SrNbO3 has a (cubic) perovskite structure, resembling CaTiO3 in phase, and crystallizes in the cubic Pm-3 m space group with 5 independent atoms per unit cell in the oxidation states O2−, Sr2+, and Nb4+, respectively. SrO12 cuboctahedra are created when Sr2+ bonds with twelve equivalent O2−atoms, sharing corners with twelve equivalent SrO12 cuboctahedra, faces with six comparable SrO12 cuboctahedra, and faces with equivalent NbO6 octahedra. NbO6 octahedra are created when Nb4+ bonds with six equivalent O2−atoms, sharing faces with eight equivalent SrO12 cuboctahedra and corners with an additional six NbO6 octahedra.

2.2 DFT Theories

The success and application of DFT may be attributed to certain extremely astute realizations made by Kohn, Hohenberg, and Sham around the middle of 1960s. DFT was created by reformulating the many-body issue as an analogous single-particle problem and focusing instead on the density of electrons as the primary one to solve. Since its inception in condensed matter physics, it has developed into a powerful tool for material science, nanotechnology, solid-state chemistry, and other computational sub-disciplines. For instance, the Schrodinger equation has trouble with the many-body system because 10 electrons need 30 dimensions, which makes it difficult to get precise answers. From this point on, DFT is effective. The many-body problem's approximations are merely briefly given here. Using these theories and approximations, DFT is developed, which operates in terms of electron density rather than just classical electrons [10, 11]. The Schrödinger equation is solved to determine an atom's ground state energy in known terms:

$$\widehat{H} \psi \left(\left\{{r}_{i}\right\},\left\{{R}_{l}\right\}\right)=E\psi (\left\{{r}_{i}\right\},\left\{{R}_{l}\right\}$$
(1)

2.2.1 The Born–Oppenheimer (BO) Estimation:

The Born–Oppenheimer approximation is one of the key concepts that underlie the description of the quantum states of molecules and enables the separation between the motion of the nuclei and the motion of the electrons [12]. By taking into account the following mathematics, presented in general form, it is possible to see how the Schrödinger equations employ the fact that the mass of an atomic nucleus is considerably more than the mass of an electron:

$$\psi \left(\left\{{r}_{i}\right\},\left\{{R}_{l}\right\}\right)= {\psi }_{N}\left\{{R}_{l}\right\} x {\psi }_{e}\left\{{r}_{i}\right\}$$
(2)

here, ψN = Nuclei wave function and ψe = Electron wavefunction.

2.2.2 The Hohenberg Kohn (HK) Postulates

It consists of two fundamental postulates that were put out by Hohenberg and Kohn [13]. The first theorem states that the total ground state energy or external potential of a many-electron system is an exclusive function of the electron density.

$${\text{E }} = {\text{ E}}_{{\text{o}}} \left[ {\rho _{{\text{o}}} \left( {\text{r}} \right)} \right]$$
(3)

here ρ(r) is density function.

But according to the second postulate, the actual ground-state electron density is the one that minimizes the functional's total energy.

$${\text{E }}\left[ {\rho \left( {\text{r}} \right)} \right]{\text{ }} > {\text{ E}}_{{\text{o}}} \left[ {\rho _{{\text{o}}} \left( {\text{r}} \right)} \right]$$
(4)

2.2.3 The Kohn Sham (KS) Strategy

According to this technique, the KS equation may be used to convert a multi-electron system with ground state eigenvalues into a single electron problem. The formula is as follows:

$$\rho \left(r\right)=\sum_{i=1}^{N}|{\varphi }_{i}\left(r\right){|}^{2}$$
(5)

\(|{\varphi }_{i}\left(r\right){|}^{2}\) is a unit electron wave function.

2.3 Exchange–Correlation Approximations (ECA) Energy Functionals

We all are already aware that, exchange–correlation functional EXC is a crucial component of DFT. LDA/LSDA (local spin density approximation), GGA (generalized gradient approximation), and BLYP (hybrid density functional) are only a few of the approximation methods that have been developed. Sham introduced LDA's core idea [14] for the first time in 1965. In 1986, Perdew and Wang presented GGA [15, 16], which was based on the LDA potential function, and indicated that in addition to the system's local electron density, the exchange energy and correlation energy also rely on the density gradient. Compared to LDA, which is better for metals but less effective for semiconductors, GGA is employed in all sorts of materials.

$${E}_{XC}^{LDA}\left[\rho \right]=\int \rho \left(r\right){\varepsilon }_{XC}\left[\rho \left(r\right)\right]dr$$
(6)
$${E}_{XC}\left[\rho \right]=\int \rho \left(r\right){\varepsilon }_{XC}\left(\rho \left(r\right)\right)dr+{E}_{xc}^{GGA} (\rho \left(r\right),\nabla \rho \left(r\right))$$
(7)

2.4 Electronic Structure Calculations and Properties

Determining a material's electrical structure is the major goal of atomistic simulations. The calculations of wave functions, often referred to as eigenstates, and related eigenvalues, or energies, of electrons surrounding stationary nuclei are the subject of this work. The knowledge of electronic ground states provides knowledge of stability, vibrational properties with a variety of thermal properties, elastic properties, and transport phenomena like diffusivity, ionic conductivity, and dielectric properties. Excited states convey knowledge of electronic transport phenomena and optical properties. This study plays a crucial role in the delicate development of microscopic phenomena as well as in the classification of materials as conductors, semiconductors, insulators, or superconductors. Following are explanations of its electrical band structure (a) and density of states (b) [17].

  1. a.

    Band Structure

    Each energy level divides into N energy levels, creating an energy continuum, as the N atoms form a solid and move towards one another at a distance equal to the lattice constant. This group of continuum energy levels is referred to as an energy band. The quantum mechanical approach offers a comprehensive grasp of the description of the band structure, as shown by the Schrodinger equation, which explains free electron mobility at a potential of zero.

    $$\frac{{d}^{2}\psi }{{dx}^{2}}+ \frac{2m}{{\hbar }^{2}}E\psi =0$$
    (8)

    The state of a free electron is represented by \(\psi\) (r) = Aexp(ikr) (wave function), which produces energy E as,

    $$E\left(k\right)= \frac{{\hbar }^{2}{k}^{2}}{2m}$$
    (9)

    where k = radius of considered sphere; ħ = planks constant; m = electron mass and above Eq. (9) is a dispersion relation and represents a single band.

  2. b.

    The Density of States (DOS)

    There are a relatively large number of energy levels in each band, and the number of them changes based on the material's composition. This constraint requires calculating the number of energy levels or states per unit of energy and per unit of physical space. States that there are per unit of energy “N” The definition of the electronic density of states “D” is “E” per unit volume “V” of the real space.

    $$D= \frac{1}{V}\frac{dN}{dE}$$
    (10)
    $$D=\frac{1}{2{\pi }^{2}}{\left(\frac{2m}{{\hbar }^{2}}\right)}^{3/2}{E}^{1/2}$$
    (11)

2.5 Optical Properties

We continue the research of SNO based on optical characteristics while keeping in mind that we have completed a variety of electronic structure calculations that serve as the foundation for calculating optical features. Materials can also be classified as translucent, opaque, or transparent in addition to this property. It frequently has to do with how responsive the material is to incoming electromagnetic radiation (EMR). Due to exposure to EMR, a number of intriguing features evolved depending on their metallic or non-metallic qualities. The energy E a photon carries is,

$$E=hv$$
(12)

Considering coefficients of absorptivity, reflectivity, and transmissivity as a,r,t, we have.

$$a + r + t = 1$$
(13)

The incident photon's energy is absorbed by the electron during the microscopic treatment of EMR interaction, causing EMR to slow down and produce the refraction phenomena, which is measured by the refractive index. The dielectric function, a key microscopic characteristic that links the electrical structure to optical events, is the next significant variable. Here, the dielectric function Er is described by two equations, the first equation is:

$${\text{d}}\left( {{\text{r}},{\text{f}}} \right){\text{ }} = ~\varepsilon _{{\text{r}}} \left( \omega \right){\text{ }}\varepsilon _{0} {\text{E}}\left( {{\text{r}},{\text{f}}} \right)$$
(14)

here,

“d = ε0E + p” is the displacement vector, “ε0” is the constant for dielectric for the vacuum and “p” is the vector of polarization, and “f” is the frequency of energy, the 2nd equation is given by,

$$\varepsilon _{{\text{r}}} = {\text{ n}}^{{\text{2}}}$$
(15)

The refractive index function may be written with “n” being the refractive index as,

$$\widehat{n}=n-ik$$
(16)

Since our case study of SNO is metal, we obtain an equation that consists of extinction coefficient “k” and plasma frequency “fp” for the metal that defines the intra-band transition of electrons owing to EMR absorption.

$${\mathrm{f}}_{p}= \frac{n{e}^{2}}{{\epsilon}_{0}m}$$
(17)

Theoretically by solving the equations, \(\mathrm{n}\left(\mathrm{f}\right)\)” and “ \(\mathrm{k}\left(\mathrm{f}\right)\)” is obtained as,

“Refractive index”

$$\mathrm{n}\left(\mathrm{f}\right)=\{{\frac{{\left[{\varepsilon }_{1}^{2}\left(\mathrm{f}\right)+{\varepsilon }_{2}^{2}(\mathrm{f})\right]}^{1/2}+ {\varepsilon }_{1}(\mathrm{f})}{2}\}}^{1/2}$$
(18)

“Extinction Coefficient”

$$\mathrm{k}\left(\mathrm{f}\right)=\{{\frac{{\left[{\varepsilon }_{1}^{2}\left(\mathrm{f}\right)+{\varepsilon }_{2}^{2}\left(\mathrm{f}\right)\right]}^{1/2}+ {\varepsilon }_{1}\left(\mathrm{f}\right)}{2}\}}^{1/2}$$
(19)

here, ε1 = real component; ε2 = imaginary component; of dielectric function “εr” which is affected by the damping parameter in a real metal case, hence complex equation for the dielectric function becomes:

$$\varepsilon _{{\text{r}}} = {\text{ }}\varepsilon _{{\text{1}}} + {\text{ i}}\varepsilon _{{\text{2}}}$$
(20)

which are connected via frequency “f” by the Kramers–Kronig relation as;

$${\varepsilon }_{1}\left(f\right)=1+\frac{2}{\pi } {\int }_{0}^{\infty }\frac{{\omega }{\prime}{\varepsilon }_{2}{(f}{\prime})}{{\omega }^{{\prime}2}-{\omega }^{2}}d{f}{\prime}$$
(21)

A material's precise dielectric function equation can be used to predict how it will react electronically to an incoming photon, given as:

$$\varepsilon _{{\text{r}}} \left( {\text{f}} \right){\text{ }} = {\text{ }}\varepsilon _{{\text{1}}} \left( {\text{f}} \right){\text{ }} + {\text{ i}}\varepsilon _{{\text{2}}} \left( {\text{f}} \right)$$
(22)

Typically, the real component ε1(f) indicates the phase lag between the incident and induced polarized field component and the imaginary component ε2(f) reflects energy loss. Calculating ε2(f) involves comparing the momentum matrix components of the empty and occupied electronic states. Using “c” as the speed of light, equations describing several other significant optical characteristics are described below.

“Reflectivity”

$$R\left(f\right)=\frac{{(n-1)}^{2}+{\left(\frac{\alpha c}{2f}\right)}^{2}}{{(n+1)}^{2}+\left(\frac{\alpha c}{2f}\right)}$$
(23)

“Energy loss spectra”

$$L\left(f\right)=\frac{{\varepsilon }_{2}(f)}{\left[{\varepsilon }_{1}^{2}(f)+{\varepsilon }_{2}^{2}(f)\right]}$$
(24)

“Absorption Coefficient”

$$\alpha \left(f\right)=\frac{2f}{c}{\left\{\frac{{\left[{\varepsilon }_{1}^{2}\left(f\right)+{\varepsilon }_{2}^{2}\left(f\right)\right]}^{1/2}-{\varepsilon }_{1}(f)}{2}\right\}}^{1/2}$$
(25)

2.6 Computational Details

Ab-initio kind of computation, i.e., the First principal calculation has been performed using the WIEN2k package [18] based on DFT. The KS equations of DFT are solved using the full-potential (linearized) augmented plane-wave and local-orbitals [FP-(L) APW + lo] basis set to look at the different properties. In the current investigation, we use many software factors to comprehend the program's variety of applications by concentrating on electronic and optical aspects. We have used GGA for the XC functional constructed with the PBE prescription. The atomic coordinate-dependent visualization of the material unit cell, i.e., atomic structure, has been done using VESTA [19] (Visualisation for Electronic Structural Analysis) for a proper understanding of the considered cell.

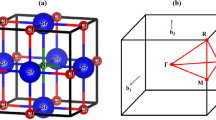
For DFT calculations, we need a crystal information file (cif), which we obtained from the materials project site [20], from which SrNbO3 cif has been obtained. The cif file reveals that the SrNbO3 is a cubic crystal system, having a cubic lattice system that has been visualized from VESTA as shown in Fig. 1, comprising Hall Number P423, and International space group name and number Pm-3 m and 221 respectively.

Fig. 1
A 3-D ball and stick diagram represents the crystal structure of S r N b O 3. N b atoms surrounded by O atoms form a cubical structure and are connected to the central atom labeled S r.

Crystal structure visualisation of (SNO) SrNbO3

Full size image

We first proceeded with the optimization of the structure formed using the cif file, which includes atoms whose coordinates have been given in Table I. After optimization, we obtained the optimized structure. We performed spin-polarized calculations of the optimized cubic structure having lattice parameters a = b = c = 7.753399 Bohr, unit cell volume = 466.09710 Bohr3, and convergence criteria for energy = 0.00001 Ry, force = 1mRy/au, and charge = 0.0001e have been applied. We have used GGA type of exchange–correlation functional for pseudopotential under Perdew-Burke-Ernzerhof, RKMAX = 7.0, smearing = TETRA, and energy separation between core and valence = -6.0 Ry with 10,000 k-points having div. 21 × 21 × 21 for all calculations for our whole study.

Table 1 Considered atomic positions
Full size table

3 Obtained Results and Discussions

In this section, the obtained results have been discussed based on below mentioned several subparts.

3.1 Structure Optimization

As we know “structure dictates the properties,” thus structure optimization should be our priority. Therefore, theoretically speaking, geometric optimization must be carried out by relaxing the structure at various volumes, determining the global minimum energy, and the proper pressure, and then fitting the structure with the appropriate equation of state (EoS). Figure 2 displays the results of using the Murnaghan EoS optimized structure, and Fig. 3 displays the results of the scf calculation's energy convergence plot.

Fig. 2
A line graph plots energy versus change in volume for S r N b O 3. The line plotted for energy follows a downward trend up to four percentage points of change in volume and starts to rise again.

Optimized energy-volume curve of SrNbO3

Full size image

The volume-energy curve shows that the minimum total energy has been obtained at a 3% change of volume w.r.t. initial structure, hence parameters corresponding to this value have been utilized further for all kinds of required calculations using DFT in the next sections.

Fig. 3
A line graph plots total energy versus the number of iterations. The line plotted for total energy has a sharp spike initially between the second and fourth iterations, falls steeply during the sixth iteration, and flattens out thereafter.

Energy convergence plot of SrNbO3

Full size image

3.2 Electronic Properties

The electronic band structure Fig. 4 and DOS. Figure 5 contribute towards the formation of electronic properties and are mentioned below.

Fig. 4
Two line graphs plot the energy band of S r N b O 3 for spin-up and spin-down conditions. Multiple energy lines in both graphs follow a fluctuating pattern and almost have a similar pattern.

Electronic band structure of SrNbO3 for both spins (different orbital configuration)

Full size image
Fig. 5
A line graph of D O S versus energy plots lines for up spin and down spin. Both lines follow a fluctuating pattern. Both lines of the up spin and down spin are symmetrical in positive and negative directions.

Total density of state comprising up and down spin for overall SrNbO3 (TCP) material

Full size image

3.2.1 Electronic Band Structure

As discussed in the theory section Eq. (9) describes a dispersion relation that represents the single band too, keeping this fact in mind, we have come across the following electronic band structure of SrNbO3, for both spins along the Brillion-zone integrations, which were carried out along the high symmetry points “R, Γ, X, M, Γ” for band structure calculations. Band structure of both up and down spins along the Fermi level (EF) can be seen in Fig. 4 within the practical energy range -8 to 8 eV, respectively.

Further, we have come across the energy band gap of 0 eV that clarifies it as metallic, under the most common one, the parameter-free GGA functional developed by Perdew, Burke, Ernzerhof (PBE).

3.2.2 DOS and PDOS Calculations

The DOS and PDOS of each and every atom's contribution has been revealed in this section, where DOS represents the number of states available to electrons, it’s the only function depending upon energy in DFT calculations. The total density of states TDOS of SrNbO3 material for different orbital configurations is shown in Fig. 5 below.

For a better insight into DOS, PDOS of every atom in SNO is shown below in Fig. 6.

From Figs. 6, 7 and 8 we note that the region of energy range –8 eV to –3.5 eV approximately in the valence band is dominated by the p-states of O and from region –1 eV, at Fermi level and that at the conduction band to is dominated by the same p-state that sums up the total contribution of O in TDOS is mostly due to p orbital compared to s-orbital.

Fig. 6
A line graph of D O S versus energy plots lines for O, s, and p. The lines for O and p follow a fluctuating pattern with sharp spikes, while the line for s almost remains flat, with a slight fluctuation at 3 electron volts on the y-axis.

PDOS of oxygen atom in up spin

Full size image
Fig. 7
A line graph of D O S versus energy plots lines for O, s, and p. The lines for O and p follow a fluctuating pattern with sharp spikes, while the line for s almost remains flat, with a slight fluctuation at 3 electron volts on the y-axis.

PDOS of oxygen atom in down spin

Full size image

From Figs. 8 and 9, we see that the same region of energy (–8 eV to –3.5 eV) in “Nb” atom is dominated by d orbital even having “p” orbital contribution in significant number, but “s” states an absence in the PDOS of Nb and from the valence band of energy range -1 eV to conduction band crossing Fermi energy level is well supported with “d” & p-orbital but in less nature.

Fig. 8
A line graph of D O S versus energy for up spin. It plots lines for N b, s, p, and d. The lines for N b, p, and d follow a fluctuating pattern with sharp spikes, while the line for s almost remains flat, with a few fluctuations at the end.

PDOS of Niobium atom in up spin

Full size image
Fig. 9
A line graph of D O S versus energy for down spin. It plots lines for N b, s, p, and d. The lines for N b, p, and d have a fluctuating pattern with sharp spikes on the negative side and the fluctuation reduces on the positive side, while the line for s almost remains flat.

PDOS of Niobium atom in down spin

Full size image

If we study the above plots in Figs. 10, 11, it follows the same trends as of “O” and “Nb” atom, the major difference is that in valence band “p” & “d” states both contribute to domination in TDOS of SNO having d-orbital in dominating character but as soon we move from valence band towards Fermi than to conduction band, we see a rapid decrease in DOS contribution of all the s, p, d states.

Fig. 10
A line graph of D O S versus energy for up spin. It plots lines for S r, s, p, and d. The lines for S r, p, and d have a fluctuating pattern with sharp spikes on the negative side and minor fluctuations on the positive side, while the line for s almost remains flat.

PDOS of Strontium atom in up spin

Full size image
Fig. 11
A line graph of D O S versus energy for down spin. It plots lines for S r, s, p, and d. The lines for S r, p, and d follow a fluctuating pattern with sharp spikes on the negative side and minor fluctuations on the positive side, while the line for s almost remains flat.

PDOS of Strontium atom in down spin

Full size image

3.3 Optical Properties

Keeping in mind that we have done all kinds of electronic structure calculations which form the basis for optical properties calculation. The calculated ε1(f) and ε2(f) for the strontium niobium oxide using PBE functionals are shown below. Figure 12 shows the reflectivity R(f) of SNO perovskite having minima at plasma edges. These characteristics shown by SNO are due to the plasmonic excitation within the material, which causes the decline within the plots of reflectivity.

Fig. 12
A line graph of reflectivity R versus energy plots lines for R subscript x and R subscript y. Both lines follow a concave-down decreasing trend, with slight fluctuations.

Reflectivity through SNO

Full size image

The n(f) in Fig. 13 shows the varying refractive index, which is the result of refraction within the material. We can conclude from both of the plots that there is negligible varying R(f) and almost constant n(f), which implies that there is not a much higher degree of refraction or reflectance within the material, it remains constant throughout the UV and visible light wavelength, bringing it in the category of transparent conducting perovskites.

Fig. 13
A line graph of refractive index n versus energy plots lines for n subscript x and n subscript y. The overlapping lines follow a steep downward trend at the start and then flatten out with increasing energy values.

Refractive index variation in SNO

Full size image

The peak of the energy loss spectrum L(f) in Fig. 12 can be used for understanding the plasmonic resonance. In Fig. 13 spectra near approaching 0 eV, and the absorption coefficient is almost approaching 0. The refractive index in Fig. 10 approaches 1 and the absorption coefficient falls to 0 at energies above plasmon energy, demonstrating the transparency of the material. The measurement of optical conductivity, which is the extension of electrical transport to high (optical) frequencies, is quantifiable, contact-free, primarily responsive to charged responses, and it is based on polarized absorption spectra. Figure 14 explains the optical conductivity spectra that designate that SNO is optically active for visible to UV light. Overall Fig. 15 explains the degree of absorption or reflection radiation taking place through SNO, dependent on atomic, chemical, and structural composition as an intrinsic property.

Fig. 14
A line graph of the extinction coefficient k versus energy plots lines for k subscript x and k subscript y. Both lines completely overlap and follow an exponentially decreasing trend.

Extinction coefficient of SNO

Full size image
Fig. 15
A line graph of electron energy loss L versus energy plots lines for L subscript x and L subscript y. The overlapping lines follow a concave-up increasing trend and drop after reaching an energy value of 2.5 electron volts.

Energy loss spectra of SNO

Full size image
Fig. 16
A line graph of the absorption coefficient alpha versus energy plots lines for alpha subscript x and alpha subscript y. Both lines increase steeply at the beginning up to an absorption coefficient of 30 and follow a fluctuating pattern with a gradual downward trend.

Absorption coefficient of SNO

Full size image
Fig. 17
A line graph of optical conductivity sigma versus energy plots 4 lines. The lines for R e of sigma subscript x and y overlap and follow a steep downward trend that flattens out. The overlapping lines of I m of sigma subscript x and y have an initial spike and follow a gradual downward trend.

Optical conductivity of SNO

Full size image

4 Conclusions

Overall, the most recent method for examining a material's electronic structure is DFT, within the framework of the DFT FP-LAPW technique, employing GGA-PBE functionals, a thorough analysis of the cubic-structured SNO's structural, electrical, and optical aspects of the optimized crystal lattice are carried out very successfully, whose lattice parameters were comparable to earlier efforts. The study of electronic properties by both the calculated band structure and density of states has been strongly explained towards its metallic behavior. As the refractive index is approaching one and absorption spectra can be seen as a maximum within the photon energy implying the UV and visible window. Therefore, we can conclude that it transmits the whole incident light rays making it TCP. The result presented here in this work can be used and helpful as a road map for experimentalists for the futuristic application of this needful material especially in the optical aspect.