Electromagnetohydrodynamic (EMHD) Flow Actuation with Patterned Wettability

Abstract

Due to the low Re flow in a microchannel, turbulent mixing is absent. Hence, there is a need to explore novel unconventional mechanisms to improve mixing efficiency. In the present study, we theoretically analyze the interplay of an externally applied electromagnetic field and wall wettability in the mixing hydrodynamics. We observe that while the discharge rate through the microchannel depends on both the electric and the magnetic field, the interplay of wall wettability and the magnetic field governs the local vortex generation, which controls the mixing phenomenon. However, the discharge rate reduces with increased magnetic field strength.

1 Introduction

Microfluidic devices have recently become popular in various medical, scientific, and industrial utilities. Advantages such as the need for only small samples, fast rates, and a wide range of applications have made them an integral area of research and popularized devices like Lab-on-a-chip, mixers, and sensors. Flows at such a small scale are manipulated with the help of different effects such as capillary effects, electric and magnetic fields, rotation, and acoustics used independently or in combination [1]. Mixing and throughput rate are the primary criteria that define the device’s efficiency for biochemical processes. Passive techniques like adding groves along the length of the microchannel to facilitate mixing [2] were used extensively. Lately, the use of active techniques such as the use of pulsating electro-osmotic flows [3], use of wall corrugations [4] or the use of surface charge modulation [5, 6] are more frequent. Ghosh and Chakraborty [7] imagined the case of mixing in the presence of patterned slip on the wall and charge-modulated surface, with a more practical example of the presence of an electric double layer (EDL).

Recently, the unique opportunity to manipulate flow using forces induced by magnetic fields has been observed [8]. Theoretical and experimental studies for flow rates Magneto hydrodynamic (MHD) mixers have shown increased flow rates. For example, Lee et al. [9] constructed a novel MHD micropump and showed various advantages of using Lorentz force as a pumping mechanism, Zhao et al. [10] studied capillary flows in the presence of the magnetic field in hydrophobic and hydrophilic channels, Tso and Sundaravadivelu [11] studied capillary flow sandwiched in parallel plates influenced by an electromagnetic field.

Mixing is one important parameter when we consider the biochemical applications of microfluidic devices. The more the mixing, the more efficient the reaction is, a general trend in chemical reactions. Thus, numerous studies to understand mixing in the microchannel are being carried out by researchers. For example, studies were done on mixing in the presence of electro-osmotic flow [3, 5,6,7], also Bau et al. [12] investigated an MHD stirrer for micromixing. More practical studies for biochemical applications such as DNA hybridization [13], thermal effects on micro-scale blood low [14], and macromolecular separation [15] have also been carried out in the last few years.

The present study explores the effect of the patterned slip length of a wall in the presence of electromagnetohydrodynamic (EMHD) flow actuation. Bau et al. [12] investigated MHD stirrers where mixing is induced with the help of alternating potential differences across the wall. Paul and Chakraborty [16] studied the effect of EMHD flow actuation in the presence of EDL, which is a more practical case. Though, they considered a no-slip condition on the walls, which is generally not the case in micro-scale flows. In the present study, the interplay between effects of patterned slip on the wall and combined EMHD flow actuation are studied. Under the same conditions, more mixing in the presence of a magnetic field as opposed to the absence of it is observed. Results at very low magnetic fields are validated against past studies.

2 Methodology

2.1 Problem Description

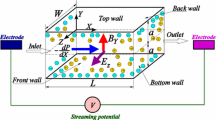
We consider a microchannel with height H (vertical direction) and length L (axial direction). We apply axial electric field-E and vertical magnetic field-B to the fluid sandwiched between the two parallel plates. Channel length in the transverse direction is assumed to be significantly larger than the height H of the channel. Thus, flow can be treated as a two-dimensional flow. The walls are imposed with patterned slip [7] given as below,

$$ u\left( 0 \right) = ls\left( {1 + \delta {\text{cos}}\left( {qx + \theta } \right)} \right)\left( {\partial u\left( {y = 0} \right)} \right)/\partial y $$

(1)

$$ u\left( 1 \right) = - ls\left( {1 + n\delta {\text{cos}}\left( {qx + \theta } \right)} \right)\left( {\partial u\left( {y = 1} \right)} \right)/\partial y $$

(2)

Newtonian fluid moves due to the influence of combined electromagnetohydrodynamic flow actuation. Flow mixing is induced by patterned slip on the walls, which creates a mismatch between wall interface velocity and velocity in the bulk of fluid, which in turn induces local vortices. Fluid in the channel is considered to have permittivity ε and dynamic viscosity µ (Fig. 1).

Fig. 1

Flow between parallel plate microchannel in the presence of axial electric field (E) and vertical magnetic field (B). Walls have patterned slip

The channel walls are assumed to have constant surface potential. This wall potential induces the formation of an electric double layer (EDL). Using the Poisson–Boltzmann equation in the limit of Debye–Huckel Linearization, the induced electrostatic potential can be described as,

$$ \Delta^{2} \psi^{*} = \lambda^{*2} \psi^{*} $$

(3)

where $\lambda \left( { = \frac{{2n_{0} ze}}{\epsilon \kappa T}} \right)$ is the inverse of length, where z is the valence of the concerned charge, e is the electronic charge, n0 is the average number of positive or negative ions in the buffer, $\kappa$ is Boltzmann constant, and T is temperature.

Equation (3) is non-dimensionalized with variables being non-dimensionalized as $(x \to \frac{{x^{*} }}{H},y \to \frac{{y^{*} }}{H},\psi \to \frac{{\psi^{*} }}{\xi }, \rho_{e} \to \frac{{\rho_{e}^{*} }}{{2\rho_{0} }}, \lambda \to \lambda^{*} H)$, where $\rho_{e}$ is the volumetric charge density normalized with the help of reference charge density $\rho_{0} = n_{0} ze$ and $\xi$ is reference zeta potential (which is the same as induced surface potential at the walls). Boundary conditions for $\psi$ read as,

$$ \psi \left( 0 \right) = \psi \left( 1 \right) = 1 $$

(4)

solving Eq. (3) with boundary conditions (4) gives non-dimensionalized $\psi$ as,

$$ \psi = \frac{{\cosh \left( {\lambda \left( {\frac{1}{2} - y} \right)} \right)}}{{\cosh \left( {\frac{\lambda }{2}} \right)}} $$

(5)

2.2 Mathematical Model

For a given charge, distribution flow is induced with the help of combined electromagnetic effects. A driving pressure gradient aids the motion of the fluid, and this electromagnetohydrodynamic (EMHD) effect is given by the Navier–Stokes equation as follows:

$$ \rho_{f} \frac{{D{\varvec{u}}^{\user2{*}} }}{Dt} = - \nabla P^{*} + \mu \nabla^{2} {\varvec{u}}^{\user2{*}} + \vec{F} $$

(6)

where $\rho_{f}$ is the fluid density, ${\varvec{u}}^{\user2{*}}$ ($\overrightarrow {{u^{*} }} = u^{*} \hat{i} + v^{*} \hat{j}$) is Eulerian velocity, P is pressure, and $\vec{F}$ is net body force acting on the fluid. In our case, this body force is given by combined electric and magnetic effects acting on the fluid. Thus, one may write,

$$ \vec{F} = \rho_{e}^{*} \vec{E} + \vec{J} \times \vec{B} $$

(7)

where

$$ \vec{J} = \sigma_{e} \left( {\vec{E} + \overrightarrow {{u^{*} }} } \right) \times \vec{B} $$

(8)

where $\sigma_{e}$ is the electrical conductivity of the medium, and $\rho_{e} = - ze\xi /\kappa T$. In our case, $\vec{E} = E\hat{i}\;{\text{and}}\;\vec{B} = B\hat{j}$.

We consider the effect of this force only in the XY plane. The simplified form of Navier–Stokes and mass balance equations in case of the fully developed steady case are given as:

$$ \begin{aligned} & - \nabla P^{*} + \mu \nabla^{2} {\varvec{u}}^{\user2{*}} + \left( {\rho_{e}^{*} E - \sigma_{e} u^{*} B^{2} } \right)\widehat{i } \\ & \partial u^{*} /\partial x^{*} + \partial v^{*} /\partial y^{*} \\ \end{aligned} $$

(9)

Subjected to slip boundary conditions (1), (2), and no penetration boundary condition as v(0) = v(1) = 0.

The above Eq. (9) is normalized further by taking non-dimensional $u \to \frac{{u^{*} }}{{u_{0} }},v \to \frac{{v^{*} }}{{v_{0} }},P \to \frac{{P^{*} }}{{P_{0} }}$; where $u_{0} = - \varepsilon \xi E/\mu \;{\text{and}}\;P_{0} = \mu u_{0} /H$, which gives the final form of normalized governing equations as:

$$ \begin{aligned} & - \partial P/\partial x + \nabla^{2} {\varvec{u}} + \lambda^{2} \psi - {\varvec{Ha}}^{2} {\varvec{u}} = 0 \\ & - \partial P/\partial y + \nabla^{2} {\varvec{v}} = 0 \\ \end{aligned} $$

(10)

where $(Ha = \sqrt {\sigma_{e} B^{2} /(\mu /H^{2} )} )$ is the Hartmann number. By introducing stream function $\phi$, and substituting the expression for $\psi$ from Eq. (5), the above governing equation can be rewritten as:

$$ \nabla^{4} \phi - {\text{Ha}}^{2} \frac{{\partial^{2} \phi }}{{\partial y^{2} }} = \frac{{\lambda^{3} {\text{ sinh}}\left( {\lambda \left( {\frac{1}{2} - y} \right)} \right)}}{{\cosh \left( {\frac{\lambda }{2}} \right)}} $$

(11)

where

$$ u = \frac{\partial \phi }{{\partial y}}\;{\text{and}}\;v = \frac{\partial \phi }{{\partial x}} $$

(12)

Normalized governing Eq. (11) can be solved analytically using the regular perturbation method with perturbation parameter $\delta$ by expressing stream function as:

$$ \phi = \phi_{0} + \delta \phi_{1} $$

(13)

Governing equation is modified using the perturbed form of $\phi$ as:

$$ \nabla^{4} \phi_{0} - {\text{Ha}}^{2} \frac{{\partial^{2} \phi_{0} }}{{\partial y^{2} }} = \frac{{\lambda^{3} {\text{ sinh}}\left( {\lambda \left( {\frac{1}{2} - y} \right)} \right)}}{{\cosh \left( {\frac{\lambda }{2}} \right)}} $$

(14)

and

$$ \nabla^{4} \phi_{1} - {\text{Ha}}^{2} \frac{{\partial^{2} \phi_{1} }}{{\partial y^{2} }} = 0 $$

(15)

The governing Eqs. (14, 15) are solved by the method of variation of parameters. The final expressions for $\phi_{0}$ and $\phi_{1}$ are given as:

$$ \phi_{0} = c1e^{{{\text{Hay}}}} + c2e^{{ - {\text{Hay}}}} + \frac{{\lambda {\text{ sinh}}\left( {\lambda \left( {\frac{1}{2} - y} \right)} \right)}}{{\left( {\lambda^{2} - Ha^{2} } \right)\cosh \left( {\frac{\lambda }{2}} \right)}} + \frac{c3y}{{{\text{Ha}}^{2} }} $$

(16)

and

$$ \phi_{1} = g(y)\cos (qx + \theta ) $$

(17)

here

$$ g(y) = e^{\frac{Hay}{2}} ((d1 + d2y)\sin h(Qy) + (d3y)\cosh (Qy)) $$

(18)

where $Q = \frac{{\sqrt {{\text{Ha}}^{2} + 4q^{2} } }}{2}$. Where the constants c1, c2, c3, d1, d2, d3 are determined using boundary conditions, but are not mentioned to maintain brevity.

3 Results and Discussion

3.1 Validation

The present model is validated against Ghosh and Chakraborty’s [7] work in the limiting case of Ha → 0. Axial velocity at the channel’s center line and vertical velocity at axial position x = 0 (here non-dimensional forms of velocities are considered) for the present model seems to fit well with the reference model (see Fig. 2).

Fig. 2

Validation of the present mathematical model with Ghosh and Chakraborty’s [7] model: a Axial velocity at microchannel’s center line, b Vertical velocity at x = 0

3.2 Hydrodynamic Analysis

We observe streamline pattern dependence on different parameters such as slip length(ls), patterning frequency(q) and Hartmann number (Ha). The flow is primarily unidirectional for no-slip conditions, and very low mixing is observed. Mixing is increased as we increase the slip length since this restricts the variation of velocity at the boundary more prominently (see Fig. 3) (Table 1).

Fig. 3

Dependence of streamline pattern on slip length(ls): a ls = 0, b ls = 0.025, and c ls = 0.05

Table 1 Values of the fixed parameters for different plots

Fig. 4

Dependence of streamline pattern on patterning frequency(q): a q = π/4, b q = π/2, and c q = 3π/4

Fig. 5

Dependence of streamline pattern on Hartmann number (Ha): a Ha = 0, b Ha = 3.5, and c Ha = 6.75

Another essential factor influencing mixing in the present model is patterning frequency(q). As we increase patterning frequency, the stream pattern is squeezed in the axial direction (refer to Fig. 4).

Hartmann number signifies the strength of the magnetic field in the microchannel. For the limiting case of Ha → 0 applied electric field determines the flow pattern, which is oriented along the axial direction. By looking at Fig. 5a), we observed that the flow is predominantly in the axial direction, and mixing is missing. As we increase the Hartmann number, the velocity gradient increases in the transverse direction; thus, enhancing the mixing dynamics (Fig. 5).

4 Conclusions

We explore the interplay between electromagnetic effects and patterned wall slip with an analytical approach. The perturbed solution of the stream function is obtained using regular perturbation analysis applied to the dimensionless form of governing equation. The obtained solution is validated against the model proposed by Ghosh and Chakraborty in the limiting condition of zero magnetic field. The parametric study is performed to understand the role of crucial parameters in flow hydrodynamics. The electric field is observed to govern the discharge rate at low Ha. However, at a higher Hartmann number, the discharge rate depends on both the electric and the magnetic field strength. Further, we observed that the wall wettability and magnetic field interplay determines the extent of mixing obtained. The outcome of the present work can play a pivotal role in the technical advancement of the microdevices used in different biochemical, scientific, and industrial processes.