Keywords

1 Introduction

Immense industrial and biomedical applications (e.g., polymer processing, magnetically controlled optics, ferrofluid-based sensors, biomedical imaging, drug delivery, and diagnosis of malignant tumors) make the droplet magnetohydrodynamics an emerging area of research for the last few decades [1,2,3,4,5].

In the case of the flow field, the droplet deformation depends on the nondimensional capillary number (Ca), which signifies the ratio between viscous force (that tries the droplet to deform) and the interfacial force (that maintains the droplet to its initial spherical shape). Following the pioneering research (on the droplet dynamics of Newtonian fluid under the governance of background flow in a small deformation regime) of Taylor [6], Han and Chin [7] experimented to show the deformation and breakup characteristics of the droplet in extensional flow. Here they considered both the droplet phase and continuous phase to be viscoelastic and showed the effects of different fluid properties (such as viscosity, elasticity, and interfacial tension) on the deformation dynamics. Moreover, droplet breakups in linear flows have been adequately examined numerically as well as experimentally by Stone [8]. Furthermore, Delaby et al. [9] experimentally exhibited the importance of the viscosity ratio on the deformation dynamics of a droplet in immiscible molten polymer blends for higher Ca limits. Minale [10] analytically shows the droplet deformation considering (i) both the phases are Newtonian, (ii) one of the phases is non-Newtonian, and (iii) considering the confined system where wall effects have been considered.

Similarly, the sole impact of a uniform magnetic field on the ferro-droplet has been thoroughly addressed in the literature [11,12,13]. On a brief note, the appearance of a magnetic field makes the ferro-droplet unstable and expands along with the applied magnetic field orientation [14]. In this context, Afkhami et al. [12, 13] analytically showed the dependency of the aspect ratio (ratio between the length of major and minor axes) of the deformed droplet on the magneto-physical properties of the ferrofluid. A complete numerical study on hysteresis phenomena for the ferro-droplet deformation in a uniform magnetic field has been studied by Lavrova et al. [15].

The dynamics of a neutrally buoyant droplet in the presence of the magnetic field or extensional flow are independently reported in the literature. The droplet dynamics in the combined effect of magnetic field and uniaxial extensional flow can provide many physical imaginations on the fluid mixing controllability. Motivated by this, here we propose to see the impact of the uniform magnetic field in the background uniaxial extensional flow on the ferro-droplet dynamics. Considering Stokes flow, the magnetohydrodynamic problem is solved by following numerical simulations in the small deformation limit.

2 Problem Formulation

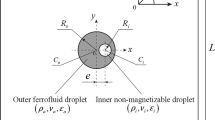
Here, we considered a Newtonian ferrofluid droplet of radius ri, density ρ, viscosity ηi, and magnetic susceptibility χi, placed in another Newtonian, non-magnetic fluid of viscosity ηe and density ρ (neutrally buoyant) as shown in Fig. 1. The droplet is directed by an externally employed magnetic field \(\overline{\user2{H}}_{0} = H_{0} {\varvec{e}}_{z}\) and uniaxial extensional flow \(\overline{\user2{U}}_{0} = \user2{\overline{\rm T}}_{0} \cdot \overline{\user2{X}}\). Here, \(H_{0}\) is the magnitude of the applied magnetic field, \(\user2{\overline{\rm T}}_{0}\) is the rate of the strain tensor, and \(\overline{\user2{X}}\) is the position vector. The far-field strain rate tensor \(\user2{\overline{\rm T}}_{0} \user2{ }\) can be defined as:

$$ \overline{{\varvec{T}}}_{0} = \frac{{G_{0} }}{2}\left[ {\begin{array}{*{20}c} { - 1} & 0 & 0 \\ 0 & { - 1} & 0 \\ 0 & 0 & 2 \\ \end{array} } \right] $$
(1)
Fig. 1
A schematic of a sphere of radius r i in a 3 D coordinate system. It is placed between the uniaxial extensional flow and uniform magnetic field.

Schematic representation of the problem description

Full size image

where G0 is the rate of strain. Further, we considered the surface tension σ is uniform along with the droplet interface.

2.1 Governing Equations

The velocity field for an incompressible flow satisfies the continuity and Navier–Stokes equation as [16, 17]:

$$ \left. \begin{gathered} \nabla \,{\mathbf{ \cdot }}\,{\mathbf{u}}\,\, = \,\,0 \\ \rho \left( {\frac{{\partial {\mathbf{u}}}}{\partial t} + {\mathbf{u}}\,{\mathbf{\nabla }}\,{\mathbf{u}}} \right) = - \nabla p + \eta \,\nabla \,{\mathbf{ \cdot }}\,\,\left( {\nabla {\mathbf{u}} + \left( {\nabla {\mathbf{u}}} \right)^{{\varvec{T}}} } \right) + {\mathbf{F}}_{{{\text{ST}}}} + {\mathbf{F}}_{{\text{M}}} \\ \end{gathered} \right\} $$
(2)

Here FST and FM represent the force due to surface tension and magnetic force, respectively. The surface tension force, FST can be described as [18]:

$$ {\mathbf{F}}_{{{\text{ST}}}} = \nabla \,{\mathbf{ \cdot }}\,\,\left[ {\sigma {\mathbf{I}} + \left( { - {\mathbf{nn}}^{{\varvec{T}}} } \right)\delta } \right] $$
(3)

where I, δ, and n are the second-order identity tensor, Dirac delta function, and unit normal to the interface. Similarly, the force due to magnetic field, FM can be defined as [18]:

$$ {\mathbf{F}}_{{\text{M}}} = \,\,\nabla \,{\mathbf{ \cdot }}\,\,{\varvec{\tau}}_{{\text{M}}} \,{\mathbf{ = }}\,\,\nabla \,{\mathbf{ \cdot }}\,\,\left( {\mu_{m} {\mathbf{HH}}^{{\text{T}}} - \frac{{\mu_{m} }}{2}\left( {{\mathbf{H}}\,{\mathbf{ \cdot H}}} \right){\mathbf{I}}} \right) $$
(4)

In the above equation, H, τM, and µm are the strength of the applied magnetic field, magnetic stress tensor, and the magnetic permeability of the fluid, respectively. To find the magnetic stress tensor, we need to solve the magneto-static Maxwell equations as given below [18].

$$ \left. \begin{gathered} \nabla \,{\mathbf{ \cdot }}\,{\mathbf{B}} = 0 \hfill \\ \nabla \times {\mathbf{H}} = 0 \hfill \\ {\mathbf{M}} = \chi_{m} {\mathbf{H}} \hfill \\ {\mathbf{B}} = \mu_{0} \left( {{\mathbf{H}} + {\mathbf{M}}} \right) \hfill \\ \end{gathered} \right\} $$
(5)

where µ0 (µ0 = 4π × 10−7 N/A2) is the permeability of the vacuum. B, M, and χm are magnetic induction, magnetization, and magnetic susceptibility, respectively.

2.2 Nondimensionalization

To nondimensionalize, we have considered the following scales: length—ri, velocity—G0ri, magnetic field strength—H0, hydrodynamic stress—ηeG0, and magnetic stress—µ0H02. Here we assumed that the viscous force is ruling over the inertia force, resulting in a low Reynolds number flow. We have tabulated all the dimensionless parameters and nondimensional numbers in Table 1.

Table 1 Different dimensionless parameters and nondimensional numbers associated with the present analysis
Full size table

3 Numerical Method

In this study, we used the phase-field technique to resolve the two-phase interface features. Phase-field model for a system of two incompressible and immiscible fluids can be described as [19]:

$$ \frac{{\partial \psi \left( {x,t} \right)}}{\partial t}\, + \,{\mathbf{u}}\,{\mathbf{ \cdot }}\nabla \psi \left( {x,t} \right)\, = \,\nabla \left( {M_{{\psi \left( {x,t} \right)}} {\mathbf{\nabla }}G} \right) $$
(6)

where Mψ(x,t) and G denote the interface mobility factor and chemical potential, respectively. Two fluids are distinguished by the definite values of the phase-field parameter ψ(x,t). The values of the phase-field parameter for suspending fluid phase and droplet phase are taken as −1 and +1, respectively; whereas it varies from −1 to +1 at the two-phase interface.

The magnetic potential follows Poisson’s equation in the following form [18]:

$$ \nabla \,{\mathbf{ \cdot }}\left( {\mu_{m} \nabla \phi^{mag} } \right) = 0 $$
(7)

where \({\mu }_{m}\) is the magnetic permeability of the fluid which can be presented in terms of the phase-field parameter as

$$ \mu_{m} = \left[ {\frac{{\left( {1 + \psi \left( {x,t} \right)} \right)}}{2}\mu_{i} } \right] + \left[ {\frac{{\left( {1 - \psi \left( {x,t} \right)} \right)}}{2}\mu_{e} } \right] $$
(8)

For simulations, a square channel of size L × L is considered (here L = 10ri to neglect the effect of channel confinement), where the droplet is situated at the center of the left side (axis of symmetry) as shown in Fig. 2.

Fig. 2
A schematic of a domain of dimensions L equal 10 r i. A droplet of radius r i is placed on the symmetry boundary. The droplet phase and carrier fluid are labeled on it.

Schematic representation of the computational domain

Full size image

3.1 Grid Independence and Cahn Number Independence Test

To check the precision of the simulation results, the grid independence and Cahn number (Cn) independence assessments are necessary. In our model, the grid size and the Cahn number are similar and close to the two-phase interface. So, an accurate grid independence study automatically confirms a correct Cahn number independence analysis [20]. For the Cahn number independence study, we have compared the temporal droplet deformation in presence of uniaxial flow as illustrated in Fig. 3. This figure confirms that the droplet deformation is almost the same for three different values of the Cahn number. Eventually, we considered Cn = 0.04 for the rest of our analysis.

Fig. 3
A multi-line graph plots D versus t. The data is plotted for C n equals 0.06, 0.05, and 0.04. The curve increases. A section of the curve is magnified, and it displays three parallel lines.

Alteration of the droplet deformation for different Cahn numbers (Cn) at Ca = 0.05, λ = 1 in the sole presence of uniaxial extensional flow

Full size image

3.2 Model Validation

For validation, we have compared the deformation parameter D [where D = (l − b)/(l + b); l and b are the lengths of the major and minor axis of the deformed droplet, respectively] with the previously reported results for two cases: (a) droplet deformation in existence of uniaxial extensional flow only and (b) droplet deformation in the sole presence of the uniform magnetic field. Figure 4a shows the steady-state droplet deformation (Dα) for different Ca values at λ = 1, which confirms that our numerical model is in harmony with the simulation of Stone and Leal [21]. Figure 4b depicts the alteration of droplet deformation at the steady-state (Dα) with the magnetic Bond number (Bom) for µr,i = 1.89. After comparison, we found that our numerical model is in the same fashion as the experimental results of Afkhami et al. [13] for Bom < 1.5.

Fig. 4
Two graphs. Graph a plots D alpha versus C a for simulation and present simulation values. Graph b plots D alpha versus B o for the experiment and present simulation values.

Alteration of the droplet deformation at the steady-state (Dα) with a Capillary number Ca at λ = 1 in uniaxial extensional flow and b Magnetic Bond number Bom for (µr,i, µr,e) = (1.89, 1) in sole existence of uniform magnetic field

Full size image

4 Results and Discussion

In external flow conditions, the viscosity ratio plays a pivotal role in the deformation dynamics of a droplet. Figure 5 confirmed the impact of the viscosity ratio on the droplet deformation in the Stokes flow regime (here, Re = 0.01). It can be seen that at a fixed Ca value (here, Ca = 0.05), as the viscosity ratio (λ) increases from 0.01 to 5, the deformation parameter (D) also increases. Contrariwise, the time taken to reach steady-state deformation is smaller at the lower viscosity ratio. Another important observation is that for λ ⩽ 1, the temporal evolution of the droplet deformation is almost independent of the viscosity ratio. More precisely, the droplet deformation plot at λ = 0.01 almost coincides with that at λ = 0.1. Considering these aspects, we considered λ = 1 to see the droplet deformation characteristics for the rest of the analysis.

Fig. 5
A multi-line graph plots D versus t for lambda equal 5, 1, 0.1, and 0.01. A section of the curves is magnified and three curves are displayed.

Effect of viscosity ratio (λ) on the droplet deformation (D) for Ca = 0.05, M = 0, and Re = 0.01

Full size image

Figure 6a illustrates the transient droplet deformation for (μr,i, μr,e) = (2, 1) and λ = 1 for different Mason numbers and α = 90°. In absence of a magnetic field (i.e., M = 0), the drop deforms into a prolate shape due to the hydrodynamic stress distribution. For all M > 0 at α = 90°, both the magnetic stress and the hydrodynamic stress are acting in the same direction which assists the droplet to deform into a prolate shape. Moreover, the deformation increases with increasing magnetic field strength. Figure 6b depicts the alteration of transient deformation of the ferro-droplet for (μr,i, μr,e) = (2, 1) and λ = 1 with different Mason numbers at α = 0°. Here the magnetic stress tries to resist the prolate deformation aided by hydrodynamic stress. For this reason, the deformation for all M > 0 is less when compared with M = 0. Fascinatingly, here we observed two distinct droplet shape deformations. For M = 0, 1, and 5, it forms a prolate shape, whereas, for higher values of M (= 10, 20), it deforms into an oblate shape. The prolate shape formation is because of the higher viscous force compared with the magnetic force. While, for M = 10 and 20, the magnetic stress becomes relatively high so that it overcomes the viscous force and deformed the droplet into an oblate shape.

Fig. 6
Two multi-line graphs plot D versus t for values at M equals 0, 1, 5, 10, and 0. In graph b, a no deformation line is drawn at D equals 0.

Alteration of droplet deformation (D) with time for (µr,i, µr,e) = (2, 1) and λ = 1 for different Mason numbers. a α = 90°and b α = 0°. Other parameters are Ca = 0.05 and Re = 0.01

Full size image

The relative magnetic permeability of a material represents the ability of that material to be magnetized in presence of an external magnetic field. The magnetic force exerted on a ferrofluid droplet directly depends on its relative magnetic permeability. Hence, the relative magnetic permeability has a key role in droplet morphology alteration. Figure 7a represents that for a system with α = 90°, the droplet deformation (D) increases monotonically with the relative magnetic permeability at a fixed magnetic field strength. This observation follows a similar trend as reported in the literature [22]. This is because the magnetic stress attributed to the droplet pole increases with an increase in relative magnetic permeability. Consequently, the magnetic force dominates the surface tension force and thus the droplet becomes more elongated along the direction of the magnetic field and forms a prolate shape with a high aspect ratio. Interestingly, for the system (M, α) = (1, 0°) as shown in Fig. 7b, the droplet morphology evolved from prolate to oblate shape with the increase of relative magnetic permeability from 1 to 10. This is because with the increase of μr,i, the magnetic stress becomes high and it governs the flow dynamics. As a result, the droplet follows the magnetic field direction and formed an oblate shape.

Fig. 7
Two multi-line graphs plot D versus t for values at mu m equals 0, 1, 5, 10, and 0. The general trend is increasing except for the curve for mu m equals 3 for graph b.

Alteration of droplet deformation (D) with time for different relative magnetic permeability of the droplet phase (μr,i) for a (M, α) = (1, 90°) and b (M, α) = (1, 0°). Other parameters are μr,e = 1, Ca = 0.05, λ = 1, and Re = 0.01

Full size image

5 Conclusions

In summary, the transient dynamics of a ferro-droplet guided by the uniform magnetic field in background uniaxial extensional flow has been studied numerically. Based on the outcomes, the major findings are as follows:

  • The droplet deforms into a prolate shape for α = 90°. On the contrary, for α = 0°, the droplet may deform into either a prolate or oblate shape depending on the Mason number.

  • For the system with α = 90°, the droplet elongates more with the higher relative magnetic permeability and forms the prolate shape. Whereas, an enhancement of relative magnetic permeability can change the droplet morphology from the prolate to an oblate shape at α = 0°.