Learning Stable Representations with Progressive Autoencoder (PAE)

Abstract

Autoencoder, which compresses the information into latent variables, is widely used in various domains. However, how to make these latent variables understandable and controllable is a major challenge. While the $\beta$-VAE family is aiming to find disentangled representations and acquire human-interpretable generative factors like what independent component analysis (ICA) does in the linear domain, we propose Progressive Autoencoder (PAE), a novel autoencoder based model, as a correspondence to principal component analysis (PCA) in the non-linear domain. The main idea is to train an autoencoder with one latent variable first, then add latent variables progressively with decreasing weights to refine the reconstruction results. This brings PAE two remarkable characteristics. Firstly, the latent variables of PAE are ordered by the importance of a downtrend. Secondly, the latent variables acquired are stable and robust regardless of the network initial states. Since our main work is to analyze the gas turbine, we create a toy dataset with a custom-made non-linear system as a simulation of gas turbine system to test the model and to demonstrate the two key features of PAE. In light of PAE as well as $\beta$-VAE is derivative of Autoencoder, the structure of $\beta$-VAE could be easily added to our model with the capability of disentanglement. And the specialty of PAE could also be demonstrated by comparing it with the original $\beta$-VAE. Furthermore, the experiment on the MNIST dataset demonstrates how PAE could be applied to more sophisticated tasks.

1 Introduction

The Autoencoders (AE) have been used to automatically extract features from data without supervision for many years. Since then, a lot of work has been done to enhance this elegant structure. A particular enhancement direction focuses on extracting latent variables with properties that are useful for non-linear system analysis, like disentanglement or interpretability. Rifai et al. (2011) restrict the learned representations within contractive space and got a better robustness using contractive autoencoder [1]. Variational autoencoder [2] by Diederik P Kingma and Max Welling (2014) root in the methods of Variational Bayesian and graphical model, mapping the input into a distribution instead of individual variables. Diederik P. Kingma, et al., in the same year also introduced conditional VAE [3] to learn with labeled data and obtain meaningful latent variables with semi-supervised learning. Then $\beta$-VAE [4, 5] is proposed by Irina Higgins, et al., (2017), trying to learn disentangled representations by strengthening the punishment of KL term with a hyperparameter beta and narrowing the information bottleneck. $\beta$-TC VAE [6] by TianQi Chen, et al., (2018) further refined their work until Babak Esmaeili, et al., (2019) unified all methods that modify the objective function with HFVAE [7].

From the GAN [8] family, some methods try to learn disentangled representations, a few milestones are conditional GAN (2014) [9] that involves label to input data, BiGAN (2017) [10] with a bidirectional structure to project data back to latent space, InfoGAN (2017) [11] that learns disentangled representations with information-theoretic extended GAN, and InfoGAN-CR (2020) [12] that references techniques from the $\beta$-VAE branch.

Behind the observable variables of an unknown system, there are usually a few independent source variables whose changes represent the entire system. These variables are usually hidden from sight and physically difficult to acquire, but once dug out, and made clear their relationship to the observable variables, they can help us fully understand the system. Excavating them from the data, however, is extremely hard and sometimes impossible. For easier understanding, Fig. 1 displays the relationship between these variables and concepts. Against the background of gas turbine condition monitoring, which is the main work of our lab, the observable variables are performance parameters collected by sensors such as temperature, pressure, and etc. These parameters are entangled with each other and incomplete as well. To get a clear and intact presentation of the state of gas turbines, we proposed a new model to achieve these aims.

Fig. 1.

The relationships between observable variables, source variables, labels, latent variables, and representations of source variables.

In this paper, Progressive Autoencoder (PAE) is proposed with a new Progressive Patching Decoder (PPD) structure to learn representations with another unique property: stability. The representations learned by PAE are ranked by their importance for reconstruction, and for the same dataset PAE always provides a stable result because latent variables always learn the same features. The reconstruction error is progressively reduced by adding new latent variables until another new freedom degree could not contribute to the reduction of reconstruction error. Good robustness is achieved by introducing a denoising structure [13] to PAE using a dropout layer, this allows the PAE to perform a self-supervised learning task [14] to understand the non-linear system better. The highly flexible structure also enables PAE to work both on a supervised and unsupervised manner.

Briefly, PAE has two outstanding features. First is that the latent variables are learned by decreasing order of importance and the second is the high stability of latent variables learned by PAE. Additionally, by combining of beta-VAE, the disentanglement ability could be added to PAE and form beta-PAE.

2 Framework of Progressive Autoencoder

The structure of PAE is illustrated in Fig. 2. Similar to a classical autoencoder, PAE is made of 2 parts, an encoder and a decoder. The encoder of PAE can be further divided into 2 neural nets, Encoder1 is used for generating unsupervised latent variables $z_i$, (i = 1, 2... n) and Encoder0 is prepared for supervised learning. Encoder0 could either provides $z_0$ as a result of unsupervised learning or gives $\hat{y}$ with the supervision of labels. The decoder of PAE is a multi-level decoder called Progressive Patching Decoder (PPD), it takes in not all the latent variable of z but one at a time to progressively patch the Median code $m_i$ with Process variable $p_i$ generated from z with neural nets named NNi, then followed by a normal Decoder to reconstruct original data x.

The main objectives for Progressive Autoencoder are: 1. minimizing the distance (usually the mean square error (MSE)) between input data vector x and reconstructed data vector $\hat{x}_i$; 2. minimizing the label loss if any label is provided; 3. Minimizing the KL-divergence between prior and posterior distribution from VAE. What’s special about PAE is that instead of having one reconstructed result, we have n of them. Each of the reconstructed result $\hat{x}_i$ uses the first i latent variables, from $z_0$ to $z_i$, as if we are training n individual autoencoders with 1 $\sim$ n latent variables simultaneously with shared weights.

Fig. 2.

Structure of Progressive Autoencoder.

2.1 Encoder Network

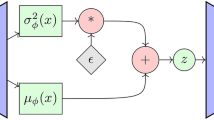
Encoder1 is like the VAE Encoder. it learns to output a distribution as latent representations from the input data x. The final result of Encoder1, z, is sampled from the Gaussian distribution $\epsilon \sim \mathcal {N}\left( 0,1\right)$ with parameters $\mu$ and $\sigma$ using the reparameterization trick proposed in VAE. $\mu$ and $\sigma$ are the outputs of the Encoder1:

$$\begin{aligned} z=\mu +\sigma \cdot \epsilon \end{aligned}$$

(1)

Encoder0 is prepared for semi-supervised learning. If looked separately, it’s exactly the same as a normal supervised Neural Network. The purpose of Encoder0 is for extracting labels (human-selected representations) from the data.

When there is no label available, it can also work without supervision to extract the “Principal latent variable” of the data. The input of Encoder0 is the data vector x, and the output is either the predicted label vector $\hat{y}$ which has the same dimension as the label or the principal latent variable $z_0$.

When used with labels, the objective of Encoder0 is to minimize the difference between actual label y and output $\hat{y}$. With an individual loss function:

$$\begin{aligned} \mathcal {L}_{{Encoder}_0}=\mathbb E_{x,y\sim Pd}\left( y-\hat{y}\right) ^2 \end{aligned}$$

(2)

With continuous labels, Mean Squared Error is used to calculate the error between the predicted and actual label, for categorical labels, Cross Entropy can be used instead.

To improve the robustness of the feature extractor Encoder0 and Encoder1, noise is added to the data x before it’s fed into the neural nets. To help handle data with missing values, a dropout layer is used in this case to add noise. The special layer can set a certain amount of input to 0, forcing the encoder nets to extract representations with fewer observable variables.

2.2 Progressive Patching Decoder

The latent vector z is generated one column at a time by the encoder network of PAE, each of them contributing a new degree of freedom to the reconstruction result. PPD takes in the n-dimensional z and produces n results using 1, 2... n latent variables. PPD is designed to be a multi-level structure where the newly added latent variable is used to “patch” the previous result and refine it by giving more information.

From a regular feature fusion point of view, the “patching” process should either be done by concatenating the vectors, or adding them together. However, we cannot add the latent variables together directly, as it would limit the width of AE bottlenecks and provide fewer degrees of freedom. Concatenating also doesn’t work in this case, as the input shape for a neural network layer should normally be fixed, the structure with adaptive shapes and elements from the continual learning domain might work, but is unnecessarily difficult for this task.

Achieving both utility and simplicity, PPD uses a hierarchical structure: the first latent variable is converted by a neural network NN0 into the base median vector $m_0$, the newly added latent variables are converted by NNi into the patcher vector $p_i$ and “patch” $m_0$ one by one, then both the patched and under-patched median vectors are used for reconstruction. The median vectors should have dimensions bigger than n, so it can include all information from latent variables. The patching process can be done by simply adding the patcher vector to the median vector:

$$\begin{aligned} m_i=p_i+m_{i-1} \end{aligned}$$

(3)

As we discovered later, a 2-step linear transformation achieves the same result and converges faster:

$$\begin{aligned} m_i=p_{i1}+p_{i2}\cdot m_{i-1} \end{aligned}$$

(4)

where $p_i1$ is called adder patcher vector and $p_i2$ is called multiplier patcher vector. The two patchers are both generated by NNi and have the same shape with $m_i$. $p_i1$ is initialized to be a gaussian distribution that is 0-mean and $p_i2$ is to have 1-mean. NNi generates the progressive patcher for median code to calculate the refined median codes. The total amount of NNi is decided according to the task. The input for NNi is $z_i$ generated by Encoder, and the output is $p_i1$ and $p_i2$ the adder and multiplier patcher.

2.3 Training Method

When dealing with an unsupervised task, for each column of z, a reconstruction result $\hat{x}_i$ is generated by the PPD, and the goal is to minimize the differences between each $\hat{x}_i$ and input data x. A hyperparameter $\xi$ is involved in the loss function to balance the optimization process, and to put equal effort on each reconstruction result - that the reconstruction error weighted by $\xi$ should be roughly the same. According to experiment results, we decided that using a geometric series is appropriate, $\alpha$ is the common ratio of the geometric series, normally $\alpha =\frac{2}{3}$. Therefore, the reconstruction loss term of the loss function is:

$$\begin{aligned} \mathcal {L}_{RL}=\mathbb {E}_{x~Pd}\left\{ \sum _{i=0}^{n}\left[ \left( x-{\hat{x}}_i\right) ^2\cdot \left( \xi \cdot \frac{1-\alpha ^i}{1-\alpha }+1\right) \right] \right\} \end{aligned}$$

(5)

Adding the KL divergence term that encourages the posterior to be as close to the Gaussian prior $p\left( z\right)$, the complete Encoder loss function is:

(6)

When it comes to a supervised task, the only difference is the training of Encoder0, the loss function is mentioned in Sect. 2.1. $\mathcal {L}_{{Encoder}_0}$ is used to update the parameters of Encoder0 and $\mathcal {L}_{complete}$ responsible for other parameters of the model.

3 Experiments

To assess the quality of the proposed network, we conducted experiments on a toy dataset sampled from a custom-made non-linear system. Results on PAE with different settings are collected and compared to the more classical VAE and beta-VAE framework. Mutual Information [15] is used to measure the relativity of the representations extracted and generative factors.

3.1 Non-linear Toy Dataset

We want to present the full potential of Progressive Autoencoder in a clear yet not too easy or challenging way. And as our ultimate aim is condition monitoring of gas turbine, we decided to design a non-linear toy dataset and test our model on this dataset. This dataset could imitate the performance parameters of gas turbine which is under the influence of internal state and environmental influence. Furthermore, the toy datasets are easy to control and allow us to discover some interesting properties of PAE.

Fig. 3.

This figure shows a few systems outputs changing accordingly to one input varying while other inputs are fixed to 0. Figure left shows the result without noise and figure right is what the dataset truly looks like when adding Gaussian noise with a std of 0.125.

For the dataset, we first created a mathematical model for the custom-made non-linear memoryless time-invariant system, and use the model to generate the data. Figure 3 shows the degree of non-linearity of the mappings used for the costume-made system. The system has 5 inputs (generative factors) and 48 outputs (observable variables), each output is determined by the 5 inputs under a random non-linear transformation with Gaussian noise.

Each input from the toy dataset is not equivalent to each other, as the “importance” of each input variable is different, determined by its overall contribution to the outputs. A less “important” input variable would have a smaller impact to output variables with the same degree of changes, and the non-linearity of the impact is also reduced. In our toy datasets, the 1st and 2nd input variables (generative factors) S1, S2 have equal importance and S3 S5 have gradually decreased importance. The dataset is then generated from the model with 5 inputs independently sampled from truncated Gaussian distributions with a standard deviation of 1.

3.2 Experiment Settings

The architecture of Progressive Autoencoder used in the experiment session is shown in Table 1. Experiments for other frameworks are also conducted on this architecture, with different NNi unit amounts. In order to avoid confusion, while describing the experiment results we use L1$\sim$Ln to represent the nth latent variable rather than $z_i$ from the architecture. S1$\sim$S5 are used to represent the generative factors or the inputs of the dataset respectively.

Table 1. Progressive Autoencoder architecture for Non-linear Toy datasets

In each experiment, 10,000 data pieces are sampled from the toy dataset and a total of 20000 training iterations are conducted (whether it’s converged or not) using Adam optimizer with batch size = 500 and learning rate = 0.001. Note that each experiment presents in this section is done individually, they have different network random initial states and do not share any trainable parameters with each other. Each experiment is done more than once with different initial states to prove reproduction stability. In the first two experiment, dataset is the toy dataset mentioned in Sect. 3.1, and in the last experiment, we test the model on MNIST.

Fig. 4.

(a) shows the distribution of adder patcher (blue) and multiplier patcher (orange) which is mentioned in Sect. 3. 2. (b) shows the reconstruction loss lowered by each latent variable. (c) and (d) show the non-linear mapping between L1 L6 and S1 S5 in two separate experiments. (Color figure online)

3.3 Results of Toy Dataset

Figure 4 shows the result of PAE with 6 latent variables. As shown in Fig. 4a, the distributions which count every vector component of patchers are gradually closing into the center, meaning that they are contributing less and less to the final result and the significance of new latent variable is on the decline. This is also reflected in Fig. 4b in which the reconstruction error is decreasing with more latent variables added at a level that also gradually reduces. Until L6 is added, the variation of loss seems to cease because there are only five generative factors and the first five latent variables have almost learned all features of them. When given the 6th latent variable, it becomes redundant could hardly refine the result any further.

Figures 4c and 4d, which come from two individual experiments with different random initialization, present the relationship between S and L. In the title of each subgraph, $S_i L_j$ means that the horizontal axis is $S_i$ and the vertical axis is $L_j$, while MI (short for mutual information) is calculated to measure the relativity of $S_i$ and $L_j$. By comparing the two graphs, we could easily find that the corresponding subgraphs are extremely similar which proves that latent variables in same place always learn same features and this is exactly the stability we talked above. However, the feature learned by PAE is still Entangled, in other to solve this problem, the structure of $\beta$-VAE is imported in next experiment.

Fig. 5.

Demonstration of the results of supervised PAE.

Figure 5 shows the result of supervised PAE with 6 latent variables. The first two latent variables have learned good features by the supervision of S1 and S2. The other latent variable could also Provide proof of the stability of PAE.

Table. 2 shows the reconstruction errors of all the PAE experiments beta-PAE and supervised PAE, with different latent variables available to use. Reconstruction errors of model with same latent variables are similar and Reconstruction errors in same row increase gradually. The reconstruction error of L2 of Supervised PAE is greater than others’ because what they learn is restricted by supervision while the reconstruction error of L6 of Supervised PAE is the smallest one because it can learn better with the “patch” of other latent variables. The experiment that will be described next is about Beta-PAE, which sacrifices some ability of reconstruction and acquires the ability of disentanglement.

Table 2. Reconstruction Errors for Different Architectures with Different Amount of Latent Variables

Fig. 6.

The result of beta-VAE and Progressive Autoencoder with 6 latent variables.

3.4 Comparison Between Beta-PAE and Beta-VAE

By combining beta-VAE and Progressive Autoencoder, we can learn disentangled representations and rank them by importance at the same time. This could be useful in industrial applications. Results of Progressive Autoencoder and beta-VAE are shown in Fig. 6.

Through comparing Fig. 6a and Fig. 5c/Fig. 5d, we find that beta-PAE gains the ability of disentanglement. From the comparison of Figs. 6a and 6b, though beta-VAE separate generation factors a little better, beta-PAE is stable. Beta-PAE always learns the generation factors in a fixed sequence, order of decreasing importance, but the result of beta-VAE is different every time as we all know.

3.5 Experiments on MNIST

Fig. 7.

The results of $\beta$-PAE with one latent variable varies each time and others fixed

From the experiments with the toy dataset, the characteristics of $\beta$-PAE are shown. In this part, we will display the property of $\beta$-PAE in a more intuitive way. For MNIST dataset, $\beta$-PAE is used with supervision to generate the digits first, then applied unsupervised approach to learn the other properties of the hand-written digits. We turn the latent variables of trained model from −1 to 1 and fix the other latent variables to 0. The result is shown in Fig. 7.

In Fig. 7, the pictures are ordered by the sequence of latent variables. For example, in Fig. 7a, the first latent variable, which is the most important one, is changed from −1 to 1 and others are always 0. The first 3 properties learned are human-interpretable: Angle, Width, and Thickness while the other properties learned are not so easily described. The 3 factors learned, according to personal experiences, might just as well be the most important factors for digit reconstruction.

Fig. 8.

(a) is the result of $\beta$-PAE with one latent variables and (b)–(d) are results of $\beta$-PAE by adding only one latent variables each time. (e) is the input that is placed here for comparison

$\beta$-PAE can also generate the digits using only the first few latent variables, the “intermediate products” as they are refined. Figure 8g shows how each latent variable refines the reconstruction results. At first, PAE could only get what number it is so that every picture of same number looks exactly the same. As new latent variables are added, the mode could acquire Angle, Width, and Thickness of the number and become increasingly clear.

4 Discussion and Conclusion

In this paper, we proposed a new Autoencoder-based model called Progressive Autoencoder. In this model, the latent variables are ordered by their consequence and have strong stability along with the structure called Progressive Patching Decoder. Progressive Autoencoder could also gain the disentanglement ability by combining the idea of $\beta$-VAE. We created a toy dataset to prove the property of PAE. The results indicate that features learned by PAE are stable and order by the way we want. We also showed how to use PAE on a supervised task and designed experiments to prove the effect. Comparison of $\beta$-PAE and $\beta$-VAE shows the combination of stability and ability of disentanglement. How does PAE work is intuitively showed by the experiments on MNIST, in which we could find variation of features which are visible.

Overall, Progressive Autoencoder is a flexible architecture that can be used in many real-life scenarios such as condition monitoring of gas turbine and can help us analyze non-linear systems better, although we haven’t mentioned any of these apps for space reasons but only explained the theory and characteristics. In this paper, we just use Multi-layer Perceptron as a substructure of PAE. By the combination of other structures such as Convolutional Neural Networks or Attention Mechanism, PAE may become stronger and applicable to a variety of fields.