Keywords

1 Introduction

The electric vehicle has been devoted a great deal of efforts in last decades because it has the advantages of energy-saving and environmental friendliness [1,2,3,4,5]. Specifically, the in-wheel motor-driven (IWMD) vehicle has the prominent advantages of independently and precisely controllable torque, high transmission efficiency, large torque, and fast response. As a result, the IWMD electric vehicle is the main development direction of electric vehicles [6]. However, in the IWMD electric vehicles, installing the motors in the drive wheels indicates that the excitation is directly transmitted to the vehicle body. At the same time, in un-sprung modes, the frequency of vertical excitation increases and the ride comfort and contact stability performance decreases. Hence, some treatments are needed to reduce the impact on ride comfort [7]. Bridgestone company has designed a suspension structure with a wheel motor, which is effective to improve the suspension performances as a dynamic vibration absorber (DVA). It can greatly counteract the road vibration inputs and improve the road holding performance compared to the conventional electric vehicles, but this structure requires the use of active suspension control [8, 9]. Hence, the advanced control technologies of the suspension systems are important to promote the development of IWMD electric vehicles.

To improve suspension responses, many control methods were presented in the field of active suspension control including the adaptive control [10], the robust control [11], the neural network control [12], the sliding model control (SMC) [13] and so on [14,15,16,17]. Among the above control methods, the SMC possesses the advantages of strong robustness and ability to maintain stability despite the system uncertainties and external disturbances. However, traditional SMC usually faces an obvious chattering phenomenon. In line of this consideration, various methods including the terminal SMC, the higher-order SMC and the adaptive sliding model control have been presented to avoid the above problem and to improve the control performances [18]. However, the former two approaches have the disadvantages of needing accurate mathematical models and complicated controller design. Based on the above-mentioned issues, the adaptive SMC approach has been widely investigated [19, 20]. The authors in [21] investigated the adaptive SMC problem for the stabilization of Markovian jump systems. The authors in [22] proposed an adaptive SMC method for the uncertain active suspensions.

The wide application of network brings many benefits, such as improving the system operation rate and communication efficiency. On the other hand, the network may also generate some problems such as time delay and cyber attacks [23]. For electric vehicles, due to the interaction of information among sensors, controllers, and actuators, the active suspension systems are easily susceptible to the cyber attacks. The cyber attacks consume or take up reasonable resources of the system by using malicious data, which may degrade the control performances of active suspensions [24]. To deal with the cyber attacks, the SMC has been widely investigated due to its obvious advantages in resisting external disturbance [25]. However, the parameter uncertainties and time delay were not fully addressed in the above adaptive SMC methods.

In the control strategy of the vehicle, the signal transmission inevitably causes time delay. It should be noted that the time delay can decrease the stability and responses of the vehicle suspension systems [5, 26]. In recent years, there are many control strategies for the time-delay active suspensions, but most of them ignored the cyber attacks [27,28,29]. Although the adaptive SMC has an advantage in handling the cyber attacks, it is still necessary to consider the time delay in the design process of adaptive sliding mode controller.

This paper aims to develop an adaptive SMC method for the IWMD vehicle active suspensions subject to time delay and cyber attacks. This paper has the following features as: (1) An active suspension model is established by considering the spring and damper dynamic nonlinearities, dynamic vibration absorber, time delay and cyber attacks. (2) An integral-type sliding surface is established with consideration of time delay. (3) An adaptive SMC method is proposed to improve the vehicle suspension performance and meet the suspension constraint requirements.

2 Problem Formulation

2.1 Suspension Model of IWMD Vehicles

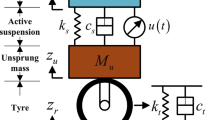
To simplify the complexity of the suspension dynamics analysis and controller design, a quarter-vehicle suspension model is considered. It can be seen from Fig. 1 that the suspension dynamics can be described as:

$$ \left\{ \begin{gathered} m_{s} \ddot{z}_{s} = - k_{s} (t)(z_{s} - z_{u} ) - c_{s} (t)\left( {\dot{z}_{s} - \dot{z}_{u} } \right) + u\left( t \right) \\ m_{u} \ddot{z}_{u} = k_{s} (t)\left( {z_{s} - z_{u} } \right) + c_{s} (t)\left( {\dot{z}_{s} - \dot{z}_{u} } \right) + k_{d} \left( {z_{d} - z_{w} } \right) + c_{d} \left( {\dot{z}_{d} - \dot{z}_{w} } \right) \\ \, - k_{t} \left( {z_{u} - z_{w} } \right) - c_{t} \left( {\dot{z}_{u} - \dot{z}_{w} } \right) - u\left( t \right) \\ m_{d} \ddot{z}_{d} = - k_{d} \left( {z_{d} - z_{u} } \right) - c_{d} \left( {\dot{z}_{d} - \dot{z}_{u} } \right) \\ \end{gathered} \right. $$
(1)

where \(z_{d}\), \(z_{u}\) and \(z_{s}\) stand for the vertical displacements of the motor mass \(m_{d}\), un-sprung mass \(m_{u}\) and sprung mass \(m_{s}\). \(z_{w}\) and \(u(t)\) denote the road disturbances and the actuator force. The suspension damping and stiffness coefficients are \(k_{s}\) and \(c_{s}\). The motor damping and stiffness coefficients are \(k_{d}\) and \(c_{d}\). The tire damping and stiffness coefficients are \(k_{t}\) and \(c_{t}\), respectively. And the nonlinear stiffness and damping coefficients are described as [30, 31]:

$$ \begin{gathered} k_{s} (t) = k_{l} \left( {1 + n\left( {{\text{z}}_{s} - {\text{z}}_{u} } \right)^{2} } \right) \hfill \\ c_{s} (t) = \left\{ \begin{gathered} c_{s1} ,{\dot{\text{z}}}_{s} - {\dot{\text{z}}}_{u} \ge 0 \hfill \\ c_{s2} ,{\dot{\text{z}}}_{s} - {\dot{\text{z}}}_{u} < 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $$
(2)

where \(n\) is the ratio of nonlinear to linear segment \(k_{l}\) of the stiffness coefficient. \(c_{s1}\) and \(c_{s2}\) represent damping coefficient of extension and compression. Defining two premise variables as \(\delta_{1} (t) = (z_{s} - z_{u} )^{2}\) and \(\delta_{2} (t) = \dot{z}_{s} - \dot{z}_{u}\), Eq. (2) can be morphed into

$$ k_{s} (t) = k_{l} + nk_{l} \delta_{1} (t), \, c_{s} (t) = c_{s1} \upsilon (\delta_{2} (t)) + c_{s2} (1 - \upsilon (\delta_{2} (t)) $$
(3)

where \(\upsilon (t)\) is a step function.

Fig. 1.
figure 1

Quarter-vehicle active suspension model with a DVA

Full size image

Regarding to the controller design, the following four key suspension performances are considered as [32]: (1) Ride comfort: It is usually characterized by the body acceleration, thus the following condition is considered:

$$ \min \, \ddot{z}_{s} (t) $$
(4)

(2) Handling stability: It can be characterized by the suspension travel, which needs to be smaller than its maximum value, namely,

$$ \left| {z_{s} (t) - z_{u} (t)} \right| \le z_{\max } $$
(5)

(3) Road holding ability: The tire should be connected to the road closely and firmly, requiring the dynamic load less than or equal to static load, namely,

$$ k_{t} \left( {z_{u} \left( t \right) - z_{w} \left( t \right)} \right) \le (m_{s} + m_{u} + m_{d} )g $$
(6)

Defining the state vector as \(x(t) = \left[ {\begin{array}{*{20}c} {z_{s} - z_{u} } & {\dot{z}_{s} } & {z_{d} - z_{u} } & {\dot{z}_{d} } & {z_{u} - z_{w} } & {\dot{z}_{u} } \\ \end{array} } \right]^{T}\) the road perturbate input as \(\omega (t) = \dot{z}_{w}\), and the control output as \(z(t) = \left[ {\begin{array}{*{20}c} {\ddot{z}_{s} } & {a_{1} (z_{s} - z_{u} )} & {a_{2} (z_{d} - z_{u} )} & {a_{3} (z_{u} - z_{w} )} \\ \end{array} } \right]^{T}\), the suspension model can be converted to

$$ \left\{ \begin{gathered} \dot{x}(t) = Ax(t) + B_{1} \omega (t) + B_{2} u(t) \hfill \\ z(t) = Cx(t) + D_{1} \omega (t) + D_{2} u(t) \hfill \\ \end{gathered} \right. $$
(7)

where

$$ A = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 & 0 & { - 1} \\ { - \frac{{k_{s} \left( t \right)}}{{m_{s} }}} & { - \frac{{c_{s} \left( t \right)}}{{m_{s} }}} & 0 & 0 & 0 & {\frac{{c_{s} \left( t \right)}}{{m_{s} }}} \\ 0 & 0 & 0 & 1 & 0 & { - 1} \\ 0 & 0 & { - \frac{{k_{d} }}{{m_{d} }}} & { - \frac{{c_{d} }}{{m_{d} }}} & 0 & {\frac{{c_{d} }}{{m_{d} }}} \\ 0 & 0 & 0 & 0 & 0 & 1 \\ {\frac{{k_{s} }}{{m_{u} }}} & {\frac{{c_{s} \left( t \right)}}{{m_{u} }}} & {\frac{{k_{d} }}{{m_{u} }}} & {\frac{{c_{d} }}{{m_{u} }}} & { - \frac{{k_{t} }}{{m_{u} }}} & { - \frac{{c_{s} \left( t \right) + c_{d} + c_{t} }}{{m_{u} }}} \\ \end{array} } \right],\,B_{1} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ { - 1} \\ {\frac{{c_{t} }}{{m_{u} }}} \\ \end{array} } \right], $$
$$ B_{2} = \left[ {\begin{array}{*{20}c} 0 \\ {\frac{1}{{m_{s} }}} \\ 0 \\ 0 \\ 0 \\ { - \frac{1}{{m_{u} }}} \\ \end{array} } \right],\,C = \left[ {\begin{array}{*{20}l} { - \frac{{k_{s} (t)}}{{m_{s} }}} \hfill & { - \frac{{c_{s} (t)}}{{m_{s} }}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\frac{{c_{s} (t)}}{{m_{s} }}} \hfill \\ {a_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {a_{2} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {a_{3} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right],\,D_{1} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right],\,D_{2} = \left[ {\begin{array}{*{20}c} {\frac{1}{{m_{s} }}} \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]. $$

Moreover, since the opening-up property of the IWMD vehicle, the cyber attacks are considered when building the suspension system model, which can be shown as

$$ \left\{ \begin{gathered} \dot{x}(t) = Ax(t) + B_{1} \omega (t) + B_{2} [u(t) + h(x(t))] \hfill \\ z(t) = Cx(t) + D_{1} \omega (t) + D_{2} [u(t) + h(x(t))] \hfill \\ \end{gathered} \right. $$
(8)

where \(h(x(t))\) represents the cyber attacks on suspension system, which meets the following condition and \(\varepsilon > 0\) is a constant:

$$ \left\| {h(x(t))} \right\| \le \varepsilon \left\| {x(t)} \right\| $$
(9)

Based on (2)-(3), the membership functions are

$$ \begin{gathered} P_{1} (\delta_{1} (t)) = (z_{\max }^{2} - \delta_{1} (t))/(z_{\max }^{2} - z_{\min }^{2} ), \, Q_{1} (\delta_{2} (t)) = \upsilon (\delta_{2} (t)) \hfill \\ P_{2} (\delta_{1} (t)) = (\delta_{1} (t) - z_{\min }^{2} )/(z_{\max }^{2} - z_{\min }^{2} ), \, Q_{2} (\delta_{2} (t)) = 1 - \upsilon (\delta_{2} (t)) \hfill \\ \end{gathered} $$
(10)

Therefore, the condition \(\delta_{1} (t) = P_{1} (\delta_{1} (t))z_{\min }^{2} + P_{2} (\delta_{1} (t))z_{\max }^{2}\) can be obtained with \(P_{1} (\delta_{1} (t)) + P_{2} (\delta_{1} (t)) = 1\). Then, the following Takagi-Sugeno (T-S) fuzzy model is obtained as:

Fuzzy Rule \(i\): IF \(\delta_{1} (t)\) is \(P_{v} (\delta_{1} (t))\) and \(\delta_{2} (t)\) is \(Q_{v} (\delta_{2} (t))\), THEN

$$ \left\{ \begin{gathered} \dot{x}(t) = A_{i} x(t) + B_{1i} \omega (t) + B_{2i} [u(t) + h(x(t))] \hfill \\ z(t) = C_{i} x(t) + D_{1i} \omega (t) + D_{2i} [u(t) + h(x(t))] \hfill \\ \end{gathered} \right. $$
(11)

where \(v = 1,2\) and \(i = 1,2,3,4\). And the matrices \(A_{i}\), \(B_{1i}\), \(B_{2i}\), \(C_{i}\), \(D_{1i}\) and \(D_{2i}\) of system can be obtain by corresponding \(\delta_{1} (t)\) and \(\delta_{2} (t)\), respectively. Furthermore, one has

$$ \left\{ \begin{gathered} \dot{x}(t) = \sum\limits_{i = 1}^{4} {\eta_{i} } [A_{i} x(t) + B_{1i} \omega (t) + B_{2i} (u(t) + h(x(t)))] \hfill \\ z(t) = \sum\limits_{i = 1}^{4} {\eta_{i} } [C_{i} x(t) + D_{1i} \omega (t) + D_{2i} (u(t) + h(x(t)))] \hfill \\ \end{gathered} \right. $$
(12)

where the grades of membership \(\eta_{i}\) satisfies \(\eta_{i} \ge 0\) and \(\sum\nolimits_{i = 1}^{4} {\eta_{i} } = 1\), and \(\eta_{1} = P_{1} (\delta_{1} (t)) \times Q_{1} (\delta_{2} (t))\), \(\eta_{2} = P_{1} (\delta_{1} (t)) \times Q_{2} (\delta_{2} (t))\), \(\eta_{3} = P_{2} (\delta_{1} (t)) \times Q_{1} (\delta_{2} (t))\), \(\eta_{4} = P_{2} (\delta_{1} (t)) \times Q_{2} (\delta_{2} (t))\).

2.2 Adaptive Sliding Mode Controller

Firstly, the following sliding surface is constructed as:

$$ s(t) = Hx(t) - \int_{0}^{t} {\sum\limits_{i = 1}^{4} {\sum\limits_{j = 1}^{4} {\eta_{i} \eta_{j} } } HA_{i} x(\alpha )} d\alpha - \int_{0}^{t} {\sum\limits_{i = 1}^{4} {\sum\limits_{j = 1}^{4} {\eta_{i} \eta_{j} } } HB_{2i} K_{j} x(\beta - \tau (\beta ))} d\beta $$
(13)

where the constant matrix \(H \in \Re^{1 \times 4}\) will be design to guarantee that \(HB_{2i}\) is nonsingular and \(HB_{1i} = 0\). Based on the parallel distribution compensation, the following control law can be obtained:

Control Rule \(j\): IF \(\delta_{1} (t)\) is \(P_{v} (\delta_{1} (t))\) and \(\delta_{2} (t)\) is \(Q_{v} (\delta_{2} (t))\), THEN

$$ u(t) = \eta_{j} K_{j} x(t - \tau (t)) - h(x(t)) $$

where the local control gain matrix \(K_{j}\) will be obtained by subsequent calculations. Hence, we have the global fuzzy controller as follows:

$$ u(t) = \eta_{j} K_{j} x(t - \tau (t)) - h(x(t)) $$
(14)

By combining Eq. (14) and Eq. (12), the closed-loop model of IWMD vehicle active suspension system is

$$ \left\{ \begin{gathered} \dot{x}(t) = \sum\limits_{i = 1}^{4} {\sum\limits_{j = 1}^{4} {\eta_{i} \eta_{j} } } [A_{i} x(t) + B_{1i} \omega (t) + B_{2i} K_{j} x(t - \tau (t))] \hfill \\ z(t) = \sum\limits_{i = 1}^{4} {\sum\limits_{j = 1}^{4} {\eta_{i} \eta_{j} } } [C_{i} x(t) + D_{1i} \omega (t) + D_{2i} K_{j} x(t - \tau (t))] \hfill \\ \end{gathered} \right. $$
(15)

As shown in Fig. 2, the control flow of the IWMD vehicles nonlinear suspension is presented. The active suspension system is subject to both road interference and cyber attacks. However, the closed-loop system (15) will be asymptotically stable and achieve the desired performance after being processed by the designed sliding mode controller. In a word, a robust adaptive SMC method is proposed for the IWMD vehicle active suspension such that the asymptotical stability and the following condition are satisfied:

$$ \left\| {z(t)} \right\|_{2} \le \gamma \left\| {\omega (t)} \right\|_{2} ,\omega (t) \in L_{2} [0,\infty ) $$
(16)
Fig. 2.
figure 2

Control workflow of the IWMD vehicles suspension system

Full size image

3 Main Results

3.1 Stability Analysis of the Sliding Motion

Theorem 1.

For the given positive scalars \(\tau_{1}\), \(\tau_{2}\), \(\gamma\), \(\kappa_{1}\), \(\kappa_{2}\), and control gains \(\overline{K}_{j}\). The closed-loop system (15) ensure the asymptotical stability and guarantee the \(H_{\infty }\) performance in (16), if there exist positive definite matrices \(\overline{E}_{1}\), \(\overline{E}_{2}\), \(\overline{F}_{1}\), \(\overline{F}_{2}\), \(\overline{X}\), general matrix \(\overline{W}\) that satisfies \(\left[ {\begin{array}{*{20}c} {\overline{F}_{2} } & {\overline{W}} \\ * & {\overline{F}_{2} } \\ \end{array} } \right] > 0\), such that

$$ \overline{\Theta }_{ii} < 0 $$
(17)
$$ \overline{\Theta }_{ij} + \overline{\Theta }_{ji} < 0 \, (i < j) $$
(18)
$$ \left[ {\begin{array}{*{20}c} {\overline{F}_{2} } & {\overline{W}} \\ * & {\overline{F}_{2} } \\ \end{array} } \right] > 0 $$
(19)

where \(i,j = 1,2,3,4\) \(\overline{\Theta }_{ij} = \left[ {\begin{array}{*{20}c} {\overline{\Lambda }_{ij}^{11} } & {\overline{\Lambda }_{ij}^{12} } \\ * & {\overline{\Lambda }_{ij}^{22} } \\ \end{array} } \right]\), and

$$ \begin{gathered} \overline{\Lambda }_{ij}^{11} = \left[ {\begin{array}{*{20}c} {\overline{\Lambda }} & {\overline{F}_{1} } & {B_{2i} \overline{K}_{j} } & 0 & {B_{1i} } \\ * & { - \overline{F}_{1} - \overline{F}_{2} - \overline{E}_{1} } & {\overline{F}_{2} - \overline{W}} & {\overline{W}} & 0 \\ * & * & {[\overline{W} - \overline{F}_{2} ]_{s} } & {\overline{F}_{2} - \overline{W}} & 0 \\ * & * & * & { - \overline{F}_{2} - \overline{E}_{2} } & 0 \\ * & * & * & * & { - \gamma^{2} I} \\ \end{array} } \right],\, \hfill \\ \overline{\Lambda }_{ij}^{12} = \left[ {\begin{array}{*{20}c} {\tau_{1} \overline{X}A_{i}^{T} } & {(\tau_{2} - \tau_{1} )\overline{X}A_{i}^{T} } & {\overline{P}C_{i}^{T} } \\ {\tau_{1} \overline{K}_{j}^{T} B_{2i}^{T} } & {(\tau_{2} - \tau_{1} )\overline{K}_{j}^{T} B_{2i}^{T} } & {\overline{K}_{j}^{T} D_{2i}^{T} } \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ {\tau_{1} B_{1i}^{T} } & {(\tau_{2} - \tau_{1} )B_{1i}^{T} } & {D_{1i}^{T} } \\ \end{array} } \right], \hfill \\ \end{gathered} $$

\(\overline{\Lambda }_{22} { = }diag\{ 2\kappa \overline{X} - \kappa^{2} \overline{F}_{1} ,2\kappa \overline{X} - \kappa^{2} \overline{F}_{2} , - I\}\), \(\overline{\Lambda } = [\overline{X}A_{i} ]_{s} + \overline{E}_{1} + \overline{E}_{2} - \overline{F}_{1}\).

Moreover, the control gain is calculated as \(K_{j} = \overline{K}_{j} \overline{X}^{ - 1}\).

Proof.

Constructing a Lyapunov function as:

$$ \begin{gathered} V(t) = x^{T} (t)Xx(t) + \int_{{t - \tau_{1} }}^{t} {x^{T} (\theta )E_{1} x(\theta )d\theta } + \int_{{t - \tau_{2} }}^{t} {x^{T} (\theta )E_{1} x(\theta )d\theta } \\ +_{1} \int_{{ - \tau_{1} }}^{0} {\int_{t + \theta }^{t} {\dot{x}^{T} (\alpha )F_{1} \dot{x}(\alpha )} d\alpha d\theta } + (\tau_{1} - \tau_{2} )\int_{{ - \tau_{2} }}^{{ - \tau_{1} }} {\int_{t + \theta }^{t} {\dot{x}^{T} (\alpha )F_{2} \dot{x}(\alpha )} d\alpha d\theta } \\ \end{gathered} $$
(20)

The derivative of (20) is obtained as

$$ \begin{gathered} \dot{V}(t) = \dot{x}^{T} (t)Xx(t) + x^{T} (t)X\dot{x}(t) + x^{T} (t)(E_{1} + E_{2} )x(t) \hfill \\ \, - x^{T} (t - \tau_{1} )E_{1} x(t - \tau_{1} ) - x^{T} (t - \tau_{2} )E_{2} x(t - \tau_{2} ) + \tau_{1}^{2} \dot{x}^{T} (t)F_{1} \dot{x}(t) \hfill \\ \, + (\tau_{2} - \tau_{1} )^{2} \dot{x}^{T} (t)F_{2} \dot{x}(t) - \tau_{1} \int_{{t - \tau_{1} }}^{t} {\dot{x}^{T} (\theta )F_{1} \dot{x}(\theta )} d\theta - (\tau_{2} - \tau_{1} )\int_{{t - \tau_{2} }}^{{t - \tau_{1} }} {\dot{x}^{T} (\theta )F_{2} \dot{x}(\theta )} d\theta \hfill \\ \end{gathered} $$
(21)

Based on Jensen’s inequality [33], the following condition holds

$$ - \tau \int_{{t - \tau_{1} }}^{t} {\dot{x}^{T} (\theta )F_{1} \dot{x}(\theta )} d\theta \le \left[ {\begin{array}{*{20}c} {x(t)} \\ {x(t - \tau_{1} )} \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} { - F_{1} } & {F_{1} } \\ * & { - F_{1} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x(t)} \\ {x(t - \tau_{1} )} \\ \end{array} } \right] $$
(22)

According to Reciprocal convex inequality [34], it follows that

$$ \begin{gathered} - (\tau_{2} - \tau_{1} )\int_{{t - \tau_{2} }}^{{t - \tau_{1} }} {\dot{x}^{T} (s)R_{2} \dot{x}(s)} ds \le \hfill \\ \, \left[ {\begin{array}{*{20}c} {x(t - \tau_{1} )} \\ {x(t - \tau (t))} \\ {x(t - \tau_{2} )} \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} { - F_{2} } & {F_{2} - W} & W \\ * & {[W - F_{2} ]_{s} } & {F_{2} - W} \\ * & * & { - F_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x(t - \tau_{1} )} \\ {x(t - \tau (t))} \\ {x(t - \tau_{2} )} \\ \end{array} } \right] \hfill \\ \end{gathered} $$
(23)

And the matrix \(W\) meets the conditions \(\left[ {\begin{array}{*{20}c} {F_{2} } & W \\ * & {F_{2} } \\ \end{array} } \right] > 0\).

Combining (21)–(23), the following condition can be obtained:

$$ {\mathcal{J}} = \dot{V}(t) + z^{T} (t)z(t) - \gamma^{2} \omega^{{\text{T}}} (t)\omega (t) \le \varsigma^{T} (t)\Omega_{ij} \varsigma (t) $$
(24)

where \(\varsigma^{T} (t) = col\{ x(t),\dot{x}(t),x(t - \tau_{1} ),x(t - \tau (t)),x(t - \tau_{2} ),\omega (t)\}\), and

$$ \Omega_{ij} = \sum\limits_{i = 1}^{4} {\sum\limits_{j = 1}^{4} {\eta_{i} \eta_{j} \Theta_{ij} } } = \sum\limits_{i = 1}^{4} {\eta_{i}^{2} \Theta_{ii} } + \sum\limits_{i = 1}^{3} {\sum\limits_{j > i}^{4} {\eta_{i} \eta_{j} (\Theta_{ij} + \Theta_{ji} )} } $$
(25)

where \(\Theta_{ij} = \Lambda_{ij}^{11} - \Lambda_{ij}^{12} \Lambda_{22}^{ - 1} (\Lambda_{ij}^{12} )^{T}\). In other words, when the following condition is true, \({\mathcal{J} < 0}\) holds:

$$ \Theta_{ii} < 0 $$
(26)
$$ \Theta_{ij} + \Theta_{ji} < 0 \, (i < j) $$
(27)

Moreover, when \(\omega (t) = 0\), the derivative \(\dot{V}(t) < 0\) of Lyapunov function can be easily obtained, thus the IWMD vehicle active suspension system (15) is asymptotically stable. Under \(V(0) = 0\) and \(V(\infty ) \ge 0\), one has

$$ \int_{0}^{\infty } {z^{T} (\theta )z(\theta )} d\theta - \gamma^{2} \int_{0}^{\infty } {\omega^{T} (\theta )\omega (\theta )} d\theta < 0 $$
(28)

Thus, the \(H_{\infty }\) performance can be guaranteed.

Define \(\Xi = diag\{ X^{ - 1} ,X^{ - 1} ,X^{ - 1} ,X^{ - 1} ,I,I,I,I\}\), and pre- and post-multiply \(\Xi\) and its transposition to (26) and (27). Define \(K_{j} = \overline{K}_{j} \overline{X}^{ - 1}\), \(\overline{E}_{1} = X^{ - 1} E_{1} X^{ - 1}\), \(\overline{E}_{2} = X^{ - 1} E_{2} X^{ - 1}\), \(\overline{F}_{1} = X^{ - 1} F_{1} X^{ - 1}\), \(\overline{F}_{2} = X^{ - 1} E_{2} X^{ - 1}\), and \(\overline{W} = X^{ - 1} W_{3} X^{ - 1}\). Based on Schur complement and \(\overline{X}\overline{F}_{\alpha }^{ - 1} \overline{X} \le 2\kappa_{\alpha } \overline{X} - \kappa_{{_{\alpha } }}^{2} \overline{F}_{\alpha }\), the Eqs. (17) and (18) can be obtained. Thus, the asymptotic stability and the performance (16) of the suspension system (15) can be guaranteed.

3.2 Reachability Analysis

Theorem 2.

The active suspension system (15), can approach a specified sliding mode surface \(s(t) = 0\) in limited time with the following SMC strategy as

$$ u(t) = \sum\limits_{j = 1}^{4} {\eta_{j} } K_{j} x(t - \tau (t)) - \varphi (t){\text{sgn}} (s(t)) $$
(29)

where \(\varphi (t) = \mu + \varepsilon (t)\left\| {x(t)} \right\|\), and the updating rule of \(\varepsilon (t)\) can be expressed as

$$ \dot{\varepsilon }(t) = \rho \left\| {s(t)} \right\|\left\| {x(t)} \right\| $$
(30)

where \(\mu > 0\) and \(\rho > 0\) the known constants.

Proof:

Considering the Lyapunov function \(V_{s} (t)\) shown below:

$$ V_{s} (t) = \frac{1}{2}s^{T} (t)\left( {\sum\limits_{j = 1}^{4} {\eta_{j} } HB_{2i} } \right)^{ - 1} s(t) + \frac{1}{2\rho }\varepsilon^{2} (t) $$
(31)

Combining (13) and (29), the derivative of sliding-surface function \(s(t)\) can be derived as

$$ \dot{s}(t) = H\sum\limits_{i = 1}^{4} {\eta_{i} } B_{1i} ( - \varphi (t){\text{sgn}} (s(t)) + h(x(t))) $$
(32)

In addition, the derivative of \(V_{s} (t)\) can be expressed as

$$ \begin{gathered} \dot{V}_{s} (t) = s^{T} (t)\left( {\sum\limits_{j = 1}^{4} {\eta_{j} } HB_{2i} } \right)^{ - 1} \dot{s}(t) + \frac{1}{\rho }\varepsilon (t)\dot{\varepsilon }(t) \\ \le - \mu \left\| {s(t)} \right\| < 0 \\ \end{gathered} $$
(33)

where \(\left\| {s(t)} \right\| \ne 0\), which indicates the trajectories of the suspension system can all arrive at the specified sliding-mode surface \(s(t) = 0\) in a finite time.

4 Simulation Results

Various simulations are carried out to verify the performance of the adaptive SMC for active suspensions of IWMD vehicles under cyber attacks. The parameters of suspension model are shown in Table 1.

Given scalars \(\tau_{1} = 0.015\) s,\(\tau_{2} = 0.020\) s,\(a_{1} = 5\), \(a_{2} = 25\), \(a_{3} = 10\), \(\kappa_{1} = 0.1\), \(\kappa_{2} = 0.1\) and \(\mu = 0.5\), \(\rho = 0.1\), and the matrix \(H = [\begin{array}{*{20}c} {100} & {100} & 0 & 0 & {100} & {100} \\ \end{array} ]\) such that \(HB_{2i}\) is nonsingular and \(HB_{1i} = 0\). And the function of cyber attacks is set as \(h(x(t)) = - \sum\nolimits_{j = 1}^{4} {0.2K_{j} x(t)}\). To highlight the effectiveness of the proposed method, the robust H∞ control method is selected as a comparison, which is labeled ‘Comparison’ in subsequent results. In addition, the \(H\infty\) performance index \(\gamma_{\min } = {17}{\text{.2039}}\) and controller gains can be obtained by solving Theorem 1.

Table 1. Parameters of active suspension model.
Full size table

4.1 Bump Response

The following bumpy road is selected as the disturbance input:

$$ z_{w} = \left\{ \begin{gathered} \frac{A}{2}(1 - \cos (\frac{2\pi V}{L}t)), \, 0 \le t \le \frac{L}{V} \hfill \\ 0, \, t > \frac{L}{V} \hfill \\ \end{gathered} \right. $$
(34)

where \(A = 0.05 \, m\) and \(l = 6 \, m\), respectively, and \(v = 10 \, m/s\).

Fig. 3.
figure 3

Bump response of IWMD vehicle suspension system

Full size image

Figure 3 plots the bump response results for IWMD vehicle active suspension systems. Figure 3(a) shows that the body acceleration of the proposed control method has lower peaks than the other two cases, which means the ride comfort is better guaranteed. Figure 3(b)-(c) illustrates that the fluctuation ranges of the suspension travel and tire deflection are smaller than that of the comparison and the passive suspension, which means the handling stability and road holding ability are ensured by the proposed control method. Figure 3(d) illustrates the actuator force under two control strategies. In other words, Fig. 3 shows the adaptive SMC method has an excellent performance.

Fig. 4.
figure 4

The trajectory of sliding mode

Full size image

Figure 4 presents the variation trends of \(s(t)\) and the adaptive parameter \(\varepsilon (t)\). It can be seen from Fig. 4(a) that the sliding variable changes with bump road interference. Figure 4(b) shows that the parameter \(\varepsilon (t)\) varies from the system states to a constant. In addition, Fig. 4 shows that the sliding motion is achieved in finite time.

4.2 Random Response

The following random road excitation is considered:

$$ \dot{z}_{w} (t) = 2\pi n_{0} \sqrt {G_{q} (n_{0} )(v_{0} + at)} n(t) - (v_{0} + at)2\pi n_{c} z_{r} (t) $$
(35)

where \(v_{0} = 5 \, m/s\), \(a = 0.5 \, m/s^{2}\), \(n_{0} { = }0.1 \, m^{ - 1}\) and \(n_{c} { = }0.01 \, m^{ - 1}\), \(n(t)\) denotes a white noise and \(G_{q} (n_{0} ) = 64 \times 10^{ - 6} m^{3}\) is selected in this simulation of random road.

Fig. 5.
figure 5

Random response of IWMD vehicle suspension system

Full size image

The dynamic responses of the IWMD vehicle suspension system under random response are plotted in Fig. 5. It is observed from Fig. 5(a) that the body acceleration is greatly reduced by the proposed controller compared to the other two cases. Figure 5(b)-(c) presents the suspension travel constraint and the tire deflection constraint are guaranteed, which also shows that the performance of the design SMC method is more outstanding than the comparison and passive suspension. The actuator forces of the proposed control scheme and comparison are revealed in Fig. 5(d).

Fig. 6.
figure 6

The trajectory of sliding mode under random road

Full size image

The changing trends of the sliding surface and adaptive parameter under random road interference are illustrated in Fig. 6. From Fig. 6(a) we can see that the sliding surface \(s(t)\) is changing along with the system state, which means the sliding mode motion can be achieved in a finite time. Figure 6(b) shows that the parameter \(\varepsilon (t)\) increases along with the time, which is in line with the trend of the definition of \(\varepsilon (t)\).

5 Conclusion

An adaptive SMC problem for active suspensions of IWMD electric vehicles under time delay and cyber attacks was investigated in this paper. First of all, a T-S fuzzy model has been constructed to capture the nonlinearity of the IWMD vehicle suspension dynamics, and it provided a powerful foundation for the controller design. Then, a set of sufficient conditions were developed to ensure the asymptotical stability and constraint performances of the sliding motion despite the occurrence of time delay and cyber attacks. Moreover, an adaptive SMC strategy was proposed to guarantee the closed-loop active suspension system can achieve the desired performances guaranteed by the specific sliding surface. Finally, the simulation results illustrated the superiority of the proposed adaptive SMC scheme. In the future, the energy-saving control issue will be investigated for the suspension systems [35, 36].