Semi-analytical Expression of Force and Stiffness of Perpendicular Polarized Ring Magnets for Nonlinear Dynamic Analysis

Abstract

Magnetic coupling arrays composed of ring permanent magnets have been widely applied in industrial occasions for achieving nonlinearity, such as passive magnetic bearings, quasi-zero stiffness isolators and multi-stable energy harvesters. These magnetic couplings can be divided into basic configurations including axial magnetization, radial magnetization, and perpendicular magnetization. For the purpose of structure design and parameter optimization, the semi-analytical expressions of first two configurations have been analyzed to obtain high accuracy and low computational cost in previous literatures, while the semi-analytical calculation of perpendicular magnetization has not still been investigated. Therefore, the semi-analytical expressions of magnetic force and stiffness for perpendicular polarized ring magnets are proposed. Then, the magnetic forces calculated by the proposed method, numerical simulation, and COMSOL software under different parameters are obtained. The results show that the proposed semi-analytical calculation has higher accuracy and less computational time than numerical simulation. Moreover, the influence of structural parameters on magnetic stiffness is analyzed. It can be demonstrated that with the increase of air gap, the decrease of the width of axial magnetized magnet, and the decrease of the height of axial magnetized magnet, the magnetic force and magnetic stiffness are both reduced. In general, the proposed semi-expression model can be applied for the design and optimization in the practical applications of ring permanent magnets.

1 Introduction

The permanent magnets have been widely used in many significant occasions. For example, passive magnetic bearings are composed of several permanent magnets polarized in axial or radial directions [1,2,3]. In these occasions, many basic magnetic coupling configurations are used to provide magnetic force and stiffness to maintain the working performance of devices, such as in quasi-zero stiffness (QZS) isolator [4, 5]. In these engineering applications, it is of great significance to design, analyze, and optimize the structural parameters of ring permanent magnets due to the limited space. Therefore, to obtain the magnetic force or magnetic stiffness produced by ring permanent magnets for nonlinear dynamic analysis is becoming an open issue.

The magnetic dipole method can be used to calculate the magnetic field or the magnetic force [6], but regarding the permanent magnet as the dipole may yield low accuracy if two magnets have close distance. Besides, the magnetic charge theory has been widely applied to calculate the magnetic force of permanent magnets [7]. This method considers the magnetization of magnets as positive and negative magnetic charges distributed in the surfaces of magnets. Then, according to the Coulomb’s law, the magnetic force can be calculated by integrating the magnetic force between magnetic charges. The fully analytical expressions of perpendicular or parallel cubic magnets [8], and rotational cubic magnets [9] were investigated. However, it is difficult to obtain the accurate fully analytical expressions of magnetic force produced by ring permanent magnets. According to the Coulomb’s law, the numerical method can be used to calculate the magnetic force by dispersing magnetic charge [10], but the high computational cost is not suitable for structural design and parametric analysis.

Some semi-analytical or analytical expressions have been proposed to calculate magnetic field produced by ring permanent magnets [11,12,13]. Ravaud et al. [14] presented analytical formulations of magnetic field of ring magnets according to Colombian approach. Babic et al. [15] proposed an improved Colombian-based analytical calculation of magnetic fields created by ring magnet. Besides, since ring permanent magnets can be approximately composed of tile magnets, the magnetic field of ring permanent magnets can be calculated by superposing the magnetic fields produced by tile magnets [16,17,18]. However, the analytical formulations of magnetic force exerted between two ring permanent magnets are difficult to be obtained up till now. To address this issue, Ravaud et al. [19, 20] deduced the semi-analytical expressions of magnetic force and stiffness of passive magnetic bearings using permanent magnets with axial magnetizations and radial magnetizations for parametric studies. Then, Ravaud et al. [21] presented simplified analytical expressions of magnetic force and stiffness for ring permanent magnets with perpendicular polarizations where the inner ring polarization is perpendicular to the outer ring polarization. Therefore, much effort has been devoted to calculating magnetic force and magnetic stiffness of ring permanent magnets by presenting semi-analytical or simplified analytical expressions. However, the semi-analytical expression of perpendicular polarization of ring magnet remains uninvestigated. In addition, the simplified calculation of perpendicular polarization does not take the magnetic charge volume density of radial-magnetized ring magnet into consideration. It would be unavailable for thick radial-magnetized ring magnet.

Therefore, the semi-analytical expressions of the magnetic force and magnetic stiffness of perpendicular polarized ring permanent magnets are presented by taking both surface and volume charge densities into consideration. Then, the accuracy and the time cost of the proposed semi-analytical expressions are compared with numerical simulation and COMSOL software. Finally, the influence of structural parameters of permanent magnets on magnetic force and magnetic stiffness is analyzed.

2 Semi-analytical Calculations of Force and Stiffness

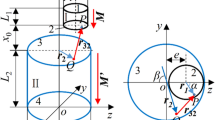
The circular Halbach array composed by ring magnets can be widely applied for QZS isolators [22] and multi-stable energy harvesters, as shown in Fig. 1. The spring and Halbach array can be combined to provide nonlinear stiffness. The QZS isolator can be applied to isolate the low-frequency vibration, while the multi-stable energy harvester can be beneficial for energy extraction from broadband excitation. In order to investigate the nonlinear characteristics, it is necessary to model the magnetic force of Halbach array.

Therefore, this section will present semi-analytical expressions of the magnetic force and stiffness exerted by perpendicular polarized ring permanent magnets for calculating the magnetic stiffness of Halbach array. The perpendicular polarization is composed of two ring magnets whose polarizations are axial and radial respectively. The perpendicular polarization can be seen in many magnetic arrays, such as Halbach array. Moreover, the semi-analytical expressions proposed in this section can improve the calculating accuracy and reduce the computational time.

Fig. 1.

QZS isolator and multi-stable energy harvester by using Halbach array

2.1 Notion and Geometry

Figure 2 shows the basic configurations of ring permanent magnets which composes the Halbach array, including axial magnetization, radial magnetization, and perpendicular magnetization. These three basic configurations can be applied to achieve a variety of magnetic couplings. In this paper, the concern is the configuration of perpendicular magnetization. Therefore, the semi-analytical expression of magnetic force and stiffness for perpendicular magnetization will be derived.

Fig. 2.

Basic configurations of ring permanent magnets: (a) axial magnetization, (b) radial magnetization, and (b) perpendicular magnetization.

The representation of perpendicular magnetization with two ring magnets is shown in Fig. 3. For the ring magnet polarized in axial direction, r₁ and r₂ are the inner and outer radiuses, z₁ and z₂ are the bottom and top heights, θ₁ is the position angle from 0 to 2π, and the magnetization is J. For the ring magnet polarized in radial direction, R₁ and R₂ are inner and outer radiuses, Z₁ and Z₂ are bottom and top heights, θ₂ is the position angle from 0 to 2π, and the magnetization is J.

Fig. 3.

Representation of perpendicular magnetization with two ring magnets: (a) space diagram, (b) sectional diagram.

2.2 Semi-analytical Expression of Magnetic Force

The axial polarized and radial polarized ring magnets can be equivalent to magnetic charges. For uniform axial polarized magnet, there is only surface charge σ₁ = J. For non-uniform radial polarized magnet, there are surface charge σ₂ = J and volume charge ρ₂ = J/R, where R is the radius where the volume charge locates. In this research, the axial magnetic force F_z is the concern. Therefore, the axial magnetic force F_z can be calculated by

$$ F_{z} = F_{SS} + F_{SV} $$

(1)

where F_SS is the axial magnetic force exerted by surface charges between axial and radial polarized magnets, F_SV is the axial magnetic force exerted by the surface charge of axial polarized magnet and the volume charge of radial polarized magnet.

For F_SS, it can be expressed as

$$ F_{SS} = f_{ss} \left( {z_{1} ,R_{1} } \right) + f_{ss} \left( {z_{1} ,R_{2} } \right) + f_{ss} \left( {z_{2} ,R_{1} } \right) + f_{ss} \left( {z_{2} ,R_{2} } \right) $$

(2)

where

$$ f_{ss} \left( {z,R} \right) = - \frac{{\sigma_{1} \sigma_{2} }}{{4\pi \mu_{0} }}\int_{{r_{1} }}^{{r_{2} }} {\int_{{Z_{1} }}^{{Z_{2} }} {\int_{0}^{2\pi } {\int_{0}^{2\pi } {\frac{{\left( {z - Z} \right)rR}}{{\left( {r^{2} + R^{2} - 2rR\cos \left( {\theta_{1} - \theta_{2} } \right) + \left( {z - Z} \right)^{2} } \right)^{\frac{3}{2}} }}} {\text{d}}\theta_{1} } {\text{d}}\theta_{2} } {\text{d}}Z{\text{d}}r} $$

(3)

where μ₀ is the permeability of the vacuum.

According to the symmetry of axial magnetic force, f_ss(z, R) can be rewritten as

$$ f_{ss} \left( {z,R} \right) = - \frac{{\sigma_{1} \sigma_{2} }}{{2\mu_{0} }}\int_{{r_{1} }}^{{r_{2} }} {\int_{{Z_{1} }}^{{Z_{2} }} {\int_{0}^{2\pi } {\frac{{\left( {z - Z} \right)rR}}{{\left( {r^{2} + R^{2} - 2rR\cos \left( \theta \right) + \left( {z - Z} \right)^{2} } \right)^{\frac{3}{2}} }}} {\text{d}}\theta } {\text{d}}Z{\text{d}}r} $$

(4)

After the integration with respect to r and Z, Eq. (4) can be rewritten as

$$ \begin{aligned} f_{ss} \left( {z,R} \right) = & - \frac{{\sigma_{1} \sigma_{2} }}{{4\pi \mu_{0} }}\int_{0}^{2\pi } {f_{1} \left( {r_{2} ,z,R,Z_{2} ,\theta } \right) - f_{1} \left( {r_{1} ,z,R,Z_{2} ,\theta } \right)} - f_{1} \left( {r_{2} ,z,R,Z_{1} ,\theta } \right) \\ & { + }f_{1} \left( {r_{1} ,z,R,Z_{1} ,\theta } \right) \\ \end{aligned} $$

(5)

where

$$ f_{1} \left( {r,z,R,Z,\theta } \right) = R\left( {R{\text{ArcTanh}}\left[ {\frac{2r - 2R\cos \left( \theta \right)}{{2\alpha }}} \right]\cos \left( \theta \right) + \alpha } \right) $$

(6)

$$ \alpha = \sqrt {r^{2} + R^{2} + \left( {z - Z} \right)^{2} - 2rR\cos \left( \theta \right)} $$

(7)

For F_SV, it can be expressed as

$$ F_{SV} = f_{sv} \left( {z_{1} } \right) + f_{sv} \left( {z_{2} } \right) $$

(8)

where

$$ f_{sv} \left( z \right) = - \frac{{\sigma_{1} \sigma_{2} }}{{4\pi \mu_{0} }}\int_{{R_{1} }}^{{R_{2} }} {\int_{{r_{1} }}^{{r_{2} }} {\int_{{Z_{1} }}^{{Z_{2} }} {\int_{0}^{2\pi } {\int_{0}^{2\pi } {\frac{{\left( {z - Z} \right)r}}{{\left( {r^{2} + R^{2} - 2rR\cos \left( {\theta_{1} - \theta_{2} } \right) + \left( {z - Z} \right)^{2} } \right)^{\frac{3}{2}} }}{\text{d}}\theta } } {\text{d}}\theta } {\text{d}}Z{\text{d}}r} {\text{d}}R} $$

(9)

According to the symmetry of axial magnetic force, f_sv(z) can be rewritten as

$$ f_{sv} \left( z \right) = - \frac{{\sigma_{1} \sigma_{2} }}{{2\mu_{0} }}\int_{{R_{1} }}^{{R_{2} }} {\int_{{r_{1} }}^{{r_{2} }} {\int_{{Z_{1} }}^{{Z_{2} }} {\int_{0}^{2\pi } {\frac{{\left( {z - Z} \right)r}}{{\left( {r^{2} + R^{2} - 2rR\cos \left( {\theta_{1} - \theta_{2} } \right) + \left( {z - Z} \right)^{2} } \right)^{\frac{3}{2}} }}} {\text{d}}\theta } {\text{d}}Z{\text{d}}r} {\text{d}}R} $$

(10)

After the integration with respect to r, R and Z, Eq. (10) can be rewritten as

$$ \begin{gathered} f_{sv} \left( z \right) = - \frac{{\sigma_{1} \sigma_{2} }}{{2\mu_{0} }}\int_{0}^{2\pi } {\left( {f_{2} \left( {r_{2} ,z,R_{2} ,Z_{2} ,\theta } \right) - f_{2} \left( {r_{1} ,z,R_{2} ,Z_{2} ,\theta } \right)} \right.} \\ - f_{2} \left( {r_{2} ,z,R_{1} ,Z_{2} ,\theta } \right){ + }f_{2} \left( {r_{1} ,z,R_{1} ,Z_{2} ,\theta } \right) + f_{2} \left( {r_{2} ,z,R_{2} ,Z_{1} ,\theta } \right) \\ \left. { - f_{2} \left( {r_{1} ,z,R_{2} ,Z_{1} ,\theta } \right) - f_{2} \left( {r_{2} ,z,R_{1} ,Z_{1} ,\theta } \right){ + }f_{2} \left( {r_{1} ,z,R_{1} ,Z_{1} ,\theta } \right)} \right){\text{d}}\theta \\ \end{gathered} $$

(11)

where

$$ \begin{gathered} f_{2} = - r^{2} + 2R\alpha + 2r^{2} \ln \left( {R - r\cos \left( \theta \right) + \alpha } \right) \\ - \left( {R^{2} - 2\left( {z - Z} \right)^{2} + R^{2} \cos \left( {2\theta } \right)} \right)\cot \left( \theta \right)\csc \left( \theta \right)\ln \left( {r - R\cos \left( \theta \right) + \alpha } \right) \\ + \left( {z - Z} \right)^{2} \csc^{2} \left( \theta \right)\ln \left( { - r^{2} - 2\left( {z - Z} \right)^{2} + r^{2} \cos \left( {2\theta } \right)} \right) \\ + \frac{{{\text{i}}\left( {z - Z} \right)^{2} \left( {iR + \left( {z - Z} \right)\cot \left( \theta \right)} \right)\csc \left( \theta \right)}}{{\sqrt {\delta + \phi } }}\ln \left( { - \frac{{4\sin^{3} \left( \theta \right)\sigma \left( {\beta + \gamma - 2\left( {R^{2} + \left( {z - Z} \right)^{2} } \right)\sin \left( \theta \right) + 2\alpha \sqrt {\left( {\delta + \phi } \right)^{2} } } \right)}}{{\left( {z - Z} \right)^{2} \left( {z - Z + {\text{i}}r\sin \left( \theta \right)} \right)\left( { - \left( {\left( {z - Z} \right)\cos \left( \theta \right) + iR\sin \left( \theta \right)} \right)^{2} } \right)^{\frac{3}{2}} }}} \right) \\ - \frac{{\left( {z - Z} \right)^{2} \left( {R + \left( {z - Z} \right)\cot \left( \theta \right)} \right)\csc \left( \theta \right)}}{{\sqrt { - \delta + \phi } }}\ln \left( { - \frac{{4{\text{i}}\sin^{3} \left( \theta \right)\left( { - \beta - \gamma - 2\left( {R^{2} + \left( {z - Z} \right)^{2} } \right)\sin \left( \theta \right) + 2\alpha \sqrt {\left( { - \delta + \phi } \right)^{2} } } \right)}}{{\left( {z - Z} \right)^{2} \left( {z - Z + {\text{i}}r\sin \left( \theta \right)} \right)\left( { - \left( {i\left( {z - Z} \right)\cos \left( \theta \right) + R\sin \left( \theta \right)} \right)^{2} } \right)^{\frac{3}{2}} }}} \right) \\ \end{gathered} $$

(12)

$$ \alpha = \sqrt {r^{2} + R^{2} + \left( {z - Z} \right)^{2} - 2rR\cos \left( \theta \right)} $$

(13)

$$ \beta = - 2{\text{i}}rz + 2{\text{i}}rZ $$

(14)

$$ \gamma = 2{\text{i}}R\left( {z - Z} \right)\cos \left( \theta \right) $$

(15)

$$ \delta = - {\text{i}}\left( {z - Z} \right)\cos \left( \theta \right) $$

(16)

$$ \phi = R\sin \left( \theta \right) $$

(17)

$$ \sigma = \left( {z - Z} \right)\cos \left( \theta \right) + {\text{i}}R\sin \left( \theta \right) $$

(18)

2.3 Semi-analytical Expression of Magnetic Stiffness

The axial magnetic stiffness K_z can be expressed as

$$ K_{z} = K_{SS} + K_{SV} $$

(19)

where K_SS is the axial magnetic force produced by surface charges between axial and radial polarized magnets, K_SV is the axial magnetic force produced by the surface charge of axial polarized magnet and the volume charge of radial polarized magnet.

For K_SS, it can be expressed as

$$ K_{SS} = k_{ss} \left( {z_{1} ,R_{1} } \right) + k_{ss} \left( {z_{1} ,R_{2} } \right) + k_{ss} \left( {z_{2} ,R_{1} } \right) + k_{ss} \left( {z_{2} ,R_{2} } \right) $$

(20)

where

$$ k_{ss} \left( {z,R} \right) = - \frac{\partial }{\partial z}\frac{{\sigma_{1} \sigma_{2} }}{{2\mu_{0} }}\int_{{r_{1} }}^{{r_{2} }} {\int_{{Z_{1} }}^{{Z_{2} }} {\int_{0}^{2\pi } {\frac{{\left( {z - Z} \right)rR}}{{\left( {r^{2} + R^{2} - 2rR\cos \left( \theta \right) + \left( {z - Z} \right)^{2} } \right)^{\frac{3}{2}} }}} {\text{d}}\theta } {\text{d}}Z{\text{d}}r} $$

(21)

After calculating the derivative with respect to z and the integration with respect to R and z, Eq. (21) can be expressed as

$$ \begin{aligned} k_{ss} \left( {z,R} \right) = & - \frac{{\sigma_{1} \sigma_{2} }}{{2\mu_{0} }}\int_{0}^{2\pi } {k_{1} \left( {r_{2} ,z,R,Z_{2} ,\theta } \right) - k_{1} \left( {r_{1} ,z,R,Z_{2} ,\theta } \right)} \\ & - k_{1} \left( {r_{2} ,z,R,Z_{1} ,\theta } \right){ + }k_{1} \left( {r_{1} ,z,R,Z_{1} ,\theta } \right){\text{d}}\theta \\ \end{aligned} $$

(22)

where

$$ k_{1} \left( {z,R} \right) = \frac{{R\left( {z{ - }Z} \right)\left( {R^{2} + \left( {z - Z} \right)^{2} - rR\cos \left( \theta \right)} \right)}}{{\sqrt {r^{2} + R^{2} + z^{2} - 2zZ + Z^{2} - 2rR\cos \left( \theta \right)} \left( {R^{2} { + }\left( {z - Z} \right)^{2} - R^{2} \cos^{2} \left( \theta \right)} \right)}} $$

(23)

For K_SV, it can be expressed as

$$ K_{SV} = k_{sv} \left( {z_{1} } \right) + k_{sv} \left( {z_{2} } \right) $$

(24)

where

$$ k_{sv} \left( z \right) = - \frac{\partial }{\partial z}\frac{{\sigma_{1} \sigma_{2} }}{{2\mu_{0} }}\int_{{R_{1} }}^{{R_{2} }} {\int_{{r_{1} }}^{{r_{2} }} {\int_{{Z_{1} }}^{{Z_{2} }} {\int_{0}^{2\pi } {\frac{{\left( {z - Z} \right)r}}{{\left( {r^{2} + R^{2} - 2rR\cos \left( \theta \right) + \left( {z - Z} \right)^{2} } \right)^{\frac{3}{2}} }}} {\text{d}}\theta } {\text{d}}Z{\text{d}}r} {\text{d}}R} $$

(25)

After calculating the derivative with respect to z and the integration with respect to r and Z, Eq. (25) can be rewritten as

$$ \begin{aligned} k_{sv} \left( z \right) = & - \frac{{\sigma_{1} \sigma_{2} }}{{2\mu_{0} }}\int_{0}^{2\pi } {\left( {k_{2} \left( {r_{2} ,z,R_{2} ,Z_{2} ,\theta } \right) - k_{2} \left( {r_{1} ,z,R_{2} ,Z_{2} ,\theta } \right)} \right.} \\ & - k_{2} \left( {r_{2} ,z,R_{1} ,Z_{2} ,\theta } \right){ + }k_{2} \left( {r_{1} ,z,R_{1} ,Z_{2} ,\theta } \right) + k_{2} \left( {r_{2} ,z,R_{2} ,Z_{1} ,\theta } \right) \\ & \left. { - k_{2} \left( {r_{1} ,z,R_{2} ,Z_{1} ,\theta } \right) - k_{2} \left( {r_{2} ,z,R_{1} ,Z_{1} ,\theta } \right){ + }k_{2} \left( {r_{1} ,z,R_{1} ,Z_{1} ,\theta } \right)} \right){\text{d}}\theta \\ \end{aligned} $$

(26)

where

$$ \begin{aligned} k_{2} = & \frac{1}{4}\left( {z - Z} \right)\left( {4{\text{a}}\tanh \left( {\frac{R - r\cos \left( \theta \right)}{\alpha }} \right)} \right.\csc^{2} \left( \theta \right) \\ & - \frac{{2\sqrt 2 {\text{a}}\tanh \left( {\frac{{ - 2R\beta + 2\gamma \sin \left( \theta \right) + 2r\cos \left( \theta \right)\left( {\beta - R\sin \left( \theta \right)} \right)}}{{\sqrt 2 \alpha \sqrt {\delta + \phi } }}} \right)\cot \left( \theta \right)\left( { - r\beta + \left( {z - Z} \right)^{2} \cot \left( \theta \right)} \right)}}{{\beta \sqrt {\delta + \phi } }} \\ & - \frac{{\left( {2\sqrt 2 {\text{a}}\tanh \left( {\frac{{\sqrt 2 \left( {R\beta + \gamma \sin \left( \theta \right) - r\cos \left( \theta \right)\left( {\beta + R\sin \left( \theta \right)} \right)} \right)}}{{\alpha \sqrt {\delta - \phi } }}} \right)\cot \left( \theta \right)} \right)\left( {r\beta + \left( {z - Z} \right)^{2} \cot \left( \theta \right)} \right)\left( {\sqrt {\delta - \phi } } \right)}}{{\beta \sqrt { - \delta + \phi } }} \\ \end{aligned} $$

(27)

$$ \alpha = \sqrt {r^{2} + R^{2} + \left( {z - Z} \right)^{2} - 2rR\cos \left( \theta \right)} $$

(28)

$$ \beta = \sqrt { - \left( {z - Z} \right)^{2} } $$

(29)

$$ \gamma = r^{2} + \left( {z - Z} \right)^{2} $$

(30)

$$ \delta = r^{2} - \left( {z - Z} \right)^{2} - \left( {r^{2} + \left( {z - Z} \right)^{2} } \right)\cos \left( {2\theta } \right) $$

(31)

$$ \phi = 2r\sin \left( {2\theta } \right)\sqrt { - \left( {z - Z} \right)^{2} } $$

(32)

3 Simulation Verification

This section is aimed to verify the effectiveness of the proposed semi-analytical model for the calculations of magnetic force and magnetic stiffness. The results from the semi-analytical model, numerical simulation, and COMSOL software are compared, including the accuracy and the computational time cost. The semi-analytical model and the numerical simulation are both finished by MATLAB. The numerical simulation is to discrete the integrating variables directly.

3.1 Size Parameters

The sizes of ring permanent magnets for simulation verification are listed in Table 1. There are three sizes used to compare the magnetic force and stiffness.

Table 1. Sizes of ring permanent magnets for simulation verification

3.2 Magnetic Force

The magnetic forces of perpendicular magnetization are compared among COMSOL, numerical simulation, and semi-analytical calculation, as shown in Fig. 4, with the magnetization J of 1.4 T. The displacement is changing from -20 mm to 20 mm, with the step of 1 mm. For numerical simulation, the steps of Z, r, R, and θ are 0.1 mm, 0.1 mm, 0.1 mm and 0.1 rad respectively. For the semi-analytical calculation, the step of θ is 0.1 rad.

It can be seen from Fig. 4 that the varying trends of magnetic forces for size 1, size 2, and size 3 are all the same. The maximal magnetic force can be seen when the displacement is 0. With the increase of displacement, the magnetic force finally reaches the peak value in +y direction. In addition, the magnetic forces calculated by numerical simulation and semi-analytical expression are both close to the result of COMSOL.

Fig. 4.

Magnetic forces under different sizes: (a) size 1, (b) size 2, (c) size 3.

For size 1 in Fig. 4(a), the maximal magnetic forces of COMSOL, semi-analytical calculation, and numerical simulation are −36.794 N, −36.472 N and −36.207 N respectively when the displacement is 0. The errors of semi-analytical calculation and numerical simulation are 0.88% and 1.60% respectively. For size 2 in Fig. 4(b), the maximal magnetic forces from COMSOL, semi-analytical calculation, and numerical simulation are −100.54 N, −98.995 N and −98.338 N respectively when the displacement is 0. The errors of semi-analytical calculation and numerical simulation are 1.54% and 2.19% respectively. For size 3 in Fig. 4(c), the maximal magnetic forces of COMSOL, semi-analytical calculation, and numerical simulation are −169.846 N, −166.024 N and −165.025 N when the displacement is 0. The errors of semi-analytical calculation and numerical simulation are 2.25% and 2.84% respectively. Therefore, it indicates that both semi-analytical calculation and numerical simulation can have high accuracy, and the semi-analytical calculation is more precise than numerical simulation.

In addition, the comparisons of error and time for magnetic force calculation are listed in Table 2. The computational times of numerical simulation for size 1, size 2, and size 3 are 88.922 s, 345.870 s, and 766.836 s respectively, while the computational times of semi-analytical calculation are only 0.505 s, 0.525 s, and 0.526 s. It can be concluded that the accuracy and the computational time of semi-analytical calculation are both better than numerical simulation.

Table 2. Comparisons of error and time for magnetic force calculation.

3.3 Magnetic Stiffness

Figure 5 illustrates the magnetic stiffness under three sizes of magnets, including COMSOL, numerical simulation, and semi-analytical calculation, with the magnetization J of 1.4 T. The displacement is changing from -20 mm to 20 mm, with the step of 1 mm. For numerical simulation, the steps of Z, r, R, and θ are 0.1 mm, 0.1 mm, 0.1 mm and 0.1 rad respectively. For the semi-analytical calculation, the step of θ is 0.1 rad.

It can be seen from Fig. 5 that when the displacement is 0, the magnetic stiffness is 0. With the increase of displacement, the magnetic stiffness can firstly increase to the peak value and then decrease to 0 for all sizes magnets. For size 1 in Fig. 5(a), the maximal magnetic stiffnesses from COMSOL, numerical simulation, and semi-analytical calculation are 4.619 × 10³ N/m, 4.486 × 10³ N/m, and 4.567 × 10³ N/m respectively. The errors of semi-analytical calculation and numerical simulation are 1.13% and 2.88% respectively. For size 2 in Fig. 5(b), the maximal magnetic stiffnesses from COMSOL, numerical simulation, and semi-analytical calculation are 1.0968 × 10⁴ N/m, 1.0544 × 10⁴ N/m, and 1.0755 × 10⁴ N/m respectively. The errors of semi-analytical calculation and numerical simulation are 1.94% and 3.87% respectively. For size 3 in Fig. 5(c), the maximal magnetic stiffnesses of COMSOL, numerical simulation, and semi-analytical calculation are 1.6581 × 10⁴ N/m, 1.5791 × 10⁴ N/m, and 1.6013 × 10⁴ N/m respectively. The errors of semi-analytical calculation and numerical simulation are 3.43% and 4.76% respectively. Therefore, the results show that the magnetic stiffness of semi-analytical calculation can have higher accuracy than numerical simulation.

Fig. 5.

Magnetic stiffnesses under different sizes: (a) size 1, (b) size 2, (c) size 3.

The comparisons of error and time for magnetic stiffness calculation is summarized in Table 3. The computational times of numerical simulation for size 1, size 2, and size 3 are 89.052 s, 345.953 s, and 766.890 s respectively, while the computational times of semi-analytical calculation are only 0.136 s, 0.136 s, and 0.138 s. Therefore, it can be concluded that the accuracy and the computational time of semi-analytical calculation are both better than numerical simulation.

Table 3. Comparisons of error and time for magnetic stiffness calculation.

4 Parameters Analysis

It is well known that structural parameters have an important impact on magnetic force and magnetic stiffness in the perpendicular magnetization. Therefore, it is necessary to analyze the influence of structural parameters including air gap, width of axial magnetized magnet, and height of axial magnetized magnet using the proposed semi-analytical expressions.

4.1 Air Gap

To analyze the influence of air gap, the widths w₁, w₂ and heights h₁, h₂ of axial polarized and radial polarized ring magnets are 10 mm and 10 mm, 10 mm and 10 mm respectively. Then, the different air gaps g can be obtained by changing R₁ and R₂. Figure 6 shows that the magnetic forces and stiffnesses under different air gaps g, ranging from 2 mm to 6 mm, with the step of 0.1 mm. It can be seen from Fig. 6 that with the increase of g, the peak value of magnetic force decreases from 335.367 N to 170.397 N. The number of extremums is 3 when g is 2 mm, but it decreases to 1 when g increases to 6 mm. In addition, with the increase of g, the peak value of magnetic stiffness decreases from 50907.7 N/m to 22356.6 N/m.

Fig. 6.

Magnetic force and stiffness under different air gaps: (a) magnetic force, (b) magnetic stiffness.

4.2 Width of Axial Magnetized Magnet

To investigate the influence of the width of axial magnetized magnet, the air gap g is 10 mm, the width w₂ of radial magnetized magnet is 10 mm, and the heights h₁, h₂ of axial polarized and radial polarized ring magnets are 10 mm and 10 mm respectively. Figure 7 shows the magnetic forces and stiffnesses under different widths of axial magnetized magnet w₁, ranging from 2 mm to 6 mm, with the step of 0.1 mm. The result shows that with the increase of w₁, the peak value of magnetic force rises from 24.601 N to 65.272 N, while the peak value of magnetic stiffness increases from 3034.14 N/m to 7462.87 N/m.

Fig. 7.

Magnetic forces and stiffnesses under different widths of axial magnetized magnet: (a) magnetic force, (b) magnetic stiffness.

4.3 Height of Axial Magnetized Magnet

For the analysis of the height of axial magnetized magnet, the air gap g is 10 mm, the widths w₁, w₂ of axial and radial magnetized magnet are 10 mm and 10 mm respectively, and the height h₂ of radial polarized ring magnets is 10 mm. Figure 8 illustrates the magnetic forces and stiffnesses under different heights of axial magnetized magnet h₁, ranging from 8 mm to 12 mm. With the increase of h₁, the peak value of magnetic force increases from 82.562 N to 112.800 N, the peak value of magnetic stiffness rises from 9143.22 N/m to 11879.2 N/m.

Fig. 8.

Magnetic forces and stiffnesses under different heights of axial magnetized magnet: (a) magnetic force, (b) magnetic stiffness.

Generally, the quantitative analysis of magnetic force and stiffness under different parameters can be very beneficial for the design and optimization of ring permanent magnets.

5 Conclusion

The semi-analytical expressions of magnetic force and stiffness induced by perpendicular polarized ring permanent magnets are presented. By comparing with the results from COMSOL software, the accuracy of the semi-analytical expression is higher than numerical simulation, and the computational time of the semi-analytical expression is much shorter than numerical simulation for magnetic force and stiffness calculation. Based on the semi-analytical expression, the parameters quantitative analysis of magnetic force and magnetic stiffness is carried out. With the increase of air gap, the decrease of the width of axial magnetized magnet, and the decrease of the height of axial magnetized magnet, the magnetic force and magnetic stiffness are both reduced. Moreover, the proposed semi-analytical expressions can be beneficial to obtaining the expected magnetic force and stiffness in the design and the optimization of ring permanent magnets.