Keywords

1 Introduction

Cancer is a life-threatening disease, and one of the most frightening among them is the brain cancer. The survival rate for people with brain cancer decreases with age (American Society of Clinical Oncology (ASCO) 2020). More than a million cases of brain tumor are diagnosed per year in India. A popular and effective technique, Magnetic Resonance Imaging (MRI) provides exquisite detail of the brain, to detect the prognosis of tumor, but sometimes the presence of surrounding soft tissues obscures the tumor outline. In this view, image segmentation is one of the most crucial steps in tumor analysis. There are several popular image segmentation techniques applied in medical imaging but a single approach is not applicable for all types of brain MRI. Hence, there is a need for more advanced and automated approach, which would mostly eliminate the inconveniences present in the conventional techniques and would provide better result for diagnosis of brain tumor.

Based on these, present work introduces a novel cluster validity index-based fuzzy c-means (FCM) clustering algorithm for segmentation of brain MRI. FCM is one of the most popular and widely used algorithms due to its robustness in presence of ambiguity and impreciseness. Two significant regional features of MRI; local entropy and brightness captured by appropriate kernel are utilized as the data of FCM model which accurately detects the prognosis of brain tumors. To combat the problem of manual selection of cluster numbers in FCM algorithm, this work employs five cluster validity indices for prediction of appropriate cluster numbers. Following this segmentation approach, discrimination of benignancy/malignancy of tumors also produces encouraging results.

The proposed method is discussed in Sect. 2. Section 3 provides the experimental results using the proposed detection model and finally Sect. 4, Sect. 5 draws some discussion and conclusion of this work.

2 Proposed Methodology

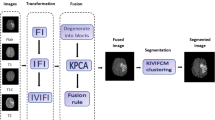
To resolve high degrees of inhomogeneity present in brain MRI, a novel cluster validity index-based FCM algorithm has been proposed using two significant spatial characteristics of MRI. The framework of the proposed approach, consisting of different blocks is shown in Fig. 1. To abide by the principles of medical ethics, multimodal brain MRIs (T1-weighted, T2-weighted, Gad, and PD) have been used from benchmarked databases from ‘The Whole Brain Atlas-Harvard Medical School’ (Johnson and Becker 2003) and ‘The Multimodal Brain Tumor Image Segmentation Benchmark (BRATS)’ (Lastname et al. 2015).

Fig. 1
figure 1

Framework of the proposed approach

Full size image

In the following sections, the different blocks of the proposed methodology have been further discussed in detail.

2.1 Significant Feature Selection

From several research works, it has been observed that statistical features like local entropy, brightness, homogeneity, relative variances have been individually used to resolve the impreciseness in edge detection (Despotovic et al. 2015). On the contrary, Das et al. (2019) studied that, the combination of local entropy and local brightness is an effective pair to model the impreciseness present in mammograms. Sometimes, in brain MRI, the presence of overlapped soft tissues flattens the brightness of tumor and hence leads to over/under segmentation problems. As local entropy of a region estimates the information carried by it, surrounding soft tissues occupy different grade of entropy compared to the tumors. Following this, the present study shows that the combinations of local entropy (E) and brightness (B) efficiently resolve the uncertainties present in the process of tumor segmentation.

Regional entropy (E) and brightness (B) are mathematically expressed by the following two equations

$$E = - \mathop \sum \limits_{i = 1}^{n} p\left( {x_{i} } \right)\log p\left( {x_{i} } \right)$$
(1)
$$B = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} I\left( {x_{i} } \right)$$
(2)

where X = {x1, x2, …, xi,…, xn} denotes the set of image pixels and p(xi) is the probability of occurrence of pixel intensity I(xi) inside the kernel.

A kernel of size 3 × 3 (n = 9) has been moved across the entire image to fetch different characteristics of E and B, which in turn are used as the data for the proposed approach.

2.2 Cluster Number Selection

A conventional clustering algorithm Fuzzy c-means (FCM) has a great advantage of being more flexible than hard clustering techniques and provides better result in case of overlapped imprecise data. In spite of being advantageous, the most important challenge in FCM algorithm is to predict the optimal number of clusters (Gueorguieva et al. 2017). In this view, present work addresses optimal cluster number selection in terms of various cluster validity indices, prior to the segmentation using FCM algorithm.

Cluster Validity Indices

Cluster validation approach evaluates the obtained results and finds the best partitioning of the given data (Gueorguieva et al. 2017). The two important criteria for selection of the cluster number are compactness and separation of the underlying data which has been clearly shown in Fig. 2.

Fig. 2
figure 2

Compactness and separation within two clusters

Full size image

Compactness refers to the closeness of the members in each cluster, measured by the variance of cluster members and it should be minimized for better clustering. Separation refers to the distance between two different clusters, the inter-cluster distance (Wang and Zhang 2007). In the present work, five effective cluster validation indices have been employed for evaluating the cluster numbers (Wang and Zhang 2007; Bataineh et al. 2011; Pakhira et al. 2004). The validation indices and their mathematical formulations are described below

  1. (i)

    Partition Coefficient (PC): It measures the overlapping between the clusters and its value lies in the range of [1/KC, 1], where KC is the number of clusters (Capitaine and Frelicot 2011). Closer the value of PC to unity, more crisp the clustering would be (Gueorguieva et al. 2017).

    $${\text{PC}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{{K_{{\text{c}}} }} \mathop \sum \limits_{j = 1}^{n} \left( {\mu_{ij}^{2} } \right)$$
    (3)

    where n is the size of the data matrix, \(\mu_{ij}\) is the membership value of jth data point in ith cluster.

  2. (ii)

    Classification Entropy (CE): CE measures the fuzziness of a given cluster (Capitaine and Frelicot 2011). Hence, CE estimates the effectiveness of partitioning and its value lies between the intervals [0, logKc]. Lower value of CE reflects better partitioning of dataset Z.

    $${\text{CE}} = - \frac{1}{n}\mathop \sum \limits_{i = 1}^{{K_{{\text{c}}} }} \mathop \sum \limits_{j = 1}^{n} \mu_{ij} \log \mu_{ij}$$
    (4)
  3. (iii)

    Separation Coefficient (SC): SC computes the ratio of sum of the separation and compactness of clusters (Gueorguieva et al. 2017). Minimum value of SC indicates the better separation between the clusters.

    $$SC = \mathop \sum \limits_{{i = 1}}^{{K_{{\text{c}}} }} \frac{{\mathop \sum \nolimits_{{j = 1}}^{n} ~\left( {\mu _{{ij}} } \right)^{x} \left\| {z_{j} - c_{i} ^{2} } \right\|}}{{n_{i} ~~~\mathop \sum \nolimits_{k}^{{K_{c} }} \left\| {c_{k} - c_{i} ^{2} } \right\|~}}$$
    (5)

    where x is the fuzzifier index taken as 2, \(\left\| {z_{j} - c_{i} } \right\|\) is the Euclidean distance for jth data point and ith cluster.

  4. (iv)

    Separation Index (SI): SI utilizes the minimum distance of separation for the partition validity (Gueorguieva et al. 2017). Lower value of SI indicates better separation.

    $${\text{SI}} = ~\frac{{\mathop \sum \nolimits_{{i = 1}}^{{K_{{\text{c}}} }} ~\mathop \sum \nolimits_{{j = 1~}}^{n} \left( {\mu _{{ij}} } \right)^{2} \left\| {z_{j} - c_{i} } \right\|^{2} }}{{n~\min _{{ik}} \left\| {c_{k} - c_{i} } \right\|^{2} }}$$
    (6)
  5. (v)

    Xie-Beni's Validation (XB): XB estimates the ratio of total variation within the given clusters and the separation between clusters and its smaller value indicates that the clusters are compact as well as well separated (Xie and Beni 1991).

    $${\text{XB}} = ~\frac{{\mathop \sum \nolimits_{{i = 1}}^{{K_{{\text{c}}} }} ~\mathop \sum \nolimits_{{j = 1~}}^{n} \left( {\mu _{{ij}} } \right)^{x} \left\| {z_{j} - c_{i} } \right\|^{2} }}{{n~\min _{{ik}} \left\| {z_{j} - c_{i} } \right\|^{2} }}$$
    (7)

The optimal number of clusters has been selected by the following selection rule—“For optimal cluster number, the majority of cluster validity indices (PC, CE, SC, SI, XB) must satisfy their respective criteria”.

2.3 FCM Algorithm

FCM is an objective function-based algorithm in which the membership values are assigned to each of the data point (E/B) corresponding to a cluster depending on the Euclidean distance between the data point and the cluster center (Bezdek et al. 1984; Kang et al. 2009; Adhikari et al. 2015). Higher degrees of membership are assigned to those data points which are close to the cluster center, and hence, the objective function gets minimized accordingly. The objective function of the FCM algorithm has been shown below

$$J^{{{\text{FCM}}}} \left( {U,Z,\left\{ {D_{i} } \right\}} \right) = \mathop \sum \limits_{i = 1}^{{K_{c} }} \mathop \sum \limits_{k = 1}^{M} \left( {\mu_{ik} } \right)^{m } \cdot d_{ik}^{2} D_{i}$$
(8)

where U = [µij] denotes the matrix of membership values, Z is the given ‘q’ dimensional data of ‘n’ objects, Di is the local norm inducing matrix which is used as an optimization variable in U = [µij], Kc denotes the center of the clusters, \(d_{ik}^{2}\) is the Euclidean metrics which depends on the corresponding Euclidean distance \(d_{ij}^{2}\) and m denotes the fuzzifier index usually taken as 2 for best results.

The degree of membership value of given dataset Z in the cluster Kc, satisfies the equation below,

$$\mathop \sum \limits_{i = 1}^{{K_{{\text{c}}} }} \mu_{ij} = 1\;{\text{for}},0 \le \mu_{ij} \le 1\;{\text{and}}\;K_{{\text{c}}} = 1,2, \ldots ,n$$
(9)

where \(\mu_{ij } = \frac{1}{{\mathop \sum \nolimits_{t = 1}^{{K_{{\text{c}}} }} \left( {\frac{{d_{ij} }}{{d_{it} }}} \right)^{{\frac{2}{m - 1}}} }}\).

Also, the equations for the cluster center (\(c_{i}\)) and the Euclidean metric (\(d_{ik}^{2}\)) has been stated below-

$$c_{i} = \frac{{\mathop \sum \nolimits_{j = 1}^{n} \mu_{ij }^{m} z_{j} }}{{\mathop \sum \nolimits_{j = 1}^{n} \mu_{ij}^{m} }}\;{\text{for}}\;\forall_{j} = 1,2, \ldots ,n$$
(10)
$$~d_{{ik}}^{2} = \mathop \sum \limits_{{j = 1}}^{{K_{{\text{c}}} }} d_{{ij}}^{2} = ~\mathop \sum \limits_{{j = 1}}^{{K_{{\text{c}}} }} \left\| {z_{j} - c_{i} } \right\|^{2} \;{\text{for}}\;\forall _{j} = 1,2, \ldots ,K_{{\text{c}}}$$
(11)

where Kc denotes the cluster number, dij2 is the Euclidean distance between jth data point and the ith cluster center.

2.4 Feature Combination Using Principal Component Analysis

To measure the contributions of each of the statistical features that is, regional entropy and brightness, a popular and extensively used computational technique known as principal component analysis (PCA) has been employed in this work. PCA is an useful approach to find out the principal component of the datasets for both of the features and henceforth, determines the respective weight factors for them (Mukherjee and Das 2020). It works on the principle of computing the covariance matrix created from the datasets of both of the regional features. Hence, it makes the segmentation approach automated and robust.

2.5 Shape-Based Feature Extraction

Several research works have been conducted, to extract information of the region of interest (ROI). The aim of this work is to determine the better feature extraction technique, in case of a particular scenario. From several studies, it has been observed that the malignant tumors consist of uneven shape irregularities in comparison with benign tumors as shown in Fig. 3. Hence, the characterization of tumors in terms of its shape has been the main focus to capture these shape irregularities.

Fig. 3
figure 3

Variation in shape of a tumor

Full size image

In this view, the proposed method addresses a combination of some conventional shape metrics with a radius vector (r) based shape descriptor (Kurtosis) to study the tumor characteristics of brain MRI. The radius vector-based feature is insensitive to image orientation and alignments (Kobayashi et al. 2008). The mathematical formulations are as follows

$${\text{Kurtosis}} = \frac{{\frac{1}{N}\mathop \sum \nolimits_{n = 1}^{N} \left[ {r\left( n \right) - m} \right]^{4} }}{{\left( {\frac{1}{N}\mathop \sum \nolimits_{n = 1}^{N} \left[ {r\left( n \right) - m} \right]^{2} } \right)^{2} }}$$
(12)

where N is the total number of contour pixels and mean \(m = \frac{1}{N}\mathop \sum \nolimits_{n = 1}^{N} \left[ {r\left( n \right)} \right]\)

$${\text{Area}}\;{\text{Mismatch}}\;{\text{Ratio}} \left( {{\text{AMR}}} \right) = \frac{{\left| {{\text{CA}} - A} \right|}}{A}$$
(13)
$${\text{Compactness}} = \frac{{P^{2} }}{4\pi A}$$
(14)
$${\text{Solidity}} = \frac{A}{{{\text{CA}}}}$$
(15)
$${\text{Eccentricity}} = \frac{W}{L}$$
(16)

where W, L, A, P, CA denotes width, length, area, perimeter and convex area of the tumor, respectively.

Based on these extracted feature characteristics, the segmented tumors have been categorized into malignant/benign groups.

2.6 Classification

In this work, a conventional k nearest neighbor (KNN) classifier has been chosen, to classify the brain tumors into malignant/benign classes. KNN is a supervised classification algorithm which classifies a data point based on its neighboring data points. From known training datasets, KNN classifies the test data based on a similarity measure. The parameter ‘k’ in KNN algorithm refers to the number of nearest neighbors which are determined based on some distance parameters (Zhang et al. 2018). In this work, Euclidean distance measures between the known and the unknown data points have been considered. The performance of the KNN classifier on the proposed FCM model has been evaluated based on some statistical measures and the performance indices such as sensitivity, specificity and accuracy have been estimated by the following mathematical formulations

Sensitivity: It estimates how correctly the classifier can predict the malignant tumors.

$${\text{Sensitivity}}\left( \% \right) = \frac{{{\text{TP}}}}{{{\text{TP}} + {\text{FN}}}} \times 100$$
(17)

Specificity: It estimates how correctly the classifier can predict the benign tumors.

$${\text{Specificity}}\left( \% \right) = \frac{{{\text{TN}}}}{{{\text{TN}} + {\text{FP}}}} \times 100$$
(18)

Accuracy: It estimates the total correctly predicted malignant and benign tumors.

$${\text{Accuracy}}\left( \% \right) = \frac{{{\text{TP}} + {\text{TN}}}}{{{\text{TP}} + {\text{FP}} + {\text{FN}} + {\text{TN}}}} \times 100$$
(19)

where (TP): number of previously known malignant tumors correctly identified as malignant; (TN): number of previously known benign tumors correctly identified as benign; (FP): number of previously known benign tumors incorrectly identified as malignant; (FN): number of previously known malignant tumors incorrectly identified as benign.

Further, this classifier has been validated using a popular technique, k-fold cross-validation. Specifically, fivefold cross-validation approach has been employed here which estimates the performance of the KNN classifier. The entire dataset is divided into k-subsets, such that every time each of the k subset is considered as test set and the remaining (k − 1) subsets as training sets, to validate the performance. The average estimation of total k number of trials provides the total effectiveness of the model.

3 Experimental Results

The dataset in the present work consists of 50 randomly chosen brain MRIs (31 benign and 19 malignant samples) specified by expert radiologists, taken from the benchmarked sources as mentioned in Sect. 2. To detect brain tumor using the proposed segmentation approach, following steps have been executed.

3.1 Cluster Number Selection Procedure

The following Tables 1 and 2 present the dataset of five validity indices computed by varying the cluster numbers (KC) from 3 to 9 with respect to the features; regional entropy and regional brightness, respectively. By thorough analysis of the datasets and following the selection rule—“For optimal cluster number, the majority of cluster validity indices (PC, CE, SC, SI, XB) must satisfy their respective criteria”, the cluster selection procedure has been carried out.

Table 1 Computation of validity indices for regional entropy
Full size table
Table 2 Computation of validity indices for regional brightness
Full size table

By analyzing from Tables 1 and 2, it can be observed that KC = 9 and KC = 3 has been selected as the optimal cluster numbers, following the above-mentioned selection rule for both the features regional entropy (E) and regional brightness (B), respectively.

3.2 Data of the Proposed Segmentation Approach

The segmentation results of brain MRIs with various illumination and contrast, obtained after successful execution of the proposed approach, are shown in Fig. 4.

Fig. 4
figure 4

Different brain MRI modalities (from the database) with their segmented outputs using validity index-based FCM algorithm; a MRI T1; b MRI T2; c MRI T1 GAD; d MRI PD; e–h shows the corresponding segmented outputs of a, b, c and d, respectively

Full size image

By varying the nearest neighbor ‘k’ of the KNN classifier, it has been found empirically that for k = 7, the maximum average accuracy of 96.0%; sensitivity of 96.42% and specificity of 95.45% have been obtained.

4 Discussion

The efficiency of the proposed segmentation approach is estimated in terms of classification accuracy. Table 3, shows a brief comparison of overall classification accuracy, of the proposed approach with other related research works. It is found that the present work shows superior/comparable performances with respect to recent studies.

Table 3 A brief comparative study of the proposed model with other related research works
Full size table

5 Conclusion

The present work has addressed an automated, robust and efficient segmentation technique based on five effective cluster validity indices to estimate the optimal cluster numbers in an automated manner. The combination of two significant regional features makes the proposed segmentation method more efficient. Moreover, following the detection procedure, the shape describing feature set makes the classification easier and the results also show the superiority of the proposed approach with other related studies. As the cluster number selection procedure takes a significant time frame hence, further investigation of more sophisticated segmentation model may lead to more robust and cost-effective diagnostic system for real-time use.