Keywords

MSC Code

Introduction

In December of 2019, a novel strain of coronavirus was found in Wuhan, China, and disease caused by it is identified as coronavirus disease 2019 (COVID-19) [1]. Transmission of COVID-19, similar to numerous airborne respiratory viruses including tuberculosis and influenza, occurs through direct contact with an infected person through respiratory droplets when a person coughs or sneezes or indirect contact through interaction with contaminated surfaces with respiratory droplets from infected person [2]. As of 18 April 2020, the disease has spread to 210 countries with 2,324,731 total confirmed new cases reported and 160,434 deaths [4]. Data we used for the current research are most recent as of 18 April 2020. Since currently there is no definitive treatment or an effective vaccine for disease control, there is a crucial need to find measures that cure or reduce morbidity due to COVID-19. There are prominent dissimilarities in how COVID-19 is affecting different countries. Although developing countries like India, Philippines and Sri Lanka reported their initial case in January, they have yet to experience extensive community spread [5]. In contrast, developed countries like Italy and UK have experienced high mortality and widespread infection despite strong curtailing of social interactions. Studies show a disproportionately smaller number of cases have been reported from disadvantaged and low-income countries [6]. It is puzzling that countries with more fragile health systems report less incidence of COVID-19. Figure 2.1 shows a figure from the European Centre for Disease Prevention and Control which indicates that much of the incidence of COVID-19 is in the developing countries such as UK and USA [3]. A possible explanation for lower number of cases detected in these developing countries with extensive travel and trade links to China may stem from the induced heterologous protective activity of the Bacillus Calmette-Guerin (BCG) immunisation [5].

Fig. 2.1
figure 1

Adapted from European Centre for Disease Prevention and Control

Geographical distribution of COVID-19 cases worldwide as of 18 April 2020 [3].

Full size image

Vaccines provide protection from particular pathogens by inducing effector mechanisms directed towards that pathogen. Certain live attenuated vaccines like the BCG vaccine increase immunity against not only a particular pathogen, but also numerous unrelated pathogens that present with similar acute respiratory tract infections [8]. Randomised controlled trials have provided evidence that the BCG vaccine’s immunomodulatory properties can protect against respiratory infections. In Guinea-Bissau, a high-mortality setting, BCG Danish reduced all-cause neonatal mortality by 38% (95% CI 17–54), mainly because there were fewer deaths from pneumonia and sepsis [9]. In South Africa, BCG Danish reduced respiratory tract infections by 73% (95% CI 39–88) in adolescents [10]. The BCG vaccine reduced yellow fever vaccine viraemia by 71% (95% CI 6–91) in volunteers in the Netherlands [11]. Previous studies have established that BCG vaccination provided non-specific protection via the induction of innate immune memory [12]. The BCG vaccine induces metabolic and epigenetic changes that enhance the innate immune response to subsequent infections, a process termed trained immunity [13]. The BCG vaccine might therefore reduce viraemia after SARS-CoV-2 exposure, with consequent less severe COVID-19 and more rapid recovery [14]. BCG is used widely across the world as a vaccine for tuberculosis, with many developing nations having a universal BCG vaccination policy for newborn [15]. Studies have indicated that countries with uniform BCG vaccination policy show significantly lower COVID-19 cases and deaths per million people compared to countries where BCG vaccination policy was ceased or was never in place [5, 16]. Figure 2.2 from the BCG world atlas shows that numerous developing countries currently employ a universal BCG vaccination programme, while many developed countries have either ceased their BCG vaccination recommendation or never recommended it [7]. Comparison of Figs. 2.1 and 2.2 also indicates that the largest number of COVID-19 cases is in countries that currently have no BCG vaccination recommendation.

Fig. 2.2
figure 2

Adapted from BCG World Atlas

Map displaying BCG vaccination policy by country. a The country currently has universal BCG vaccination programme. b The country used to recommend BCG vaccination for everyone, but currently does not. c The country never had universal BCG vaccination programmes [7].

Full size image

Furthermore, the year that universal BCG vaccination was established within a country has a significant correlation with the mortality rate, indicating that earlier implementation of the policy leads to protection of a larger fraction of the elderly population. For instance, although Iran currently employs a universal BCG vaccination policy, it was implemented as recently as 1984. Consequently, it reports an elevated mortality with 19.7 deaths per million inhabitants [6]. In contrast, Japan started its universal BCG policy in 1947 and found that Japan has around 100 times less deaths per million people, with 0.28 deaths. Similarly, Brazil started universal vaccination in 1920 and also has an even lower mortality rate of 0.0573 deaths per million inhabitants [6].

Exploring this relationship between BCG vaccination and COVID-19 further is crucial in establishing a potential short- or long-term prevention measure that is effective in reducing incidence and mortality of COVID-19. Four clinical trials have been registered with BCG vaccination to prevent or reduce the severity of COVID-19 in the elderly population and healthcare workers [17]. While previous studies have explored a possible link between the BCG vaccine and incidence of COVID-19, they have not modelled the impact of implementing a nationwide BCG immunisation policy [6, 7]. Mathematical modelling is ideal for predicting the rate of disease transmission as well as evaluating efficacy of possible public health prevention measures [18]. This study aims to create a model to evaluate the effect of nationwide BCG vaccine recommendations on incidence, severity and mortality rates of COVID-19. Furthermore, our study aims to model the protentional implications of an immediate implementation of the universal BCG vaccination policy.

Mathematical Model

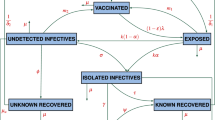
A novel coronavirus pandemic is occurring around the world, both in countries with and without the BCG vaccine. To analyse the importance of this vaccine against the fight of COVID-19, we have developed a mathematical model. This model has seven various compartments. First compartment is the class of exposed individuals to COVID-19 noted as \(E.\) From these individuals, some are vaccinated with BCG vaccine noted as \(V\) and those who have not taken it are noted as \(N_{V}\). Now, with the certain rate these individuals transfer into infected stage noted as \(I\) and some can become critically infected noted as \(C\) compartment. The individuals suffering from COVID-19 that need to be hospitalised are noted as \(H\). The infected and hospitalised individuals that recover are noted as \(R\).

With the help of transmission shown in Fig. 2.3 and notation of parameter given in Table 2.1, the system of nonlinear ODE is derived as:

$$\begin{aligned}& \frac{{{\text{d}}E}}{{{\text{d}}t}} = B - \beta_{1} EV - \left( {1 - \beta_{1} } \right)EN_{V} + \beta_{9} R - \mu E \\ & \frac{{{\text{d}}V}}{{{\text{d}}t}} = \beta_{1} EV - \beta_{2} V - \mu V \\ & \frac{{{\text{d}}N_{V} }}{{{\text{d}}t}} = \left( {1 - \beta_{1} } \right)EN_{V} - \beta_{3} N_{V} - \mu N_{V}\\ & \frac{{{\text{d}}I}}{{{\text{d}}t}} = \beta_{2} V + \beta_{3} N_{V} - \beta_{4} I - \beta_{5} I - \beta_{6} I - \mu_{d} I \\ & \frac{{{\text{d}}C}}{{{\text{d}}t}} = \beta_{4} I - \beta_{7} C - \mu_{d} C\\ & \frac{{{\text{d}}H}}{{{\text{d}}t}} = \beta_{5} I + \beta_{7} C - \beta_{8} H - \mu_{d} H\\ & \frac{{{\text{d}}R}}{{{\text{d}}t}} = \beta_{6} I + \beta_{8} H - \beta_{9} R - \mu R\end{aligned}$$
(2.1)

with \(E > 0;V,N_{V} ,I,C,H,R \ge 0\).

Fig. 2.3
figure 3

Transmission diagram of COVID-19 with BCG vaccine

Full size image
Table 2.1 Notation and its description
Full size table

Hence, the feasible region of given system is

$$\Lambda = \left\{ {\left( {E,V,N_{V} ,I,C,H,R} \right) \in R_{ + }^{7} :E + V + N_{V} + I + C + H + R \le \frac{B}{\mu }} \right\}.$$

Now, consider \(\beta_{2} + \mu = k_{1}\), \(\beta_{3} + \mu = k_{2}\), \(\beta_{4} + \beta_{5} + \beta_{6} + \mu_{d} = k_{3}\), \(\beta_{7} + \mu_{d} = k_{4}\), \(\beta_{8} + \mu_{d} = k_{5}\), \(\beta_{9} + \mu = k_{6}\); then, we get new system as follows

$$\begin{aligned} & \frac{{{\text{d}}E}}{{{\text{d}}t}} = B - \beta_{1} EV - \left( {1 - \beta_{1} } \right)EN_{V} + \beta_{9} R - \mu E\\ & \frac{{{\text{d}}V}}{{{\text{d}}t}} = \beta_{1} EV - k_{1} V\\ & \frac{{{\text{d}}N_{V} }}{{{\text{d}}t}} = \left( {1 - \beta_{1} } \right)EN_{V} - k_{2} N_{V}\\& \frac{{{\text{d}}I}}{{{\text{d}}t}} = \beta_{2} V + \beta_{3} N_{V} - k_{3} I \\& \frac{{{\text{d}}C}}{{{\text{d}}t}} = \beta_{4} I - k_{4} C \\& \frac{{{\text{d}}H}}{{{\text{d}}t}} = \beta_{5} I + \beta_{7} C - k_{5} H \\& \frac{{{\text{d}}R}}{{{\text{d}}t}} = \beta_{6} I + \beta_{8} H - k_{6} R\end{aligned}$$
(2.2)

The dynamical behaviour of system (2.1) is equivalent to the system (2.2). Hence, every solution of system (2.2) will remain in the region \(\Lambda\).

The above system (2.2) has three equilibrium points by setting the equation as zero.

  1. 1.

    Diseases-free equilibrium point \(E_{P}^{0} \left( {E_{0} ,0,0,0,0,0,0} \right)\) where

    $$E_{0} = \frac{B}{\mu }$$
  2. 2.

    Vaccine-free equilibrium point \(E_{P}^{1} \left( {E_{1} ,0,N_{{V_{1} }} ,I_{1} ,C_{1} ,H_{1} ,R_{1} } \right)\) where

    $$E_{1} = \frac{{k_{2} }}{{1 - \beta_{1} }}$$
    $$N_{{V_{1} }} = \frac{{k_{3} k_{4} k_{5} k_{6} \left( {B\beta_{1} + k_{2} \mu - B} \right)}}{{\left( {1 - \beta_{1} } \right)\left[ {\beta_{3} \beta_{8} \beta_{9} \left( {\beta_{4} \beta_{7} + \beta_{5} k_{5} } \right) + k_{4} k_{5} \left( {\beta_{3} \beta_{6} \beta_{9} - k_{2} k_{3} k_{6} } \right)} \right]}}$$
    $$I_{1} = \frac{{\beta_{3} k_{4} k_{5} k_{6} \left( {B\beta_{1} + k_{2} \mu - B} \right)}}{{\left( {1 - \beta_{1} } \right)\left[ {\beta_{3} \beta_{8} \beta_{9} \left( {\beta_{4} \beta_{7} + \beta_{5} k_{5} } \right) + k_{4} k_{5} \left( {\beta_{3} \beta_{6} \beta_{9} - k_{2} k_{3} k_{6} } \right)} \right]}}$$
    $$C_{1} = \frac{{\beta_{3} \beta_{4} k_{5} k_{6} \left( {B\beta_{1} + k_{2} \mu - B} \right)}}{{\left( {1 - \beta_{1} } \right)\left[ {\beta_{3} \beta_{8} \beta_{9} \left( {\beta_{4} \beta_{7} + \beta_{5} k_{5} } \right) + k_{4} k_{5} \left( {\beta_{3} \beta_{6} \beta_{9} - k_{2} k_{3} k_{6} } \right)} \right]}}$$
    $$H_{1} = \frac{{\beta_{3} k_{6} \left( {B\beta_{1} + k_{2} \mu - B} \right)\left( {\beta_{4} \beta_{7} + \beta_{5} k_{4} } \right)}}{{\left( {1 - \beta_{1} } \right)\left[ {\beta_{3} \beta_{8} \beta_{9} \left( {\beta_{4} \beta_{7} + \beta_{5} k_{5} } \right) + k_{4} k_{5} \left( {\beta_{3} \beta_{6} \beta_{9} - k_{2} k_{3} k_{6} } \right)} \right]}}$$
    $$R_{1} = \frac{{\beta_{3} \left( {B\beta_{1} + k_{2} \mu - B} \right)\left( {\beta_{4} \beta_{7} \beta_{8} + \beta_{5} \beta_{8} k_{4} + \beta_{6} k_{4} k_{5} } \right)}}{{\left( {1 - \beta_{1} } \right)\left[ {\beta_{3} \beta_{8} \beta_{9} \left( {\beta_{4} \beta_{7} + \beta_{5} k_{5} } \right) + k_{4} k_{5} \left( {\beta_{3} \beta_{6} \beta_{9} - k_{2} k_{3} k_{6} } \right)} \right]}}$$
  3. 3.

    Non-vaccine-free equilibrium point \(E_{P}^{2} \left( {E_{2} ,V_{2} ,0,I_{2} ,C_{2} ,H_{2} ,R_{2} } \right)\)

    $$E_{2} = \frac{{k_{1} }}{{\beta_{1} }}$$
    $$V_{2} = \frac{{k_{3} k_{4} k_{5} k_{6} \left( {k_{1} \mu - B\beta_{1} } \right)}}{{\beta_{1} \left[ {\beta_{2} \beta_{8} \beta_{9} \left( {\beta_{4} \beta_{7} + \beta_{5} k_{4} } \right) + k_{4} k_{5} \left( {\beta_{2} \beta_{6} \beta_{9} - k_{1} k_{3} k_{6} } \right)} \right]}}$$
    $$I_{2} = \frac{{\beta_{2} k_{4} k_{5} k_{6} \left( {k_{1} \mu - B\beta_{1} } \right)}}{{\beta_{1} \left[ {\beta_{2} \beta_{8} \beta_{9} \left( {\beta_{4} \beta_{7} + \beta_{5} k_{4} } \right) + k_{4} k_{5} \left( {\beta_{2} \beta_{6} \beta_{9} - k_{1} k_{3} k_{6} } \right)} \right]}}$$
    $$C_{2} = \frac{{\beta_{2} \beta_{4} k_{5} k_{6} \left( {k_{1} \mu - B\beta_{1} } \right)}}{{\beta_{1} \left[ {\beta_{2} \beta_{8} \beta_{9} \left( {\beta_{4} \beta_{7} + \beta_{5} k_{4} } \right) + k_{4} k_{5} \left( {\beta_{2} \beta_{6} \beta_{9} - k_{1} k_{3} k_{6} } \right)} \right]}}$$
    $$H_{2} = \frac{{\beta_{2} k_{6} \left( {k_{1} \mu - B\beta_{1} } \right)\left( {\beta_{4} \beta_{7} + \beta_{5} k_{4} } \right)}}{{\beta_{1} \left[ {\beta_{2} \beta_{8} \beta_{9} \left( {\beta_{4} \beta_{7} + \beta_{5} k_{4} } \right) + k_{4} k_{5} \left( {\beta_{2} \beta_{6} \beta_{9} - k_{1} k_{3} k_{6} } \right)} \right]}}$$
    $$R_{2} = \frac{{\beta_{2} \left( {k_{1} \mu - B\beta_{1} } \right)\left( {\beta_{4} \beta_{7} \beta_{8} + \beta_{5} \beta_{8} k_{4} + \beta_{6} k_{4} k_{5} } \right)}}{{\beta_{1} \left[ {\beta_{2} \beta_{8} \beta_{9} \left( {\beta_{4} \beta_{7} + \beta_{5} k_{4} } \right) + k_{4} k_{5} \left( {\beta_{2} \beta_{6} \beta_{9} - k_{1} k_{3} k_{6} } \right)} \right]}}$$

The diseases-free equilibrium point is not valid according to current scenario, and therefore we will discuss only two equilibrium points.

Basic Reproduction Number

In this section, basic reproduction number is derived using next-generation matrix method [19]. The quantity of basic reproduction number helps to understand the behaviour of the spread of COVID-19 among the population. The basic reproduction number is denoted as \(R_{0}\). If the value of \(R_{0}\) is less than 1, then the diseases is in the controllable stage. Otherwise, it has reached the epidemic stage. This is the ratio of affected infected individual by secondary infected individuals within the population. Using next-generation matrix method, \(f\) and \(v\) are derived as

$$f = \left[ {\begin{array}{*{20}c} {\beta_{1} EV} \\ {\left( {1 - \beta_{1} } \right)EN_{V} } \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]\,{\text{and}}\,v = \left[ {\begin{array}{*{20}c} {k_{1} V} \\ {k_{2} N_{V} } \\ { - \beta_{2} V - \beta_{3} N_{V} + k_{3} I} \\ { - \beta_{4} I + k_{4} C} \\ { - \beta_{5} I - \beta_{7} C + k_{5} H} \\ { - \beta_{6} I - \beta_{8} H + k_{6} R} \\ { - B + \beta_{1} EV + \left( {1 - \beta_{1} } \right)EN_{V} - \beta_{9} R + \mu E} \\ \end{array} } \right].$$

The Jacobian matrices of \(f\) and \(v\) are \(F\) and \(V\) defined as below

$$F = \left[ {\begin{array}{*{20}c} {\beta_{1} E} & 0 & 0 & 0 & 0 & 0 & {\beta_{1} V} \\ 0 & {\left( {1 - \beta_{1} } \right)E} & 0 & 0 & 0 & 0 & {\left( {1 - \beta_{1} } \right)N_{V} } \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\,{\text{and}}$$
$$V = \left[ {\begin{array}{*{20}c} {k_{1} } & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {k_{2} } & 0 & 0 & 0 & 0 & 0 \\ { - \beta_{2} } & { - \beta_{3} } & {k_{3} } & 0 & 0 & 0 & 0 \\ 0 & 0 & { - \beta_{4} } & {k_{4} } & 0 & 0 & 0 \\ 0 & 0 & { - \beta_{5} } & { - \beta_{7} } & {k_{5} } & 0 & 0 \\ 0 & 0 & { - \beta_{6} } & 0 & { - \beta_{8} } & {k_{6} } & 0 \\ {\beta_{1} E} & {\left( {1 - \beta_{1} } \right)E} & 0 & 0 & 0 & { - \beta_{9} } & {\beta_{1} V + \left( {1 - \beta_{1} } \right)N_{V} + \mu } \\ \end{array} } \right]$$

These Jacobian matrices are used to derive \(FV^{ - 1}\) whose spectral radius is our desired basic reproduction number \(\left( {R_{0} } \right)\). Here, we have computed two basic reproduction numbers: one at vaccine-free equilibrium point and other at non-vaccine-free equilibrium point.

The expression of basic reproduction number for non-vaccinated individuals, i.e. at vaccine-free equilibrium point, is denoted by \(R_{0}^{(1)}\) given by

$$\begin{aligned} R_{0}^{(1)} & = \left( {\left( {1 - \beta_{1} } \right)k_{3} k_{4} k_{5} k_{6} \left( {B\beta_{1} + k_{2} - B} \right)\left( {\beta_{1} k_{2} k_{6} \mu_{d}^{3} } \right.} \right. + \left( { - \beta_{2} \beta_{6} \beta_{9} } \right.\left( {1 - \beta_{1} } \right) \\ & \quad + \beta_{1} k_{2} k_{6} \left( {\beta_{4} } \right. + \beta_{5} + \beta_{6} + \beta_{7} + \left. {\left. {\beta_{8} } \right)} \right)\mu_{d}^{2} \\ & \quad + \left( { - \beta_{2} \beta_{9} } \right.\left( {1 - \beta_{1} } \right)\left( {\beta_{5} \beta_{8} + \beta_{6} \beta_{7} + \beta_{6} \beta_{8} } \right) + \beta_{1} k_{2} k_{6} \left( {\beta_{4} \beta_{7} } \right. \\ & \quad + \beta_{4} \beta_{8} + \beta_{5} \beta_{7} + \beta_{5} \beta_{8} + \beta_{6} \beta_{7} + \beta_{6} \beta_{8} + \left. {\left. {\beta_{7} \beta_{8} } \right)} \right)\mu_{d} \\ & \quad + \beta_{7} \beta_{8} \left( {\beta_{4} + \beta_{5} + \beta_{6} } \right)\left. {\left( { - \beta_{2} \beta_{9} \left( {1 - \beta_{1} } \right) + \beta_{1} k_{2} k_{6} } \right)} \right)\left( {\beta_{3} \beta_{8} \beta_{9} } \right.\left( {\beta_{4} \beta_{7} } \right. + \left. {\beta_{5} k_{4} } \right) \\ & \quad + k_{4} k_{5} {{\left. {\left. {\left( {\beta_{3} \beta_{6} \beta_{9} - k_{2} k_{3} k_{6} } \right)} \right)} \right)} \mathord{\left/ {\vphantom {{\left. {\left. {\left( {\beta_{3} \beta_{6} \beta_{9} - k_{2} k_{3} k_{6} } \right)} \right)} \right)} {\left( {\left( {1 - \beta_{1} } \right)} \right.}}} \right. \kern-\nulldelimiterspace} {\left( {\left( {1 - \beta_{1} } \right)} \right.}}^{2} k_{1} k_{3} k_{4} k_{5} k_{6} \left( {\beta_{3} \beta_{8} \beta_{9} } \right.\left( {\beta_{4} \beta_{7} + \left. {\beta_{5} k_{4} } \right)} \right. \\ & \quad + k_{4} k_{5} \left( {\beta_{3} \beta_{6} \beta_{9} } \right. - \left. {\left. {k_{2} k_{3} k_{6} } \right)} \right)\left( { - Bk_{3} k_{4} k_{5} k_{6} \left( {1 - \beta_{1} } \right)} \right. \\ & \quad \left. +{ \beta_{3} \beta_{9} \mu \left( {\beta_{4} \beta_{7} \beta_{8} + \beta_{5} \beta_{8} k_{4} + \beta_{6} k_{4} k_{5} } \right)} \right) \\ \end{aligned}$$

whereas the expression of basic reproduction number for vaccinated individuals, i.e. at non-vaccine-free equilibrium point, is denoted by \(R_{0}^{(2)}\) given by

$$\begin{aligned} R_{0}^{(2)} & = \frac{{k_{1} }}{{\beta_{2} + \mu }} - \left( {k_{3} k_{4} k_{5} k_{6} } \right.\left( {B\beta_{1} - k_{1} \mu } \right)\left( {k_{1} k_{6} \mu_{d}^{3} } \right. \\ & \quad + \left( {k_{1} k_{6} } \right.\left( {\beta_{4} + \beta_{5} + \beta_{6} + \beta_{7} + \beta_{8} } \right) - \left. {\beta_{2} \beta_{6} \beta_{9} } \right)\mu_{d}^{2} \\ & \quad + \left( { - \beta_{2} \beta_{9} } \right.\left( {\beta_{5} \beta_{8} + \beta_{6} \beta_{7} + \beta_{6} \beta_{8} } \right) + k_{1} k_{6} \left( {\beta_{4} \beta_{7} } \right. \\ & \quad + \beta_{4} \beta_{8} + \beta_{5} \beta_{7} + \beta_{5} \beta_{8} + \beta_{6} \beta_{7} + \beta_{6} \beta_{8} + \left. {\left. {\beta_{7} \beta_{8} } \right)} \right)\mu_{d} \\ & \quad + \beta_{7} \beta_{8} \left( {\beta_{4} + \beta_{5} + \beta_{6} } \right){{\left( { - \beta_{2} \beta_{9} + k_{1} k_{6} } \right)} \mathord{\left/ {\vphantom {{\left( { - \beta_{2} \beta_{9} + k_{1} k_{6} } \right)} {\left( {k_{2} k_{3} k_{4} k_{5} k_{6} } \right.\left( {k_{4} k_{5} } \right.}}} \right. \kern-\nulldelimiterspace} {\left( {k_{2} k_{3} k_{4} k_{5} k_{6} } \right.\left( {k_{4} k_{5} } \right.}}\left( {B\beta_{1} k_{3} k_{6} } \right. \\ & \quad - \left. {\beta_{2} \beta_{6} \beta_{9} \mu } \right) - \beta_{2} \beta_{8} \beta_{9} \left. {\left. {\left( {\beta_{4} \beta_{7} + \beta_{5} k_{4} } \right)} \right)} \right) \\ \end{aligned}$$

Moreover, the basic reproduction for the system is \(R_{0} = \frac{{R_{0}^{(1)} + R_{0}^{(2)} }}{2}\).

Local Stability Analysis

In this section, we will be discussing the local stability for vaccine and non-vaccine-free equilibrium point utilising the concept of eigenvalues. To find the eigenvalues, the Jacobian matrix of the system (2.2) is calculated as

$$J: = \left[ {\begin{array}{*{20}c} { - \beta_{1} V - \left( {1 - \beta_{1} } \right)N_{V} - \mu } & { - \beta_{1} E} & { - \left( {1 - \beta_{1} } \right)E} & 0 & 0 & 0 & {\beta_{9} } \\ {\beta_{1} V} & {\beta_{1} E - k_{1} } & 0 & 0 & 0 & 0 & 0 \\ {\left( {1 - \beta_{1} } \right)N_{V} } & 0 & {\left( {1 - \beta_{1} } \right)E - k_{2} } & 0 & 0 & 0 & 0 \\ 0 & {\beta_{2} } & {\beta_{3} } & { - k_{3} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {\beta_{4} } & { - k_{4} } & 0 & 0 \\ 0 & 0 & 0 & {\beta_{5} } & {\beta_{7} } & { - k_{5} } & 0 \\ 0 & 0 & 0 & {\beta_{6} } & 0 & {\beta_{8} } & { - k_{6} } \\ \end{array} } \right]$$

Eigenvalues for above Jacobi matrix about the vaccine-free equilibrium point are 0.1225, −0.0664, −0.1375, −0.1375, −0.8463, −0.9431, 0.7019.

Eigenvalues for above Jacobi matrix about the non-vaccine-free equilibrium point are 0.2298, −0.0655, −0.1595, −0.2296, −0.8464, −0.9431, −0.1021.

Hence, both the equilibrium points are not locally asymptotically stable.

Sensitivity Analysis

Here, sensitivity analysis is carried out to see which parameter is conferring a positive effect on the model. The sensitivity analysis is conducted on the basic reproduction number. It is to be done using Christoffel formula which is \(\Gamma_{\alpha }^{{R_{0} }} = \frac{{\partial R_{0} }}{\partial \alpha } \cdot \frac{\alpha }{{R_{0} }}\) where \(\alpha\) is the model parameter.

From Table 2.2, it can be observed that the growth rate is producing negative impact. Precisely, growth rate is more negative when there is no vaccinated individual. The rate of individual vaccinated with BCG \(\left( {\beta_{1} } \right)\) shows the positive impact among all. Moreover, the disease-induced death rate is lower for \(R_{0}^{(1)}\) when compared to \(R_{0}^{(2)}\). Additionally, considering the sensitivity analysis for both the basic reproduction numbers, we conclude that BCG vaccine is beneficial in preventing COVID-19.

Table 2.2 Sensitivity analysis
Full size table

Numerical Simulation

In this section, results of transmission of COVID-19 outbreak are simulated numerically, helping validate model results.

Figure 2.4 shows the change in the behaviour of individuals. This suggests that exposed individuals quickly progress into infected ones. Infected individuals increase in first 1.5 weeks and then start to decrease, whereas critically infected individuals stay in lower numbers. Hospitalisation increases rapidly for at least 3 weeks, and then it flattens. Recovery rate increases but at lower rate.

Fig. 2.4
figure 4

Transmission of COVID-19

Full size image

To get precise results, four clusters of Fig. 2.5 are magnified. Our data indicates that individuals should go into isolation earlier to prevent exposure to COVID-19. BCG-vaccinated individual may get exposed in 0.2 week, while, at the same time, non-vaccinated individual may get critically infected. Moreover, recovered individual also may become exposed and get re-infected after 2 weeks.

Fig. 2.5
figure 5

Magnified plots of transmission of COVID-19

Full size image

Figure 2.6 indicates the cyclic behaviour of recovered individuals. The first graph shows vaccinated individuals, while the other displays non-vaccinated individuals. The graphs show that the cycle of vaccinated individuals is larger than non-vaccinated individuals. Furthermore, vaccinated individuals have greater time to reinfection when compared to that of non-vaccinated individuals.

Fig. 2.6
figure 6

Cyclic behaviour of recovered individuals

Full size image

Figure 2.7 compares the behaviour of exposed individuals with vaccinated individuals, non-vaccinated individuals and infected individuals, respectively. The rate of exposure is consecutive for non-vaccinated individuals when compared to vaccinated individuals. Furthermore, the transmission from exposed to infected is quite quick; i.e. almost every individual who is exposed will get infected.

Fig. 2.7
figure 7

Behaviour of exposed individuals

Full size image

Figure 2.8 indicates that vaccinated individuals are infected gradually while non-vaccinated individuals are infected quickly. Consequently, non-vaccinated individuals are at higher risk of becoming infected with COVID-19.

Fig. 2.8
figure 8

Behaviour of vaccinated and non-vaccinated individuals

Full size image

Figure 2.9 shows the behaviour of infected individuals towards critical, hospitalised and recovered individuals, respectively. If individuals are vaccinated early, the chances of becoming critically infection are low. However, this also indicates that infected individuals must receive treatment in hospitals before the infection progresses to critical stage. This is further elaborated by the last graph, which indicates that the chances of recovering by staying at home are negligible.

Fig. 2.9
figure 9

Behaviour of infected individual

Full size image

Figure 2.10 shows the behaviour of hospitalised individuals and their recovery. This figure further emphasises that individuals recover only after proper hospitalisation is received.

Fig. 2.10
figure 10

Behaviour of hospitalised individuals

Full size image

Conclusion

Our model indicates that a universal recommendation of BCG vaccination is beneficial in reducing the incidence rate of COVID-19. Moreover, the vaccination reduces the severity of the disease by reducing the hospitalisation time for infected individuals. It also contributed to a higher rate of recovery for vaccinated individuals when compared to non-vaccinated individuals. The risk of reinfection is also reduced in vaccinated populations. Finally, the overall disease-specific mortality of infected individuals is also reduced in vaccinated populations. Consequently, we validate the effectiveness of universal BCG vaccination policy in increasing herd immunity against COVID-19.

Considering that the BCG vaccination is established in preventing acute respiratory tract infections even in the elderly [15], vulnerable populations may be immunised with BCG vaccines until a COVID-19-specific vaccine is developed. This strategy would be especially beneficial in the newborns, elderly and front-line essential workers. This study validates the call for clinical trials of BCG vaccine against COVID-19. Given that our model shows a significant reduction in incidence of COVID-19 in countries with universal BCG vaccination, we recommend all countries to conduct more clinical trials to establish and consider policy regarding BCG vaccinations for its citizens.

Our study may be subject to a few limitations. The study does not take into account confounding variables such as the potential differences in geographical and biological factors such as temperature, humidity, life expectancy, average income, social–cultural norms, ethnical genetic background and mitigation between developing and developed countries. Due to these confounding variables, we cannot establish causality [20]. The epidemiological data comparing vaccinated countries and non-vaccinated countries must be monitored throughout this pandemic to establish a causal impact in reducing incidence and mortality. Overall, our study serves to establish that individuals with BCG vaccinations have lower risk of getting COVID-19 infection, shorter hospital stays and increased rate of recovery. Furthermore, countries with long-standing universal BCG vaccination policies have reduced incidence, mortality and severity of COVID-19. Considering the remarkable dissemination capacity and the mortality rates of COVID-19, vaccination capable of conferring even transient protection (e.g. 6–12 months) may be useful in individuals at high risk, such as health workers, first responders and police officers, or those with pre-existing conditions such as obesity, diabetes or cardiovascular disease. Similarly, even enhanced unspecific immunity through BCG vaccination in vulnerable age groups could ameliorate severe COVID-19. Temporarily induced trained immunity could buy time until specific vaccines and/or effective treatments against severe acute respiratory syndrome coronavirus 2 infections become available [21]. Studies done by Moolag et al. [15] and Esobar et al. [21] showed possible benefit of BCG vaccination and suggest that vulnerable population may get benefit from it to ameliorate the severity of COVID-19 and buy some time till specific vaccine and or effective treatment against COVID-19 becomes available. Further research will focus on exploring the immediate benefits of vaccination to healthcare workers and patients as well as benefits of BCG re-vaccination. The results of this study will serve to inform and encourage further research and, ultimately, the creation of policy regarding universal BCG vaccination.