Keywords

1 Introduction

Scholars in social sciences often refer to “social capital” to explain a wide list of economic and social phenomena, notably including national and regional economic performance and growth (Westlund 2006; Fazio and Piacentino 2010; Tabellini 2010), starting from the seminal work such as Putnam (2001). Notwithstanding its wide use, there is no definition of social capital which is commonly accepted, in particular across disciplines, and social capital can be easily confused with other forms of capital (for example, human capital). In this chapter, we will follow the economic perspective put forth by Guiso et al. (2011), who rephrase social capital in terms of civic capital, intended as “those persistent and shared beliefs and values that help a group overcome the free rider problem in the pursuit of socially valuable activities”.

While the impact of social capital on economic and social outcome is well-documented, the process driving its accumulation or depreciation is still an active area of research. Guiso et al. (2011) distinguish civil capital from human capital because the former is the result of a social process of investment and requires individual values and beliefs to be shared by other members of the community. Particular attention has been paid to intergenerational transmission mechanism, in which values to transmit to children are influenced by the spatial pattern of external values and beliefs, and the process of cultural transmission evolves slowly over time, explaining the persistence of the cultural traits of a community even over centuries (Tabellini 2008). Recent contributions have also highlighted the role of spatial interaction (see Durlauf and Ioannides 2010; Fazio and Lavecchia 2013). Civic capital can be transmitted also horizontally (intragenerational transmission, i.e. among peers), although this form of transmission has received less attention. Approaches to social/civic capital analysis are very diverse, and analytical solutions for its transmission mechanisms are possible only for relatively simple hypotheses.

To overcome this obstacle, this chapter develops an agent-based model in which the emergence of cooperation and the horizontal transmission of civic capital are jointly considered in a spatial interaction setting. It does this within the context of the so-called threshold models (Schelling 1973; Granovetter 1978; Watts 2002). Threshold models are a class of models aimed at representing collective actions in which: (1) individuals have a binary choice (in our case being “cooperative” or “defective”); (2) the probability that an individual chooses a certain action positively depends on the fraction of individuals in society (or in a relevant sub-group) choosing the same action, that is, such a fraction is above an (individual-specific) threshold. These models are well-suited to represent individual behaviour in social dilemmas situations (those at risk of free-riding), since a consolidated experimental literature now exists showing that conditional cooperation, that is, to be “cooperative” if others are, often characterizes human behaviour, while at the same time a significant level of heterogeneity exists across subjects. In our model, the lower is the threshold, the higher is the “propensity” towards cooperation, this propensity being affected by those “beliefs and values” constituting the definition of civic capital in Guiso et al. In other words, at the social level, civic capital is inversely related to the average threshold level in the population. In addition, a distinctive feature of threshold models is that not only the average, but also the distribution of thresholds matters for determining collective behaviour. In our model, the process of horizontal transmission of civic capital is given by social influence determining how thresholds evolve over time. In other terms, it is not an actual behaviour which diffuses, but rather beliefs and values which in turn determine, mediated by individual choices, collective cooperative behaviour. Space matters as well, because interactions can be global or local, depending on the size of the group affecting both behaviour and the transmission of civic capital.

The rest of the chapter is organized as follows. In Sect. 11.2, we briefly review those streams of literature which are relevant to support our hypotheses and to which we intend to contribute. Section 11.3 describes the model. Section 11.4 derives a few analytical results which are used as benchmark for the results from the numerical simulations reported and discussed in Sect. 11.5. Section 11.6 concludes the chapter.

2 Literature Review

In the first part of this section, we review those studies which connect civic capital to various kinds of economic outcomes, thus supporting the relevance of our work. Secondly, we look at the mix of experimental evidence and theoretical insights which identified human regularities behaviour in social dilemma situations and mechanisms for sustaining cooperation. These streams of research are key to motivate our model assumption. Finally, we introduce the class of threshold models of collective action, to which our contribution belongs.

2.1 Civic Capital and Economic Outcomes

In a review of the debate about the role of social capital in economics, Guiso et al. (2011) try to overcome the vagueness of the previous literature by relabelling social capital as civic capital. According to the authors, this definition has several advantages. First, it restricts the above concept to a notion of capital that has a positive and durable economic payoff. Second, social capital as beliefs and values becomes measurable through experiments and surveys. Third, as the other notions of capital, it attributes importance to the mechanism of accumulation and depreciation of civic capital.

The literature on civic capital has analysed its antecedents and consequences. As for antecedents, the cultural transmission of cooperative values is at the core of Tabellini (2008). In this model, parents choose what values to pass on to their children, while assessing their children’s welfare in terms of their values. This creates a complementarity between norms and behaviour: when more people cooperate, the payoff from cooperation increases, consequently increasing the scope of cooperation. Guiso et al. (2008) consider a model in which beliefs are transmitted by parents to children. It turns out that, in order to protect their children, parents transmit conservative priors, which could create a “mistrust equilibrium”. Both models generate a distinctive feature of civic capital, which is persistence (Guiso et al. 2016; Giavazzi et al. 2019).

As for its consequences, civic capital has been shown to impact on both macro and micro phenomena. Using historical variables as instruments for civic capital, Tabellini (2010) shows how the latter strongly correlates with current regional economic development in Europe. Nannicini et al. (2013) show that civic capital may increase economic wellbeing by improving the functioning of institutions through political accountability, since the electorate punishes political misbehaviour more severely in Italian districts with higher civic capital. Using regional background as proxy for civicness, Ichino and Maggi (2000) show that it can explain shirking differentials in a large Italian firm. Bürker et al. (2013) argue that civic capital may also affect the governance of firms, and show, using Italian data, that the productivity effect of foreign ownership depends on the stock of civic capital in the area where the firm is located.

2.2 Overcoming the Free-Rider Problem: The Experimental Evidence and the Theoretical Insights

In the definition of Guiso and coauthors, civic capital is inherently seen as a solution for social dilemmas, that is, those situations in which a conflict exists between individual and social interests. In social dilemmas, each person has a dominant strategy which yields the best outcome for all possible circumstances (the non-cooperative choice), but if all individuals pursue this strategy, a sub-optimal collective outcome emerges, as everyone would be better off by cooperating. Several games exhibit these characteristics, in particular the prisoner’s dilemma and public good games. In one-shot games, or finitely repeated games, if individuals are rational and self-interested, game theory predicts that they should play their dominant strategy, that is, they should not cooperate. Experimental evidence on such games does not (fully) support this view. In a summary of early work on public goods experiments, Ledyard (1995) identifies as a “stylized fact” that individuals tend to contribute positive amounts to public goods (while they should not if rational and self-interested), although their contributions decline over time across repetitions of the game. Subsequent work has tried to identify in a more precise way the deviation of the observed evidence with respect to classical game theory predictions. One strong regularity that has emerged is that individuals tend to be conditionally cooperative. In public good games, for instance, this means that contributions to the public good are positively correlated with expectations about average group contribution (Fischbacher et al. 2001; Chaudhuri 2011), although a self-serving bias, for which individuals contribute less than the expected average, is observed (Fischbacher and Gächter 2010). Heterogeneity across individuals also emerges as a recurrent fact: while most subjects are conditionally cooperative, unconditionally cooperative and free-riding agents are also observed (Kurzban and Houser 2005), with evidence that the distribution of such types may vary across countries (Kocher et al. 2008). Evidence of conditional cooperation has emerged also in prisoner’s dilemma games (Grujić et al. 2010; Cimini and Sánchez 2014).

Although the predictions based on rationality and self-interest are not fully confirmed in the experimental evidence, the observed decay in cooperative behaviour has nevertheless reinforced the interest towards those mechanisms which are able to sustain cooperation, which we indeed observe in human interactions and, more generally, in the biological world (Nowak and Highfield 2011). Some mechanisms are known. If interaction is repeated within the same group of players, the folk theorems for repeated games (Mailath and Samuelson 2006) show that cooperative behaviour may indeed be the equilibrium outcome in the supergame. Experimental evidence also shows that cooperation may be favoured by mechanisms such as altruistic punishment (Fehr and Gächter 2000), in which cooperators bear a cost to punish defectors, or rewards (Rand et al. 2009). Finally, in an evolutionary perspective, where the frequency of individuals playing a certain strategy increases with their “fitness”, local interaction has been identified as an important channel towards the emergence of cooperation (Nowak and May 1992). While with global interaction cooperators, who played a dominated strategy, tend to disappear, local interaction may lead to the emergence of clusters of cooperators which can succeed in invading the population.

2.3 Threshold Models of Collective Action

Threshold models of collective action find their origins in the work of Schelling (1973) and Granovetter (1978). In abstract terms, they represent binary decision problems with externalities, in which agents choose a certain action if the fraction of other agents choosing that action is above a certain threshold. The existence of such a threshold may be explicitly microfounded (Schelling 1973) or not (Granovetter 1978). Threshold models belong to a more general class of models that analytical sociologists define as the class of conditional choice models (Rolfe 2009).

Due to their generality, threshold models have been applied to various social phenomena, such as crowd behaviour, participation to social movements, voting or adoption of innovations (Watts and Dodds 2009). Most models are interested in determining the conditions for certain collective behaviour to be observed, such as a riot or the diffusion of an innovation. In this case, individuals are initially “inactive”, and the probability of a cascade of active behaviour is investigated, as a function of the threshold distribution and the nature of interaction (Watts 2002). In a very simple example, Granovetter considers the case of 100 individuals considering if participating or not to a riot. He notices that if the thresholds are uniformly distributed, then the riot will be observed with probability equal to 1. However, if no agent has a threshold of 2, while two agents have a threshold of 3 (and the rest of the distribution is as before), then the riot will be observed with zero probability. This suggests that the outcome of the collective action may be very sensitive to the threshold distribution.

In Sect. 11.5, we present both analytical results on civic capital horizontal transmission and, for more complex solutions that cannot be solved analytically, an agent-based version of our model. Agent-Based Models (ABMs) are usually based on a set of autonomous agents, capable of interacting with each other, as well as with the environment, according to given behavioural rules. Such rules can be simple or complex, deterministic or stochastic, fixed or adaptive. Adaptive agents have the ability to learn, and they evolve in a learning cycle (Billari et al. 2006). Rules are typically derived from published literature (van Leeuwen and Lijesen 2016), expert knowledge, data analysis or numerical work, and are the foundation of an agent’s behaviour (Crooks and Heppenstall 2012). ABMs allow one to simulate the individual actions of a diverse number of agents, assessing the resulting system behaviour and outcomes over time, and they are models that generally deal with systems that are complex, open-ended, hence emergent and thus exhibit novelty and surprise (Crooks et al. 2008). They have their roots in an interdisciplinary computing movement and in the field of artificial intelligence. Today, ABMs are often used to investigate the interplay occurring at the micro and macro structures of a given system, in which the interaction structure itself plays an important role. Furthermore, ABMs allow a flexible design of how individual entities behave and interact, since the results are computed and need not to be solved analytically (Leombruni and Richiardi 2005). They have been applied to a diverse range of subject areas, such as: archaeological reconstruction of ancient civilizations; understanding theories of political identity and stability; biological models of infectious diseases; modelling economic processes as dynamic systems of interacting agents; geographical retail markets and so on (see Crooks and Heppenstall 2012 for a more extensive overview).

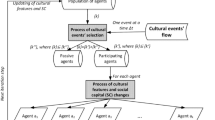
3 The Model

We will now describe the model in its most general formulation, while for both the analytical solution and the numerical experiments we will consider specific versions of the same. Our model is dynamic in discrete time. Consider a fixed population of N agents. At each moment of time, each agent i faces a binary choice, represented by function \( {\alpha}_i^t \): being cooperative (\( {\alpha}_i^t=1 \)) or not (\( {\alpha}_i^t=0 \)). Each agent is characterized by a threshold \( {\alpha}^t \) in the unit interval, affecting her choice, with \( \underset{\_}{\alpha_i} \) being the vector of thresholds in the population. From agent i’s viewpoint, the rest of the individuals differ in their influence on his behaviour. The behaviour-influencing network gb is a (possibly directed) graph over N such that, for each agent i, a weighting function wi(gb) assigns a weight \( {w}_i^j>0 \) to agent j ≠ i, with \( {\sum}_{j\ne i}{w}_i^j=1 \). This leads to define \( {\alpha}_{-i}^t={\sum}_{j\ne i}{w}_i^j{\alpha}_j^t \). If all agents are assigned the same weight, that is, the case of global interaction, then \( {\alpha}_{-i}^t \) denotes the actual fraction of agents (excluding i) who are cooperative at time t (therefore \( {\alpha}_{-i}^t={\sum}_{j\ne i}\frac{1}{N-1}{\alpha}_j^t \)). This is a case for which analytical results can be easily obtained. Alternatively, we will consider individuals located on a bounded two-dimensional grid. In this case, agents are only (equally) influenced by others in their “neighbourhood”, whose characteristics will be specified in the following. Denoting with Ei(\( {\alpha}_{-i}^t \)) the expectation for the behaviour of agent i, he cooperates if \( {E}_i\left({\alpha}^t\right)>\underset{\_}{\alpha_i^t} \), and he does not cooperate otherwise. We shall assume adaptive expectations, that is, Ei(\( {\alpha}_{-i}^t \)) = \( {\alpha}_{-i}^t \), therefore leading to the following (deterministic) choice rule:

$$ {\alpha}_i^t=\{{\displaystyle \begin{array}{c}0\ \mathrm{if}\ {\alpha}_{-i}^t<\underset{\_}{\alpha_i^t}\\ {}1\ \mathrm{if}\ {\alpha}_{-i}^t\ge \underset{\_}{\alpha_i^t}\end{array}}\operatorname{}. $$
(11.1)

Agents are heterogeneous in \( \underset{\_}{\alpha_i^t} \), and this captures the extent to which an individual is a conditional cooperator. Notice that, for \( \underset{\_}{\alpha_i^t}\to 0 \), agent i (almost) always cooperates, that is, he is an unconditional cooperator. For \( \underset{\_}{\alpha_i^t}\to 1, \) agent i (almost) never cooperates, that is, he is a free-rider. Social capital (defined as civic capital) is then inversely related to the average value of \( \underset{\_}{\alpha_i^t} \), but its overall distribution is also relevant, and a parameter we will control in our numerical experiment.

As mentioned earlier, \( \underset{\_}{\alpha_i^t} \) evolves over time as the outcome of a process of social transmission. In order to model such a process, we introduce the notion of value-influencing network gv, where gv is a (possibly directed) graph over population N. For each agent i, we then introduce a weighting function θi(gv) which assigns a weight \( {\theta}_i^j>0 \) to agent j ≠ i, with \( {\sum}_{j\ne i}{\theta}_i^j=1 \). In general terms, the law of motion of \( \underset{\_}{\alpha_i^t} \) can be written as \( \underset{\_}{\alpha_i^t}=\underset{\_}{\alpha_i^t}\left[\underset{\_}{\alpha^{t-1}};{\theta}_i\left({g}^v\right)\right] \). In our simulation experiments, we will consider the process given by:

$$ \underset{\_}{\alpha_i^t}=\rho \underset{\_}{\alpha_i^{t-1}}+\left(1-\rho \right)\sum \limits_{j\ne i}{\theta}_i^j\underset{\_}{\alpha_j^{t-1}}, $$
(11.2)

with 0 < ρ < 1. This in an example of assimilative social influence model (Degroot 1974; Flache et al. 2017). In particular, we will consider the case of global interaction (\( {\theta}_i^j=\frac{1}{N-1} \) for each i,j) and cases where weights are determined by the agents’ location on the grid. From this last perspective, the matrix containing all the weights \( {\theta}_i^j \) may be compared to the spatial weights matrices used in spatial econometrics.

4 Analytical Results

A model which can be easily studied analytically (and graphically), being substantially equivalent to Granovetter (1978), is the one of global interaction with time-invariant—but heterogenous—thresholds. In this case, the threshold of one individual is compared to the average cooperative behaviour of all the remaining agents. For tractability, let us assume that the set of individuals in the society is given by a continuum of agents of mass 1, and that \( \underset{\_}{\alpha_i} \) is distributed across individuals with a cumulative (density) function F(∙) (f(∙)).

At time t, the fraction of cooperating individuals is given by \( {\alpha}^t\equiv \Pr \left(\underset{\_}{\alpha_i}<{\alpha}^{t-1}\right)\equiv F\left({\alpha}^{t-1}\right) \) (notice that by considering a continuum of agents, including individual i does not affect the fraction of cooperating agents in society). Therefore, the evolution of the system is described by the difference equation αt = F(αt − 1). As usual, the equilibrium is identified by αt = αt − 1.

Standard graphical analysis (through staircase diagrams) can help analysing the stability properties of such equilibria. In Fig. 11.1, we represent a case of a distribution function for which a unique interior stable equilibrium is observed.

Fig. 11.1
figure 1

Case with a unique interior stable equilibrium

Full size image

In terms of interpretation, the distribution function represented in Fig. 11.1 corresponds to a case where both (almost) unconditional cooperators and free-riders are common in the population. As a result, both cooperative and non-cooperative behaviours coexist in equilibrium.

Consider now the case of a uniform distribution between \( {\underset{\_}{\alpha}}_{\mathrm{min}}>0 \) and \( {\underset{\_}{\alpha}}_{\mathrm{max}}<1 \). As shown in Fig. 11.2, we have one unstable interior equilibrium and two stable corner equilibria, where all agents cooperate or all agents do not.

Fig. 11.2
figure 2

Case with one unstable interior equilibrium and two stable corner equilibria

Full size image

In this case, initial conditions will determine which equilibrium prevails, while the min and max values will determine the basin of attractions of the equilibria (with lower values, i.e. higher values of civic capital, leading to full cooperation for a larger set of initial conditions). Notice that this case corresponds to a relatively homogenous society (in terms of types of individuals). Interestingly, social homogeneity leads to less predictable outcomes in terms of social behaviour.

5 Simulation Results

In this section, we report on simulation results for the different configurations of model parameters we consider, varying the value of ρ in Eq. (11.2), the global/local nature of interaction in the diffusion of values and behaviour, and the initial distribution of civic capital (distribution of \( \underset{\_}{\alpha } \)). In particular, we analyse five scenarios, in which the distribution of \( \underset{\_}{\alpha } \) at t = 0 is uniform:

  • Scenario 1: ρ = 1, with global influence for both behaviour and values. This scenario illustrates numerically the conclusion we reached analytically in the previous section.

  • Scenario 2: ρ = 1, with local influence for behaviour.

  • Scenario 3: ρ < 1, with global influence for both behaviour and values.

  • Scenario 4: ρ < 1, with local influence for values and global influence for behaviour.

  • Scenario 5: ρ < 1, with local influence on both behaviour and values.

Then, we briefly comment on what happens when the distribution of \( \underset{\_}{\alpha } \) at t = 0 is normal. In our simulations, “equilibria” take two forms: i) a stationary state in which αt = αt − 1; ii) a 2-cycle, in which very few agents (in most cases a single one) alternate between cooperative and non-cooperative behaviour.

5.1 Scenario 1

Focusing on the uniform distribution, we tested different values for \( {\underset{\_}{\alpha}}_{\mathrm{min}} \) and \( {\underset{\_}{\alpha}}_{\mathrm{max}} \). \( {\underset{\_}{\alpha}}_{\mathrm{min}} \) ranges between 0.05 and 0.5 (in 0.05 increments), while \( {\underset{\_}{\alpha}}_{\mathrm{max}} \) ranges between 0.6 and 0.95 (with increments of 0.05). We run 100 replications for each parameter pair (\( {\underset{\_}{\alpha}}_{\mathrm{min}} \), \( {\underset{\_}{\alpha}}_{\mathrm{max}} \)).

Results for the equilibrium values of the average levels of cooperation (that is, the fraction of agents being cooperative in the population) are reported in Table 11.1. The effects of the initial random distribution of \( \underset{\_}{\alpha } \) are clear: when \( {\underset{\_}{\alpha}}_{\mathrm{min}}+{\underset{\_}{\alpha}}_{\mathrm{max}}<1 \), the model always ends with a fully cooperating society; when \( {\underset{\_}{\alpha}}_{\mathrm{min}}+{\underset{\_}{\alpha}}_{\mathrm{max}}>1 \), the model always ends with a fully non-cooperating society. If \( {\underset{\_}{\alpha}}_{\mathrm{min}}+{\underset{\_}{\alpha}}_{\mathrm{max}}=1 \), such that the expected value of \( \underset{\_}{\alpha } \)at t = 0 is 0.5, each corner solution is almost equally likely.

Table 11.1 Average levels of cooperation for different ranges of personal values
Full size table

5.2 Scenario 2

In our second experiment, the focus is on the extent to which neighbourhood effects happen. This time, the agents do not compare their personal values with the observed behaviour of society as a whole, but with the one of their neighbours. We compare the difference of being affected by the 4 nearest neighbours (rook contiguity order 1), the 8 nearest neighbours (queen contiguity order 1), 24 neighbours (queen contiguity order 2) or 48 neighbours (queen contiguity order 3). Based on the literature, we expect clusters of cooperation to emerge, especially when the influence is very local, as is the case when the rook contiguity is used.

The model results, provided in Table 11.2, indicate that the more local the interaction, the larger the deviation from the results of Scenario 1. Now, simulation results are mixed also for initial personal values that are drawn from ranges that sum up to 0.9 or 1.05. In these cases, generally, no corner solutions are found, but patches of cooperating and non-cooperating agents coexist next to each other (as shown in Fig. 11.3). The number of iterations needed to reach an equilibrium lies between 5 and 54, with an average of 16.

Table 11.2 Average level of cooperation of society as a whole with different levels of neighbourhood effects and different minimum ranges for the random personal value of each agent (\( {\underset{\_}{\alpha}}_{\mathrm{max}} \) = 0.6)
Full size table
Fig. 11.3
figure 3

Example of a final outcome of Scenario 2

Full size image

5.3 Scenarios 3–4

In Scenario 3, not only behaviour, but also personal values are influenced by society as a whole. Allowing different values of ρ, values in society affect the ones of the individual agent. It means that, in each period, each agent becomes more similar to society as a whole. The results show that the outcomes are very similar to the first experiment. Again, all model runs result in corner solutions of either fully cooperating or non-cooperating society.

In Scenario 4, it is neighbouring agents that influence each other’s personal values. However, the final choice to cooperate or not is still based on the average behaviour of society as a whole. Again, all model runs result in a corner solution, and only when \( {\underset{\_}{\ \alpha}}_{\mathrm{min}}+{\underset{\_}{\alpha}}_{\mathrm{max}}=1 \), the outcome whether everyone cooperates or not depends on the (spatial distribution of the) initial values.

5.4 Scenario 5

In this final basic scenario, we combine the insights from all the previous ones. We combine different levels of neighbourhood effects with different combinations of values for ρ and different levels of the initial random variables. This means that neighbours influence both the choice to cooperate or not, as well as the personal values of the agent.

For this scenario, we report, in Table 11.3, the share of model runs that find an equilibrium (each configuration is repeated 100 times, with the maximum number of iterations equal to 600). The main conclusion that can be drawn here is that smaller values of ρ (that is, social influence) result in fewer model runs that reach an equilibrium: the model becomes more unstable. Furthermore, the range from which the initial values of \( \underset{\_}{\alpha } \) are drawn appears to matter, since if \( {\underset{\_}{\ \alpha}}_{\mathrm{min}}+{\underset{\_}{\alpha}}_{\mathrm{max}}\ne \) 1, our simulations result much more often in an equilibrium. The average number of iterations required to reach an equilibrium lays around 20. The range of the neighbours’ sphere of influence is important as well: when only the four nearest neighbours are taken into account (rook contiguity of order 1), the probability of reaching an equilibrium is higher when \( {\underset{\_}{\ \alpha}}_{min}+{\underset{\_}{\alpha}}_{max}= \) 1, and lower otherwise. This setting is the one needing on average the most iterations to find a solution (more than 200). Furthermore, when taking eight neighbours into account (queen contiguity of order 1), the share of models that reach an equilibrium is the lowest. Similarly to Scenario 2, this scenario generates coexisting patches of collaborating and non-collaborating agents, more clearly defined than before (see Fig. 11.4).

Table 11.3 The share of model runs finding an equilibrium for Scenario 5
Full size table
Fig. 11.4
figure 4

Example of a final outcome of Scenario 5

Full size image

5.5 Normal Distribution

In a further simulation exercise, we hypothesized a normal distribution for \( \underset{\_}{\alpha } \) at t = 0, with a mean of 0.5 and a standard deviation of 0.1. When running 1600 simulations, only 79 resulted in corner solutions (of which 47 for ρ = 0.95, and neighbourhood radius at Queen-2 or 3). Table 11.4 shows the share of models that reach an equilibrium when the maximum number of runs is set to 600. Again, queen contiguity of order 1 results in the lowest share of models with a solution, and rook contiguity in the highest one. The average number of iterations was 142, but for ρ = 1, the average number of steps was 19.

Table 11.4 The share of model runs finding an equilibrium with a normal distribution
Full size table

5.6 Statistical Analysis

The above simulation findings depict pictures of the average performance of the system when certain population and behavioural parameters are used. However, it is difficult, within this framework, to assess the role played by each single model parameter in shaping the final population outcome. We can go more in-depth in our analysis from this viewpoint by analysing single simulation outcomes in a regression framework, by considering their related simulation parameters. In particular, it is worth examining two types of information in this regard: (1) the share of collaborating agents in the final population (behaviour of society), that is, at time t = T; and (2) the related level of clustering found.

While fully cooperating or non-cooperating societies show no clustering, it is interesting to understand what are the parameters that lead to local pockets of collaborating individuals, a dichotomic population (split 50–50 either horizontally or vertically on the grid) being the strongest possible clustering. Such clustering can be measured, given the binary nature of the simulations’ outcome variable, by join count statistics. Similarly to standard spatial autocorrelation indices like Moran’s I, join count statistics can signal positive or negative clustering, as well as no statistically significant clustering. Given a binary variable classified as 1 s and 0 s, and a spatial weights matrix W (in our case, a rook contiguity matrix), the number of “joins” of grid cells of the same type (1–1, or 0–0) is counted, and compared against the theoretically expected number of joins. A simple test for significance of the difference between the two can be used to detect clustering (Cliff and Ord 1981).

We then focus on Scenario 5, which has local influence on both behaviour and values, and estimate simple regression models as follows:

$$ {\alpha}^T=\mathrm{const}+{\beta}_1{\underset{\_}{\alpha}}_{\mathrm{min}}+{\beta}_2\rho +\mathrm{neighouring}, $$
(11.3)
$$ {JC}^T=\mathrm{const}+{\beta}_1{\underset{\_}{\alpha}}_{\mathrm{min}}+{\beta}_2\rho +\mathrm{neighouring}+{\beta}_3{JC}^0, $$
(11.4)

where, in addition to what was defined above, neighbouring is a set of indicator variables—and related coefficients—for the type of neighbours influence simulated (between Rook-1, Queen-1, Queen-2, Queen-3), while JCT and JC0 are the join count statistics measured (for the collaborating agents) at the final iteration and at t = 0, respectively.

The model in Eq. (11.3) explains the final share of collaborating agents, while in Eq. (11.4) we model its level of spatial clustering. Both models employ, as explanatory variables, the lower bound of the uniform distribution of thresholds \( {\underset{\_}{\alpha}}_{min} \) (\( {\underset{\_}{\alpha}}_{\mathrm{max}} \) is fixed in Scenario 5), the inertia parameter ρ and the type of neighbours influence. In addition, Eq. (11.4) includes the level of clustering at t = 0. We estimate OLS regression models and present our empirical estimates in Table 11.5.

Table 11.5 Regression results for Eqs. (11.3) and (11.4)
Full size table

Regression results highlight the different roles played by simulation parameters in shaping the final population behaviour. Extending (downward) the range of possible individual thresholds logically increases the share of collaborating agents, but it leads to more homogeneous behaviour (less clustering). Instead, behavioural inertia (ρ) appears to have a limited effect in terms of decreasing the share of collaborating agents, as well as, to a greater degree, clustering. Coefficients for the different types of spatial influence (Rook-1 being the benchmark) suggest that the more spatially extended the observation, the higher the chances of collaborating, and the higher the clustering. As expected, the initial level of clustering has a positive correlation with the final clustering.

6 Conclusions

This chapter addressed the issue of civic capital development (emergence of cooperation) from a spatial viewpoint, using agent-based modelling (ABM). We first developed a simple analytical model for the most general case of a threshold model in which single individuals choose to collaborate based on a set of personal values and a minimum share of society following the same behaviour. In order to look deeper into this issue, we set up five scenarios and ran a high number of simulations to inspect regularities in the aggregate (population-level) outcomes of collaboration. We found that the most interesting cases are the ones in which interaction between agents, in terms of both reciprocal influence on values and observation of others behaviour, happens at the local (instead of global) level, that is, between nearby individuals. Finally, we conducted a preliminary regression analysis to relate aggregate behavioural outcomes (also in terms of spatial clustering) to the simulation parameters used.

Our results provide a number of insights.

  • When individual behaviour responds to the aggregate behaviour, society quickly converges to homogenous choices, where all individuals behave cooperatively, or none does. Which outcome is observed depends on the initial distribution of civic capital, but it is not affected by the social process of influence in values.

  • When individual behaviour responds instead to the behaviour of neighbours only, spatial clusters of cooperating and non-cooperating agents are often observed. In addition, when the propensity towards cooperation is socially affected, the system becomes less stable, and is less likely to find a stable equilibrium in the observed time horizon of our simulations. We believe this issue to be due to expectable feedback effects happening between individuals over space.

  • When focussing on local mechanisms of influence, we observe, through regression models, that a behavioural inertia and the extent of the range of individual threshold for cooperation matter in shaping societal outcomes and the level of spatial clustering.

  • The latter further depends on the spatial extent of observation and influence. The larger this is, the higher the level of spatial clustering observed. This finding suggests that, while neighbourhood effects matter in setting the condition for the development of pockets of heterogeneous behaviour, there is most likely an “optimal” extent of spatial influence that leads to the strongest spatial clustering and, therefore, in real-life settings, to possible issues of segregation and isolation.

The above findings represent a first exploration of how horizontal transmission of civic capital may be modelled, explored and analysed. Further experiments are of course needed in this regard. For instance, the role played by urban infrastructure (positioned on the urban grid), like highways, in causing isolation and clustering of homogeneous behaviour by interrupting proximity relations may be fruitfully explored in an ABM simulation framework. At the same time, recent advancements in urban transportation, which facilitate cross-neighbourhood mobility, could have the opposite effect, and favour interaction between more distant individuals. We leave this and other model expansions for future developments.